HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल InText Questions

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल InText Questions

इन्हें कीजिए (पृष्ठ सं. 221-222)

प्रश्न 1.
नीचे दिए गए प्रश्नों के उत्तर देने के लिए आपको क्षेत्रफल या परिमाप में से किसको ज्ञात करने की आवश्यकता होगी।
1. एक श्यामपट कितनी जगह घेरता है ?
2. एक आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए आवश्यक तार की लम्बाई क्या है ?\
3. एक तिकोने पार्क के चारों ओर दो बार चक्कर लगाने पर आप कितनी दरी तय करेंगे ?
4. एक आयताकार स्वीमिंग पूल को ढकने के लिए आपको कितनी प्लास्टिक शीट की आवश्यकता होगी ?
हल :
1. श्यामपट द्वारा घेरे गए क्षेत्र/स्थान के लिए श्यामपट का क्षेत्रफल ज्ञात करना होगा।
क्षेत्रफल = लम्बाई × चौड़ाई
2. आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए फूलों की क्यारी का परिमाप ज्ञात करना होगा।
परिमाप = 2 × (लम्बाई + चौड़ाई)
3. तिकोने पार्क के चारों ओर दो बार चक्कर लगाने की दूरी = 2 × पार्क का परिमाप।
4. आयताकार स्वीमिंग पुल को ढकने के लिए प्लास्टिक शीट की आवश्यकता = तालाब का क्षेत्रफल।

पृष्ठ सं. 222

प्रश्न 1.
छात्र स्वयं करें।

प्रश्न 2.
दो ऐसे उदाहरण दीजिए जहाँ परिमाप के बढ़ने पर उसका क्षेत्रफल भी बढ़ जाए।
हल :
(i) माना एक आयत ABCD है।

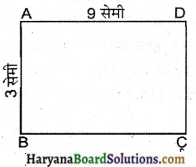
क्षेत्रफल (ABCD) = A₁ = 9 × 3 वर्ग सेमी
= 27 वर्ग सेमी
परिमाप (ABCD) = P₁ = 2(9 + 3) सेमी
= 24 सेमी
दूसरा आयत ABEF मानते हैं।

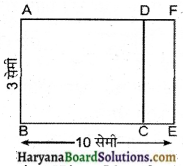
क्षेत्रफल (ABEF) = A₂ = 10 × 3 वर्ग सेमी
= 30 वर्ग सेमी
परिमाप (ABEF) = P₂ = 2(10 + 3) सेमी
= 26 सेमी
A₂ > A₁ ⇒ P₂ > P₁ अर्थात् जब क्षेत्रफल बढ़ता है, परिमाप बढ़ता है।

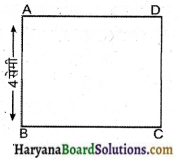
(ii) एक वर्ग ABCD मानते हैं।
क्षेत्रफल (ABCD) = 4 × 4 वर्ग सेमी
= 16 वर्ग सेमी
परिमाप (ABCD) = 2 × (4 + 4) सेमी
= 2 × 8 = 16 सेमी

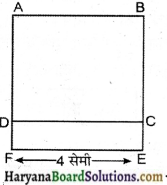
आयत ABFE मानते हैं।
क्षेत्रफल (ABFE) = 4 × 5 वर्ग सेमी
= 20 वर्ग सेमी

परिमाप (ABFE) = 2 × (4 + 5) सेमी
= 2 × 9 = 18 सेमी
अतः क्षेत्रफल बढ़ता है तो परिमाप बढ़ता है।

प्रश्न 3.
ऐसे दो उदाहरण दीजिए, जहाँ परिमाप के बढ़ने पर उसके क्षेत्रफल में बढ़ोत्तरी न हो।
हल :
(i) आयत ABCD में,
क्षेत्रफल (ABCD) = A₁ = 8 × 10 सेमी²
= 80 सेमी²

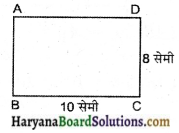
परिमाप (ABCD) = P₁ = 2 × (8 + 10) सेमी
= 2 × 18 = 36 सेमी
अब आयत ABCD में से एक त्रिभुज काटते हैं।
इसी आकृति का क्षेत्रफल (A₂)
= [8 × 10 – \(\frac{1}{2}\) × 3 × 4] सेमी²

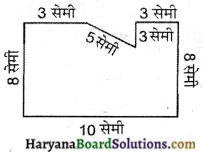
= (80 – 6) सेमी
= 74 सेमी²
इसका परिमाप (P₂)
= (8 + 10 + 8 + 3 + 3 + 5 + 3) सेमी
= 40 सेमी
स्पष्ट है कि A₁ < A₂ क्षेत्रफल घटता है।
परन्तु P₂ > P₁ परिमाप बढ़ता है।

(ii) उपर्युक्त आकृति में से एक कट और करने पर, इस आकृति का क्षेत्रफल (A₃)
= (A₂ – 4 × 3) सेमी²
= (74 – 12) सेमी²
= 62 सेमी²

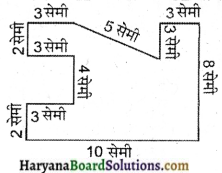
सेमी इस आकृति का परिमाप (P₃)
= (2 + 3 +4+ 3 + 2 + 10 + 8 + 3 + 3 + 5 + 3) सेमी
= 46 सेमी
स्पष्ट है कि A₃ < A₂ क्षेत्रफल घटता है।
परन्तु P₃ > P₂ परिमाप बढ़ता है।

पृष्ठ सं. 226

प्रश्न 1.
नीचे दिए गए प्रत्येक आयत जिसकी लम्बाई 6 सेमी और चौड़ाई 4 सेमी है, सर्वांगसम बहुभुजों से मिलकर बने हैं। प्रत्येक बहुभुज का क्षेत्रफल ज्ञात कीजिए।

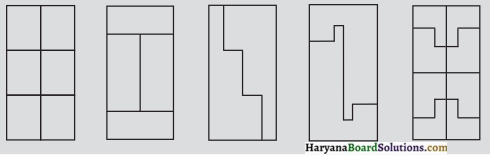
हल:
लम्बाई = 6 सेमी
चौड़ाई = 4 सेमी
प्रत्येक बहुभुज का क्षेत्रफल = आयत का क्षेत्रफल
= लम्बाई × चौड़ाई
= (6 × 4) सेमी
= 24 सेमी²।

पृष्ठ सं. 229

प्रश्न 1.
निम्न समांतर चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए :

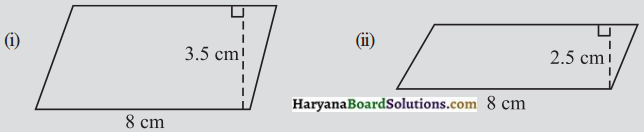
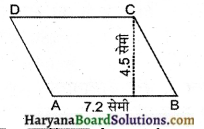
(iii) समान्तर चतुर्भुज ABCD में, AB = 7.2 सेमी और C से AB पर लम्ब 4.5 सेमी है।
हल :
(i) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= 8 × 3.5 = 28 सेमी²

(ii) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 8 × 2.5 = 20 सेमी²

(iii) समान्तर चतुर्भुज ABCD का क्षेत्रफल
= AB × C से AB पर लम्ब की लम्बाई
= 7.2 × 4.5 = 32.4 सेमी²।

पृष्ठ सं. 230

प्रश्न 1.
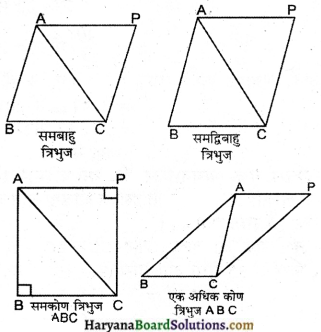
ऊपर दिए गए क्रियाकलापों को अलग-अलग प्रकार के त्रिभुज लेकर कीजिए।
हल :
एक त्रिभुज ABC दिया है। सर्वांगसम त्रिभुज ACP है। दोनों मिलाने पर ABCP समान्तर चतुर्भुज जैसी आकृति प्राप्त होती है।

प्रश्न 2.
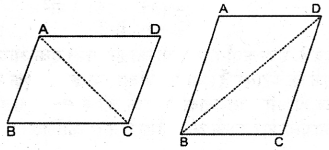
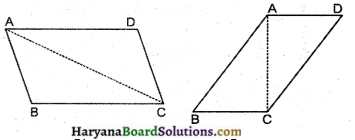
अलग-अलग प्रकार के समांतर चतुर्भुज लीजिए। प्रत्येक समान्तर चतुर्भुज को दो त्रिभुजों में एक विकर्ण के अनुदिश काटिए। क्या ये त्रिभुज सर्वांगसम हैं ?
हल :
ABCD एक समान्तर चतुर्भुज है (दिया है)। प्रत्येक समान्तर चतुर्भुज को विकर्ण AC अथवा BD के अनुदिश काटने पर। दो त्रिभुजों में विभाजित होता है।

ये दोनों त्रिभुज आपस में सर्वांगसम होंगे।

पृष्ठ सं. 235

प्रश्न 1.
एक बोतल का ढक्कन एक चूड़ी या कोई अन्य वृत्ताकार वस्तु लीजिए और उसकी परिधि ज्ञात कीजिए।
हल :
छात्र स्वयं करें।

पृष्ठ सं. 236

प्रश्न 1.
आकृति में :
(a) किस वर्ग का परिमाप अधिक है?
(b) कौन-सा अधिक है, छोटे वर्ग का परिमाप या वृत्त की परिधि ?

हल :
(a) बाहरी वर्ग का परिमाप सबसे अधिक होगा।
(b) छोटे वर्ग के परिमाप से वृत्त की परिधि अधिक होगी।

पृष्ठ सं. 239

प्रश्न 1.
ग्राफ पेपर पर अलग-अलग त्रिज्याओं के वृत्तों को बनाइए। वर्गों की संख्या को गिनकर क्षेत्रफल ज्ञात कीजिए। सूत्र का प्रयोग करके भी क्षेत्रफल ज्ञात कीजिए। दोनों उत्तरों की तुलना कीजिए।
हल :
1 वर्ग सेमी के ग्राफ पर 1 सेमी और 2 सेमी त्रिज्या के दो वृत्त खींचने पर,

ग्राफ पेपर पर प्रयोग करने पर, हमें दोनों वृत्तों का क्षेत्रफल क्रमशः 4 सेमी2 और 12 सेमी2 प्राप्त होता है।
सूत्र का प्रयोग करके हम उनका क्रमशः क्षेत्रफल
πr₁² = (\(\frac{22}{7}\) × 12 ) सेमी² = 3.14 सेमी² (लगभग)
और πr₂² = (\(\frac{22}{7}\) × 22 ) सेमी² = (\(\frac{22}{7}\) × 4) सेमी²
= 12.57 सेमी² (लगभग)
हम देखते हैं कि दोनों मान भिन्न हैं।

पृष्ठ सं. 241

प्रश्न 1.
निम्न को बदलिए :
(i) 50 सेमी² को मिमी² में
(ii) 2 हेक्टेअर को मीटर² में
(iii) 10 मीटर² को सेमी² में
(iv) 1000 सेमी² को मिमी²
हल :
(i) 1 सेमी² = 1 सेमी × 1 सेमी
= 10 मिमी × 10 मिमी
= 100 मिमी²
∴ 50 सेमी² = (50 × 100) मिमी²
= 5000 मिमी²।

(ii) 1 हेक्टेअर = 100 मीटर भुजा वाले वर्ग का क्षेत्रफल
= 100 मीटर × 100 मीटर
= 10000 मीटर²
हेक्टेअर = 20000 मीटर²।

(iii) 1 मीटर² = 1 मीटर × 1 मीटर
= 100 सेमी × 100 सेमी
= 10000 सेमी²
∴ 10 मीटर² = 10 × 10000 सेमी²
= 100000 सेमी²

(iv) 1 सेमी² = 100 मिमी²
1000 सेमी² = 100 × 1000 मिमी
= 100000 मिमी²।