Haryana State Board HBSE 9th Class Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Exercise 9.4
[This exercise is not from examination point of view]
Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:
Given: Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas.
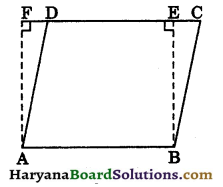
To prove : Perimeter of ||gm ABCD > Perimeter of rectangle ABEF.
Proof : Since opposite sides of a parallelogram are equal.
∴ Perimeter of ||gm
ABCD = 2(AB + BC) …(i)
and perimeter of rectangle
ABEP = 2(AB + BE) …..(ii)
In right ΔBEC, ∠BEC = 90° and ∠BCE is an acute angle (< 90°)
∴ ∠BEC > ∠BCE
⇒ BC > BE
(side opposite to greater angle is greater)
⇒ 2BC > 2BE
⇒ 2AB + 2BC > 2AB + 2BE
[Adding 2AB on both sides]
⇒ 2(AB + BC) > 2(AB + BE) ……(iii)
From (i), (ii) and (iii), we get
Perimeter of ||gm
ABCD > Perimeter of rectangle ABEF.
Hence proved
![]()
Question 2.
In figure 9.30, D and E are two points on BC such that BD = DE = EC. Show that: ar (ABD) = ar (ADE) = ar (AEC).
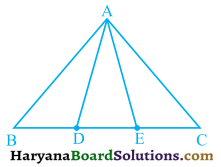
Solution:
Draw
AP ⊥ BC
Let BD = DE = EC = x
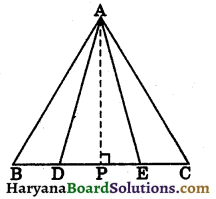
Now area of ΔABD = \(\frac{1}{2}\) × BD × AP
⇒ area of ΔABD = \(\frac{1}{2}\) × x × AP …….(i)
area of ΔADE = \(\frac{1}{2}\) × DE × AP
⇒ area of ΔADE = \(\frac{1}{2}\) × x × AP …(ii)
and area of ΔAEC = \(\frac{1}{2}\) × EC × AP
⇒ area of ΔAEC = \(\frac{1}{2}\) × x × AP …(iii
From (i), (ii) and (ii), we get
ar (ΔABD) = ar (ΔADE) = ar (ΔAEC).
Hence proved
Question 3.
In figure 9.31, ABCD, DCFE and ABFE are parallelograms. Show that: ar (ADE) = ar (BCF).
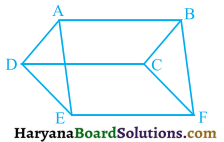
Solution:
Since ABCD is a paralllelogram.
∴ AD = BC …..(i)
Again DCFE is a parallelogram.
∴ DE = CF …..(ii)
and ABFE is a parallelogram.
∴ AE = BF …..(iii)
In ΔADE and ΔBCF, we have
AD = BC [From (i)]
DE = CF [From (ii)]
and AE = BF [From (iii)]
∴ ΔADE ≅ ΔBCF
(By SSS congruence rule)
ar (ADE) = ar (ABCF).
Hence proved
Question 4.
In figure 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (ΔBPC) = ar (ΔDPQ).

Solution:
Join AC.
Since, ΔADC and ΔADQ are on the same base AD and between the same parallels AD and CQ.
∴ ar (ΔADC) = ar (ΔADQ)
⇒ ar (ΔADC) – ar (ΔADP) = ar (ΔADQ) – ar (ΔADP)
⇒ ar (ΔAPC) = ar (ΔDPQ) …(i)
and ΔAPC and ΔBPC are on the same base PC and between the same parallels
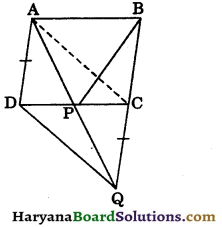
AB and CD.
∴ ar (ΔAPC) = ar (ΔBPC) …(ii)
From (i) and (ii), we get
ar (ΔBPC) = ar (ΔDPQ).
Hence proved
![]()
Question 5.
In figure 9.33, ABC and BDE are two equilateral triangles such that D is the mid point of BC. If AE intersects BC at F, then show that:
(1) ar(BDE) = \(\frac{1}{4}\)ar (ABC)
(i) ar (BDE) = \(\frac{1}{2}\) ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC).
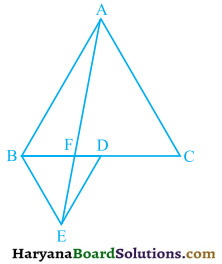
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
Solution:
(i) Let
AB = BC = AC = x
Then BD = ED = BE = \(\frac{x}{2}\)
ar (ΔABC) = \(\frac{\sqrt{3}}{4} x^2\) ……(1)
ar (BDE) = \(\frac{\sqrt{3}}{4}\left(\frac{x}{2}\right)^2\)
⇒ ar (ΔBDE) = \(\frac{\sqrt{3}}{4} x^2\)
⇒ 4 ar (ΔBDE) = \(\frac{\sqrt{3}}{4} x^2\) …..(2)
From (1) and (2), we get
4 ar (ΔBDE) = ar (AABC)
⇒ ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
Join AD and EC and draw EP ⊥ BD.
(ii) In ΔBEC, ED is the median.
ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC)

Since, ABC and BDE are equilateral triangles.
∴ ∠ACB = ∠CBE = 60°
But these are alternate interior angles.
∴ BE || AC
Now ΔBAE and BDE are on the same base BE and between the same paralles BE and
∴ ar (ΔBAE) = ar (ΔBAE)
⇒ ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE).
(iii) In DBEC, ED is the median.
∴ (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC)
⇒ \(\frac{1}{4}\)ar (ΔABC) = \(\frac{1}{2}\)ar (ΔBEC),
[From (i) part, ar (ΔBDE) = \(\frac{1}{4}\)ar ΔABC]]
⇒ ar(ΔABC) = \(\frac{4}{2}\) ar (ΔBEC)
⇒ ar (ΔABC) = 2 ar (ΔBEC).
(iv) Since, ABC and BDE are equilaterla triangles.
∴ ∠ABC = ∠BDE = 60°
But these are alternate interior angles.
∴ AB || DE
Now, ΔBED and ΔAED are on the same base DE and between the same parallels DE = AB.
∴ ar (ΔBED) = ar (ΔAED)
⇒ ar (ΔBED) – ar (ΔFED) = ar (ΔAED) – ar (ΔFED)
⇒ ar (ΔBEF) = ar (ΔAFD)
(v) In equilateral triangles median is a;sp a;totide.
∴ AD ⊥ BC
[ΔABD ≅ ΔACD ⇒ ∠ADB = ∠ADC = 90°]
Let AD = h
at (ΔABC) = 4 ar (ΔBDE)
[as proved in part (i)]
⇒ \(\frac{1}{2}\)x × h = 2 × \(\frac{x}{2}\) × EP


From (6) and (7), we get
ar (ΔBFE) = 2 ar (ΔFED)
(vi) FC = FD + CD

⇒ 24 ar (ΔFED) = xh
From (8) and (9), we get
24 ar (ΔFED) = 3 ar (ΔAFC)
⇒ ar (ΔFED) = \(\frac{3}{24}\)ar (ΔAFC)
⇒ ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
Hence proved
![]()
Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC).
Solution:
Draw
AE ⊥ BD and CF ⊥ BD
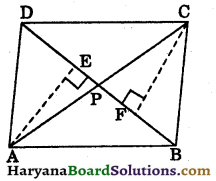
ar (ΔAPB) × ar (ΔCPD) = \(\left(\frac{1}{2} P B \times A E\right) \times\left(\frac{1}{2} D P \times C F\right)\) ….(i)
ar (ΔAPD) × ar (ΔBPC) = \(\left(\frac{1}{2} P D \times A E\right) \times\left(\frac{1}{2} P B \times C F\right)\) …..(ii)
From (i) and (ii), we get
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC). Hence proved
Question 7.
P and Q are respectively the mid points of sides AB and BC of a triangle ABC and R is the mid point of AP. Show that :
(i) ar (ΔPRQ) = \(\frac{1}{2}\)ar (ΔARC)
(ii) ar (ΔRQC) = \(\frac{3}{8}\)ar (ΔABC)
(iii) ar (ΔPBQ) = ar (ΔARC).
Solution:
We know that each median of a triangle divides it into two triangles of equal areas.
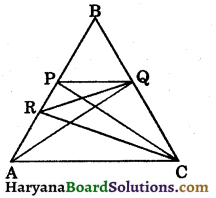
(i) Since, CR is the median of ΔCAP.
∴ ar (ΔARC) = \(\frac{1}{2}\)ar (ΔCAP) …..(i)
In AABC, CP is the median.
∴ ar (ΔCAP) = \(\frac{1}{2}\)ar (ΔABC) …(ii)
From (i) and (ii), we get
ar (ΔARC) = \(\frac{1}{2} \cdot \frac{1}{2}\) ar (ΔABC)
⇒ ar (ΔARC) = \(\frac{1}{4}\) ar (ΔABC)
⇒ 4 ar (ΔARC) = ar (ΔABC) ……(iii)
In ΔAPQ, QR is a median.
∴ ar (ΔPRQ) = \(\frac{1}{2}\)ar (ΔAPQ) ……..(iv)
In ΔAQB, QP is a median.
∴ ar (ΔAPQ) = \(\frac{1}{2}\)ar (ΔAQB) ……(v)
From (iv) and (v), we get
∴ ar (ΔPRQ) = \(\frac{1}{2} \cdot \frac{1}{2}\)ar (ΔAQB)
ar (ΔPRQ) = \(\frac{1}{4}\)ar (ΔAQB) ……(vi)
In a ΔABC, AQ is a median.
ar (ΔAQB) = \(\frac{1}{2}\)ar (ΔABC) …(vii)
From (vi) and (vii), we get
ar (ΔPRQ) = \(\frac{1}{4} \cdot \frac{1}{2}\)(ΔABC)
ar (ΔPRQ) = \(\frac{1}{8}\)ar (ΔABC)
⇒ 8 ar (ΔPRQ)= ar (ΔABC) …(viii)
From (iii) and (viii), we get
8 ar (ΔPRQ) = 4 ar (ΔARC)
⇒ ar (ΔPRQ) = \(\frac{4}{8}\)ar (ΔARC)
⇒ ar (ΔPRQ) = \(\frac{1}{4}\)ar (ΔARC).
(ii) 4 ar (ΔARC) = ar (ΔABC) [From (iii)]
⇒ ar (ΔARC) = \(\frac{1}{4}\)(ΔABC) …(ix)
In ΔRBC, RQ is a median.
∴ ar (ΔRQC) = \(\frac{1}{2}\)ar (ΔRBC)
⇒ ar (ΔRQC) = \(\frac{1}{2}\)[ar (ΔABC) – ar (ΔARC)]
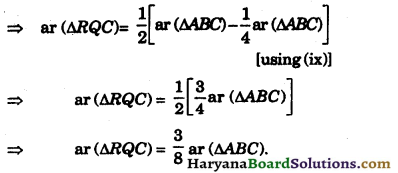
(iii) In ΔABC, CP is the median.
∴ ar (ΔCAP) = ar (ΔCBP) …(x)
From (i) and (x), we get
ar (ΔARC) = \(\frac{1}{2}\)ar (ΔCBP) …..(xi)
In ΔCBP, PQ is a median.
∴ ar (ΔPBQ) = \(\frac{1}{2}\)ar (ΔCBP) …(xii)
From (xi) and (xii), we get
ar (ΔPBQ) = ar (ΔARC).
Hence proved
![]()
Question 8.
In figure 9.66, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:

(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Results (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Solution:
(i) ∠MBC = 90° + ∠ABC
[∵ ∠ABM = 90°) … (i) and
and ∠ABD = 90° + ∠ABC
[∵ CBD = 90°] … (ii)
From (i) and (ii), we get
∠MBC = ∠ABD …(iii)
In ΔMBC and ΔABD, we have
MB = AB
[sides of the square ABMN]
∠MBC = ∠ABD [From (iii)]
and BC = BD
[sides of the square BCED]
∴ ΔMBC ≅ ΔABD
(By SAS congruence rule)
(ii) AX ⊥ DE (given) and BD ⊥ DE,
(∵ BCED is a square)
∴ AX || BD
Now, ΔABD and rectangle BYXD are on the same base BD and between the same parallels BD and AX.
ar (ΔABD) = \(\frac{1}{2}\)ar (BYXD) …(iv)
ΔABD ≅ ΔMBC [Proved in (i)]
⇒ ar (ΔABD) = ar (ΔMBC) …(v)
From (iv) and (v), we get
\(\frac{1}{2}\)ar (BYXD) = ar (ΔMBC)
⇒ ar (BYXD) = 2 ar (ΔMBC) …(vi)
(iii) Square ABMN and ΔMBC are on the same base MB and between the same parallels MB and NC.
∴ Ar (ΔMBC) = \(\frac{1}{2}\)ar (ABMN)
[a square is a ||gm]
⇒ ar (ABMN) = 2 ar (ΔMBC) …(vii)
From (vi) and (vii), we get
ar (BYXD) = ar (ABMN)
(iv) In ΔFCB and ΔACE, we have
FC = AC
[∵ sides of a square ACFG]
∠BCF = ∠ECA
[∵ each = 90° + ∠ACB]
and BC = EC
[∵ sides of a square BCED]
ΔFCB ≅ ΔACE
(By SAS congruence rule)
(v) Since ΔFCB ≅ ΔACE
(as proved above)
∴ ar (ΔFCB) = 2 ar (ΔACE)
⇒ 2 ar (ΔFCB) = 2 ar (ΔACE) …(viii)
Now, ΔACE and rectangle CYXE are on same base CE and between the same parallels CE and AX.
∴ ar(ΔACE) = \(\frac{1}{2}\)ar (CYXE)
⇒ ar(CYXE) = 2 ar (ΔACE) …(ix)
From (8) and (9), we get
ar (CYXE) = 2 ar (ΔFCB) …(x)
(vi) ΔBCF and square ACFG are on the same base CF and between the same parallels CF and BG.
∴ ar (ΔBCF) = \(\frac{1}{2}\)ar (ACFG)
⇒ ar (ΔCFG) = 2 ar (ΔFCB)
[∵ ΔFCB = ΔBCF) …(xi)
From (x) and (xi), we get
ar (CYXE)= ar (ACFG)
(vii) ar (BCED) = ar (BYXD) + ar (CYXE)
⇒ ar (BCED) = ar (ABMN) + ar (ACFG)
[From part (iii) and
ar (BYXD) = ar (ABMN)
ar (CYXE) = ar (ACFG)]
Hence proved