Haryana State Board HBSE 9th Class Maths Solutions Chapter 6 Lines and Angles Ex 6.3 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 6 Lines and Angles Exercise 6.3
Question 1.
In figure 6.79, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
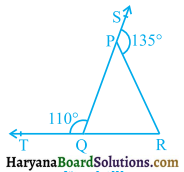
Solution:
Since, TQR is a straight line.
∴ ∠PQT + ∠PQR = 180°,
(Linear pair axiom)
⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° – 110°
⇒ ∠PQR = 70° …(i)
In ΔPQR, we have
∠SPR = ∠PQR + ∠PRQ,
[By theorem 6.8]
⇒ 135° = 70° + ∠PRQ,
[∵ ∠SPR = 135 and using (i)]
⇒ 135° – 70° = ∠PRQ
⇒ ∠PRQ = 65°
Hence, ∠PRQ = 65°.
![]()
Question 2.
In figure 6.80, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
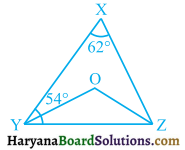
Solution:
In ΔXYZ, we have
∠X + ∠Y + ∠Z = 180°,
[∵ Sum of angles of a triangle = 180°
⇒ 62° + 54° + ∠Z = 180°,
(∵ ∠X = 62° and ∠Y = 54°)
⇒ 116° + ∠Z = 180°
⇒ ∠Z = 180° – 116° = 64°
Now, ∠OZY = \(\frac {1}{2}\)∠XZY [∵ ZO is the bisector of ∠XZY]
⇒ ∠OZY = \(\frac {64°}{2}\)
⇒ ∠OZY = 32° …….(i)
and ∠OYZ = \(\frac {1}{2}\)∠XYZ (∵ YO is the bisector of ∠XYZ)
⇒ ∠OYZ = \(\frac {54°}{2}\)
⇒ ∠OYZ = 27° …….(ii)
Now, in ΔYOZ, we have
∠OYZ + ∠OZY + ∠YOZ = 180°,
(Sum of angles of a triangle = 180°)
⇒ 27° + 32° + ∠YOZ = 180°,
[Using (i) and (ii)]
⇒ 59° + ∠YOZ = 180°
⇒ ∠YOZ = 180° – 59°
⇒ ∠YOZ = 121°
Hence, ∠OZY = 32° and ∠YOZ = 121°.
Question 3.
In figure 6.81, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
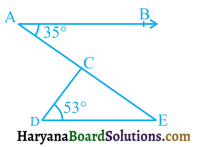
Solution :
∵ AB || DE and AE is the transversal
∴ ∠AED = ∠BAE,
(Alternate interior angles)
⇒ ∠AED = 35°
⇒ ∠CED = 35°,
[∵ ∠AED = ∠CED]
In ΔCDE, we have ∠CDE + ∠DCE + ∠CED = 180°
(∵ Sum of angles of a triangle = 180°)
⇒ 53° + ∠DCE + 35° = 180°
⇒ 88° + ∠DCE = 180°
⇒ ∠DCE = 180° – 88°
⇒ ∠DCE = 92°
Hence, ∠DCE = 92°
![]()
Question 4.
In figure 6.82, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95o and ∠TSQ = 75°, find ∠SQT.
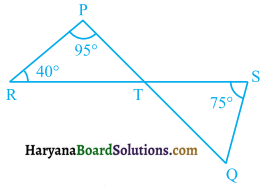
Solution:
In ΔPRT, we have
∠RPT + ∠PRT + ∠PTR = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ 95° + 40° + ∠PTR = 180°
⇒ 135° + ∠PTR = 180°
⇒ ∠PTR = 180° – 135°
⇒ ∠PTR = 45°
Now, ∠STQ = ∠PTR,
(Vertically opposite angles)
⇒ ∠STQ = 45°
Now in triangle ΔTSQ, we have
∠STQ + ∠TSQ + ∠SQT = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ 45° + 75° + ∠SQT = 180°
⇒ 120° + ∠SQT = 180°
⇒ ∠SQT = 180° – 120°
⇒ ∠SQT = 60°
Hence, ∠SQT = 60
Question 5.
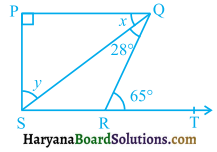
In figure 6.83, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
Solution :
Since, PQ || SR and QR is the transversal
∴ ∠PQR = ∠QRT,
(Alternate interior angles)
⇒ ∠PQR = 65°
⇒ x + 28° = 65°,
(∵ ∠PQR = x + 28°)
⇒ x = 65° – 28°
⇒ x = 37°
Now, in ΔPSQ, we have
∠SPQ + ∠PSQ + ∠PQS = 180°,
(Sum of angles of a triangle = 180°)
⇒ 90° + y + x = 180°
⇒ 90° + y + 37° = 180°
⇒ 127° + y = 180°
⇒ y = 180° – 127°
⇒ y = 53°
Hence, x= 37° and y = 53°.
![]()
Question 6.
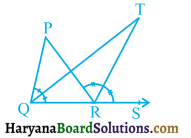
In figure 6.84, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that:
∠QTR = \(\frac {1}{2}\)∠QPR.
Solution:
In ΔPQR, we have
∠PRS = ∠QPR + ∠PQR, (By theorem 6.8)
⇒ \(\frac {1}{2}\)∠PRS = \(\frac {1}{2}\)∠QPR + \(\frac {1}{2}\)∠PQR
⇒ ∠TRS = \(\frac {1}{2}\)∠QPR + ∠TQR …….(i)
[∵ RT and QT are the bisectors of ∠PRS and ∠PQR respectively
∴ ∠TRS = \(\frac {1}{2}\)∠PRS and ∠TQR = \(\frac {1}{2}\)∠PQR]
In ΔTQR, we have
∠TRS = ∠QTR + ∠TQR …(ii)
(By theorem 6.8)
From (i) and (ii), we get
\(\frac {1}{2}\)∠QPR + ∠TQR = ∠QTR + ∠TQR
⇒ \(\frac {1}{2}\)∠QPR = ∠QTR
⇒ ∠QTR = \(\frac {1}{2}\)∠QPR.
Hence proved