HBSE 9th Class Maths Solutions Chapter 15 Probability Ex 15.1

Haryana State Board HBSE 9th Class Maths Solutions Chapter 15 Probability Ex 15.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 15 Probability Exercise 15.1

Question 1.
In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
Number of balls thrown = 30
∴ Total number of possible outcomes = 30
Number of times, the boundary is hit by the ball = 6
Number of times, the boundary is not hit by the ball= 30 – 6 = 24
∴ Number of favourable outcomes = 24
Let E be event that the boundary is not hit by the ball
∴ P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{24}{30}\) = \(\frac{4}{5}\)
Hence, P(E) = \(\frac{4}{5}\)

Question 2.
1500 families with 2 children were selected randomly, and the following data were recorded :

Number of girls in a family	2	1	0
Number of families	475	814	211

Compute the probability of a family, chosen at random, having :
(i) 2 girls
(ii) 1 girl
(iii) No girl.
Also check whether the sum of these probabilities is 1.
Solution:
Total number of families = 1500
∴ Total number of possible outcomes = 1500
(i) Number of families having 2 girls = 475
∴ Number of favourable outcomes = 475
Let E₁ be event that the selected family has 2 girls, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{475}{1500}\) = \(\frac{19}{60}\)

(ii) Number of families having 1 girl = 814
∴ Number of favourable outcomes = 814
Let E₂ be the event that the selected family has 1 girl, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{814}{1500}\) = \(\frac{407}{750}\)

(iii) Number of families having no girl = 211
∴ Number of favourable outcomes = 211
Let E₃ be the event that the selected family has no girl; then
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{211}{1500}\)

(iv) Sum of the probabilities
= \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}\)
= \(\frac{475+814+211}{1500}\)
= \(\frac{1500}{1500}\) = 1
Hence, (i) P(E₁) = \(\frac{19}{60}\), (ii) P(E₂) = \(\frac{407}{750}\) (iii) P(E₃) = \(\frac{211}{1500}\) (iv) Sum of the probabilities = 1.

Question 3.
In a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for the data so obtained :

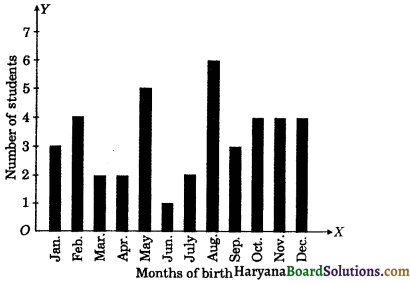
Find the probability that a student of the class was born in August.
Solution :
Total number of students = 40
∴ Total number of possible outcomes = 40
Number of students was born in August = 6
∴ Number of favourable outcomes = 6
Let E be the event that a student of the class was born in August, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{6}{40}\) = \(\frac{3}{20}\)
Hence, P(E) = \(\frac{3}{20}\)

Question 4.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :

Outcome	3 heads	2 heads	1 head	No head
Frequency	23	72	77	28

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution :
Total number of tosses of three coins simultaneously = 200
∴ Total number of possible outcomes = 200
Number of outcomes of 2 heads = 72
∴ Number of favourable outcomes = 72
Let E be the event of 2 heads coming up, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{72}{200}\) = \(\frac{9}{25}\)
Hence, P(E) = \(\frac{9}{25}\)

Question 5.
An organisation selected 2400 families at random and surveyed them to determine their income level and the number of vehicles in a family. The information gathered is listed in the table below :

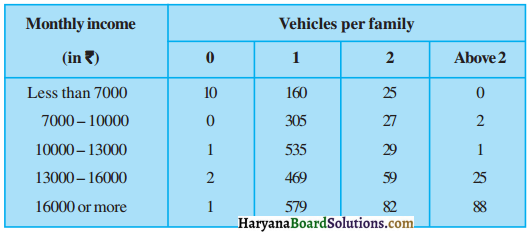
Suppose a family is chosen. Find the probability that the family chosen is :
(i) earning Rs. 10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning Rs. 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs. 7000 per month and does not own any vehicle.
(iv) earning Rs. 13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Solution:
The total number of families = 2400
∴ Total number of possible outcomes= 2400
(i) Number of families earning Rs. 10000 – 13000 per month and owning exactly 2 vehicles = 29
∴ Number of favourable outcomes = 29
Let E₁ be the event that a family’s earning 10000 – 13000 per month and owning exactly 2 vehicles, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{29}{2400}\)

(ii) Number of families earning Rs. 16000 or more per month and owning exactly 1 vehicle = 579
∴ Number of favourable outcomes = 579
Let E₂ be the event that a family’s earning Rs. 16000 or more per month and owning exactly 1 vehicle, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{579}{2400}\)

(iii) Number of families earning less than Rs. 7000 per month and does not own any vehicle = 10
∴ Number of favourable outcomes = 10
Let E₃ be the event that a family’s earning less than Rs. 7000 per month and does not own any vehicle, then
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{10}{2400}\) = \(\frac{1}{240}\)

(iv) Number of families earning Rs. 13000 – 16000 per month and owning more than 2 vehicles = 25
∴ Number of favourable outcomes = 25
Let E₄ be the event that a family’s earning Rs. 13000 – 16000 per month and owning more than 2 vehicles, then
P(E₄) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{25}{2400}\) = \(\frac{1}{96}\)

(v) Number of families owning not more than 1 vehicle = 10 + 0 + 1 + 2 + 1 + 160 + 305 + 535 + 469 + 579
= 2062
∴ Number of favourable outcomes= 2062
Let E₅ be the event that a family owning not more than 1 vehicle, then
P(E₅) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{2062}{2400}\) = \(\frac{1031}{1200}\)
Hence,
(i) P(E₁) = \(\frac{29}{2400}\);
(ii) P(E₂) = \(\frac{579}{2400}\)
(i) P(E₃) = \(\frac{1}{240}\)
(iv) P(E₄) = \(\frac{1}{96}\)
(v) P(E₅) = \(\frac{1031}{1200}\)

Question 6.
A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. A data of their performances is given below in the table :

Marks	Number of students
0 – 20	7
20 – 30	10
30 – 40	10
40 – 50	20
50 – 60	20
60 – 70	15
70 – above	8
Total	90

(i) Find the probability that a student obtained less than 20% marks in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Solution:
Total number of students = 90
∴ Total number of possible outcomes = 90
(i) Number of students who obtained less than 20% marks in the test = 7
∴ Number of favourable outcomes = 7
Let E₁ be the event of a student obtaining less than 20% marks in the test.
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{7}{90}\)

(ii) Number of students who obtained marks 60 or above in the test = 15 + 8 = 23
∴ Number of favourable outcomes = 23
Let E₂ be the event of a student obtaining 60 or above marks in the test.
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{23}{90}\)
Hence, (i) P(E₁) = \(\frac{7}{90}\),
(ii) P(E₂) = \(\frac{23}{90}\)

Question 7.
To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table :

Opinion	Number of students
like	135
dislike	65

Find the probability that a student chosen at random :
(i) likes statistics,
(ii) does not like it.
Solution:
Total number of students = 200
∴ Total number of possible outcomes = 200
(i) Number of students who likes statistics = 135
∴ Number of favourable outcomes = 135
Let E₁ be the event of a student likes statistics, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{135}{200}\) = \(\frac{27}{40}\)

(ii) Number of students who dislikes statistics = 65
∴ Number of favourable outcomes = 65
Let E₂ be the event of a student dislikes statistics, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{65}{200}\) = \(\frac{13}{40}\)
Hence, (i) P(E₁) = \(\frac{27}{40}\) (ii) P(E₂) = \(\frac{13}{40}\)

Question 8.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:

Construct a grouped frequency distribution table with class size 7 for the data given above taking the first interval as 0-7 (7 is not included).
What is the empirical probability that an engineer lives :
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work ?
(iii) within \(\frac{1}{2}\) km from her place of work?
Solution:
First we construct the frequency distribution table taking class interval 0 – 7, 7 – 14, 14 – 21, … as follows :

Distance (in km)	No. of Engineers
0 – 7	9
7 – 14	17
14 – 21	11
21 – 28	1
28 – 35	2
Total	40

Total number of engineers = 40
∴ Total number of possible outcomes = 40
(i) Number of engineers who live at a distance less than 7 km from their place of work = 9
∴ Number of favourable outcomes = 9
Let E₁ be the event of a engineer lives at a distance less than 7 km from their place, then
P(E₁) = \(\frac{9}{40}\)
(ii) Number of engineers who live at a distance more than or equal to 7 km from their place of work = 17 + 11 + 1 + 2 = 31
∴ Number of favourable outcomes = 31
Let E₂ be the event of a engineer lives at a distance more than or equal to 7 km from their place, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{31}{40}\)

(iii) Number of engineers who live within \(\frac{1}{2}\) km from their place of work = 0
Number of favourable outcomes = 0
Let E₃ be the event of a engineer lives within \(\frac{1}{2}\) km from their place of work.
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{0}{40}\) = 0
Hence, (i) P(E₁) = \(\frac{9}{40}\), P(E₂) = \(\frac{31}{40}\), (iii) P(E₃) = 0.

Question 9.
Activity: Note the frequency of two wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Solution :
Collect the data according to activity and find the required probability.

Question 10.
Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Solution :
According to activity, collect the data and find required probability

Question 11.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Total number of bags = 11
∴ Total number of possible outcomes = 11
Number of bags containing more than 5 kg of flour = 7
∴ Number of favourable outcomes = 7
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{7}{11}\)
Hence, P(E) = \(\frac{7}{11}\)

Question 12.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows :

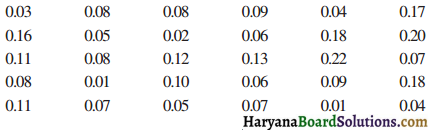
make a grouped frequency distribution table for this data with class intervals as 0.00 – 0.04, 0.04 – 0·08 and so on. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Solution :
First we construct frequency distribution table taking class intervals as 0.00 – 0.04, 0.04 – 0.08, …, as follows:

Concentration of SO2 (in ppm)	Frequency
0.00 – 0.04	4
0.04 – 0.08	9
0.08 – 0.12	9
0.12 – 0.16	2
0.16 – 0.20	4
0.20 – 0.24	2
Total	30

Total number of days = 30
∴ Total number of possible outcomes = 30
Concentration of sulphur dioxide in the interval 0.12 – 0.16 on any day = 2
∴ Number of favourable outcomes = 2
Let E be the event of concentration of sulphur dioxide in the interval 0·12 – 0.18 on any day. Then,
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{2}{30}\) = \(\frac{1}{15}\)
Hence, P(E) = \(\frac{1}{15}\)

Question 13.
The blood groups of 30 students of class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Represent this data in the form of a frequency distribution table. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
Solution :
First prepare the frequency distribution table as follows :

Blood groups	Number of students
A	9
B	6
AB	3
O	12
Total	30

Total number of students = 30
∴ Total number of possible outcomes = 30
Number of students having blood group AB = 3
∴ Number of favourable outcomes = 3
Let E be event of a student having blood group AB, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{30}\) = \(\frac{1}{10}\)
Hence, P(E) = \(\frac{1}{10}\)