HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.4

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 Statistics Exercise 14.4

Question 1.
The following number of goals were scored by a team in a series of 10 matches :
2, 3, 4, 5,0, 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
Solution:
Here, n = 10
\(\sum_{i=1}^{10} x_i\) = 2 + 3 + 4 + 5 + 0 + 1 + 3 + 3 + 4 + 3 = 28
∴ mean = \(\frac{\sum_{i=1}^{10} x_i}{n}=\frac{28}{10}\) = 2.8
To obtain the median, we arrange the data in ascending order :
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
n = 10, which is even


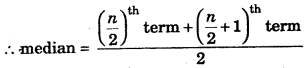
Again, in the data 3 occurs most frequently i.e., 4 times, so mode = 3.
Hence, mean = 2.8, median = 3 and mode = 3.

Question 2.
In a mathematics test given to 15 students, the following marks (out of 100) are recorded:
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60.
Find the mean, median and mode of this data.
Solution:
Here, n = 15
\(\sum_{i=1}^{15} x_i\) = 41 + 39 + 48 +52 + 46 +62 + 54 + 40 + 96 +52 +98 + 40 + 42 +52 + 60
= 822
∴ mean = \(\frac{\sum_{i=1}^{15} x_i}{n}=\frac{822}{15}\) = 54.8
To obtain the median, we arrange the data in ascending order:
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
n = 15, which is odd
∴ median = \(\left(\frac{n+1}{2}\right)^{\text {th }}\) term
median = \(\left(\frac{15+1}{2}\right)^{\text {th }}\) term
= 8^th term = 52
Again, in the data 52 occurs most frequently i.e., 3 times.
∴ mode = 52
Hence, mean = 54.8, median = 52 and mode = 52.

Question 3.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95.
Solution:
The given data arranged in ascending order is :
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95 and median = 63
Here, n = 10, which is even

⇒ 63 = \(\frac{2 x+2}{2}\)
⇒ 63 = x + 1
⇒ x = 63 – 1 = 62
Hence, x = 62

Question 4.
Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Solution:
We arrange the data in the following form:
14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28 Here, 14 occurs most frequently, i.e., 4 times.
Hence, mode = 14.

Question 5.
Find the mean salary of 60 workers of a factory from the following table:

Salary (in Rs.)	Number of workers
3000	16
4000	12
5000	10
6000	8
7000	6
8000	4
9000	3
10000	1
Total	60

Solution:
For calculating the mean, we prepare the following table:

Salary (in Rs.) xi	Number of workers fi	fixi
3000	16	48000
4000	12	48000
5000	10	50000
6000	8	48000
7000	6	42000
8000	4	32000
9000	3	27000
10000	1	10000
	\(\sum_{i=1}^{30} f_i=60\) = 60	\(\sum_{i=1}^{30} f_i x_i\) = 305000

Hence, mean salary of 60 workers = Rs. 5083.33 (approx.).

Question 6.
Give one example of a situation in which :
(i) the mean is an approximate measure of central tendency.
(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Solution:
(i) The marks obtained by a student in 5 subjects (out of 20) are:
10, 12, 12, 14, 16
Here, n = 5
\(\sum_{i=1}^5 x_i\) = 10 + 12 + 12 + 14 + 16 = 64
mean = \(\frac{\sum_{i=1}^5 x_i}{n}=\frac{64}{5}\) = 12:8
n = 5, which is odd
∴ median = \(\left(\frac{n+1}{2}\right)^{\text {th }}\) term
= \(\left(\frac{5+1}{2}\right)^{\text {th }}\) term
= 3^th term = 12
Again, data 12 occurs most frequently i.e., 2 times.
∴ mode = 12
Hence, mean more appropriate measure of central tendency. Ans.

(ii) Mean is highly effected by the extreme value. But median is uneffected by the extreme value of the variable.
e.g., Runs scored by a batsman in 5 innings are 8, 10, 12, 15, 65.
Here, n = 5
\(\sum_{i=1}^5 x_i\) = 8 + 10 + 12 + 15 + 65 = 110
mean = \(\frac{\sum_{i=1}^5 x_i}{n}\)
= \(\frac{110}{5}\) = 22
n = 5, which is odd
∴ median = \(\left(\frac{5+1}{2}\right)^{\text {th }}\) term
= \(\left(\frac{5+1}{2}\right)^{\text {th }}\) term
= 3^th term = 12
Hence, mean is not appropriate measure of central tendency but the median is an appropriate measure of central tendency.