HBSE 9th Class Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.2

Haryana State Board HBSE 9th Class Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 12 हीरोन का सूत्र Exercise 12.2

प्रश्न 1.
एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90°, AB = 9 m, BC = 12 m, CD =5 m और AD = 8 m है। इस पार्क का कितना क्षेत्रफल है ?
हल :
ΔBCD का क्षेत्रफल = \(\frac{1}{2}\) × BC × CD
= (\(\frac{1}{2}\) × 12 × 5) m² = 30 m²
पाइथागोरस प्रमेय से,

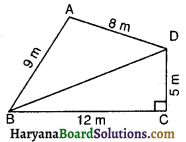
BD² = BC² + CD²
⇒ BD² = 12² + 5²
⇒ BD² = 144 + 25
⇒ BD² = 169
BD = \(\sqrt{169}\) = 13 m
Δ ABD के लिए
a = 13 m , b = 8 m site c = 9m
अब s = \(\frac{1}{2}\)(a + b + c)
= \(\frac{1}{2}\)(13 + 8 + 9) m
= \(\frac{1}{2}\) × 30 m = 15 m

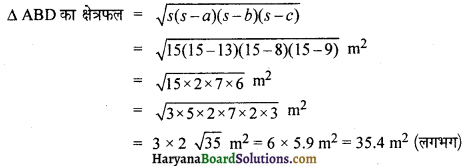
अतः चतुर्भुजाकार पार्क Δ BCD का क्षेत्रफल = (Δ BCD + Δ ABD) का क्षेत्रफल
= (30 + 35.4) m² = 65.4 m² (लगभग) उत्तर

प्रश्न 2.
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5cm और AC = 5 cm है।
हल :
यहाँ पर ΔABC के लिए a = 3 cm, b = 4 cm, c = 5 cm

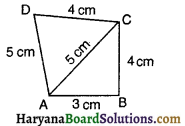
s = \(\frac{a+b+c}{2}=\frac{3+4+5}{2}\) cm
= \(\frac{12}{2}\) cm = 6 cm

अतः चतुर्भुज (ΔBCD) का क्षेत्रफल = (ΔABC) + (ΔADC) का क्षेत्रफल
= (6 + 9.2) cm²
= 15.2 cm² (लगभग) उत्तर

प्रश्न 3.
राधा ने एक रंगीन कागज से एक हवाई जहाज का चित्र बनाया, जैसा कि आकृति में दिखाया गया है। प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।

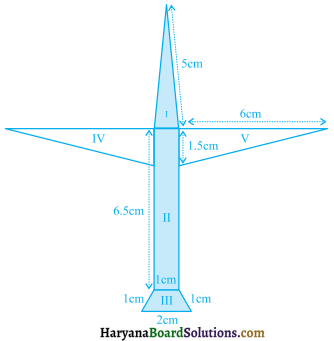
हल :
यहाँ पर भाग I के लिए
a = 5 cm, b = 5 cm, c = 1 cm

भाग II के लिए
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= 6.5 × 1 cm² = 6.5 cm²
भाग III के लिए
समलंब का क्षेत्रफल = 3 × समबाहु त्रिभुज का क्षेत्रफल
= 3 × \(\frac{\sqrt{3}}{4}\) (1)²cm²
= 3 × \(\frac{1.732}{4}\) cm²
= \(\frac{5.196}{4}\) = 1.3 cm²
भाग IV के लिए
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × 6 × 1.5 cm² = 4.5 cm²
भाग V के लिए
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × 6 x 1.5 cm² = 4.5 cm²
अतः राधा द्वारा प्रयोग किए गए कागज का कुल क्षेत्रफल
= भाग [I + II + III + IV + V] का क्षेत्रफल
= [2.5 + 6.5 + 1.3 + 4.5 + 4.5] cm²
= 19.3 cm² (लगभग) उत्तर

प्रश्न 4.
एक त्रिभुज और एक समांतर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समांतर चतुर्भुज 28 cm के आधार पर स्थित है, तो उसकी संगत ऊँचाई ज्ञात कीजिए।
हल :
यहाँ त्रिभुज के लिए
a = 26 cm, b = 28 cm, c = 30 cm

समांतर चतुर्भुज का आधार = 28 cm
प्रश्नानुसार
समांतर चतुर्भुज का क्षेत्रफल = त्रिभुज का क्षेत्रफल
⇒ आधार × संगत ऊँचाई = 336
या 28 × संगत ऊँचाई = 336
या संगत ऊँचाई = \(\frac{336}{28}\) = 12 cm उत्तर

प्रश्न 5.
एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा ? [B.S.E.H. March, 2019]
हल :
हम जानते हैं कि समचतुर्भुज का विकर्ण इसे दो बराबर त्रिभुजों में बाँटता है।

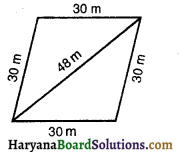
प्रत्येक त्रिभुज के लिए
a = 30m
b = 30m
c = 48m

अतः समचतुर्भुजाकार खेत का क्षेत्रफल = 2 × त्रिभुज का क्षेत्रफल
= 2 × 432 m² = 864 m²
18 गायों को चरने के लिए उपलब्ध क्षेत्रफल = 864 m²
1 गाय को चरने के लिए उपलब्ध क्षेत्रफल = \(\frac{864}{18}\) m²
= 48 m² उत्तर

प्रश्न 6.
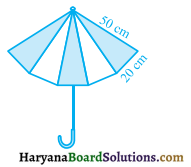
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है (देखिए आकृति)। प्रत्येक टुकड़े के माप 20 cm, 50 cm और 50 cm हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है ?

हल :
यहाँ पर प्रत्येक त्रिभुजाकार टुकड़े के लिए
a = 20 cm
b = 50 cm
c = 50 cm

अतः छाते में प्रत्येक रंग के कपड़े का क्षेत्रफल = 5 × 200\(\sqrt{6}\) cm²
= 1000\(\sqrt{6}\) cm² उत्तर

प्रश्न 7.
एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है ?

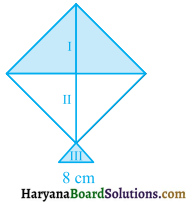
हल :
पतंग के ऊपरी भाग का विकर्ण = 32 cm
∴ ऊपरी भाग का कुल क्षेत्रफल = \(\frac{1}{2}\) × पहला विकर्ण × दूसरा विकर्ण
= \(\frac{1}{2}\) × 32 × 32 cm²
= 16 × 32 cm² = 512 cm²
512 अतः छायांकित भाग I का क्षेत्रफल = छायांकित भाग II का क्षेत्रफल = \(\frac{512}{2}\)
= 256 cm² उत्तर
अब भाग III के लिए
a = 6 cm, b = 6 cm, c = 8 cm

प्रश्न 8.
फर्श पर एक फूलों का डिज़ाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 cm, 28 cm और 35 cm हैं (देखिए आकृति)। इन टाइलों को 50 पैसे प्रति cm² की दर से पॉलिश कराने का व्यय ज्ञात कीजिए।

हल :
प्रत्येक त्रिभुजाकार टाइल के लिए
a = 9 cm, b = 28 cm, c = 35 cm

= \(\sqrt{36 \times 27 \times 8 \times 1}\) cm²
= \(\sqrt{6 \times 6 \times 3 \times 3 \times 3 \times 2 \times 2 \times 2}\) cm²
= 6 × 3 × 2 × \(\sqrt{6}\) cm²
= 36\(\sqrt{6}\) cm²
अतः फर्श में लगी 16 टाइलों का कुल क्षेत्रफल = 16 × 36\(\sqrt{6}\) cm²
= 576 × 2.45 cm²
= 1411.2 cm²
1 वर्ग सें०मी० टाइल पर पॉलिश करने का व्यय = 50 पैसे = ₹ \(\frac{50}{100}\)
1411.2 वर्ग सें०मी० टाइल पर पॉलिश करने का व्यय = ₹\(\frac{50}{100}\) × 1411.2
₹ 705.60 उत्तर

प्रश्न 9.
एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 m और 10 m हैं। इसकी असमांतर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल :

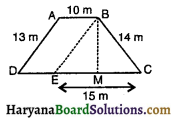
माना ABCD एक समलंब के आकार का खेत है जिसमें
AB = 10 m, BC = 14 m
CD = 25 m, DA = 13 m
BE||AD खींचिए जो CD को E पर काटे तथा BM⊥CD खींचे जो CD को M पर मिले। इस प्रकार ABED एक समांतर चतुर्भुज है।
AB = DE = 10 m
BE = DA = 13 m
CE = DC – DE = 25 – 10 = 15 m
अब ΔBEC में
a = 13 m
b = 15 m
c = 14 m

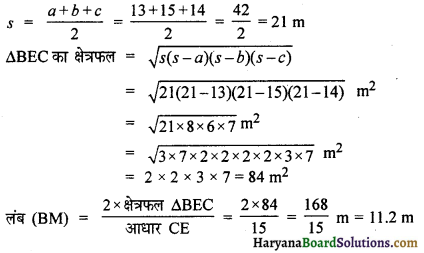
अतः समलंब ABCD का क्षेत्रफल = \(\frac{1}{2}\) × (AB + CD) × BM
= \(\frac{1}{2}\) × (10 + 25) × 11.2 m²
= \(\frac{1}{2}\) × 35 × 11.2 m²
= 35 × 5.6 m²
= 196 m² उत्तर