Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 11 Constructions Exercise 11.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
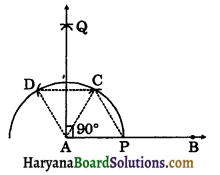
Steps of construction:
Step – I: Draw a ray AB with initial point A.
Step – II: Taking A as centre and suitable radius, draw an arc which intersects AB at P.
Step – III: Taking P as centre and same radius as before, draw an arc intersecting previous arc at C.
Step – IV: Taking C as centre and same radius as before, draw an arc intersecting the previous, arc at D.
Step – V: Taking C and D as centres draw two arcs intersecting each other at Q.
Step – VI: Join AQ. Then ∠QAB is the required angle of measure 90°.
Justification: Join CP, AC, CD and AD.
∵ AP = CP = AC (By construction)
∴ ACP is an equilateral triangle.
⇒ ∠CAP = 60°
[∵ Each angle of equilateral triangle is 60°]
Again, AC = CD = AD
(By construction)
∴ CAD is an equilateral triangle.
⇒ ∠CAD = 60°
Since, AQ is the bisector of ∠CAD.
∴ ∠CAQ = \(\frac{1}{2}\) × 60° = 30°
Now, ∠QAB = ∠CAP + ∠CAQ
⇒ ∠QAB = 60° + 30°
⇒ ∠QAB = 90°.
![]()
Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
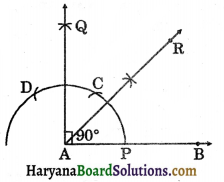
Steps of construction:
Step – I: Draw ∠QAB = 90° by the following steps given in 1.
Step – II: Draw the bisector of ∠QAB.
Then ∠RAB = 45°
Justification: ∠QAB = 90° (By construction)
Since AR is the bisector of ∠QAB.
∠RAB = \(\frac{1}{2}\) × 90°
= 45°.
Question 3.
Construct the angles of the following measurements:
(i) 30°
(ii) 22°
(iii) 15°
Solution:
(i) Steps of construction:
Step – I: Draw a ray AB with initial pointA.
Step – II: Taking A as centre and suitable radius, draw an arc intersecting AB at C.
Step – III: Taking C as centre and same radius as before, draw an arc intersecting the previous arc at D.

Step – IV: Taking C and D as centres and a suitable radius more than \(\frac{1}{2}\)CD, draw two arcs intersecting each other at E.
Step – V: Join AE. Then ∠BAE = 30°.
(ii) Steps of construction:
Step – I: Draw ∠CAB = 90° as followed by the steps in 1.
Step – II: Draw the bisector AD of ∠CAB.
∠CAD = ∠BAD = \(\frac{90^{\circ}}{2}\) = 45°.
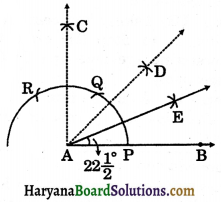
Step – III: Draw the bisector AE of ∠BAD
∴ ∠BAE = \(\frac{1}{2}\) × 45° = \(22 \frac{1}{2}^{\circ}\)
(iii) Steps of construction :
Step – I: Draw ∠CAB = 30° as followed by the steps in 3(a).
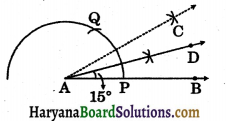
Step – II: Draw the bisector AD of ∠CAB.
∴ ∠BAD = \(\frac{1}{2}\) × 30°
= 15°
![]()
Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°.
Solution:
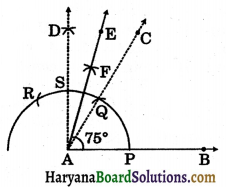
(i) Steps of construction:
Step – I: Draw ∠CAB = 60° as followed by the steps in Construction 11.3.
Step – II: Draw ∠DAB = 90° as followed by the steps in 1. So, ∠CAD = 90° – 60° = 30°.
Step – III: Draw the bisector AE of CAD.
Then ∠EAB = 75° is required angle.
Verification: On measuring ∠EAB, with the help of protractor. We observe that ∠EAB = 75°.
(ii) Steps of construction:
Step – I:Draw a ray AB with initial point A.
Step – II:Taking A as centre and suitable radius, draw an arc intersecting AB at P.
Step – III:Taking P as a centre and same radius as before, draw an arc intersecting previous are at Q.
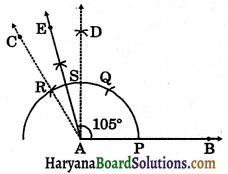
Step – IV: Taking Q as a centre and same radius as before, draw an arc intersecting previous arc at R.
Step – V: Draw a ray CA passing through R. Then
∠CAB = 120°
Step – VI: Draw ∠DAB = 90° as followed by the steps in 1.
∴ ∠CAD = 120° – 90° = 30°.
Step – VII: Draw the bisector AE of ∠CAD.
∠EAD = \(\frac{1}{2}\) × 30° = 15°
Then, ∠EAB = 90° + 15° = 105°
Hence, ∠EAB = 105°.
Verification: On measuring ∠EAB with the help of protractor we observe that ∠EAB = 105°.
(iii) Steps of construction :
Step – I: Draw a ray AB with initial point
Step – II: Taking A as centre and suitable radius draw an arc intersecting AB at P.
Step – III: Taking Pas centre and same radius as before, draw an arc intersecting previous arc at Q.
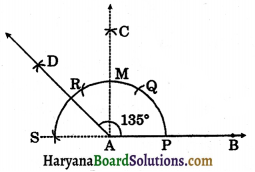
Step – IV: Taking Q as centre and same radius as before, draw an arc intersecting previous arc at R.
Step – V: Taking R as the centre and same radius as before, draw an arc intersecting previous arc at S. Produce BA to S. Then ∠SAB = 180°.
Step – VI: Taking Q and R as the centres and radius more than \(\frac{1}{2}\)PQ draw two arcs intersecting each other at C.
Step – VII: Join AC intersecting previous arc at M. Then ∠CAB = 90°. ∠CAS = 180° – 90° = 90°.
Step – VIII: Draw bisector AD of ∠CAS.
Then ∠CAD = \(\frac{1}{2}\) × 90o = 45°.
∴ ∠BAD = 90° + 45° = 135°.
Verification: On measuring ∠BAD with the help of protractor we osberve that ∠BAD = 135°.
![]()
Question 5.
Construct an equilateral triangle, given its side and justify the construction. Let us draw an equilateral triangle of side 3.7 cm (say).
Solution:
Steps of construction:
Step – I: Draw a line segment length 3.7 cm.
Step – II: Taking B draw an arc, that cut BC at D.
Step – III: By same radius taking D as centre, draw an arc that cut previous arc at E join BE.
Step – IV: Cut 3.7 cm from BE at A, Join ABC.
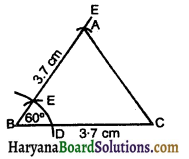
Justification:
∵ AB = BC = CA (By construction)
∴ ABC is an equilateral triangle.