HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.3

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 Circles Exercise 10.3

Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
The different pair of circles are

These pairs may have 0, 1 and 2 points common.
A pair of circles have maximum two points common.

Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Solution:

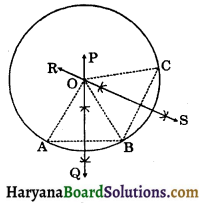
There is one and only one circle passing through three given non-collinear points.
Given: Three non-collinear points A, B and C.
To prove: There is one and only one circle passing through three points A, B and C.
Construction: Join AB and BC. Draw the I bisectors PQ and RS of AB and BC. Since A, B and C are non-collinear, PQ and RS are not parallel and will intersect, say the point O. Join OA, OB and OC.
Proof: Since O lies on the perpendicular bisector of AB, we have
OA = OB …….(i)
Similarly, O lies on the perpendicular bisector of BC, we have
OC = OB ……(ii)
From (i) and (ii), we get
OA = OB = OC = r (say)
With O as the Centre and r the radius, draw circle C(O, r) which will pass through A, B and C.
Hence, there is one and only one circle passing through three non-collinear points.

Remark: If ABC is a triangle, then by Theorem 105, there is a unique circle passing through the three vertices A, B and C of the triangle. This circle is called the circumcircle of the MBC. Its centre and radius are called respectively the circumcentre and the circumradius of the triangle.

Equal chords and their distances from the centre: Let AB be a line and P be a point (not on the line). There are many infinite number of points L₁, L₂, L₃, L₄, L₅ on the line. If we join these points to P, we will get many line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅, where PM is the perpendicular from P to AB. On measuring these line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅ we find that PM is the shortest line segment.

So, we conclude that the length of the perpendicular from a point to a line is the distance of the line from the point.

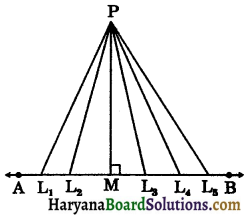
Note: If the point lies on the line, the distance of the line from the point is zero.

Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
Given: Two circles C(O, r₁) and C(Oʻ, r₂) intersecting at points A and B.
To prove: OO’ is the perpendicular bisector of AB.
Construction: Join OA, OB, O’A and OB’. Let OO’ intersects AB at M.
Proof: In ΔOAO and ΔOBO’, we have

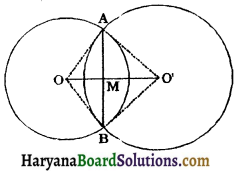
OA = OB [Radii of a same circle]
AO’ = BO’ [Radii of a same circle]
OO’ = OO’ (Common)
∴ ΔOAO’ ≅ ΔOBO’ [By SSS congruence rule]
⇒ ∠AOO’ = ∠BOO’ (CPCT)
⇒ ∠AOM = ∠BOM
In ΔAOM and ΔBOM, we have
ОА = OB [Radii of a same circle]
∠AOM = ∠BOM (as proved above)
OM = OM (Common)
∴ ΔAOM ≅ ΔBOM (By SAS congruence rule)
⇒ AM = BM (CPCT)
and ∠AMO = ∠BMO (CPCT) …(i)
But ∠AMO + ∠BMO = 180° (By linear pair axiom)
∠AMO + ∠AMO = 180° [using (i)]
2∠AMO = 180°
∠AMO = \(\frac{180^{\circ}}{2}\) = 90°
Thus AM = BM and
∠AMO = ∠BMO = 90°
Hence, OO’ is the perpendicular bisector of AB.
Proved.