HBSE 9th Class Maths Notes Chapter 10 Circles

Haryana State Board HBSE 9th Class Maths Notes Chapter 10 Circles Notes.

Haryana Board 9th Class Maths Notes Chapter 10 Circles

Introduction
We used various objects in our daily life which are round in shape, such as coins of dimensions ₹ 1, ₹ 2 and ₹ 5, buttons of shirts, key rings, dials of clocks, wheels of vehicles etc. (see in figure 10.1). In a clock we have observed that the second’s hand goes round the dial of the clock rapidly and its tip moves round path. This path traced by the tip of the second’s hand is called a circle.

If we fix a pencil in compass and put its pointed leg on a point on a sheet of a paper, open the other leg to some distance. Keeping the pointed leg on the same point, rotate the other leg through one revolution we get a closed figure traced by the pencil on the paper which is known as the circle (see in figure 10.2). In this chapter we will study about circles, it’s related terms and some properties of a circle.

Key Words
→ Circle: A circle is a plane figure bounded by one curved line and is such that all straight lines drawn to this line from certain point within it are equal.

→ Radius: A line segment joining the centre and a point on the circle is called its radius.

→ Circular Region: The region consisting of all points which are either on the circle or lies inside the circle is called the circular region or circular disc.

→ Concentric Circles: The circles which have same centre and different radii are called concentric circles.

→ Centroid: The point of concurrency of the three medians of a triangle is called the centroid of the triangle.

→ Circumcentre: The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcentre of the triangle.

→ Circumcircle: The circumcentre O is equidistant from the three vertices of a triangle. A circle with centre O and radius OA is called the circumcircle of the triangle. It passes through all the three vertices.

→ Concyclic: A number of points are concyclic if there is a circle that passes through all of them.

Basic Concepts
Circles and Its Related Terms: A Review
(i) Circle: The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
(ii) Centre: The fixed point is called the centre of the circle. In the figure, O is the centre.

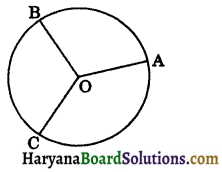
(iii) Radius: The constant distance from its centre is called the radius of the circle. The plural of radius is radii.
In the figure, OA, OB and OC are radii of the circle C(O, r).

(iv) Circumference: The length of the complete circle is called its circumference. The perimeter of a circle is also known as the circumference of the circle.

(v) Chord: A line segment joining any two points on the circle is known as the chord of the circle. In the figure, AB and CD are chords of a circle with centre O.

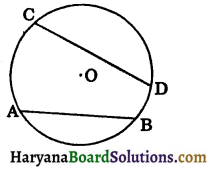
(vi) Diameter: The chord, which passes through the centre of the circle is called a diameter of the circle. A diameter is the longest chord and all diameters are equal in lengths. In the figure, AOB is the diameter.
Diameter = 2 × radius
A diameter divides the circle into two equal arcs. Each of these two arcs is called a semicircle. In the figure, \(\widehat{A P B}\) and \(\widehat{A Q B}\) are two semicircles. The degree measure of a semicircle is 180°.

(vii) Secant: A line which intersects a circle in two distinct points is called a secant of the cricle. In the figure, the line l cuts the circle in two points A and B. So, l is a secant of the circle.

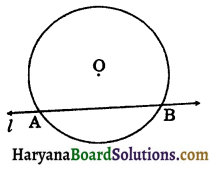
(viii) Arc: A piece of a circle between two points is called an arc.

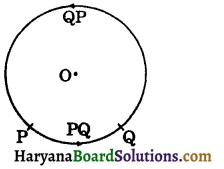
Let P and Q be two points on the circle. These points P and Q divide the circle into two pieces. Each piece is an arc. These arcs are denoted in anticlockwise direction from P to Q as PQ and from Q to Pas QP. The arc PQ is called the minor are and arc QRP is called the major arc,

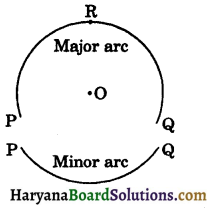
where R is any point (figure 10.9) on the arc between P and Q. When arcs PQ and QRP are equal, then each is called a semicircle.

(ix) Interior and Exterior of a circle: A circle divides the plane on which it lies into three parts. They are:

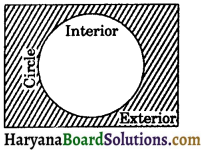
(a) Inside the circle, which is also called the interior of the circle.
(b) Circle.
(c) Outside the circle, which is also called the exterior of the circle (see in figure).
The circle and its interior make up the circular region.
(x) Position of a point with respect to a circle:
(a) Point inside the circle: A point P is said to lie inside the circle C(O, r), if OP < r.

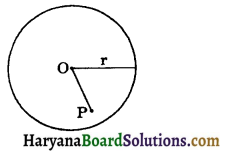
(b) Point on the circle: A point is said to lie on the circle C(O, r), if OP = r.

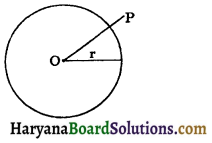
(c) Point outside the circle: A point is said to lie outside the circle C(O, r), if OP > r.

(xi) Segment of a circle: The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle.

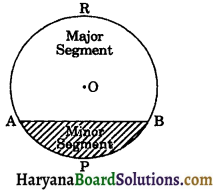
The segment containing the minor area is called the minor segment. Thus APBA is the minor segment of the circle.
The segment containing the major arc is called the major segment. Thus ARBA is the major segment of the circle.
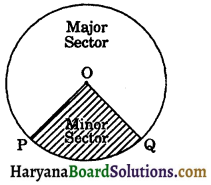
(xii) Sector of a circle: The region between an arc and the two radii, joining the centre to the end points of the arc is called a sector. The minor are corresponds to the minor sector and the major arc corresponds to the major sector. In the figure, the region OPQO is the minor. sector and remaining part of the circular region is the major sector.

(xiii) Quadrant of a circle: One fourth of a circle is called a quadrant of a circle. In the figure, OABO is the quadrant of the circle C(O, r).

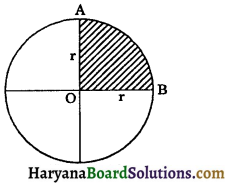
(xiv) Central angle: Let C(O, r) be any circle, then any angle whose vertex is O, is called a central angle of the circle. In the figure, ∠AOB is a central angle of the circle C (O, r).

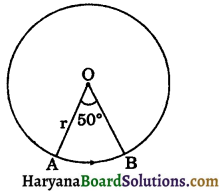
(xv) Degree measure of an arc: Degree measure of a minor arc is the measure of the central angle subtended by the arc. In the given figure 10.17, the measure of the minor are AB is 50° ie., m\(\widehat{A B}\) = 50°. The degree measure of the major are is 360° – 50° = 310°.
⇒ m\(\widehat{B A}\) = 310°
The degree measure of a circle is 360°.
∴ mC(O, r) = m arc AB + m arc BA
= 50° + 310° = 360°.

(xvi) Congruent circles: Two circles are said to be congruent, if and only if one of them can be superposed on the other so as to cover it exactly. This is possible only when the radii of the two circles are equal. Let C(O, r₁) and C(O’, r₂) be two circles such that C(O, r₁) is superposed on C(O’, r₂) so that O’ coincides with O. Then C(O, r₁) will cover C(O’, r₂) completely if and only if r₁ = r₂.

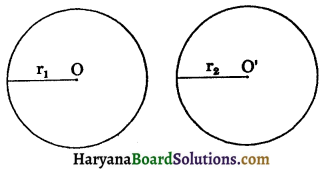
Thus two circles are congruent, if and only if, they have equal radii.

(xvii) Congruent arcs: Two arcs of a circle are said to be congruent if and only if they have the same degree measures.
If arc AB is congruent to arc CD. They are written as
AB = CD

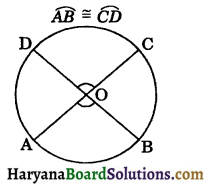
In particular case, arcs of semicircles will be congruent because each has degree. measure = 180°.

Angle subtended by a chord at a point: The angle subtended by chord PQ at a point R (not on the chord PQ) on the circumference of the circle is ∠PRQ. And the angle subtended by chord PQ at the centre O is ∠POQ.

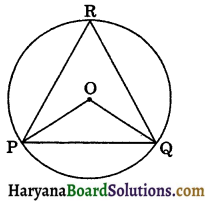
Theorem 10.1:
Equal chords of a circle subtend equal angles at the centre.
Given: Two equal chords AB and CD of a circle with centre O.

To prove: ∠AOB = ∠COD.
Proof: In ΔAOB and ΔCOD, we have
OA = OC (Equal radii of a circle)
OB = OD (Equal radii of a circle)
AB = CD (given)
∴ ΔAOB ≅ ΔCOD (By SSS congruence rule)
⇒ ∠AOB = ∠COD (CPCT)
Hence proved

Theorem 10.2: [Converse of theorem 10.1]
If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.

Given: Two chords AB and CD of a circle are such that
∠AOB = ∠COD.
To prove: AB = CD.
Proof: In ΔAOB and ΔCOD, we have
OA = OC [Equal radii of a circle]
∠AOB = ∠COD (given)
OB = OD [Equal radii of a circle]
∴ ΔAOB ≅ ΔCOD (By SAS congruence rule)
⇒ AB = CD (CPCT)
Hence proved

Perpendicular from the centre to a chord :
Theorem 10.3:
The perpendicular from the centre of a circle to a chord bisects the chord.

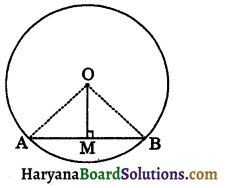
Given: A chord AB of a circle C(O, r) and OM ⊥ to the chord AB.
To prove: AM = MB.
Construction: Join OA and OB.
Proof: In the right ΔOMA and ΔOMB, we have
OA = OB (Equal radii of a circle)
∠OMA = ∠OMB (Each is 90°)
OM = OM (Common)
ΔΟΜΑ ≅ ΔΟΜΒ (By RHS congruence rule)
⇒ AM = MB (CPCT)
Hence proved

Theorem 10.4:
[Converse of theorem 10.3]
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

Given: A chord AB of a circle C(O, r) with mid point M.
To prove: OM ⊥ AB.
Construction: Join OA and OB.
Proof: In ΔOAM and ΔOBM, we have
OA = OB (Equal radii of a circle)
AM = BM
[∵ M is the mid point of AB]
OM = OM (common)
∴ ΔOAM ≅ ΔOBM (By SSS congruence rule)
⇒ ∠OMA = ∠OMB (CPCT) …..(i)
But ∠OMA + ∠OMB = 180° (Linear pair axiom)
⇒ ∠OMA + ∠OMA = 180° [using (i)]
⇒ ∠OMA = 180°
⇒ ∠OMA = \(\frac{180^{\circ}}{2}\) = 90°
∠OMA = ∠OMB = 90°
Hence OM ⊥ AB.
Hence proved

Circle Through Three Points: We take a point P on a paper. There are many circles passing through this point.
Take two points P and Q. There are many infinite number of circle passing through P and Q.
If you take three non-collinear points A, B and C. There is only one circle passing through these points (see in figure below).

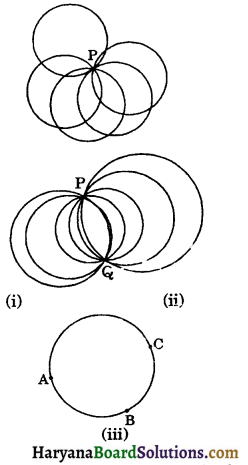
Theorem 10.5:
There is one and only one circle passing through three given. noncollinear points.

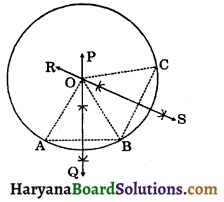
Given: Three non-collinear points A, B and C.
To prove: There is one and only one circle passing through three points A, B and C.
Construction: Join AB and BC. Draw the 1 bisectors PQ and RS of AB and BC. Since A, B and C are non-collinear, PQ and RS are not parallel and will intersect, say the point O. Join OA, OB and OC.
Proof: Since, O lies on the perpendicular bisector of AB, we have
OA = OB …..(i)
Similarly, O lies on the perpendicular bisector of BC, we have
OC = OB …..(ii)
From (i) and (ii), we get
OA = OB = OC = r (say)
With O as the centre and r the radius, draw circle C(O, r) which will pass through A, B and C.
Hence, there is one and only one circle passing through three non-collinear points.
Remark: If ABC is a triangle, then by Theorem 10.5, there is a unique circle passing through the three vertices A, B and C of the triangle. This circle is called the circumcircle of the ΔABC. Its centre and radius are called respectively the circumcentre and the circumradius of the triangle.

Equal chords and their distances from the centre: Let AB be a line and P be a point (not on the line). There are many infinite number of points L₁, L₂, L₃, L₄, L₅ on the line. If we join these points to P, we will get many line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅, where PM is the perpendicular from P to AB. On measuring these line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅, we find that PM is the shortest line segment.

So, we conclude that the length of the perpendicular from a point to a line is the distance of the line from the point.

Note: If the point lies on the line, the distance of the line from the point is zero.

Theorem 10.6:
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

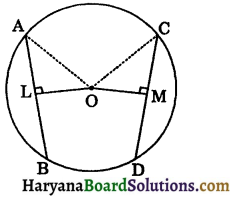
Given: A circle C(O, r) in which chord AB is equal to chord CD, OL ⊥ AB and OM ⊥ CD.
To prove: OL = OM.
Construction: Join OA and OC.
Proof: We have
AB = CD
\(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD ……(i)
∵ OL ⊥ AB
∴ AL = LB = \(\frac{1}{2}\)AB
(By theorem 10.3)…(ii)
and OM ⊥ CD
∴ CM = MD = \(\frac{1}{2}\)CD
(By theorem 10.3)…(iii)
From (i), (ii) and (iii), we get
AL = CM
Now, right ΔOLA and ΔOMC, we have
Hyp. OA = Hyp. OC [Equal radii of a circle]
AL = CM (as proved above)
∠OLA = ∠OMC (Each is 90°)
ΔOLA ≅ ΔOMC (By RHS congruence rule)
⇒ OL = OM (CPCT)
Hence, equal chords of a circle are equidistant from the centre. Proved.

Theorem 10.7:
Chords equidistant from the centre of a circle are equal in length.

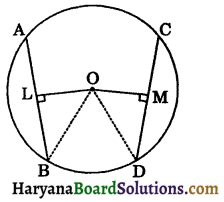
Given: Two chords AB and CD of a circle C(O, r) are such that OL = OM, OL ⊥ AB and OM ⊥ CD.
To prove: AB = CD.
Construction: Join OB and OD.
Proof: ∵ OL ⊥ AB and OM ⊥ CD
∴ LB = \(\frac{1}{2}\)AB and MD = \(\frac{1}{2}\)CD ……(i)
(By theorem 10.3)
Now, right ΔOLB and ΔOMD, we have
Hyp. OB = Hyp. OD [Equal radii of a circle]
∠OLB = ∠OMD (Each is 90°)
OL = OM (given)
∴ ΔΟLΒ ≅ ΔΟΜD (By RHS congruence rule)
⇒ LB = MD (CPCT)
⇒ 2LB = 2MD
⇒ AB = CD [using (i)]
Hence, chords of a circle, which are equidistant from the centre are equal.
Proved

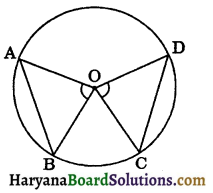
Angle Subtended by an Arc of a Circle: If we cut two arcs corresponding to the equal chords AB and CD respectively. We observe that are AB superimpose the arc CD completely (see in figure). This shows that equal chords make congruent arcs and conversely congruent arcs make equal chords of a circle. You can state it as follows:

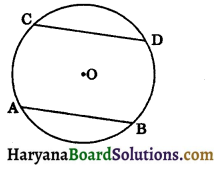
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
In the given figure, minor are AB subtends ∠AOB at the centre O and major are BA subtends reflex ∠AOB at the centre.

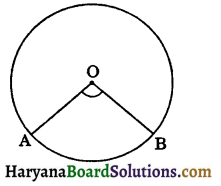
In view of the property above and theorem 10.1, the following result is true:
Congruent ares (or equal arcs) of a circle subtend equal angles at the centre.

Theorem 10.8:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Given: An arc PQ of a circle subtends ∠POQ at the centre and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
Construction: Join AO and produced it to B.

Proof : Consider three different cases as given in figures. In figure (i) \(\widehat{P Q}\) is minor arc, in (ii) \(\widehat{P Q}\) is a semi-circle and in (iii) \(\widehat{P Q}\) is major arc.
In figure (i) and (ii), In ΔAOP, we have
AO = OP [Equal radii of same circle]
⇒ ∠1 = ∠2 [Angles to the opposite sides are equal]
∠POB = ∠1 + ∠2
[Exterior angle is equal to sum of its two opposite interior angles]
⇒ ∠POB = ∠1 + ∠1
⇒ ∠POB = 2∠1 …..(i)
Similarly, In ΔAOQ, we have
∠3 = ∠4 [∵ AO = OQ]
∠QOB = ∠3 + ∠4
⇒ ∠QOB = ∠3 + ∠3
⇒ ∠QOB = 2∠3 ……(ii)
Adding (i) and (ii), we get
∠POB + ∠QOB = 2∠1 + 2∠3
⇒ ∠POQ = 2(∠1 + ∠3)
⇒ ∠POQ = 2∠PAQ
In figure (iii),
∠POB + ∠QOB = 2 (∠1 + ∠3)
⇒ Reflex ∠POQ = 2∠PAQ. Hence proved

Corollary: The angle in a semicircle is a right angle.
Given: In a circle C(O, r), AB is the diameter with centre O and ∠ACB is an angle in a semicircle.

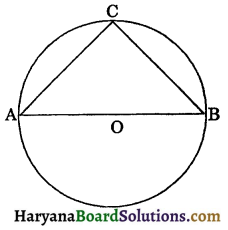
To prove: ∠ACB = 90°,
Proof: ∠AOB = 2∠ACB (By theorem 10.8)
⇒ 180° = 2∠ACB (∵ AOB is a straight line)
∠ACB = \(\frac{180^{\circ}}{2}\)
∠ACB = 90°
Hence, angle in a semicircle is a right angle. Proved

Theorem 10.9:
Angles in the same segment of a circle are equal.
Given: A circle C(O, r) in which ∠ACB and ∠ADB are two angles made by arc AB in the same segment ACDB of the circle.
To prove: ∠ACB = ∠ADB.
Construction: Join OA and OB.

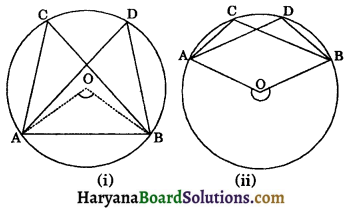
Proof: In figure (i), by theorem 10.8, we have
∠AOB = 2∠ACB…(i)
and ∠AOB = 2∠ADB…(ii)
From (i) and (ii), we get
2∠ACB = 2∠ADB
∠ACB = ∠ADB
In figure (ii), by theorem 10.8, we have
reflex ∠AOB = 2∠ACB…(iii)
and reflex ∠AOB = 2∠ADB…(iv)
From (iii) and (iv), we get
2∠ACB = 2∠ADB
∠ACB = ∠ADB
In both cases, ∠ACB = ∠ADB
Hence, angles in the same segment of a circle are equal. Hence proved

Theorem 10.10:
If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e., they are concyclic).

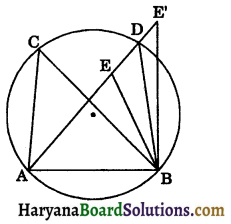
Given: AB is a line segment, which subtends equal angles at two points C and D, such that
∠ACB = ∠ADB.
To prove: The points A, B, C and D lie on a circle (i.e., they are concyclic).
Construction: Draw a circle through three non-collinear points A, B, C.
Proof: Suppose circle does not pass through D. Let it will intersect AD (or extended AD) at point, say E (or E’). If points A, C, E and B lie on a circle, then
∠ACB = ∠AEB …(i) (By theorem 10.9)
But, ∠ACB = ∠ADB (given)…(ii)
From (i) and (ii), we get
∠AEB = ∠ADB
This is not possible unless E coincides with D.
Therefore D lies on the circle passing through A, B, C.
Similarly, E’ should also coincide with D.
Hence, the points A, B, C and D are concylic. Hence Proved

Cyclic Quadrilaterals: A quadrilateral ABCD is called cyclic, if all the four vertices of it lie on a circle.
Theorem 10.11:
The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Or
The opposite angles of a cyclic quadrilateral are supplementary.

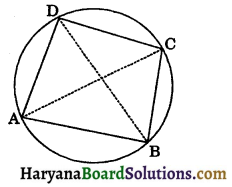
Given: A cyclic quadrilateral ABCD.
To prove: ∠A + ∠C = 180° and ∠B + ∠D = 180°.
Construction: Join AC and BD.
Proof: ∠ADB = ∠ACB [Angles in a same segment are equal]…(i)
∠ABD = ∠ACD [Angles in a same segment are equal]…(ii)
Adding (i) and (ii), we get
∠ADB + ∠ABD = ∠ACB + ∠ACD
⇒ ∠ADB + ∠ABD = ∠C
Adding ∠BAD on both sides, we get
∠ADB + ∠ABD + ∠BAD = ∠C + ∠BAD
⇒ 180° = ∠C + ∠A
[∵ Sum of angles of a ΔBAD is 180°]
∠A + ∠C = 180° …(iii)
But, we know that the sum of angles of a quadrilateral is 360°.
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠B + ∠D + 180° = 360° [using (iii)]
⇒ ∠B + ∠D = 360° – 180° = 180°
Hence, ∠A + ∠C = 180° and
∠B + ∠D = 180°. Proved

Theorem 10.12:
If the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic.
Given: A quadrilateral ABCD in which ∠A + ∠C = 180°.
To prove: ABCD is a cyclic quadrilateral.
Construction: If possible, let ABCD be not a cyclic quadrilateral. Draw a circle, passing through non-collinear points D, A, B. Let this circle meet DE or DE produced at C. Join EB.

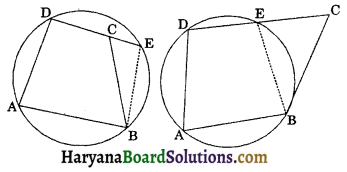
Proof: ∠A + ∠C = 180° (given) …(i)
Now ABED is a cyclic quadrilateral.
∠A + ∠E = 180° ….(ii)
[∵ opposite angles of a cyclic quadrilateral is 180°]
From (i) and (ii), we get
∠A + ∠C = ∠A + ∠E
⇒ ∠C = ∠E
This is not possible, since an exterior angle of a triangle can never be equal to its interior opposite angle.
So, ∠C = ∠E is possible only when C coincides with E.
Hence, the circle passing through D, A, B must pass through C also.
Hence, ABCD is a cyclic quadrilateral.
Proved