Haryana State Board HBSE 8th Class Maths Solutions Chapter 7 घन और घनमूल Ex 7.1 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 7 घन और घनमूल Ex 7.1
![]()
प्रश्न 1.
निम्नलिखित में से कौनसी संख्याएँ पूर्णघन नहीं है?
(i) 216
हल:
216 का अभाज्य गुणनखण्ड करने पर
216 = 6 × 6 × 6
अत: यहाँ 6 का त्रिक् बन रहा है ।
इसलिए 216 पूर्ण घन है ।
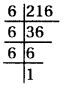
(ii) 128
हल:
28 का अभाज्य गुणनखण्ड करने पर
128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2
यहाँ, 2 का त्रिक् बनने के बाद 2 शेष रहता है ।
अतः 128 पूर्ण घन नहीं है ।
(iii) 1000
हल:
1000 का अभाज्य गुणनखंड करने पर
1000 = 10 × 10 × 10
अत: यहाँ 10 का त्रिक् बन रहा है ।
इसलिए 1000 पूर्ण घन है ।
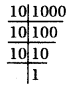
(iv) 100
हल:
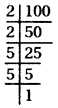
100 के अभाज्य गुणनखंड करने पर
100 = 2 × 2 × 5 × 5
यहाँ, 2, 5 का त्रिक् नहीं बन शेष रहा है ।
अतः 100 पूर्ण घन नहीं है ।

(v) 46656
हल:
46656 के अभाज्य गुणनखंड करने पर
46656 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)
यहाँ, 2, 3 का त्रिक् नहीं बन शेष रहा है ।
अतः 46656 पूर्ण घन नहीं है ।

प्रश्न 2.
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को गुणा करने पर पूर्ण घन प्राप्त हो जाए-
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
हल:
(i) 243
243 को अभाज्य गुणनखंडों के गुणनफल के रूप में लिखने पर
243 = \(\underline{3 \times 3 \times 3}\) × 3 × 3
इस गुणनखण्ड में, 3 का त्रिक नहीं हैं।
अत: 243 पूर्ण घन नहीं है ।
हमें पूर्ण घन बनाने के लिए 3 से और गुणा करना पड़ेगा ।
अत: 243 × 3 =\(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)
= 729
अतः 729 एक पूर्ण घन संख्या है ।

(ii) 256 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2 × 2
इस गुणनखण्ड में, 2 का त्रिक नहीं हैं।
अत: 256 पूर्ण घन नहीं है ।
हमें पूर्ण घन बनाने के लिए 2 से और गुणा करना पड़ेगा ।
अत: 256 पूर्ण घन नहीं है। हमें पूर्ण घन बनाने के लिए 2 से और गुणा करना पड़ेगा।
अत: 256 × 2 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
= 512
अतः 512 एक पूर्ण घन संख्या है ।

(iii) 72 = \(\underline{2 \times 2 \times 2}\) × 3 × 3
इस गुणनखण्ड में, 3 का त्रिक नहीं हैं।
पूर्ण घन बनाने के लिए एक 3 से गुणा करना पड़ेगा ।
अत: 72 × 3 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)
= 216
अतः 216 एक पूर्ण घन संख्या है ।

(iv) 675 = \(\underline{3 \times 3 \times 3}\) × 5 × 5
इस गुणनखण्ड में 5 का त्रिक नहीं है।
अत: 675 पूर्ण घन नहीं है ।
पूर्ण घन बनाने के लिए 5 से और गुणा करना पड़ेगा।
अत: 675 × 5 = 3× 3 × 3 × 5 × 5 × 5
= 3375
अत: 3375 एक पूर्ण घन संख्या है।

(v) 100 = 2 × 2 × 5 × 5
इस गुणनखण्ड में 2 तथा 5 दोनों का त्रिक नहीं है।
अत: 100 पूर्ण घन नहीं है ।
पूर्ण घन बनाने के लिए 2 तथा 5 से गुणा करना पड़ेगा।
अत: 100 × 10 = 2 × 2 × 5 × 5 × 2 × 5
= 1000
अतः 1000 पूर्ण घन संख्या है।
प्रश्न 3.
वह सबसे छोटी संख्या ज्ञात कीजिए, जिससे निम्नलिखित संख्याओं को भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाये
(i) 81
(ii) 128
(iii) 135
(iv)192
(v) 704
हल :
(i) 81 = \(\underline{3 \times 3 \times 3}\) × 3
![]()
अभाज्य गुणनखण्ड में 3 त्रिक में नहीं 3/81 आ रहा है ।
अत: 81 एक पूर्ण घन नहीं है।
अतः इसे पूर्ण घन बनाने के लिए 81 में 39 3 का भाग दें, तो भागफल के अभाज्य 33 गुणनखण्ड में 3 नहीं आयेगा ।
इस प्रकार, 81 ÷ 3 = 3 × 3 × 3 = 27
अत: वह सबसे छोटी संख्या 3 है जिससे 81 को भाग देने पर भागफल एक पूर्ण घन प्राप्त होगा ।
अत: छोटी संख्या 3 है।
(ii) 128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2

इस गुणनखण्ड में 2 का त्रिक नहीं है।
अत: 128 पूर्ण घन नहीं है ।
अत: 128 को 2 से भाग देने पर-
128 ÷ 2 = 2 × 2 × 2 × 2 × 2 × 2
= 64
अत: 2 से भाग देने पर, भागफल के अभाज्य गुणनखण्ड में 2 नहीं आयेगा ।
अत: सबसे छोटी संख्या 2 है, जिससे 128 में भाग देने पर भागफल पूर्ण घन संख्या प्राप्त होती है ।
अतः छोटी से छोटी संख्या = 2
(iii) 135 = \(\underline{3 \times 3 \times 3}\) × 5
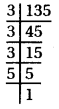
गुणनखण्ड में 5 का त्रिक नहीं है ।
अत: 5 का भाग देने पर –
135 ÷ 5 = 3 × 3 × 3
= 27
संख्या 27 एक पूर्ण घन है।
अत: छोटी से छोटी संख्या = 5
(iv) 192 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 3

गुणनखण्ड में 3 का त्रिक नहीं है ।
अत: 3 का भाग देने पर
192 ÷ 3 = 2 × 2 × 2 × 2 × 2 × 2
= 64
जो कि एक पूर्ण घन है ।
अतः छोटी से छोटी संख्या = 3
(v) 704 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 11

गुणनखण्ड में 11 का त्रिक नहीं है।
अत: 11 से भाग देने पर-
704 ÷ 11 = 2 × 2 × 2 × 2 × 2 × 2
= 64 जोकि एक पूर्ण घन संख्या है ।
अत: छोटी से छोटी संख्या = 11
प्रश्न 4.
परीक्षित प्लास्टिसिन का एक घनाभ बनाता है, जिसकी भुजाएँ 5cm, 2cm और 5cm हैं। एक घन बनाने के लिए ऐसे कितने घनाभों की आवश्यकता होगी?
हल :
माना, उसे । घनाभों की आवश्यकता होगी ।
तथा उसकी भुजाएँ = 5 cm, 2 cm तथा 5 cm हैं ।
तो घनाभ का आयतन = n × 5 × 2 ×5
अत: इसे पूर्ण घन बनाने के लिए 2 × 2 × 5 से गुणा करना पड़ेगा ।
अतः = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
अत: घन बनाने के लिए उसे (2 × 2 × 5) = 20 घनाभों की आवश्यकता होगी ।