HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण InText Questions

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण InText Questions

पृष्ठ सं. 125-126 (प्रयास कीजिए)

प्रश्न 1.
ΔABC के छः अवयवों (तीन भुजाओं तथा तीन कोणों) के नाम लिखिए।
हल :
ΔABC की तीन भुजाएँ AB, BC और CA तथा तीन कोण ∠A, ∠B और ∠C हैं।

प्रश्न 2.
लिखिए :
(i) ΔPQR के शीर्ष Q की सम्मुख भुजा
(ii) ΔLMN की भुजा LM का सम्मुख कोण
(iii) ΔRST की भुजा RT का सम्मुख शीर्ष
हल :
(i) ΔPQR के शीर्ष Q की सम्मुख भुजा RP है।
(ii) ΔLMN की भुजा LM का सम्मुख कोण = ∠N है।
(iii) ΔRST की भुजा RT का सम्मुख शीर्ष s है।

प्रश्न 3.
आकृति देखिए तथा त्रिभुजों में प्रत्येक का वर्गीकरण कीजिए:
(a) भुजाओं के आधार पर
(b) कोणों के आधार पर

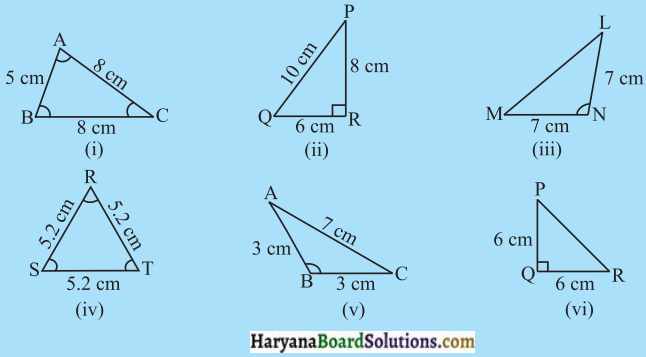
हल :
(a) भुजाओं के आधार पर वर्गीकरण
विषमबाहु त्रिभुज : (ii)
समद्विबाहु त्रिभुज : (i), (iii), (v) तथा (vi)
समबाहु त्रिभुज : (iv)

(b) कोणों के आधार पर वर्गीकरण :
न्यून कोण त्रिभुज : (i) और (iv)
समकोण त्रिभुज : (ii) और (vi)
अधिक कोण त्रिभुज : (iii) और (v)

पृष्ठ सं. 130

प्रश्न 1.
किसी त्रिभुज में एक बाह्य कोण की माप 70° है और उसके अंत: सम्मुख कोणों में से एक की माप 25° है। दूसरे अंत: सम्मुख कोण की माप ज्ञात कीजिए।
इल :

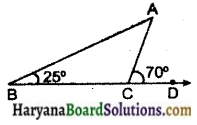
माना ΔABC की भुजा BC को आगे बढ़ाने पर बाह्य कोण ∠ACD इस प्रकार बना कि ∠ACD = 70°
माना ∠B = 25°
∴ ∠ACD = ∠B + ∠A (बाह्य कोण प्रमेय से)
70° = 25° + ∠A
∠A = 70° -25° = 45°
अत: दूसरा अन्तः सम्मुख कोण 45° का है।

प्रश्न 2.
किसी त्रिभुज के दो अंतः सम्मुख कोणों की माप 60° तथा 80° है। उसके बाल कोण की माप ज्ञात कीजिए।
हल :

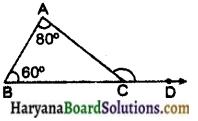
माना ΔABC की भुजा \(\overline{B C}\) को आगे बढ़ने पर एक बाहा कोण ∠ACD प्राप्त होता है।
माना ∠A = 80° और ∠B = 60°
∠ACD = ∠A + ∠B (बाह्य कोण प्रमेय से)
∠ACD = 80° + 60°
∠ACD = 140°
अतः बाह्य कोण की माप = 140°

प्रश्न 3.
क्या इस आकृति में कोई त्रुटि है। टिप्पणी करें।
हल :

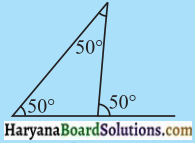
आकृति में बाह्य कोण अन्त: सम्मुख कोणों के योग के बराबर नहीं है।
50° ≠ 50° + 50°
अतः दिए गए कोण गलत हैं।

पृष्ठ सं. 134

प्रश्न 1.
एक त्रिभुज के दो कोण 30° तथा 80 हैं। इस त्रिभुज का तीसरा कोण ज्ञात कीजिए।
हल :
हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है।
माना ΔABC में ∠A = 30° और ∠B = 80° हो, तो
∠A + ∠B + ∠C = 180°
30° + 80° + ∠C = 180°
∠C = 180° – 30° – 80°
= 180° – 110° = 70°
अत: तीसरा कोण 70° होगा।

प्रश्न 2.
किसी त्रिभुज का एक कोण 80° है तथा शेष दोनों कोण बराबर हैं। बराबर कोणों में प्रत्येक की माप ज्ञात कीजिए।
हल :
माना त्रिभुज ABC में ∠A = 80° और ∠B = ∠C
∵ त्रिभुज के तीनों कोणों का योग 180° होता है।
∴ ∠A + ∠B + ∠C = 180°
⇒ 80° + ∠B + ∠B = 180°,
[∵ ∠A = 80° और ∠C = ∠B]
⇒ 80° + 2∠B = 180°
⇒ 2∠B = 180° – 80°
⇒ 2∠B = 100°
⇒ ∠B + = 50°
अत: शेष दो कोणों की माप 50° है।

प्रश्न 3.
किसी त्रिभुज के तीनों कोणों में 1 : 2 : 1 का अनुपात है। त्रिभुज के तीनों कोण जात कीजिए। त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए। हल :
माना त्रिभुज के कोण x, 2x और x है, तो
x + 2x + x = 180°
4x = 180°
x = \(\frac {180°}{4}\) = 45°
अत:त्रिभुज का पहला कोण (x) = 45°
दूसरा कोण (2x) = 2 × 45° = 90°
तीसरा कोण (x) = 45°
अत: समकोण त्रिभुज है और यह एक समद्विबाहु त्रिभुज भी है।

पृष्ठ सं. 135

प्रश्न 1.
प्रत्येक आकृति में कोण x का मान ज्ञात कीजिए


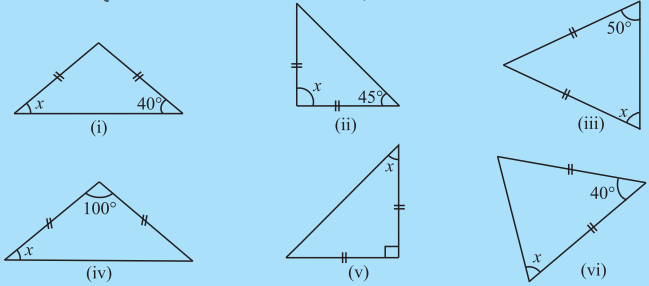
हल :
त्रिभुज (i) समद्विबाहु त्रिभुज है।
∴ ∠B = ∠C
∴ x = 40°

त्रिभुज (ii) समद्विबाहु त्रिभुज है, जिसमें
AB = BC
∠A = ∠C = 45°
कोण योग गुण से :
∠A + ∠B + ∠C = 180°
⇒ 45° + x + 45° = 180°
⇒ x = 180° – 45° – 45°
⇒ x = 90°

त्रिभुज (iii) समद्विबाहु त्रिभुज है, जिसमें
AC = AB
तथा ∠B = ∠C = 50°
∴ x = 50°

त्रिभुज (iv) समद्विबाहु त्रिभुज है, जिसमें
AC = AB
∠B = ∠C = x
कोण योग गुण से
∠A + ∠B + ∠C = 180°
⇒ 100° + x + x = 180°
⇒ 2x = 180° – 100°
⇒ 2x = 80°
⇒ x = \(\frac {80°}{2}\) = 40°

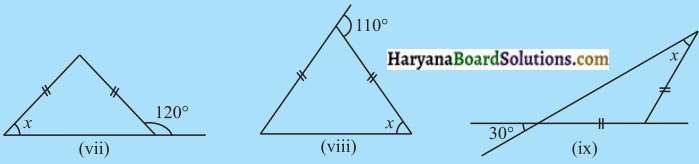
त्रिभुज (v) समद्विबाहु त्रिभुज है, जिसमें
AC = BC
तथा ∠A = ∠B = x
कोण योग गुण से
∠A + ∠B + ∠C = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° – 90°
⇒ 2x = 90°
⇒ x = \(\frac {90°}{2}\) = 45°

त्रिभुज (vi) समद्विबाहु त्रिभुज है, जिसमें
AC = BC
तथा ∠A = ∠B = x
कोण योग गुण से,
∠A + ∠B + ∠C = 180°
⇒ x + x + 40° = 180°
⇒ 2x = 180° – 40°
⇒ 2x = 140°
⇒ x = \(\frac {140°}{2}\) = 70°

त्रिभुज (vii) समद्विबाहु त्रिभुज है, जिसमें
AB = AC
∴ ∠B = ∠C
⇒ x = ∠C
क्योंकि बाह्य कोण और संलग्न अंत: कोण रैखिक युग्म बनाते हैं।
∠C + 120° = 180°
⇒ x = 180° – 120° = 60°
त्रिभुज (viii) समद्विबाहु त्रिभुज है, जिसमें
AB = AC
∴ ∠B = ∠C ⇒ ∠B = x
क्योंकि बाह्य कोण और संलग्न अंत: कोण रैखिक युग्म बनाते हैं।
110° + ∠A = 180°
∠A = 180° – 110° = 70°
कोण योग गुण से,
∠A + ∠B + ∠C = 180°
⇒ 70° + x + x = 180°
⇒ 2x = 180° – 70°
⇒ 2x = 110°
⇒ x = 55°

त्रिभुज (ix) समद्विबाहु त्रिभुज है, जिसमें
AB = AC
∠B + ∠C = x
∠B = 30°, (शीर्षाभिमुख कोण)
∴ x = 30°

प्रश्न 2.
प्रत्येक आकृति में कोण x तथा y का मा ज्ञात कीजिए।

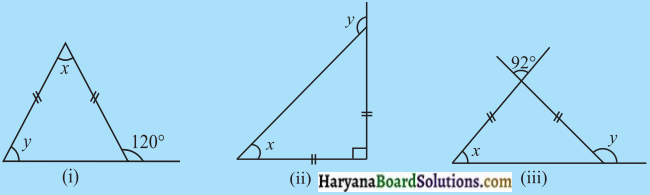
हल :
(i) अन्त: कोण ∠C + 120° = 180°
∠C = 180° – 120°
∠C = 60°
∵ ΔABC समद्विबाहु Δहै, जिसमें
AB = AC
तथा ∠B = ∠C = 60°
∴ ∠B = y = 60°
कोण योग गुण से,
∠A + ∠B + ∠C = 180°
x + 60° + 60° = 180°
x = 180° – 120°
x = 60°
अत: x = 60° और y = 60°

(ii) त्रिभुज ABC एक समद्विबाहु Δ है, जिसमें
BC = AC
∠A = ∠B = x
और ∠A + ∠B = 90°
x + x = 90°
2x = 90°
x = \(\frac {90°}{2}\)
x = 45°
लेकिन ∠B + y = 180°
x + y = 180°
45° + y = 180°
y = 180°- 45° = 135°
अतः x = 45° और y = 135°

(iii) त्रिभुज ABC समद्विबाहु त्रिभुज है, जिसमें
AB = AC
∠B = ∠C अर्थात्
∠B = ∠C = x
और ∠A = 92°, [शीर्षाभिमुख कोण]
कोण योग गुण से,
∠A + ∠B + ∠C = 180°
⇒ 92°+ x + x = 180°
⇒ 2x = 180° – 92° = 88°
⇒ x = (\(\frac {88}{2}\))° = 44°
और ∠C + y = 180°, [रैखिक युग्म]
⇒ y = 180° – 44° = 136°, [∵ ∠C = x = 44°]
अतः x = 44° और y = 136°

पृष्ठ सं. 141

प्रश्न 1.
निम्न आकृति में अज्ञात लम्बाई x ज्ञात कीजिए :

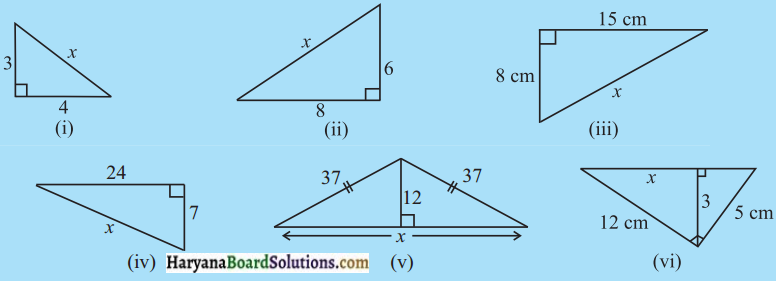
हल :
(i) ΔABC में कोण B समकोण है।
∴ पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ x² = 3² + 4²
⇒ x² = 9 + 16
⇒ x² = 25
⇒ x = \(\sqrt{25}\) = 5

(ii) ΔABC में, ∠B समकोण है।
∴ पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ x² = 8² + 6²
⇒ x² = 64 + 36
⇒ x² = 100
⇒ x = \(\sqrt{100}\) = 10

(iii) ΔABC में, ∠B समकोण है।
∴ पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ x² = 8² + 15²
⇒ x² = 64 + 225
⇒ x²= 289
⇒ x = \(\sqrt{289}\) = 17

(iv) ΔABC का ∠B समकोण है।
∴ पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ x² = 24² + 7²
⇒ x² = 576 + 49
⇒ x² = 625
⇒ x = \(\sqrt{625}\) = 25

(v) समकोण ΔALB और ΔALC में पाइथागोरस प्रमेय का प्रयोग करने पर,
ΔALB में, BL² = AB² – AL² = 37² – 12²
= (37 + 12) (37 – 12)
= 49 × 25
BL = \(\sqrt{49 \times 25}\)
BL = 7 × 5 = 35
इसी प्रकार, CL = 35
∴ BC = BL + LC = 35 + 35 = 70
∴ x = 70

(vi) समकोण त्रिभुज ALB में पाइथागोरस प्रमेय का प्रयोग करने पर,
BL² = AB² – AL²
= 12² – 3² = 144 – 9
BL² = 135
BL = \(\sqrt{135}\)
x = \(\sqrt{135}\) = 11.6 सेमी