Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 भिन्न InText Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 7 भिन्न InText Questions
पृष्ट सं. 147 से
प्रश्न 1.
भिन्न \(\frac {3}{7}\) का अंश बताइए। \(\frac {4}{15}\) का हर क्या है?
हल :
भिन्न 2 का अंश 3 है। तथा भिन्न है, का हर 15 है। उत्तर
![]()
पृष्ठ सं. 150 से
प्रश्न 1.
संख्या रेखा पर \(\frac {3}{5}\) को दर्शाइए।
हल :
हम जानते हैं कि \(\frac {3}{5}\) शून्य से बड़ा है और 1 से कम है।
∴ भिन्न \(\frac {3}{5}\), 0 और के बीच में होगी।
अब हमें \(\frac {3}{5}\) को दर्शाना है, इसलिए हम 0 और 1 के बीच की दूरी को पाँच बराबर भागों में बाँटते हैं। इसके तीसरे भाग पर बिन्दु P अंकित करते हैं।

इस प्रकार, संख्या रेखा पर बिन्दु P, \(\frac {3}{5}\) को दर्शाता है।
प्रश्न 2.
संख्या रेखा पर \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac {10}{10}\) दर्शाइए।
हल :
हम जानते हैं कि भिन्न \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac {10}{10}\) इस प्रकार हैं :
0 ≤ \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac {10}{10}\) ≤ 1
अब हमें \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac {10}{10}\) को संख्या रेखा पर दर्शाना है। इसलिए हम 0 और 1 के बीच की दूरी को 10 बराबर भागों में बाँटते हैं। इसके पहले भाग पर बिन्दु P, पाँचवें भाग पर बिन्दु Q तथा दसवें भाग पर बिन्दु A अंकित करते हैं।
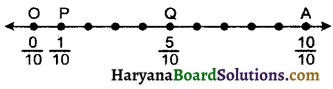
इस प्रकार बिन्दु \(\frac {1}{10}\) बिन्दु P पर, \(\frac {0}{10}\) = 0 बिन्दु O पर, \(\frac {5}{10}\) बिन्दु Q पर और \(\frac {10}{10}\) = 1 बिन्दु A पर अंकित किया। उत्तर
![]()
प्रश्न 3.
क्या आप 0 और 1 के बीच कोई अन्य भिन्न को दर्शा सकते हैं? ऐसी पाँच भिन्न और लिखिए जिन्हें आप दर्शा सकते हैं और उन्हें संख्या रेखा पर दर्शाइए।
हल :
हाँ, हम 0 और 1 के बीच अन्य भिन्न दर्शा सकते हैं। जैसे : \(\frac{1}{7}, \frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}\) इस प्रकार ये 5 भिन्न हैं जिन्हें संख्या रेखा पर बिन्दु A, B, C, D और E द्वारा दर्शाया गया है।
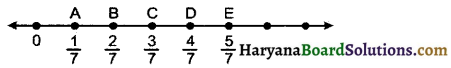
प्रश्न 4.
0 और 1 के बीच में कितनी भिन्न स्थित हैं? सोचिए, चर्चा कीजिए और अपने उत्तर को लिखिए।
हल :
0 और 1 के बीच संख्या रेखा पर अंसख्य भिन्न स्थित हैं।
पृष्ठ सं. 151 से
प्रश्न 1.
एक उचित भिन्न लिखिए :
(a) जिसका अंश 5 और हर 7 है।
(b) जिसका हर 9 और अंश 5 है।
(c) जिसके अंश और हर का योग 10 है। आप इस प्रकार की कितनी भिन्न लिख सकते हैं ?
(d) जिसका हर उसके अंश से 4 अधिक है।
(कोई पाँच भिन्न बनाइए। आप और कितनी भिन्न बना सकते हैं?)
हल :
(a) अभीष्ट भिन्न = \(\frac {5}{7}\)
(b) अभीष्ट भिन्न = \(\frac {5}{9}\)
(c) जिनके अंश और हर का योग 10 है ऐसे सम्भवतः युग्म (0, 10); (1, 9); (2, 8); (3, 7); (4, 6) हैं।
इनकी उचित भिन्न \(\frac{0}{10}, \frac{1}{9}, \frac{2}{8}, \frac{3}{7}\) और \(\frac {4}{6}\) हैं, जो कि संख्या में 5 हैं।
(d) ऐसी 5 भिन्न जिनके हर, अंश से 4 अधिक हैं :
\(\frac{0}{4}, \frac{1}{5}, \frac{2}{6}, \frac{3}{7}, \frac{4}{9}\)
अत: हम दी गई परिस्थितियों के अनुसार असंख्य भिन्न बना सकते हैं।
प्रश्न 2.
एक भिन्न दी हुई है। इसे देखकर आप कैसे बता सकते हैं कि यह भिन्न :
(a) 1 से छोटी है
(b) 1 के बराबर है ?
हल :
(a) यदि किसी भिन्न में अंश उसके हर से छोटा है, तो भिन्न 1 से छोटी है।
(b) यदि किसी भिन्न में अंश और हर बराबर हैं, तो वह भिन्न 1 के बराबर होती है।
प्रश्न 3.
संकेत ‘>’, ‘<‘ या ‘=’ का प्रयोग करके रिक्त स्थानों को भरिए।
हल :

पृष्ठ सं. 152 से (विषम भिन्न)
प्रश्न 1.
हर 7 वाली पाँच विषम भिन्न लिखिए।
हल :
पाँच विषम भिन्न जिनका हर 7 है :
\(\frac{8}{7}, \frac{9}{7}, \frac{10}{7}, \frac{11}{7}\) और \(\frac {12}{7}\) उत्तर
![]()
प्रश्न 2.
अंश 11 वाली पाँच विषम भिन्न लिखिए।
हल :
पाँच विषम भिन्न जिनका अंश 11 है :
\(\frac{11}{10}, \frac{11}{9}, \frac{11}{8}, \frac{11}{7}\) और \(\frac {11}{6}\) उत्तर
पृष्ठ सं. 155 से
प्रश्न 1.
क्या \(\frac {1}{3}\) और \(\frac {2}{7}\) तुल्य भिन्न हैं? कारण दीजिए।
हल :
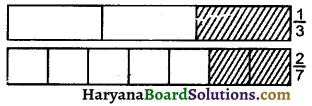
स्पष्ट रूप से, आकृतियाँ समान आकार की हैं तथा छायांकित भाग आकृति का बराबर हिस्सा नहीं दिखाता है।
इसलिए \(\frac {1}{3}\) और \(\frac {2}{7}\) तुल्य भिन्न नहीं हैं। उत्तर
प्रश्न 2.
क्या और \(\frac {2}{5}\) और \(\frac {2}{7}\) तुल्य भिन्न हैं? कारण दीजिए।
हल :

स्पष्ट रूप से, आकृतियाँ समान आकार की हैं तथा छायांकित भाग आकृति का बराबर हिस्सा नहीं है।
∴ \(\frac {2}{5}\) और \(\frac {2}{7}\) तुल्य भिन्न नहीं हैं। उत्तर
प्रश्न 3.
क्या \(\frac {2}{9}\) और \(\frac {6}{27}\) तुल्य भिन्न हैं ? कारण दीजिए।
हल:
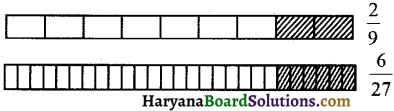
स्पष्ट रूप से, आकृतियाँ समान आकार की हैं तथा छायांकित भाग आकृति का बराबर हिस्सा दिखाता है।
∴ \(\frac {2}{9}\) और \(\frac {6}{27}\) तुल्य भिन्न हैं। उत्तर
प्रश्न 4.
चार तुल्य भिन्नों का एक अन्य उदाहरण दीजिए।
हल:

स्पष्ट रूप से, इन आकृतियों का आकार समान है और छायांकित भाग आकृतियों का बराबर हिस्सा दिखाता है।
∴ \(\frac{1}{5},\frac{2}{10}, \frac{3}{15}\) और में चारों तुल्य भिन्न हैं। उत्तर
![]()
प्रश्न 5.
प्रत्येक भिन्न को पहचानिए। क्या ये भिन्न तुल्य हैं ?
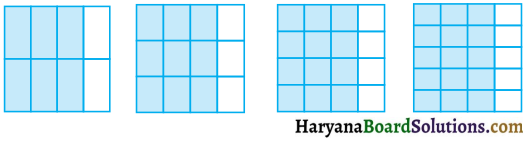
हल :
इन भिन्नों को पहचानने पर हम पाते हैं कि ये भिन्न \(\frac{6}{8}, \frac{9}{12}, \frac{12}{16}\) और \(\frac {15}{20}\) है।
स्पष्ट रूप से, इन आकृतियों का आकार समान है और छायांकित भाग आकृतियों का बराबर हिस्सा दिखाता है।
∴ \(\frac{6}{8}, \frac{9}{12}, \frac{12}{16}\) और \(\frac {15}{20}\) तुल्य भिन्न हैं। उत्तर
पृष्ठ सं. 155 से (सोचिए, चर्चा कीजिए और लिखिए)
प्रश्न 1.
तुल्य भिन्न एक पूर्ण का संमान भाग क्यों निरूपित करती है? हम इनमें से एक भिन्न को अन्य भिन्न से किस प्रकार प्राप्त कर सकते हैं?
हल :
तुल्य भिन्न एक पूर्ण के समान भाग को निरूपित करती हैं, क्योंकि इन भिन्नों के चित्रीय निरूपणों को एकदूसरे के ऊपर रखें, तो वे बराबर होंगे।
एक भिन्न से अन्य भिन्न प्राप्त करना :
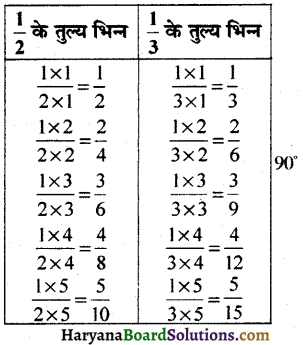
प्रश्न 2.
रजनी कहती है कि \(\frac {1}{3}\) की समतुल्य भिन्न हैं :
\(\frac{1 \times 2}{3 \times 2}=\frac{2}{6}, \frac{1 \times 3}{3 \times 3}=\frac{3}{9}, \frac{1 \times 4}{3 \times 4}=\frac{4}{12}\) और अन्य कई।
क्या आप इससे सहमत हैं? कारण सहित स्पष्ट कीजिए।
हल :
हाँ, तुल्य भिन्नों की संख्या बहुत अधिक है, क्योंकि ये दी गई भिन्न के अंश और हर को समान संख्या से गुणा करके प्राप्त की जा सकती हैं। प्राकृत संख्याएँ असीमित होती हैं। इसलिए असीमित तुल्य भिन्न बना सकते हैं। उत्तर
![]()
पृष्ठ सं. 156 से
प्रश्न 1.
निम्नलिखित में से प्रत्येक की पाँच तुल्य भिन्न ज्ञात कीजिए:
(i) \(\frac {2}{3}\)
(ii) \(\frac {1}{5}\)
(iii) \(\frac {3}{5}\)
(iv) \(\frac {5}{9}\)
हल :


पृष्ठ सं. 159 से
प्रश्न 1.
क्या आप \(\frac {9}{15}\) के तुल्य एक ऐसी भिन्न ज्ञात कर सकते हैं जिसका हर 5 हो?
हल :
हाँ, हम जानते हैं कि 15 ÷ 3 = 5 है। इसका अर्थ है कि तुल्य भिन्न प्राप्त करने के लिए, हमें दी हुई भिन्न के अंश व हर में 3 से भाग देना होगा।
इस प्रकार, \(\frac{9}{15}=\frac{9 \div 3}{15 \div 3}=\frac{3}{5}\)
अतः वांछित तुल्य भिन्न \(\frac {3}{5}\) है। उत्तर
![]()
प्रश्न 2.
निम्न को सरलतम रूप में लिखिए :
(i) \(\frac {15}{75}\)
(ii) \(\frac {16}{72}\)
(iii) \(\frac {17}{51}\)
(iv) \(\frac {42}{28}\)
(v) \(\frac {80}{24}\)
हल :
(i) \(\frac {15}{75}\) को सरलतम रूप में लिखने के लिए, 15 और 75 का महत्तम समापवर्तक निकालते हैं।
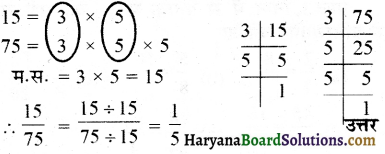
(ii) \(\frac {16}{72}\) का सरलतम रूप लिखने के लिए, 16 और 72 का म.स. निकालते हैं :
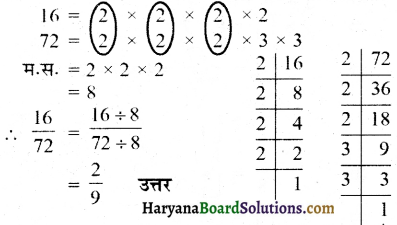
(iii) \(\frac {17}{51}\) का सरलतम रूप लिखने के लिए, 17 और 51 का म.स. निकालते हैं।

(iv) \(\frac {42}{28}\) का सरलतम रूप लिखने के लिए, 42 और 28 का म.स. निकालते हैं :
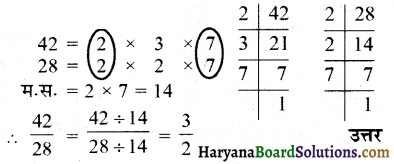
(v) \(\frac {80}{24}\) का सरलतम रूप लिखने के लिए, 80 और 24 का म.स. निकालते हैं।

प्रश्न 2.
क्या \(\frac {169}{289}\) अपने सरलतम रूप में है ?
हल :
169 और 289 का म.स. निकालने पर,
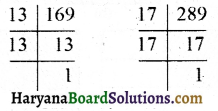
169 = 13 × 13
∴ 289 = 17 × 17
और म.स. = 1
अतः \(\frac {169}{289}\) अपने सरलतम रूप में है। उत्तर
पृष्ठ स. 161 से (समान भिन्न)
प्रश्न समान भिन्नों के पाँच युग्म और असमान भिन्नों के पाँच युग्म लिखिए।
हल :
समान भिन्नों के पाँच युग्म \(\frac{2}{37}, \frac{5}{37}, \frac{7}{37}, \frac{9}{37}, \frac{11}{37}\) है।
असमान भिलों के पाँच युग्म \(\frac{2}{9}, \frac{2}{11}, \frac{2}{17}, \frac{2}{19}, \frac{2}{23}\) है। उत्तर
![]()
पृष्ठ सं. 161 से
प्रश्न 1.
आप जूस की बोतल का \(\frac {1}{5}\) वाँ भाग प्राप्त करते हैं और आपकी बहिन को उस बोतल का एक-तिहाई भाग मिलता है। किसको अधिक जूस मिलता है ?
हल :

अतः \(\frac {1}{5}\) और \(\frac {1}{3}\) के अंश समान हैं। इसलिए भिन्न जिसका हर छोटा हो, वह बड़ी भिन्न होगी। इस प्रकार बहिन को ज्यादा जूस मिलता है। उत्तर
पृष्ठ सं. 162 से
प्रश्न 1.
कौन-सी भिन्न बड़ी है ?
(i) \(\frac {7}{10}\) या \(\frac {8}{10}\)
(ii) \(\frac {11}{24}\) या \(\frac {13}{24}\)
(iii) \(\frac {17}{102}\) या \(\frac {12}{102}\)
ऐसी भिन्नों की तुलना करना क्यों सरल है ?
हल :
हम जानते हैं कि समान हरों वाली दो भिन्नों में, बड़े अंश वाली भिन्न बड़ी होती है।
दी गई भिन्न हैं:
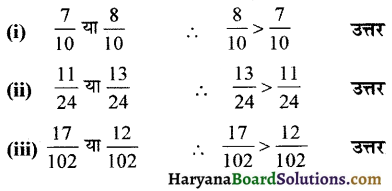
ऐसी भिन्नों की तुलना करना सरल है, क्योंकि इन स्थितियों में केवल अशों की तुलना की गई है।
![]()
प्रश्न 2.
निम्न को आरोही क्रम में लिखिए और साथ ही अवरोही क्रम में भी लिखिए :
(a) \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)
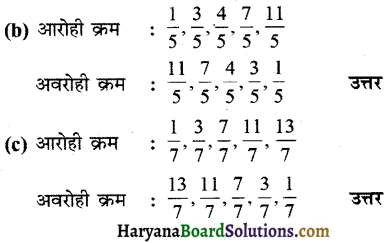
(b) \(\frac{1}{5}, \frac{11}{5}, \frac{4}{5}, \frac{3}{5}, \frac{7}{5}\)
(c) \(\frac{1}{7}, \frac{3}{7}, \frac{13}{7}, \frac{11}{7}, \frac{7}{7}\)
हल :
हम जानते हैं कि वे भिन्न जिनके हर समान हों तथा अंश का मान जितना बड़ा होगा, उस भिन्न का मान उतना ही बड़ा होगा।

पृष्ठ सं. 164 से
प्रश्न 1.
निम्नलिखित भिन्नों को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए :
(a) \(\frac{1}{12}, \frac{1}{23}, \frac{1}{5}, \frac{1}{7}, \frac{1}{50}, \frac{1}{9}, \frac{1}{17}\)
(b) \(\frac{3}{7}, \frac{3}{11}, \frac{3}{5}, \frac{3}{2}, \frac{3}{13}, \frac{3}{4}, \frac{3}{17}\)
(c) उपर्युक्त प्रकार के तीन और उदाहरण लिखिए तथा उन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
हल :
हम जानते हैं कि वे भिन्न जिनका अंश समान हो, परन्तु हर जितना बड़ा होगा, वह भिन्न उतनी ही छोटी होगी।

अब इन्हें आरोही तथा अवरोही क्रम में निम्न प्रकार लिख सकते हैं :

पृष्ठ सं. 168 से
प्रश्न 1.
मेरी माँ ने एक सेब को चार बराबर भागों में बाँटा। उन्होंने मुझे 2 भाग और मेरे भाई को एक भाग दिया। उन्होंने हम दोनों को कुल सेब का कितना भाग दिया?
हल :
उक्त प्रश्न को सेब की आकृति बनाकर स्पष्ट रूप से समझा सकते हैं:
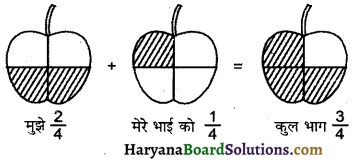
अर्थात् \(\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\)
अतः उन्होंने हम दोनों को कुल सेब का \(\frac {3}{4}\) भाग दिया।
![]()
प्रश्न 2.
माँ ने नीलू और उसके भाई से गेहूँ में से कंकड़ बीनने के लिए कहा। नीलू ने कुल कंकड़ों के \(\frac {1}{4}\) कंकड़ बीने और उसके भाई ने भी कुल कंकड़ों के \(\frac {1}{4}\) कंकड़ बीने। दोनों ने मिलकर कुल कंकड़ों की कितनी भिन्न बीनी ?
हल :
नीलू ने गेहूँ में से कुल कंकड़ों के \(\frac {1}{4}\) भाग बीने और उसके भाई ने भी \(\frac {1}{4}\) भाग बीने।
दोनों ने मिलकर कुल कंकड़ बीने
= \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) भाग। उत्तर
प्रश्न 3.
सोहन अपनी अभ्यास पुस्तिका पर कवर चढ़ा रहा था। उसने सोमवार को \(\frac {1}{4}\) भाग पर कवर चढ्न लिया। मंगलवार को उसने अन्य \(\frac {1}{4}\) भाग पर कवर चढ़ा लिया और शेष बुधवार को। बुधवार को उसने कवर का कौन सा भाग चढ़ाया ?
हल :
सोहन ने सोमवार को कवर चढ़ाया = \(\frac {1}{4}\) भाग
और मंगलवार को कवर चढ़ाया = \(\frac {1}{4}\) भाग
शेष भाग जिस पर बुधवार को कवर चढ़ाना है :
= 1 – (\(\frac{1}{4}+\frac{1}{4}\)) = 1 – (\(\frac{1+1}{4}\))
= 1 – \(\frac{2}{4}=\frac{4-2}{4}=\frac{2}{4}=\frac{1}{2}\) भाग पर। उत्तर
पृष्ठ सं. 170 से
प्रश्न 1.
आकृतियों की सहायता से जोड़िए :
(i) \(\frac{1}{8}+\frac{1}{8}\)
(ii) \(\frac{2}{5}+\frac{3}{5}\)
(iii) \(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}\)
हल :
(i) एक 2 × 4 विमाओं वाला कागज लेते हैं। इसमें लम्बाई के अनुदिश 2 खाने तथा चौड़ाई के अनुदिश 4 खाने बनाते हैं जिसमें एक खाने को क्षैतिज तथा दूसरे खाने को ऊर्ध्वाधर रूप में छायांकित करते हैं।

आकृति को देखने पर, \(\frac{1}{8}+\frac{1}{8}=\frac{2}{8}=\frac{1}{4}\) उत्तर
(ii) एक कागज लेते हैं जिसमें लम्बाई के अनुदिश बराबर-बराबर के पाँच खाने बनाते हैं। इनमें से दो खानों को छायांकित करके 3 खानों को ऊर्ध्वाधर छायांकित करते हैं।

आकृति को देखने पर, \(\frac{2}{5}+\frac{3}{5}=\frac{5}{5}\) = 1 उत्तर
(iii) 4 × 3 का एक कागज लेकर उसमें 12 खाने बनाते हैं जिसमें से एक खाने को दो बार, एक खाने को क्षैतिज रूप में और एक खाने को ऊध्याधर छायांकित करते हैं।
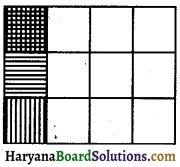
आकृति को देखने पर, \(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{12}=\frac{1}{4}\) उत्तर
![]()
प्रश्न 2.
\(\frac{1}{12}+\frac{1}{12}\) को जोड़ने पर हम क्या प्राप्त करते हैं?
आप चित्र रूप में इसे कैसे दर्शा सकते हो? कागज मोड़ने की क्रिया द्वारा कैसे दर्शाया जा सकता है?
हल:

\(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{2}{6}\) उत्तर
चित्र द्वारा दर्शाना –
4 × 3 विमाओं वाला एक कागज लेकर उसमें 12 खाने बनाते हैं जिसमें से एक खाने को क्षैतिज रूप में और एक खाने को ऊर्ध्वाधर रूप में छायांकित करते हैं। आकृति को देखने पर
\(\frac{1}{12}+\frac{1}{12}=\frac{2}{12}=\frac{1}{6}\) उत्तर
कागज मोड़ने की क्रिया द्वारा दर्शाना –

एक आयताकार कागज लेकर उसे लम्बाई के अनुदिश तीन बार मोड़ते हैं तथा चौड़ाई के अनुदिश चार बार मोड़ते हैं। अब कागज को खोलते है इस प्रकार कागज में 12 खाने बन जाते है (चित्र के अनुसार)। अब एक खाने को क्षैतिक रूप में और एक खाने को ऊर्ध्वाधर रूप में छायांकित करते हैं। कागज को देखने पर,
\(\frac{1}{12}+\frac{1}{12}=\frac{2}{12}=\frac{1}{6}\) उत्तर
प्रश्न 3.
\(\frac {7}{8}\) और \(\frac {3}{8}\) का अन्तर ज्ञात कीजिए।
हल :
\(\frac{7}{8}-\frac{3}{8}=\frac{7-3}{8}=\frac{4}{8}=\frac{1}{2}\) उत्तर
प्रश्न 4.
माँ ने एक गुड़ की पट्टी गोल आकृति में बनाई। उसने उसे बराबर भागों में विभाजित किया। सीमा ने उसमें से एक टुकड़ा खा लिया। यदि मैं एक अन्य टुकड़ा खा लूँ, तो कितनी गुड़ की पट्टी शेष रहेगी ?
हल :
माँ द्वारा गोल आकार में गुड़ की पट्टी को 5 बराबर भागों में विभाजित करने पर प्रत्येक भाग = \(\frac {1}{5}\)
सीमा ने खाया = \(\frac {1}{5}\) भाग
मेरे द्वारा खाया गया = \(\frac {1}{5}\) भाग
गुड़ की पट्टी का शेष भाग = \(\frac{1}{1}-\left(\frac{1}{5}+\frac{1}{5}\right)\)
\(\frac{5-1-1}{5}=\frac{5-2}{5}=\frac{3}{5}\) भाग उत्तर
![]()
प्रश्न 5.
मेरी बड़ी बहिन ने एक तरबूज को 16 बराबर भागों में विभाजित किया। मैंने इसके 7 टुकड़े खा लिए। मेरे मित्र ने 4 टुकड़े खाए। हमने मिलकर कुल कितना तरबूज खाया? मैंने अपने मित्र से कितना अधिक तरबूज खाया? कितना तरबूज शेष रह गया ?
हल :
एक तरबूज को मेरी बहिन ने 16 भागों में विभाजित किया।
∴ प्रत्येक भाग = \(\frac {1}{16}\)
मेरे द्वारा तरबूज खाया गया = \(\frac {7}{16}\) भाग
मेरे मित्र द्वारा खाया गया = \(\frac {4}{16}\) भाग
हम दोनों द्वारा खाया गया तरबूज का भाग
= \(\frac{7}{16}+\frac{4}{16}=\frac{7+4}{16}=\frac{11}{16}\) उत्तर
मेरे द्वारा खाया गया अधिक भाग
= \(\frac{7}{16}-\frac{4}{16}=\frac{7-4}{16}=\frac{3}{16}\) उत्तर
बचा हुआ तरबूज = 1 – (\(\frac{7}{16}+\frac{4}{16}\))
= \(\frac{16-(7+4)}{16}=\frac{16-11}{16}=\frac{5}{16}\) भाग। उत्तर
पृष्ठ सं. 173 से
प्रश्न 1.
\(\frac {2}{5}\) और \(\frac {3}{7}\) को जोड़िए।
हल :
पहला तरीका : \(\frac{2}{5}+\frac{3}{7}\)
5 और 7 का लघुतम समापवर्त्य = 5 × 7 = 35
अब, हर 5 और 7 को 35 में बदलते हैं :

![]()
प्रश्न 2.
\(\frac {5}{7}\) में से \(\frac {2}{5}\) को घटाइए।
हल :
पहला तरीका : \(\frac {5}{7}\) – \(\frac {2}{5}\)
7 और 5 का ल.स. = 7 × 5 = 35.
अब, हर 7 और 5 को 35 में बदलते हैं :
