Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 भिन्न Ex 7.3 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 7 भिन्न Exercise 7.3
प्रश्न 1.
प्रत्येक चित्र में छायांकित भागों के लिए भिन्न लिखिए। क्या ये सभी भिन्न तुल्य है?
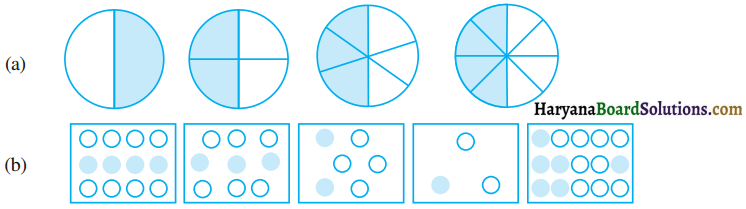
हल :

![]()
प्रश्न 2.
छायांकित भागों के लिए भिन्नों को लिखिए और प्रत्येक पंक्ति में से तुल्य भिन्नों को चुनिए :
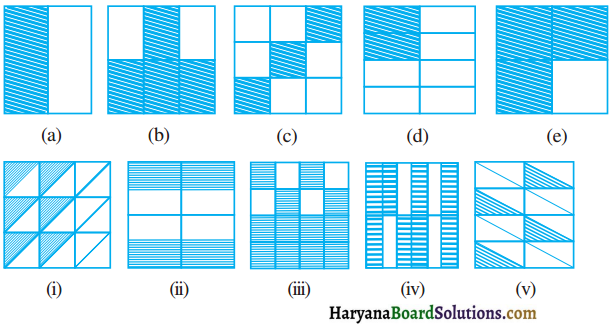
हूल :
दिये गए चित्रों में छायांकित भागों के लिए भिन्न निम्न हैं:
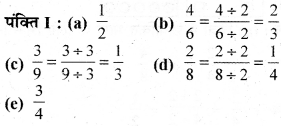

पंक्ति I और पंक्ति II में तुल्य भिन्नों के जोड़े : (a) → (ii), (b) → (iv), (c) → (i), (d) → (v) और (e) → (iii).
प्रश्न 3.
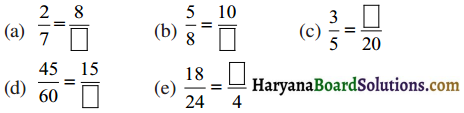
हूल :


![]()
प्रश्न 4.
के तुल्य वह भिन्न ज्ञात कीजिए, जिसका :
(a) हर 20 है,
(b) अंश 9 है,
(e) हर 30 है
(d) अंश 27 है।
हल :
(a) ∵ 20 ÷ 5 =4
∴ हर को 20 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 4 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 4}{5 \times 4}=\frac{12}{20}\) उत्तर
(b) ∵ 9 ÷ 3 = 3
∴ अंश को 9 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 3 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\) उत्तर
(c) ∵ 30 ÷ 5 = 6
हर को 30 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश व हर में 6 से गुणा करने पर, \(\frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}\) उत्तर
(d) ∵ 27 ÷ 3 = 9
अंश को 27 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 9 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 9}{5 \times 9}=\frac{27}{45}\) उत्तर
प्रश्न 5.
\(\frac {36}{48}\) के तुल्य वह भिन्न ज्ञात कीजिए, जिसका :
(a) अंश 9 है
(b) हर 4 है।
हल :
(a) ∵ 36 ÷ 9 = 4
∴ अंश को 9 बनाने के लिए भिन्न \(\frac {36}{48}\) के अंश और हर में 4 से भाग करते हैं :
\(\frac{36}{48}=\frac{36 \div 4}{48 \div 4}=\frac{9}{12}\) उत्तर
(b) ∵ 48 ÷ 4 = 12
∴ हर को 4 बनाने के लिए भिन्न \(\frac {36}{48}\) के अंश और हर में 12 से भाग करते हैं:
\(\frac{36}{48}=\frac{36 \div 12}{48 \div 12}=\frac{3}{4}\) उत्तर
![]()
प्रश्न 6.
जाँच कीजिए कि निम्न भिन्न तुल्य हैं या नहीं :
(a) \(\frac {5}{9}\), \(\frac {30}{54}\)
(b) \(\frac {3}{10}\), \(\frac {12}{50}\)
(c) \(\frac {7}{13}\), \(\frac {5}{11}\)
हल :
(a)

तिर्यक गुणा करने पर
5 × 54 = 270 और 9 × 30 = 270
∵ 270 = 270
∴ दोनों भिन्न तुल्य हैं। उत्तर
(b)
![]()
तिर्यक गुणा करने पर
3 × 50 = 150 और 12 × 10 = 120
150 ≠ 120
अतः \(\frac {3}{10}\) और \(\frac {12}{50}\) तुल्य भिन्न नहीं हैं। उत्तर
(c)

तिर्यक गुणा करने पर
7 × 11 = 77 और 13 × 5 = 65
⇒ 77 ≠ 65
\(\frac {7}{13}\) और \(\frac {5}{11}\) तुल्य भिन्न नहीं हैं। उत्तर
प्रश्न 7.
निम्नलिखित भिन्नों को उनके सरलतम रूप में बदलिए:
(a) \(\frac {48}{60}\)
(b) \(\frac {150}{60}\)
(c) \(\frac {84}{98}\)
(d) \(\frac {12}{52}\)
(e) \(\frac {7}{28}\)
हल :
(a) \(\frac {48}{60}\) को सरलतम रूप में लिखने के लिए पहले इम 48 और 60 का म.स. निकालते हैं:
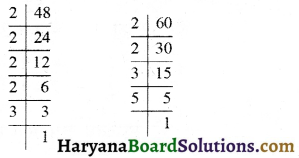
∴ 48 = 2 × 2 × 2 × 2 × 3, 60 = 2 × 2 × 3 × 5
∴ 48 और 60 का म.स. = 2 × 2 × 3 = 12
48 48+12 4 अतः 60-60+12
अतः \(\frac{48}{60}=\frac{48 \div 12}{60 \div 12}=\frac{4}{5}\) उत्तर
(b) \(\frac {150}{60}\) को सरलतम रूप में लिखने के लिए पहले हम 150 और 60 का म.स. निकालते हैं :
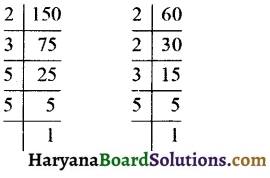
∴ 150 = 2 × 3 × 5 × 5
और 60 = 2 × 2 × 3 × 5
∴ 150 और 60 का म.स. = 2 × 3 × 5 = 30
\(\frac{150}{60}=\frac{150+30}{60 \div 30}=\frac{5}{2}\) उत्तर
(c) \(\frac {84}{98}\) को सरलतम रूप में लिखने के लिए पहले हम 84 और 98 का म.स. निकालते हैं:
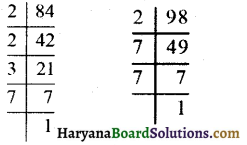
∴ 84 = 2 × 2 × 3 × 7 और 98 = 2 × 7 × 7
∴ 84 और 98 का म.स. = 2 × 7 = 14
अतः \(\frac{84}{98}=\frac{84 \div 14}{98 \div 14}=\frac{6}{7}\) उत्तर
(d) \(\frac {12}{52}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 12 और 52 का म.स. निकालते हैं :
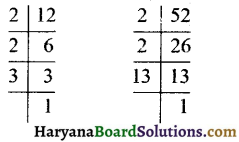
∴ 12 = 2 × 2 × 3 और 52 = 2 × 2 × 13
∴ 12 और 52 का म.स. = 2 × 2 = 4
अत: \(\frac{12}{52}=\frac{12 \div 4}{52 \div 4}=\frac{3}{13}\) उत्तर
(e) \(\frac {7}{28}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 7 और 28 का म.स. निकालते हैं:

7 = 1 × 7 और 28 = 2 × 2 × 7
∴ 7 और 28 का स.स. = 7
अतः \(\frac{7}{28}=\frac{7 \div 7}{28 \div 7}=\frac{1}{4}\) उत्तर
प्रश्न 8.
रमेश के पास 20 पेंसिल थीं। शीलू के पास 50 पेंसिल और जमाल के पास 80 पेंसिल थीं। 4 महीने के बाद रमेश ने 10 पेंसिल प्रयोग कर ली,शीलू ने 25 पेंसिल प्रयोग कर ली और जमाल ने 40 पेंसिल प्रयोग कर लीं। प्रत्येक ने अपनी पेंसिलों की कौन-सी भिन्न प्रयोग कर ली? जाँच कीजिए कि प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग की है।
हल :
रमेश, शीलू और जमाल द्वारा प्रयोग की जाने वाली पेंसिलों के भाग क्रमशः
\(\frac {10}{20}\), \(\frac {25}{50}\) और \(\frac {40}{80}\) हैं।
यहाँ \(\frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\)
\(\frac{25}{50}=\frac{25 \div 25}{50 \div 25}=\frac{1}{2}\)
\(\frac{40}{80}=\frac{40 \div 40}{80 \div 40}=\frac{1}{2}\)
ये सभी भिन्न बराबर हैं, अतः प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग में है। उत्तर
![]()
प्रश्न 9.
तुल्य भिन्नों का मिलान कीजिए और प्रत्येक के लिए दो भिन्न और लिखिए :

हल :
(i) \(\frac {250}{400}\) को सरलतम रूप में लिखने के लिए पहले हम 250 और 400 का म.स. निकालते हैं :
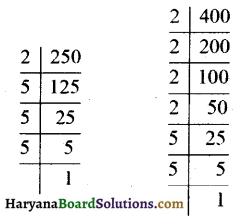
∴ 250 = 2 × 5 × 5 × 5
और 400 = 2 × 2 × 2 × 2 × 5 × 5
∴ म.स. = 2 × 5 × 5 = 50
\(\frac{250}{400}=\frac{250 \div 50}{400 \div 50}=\frac{5}{8}\)
∴ (i) का मिलान (d) से होगा। उत्तर
दो अन्य तुल्य भिन्न
\(\frac{5 \times 2}{8 \times 2}=\frac{10}{16}\) और \(\frac{5 \times 3}{8 \times 3}=\frac{15}{24}\) उत्तर
(ii) \(\frac {180}{200}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 180 और 200 का म.स. निकालते हैं :
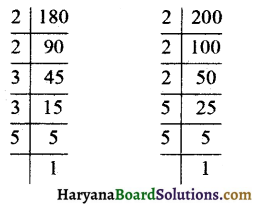
∴ 180 = 2 × 2 × 3 × 3 × 5
और 200 = 2 × 2 × 2 × 5 × 5
∴ 180 और 200 का म.स. = 2 × 2 × 5 = 20
\(\frac{180}{200}=\frac{180 \div 20}{200 \div 20}=\frac{9}{10}\)
अत: (ii) का मिलान (e) से होगा। उत्तर
दो अन्य तुल्य भिन्न:
\(\frac{9 \times 2}{10 \times 2}=\frac{18}{20}\) और \(\frac{9 \times 3}{10 \times 3}=\frac{27}{30}\) उत्तर
(iii) \(\frac {660}{990}\) को सरलतम रूप में लिखने के लिए पहले हम 660 और 990 का म.स. निकालते हैं
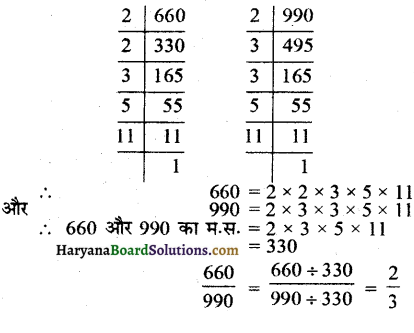
अत: (iii) का मिलान (a) से होगा।
दो अन्य तुल्य भिन्न : \(\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\) और \(\frac{2 \times 3}{3 \times 3}=\frac{6}{9}\) उत्तर
(iv) \(\frac {180}{360}\) को सरलतम रूप में लिखने के लिए पहले हम 180 और 360 का म.स. निकालते हैं :
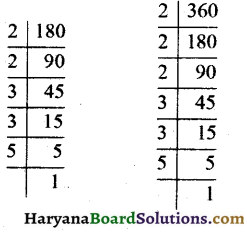
∴ 180 = 2 × 2 × 3 × 3 × 5
360 = 2 × 2 × 2 × 3 × 3 × 5
∴ अभीष्ट म.स. = 2 × 2 × 3 × 3 × 5 = 180
\(\frac{180}{360}=\frac{180 \div 180}{360 \div 180}=\frac{1}{2}\)
अत: (iv) का मिलान (c) से होगा। उत्तर
दो अन्य तुल्य भिन्न :
\(\frac{1 \times 2}{2 \times 2}=\frac{2}{4}\) और \(\frac{1 \times 3}{2 \times 3}=\frac{3}{6}\) उत्तर
(v) \(\frac {220}{550}\) को सरलतम रूप में लिखने के लिए पहले हम 220 और 550 का म.स. निकालते हैं :

अतः (v) का मिलान (b) से होगा। उत्तर
दो अन्य तुल्य भिन्न:
\(\frac{2 \times 2}{5 \times 2}=\frac{4}{10}\) और \(\frac{2 \times 3}{5 \times 3}=\frac{6}{15}\) उत्तर