HBSE 6th Class Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.5

Haryana State Board HBSE 6th Class Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Exercise 14.5

प्रश्न 1.
7.3 सेमी लंबाई का एक रेखाखंड \(\overline{A B}\) खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
हल :
रचना के पद :

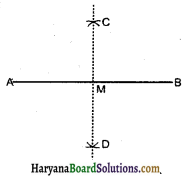
(1) रेखाखंड AB = 7.3 सेमी खींची।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी लेकर AB के दोनों ओर एक-एक चाप लगाया।
(3) अब B को केन्द्र मानकर उसी दूरी को लेकर AB के दोनों ओर चाप लगाया जो पहले वाले चापों को C तथा D पर काटते हैं।
(4) CD को मिलाया। CD, रेखाखंड AB को M पर काटता है। बिन्दु M रेखाखंड AB को समद्विभाजित करता है।
इस प्रकार प्राप्त रेखाखंड CD सममित अक्ष है।

प्रश्न 2.
9.5 सेमी लंबा एक रेखाखंड खींचिए और उसका लंब समद्विभाजक खींचिए।
हल :
रचना के पद :

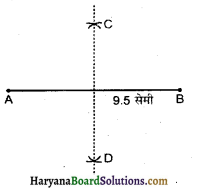
(I) एक रेखाखण्ड AB = 9.5 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी की त्रिज्या लेकर AB के दोनों ओर चाप लगाया।
(3) B को केन्द्र मानकर इसी त्रिज्या का AB के दोनों ओर चाप लगाया जो पहले चापों को C व D पर काटते हैं।
(4) CD को मिलाया। रेखाखण्ड CD रेखाखण्ड AB का लम्ब समद्विभाजक है।

प्रश्न 3.
एक रेखाखंड \(\overline{X Y}\) का लम्ब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
(a) इस लंब समद्विभाजक पर कोई बिन्दु P लीजिए। जाँच कीजिए कि PX = PY है।
(b) यदि M रेखाखंड \(\overline{X Y}\) का मध्य बिन्दु है, तो MX और XY के विषय में आप क्या कह सकते हैं ?
हल :
रचना के पद :

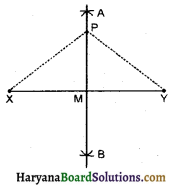
(1) रेखाखण्ड XY = 10.3 सेमी खींचा।
(2) X को केन्द्र मानकर XY के आधे से अधिक दूरी की त्रिज्या लेकर XY के दोनों ओर चाप लगाया।
(3) इसी प्रकार Y को केन्द्र मानकर इसी त्रिज्या वाली दूरी से चाप लगाया जो पहले चापों को A व B पर काटता है।
(4) AB को मिलाया, जो XY को M पर काटता है। अत: AB XY का लम्ब समद्विभाजक है।
(a) AB पर कोई बिन्दु P लिया। मापने पर, PX = PY.
(b) M, रेखाखण्ड XY का मध्य बिन्दु है।
अत: MX = \(\frac{1}{2}\)XY
= \(\frac{1}{2}\) × 10.3 = 5.15 सेमी।

प्रश्न 4.
लम्बाई 12.8 सेमी वाला एक रेखाखण्ड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कीजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
रचना के पद :

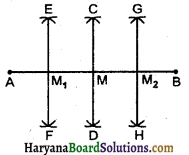
(1) रेखाखंड AB = 12.8 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी लेकर AB के दोनों ओर चाप लगाया।
(3) अब B को केन्द्र मानकर पहले वाली चाप से AB के दोनों ओर चाप लगाया, जो पहले वाले चापों को C तथा D पर काटते हैं।
(4) CD को मिलाया, जो AB को M पर काटती है।
(5) इस विधि से AM और AB के मध्य बिन्दु क्रमशः M₁ और M₂ प्राप्त होते हैं।
∴ AM₁ = M₁M = MM₂ = M₂B। इनको मापने पर प्रत्येक 3.2 सेमी प्राप्त होती है।

प्रश्न 5.
6.1 सेमी लंबाई का एक रेखाखंड \(\overline{P Q}\) खींचिए और फिर \(\overline{P Q}\) को व्यास मानकर एक वृत्त खींचिए।
हल :
रचना के पद :

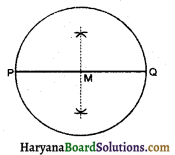
(1) रूलर की सहायता से PQ रेखाखण्ड 6.1 सेमी खींचा।
(2) रेखाखण्ड PQ का लम्ब समद्विभाजक खींचा जो PQ को M बिन्दु पर काटता है।
(3) M के केन्ड मान कर MP त्रिज्या का परकार में चाप लेकर वृत्त खींचते हैं। इस प्रकार प्राप्त वृत्त वांछित वृत्त है।

प्रश्न 6.
केन्द्र और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा \(\overline{A B}\) खींचिए। इस जीवा \(\overline{A B}\) का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केन्द्र C से होकर जाता है।
हल :
रचना के पद :

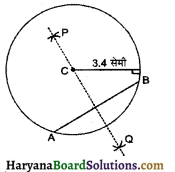
(1) कागज पर कोई बिन्दु C अंकित किया।
(2) C को केन्द्र मानकर 3.4 सेमी त्रिज्या का एक वृत्त खींचा।
(3) वृत्त के अन्दर एक जीवा AB खींची।
(4) जीवा AB का लम्ब समद्विभाजक PQ खींचा।
स्पष्ट है कि लम्ब समद्विभाजक वृत्त के केन्द्र C से होकर जाता है।

प्रश्न 7.
प्रश्न 6 को उस स्थिति के लिए दोबारा कीजिए जब \(\overline{A B}\) एक व्यास है।
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु C अंकित किया।
(2) C का केन्ड मानकर 3.4 सेमी त्रिज्या का एक वृत्त खींचा।
(3) वृत्त के अन्दर एक व्यास AB खींचा।
(4) व्यास AB का समद्विभाजक PQ खींचा।
स्पष्ट है कि लम्ब समद्विभाजक वृत्त के केन्ड C से होकर जाता है। मापने पर बिन्दु C, व्यास AB का मध्य बिन्दु है।

प्रश्न 8.
4 सेमी त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जीवाओं के लंब समद्विभाजक खींचिए। ये कहाँ मिलते हैं ?
हल :
रचना के पद:

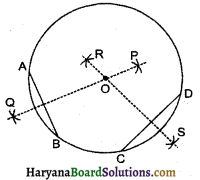
(1) कागज पर कोई बिन्दु O अंकित किया।
(2) O को केन्द्रः A मानकर 4 सेमी त्रिज्या का एक वृत्त खींचा।
(3) वृत्त के अन्दर AB व CD दो जीवाएँ खींची।
(4) जीवा AB और CD के क्रमशः लम्ब समद्विभाजक PQ और RS खींचे।
स्पष्ट है कि ये लम्ब समद्विभाजक वृत्त के केन्द्र बिन्दु O पर मिलते हैं।

प्रश्न 9.
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिन्दु A और दूसरी भुजा पर एक अन्य बिन्दु B इस प्रकार लीजिए कि 0A = OB है। \(\overline{O A}\) और \(\overline{O B}\) के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिच्छेद करते हैं। क्या PA = PB है ?
हल :
रचना के पद :

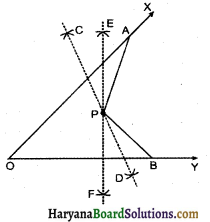
(1) कोई कोण XOY खींचते हैं।
(2) एक बिन्दु A, OX पर तथा एक बिन्दु B, OY पर इस प्रकार लेते हैं कि
OA = OB.
(3) OA तथा OB के लम्ब समद्विभाजक क्रमशः CD और EF परस्पर P बिन्दु पर काटते हैं।
मापने पर ज्ञात होता है कि PA = PB.