HBSE 11th Class Physics Important Questions Chapter 9 ठोसों के यांत्रिक गुण

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 9 ठोसों के यांत्रिक गुण Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 9 ठोसों के यांत्रिक गुण

वस्तुनिष्ठ प्रश्न (Multiple Choice Questions)

प्रश्न 1.
प्रत्यास्थता का विमीय सूत्र है-
(a) [MLT^-2]
(b) [ML²T^-2]
(c) [ML^-1T^-2]
(d) [M^-1L^-1T^-2]
उत्तर:
(b) [ML²T^-2]

प्रश्न 2.
यंग प्रत्यास्थता गुणांक का सही सूत्र है-
(a) \(\mathrm{Y}=\frac{\mathrm{Mg} \Delta \mathrm{L}}{\pi r^2 \mathrm{~L}}\)
(b) \(\mathrm{Y}=\frac{\mathrm{Mg}}{\pi r^2 \mathrm{~L}}\)
(c) \(\mathrm{Y}=\frac{\mathrm{MgL}}{\pi r^2 \Delta \mathrm{L}}\)
(d) \(\mathrm{Y}=\frac{\mathrm{Mgr^2}}{\pi \mathrm{L} \dot \Delta \mathrm{L}}\)
उत्तर:
(b) \(\mathrm{Y}=\frac{\mathrm{Mg}}{\pi r^2 \mathrm{~L}}\)

प्रश्न 3.
निम्न में से सबसे अधिक प्रत्यास्थ पदार्थ है-
(a) स्टील
(b) क्वार्ट्ज
(c) काँच
(d) रबर ।
उत्तर:
(b) क्वार्ट्ज

प्रश्न 4.
पदार्थ का प्रत्यास्थता गुणांक ताप बढ़ाने पर –
(a) बढ़ता है
(b) घटता है
(c) निर्भर नहीं करता घटने लगता है।
(d) एक सीमा तक बढ़ता है फिर
उत्तर:
(b) घटता है

प्रश्न 5.
जब तार को संपीडित किया जाये तो उसके अणुओं की स्थितिज ऊर्जा-
(a) घटती है
(b) बढ़ती है
(c) अपरिवर्तित रहती है
(d) निश्चित नहीं ।
उत्तर:
(b) बढ़ती है

प्रश्न 6.
वे ठोस, जो प्रत्यास्थता सीमा के आगे टूट जाते हैं, कहलाते
(a) तन्य
(b) आघातवर्धनीय
(c) भंगुर
(d) प्रत्यास्थ
उत्तर:
(c) भंगुर

प्रश्न 7.
दो अणुओं के मध्य अन्तर- आण्विक बल-
(a) सदा आकर्षण का बल होता है।
(b) सदा प्रतिकर्षण का बल होता है।
(c) अधिक दूरी पर नगण्य उससे कम दूरी पर आकर्षण व बहुत कम दूरी पर प्रतिकर्षण बल हो जाता है
(d) अधिक दूरी पर प्रतिकर्षण बल होता है व कम दूरी पर आकर्षण बल होता है।
उत्तर:
(c) अधिक दूरी पर नगण्य उससे कम दूरी पर आकर्षण व बहुत कम दूरी पर प्रतिकर्षण बल हो जाता है

प्रश्न 8.
रबर स्टील, काँच को प्रत्यास्थता के बढ़ते हुए क्रम में लिखने पर सही क्रम होगा-
(a) स्टील, रबर, काँच
(b) रवर, काँच, स्टील
(c) काँच, स्टील, रबर
(d) काँच, रबर स्टील ।
उत्तर:
(b) रवर, काँच, स्टील

प्रश्न 9.
किसी खिंचे हुए तार की प्रति एकांक आयतन की स्थितिज ऊर्जा होती है-
(a) \(\frac{1}{2}\) × प्रतिबल x विकृति
(b) \(\frac{1}{2}\) \(\frac{\text { प्रतिबल }}{\text { विकृति }}\)
(c) \(\frac{1}{2}\) × बंग प्रत्यास्थता गुणांक × विकृति
(d) \(\frac{1}{2}\) × बंग प्रत्यास्थता गुणांक × विकृति ।
उत्तर:
(c) \(\frac{1}{2}\) × बंग प्रत्यास्थता गुणांक × विकृति

प्रश्न 10.
एक ही पदार्थ तथा समान परिच्छेद क्षेत्रफल के दो तारों को लम्बाइयाँ 1 व 21 हैं। इन्हें लम्बाई के अनुदिश समान बल F लगाकर खींचा जाता है। तारों में उत्पन्न तनावों का अनुपात होगा-
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 4 : 1.
उत्तर:
(a) 1 : 1

प्रश्न 11.
एक ही पदार्थ के दो तारों पर जिनकी लम्बाईयाँ क्रमश: L तथा 2L और त्रिज्याएँ क्रमश: 2r तथा r हैं, समान भार लटकाया गया है। तारों की लम्बाई में वृद्धि का अनुपात होगा-
(a) 1 : 4
(b) 1 : 8
(c) 4 : 1
(d) 8 : 1.
उत्तर:
(b) 1 : 8

प्रश्न 12.
एक तार से Mg भार लटकाने पर, तार की लम्बाई में वृद्धि l हो जाती है। इस प्रक्रिया में कृत कार्य होगा-
(a) Mgl
(b) 2mgl
(c) \(\frac{Mgl}{2}\)
(d) शून्य ।
उत्तर:
(c) \(\frac{Mgl}{2}\)

प्रश्न 13.
यदि किसी तार को खींचकर उसकी लम्बाई दोगुनी कर दी जाये, तो इसका यंग प्रत्यास्थता गुणांक होगा-
(a) आधा
(b) अपरिवर्तित
(c) दोगुना
(d) चार गुना।
उत्तर:
(b) अपरिवर्तित

प्रश्न 14.
एक आदर्श दृढ़ पिण्ड के लिए यंग प्रत्यास्थता गुणांक का मान-
(a) शून्य
(b) अनन्त
(c) 1
(d) 100.
उत्तर:
(b) अनन्त

प्रश्न 15.
अनुप्रस्थ काट क्षेत्रफल A व लम्बाई L का एक तार एक दृढ़ आधार से लटका है जिस पर M भार आरोपित है। इसकी लम्बाई में वृद्धि –
(a) L के व्युत्क्रमानुपाती होती है
(b) M के समानुपाती होती है
(c) यंग प्रत्यास्थता के समानुपाती होती है
(d) A के समानुपाती होती है।
उत्तर:
(b) M के समानुपाती होती है

प्रश्न 16.
रबर स्टील, काँच की प्रत्यास्थता के घटते क्रम में सही क्रम है-
(a) स्टील, रबर, काँच
(b) रबर, काँच, स्टील
(c) स्टील, काँच, रबर
(d) काँच, रबर, स्टील।
उत्तर:
(c) स्टील, काँच, रबर

प्रश्न 17.
किसी पदार्थ का यंग प्रत्यास्थता गुणांक उस प्रतिबल के बराबर है, जो-
(a) तार की लम्बाई दोगुनी कर दें
(b) तार की लम्बाई अपरिवर्तित रहे
(c) तार की लम्बाई 50% बढ़ा दें
(d) तार की लम्बाई 25% बढ़ा दें।
उत्तर:
(a) तार की लम्बाई दोगुनी कर दें

अतिलघुत्तरात्मक प्रश्न (Very Short Answer Questions)

प्रश्न 1.
प्रतिबल का मात्रक लिखिए।
उत्तर:
प्रतिबल = \(\frac{F}{A}\)
प्रतिबल का मात्रक = \(\frac{N}{m^2}\) = Nm^-2.

प्रश्न 2.
वह गुण जिससे बाह्य बल हटा लिए जाने पर वस्तु अपने प्रारम्भिक स्वरूप को प्राप्त कर लेती है, क्या कहलाता है ?
उत्तर:
प्रत्यास्थता ।

प्रश्न 3.
प्रत्यास्थता सीमा में प्रतिबल एवं विकृति का अनुपात क्या कहलाता है ?
उत्तर:
प्रत्यास्थता गुणांक ।

प्रश्न 4.
अनुप्रस्थ विकृति एवं अनुदैर्घ्य विकृति का अनुपात क्या कहलाता है ?
उत्तर:
पॉयसन अनुपात ।

प्रश्न 5.
यंग प्रत्यास्थता गुणांक का मात्रक लिखो ।
उत्तर:
न्यूटन / मी² या पॉस्कल ।

प्रश्न 6.
किसी द्रव का अपरूपण व बंग गुणांक कितना होता है?
उत्तर:
दोनों शून्य होते हैं।

प्रश्न 7.
किसी ठोस के यंग प्रत्यास्थता गुणांक पर ताप वृद्धि का क्या प्रभाव पड़ेगा?
उत्तर:
ताप वृद्धि के साथ यंग प्रत्यास्थता गुणांक का मान घटता है।

प्रश्न 8.
मशीनों को घूर्णी गति देने के लिए शाफ्ट कैसी होनी चाहिए?
उत्तर:
खोखली तथा छोटी ताकि बलयुग्म अधिक उत्पन्न हो सके।

प्रश्न 9.
प्रतिबल तथा विकृति के बीच खिंचे ग्राफ का ढलान क्या प्रदर्शित करता है?
उत्तर:
प्रत्यास्थता गुणांक ।

प्रश्न 10.
एक पूर्ण दृढ़ पिण्ड का दृढ़ता गुणांक कितना होता है?
उत्तर:
अनन्त (00)।

प्रश्न 11.
जब एक ठोस को दबाया जाता है, तो उसके अणुओं की स्थितिज ऊर्जा पर क्या प्रभाव पड़ता है? यदि ठोस खींचा जाये, तब ?
उत्तर:
दोनों स्थितियों में स्थितिज ऊर्जा बढ़ती है।

प्रश्न 12.
ठोस, द्रव तथा गैस में से किसकी संपीड्यता सबसे अधिक होती है ?
उत्तर:
गैस ।

प्रश्न 13.
क्या प्रतिबल सदिश राशि है ?
उत्तर:
नहीं।

प्रश्न 14.
सुग्राही उपकरणों में निलम्बन तार प्रायः क्वार्ट्ज या फॉस्कर ब्रॉन्ज के ही क्यों बनाये जाते हैं ?
उत्तर:
क्योंकि इन दोनों में प्रत्यास्थ उत्तर प्रभाव नगण्य होता है।

प्रश्न 15.
भंजन प्रतिबल किस पर निर्भर करता है ?
उत्तर:
तार के पदार्थ पर।

प्रश्न 16.
गर्डर की आकृति के रूप में बनाने का क्या कारण है ?
उत्तर:
भार के कारण अवनमन कम से कम हो।

प्रश्न 17.
आयतन प्रत्यास्थता गुणांक के व्युत्क्रम को क्या कहते हैं?
उत्तर:
संपीड्यता ।

प्रश्न 18.
सर्वाधिक प्रबल अन्तर- परमाण्विक बल कौन-सा है ?
उत्तर:
आयनी आबन्ध

प्रश्न 19.
अन्तर- आण्विक व अन्तर- परमाण्विक बल किस प्रकृति के होते हैं ?
उत्तर:
वैद्युत् चुम्बकीय प्रकृति के

प्रश्न 20.
किसी ठोस को संपीडित करने पर परमाणुओं की स्थितिज ऊर्जा बढ़ेगी या घटेगी ?
उत्तर:
बढ़ेगी।

प्रश्न 21.
वे वस्तुएँ क्या कहलाती हैं जो अपना प्रारम्भिक आकार प्राप्त करने की प्रवृत्ति नहीं होती है और स्थायी रूप से विकृत हो जाते हैं ?
उत्तर:
सुघट्य या प्लास्टिक ।

प्रश्न 22.
जब प्रतिबल शून्य होने पर भी विकृति शून्य नहीं होती तब द्रव्य में स्थायी विरूपण हो जाता है। ऐसे विरूपण को क्या कहते हैं ?
उत्तर:
प्लास्टिक विरूपण ।

प्रश्न 23.
प्रत्यास्थालक (इलास्टोमर्स) के दो उदाहरण लिखो ।
उत्तर:
महाधमनी व रबड़ ।

प्रश्न 24.
किसी प्रारूपिक चट्टान की प्रत्यास्थता सीमा कितनी होती है ?
उत्तर:
30 × 10⁷ Nm^-2

प्रश्न 25.
दृढ़ता गुणांक का विमीय सूत्र क्या है ?
उत्तर:
[M¹L^-1T^-2],

प्रश्न 26.
अन्तर- परमाण्विक बल किसे कहते हैं ?
उत्तर:
विभिन्न परमाणुओं के मध्य लगने वाले बलों को अन्तर- परमाण्विक बल कहते हैं।

प्रश्न 27.
मशीनों को घूर्णी गति देने के लिए शॉफ्ट कैसी होनी चाहिए ?
उत्तर:
खोखली तथा छोटी ताकि अधिक बलयुग्म संचरित हो सके।

प्रश्न 28.
यंग प्रत्यास्थता गुणांक Y तथा अनुदैर्घ्य विकृति a के पदों में खिंचे तार के एकांक आयतन की प्रत्यास्थ स्थितिज ऊर्जा का सूत्र लिखिए।
उत्तर:
U= \(\frac{1}{2}\)Yσ²

प्रश्न 29.
जब किसी तार को खींचते हैं तो हमें कार्य क्यों करना पड़ता है ?
उत्तर:
आन्तरिक प्रतिक्रिया बलों के विरुद्ध कार्य करना पड़ता है।

प्रश्न 30.
विकृति की विमा लिखिए।
उत्तर:
विकृति विमाहीन राशि है।

प्रश्न 31.
क्या द्रवों में दृढ़ता का गुण पाया जाता है ?
उत्तर:
नहीं, द्रवों में दृढ़ता का गुण नहीं पाया जाता है, क्योंकि द्रवों की कोई आकृति नहीं होती है।

लघु उत्तरीय प्रश्न (Short Answer Questions)

तो
प्रश्न 1.
प्रत्यानयन बल क्या होते हैं ?
उत्तर:
जब विकृतकारी बल के प्रभाव में कोई वस्तु विकृत होती है। वस्तु के अन्दर प्रतिक्रियात्मक बल उत्पन्न होते हैं जो विकृतकारी का विरोध करते हैं और इन्हीं बलों के कारण बाध्य बल हटाने पर वस्तु अपनी प्रारम्भिक अवस्था में आ जाती है। इसीलिए इन बलों को प्रत्यानयन बल (Restoring Forces) कहते हैं।

प्रश्न 2.
प्रतिबल किसे कहते हैं ?
उत्तर:
वस्तु के अनुप्रस्थ काट के एकांक क्षेत्रफल पर लगने वाले प्रत्यानयन बल को प्रतिबल कहते हैं। अतः
प्रतिबल = \(\frac{\text { प्रत्यानयन बल }}{\text { क्षेत्रफल }}=\frac{F}{A}\)
∴ प्रतिबल का मात्रक – N/m².

प्रश्न 3.
प्रत्यास्थता की सीमा से क्या अभिप्राय है ?
उत्तर:
विकृतकारी बल की वह सीमा जहाँ तक वस्तु पूर्ण प्रत्यास्थ रहती है ओर इससे अधिक बल लगाने पर वस्तु में स्थायी विकृति उत्पन्न हो जाती है, प्रत्यास्थता सीमा कहलाती है।

प्रश्न 4.
यदि हाथी दाँत तथा गीली मिट्टी की एक जैसी ठोस गोलियाँ एक ही ऊँचाई से फर्श पर गिरायी जाती हैं तो फर्श से टकराने के बाद कौन सी गोली अधिक ऊँचाई तक उठेगी और क्यों ?
उत्तर:
यदि विभिन्न पदार्थों से बनी दो ठोस गोलियाँ फर्श पर एक ही ऊँचाई से गिरायी जायें तो अधिक ऊँचाई तक उठने वाली गोली अधिक प्रत्यास्थ होगी। हाथी दाँत की प्रत्यास्थता गीली मिट्टी से अधिक है, अतः हाथी दाँत की गोली अधिक ऊँचाई तक उठेगी।

प्रश्न 5.
साइकिल खोखले पाइप की क्यों बनायी जाती है ?
उत्तर:
यदि बेलनाकार छड़ है तो उसके अवनमन का सूत्र होता है-
\(\delta=\frac{\mathrm{W} l^3}{12 \mathrm{Y} \pi \mathrm{R}^4}\)
जहाँ R छड़ के काट की त्रिज्या है।
उपर्युक्त सूत्र से स्पष्ट है कि समान द्रव्यमान की खोखली बेलनाकार छड़ ठोस छड़ से अधिक मजबूत होगी क्योंकि उसी द्रव्यमान की खोखली छड़ की त्रिज्या अधिक होगी। यही कारण है कि साइकिलों में ठोस छड़ की अपेक्षा खोखला पाइप प्रयोग करते हैं जिससे पाइप की सामर्थ्य भी बढ़े तथा धातु की बचत होने पर कम खर्च आये ।

प्रश्न 6.
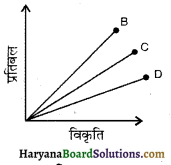
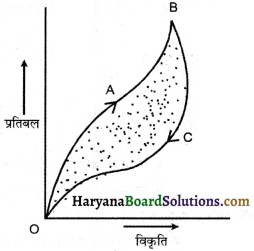
पीतल, स्टील व रबर के प्रतिबल – विकृति वक्र चित्र में प्रदर्शित हैं।
रेखा A, B और C क्रमशः किन-किन वक़ों पर प्रदर्शित करती हैं?

उत्तर:
प्रदर्शित ग्राफ में-
वक्र का ढलान = \(\frac{\text { y-अक्ष }}{\text { x-अक्ष }}=\frac{\text { प्रतिबल }}{\text { विकृति }}\) = यंग प्रत्यास्थता गुणांक
θ_A > θ_B > θ_C
अत: Y_A > Y_B > Y_C (ग्राफ द्वारा)
लेकिन तालिका से Y_खुर < Y_पीतल < Y_{स्टील}
वक्र A = स्टील = 20 × 10¹⁰ M/m²
वक्र B = पीतल = 9 × 10¹⁰ M/m²
वक्र C = रबर = 0.05 × 10¹⁰ M/m²

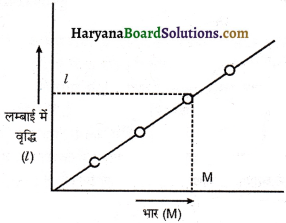
प्रश्न 7.
चित्रानुसार ग्राफ तार की लम्बाई के व्यवहार को, तार के पदार्थ के लिए उस क्षेत्र को प्रदर्शित करता है जहाँ हुक के नियम का पालन होता है। A तथा B क्या प्रदर्शित करते हैं?

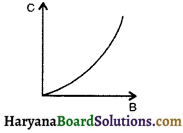
उत्तर:
प्रत्यास्थता की सीमा के अन्दर
प्रतिबल ∝ विकृति (हुक के नियम से)
ग्राफ की प्रकृति = एक सरल रेखा
जो ग्राफ में प्रदर्शित नहीं है।
तार में संचित ऊर्जा के लिए-
U = \(\frac{1}{2}\)kx² या U ∝ x²
ग्राफ की प्रकृति = परवलयाकार
जो ग्राफ में प्रदर्शित है।
अत: A तथा B, ऊर्जा तथा लम्बाई में वृद्धि को प्रदर्शित करते हैं।

प्रश्न 8.
छोटी खोखली शाफ्ट लम्बी ठोस शाफ्ट से अधिक मजबूत होती है, क्यों?
उत्तर:
शाफ्ट एक ऐसी बेलनाकार छड़ है जो अन्य मशीनों को घूर्णन गति प्रदान करने में प्रयोग की जाती है। यदि शाफ्ट का एक सिरा दृढ़ता से कसकर दूसरे सिरे पर मरोड़ देने वाला बल लगायें तब छड़ में अपरूपण विकृति उत्पन्न हो जायेगी किसी ऐंठन कोण θ के लिए लगाये जाने वाले बल आघूर्ण का मान निम्न होता है-
\(\tau=\frac{\eta \pi r^4 \theta}{2 l}\)
जहाँ l = लम्बाई, r = शाफ्ट की त्रिज्या तथा η = शाफ्ट के पदार्थ का अपरूपण गुणांक है।
ठोस शाफ्ट में एकांक ऐंठन उत्पन्न करने के लिए आवश्यक बलयुग्म आघूर्ण –

अर्थात् समान द्रव्यमान व पदार्थ की खोखली व ठोस शाफ्टों में, खोखली शाफ्ट को ऐंठने में ठोस शाफ्ट को ऐंठने की अपेक्षा अधिक कार्य करना होगा, अतः छोटी खोखली शाफ्ट लम्बी ठोस शाफ्ट से अधिक मजबूत होती है।

प्रश्न 9.
रेल की पटरी आकार की क्यों बनाई जाती है?
उत्तर:
रेल की पटरी के ऊपरी तथा नीचे के भागों में अधिक विकृति उत्पन्न होती है, जबकि बीच के भाग में कम विकृति होती है, इस कारण से ऊपरी व निचले भागों का क्षेत्रफल अधिक रखा जाता है जिससे कि इन भागों पर अभिलम्ब प्रतिबल (PA) कम लगे। बीच के भागों की विकृति कम होने के कारण ये भाग कम चौड़ाई के बनाए जाते हैं। इससे लोहे की भी बचत होती है तथा पटरी की मजबूती भी उसी प्रकार की बनी रहती है।

प्रश्न 10.
L लम्बाई तथा A परिच्छेद क्षेत्रफल वाले एक ऊर्ध्वाधर तार के निचले सिरे से M द्रव्यमान का एक गोला लटकाया जाता है। यदि तार का यंग प्रत्यास्थता गुणांक ४ हो तो ऊर्ध्वाधर तल में पिण्ड के दोलन करने की आवृत्ति ज्ञात कीजिए।
उत्तर:
माना किसी तार में खिंचाव हैं तथा तार में प्रत्यानयन बल F है-
सूत्र-

प्रश्न 11.
त्रिज्या की तार दो बिन्दुओं A व B के बीच बंधी है। सामान्य अवस्था में इसमें तनाव नहीं है। जब इसे खींचकर ACB के रूप का कर दिया जाता है तो तार में कितना तनाव है?

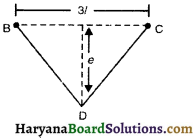
उत्तर:
प्रारम्भिक लम्बाई AB = 2l

प्रश्न 12.
विभिन्न पदार्थों के तीन तारों के लिए प्रतिबल – विकृति ग्राफ चित्र में प्रदर्शित हैं A,B व C तारों की प्रत्यास्थता की सीमाएँ हैं। चित्र से A, B C के बारे में क्या निष्कर्ष निकलते हैं?

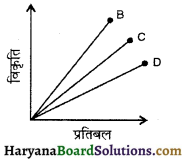
उत्तर:
ग्राफ में प्रतिबल, X- अक्ष व विकृति Y-अक्ष पर प्रदर्शित है,
अतः ग्राफ से, Y = cot θ = \(\frac{1}{tan θ}\) ∝ \(\frac{1}{θ}\)
[जहाँ θ = प्रतिबल अक्ष से कोण है]
अर्थात् A की प्रत्यास्थता न्यूनतम व की अधिकतम है।

प्रश्न 13.
जब किसी तार को (i) खींचा जाता है तथा (ii) सम्पीडित किया जाता है तो प्रत्यानयन प्रतिबल किस कारण उत्पन्न होता है?
उत्तर:
जब किसी तार को खींचा जाता है तो अन्तर- परमाण्विक आकर्षण बलों के कारण प्रत्यानयन प्रतिबल उत्पन्न होता है तथा जब तार को सम्पीडित किया जाता है तो अन्तरपरमाण्विक प्रतिकर्षण के कारण प्रत्यानयन प्रतिबल उत्पन्न होता है।

प्रश्न 14,
यंग प्रत्यास्थता गुणांक का मात्रक प्राप्त कीजिए। पीतल का बंग प्रत्यास्थता गुणांक लोहे से आधा है, पीतल के एक तार की लम्बाई लोहे के एक अन्य तार की लम्बाई के बराबर है। दोनों तारों पर एक-सा प्रतिबल लगा है। इन दोनों तारों की लम्बाई में वृद्धि के अनुपात की गणना कीजिए।
उत्तर:
Y का मात्रक = \(\frac{\text { प्रतिबल का मात्रक }}{\text { विकृति का मात्रक }}\)
= न्यूटन / मीर²
किसी पदार्थ का यंग प्रत्यास्थता गुणांक

प्रश्न 15.
समान पदार्थ के चार तारों (P, Q, R व S) के भारों का उनकी लम्बाई वृद्धि के साथ ग्राफ प्रदर्शित है। अधिकतम मोटाई का तार किस रेखा द्वारा प्रदर्शित होगा ?
उत्तर:
यंग प्रत्यास्थता गुणांक
Y = \(\frac{FL}{Al}\) ∴ l ∝ \(\frac{F}{A}\)
(∵ Y, L व F नियत हैं)
ग्राफ से स्पष्ट है कि समान भार के लिए न्यूनतम लम्बाई वृद्धि OS से प्रदर्शित है,

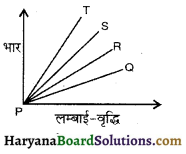
∵ लम्बाई वृद्धि (l) न्यूनतम होने पर अनुप्रस्थ काट का क्षेत्रफल A अधिकतम है।
अतः अधिकतम मोटाई का तार OS से प्रदर्शित है।

प्रश्न 16.
इस्पात तथा तांबे की समान आकारों की स्प्रिंगों को समान वृद्धि तक खींचा जाता है किस पर अधिक कार्य करना पड़ेगा ?
उत्तर:
इस्पात का यंग प्रत्यास्थता गुणांक (Y) ताँबे की तुलना में अधिक होता है अतः यदि स्प्रिंगें समान प्रकार की हैं (A. L बराबर हैं) तो बराबर-बराबर खींचने ( वृद्धि x) के लिए इस्पात की स्प्रिंग पर अधिक कार्य करना पड़ेगा।
चूँकि W = \(\frac{1}{2}\) \(\frac{YA}{L}\)x² ∴ W ∝ Y

प्रश्न 17.
यदि इन्हीं स्प्रिंगों को बराबर बल लगाकर खींचा जाये तब ?
उत्तर:
इस्पात की स्प्रिंग कम खिंचेगी। अतः अब की बार ताँबे की स्प्रिंग पर अधिक कार्य करना पड़ेगा।

प्रश्न 18.
पॉयसन अनुपात क्या होता है ?
उत्तर:
प्रत्यास्थता की सीमा के अन्दर अनुप्रस्थ (पार्श्व) विकृति एवं अनुदैर्घ्य विकृति का अनुपात पदार्थ का पॉयसन अनुपात कहलाता है। इसे σ से व्यक्त करते हैं।
पॉयसन अनुपात σ = \(\frac{\text { पार्श्व विकृति}}{\text { अनुदैर्ध्य विकृति }}\)

प्रश्न 19.
हुक का नियम लिखिए।
उत्तर:
प्रत्यास्थता सीमा के अन्दर, प्रतिबल विकृति के समानुपाती होता है।
अर्थात् प्रतिवल ∝ विकृति

प्रश्न 20.
स्प्रिंगें इसपात की ही क्यों बनायी जाती हैं ?
उत्तर:
इस्पात का यंग प्रत्यास्थता गुणांक अन्य धातुओं जैसे- ताँबा, ऐल्यूमिनियम आदि से अधिक होता है इसीलिए स्प्रिंगें इस्पात की बनायी जाती है ताकि बाहरी बल हटाने पर स्प्रिंग शीघ्र अपनी पूर्वावस्था में आ जाये।

प्रश्न 21.
हम तार को बार-बार मोड़कर उसे तोड़ने में सफल क्यों हो जाते हैं ?
उत्तर:
जब किसी पदार्थ को बार बार विकृत किया जाता है तो पदार्थ का प्रत्यास्थ गुण तेजी से घटने लगता है, इसी को प्रत्यास्थता श्रांति कहते हैं। इसलिए तार को बार-बार मोड़कर हम उसे तोड़ने में सफल हो जाते हैं।

प्रश्न 22.
अनुदैर्घ्य विकृति तथा अनुदैर्घ्य प्रतिबल को परिभाषित कीजिए।
उत्तर:
अनुदैर्घ्य विकृति : लम्बाई में परिवर्तन तथा आरम्भिक लम्बाई के अनुपात को अनुदैर्ध्य विकृति कहते हैं। तनन प्रतिबल के कारण, तार या छड़ की प्रारम्भिक लम्बाई L में ∆L वृद्धि हो तो,
अनुदैर्घ्य विकृति = \(\frac{∆L}{L}\)
अनुदैर्घ्य प्रतिबल : जब किसी तार पर बल आरोपित किया जाये तो वस्तु के प्रति एकांक काट क्षेत्र पर उत्पन्न प्रत्यानयन बल को अनुदैर्घ्य प्रतिबल कहते हैं।
अनुदैर्घ्यं प्रतिबल = \(\frac{F}{A}\)

प्रश्न 23.
पूर्ण प्रत्यास्थ, प्लास्टिक एवं दृढ़ पिण्ड किन्हें कहते हैं ? इनकी सीमाओं का उल्लेख कीजिए।
उत्तर:
जो वस्तुएँ विरूपक बल हटाने से अपनी पूर्व अवस्था में लौट आती है। उन्हें पूर्ण प्रत्यास्थ कहते हैं जैसे- क्वार्ट्ज, फॉस्फर ब्रांज ।
जो वस्तुएँ विरूपक बल हटाने पर अपनी पूर्व अवस्था में नहीं लौटती हैं, बल्कि सदैव के लिए विरूपित हो जाती हैं, उन्हें प्लास्टिक या पूर्ण सुघट्य कहते हैं; जैसे – मोम, गीली मिट्टी।
यदि किसी पदार्थ में अणु या परमाणुओं के मध्य दूरी निश्चित हो एवं बाह्य बल के प्रभाव में भी अपरिवर्तित हो तो वह दृढ़ पिण्ड कहलाता है।

दीर्घ उत्तरीय प्रश्न (Long Answer Questions)

प्रश्न 1.
यंग प्रत्यास्थता गुणांक को परिभाषित कीजिए। यंग प्रत्यास्थता गुणांक ज्ञात करने की सल की विधि का वर्णन कीजिए।
उत्तर:
यंग प्रत्यास्थता गुणांक (Young’s Modulus of Elasticity):
“प्रत्यास्थता सीमा में अनुदैर्घ्य प्रतिबल एवं अनुदैर्घ्य विकृति के अनुपात को यंग प्रत्यास्थता गुणांक कहते हैं।” इसे Y से व्यक्त करते हैं।
यंग प्रत्यास्थता गुणांक \(Y=\frac{\text { अनुदैर्घ्य प्रतिबल }}{\text { अनुद्र्घ्य विकृति }}=\frac{\sigma}{\varepsilon}\)
यदि L लम्बाई एवं A अनुप्रस्थ परिच्छेद के तार पर F बल लगाने पर उसकी लम्बाई में वृद्धि $\Delta \mathrm{L}$ हो जाती है तो
अनुदुर्घ्य प्रतिबल \(\sigma=\frac{\mathrm{F}}{\mathrm{A}}\)
तथा अनुदैर्घ्य विकृति \(\varepsilon=\frac{\Delta \mathrm{L}}{\mathrm{L}}\)
\(\mathrm{Y}=\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}\)
या \(\mathrm{Y}=\frac{\mathrm{F} \cdot \mathrm{L}}{\Delta \mathrm{L} \cdot \mathrm{A}}\)
यंग प्रत्यास्थता गुणांक का मात्रक न्यूटन / मीटर² \(\left(\mathrm{~N}-\mathrm{m}^{-2}\right)\) या पॉस्कल (Pa) तथा विमीय सूत्र \(\left[\mathrm{M}^1 \mathrm{~L}^{-1} \cdot \mathrm{T}^{-2}\right]\) है। यंग प्रत्यास्थता गुणांक Y केवल ठोस पदार्थों के लिए ही होता है।

यदि तार के परिच्छेद की त्रिज्या r तथा Mg भार लटकाकर विरूपक बल लगाया गया हो तो
\(\mathrm{Y}=\frac{\mathrm{MgL}}{\pi r^2 \Delta \mathrm{L}}\)
यदि तार का अनुप्रस्थ काट क्षेत्रफल \(\mathrm{A}=\pi r^2=1 \mathrm{~m}^2\) तथा लम्बाई में वृद्धि ∆L = L हो तो Y = F
“अर्थात् किसी पदार्थ का यंग प्रत्यास्थता गुणांक उस बल के तुल्य होता है जो प्रत्यास्थता सीमा के अन्दर उस पदार्थ के एकांक अनुप्रस्थ परिच्छेद के तार की लम्बाई को दोगुना कर दे।”

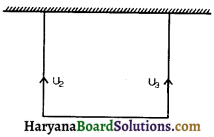
किसी तार के पदार्थ का यंग गुणांक का मापन (Measurement of Young’s Modulus of Elasticity of Material of a Wire):
किसी तार के पदार्थ का यंग प्रत्यास्थता गुणांक ज्ञात करने की सर्ल विधि (Searl Method) के लिए प्रयुक्त उपकरण चित्र में दर्शाया है।

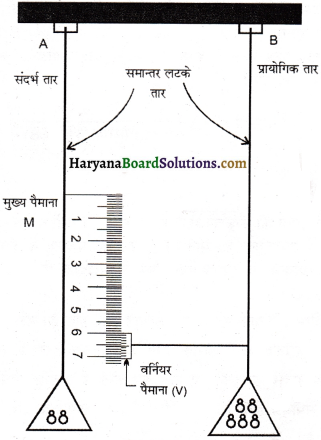
इसमें समान लम्बाई एवं समान त्रिज्या के दो ऊर्ध्वाधर पास-पास दृढ़ आधार से लटके होते हैं। इनमें तार A को सन्दर्भ तार (Reference wire) कहते हैं। इस निचले सिरे पर मिलीमीटर में अंकित प्रधान स्केल (Main Scale) M लगी होती है और एक स्थिर भार लटकाया जाता है, ताकि तार तना रहकर अपनी मूल लम्बाई में रहे। दूसरा तार B प्रायोगिक तार (Experimental Wire) होता है। जिसके निचले सिरे पर एक वर्नियर स्केल V लगी होती है जिसका सम्बन्ध मुख्य स्केल से रहता है और तार पर भार लटकाने के लिए एक हैंगर लगा होता है।

स्क्रूगेज की सहायता से तार B का व्यास कई स्थानों पर ज्ञात करके उसका औसत लेकर तार की त्रिज्या r ज्ञात कर लेते हैं। मीटर स्केल की सहायता से इस तार की प्रारम्भिक लम्बाई L ज्ञात कर लेते हैं। अब लम्बाई में वृद्धि ∆L ज्ञात करने के लिए मुख्य स्केल का पाठ पहले ज्ञात कर लेते हैं। इसके पश्चात् तार B के हैंगर पर क्रमशः वजन रखकर वर्नियर स्केल की सहायता से विभिन्न भारों के लिए लम्बाई में वृद्धि के मान ज्ञात कर लेते हैं। लम्बाई में वृद्धि एवं आरोपित भार के साथ ग्राफ खींचते हैं जो चित्र की भाँति सरल रेखा प्राप्त होती है। ग्राफीय रेखा के किसी एक बिन्दु के संगत M व ∆l के मान नोट कर लेते हैं। इसके मान को निम्न सूत्र में रखकर तार के पदार्थ का यंग गुणांक का मान ज्ञात कर लेते हैं-
\(\mathrm{Y}=\frac{\mathrm{MgL}}{\pi r^2 \Delta \mathrm{L}}\)

पदार्थ	यंग गुणांक (×109 Nm-2))
एल्युमिनियम	70
ताँबा	110
लोहा	190
इस्पात	200
काँच	65
कक्रीट	30
लकड़ी	13
अस्थि	9
पॉलीस्टीरीन	3

प्रश्न 2.
बढ़ते भार के अन्तर्गत खिंचे तार के व्यवहार को प्रतिबल – विकृति ग्राफ की सहायता से समझाइए पराभव सामर्थ्य तथा चरम तनन सामर्थ्यं भी स्पष्ट कीजिए।
उतर:
प्रतिबल – विकृति वक्र (Stress-Strain Curve):
तनन प्रतिबल के प्रभाव में किसी दिए गए द्रव्य के लिए प्रतिबल तथा विकृति के मध्य सम्बन्ध एक प्रयोग द्वारा ज्ञात किया जा सकता है। किसी बेलन या तार को एक प्रत्यारोपित बल (भार) द्वारा विस्तारित किया जाता है। लम्बाई में भिन्नात्मक परिवर्तन (विकृति) तथा इस विकृति के लिए आवश्यक विरूपक बल को नोट कर लेते हैं प्रत्यारोपित बल (या भार) को धीरे-धीरे बढ़ाते हैं और लम्बाई में वृद्धि के मान को नोट कर लेते हैं। अब सभी प्रेक्षणों के लिए प्रतिबल (\(\frac{F}{A}\)) तथा विकृति (\(\frac{∆l}{L}\)) के मान ज्ञात कर लेते हैं। प्रतिबल तथा विकृति के बीच ग्राफ खींचते हैं। किसी दी गई धातु के लिए एक प्रारूपिक प्रतिबल – विकृति ग्राफ चित्र में दर्शाया है।

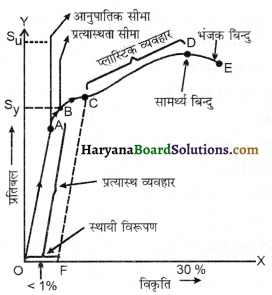
प्रतिबल-विकृति ग्राफ के अध्ययन से निम्न निष्कर्ष प्राप्त होते हैं-
(1) O से A तक वक्र रैखिक है अर्थात् इस क्षेत्र में हुक के नियम का पालन होता है। जब विरूपक बल हटा लिया जाता है तो तार पुनः अपनी प्रारम्भिक स्थिति में आ जाता है इस क्षेत्र में ठोस एक प्रत्यास्थ वस्तु जैसा आचरण करता है। A विन्दु को अनुक्रमानुपातीय सीमा- (Proportionality Limit) कहते हैं।

(2) A से B तक के क्षेत्र में प्रतिबल तथा विकृति अनुक्रमानुपाती नहीं है फिर भी भार हटा लेने पर तार अपनी प्रारम्भिक अवस्था में आ जाता है। बिन्दु B को पराभव बिन्दु अथवा प्रत्यास्थता सीमा कहते हैं तथा उसके संगत प्रतिबल को द्रव्य की पराभव सामर्थ्य (S) कहते हैं।

(3) भार को और अधिक बढ़ाने पर विकृति का मान बढ़ते प्रतिबल की तुलना में शीघ्रता से बढ़ता है तथा वक्र का B से D तक का भाग प्राप्त होता है। यदि B व D के मध्य कोई बिन्दु C माना जाये तो इस बिन्दु के संगत भार हटा लेने पर तार अपनी प्रारम्भिक स्थिति को प्राप्त नहीं कर पाता है। अर्थात् तार का प्रत्यास्थ गुणं समाप्त हो जाता है। इस स्थिति में प्रतिबल को शून्य कर देने पर भी विकृति का मान शून्य नहीं होता है। अर्थात् तार में स्थायी विरूपण हो जाता है। स्थायी विरूपण को ‘प्लास्टिक विरूपण’ कहते हैं। ग्राफ पर बिन्दु D को द्रव्य की चरम तनन सामर्थ्य कहते हैं और इसे S से प्रदर्शित करते हैं। बिन्दु D पर प्रतिबल अपने अधिकतम सम्भव मान पर होता है इसे भंजक प्रतिबल (Breaking Stress) कहते हैं। बिन्दु D पर लगाये गये भार को विच्छेदन भार (Breaking Load) कहते हैं।

(4) बिन्दु D से आगे यदि आरोपित बल को घटाया भी जाये तब भी अतिरिक्त विकृति उत्पन्न हो जाती है तथा बिन्दु E पर तार टूट जाता है। यदि D और E पास-पास है तो पदार्थ भंगुर है तथा D व E अधिक दूरी पर होने पर द्रव्य को ‘तन्य’ पदार्थ कहते हैं।

(5) कुछ पदार्थों जैसे रबड़ के लिए ग्राफ का OA भाग सरल रेखा में नहीं होता क्योंकि ऐसे पदार्थों की प्रत्यास्थता की सीमा बहुत अधिक होती है, लेकिन हुक के नियम का पालन नहीं करते। इन्हें प्रत्यास्थक (Elastomer) कहते हैं।

प्रत्यास्थता से सम्बन्धित महत्वपूर्ण परिभाषाएँ (Important Definition Related to Elasticity):
प्रत्यास्थता की सीमा (Limit of Elasticity) : विरूपक बल के उस अधिकतम मान को जिसके परे पदार्थ की प्रत्यास्थता का गुण समाप्त हो जाता है, उस पदार्थ की प्रत्यास्थता की सीमा कहते हैं।

प्रत्यास्थता भ्रांति (Elastic Fatigue) : जब किसी वस्तु पर प्रत्यास्थता की सीमा के अन्दर एक विरूपक बल अधिक समय तक लगाये रखा जाता है, तो वस्तु में उत्पन्न विकृति का मान समय के साथ धीरे-धीरे कम होता जाता है। ऐसा लगता है कि वस्तु थक गई। यदि कुछ समय के लिए वस्तु पर से विरूपक बल हटा लिया जाए, तो उसमें पुनः नियमित विकृति होने लगती है। इसे प्रत्यास्थता श्रांति कहते हैं।

प्रत्यास्थ उत्तर प्रभाव (Elastic After Effect) : जब किसी वस्तु पर प्रत्यास्थता सीमा के अन्दर विरूपक बल लगाया जाता है तो विकृति उत्पन्न होती है। विरूपक बल हटा लेने पर वस्तु तुरन्त ही अपनी पूर्वावस्था ग्रहण नहीं कर पाती, बल्कि कुछ समय लगता है। इसे प्रत्यास्थ उत्तर प्रभाव कहते हैं।
धारामापी जैसे सुग्राही यंत्रों में निलम्बन तार फॉस्फर ब्रॉज तथा क्वार्टज के बनाने का कारण इन पदार्थों की नगण्य प्रत्यास्थ उत्तर प्रभाव ही है।

प्रत्यास्थ शैथिल्य (Elastic Hysteresis) : “विकृति को प्रतिलोमत करने पर प्रतिबल – विकृति वक्र का अपने मार्ग की पुनरावृत्ति न करना प्रत्यास्थ शैथिल्य कहलाता है।” सभी प्रत्यास्थकों जैसे रबड़, हृदय से रक्त ले जाने वाली महाधमनी में प्रत्यास्थ शैथिल्य पाया जाता है। रबड़ के एक नमूने के लिए प्रतिबल – विकृति वक्र चित्र 9.8 में प्रदर्शित है जिनमें भार बढ़ाते समय का वक्र OAB एवं भार घटाते समय का वक्र BCO है। स्पष्ट है कि उक्त दोनों वक्र भिन्न हैं।

प्रश्न 3.
ठोसों के प्रत्यास्थ व्यवहार को स्प्रिंग गेंद मॉडल की सहायता से समझाइए ।
उत्तर:
ठोसों का प्रत्यास्थ व्यवहार (Elastic Behaviour Of Solids)
ठोसों के प्रत्यास्थ व्यवहार को परमाणवीय मॉडल के आधार पर भली प्रकार समझा जा सकता है। प्रत्येक पदार्थ परमाणुओं से मिलकर बना है। एक ठोस क्रिस्टल में ये परमाणु एक निश्चित व्यूह में वैद्युत आकर्षण बलों के द्वारा बँधे रहते हैं। इन वैद्युत बलों को अंतरा परमाणुक बल या अंतरा आणविक बल कहते हैं।

परमाणुओं के मध्य एक निश्चित दूरी पर आण्विक बल शून्य होता है अर्थात् वैद्युत आकर्षण बल एवं प्रतिकर्षण बल परिमाण में समान होता है। जब अन्तर परमाण्विक दूरी का मान से अधिक बढ़ता है तो To आकर्षण बल पहले बढ़ता है परन्तु एक सीमा से अधिक दूरी बढ़ाने पर आकर्षण बल घटने लगता है। बल की इस सीमा को प्रत्यास्थता सीमा कहते हैं। इसके बाद भी यदि बाह्य बल बढ़ाया जाता है तो आकर्षण बल घटते घटते शून्य हो जाता है और विच्छेद / भंजन (Breaking) की स्थिति आ जाती है ।

यदि अन्तर परमाण्विक दूरी का मान से कम हो जाता है तो इस दशा में परमाणुओं के बीच आवेश का वितरण इस प्रकार बदल जाता है। कि उनके बीच एक नेट प्रतिकर्षण बल लगने लगता है। बाह्य विरूपक बल हटा लेने पर परमाणु इसी प्रतिकर्षण बल के कारण एक-दूसरे से दूर हट कर अपनी पूर्व प्रारम्भिक स्थिति में लौटता है।

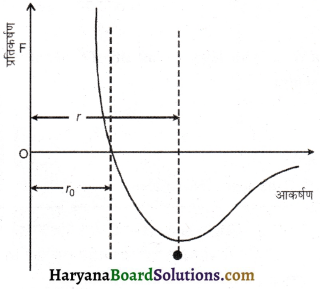
उक्त विवेचना में प्रत्यानयन बल की क्रियाविधि को समझने के लिए चित्र पर विचार करें, इसमें गेंद स्प्रिंग मॉडल में गेंद परमाणुओं को तथा स्प्रिंग अंतरा परमाण्विक बलों को निरूपित करती है। यदि किसी गेंद को अपनी स्थिति से विस्थापित करने का प्रयास करते हैं तो स्प्रिंग तन्त्र उस गेंद को वापस लाने का प्रयास करेगा। इस प्रकार ठोसों का प्रत्यास्थ व्यवहार ठोस की सूक्ष्मीय प्रकृति के आधार पर समझाया जा सकता है।

प्रश्न 4.
किसी तार को खींचने में किये गये कार्य का सूत्र व्युत्पन्न कीजिए।
उत्तर:
खिंचे हुए तार में स्थितिज ऊर्जा (Potential Energy in Astretching Wire)
जब किसी तार पर बाह्य बल लगाकर उसे खींचा जाता है तो तार में विकृति उत्पन्न होने पर उसके अन्दर प्रत्यानयन बल उत्पन्न होता है।
इसी प्रत्यानयन बल के विरुद्ध तार की लम्बाई बढ़ाने में जो कार्य करना पड़ता है, वह खिचे हुए तार में उसकी ‘प्रत्यास्थ स्थितिज ऊर्जा’ के रूप में निहित हो जाता है। इसका मान निम्न प्रकार ज्ञात करते हैं-
माना तार पर P बल लगाने पर इसकी लम्बाई में वृद्धि हो जाती है। चूँकि जो प्रत्यानयन बल उत्पन्न होते हैं, उनका प्रारम्भिक मान शून्य होता है जो अन्त में F हो जाता है अतः

आंकिक प्रश्न

यंग प्रत्यास्थता गुणांक पर आधारित

प्रश्न 1.
4 मीटर लम्बे तथा 1.2 सेमी² अनुप्रस्थ काट वाले ताँबे के तार को 4.8 × 10³ न्यूटन कल द्वारा खींचा जाता है। यदि ताँबे के लिए यंग प्रत्यास्थता गुणांक Y = 1.2 × 10¹¹ न्यूटन / मी हो तो ज्ञात कीजिए- (i) प्रतिबल (ii) विकृति
उत्तर:
(i) 4 × 10⁷ न्यूटन /मी²
(ii) 3.3 × 10^-4

प्रश्न 2.
ताँबे के तार की लम्बाई 10 मीटर है तथा इसका द्रव्यमान 50 ग्राम/मी है। यदि इस तार पर 2 किग्रा का भार लटकाया जाता है, तो लम्बाई में वृद्धि की गणना कीजिए ताँबे का यंग प्रत्यास्थता गुणांक = 1.2 × 10¹¹ न्यूटन / मी तथा ताँबे का घनत्व p = 8.9 × 10³ kg/m³ है।
उत्तर:
10.29 मिमी

प्रश्न 3.
2 मीटर लम्बी एक हल्की छड़ समान लम्बाई के दो ऊर्ध्वाधर तारों से क्षैतिज लटकाई गई है। एक तार स्टील का है जिसका अनुप्रस्थ परिच्छेद 0.1 सेमी² है दूसरा तार पीतल का है जिसकी अनुप्रस्थ काट का क्षेत्रफल 0.2 सेमी² है। दोनों तारों में (i) समान प्रतिबल (ii) समान विकृति उत्पन्न करने के लिए किसी भार को छड़ पर कहाँ लटकाना चाहिए? (स्टील के लिए Y = 2.0 ×10¹¹ N/m² तथा पीतल के लिए Y = 10× 10¹¹ N/m²)

उत्तर:
(i) स्टील के तार से 4/3m दूर
(ii) स्टील के तार से 1 m दूर

प्रश्न 4.
एक तार A पर kg भार लटकाने से उसकी लम्बाई में 1 mm की वृद्धि होती है, इसी धातु के दूसरे तार B के लिए 1.5 kg का भार लटकाने पर लम्बाई में वृद्धि का परिकलन कीजिए जबकि तार B की लम्बाई A की लम्बाई की 4/5 तथा उसका व्यास A के व्यास का 5/2 गुना है,
उत्तर:
0.192mm

प्रश्न 5.
एक पीतल की छड़ का व्यास 4.00 मिमी है। पीतल का बंग प्रत्यास्थता गुणांक 9.2 × 10¹⁰ न्यूटन / मी² है। (i) पीतल की छड़ की लम्बाई में 0.25% की वृद्धि करने पर प्रतिबल एवं विकृति की गणना कीजिए। (ii) आरोपित बल का मान क्या होगा ?
उत्तर:
2.3 × 10⁸ Nm², 2.5 × 10^-3, 2889 न्यूटन

प्रश्न 6.
1 मीटर लम्बे स्टील के एक खम्भे को 5000 किग्रा की इमारत को सँभालना है। यदि खम्भे की लम्बाई में अधिक-से-अधिक 2 मिमी का परिवर्तन सम्भव हो, तो खम्भे के न्यूनतम अनुप्रस्थ काट के क्षेत्रफल की गणना कीजिए। स्टील का यंग प्रत्यास्थता गुणांक Y = 2.2 × 10¹¹ न्यूटन / मी²
उत्तर:
1.114 × 10^-4 मीटर²

प्रश्न 7.
एक लिफ्ट का द्रव्यमान 3200 किग्रा है तथा लोहे के मोटे तारों से बंधा है। यदि लिफ्ट का महत्तम त्वरण 1.2 मी/से² हो राधा तार का अधिकतम सुरक्षित प्रतिबल 2.8 × 10⁸ न्यूटन / मी² हो, तो तार का न्यूनतम व्यास क्या होना चाहिए ?
उत्तर:
1.27 मिमी

प्रश्न 8.
लोहे की एक छड़ जिसकी लम्बाई 2 मी है दो दृढ़ आधारों के मध्य बंधी है। यदि छड़ को 100°C तक गर्म किया जाये तो छड़ की विकृति ऊर्जा की गणना कीजिए। यदि रेखीय प्रसार गुणांक = 18 × 10^-6/°C तथा अनुप्रस्थ काट का क्षेत्रफल A- 1 cm² |
उत्तर:
64.8 जूल

भंजक प्रतिबल तथा भंजक बल पर आधारित

प्रश्न 9.
स्टील के लिए भंजक प्रतिबल 8.5 × 10⁶ Nm^-2 है इसका घनत्व 8.5 × 10³ किग्रा / मी³ है इसके लिए किसी तार की वह अधिकतम लम्बाई ज्ञात कीजिए जिससे वह अपने ही भार के अन्तर्गत बिना टूटे लटकाया जा सके। (g = 10m / sec²)
उत्तर:
100 मी

प्रश्न 10.
ऐलुमिनियम का भंजक प्रतिबल 7.5 × 10⁸ डाइन / सेमी² है। ऐलुमिनियम के तार की वह अधिकतम लम्बाई ज्ञात कीजिए जिसे तार टूटे बिना प्राप्त किया जा सकता है ऐलुमिनियम का घनत्व 2.7 ग्राम / सेमी³ है।
उत्तर:
2.834 किमी

तार में संचित ऊर्जा पर आधारित

प्रश्न 11.
एक तार (Y = 2 × 10¹¹ N/m²) जिसकी लम्बाई 2 m तथा काट क्षेत्रफल 10^-6 m² है तो 0.1mm खींचने में कितना कार्य करना पड़ेगा ?
उत्तर:
5 × 10^-4 J

आयतन प्रत्यास्थता गुणांक पर आधारित

प्रश्न 12.
रबर की एक गेंद को किसी झील की तली में 300 m गहराई पर ले जाने से उसके आयतन में 0.15% की कमी हो जाती है। रबर के आयतन प्रत्यास्थता गुणांक की गणना कीजिए। झील के जल का घनत्व 1.0 × 10³ kg/m³ है तथा g 10m/sec²|
उत्तर:
2.0 × 10⁹ N/m²

प्रश्न 13.
जब 1 cm त्रिज्या के एक वायु के बुलबुले को पारे के एक पात्र में । m की गहराई तक डुबोया जाता है तो बुलबुले की त्रिज्या में परिवर्तन क्या होगा ? पारे की सम्पीड्यता 3.7 × 10^-11N^-1m² तथा पारे का घनत्व 13.6 ग्राम / सेमी’ दिया गया है।
उत्तर:
0.162 mm

प्रश्न 14.
हिन्द महासागर की औसत गहराई लगभग 3 km है महासागर की तली में पानी के भिन्नात्मक संपीडन \(\frac{∆V}{V}\) की गणना कीजिए। दिया है कि पानी का आयतन गुणांक 2.2 × 10⁹ N-m² है। g = 10 ms^-2)
उत्तर:
1.36%

दृढ़ता गुणांक पर आधारित

प्रश्न 15.
एक 7 cm भुजा वाले रबर के घन का एक फलक स्थिर है जबकि 200 kg भार का एक स्पर्शरेखीय बल विपरीत फलक पर आरोपित किया गया है। उत्पन्न अपरूपण विकृति और विकृत भुजा द्वारा तय दूरी ज्ञात कीजिए। रबर के लिए η = 2 × 10⁷ डाइन/सेमी
उत्तर:
0.2 रेडियन, 1.4cm

प्रश्न 16.
किसी 5 cm भुजा वाले रबर के घन का एक फलक स्थिर है जबकि इसके विपरीत फलक पर एक 180 kg का स्पर्शरेखीय बल आरोपित किया गया है, इसके द्वारा अपरूपण विकृति तथा धन की विकृत भुजा का पाश्र्व विस्थापन ज्ञात कीजिए। रबर का दृढ़ता प्रत्यास्थता गुणांक 2.4 × 10⁶ न्यूटन मी दिया गया है।
उत्तर:
0.294 रेडियन, 0.0147 मी