HBSE 11th Class Physics Important Questions Chapter 4 समतल में गति

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 4 समतल में गति Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 4 समतल में गति

बहुविकल्पीय प्रश्न:

प्रश्न 1.
किसी प्रक्षेप्य पर ऊँचाई y तथा क्षैतिज तल के अनुदिश दूरी x क्रमश: y = 8t – 5t² तथा x = 6t है, जहाँ t सेकण्ड में तथा दूरियाँ मीटर में हैं। प्रक्षेप्य का प्रक्षेपण वेग होगा:
(a) 8 मीटर/सेकण्ड
(b) 6 मीटर/सेकण्ड
(c) 10 मीटर/सेकण्ड
(d) उपर्युक्त विवरण से प्राप्त नहीं किया जा सकता है।
उत्तर:
(c) 10 मीटर/सेकण्ड

प्रश्न 2.
आकाश में उड़ता एक वायुयान क्षैतिज तल में मोड़ ले रहा है। ऐसा करते समय उसके पंख:
(a) क्षैतिज रहते हैं
(b) ऊर्ध्वाधर हो जाते हैं।
(c) भीतर की ओर झुक जाते हैं।
(d) बाहर की ओर झुक जाते हैं।
उत्तर:
(c) भीतर की ओर झुक जाते हैं।

प्रश्न 3.
यदि एक बन्दूक से वेग से छोड़ी गयी गोली की परास R हो, तो बन्दूक का क्षैतिज से झुकाव होगा।
(a) cos^-1\(\frac{v^2}{R g}\)
(b) cos^-1\(\frac{R g}{v^2}\)
(c) tan^-1\(\frac{v^2}{R g}\)
(d) sin^-1\(\frac{g R}{v^2}\)
उत्तर:
(d) sin^-1\(\frac{g R}{v^2}\)

प्रश्न 4.
एक कण x y तल में गति कर रहा है और किसी बिन्दु पर उसके निर्देशांक, x = Asin ωt तथा y = Acosωt हैं, जहाँ ω एक नियत राशि है। कण का पथ है।
(a) सरल रेखा
(b) दीर्घ वृत्ताकार
(c) वृत्ताकार
(d) परवलयाकार
उत्तर:
(c) वृत्ताकार

प्रश्न 5.
एक नाव जिसकी शान्त जल में चाल 5 km/hr है, 1 km चौड़ी नदी को सबसे छोटे सम्भव मार्ग से 15 मिनट में पार करती है। नदी के जल का km/hr में वेग है।
(a) 1
(b) 3
(c) 4
(d) √41
उत्तर:
(b) 3

प्रश्न 6.
दो कण A व B एक दृढ़ छड़ AB द्वारा जुड़े हैं। छड़ लम्बवत् पटरियों पर फिसलती है, जैसा कि चित्र में प्रदर्शित है । कण 4 का बायीं ओर वेग 10 m/s है। जब कोण α = 60° है, तो कण B का वेग होगा।

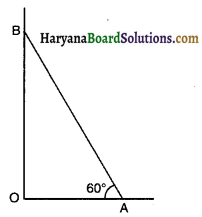
(a) 5.8m/s
(b) 9.8m/s
(c) 10m/s
(d) 17.3m/s
उत्तर:
(a) 5.8m/s

प्रश्न 7.
एक कण एक समान चाल से वृत्ताकार पथ पर चक्कर लगाता है। कण का त्वरण है।
(a) वृत्त की परिधि के अनुदिश
(b) स्पर्श रेखा के अनुदिश
(c) त्रिज्या के अनुदिश
(d) शून्य।
उत्तर:
(c) त्रिज्या के अनुदिश

प्रश्न 8.
किसी प्रक्षेप्य का पथ होता है?
(a) सरल रेखीय
(b) परवलयिक
(c) दीर्घवृत्तीय
(d) अतिपरवलयिक
उत्तर:
(b) परवलयिक

प्रश्न 9.
एक प्रक्षेप्य से किस कोण से प्रक्षेपित किया जाये कि उसकी परास एवं अधिकतम ऊँचाई समान हो।
(a) tan^-1 (√3)
(b) tan^-1 (√2)
(c) tan^-1 (4)
(d) tan^-1 (√4)
उत्तर:
(c) tan^-1 (4)

प्रश्न 10.
एक कण r त्रिज्या के वृत्तीय पथ में गति करता हैं। अर्द्धवृत्त पूर्ण करने पर उसका विस्थापन होगा।
(a) 2r
(b) \(\frac{r}{2}\)
(c) \(\frac{r}{4}\)
(d) r
उत्तर:
(a) 2r

प्रश्न 11.
एक गेंद को क्षैतिज θ कोण पर किसी वेग फेंका जाता है। उसकी क्षैतिज परास अधिकतम होने के लिए θ का मान होगा:
(a) 30°
(b) 0°
(c) 45°
(d) 60°
उत्तर:
(c) 45°

प्रश्न 12.
समान परास के लिए एक पिण्ड को समान चाल से कितनी दिशाओं में (कोणों पर) प्रेक्षित किया जा सकता है?
(a) 2
(b) 3
(c) 4
(d) 1
उत्तर:
(a) 2

प्रश्न 13.
एक प्रक्षेप्य की अधिकतम ऊँचाई पर चाल उसकी प्रारम्भिक चाल की आधी है। प्रक्षेप्य की क्षैतिज परास है।
(a) \(\frac{3 u^2}{g}\)
(b) \(\frac{\sqrt{3} u^2}{2 g}\)
(c) \(\frac{u^2}{2 g}\)
(d) \(\frac{2 u^2}{g}\)
उत्तर:
(b) \(\frac{\sqrt{3} u^2}{2 g}\)

प्रश्न 14.
एक मोटर कार 30 मीटर / सेकण्ड की चाल से 500 मीटर त्रिज्या के वृत्तीय पथ पर गतिमान है। यदि इसकी चाल 2 मीटर/सेकण्ड² की दर से बढ़ रही है तब इसका परिणामी त्वरण है।
(a) 2 मी/से²
(b) 2.2 मी/से²
(c) 2.7 मी/से²
(d) 3.8 मी/से²
उत्तर:
(c) 2.7 मी/से²

अति लघुत्तरीय प्रश्न:

प्रश्न 1.
एकांक सदिश किसे कहते हैं?
उत्तर:
वह सदिश जिसका परिमाण इकाई होता है, एकांक सदिश कहलाता है। इसका उपयोग सदिश को दिशा देने के लिए किया जाता है।

प्रश्न 2.
X- अक्ष, Y-अक्ष तथा Z-अक्ष के अनुदिश एकांक सदिश बताइये।
उत्तर:
X- अक्ष की दिशा में एकांक वेक्टर \(\hat{i}\), Y-अक्ष के अनुदिश \(\hat{j}\) तथा Z-अक्ष के अनुदिश \(\hat{k}\) होता है।

प्रश्न 3.
शून्य सदिश किसे कहते हैं?
उत्तर:
ऐसा सदिश जिसका परिमाण शून्य होता है, शून्य सदिश कहलाता है। इस सदिश की दिशा का निर्धारण सम्भव नहीं है।

प्रश्न 4.
सदिशों का वियोजन कितने प्रकार का होता है?
उत्तर:
सदिशों का वियोजन दो प्रकार का होता है:

1.  द्विविमीय वियोजन
2.  त्रिविमीय वियोजन।

प्रश्न 5.
क्या दो सदिशों के परिणामी सदिश का परिमाण दिये गये सदिशों में से किसी एक सदिश के परिमाण से कम हो सकता है?
उत्तर:
हाँ, यदि दोनों सदिशों के मध्य कोण 90° से अधिक हो।

प्रश्न 6.
निम्न भौतिक राशियों में से अदिश तथा सदिश राशियों को अलग-अलग कीजिए-
बल आघूर्ण, पृष्ठ तनाव, संवेग, ताप, ऊर्जा, वेग, त्वरण, चाल।
उत्तर:
अदिश राशियाँ: पृष्ठ तनाव, ताप, ऊर्जा, वेग, त्वरण चाल।
सदिश राशियाँ: बल आघूर्ण, संवेग।

प्रश्न 7.
क्या एक अदिश और एक सदिश राशि को जोड़ा जा सकता है?
उत्तर:
नहीं, क्योंकि एक सी प्रकार की राशियों का योग सम्भव है। और अदिश में दिशा नहीं होती है, जबकि सदिश में परिमाण के साथ-साथ दिशा भी होती है।

प्रश्न 8.
यदि किसी सदिश राशि का एक घटक शून्य हो व अन्य घटक शून्य न हो, तो क्या वह सदिश राशि शून्य हो सकती है?
उत्तर:
नहीं।

प्रश्न 9.
दो सदिशों के सदिश गुणनफल से प्राप्त सदिश की दिशा क्या होती है?
उत्तर:
दो सदिशों के सदिश गुणनफल की दिशा (\(\hat{n}\)) दोनों सदिशों के तल की लम्ब दिशा में होती है।

प्रश्न 10.
दो समान्तर सदिशों का सदिश गुणनफल क्या होता है?
उत्तर:
यदि \(\vec{A} \| \vec{B}\) A x B = A. B. sin O \(\hat{n}\) = 0 (शून्य) अर्थात् दो समान्तर सदिशों का सदिश गुणनफल शून्य होता है।

प्रश्न 11.
क्या एक स्केलर को वेक्टर से गुंणा किया जा सकता
उत्तर:
हाँ ; बल \(\vec{F}=m \vec{a}\) एवं संवेग \(\vec{p}=m \vec{v}\) इसी के उदाहरण हैं।

प्रश्न 12.
क्या विभिन्न परिमाणों के दो सदिशों को ऐसे जोड़ा जा सकता है कि उनका परिणामी शून्य हों?
उत्तर:
नहीं।

प्रश्न 13.
बल F एक स्थिर पिण्ड को दूरी तक विस्थापित करता है। इस क्रिया को सदिश संकेत से कैसे दिखायेंगे?
उत्तर:
W = \(\vec{F} \cdot \vec{d}\)
= F.d.cos θ

प्रश्न 14.
किस अवस्था में दो अशून्य सदिशों का स्केलर गुणनफल अधिकतम होता है?
उत्तर:
\(\vec{A} \cdot \vec{B}\)
= ABcos θ
जब
θ = 0° तो cos θ = 1
\((\vec{A} \cdot \vec{B})\)_max = AB
अतः समान दिशा में होने पर स्केलर गुणनफल अधिकतम होगा।

प्रश्न 15.
किसी सदिश का ग्राफीय निरूपण कैसे किया जाता।
उत्तर:
तीर (Arrow) चिन्ह द्वारा।

प्रश्न 16.
क्या सदिशों की वियोजन संक्रिया में साहचर्य गुणधर्म लागू होता है?
उत्तर:
हाँ; क्योंकि \((\vec{P}+\vec{Q})-\vec{R}=\vec{P}+(\vec{Q}-\vec{R})\)

प्रश्न 17.
क्या चार असमतलीय सदिशों का परिणामी शून्य हो सकता है?
उत्तर:
हाँ।

प्रश्न 18.
यदि a अदिश राशि है और b सदिश राशि हो तो ab किस प्रकार की राशि होगी?
उत्तर:
सदिश।

प्रश्न 19.
यदि \(\vec{P} \cdot \vec{R}=\vec{Q} \cdot \vec{R}\) तो क्या \(\overrightarrow{\boldsymbol{P}}\) और \(\overrightarrow{\boldsymbol{Q}}\) सदैव परस्पर बराबर होंगे?
उत्तर:
\(\vec{P}\) और \(\vec{Q}\) परस्पर तभी बराबर होंगे, जब दोनों में से प्रत्येक \(\vec{R}\) के साथ समान कोण बनाए।

प्रश्न 20.
दो अक्षीय सदिशों के उदाहरण दीजिए।
उत्तर:
कोणीय वेग, बल-आघूर्ण।

प्रश्न 21.
बल तथा दाब में कौन सी सदिश राशि है?
उत्तर:
बल।

प्रश्न 22.
क्या \(\vec{A}+\vec{B}\) का परिमाण वही है जो \(\vec{B}+\vec{A}\) का है?
उत्तर:
हाँ दोनों के परिमाण एवं दिशाएं समान हैं।

प्रश्न 23.
क्या \(\vec{A}-\vec{B}\) का परिमाण वही है जो \(\overrightarrow{\boldsymbol{B}}-\overrightarrow{\boldsymbol{A}}\) का है? क्या दोनों की दिशाएं भी समान हैं?
उत्तर:
\(\vec{A}-\vec{B}\) व \(\overrightarrow{\boldsymbol{B}}-\overrightarrow{\boldsymbol{A}}\) दोनों के परिमाण तो समान होंगे लेकिन दिशाएं परस्पर विपरीत होंगी।

प्रश्न 24.
दो सदिशों का योग कब अधिकतम व कब न्यूनतम होता है?
उत्तर:
जब दोनों सदिश एक ही दिशा में होते हैं (अर्थात् θ = 0) तो उनका योग अधिकतम होता है और जब परस्पर विपरीत दिशा में (अर्थात् θ = 180°) होते हैं तो उनका योग न्यूनतम होता है।

प्रश्न 25.
यदि किन्हीं दो सदिशों के पीरमाण को अपरिवर्तित रखते हुए केवल उनके बीच का कोण परिवर्तित कर दें तो उनके परिणामी सदिश पर क्या प्रभाव पड़ेगा?
उत्तर:
परिणामी सदिश के परिमाण व दिशा दोनों बदल जायेंगे।

प्रश्न 26.
क्या किसी सदिश के वियोजित घटक का मान उस सदिश के मान से अधिक हो सकता है?
उत्तर:
नहीं; किसी सदिश के वियोजित घटक का अधिकतम मान सदिश के मान के बराबर हो सकता है।

प्रश्न 27.
क्या दो सदिशों का अदिश गुणन ऋणात्मक हो सकता है?
उत्तर:
हाँ, यदि दोनों सदिशों के मध्य कोण 90° से 270° के मध्य हों।

प्रश्न 28.
प्रक्षेप्य पथ के किस बिन्दु पर चाल न्यूनतम होती है?
उत्तर:
उच्चतम बिन्दु पर।

प्रश्न 29.
प्रक्षेप्य पथ किस प्रकार का होता है? क्या यह ऋजुरेखीय हो सकता है?
उत्तर:
प्रक्षेप्य पथ परवलयाकार होता है। प्रक्षेपण कोण θ = 90° के लिए यह ऋजुरेखीय होगा।

प्रश्न 30.
प्रक्षेप्य गति में अधिकतम परास के लिए प्रक्षेपण कोंण कितना होना चाहिए?
उत्तर:
45°

प्रश्न 31.
वायु के प्रतिरोध का प्रक्षेप्य के उड्डयन काल तथा परास क्या प्रभाव पड़ता है?
उत्तर:
वायु के प्रतिरोध के कारण उड्डयन काल बढ़ जाता है। लेकिन परास घट जाता है।

प्रश्न 32.
किस प्रक्षेपण कोण के लिए महत्तम ऊँचाई एवं परास बराबर होते हैं?
उत्तर:
0 = tan^-1(4) = 76°

प्रश्न 33.
जब प्रक्षेप्य को क्षैतिज के साथ किसी कोण (90° को छोड़कर) पर प्रक्षेपित किया जाता है तो गति के दौरान वेग का कौन सा घटक नियत रहता है?
उत्तर:
वेग का क्षैतिज घटक (ucosθ) नियत रहता है।

लघु उत्तरीय प्रश्न:

प्रश्न 1.
दो बराबर सदिशों का परिणामी सदिश कब:
1. शून्य हो सकता है
2. प्रत्येक के बराबर हो सकता है?
उत्तर:

1. परिमाण में समान दो सदिश के मध्य जब 180° का कोण होता है तो उनका परिणामी शून्य होगा।
2. जब परिमाण में समान दो सदिश 120° के कोण पर होते हैं तो उनके परिणामी का परिमाण उनके परिमाण के बराबर प्राप्त होता है।

प्रश्न 2.
दो सदिश \(\vec{A}\) व \(\vec{B}\) इस प्रकार हैं कि \(\vec{A} \cdot \vec{B}\) = 0 \(\vec{A}\) व \(\vec{B}\) के विषय में क्या जानकारी मिलती है?
उत्तर:
यदि \(\vec{A} \cdot \vec{B}\) = 0 तो निम्नलिखित दो सम्भावनाएँ हैं:

1. \(\vec{A}\) व \(\vec{B}\) में कोई एक शून्य है।
2.  \(\vec{A} \cdot \vec{B}\) = 0 या ABcosθ = 0

AB ≠ 0 या cos θ = 0
अतः θ = 90°
इस प्रकार \(\vec{A} \perp \vec{B}\) अर्थात् दोनों सदिश परस्पर लम्बवत् होंगे।

प्रश्न 3.
यदि \(\vec{A} \cdot \vec{B}\) = AB तो \(\vec{A}\) व \(\vec{B}\) के विषय में क्या जानकारी मिलती है?
उत्तर:
\(\vec{A} \cdot \vec{B}\) = AB
या
AB cosθ = AB
या
cos θ = 1
∴ θ = 0°
अर्थात् \(\vec{A}\) व \(\vec{B}\) परस्पर समान्तर होंगे।

प्रश्न 4.
यदि \(\vec{R}=\vec{A} \times \vec{B}\) तो
(i) R तथा 1 के बीच कोण क्या है?
(ii) में तथा 8 के बीच कोण क्या है?
उत्तर:
दिया है:
R = 1 x B
अतः की दिशा व के तल के लम्बवत् होगी।
∴ की दिशा व B दोनों के लम्बवत् होगी अर्थात् दोनों के साथ कोण 90° होगा।

प्रश्न 5.
क्या तीन असमतलीय सदिशों का परिणामी शून्य हो सकता है?
उत्तर:
नहीं; किन्हीं दो सदिशों का परिणामी उन सदिशों के तल में ही होता है, अतः यह तीसरे सदिश जो कि भिन्न तल में है, के प्रभाव को निरस्त नहीं कर सकता है।

प्रश्न 6.
जब सदिश \(\vec{A}\) का सदिश \(\vec{B}\) में की दिशा में घटक शून्य है तो आप दोनों सदिशों के बारे में क्या निष्कर्ष निकाल सकते हैं?
उत्तर:
माना दो सदिशों \(\vec{A}\) का \(\vec{B}\) के मध्य कोण θ है। सदिश \(\vec{B}\) की दिशा में सदिश \(\vec{A}\) का घटक Acosθ होगा।
यदि यह घटक शून्य है अर्थात्
या
A cosθ = 0
cos θ = 0
⇒ θ = 90°
स्पष्ट है कि \(\vec{A} \perp \vec{B}\) अर्थात् दोनों सदिश परस्पर लम्बवत् होंगे।

प्रश्न 7.
क्या शून्य सदिश (\(\overrightarrow{\mathbf{0}}\)) को सदिश कहना सही है?
उत्तर:
दो सदिशों का अन्तर भी सदिश होता है अत: \(\vec{R}-\vec{R}=\overrightarrow{0}\) अतः शून्य सदिश को सदिश कहना सही है।

प्रश्न 8.
यद्यपि बल \(\vec{F}\) है व विस्थापन \(\overrightarrow{\boldsymbol{S}}\) दोनों सदिश राशियाँ हैं, फिर भी इन दोनों के गुणन से प्राप्त कार्य अदिश राशि है क्यों? यदि
\(\overrightarrow{\boldsymbol{F}}\) व \(\overrightarrow{\boldsymbol{s}}\) शून्य न हों फिर भी W का मान शून्य हो सकता है, कब?
उत्तर:
दो सदिश राशियों का डॉट गुणनफल अदिश राशि होती है
और कार्य W = \(\vec{F}\)\(\vec{S}\) डे, अतः कार्य अदिश राशि है।
पुन:
W = \(\vec{F}\)\(\vec{S}\) = F S cosθ
स्पष्ट है कि जब cosθ = 0 तो W = 0 होगा।
अर्थात्
θ = 90° हो \(\overrightarrow{\boldsymbol{F}}\) व \(\overrightarrow{\boldsymbol{s}}\) के अशून्य होने पर भी W का मान शून्य होगा।

प्रश्न 9.
सदिशों के योग का समान्तर चतुर्भुज नियम लिखिए।
उत्तर:
सदिशों के संयोजन का समान्तर चतुर्भुज नियम (Law of Parallelogram of Vectors Addition): इस नियम की सहायता से हम दो सदिशों को जोड़ सकते हैं। इस नियम के अनुसार, “यदि दो सदिशों को परिमाण व दिशा दोनों में किसी समान्तर चतुर्भुज की दो आसन्न भुजाओं द्वारा व्यक्त किया जा सके तो उनका परिणामी परिमाण व दिशा दोनों में चतुर्भुज के उस विकर्ण द्वारा प्रदर्शित होगा जो उन भुजाओं के कटान बिन्दु से होकर जाता है। ”

“चित्र 4.15 में माना दो सदिश व परिमाण व दिशा दोनों में समान्तर चतुर्भुज OABC की आसन्न भुजाओं OA व OB द्वारा व्यक्त किये जाते हैं तो इनका परिणामी विकर्ण OB द्वारा व्यक्त होगा अर्थात्

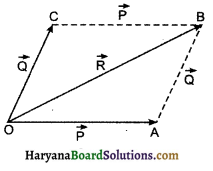
प्रश्न 10.
सदिशों के योग के लिए बहुभुज नियम लिखिए।
उत्तर:
(C) सदिशों के संयोजन का बहुभुज नियम (Law of Polygon of Vectors Addition): इस नियम की सहायता से दो से अधिक सदिशों को जोड़ा जा सकता है। इस नियम के अनुसार, यदि (n-1) सदिशों को भुजाओं वाले बहुभुज की (n-1) क्रमागत भुजाओं द्वारा प्रदर्शित किया जा सके तो उनका परिणामी बहुभुज की अन्तिम (n वीं) भुजा द्वारा नियमित क्रम में प्रदर्शित होगा।” सदिशों के बहुभुज नियम को दूसरे शब्दों में इस प्रकार भी व्यक्त कर सकते हैं, “यदि दो से अधिक सदिशों को परिमाण व दिशा दोनों में एक खुले बहुभुज की भुजाओं द्वारा एक क्रम में निरूपित किया जा सके तो बहुभुज को बन्द करने वाली भुजा द्वारा परिमाण व दिशा दोनों में उनका परिणामी व्यक्त होगा।”

विधि – बहुभुज नियम द्वारा सदिश योग ज्ञात करने के लिए उचित पैमाना मानकर योग की क्रिया किसी एक सदिश को खींचकर प्रारम्भ करते हैं, फिर उसके शीर्ष पर दूसरे सदिश का पुच्छ रखकर दूसरा सदिश खींचते हैं। इसी प्रकार दिये गये सभी सदिश क्रमशः खींच लेते हैं। प्रथम सदिश के पुच्छ एवं अंतिम वेक्टर के शीर्ष को मिला देते हैं। यही परिणामी वेक्टर होता है। इसे नापकर पैमाने का गुणा करके परिणामी का परिमाण ज्ञात करं – लेते हैं।
उदाहरणार्थ: माना चार सदिश A, B, C, D का योग बहुभुज नियम द्वारा ज्ञात करना है।

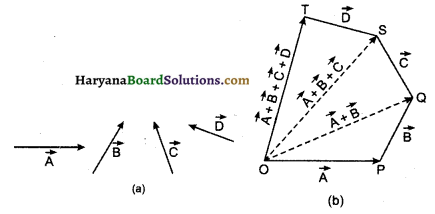
सत्यापन: त्रिभुज नियम के आधार पर

प्रश्न 11.
निम्न कथन की विवेचना कीजिए।
विस्थापन सदिश मूलतः स्थिति सदिश है।
उत्तर:
संलग्न चित्र में A व B के स्थिति सदिश क्रमशः \(\overrightarrow{r_A}\) व \(\overrightarrow{r_B}\) हैं। यदि कोई वस्तु A से B तक विस्थापित होती है तो विस्थापन सदिश

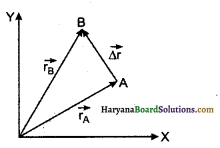
यदि प्रारम्भिक बिन्दु A मूल बिन्दु पर हो तो \(\overrightarrow{r_A}\) = 0 होगा, अतः
\(\overrightarrow{\Delta r}\) = \(\overrightarrow{r_B}\) जो कि B का स्थिति सदिश है।
स्पष्ट है कि विस्थापन सदिश मूलतः स्थिति सदिश है।

प्रश्न 12.
क्या सदिश को अदिश से गुणा करने पर इसकी प्रकृति बदल जाती है?
उत्तर:
बदल भी सकती है और नहीं भी उदाहरण के लिए जब एक सदिश शुद्ध अंक (जैसे, 1, 2, 3….. ) से गुणा करते हैं तो सदिश की प्रकृति नहीं बदलती है लेकिन यदि सदिश को अदिश भौतिक राशि से गुणा करते हैं तो सदिश की प्रकृति बदल जाती है। उदाहरण के लिए जब वेग \(\vec{v}\) सदिश को द्रव्यमान (m) अदिश से गुणा करते हैं तो सदिश राशि संवेग \(\vec{p}\) प्राप्त होता है जिसकी प्रकृति वेग से भिन्न है।

प्रश्न 13.
किसी चुम्बकीय क्षेत्र में स्थित एक समतल से सम्बद्ध चुम्बकीय फ्लक्स (अदिश), समतल के क्षेत्रफल तथा चुम्बकीय क्षेत्र की तीव्रता (सदिश) के गुणनफल के बराबर होता है। बताइये कि समतल का क्षेत्रफल सदिश है या अदिश?
उत्तर:
दो सदिश राशियों का स्केलर गुणनफल एक अदिश राशि होता है।
चुम्बकीय फ्लक्स Φ = \(\vec{B}\) . \(\vec{A}\)
अतः समतल का क्षेत्रफल सदिश राशि (\(\vec{A}\)) है।

प्रश्न 14.
क्या परिमाण व दिशा दोनों वाली राशियाँ निश्चित रूप से सदिश राशियाँ होती हैं? उदाहरण देकर स्पष्ट कीजिए।
उत्तर:
नहीं; क्योंकि परिमाण व दिशा वाली राशियाँ यदि सदिश योग के नियम का पालन करती हैं तो वे सदिश राशियाँ होती हैं परन्तु यदि वे सदिश योग के नियम का पालन नहीं करती हैं तो वे अदिश राशि की श्रेणी में आती हैं; उदाहरणार्थ – विद्युत् धारा, समय आदि।

प्रश्न 15.
एक गेंद को वेग से ऊर्ध्वाधर ऊपर फेंकने पर यह ऊँचाई तक जाती है। यदि वेग को दोगुना (2u) कर दें तो ऊँचाई पर क्या प्रभाव पड़ेगा?
उत्तर:
गेंद का वेग उच्चतम बिन्दु पर शून्य हो जायेगा, अत: सूत्र
v² = u² + 2as’
से
0 = u² – 2gh
या
2gh = u²
h = \(\frac{u^2}{2 g}\)
यदि वेग (2u) कर दिया जाये तो माना ऊँचाई ‘ हो जाती है अतः
h = \(\frac{(2 u)^2}{2 g}\) = \(\frac{4 u^2}{2 g}\) = \(4 \times\left(\frac{u^2}{2 g}\right)\)
या
h = 4h
अर्थात् वेग दो गुना कर देने पर ऊँचाई चार गुनी हो जायेगी।

प्रश्न 16.
प्रक्षेप्य गति किसे कहते हैं?
उत्तर:
प्रक्षेप्य गति: जब किसी वस्तु को क्षैतिज से किसी कोण पर ऊर्ध्वाधर तल में किसी प्रारम्भिक वेग से प्रक्षेपित की जाती है तो फेंके जाने के पश्चात् यह वस्तु पृथ्वी के गुरुत्वाकर्षण के प्रभाव में गति करती है। इस प्रकार की गति को प्रक्षेप्य गति कहा जाता है। इस गति के दौरान वस्तु परवलयाकार पथ का अनुसरण करती है।

प्रश्न 17.
क्रिकेट का एक खिलाड़ी किसी गेंद को 100 मी० की अधिकतम क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊँचाई तक फेंक सकता है?
उत्तर:
दिया है, R_max = 100 मी०
किसी प्रक्षेप्य की अधिकतम ऊँचाई
⇒ \(Y=\frac{T^2}{4 \pi^2 L}\)
= 100 मी०
\(h_m=\frac{v_0^2 \sin ^2 \theta_0}{2 g} \)
\(\left(h_m\right)_{\max }=\frac{v_0^2}{2 g} \)
जबकि θ° = 90°
H = \(\frac{1}{2}\) x \(\frac{v_0^2}{g}\)
= \(\frac{1}{2}\) x 100 मी० = 50 मी०

प्रश्न 18.
एक प्रक्षेप्य की महत्तम ऊँचाई H तथा उड्डयन काल T है। सिद्ध कीजिए कि 8H = gT²
उत्तर:
महत्तम ऊँचाई, H = \(\frac{u^2 \sin ^2 \theta}{2g}\)
एवं उड्डयन काल T = \(\frac{2 u \sin \theta}{g}\)
∴ \(\frac{H}{T^2}=\frac{\frac{u^2 \sin ^2 \theta}{2 g}}{\frac{4 u^2 \sin ^2 \theta}{g^2}}=\frac{g}{8}\)
∴ 8H = gT²

प्रश्न 19.
सिद्ध कीजिए H ऊँचाई (महत्तम ऊँचाई) तक पहुँचाने के लिए प्रक्षेपण वेग u = \(\frac{\sqrt{2 g H}}{\sin \theta}\) होगा।
उत्तर:
प्रक्षेप्य द्वारा प्राप्त महत्तम ऊँचाई
\(H=\frac{u^2 \sin ^2 \theta}{2 g}\)
u² sin² θ = 2Hg
या
u² = \(\frac{2 H g}{\sin ^2 \theta}\) ⇒ u = \(\sqrt{\frac{2 H g}{\sin ^2 \theta}}\)
या
u = \(\frac{\sqrt{2 H g}}{\sin \theta}\)

प्रश्न 20.
यदि प्रक्षेप्य का परास एवं महत्तम ऊँचाई बराबर हों तो प्रक्षेपण कोण ज्ञात कीजिए।
उत्तर:
∵ क्षैतिज परास = महत्तम ऊँचाई
\(\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin ^2 \theta}{2 g}\)
या
sin 2θ = \(\frac{\sin ^2 \theta}{2}\)
या
2sinθ.cosθ = \(\frac{\sin ^2 \theta}{2}\)
या
2cos θ = \(\frac{\sin \theta}{2}\)
या
4 = \(\frac{\sin \theta}{\cos \theta}\)
= tan θ
∴ θ = tan^-1 (4) = 75.96°

प्रश्न 21.
समान ऊँचाई से एक ही क्षण एक गोली 4 स्वतन्त्रता पूर्वक गिराई जाती है तथा दूसरी गोली B क्षैतिज दिशा में फेंकी जाती है। यदि वायु का प्रतिरोध नगण्य हो तो बताइये।
1. कौन सी गेंद जमीन पर पहले टकरायेगी?
2. जमीन से टकराते समय किस गोली का ऊर्ध्वं वेग अधिक होगा?
3. क्या गोलियाँ एक ही स्थान पर गिरेंगी?
4. गोली B का क्षैतिज परास किस बात पर निर्भर करेगा?
उत्तर:

1. दोनों गोलियाँ एक साथ जमीन से टकरायेंगी।
2.  दोनों का ऊर्ध्व वेग समान होगा।
3. नहीं।
4.  ऊँचाई तथा क्षैतिज वेग पर।

प्रश्न 22.
सभी दिशाओं में, वेग से कई गोलियाँ दागी जाती हैं. पृथ्वी तल पर वह अधिकतम क्षेत्रफल क्या होगा। जिस पर ये गोलियाँ फैल जायेंगी?
उत्तर:
वह क्षेत्रफल जिसमें गोलियाँ फैलेगी = πr²
जहाँ r = अधिकतम परास Rmax = \(\frac{u^2}{g}\)
यहाँ
u = v
∴ r = \(\frac{v^2}{g}\)
(जब θ = 45°)
अतः प्रभावित क्षेत्रफल = πr² = π \(\left(\frac{v^2}{g}\right)^2\) = \(\frac{\pi v^4}{g^2}\)

प्रश्न 23.
वृत्तीय गति में अभिकेन्द्रीय त्वरण क्या होता है? इसके लिए सूत्र प्राप्त कीजिए।
उत्तर:
अभिकेन्द्रीय त्वरण (Centripetal Acceleration):
चित्र 4.30 के अनुसार हम एक कण की वृत्ताकार गति पर विचार करते हैं। किसी भी क्षण t पर कण बिन्दु P पर है जिसकी कोणीय स्थिति θ है। अब P बिन्दु पर एक एकांक सदिश \(\overrightarrow{P A}=\hat{e_r}\) वृत्त की त्रिज्या के बाहर की ओर की दिशा में खींचते हैं तथा एक एकांक सदिश \(\overrightarrow{P B}=\hat{e_t}\) इस बिन्दु P पर स्पर्श रेखा की ओर कोण θ के बढ़ने की दिशा में खींचते हैं। \(\hat{e_r}\) को हम त्रिज्या एकांक सदिश तथा \(\hat{e_t}\) को स्पर्श रेखीय एकांक संदिश कहते हैं।

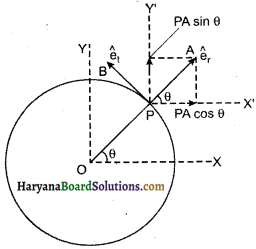
अब X- अक्ष के समान्तर PX’ एवं Y-अक्ष के समान्तर PY’ रेखाएं खींचते हैं। अब चित्र 4.30 से स्पष्ट है
\(\overrightarrow{P A}=P A \cdot \cos \theta \hat{i}+P A \sin \theta \hat{j}\)
या
\(\frac{\overrightarrow{P A}}{P A}=\hat{i} \cos \theta+\hat{j} \sin \theta\)
या
\(\hat{e}_r=\hat{i} \cdot \cos \theta+\hat{j} \sin \theta\) ……(1)
यहाँ PA = \(|\overrightarrow{P A}|\) = 1 तथा \(\hat{i}\) एवं \(\hat{j}\) क्रमश: X – एवं Y अक्षों की दिशाओं में एकांक सदिश हैं।
इसी प्रकार
\(\frac{\overrightarrow{P B}}{P B}=-\hat{i} \sin \theta+\hat{j} \cos \theta\)
या
\(\overrightarrow{e_t}=-\hat{i} \sin \theta+\hat{j} \cos \theta\) ……(2)
अब समय t पर कण का स्थिति सदिश
\(\vec{r}=\overrightarrow{O P}\)
या
\(\vec{r}=\hat{i} \cdot r \cos \theta+\hat{j} r \sin \theta\)
या
\(\vec{r}=r(\hat{i} \cdot \cos \theta+\hat{j} \sin \theta)\) ……..(3)
समीकरण (3) का समय के साथ अवकलन करने पर हमें किसी भी
समय t पर कण का वेग ज्ञात होता है।
अतः कण का वेग
\(\vec{v}=\frac{d \vec{r}}{d t}=\frac{d}{d t}[r(\hat{i} \cos \theta+\hat{j} \sin \theta)]\)
= \(\left[\hat{i}\left(-\sin \theta \cdot \frac{d \theta}{d t}\right)+\hat{j}\left(\cos \theta \cdot \frac{d \theta}{d t}\right)\right]\)
= rω[-\(\hat{i}\)sinθ +[-\(\hat{j}\)cosθ] ……….(4)
क्योंकि
\(\frac{d \theta}{d t}\) = ω
या
\(\vec{v}\) = rω.\(\hat{e_t}\) ……..(5)
[समी० (2) से]
उपरोक्त समी० (5) से हम देखते हैं कि पद rω किसी भी समय t पर कण की चाल है और इसकी दिशा \(\hat{e}_t\) की ओर अर्थात् स्पर्श रेखा की ओर है।
किसी समय t पर कण का त्वरण समी० (4) को समय t के सापेक्ष अवकलन करके ज्ञात किया जा सकता है। अतः कण का त्वरण

या \(\vec{a}\) = -ω².r.\(\hat{e}_r\) + rα\(\hat{e}_t\) ………..(6)
यहाँ पर सभी ० (1) व (2) का उपयोग किया गया है। समी० (6) से हम देखते हैं कि एक कण की सामान्य वृत्तीय गति में त्वरण \(\vec{a}\) के दो घटक होते हैं
(i) \(\vec{a}\) = -ω² r\(\hat{e}_r\), जिसकी दिशा (-\(\hat{e}_r\)) की ओर अर्थात् वृत्त के केन्द्र की ओर होती है। अतः इसे ‘अभिकेन्द्रीय त्वरण’ (centripetal acceleration) कहते हैं होती है अत: ‘स्पर्श रेखीय त्वरण’ (tangential acceleration) कहते हैं। इसका मान होगा। एक कण की असमान वृत्तीय गति में ये दोनों त्वरण होंगे। एक कण की एक समान वृत्तीय
ω नियत रहता है (क्योंकि v = rω)।
अत: \(\frac{d v}{d t}\) = \(r \frac{d \omega}{d t}\) = 0
अतः स्पर्श रेखीय त्वरण \(\vec{a}_t\) का मान शून्य होगा। अत: समी० (6) से अभिकेन्द्रीय त्वरण
\(\vec{a}_r\) = -ω².r.\(\hat{e}_r\) ………..(7)
इस त्वरण की दिशा केन्द्र की ओर होगी। इस त्वरण का परिणाम
a_r = ω².r = \(\frac{\omega^2 r^2}{r}\) = \(\frac{v^2}{r}\) ……..(8)
यहाँ यह ध्यान रखने की बात है कि एक समान वृत्तीय गति में कण की चाल तो नियत रहती है, परन्तु वेग की दिशा प्रति क्षण बदलने से वेग परिवर्तित होता रहता है। इसीलिए कण में अभिकेन्द्र त्वरण होता है।

दीर्घ उत्तरीय प्रश्न:

प्रश्न 1.
निम्न की परिभाषा दीजिए:
1. एकांक सदिश
2. समान या तुल्य सदिश
3. विपरीत सदिश
4. शून्य सदिश
5. समान्तर संदिश।
उत्तर:
1. तुल्य या समान सदिश (Equivalent Vectors): वे सदिश जिनके परिमाण एवं दिशाएँ समान होते हैं, समान वेक्टर या तुल्य सदिश कहलाते हैं।

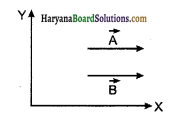
संलग्न चित्र में प्रदर्शित दो वेक्टर \(\vec{A}\) व \(\vec{B}\) बराबर वेक्टर हैं अर्थात्
\(\vec{A}\) = \(\vec{B}\)
तथा
A = B

2. असमान सदिश (Unequal Vectors): यदि दो सदिशों के परिमाण समान हों परन्तु दिशाएँ भिन्न हों अथवा परिमाण भिन्न हों किन्तु दिशाएँ समान हों अथवा परिमाण व दिशाएँ दोनों भिन्न हों तो दोनों सदिश असमान सदिश कहलाते हैं। चित्र 4.6 में असमान सदिशों की उक्त तीनों स्थितियाँ प्रदर्शित की गई हैं-

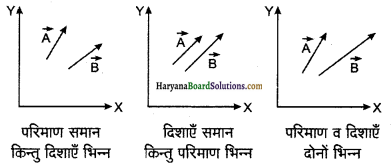
3. विपरीत सदिश (Opposite Vectors): जब दो सदिशों के परिमाण तो समान हों किन्तु दिशाएँ विपरीत हों तो वे परस्पर विपरीत सदिश कहलाते हैं। संलग्न चित्र 4.7 में दो सदिश \(\vec{A}\) व \(\vec{B}\) दिये हैं तो

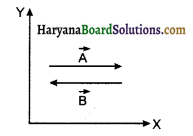
\(\vec{A}\) = \(\vec{B}\)
अथवा
\(\vec{B}\) = –\(\vec{A}\)

4. एकांक सदिश (Unit Vectors): वह सदिश जिसका परिमाण इकाई अर्थात् 1 होता है, एकांक सदिश कहलाता है।
एकांक सदिश को किसी सदिश की दिशा प्रदर्शित करने के लिए प्रयुक्त किया जाता है। उदाहरणार्थ: माना किसी सदिश का परिमाण है एवं सदिश की दिशा में एकांक सदिश है। [ एकांक सदिश को व्यक्त करने के लिए कैप (^) का प्रयोग किया जाता है।]
\(\vec{r}\) = r.r
या
\(\hat{r}=\frac{\vec{r}}{r}=\frac{\vec{r}}{|\vec{r}|}\)

5. समकोणिक एकांक सदिश (Orthogonal Unit Vectors): X- अक्ष, Y-अक्ष एवं Z अक्ष के अनुदिश एकांक सदिश क्रमश: \hat{i} \hat{j} एवं \hat{k} समकोणिक एकांक सदिश कहलाते हैं। संलग्न चित्र 4.8 में इन एकांक सदिशों को प्रदर्शित किया गया है।

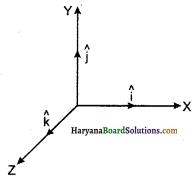
6. सरेखीय सदिश (Collinear Vectors): ऐसे सदिश जो एक ही रेखा के अनुदिश होते हैं, संरेखीय सदिश कहलाते हैं। ये सदिश दिशीय अथवा विपरीत दिशीय हो सकते हैं जैसा कि संलग्न चित्र 4.9 में प्रदर्शित है।

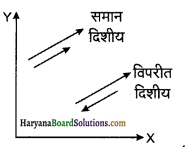
7. शून्य सदिश (Zero Vectors): वह सदिश जिसका परिमाण शून्य हो, शून्य सदिश कहलाता है। इसकी दिशा का निर्धारण नहीं किया जा सकता है। यह निम्न स्थितियों में प्राप्त किया जाता है:

1. \(\vec{A}\) व –\(\vec{A}\) सदिशों को जोड़ने पर \(\vec{A}\) + –\(\vec{A}\) = \(\overrightarrow{0}\)
2. सदिश \(\vec{A}\) को शून्य से गुणा करने पर \(\vec{A}\) .0 = \(\overrightarrow{0}\)
3.  वस्तु गति करने के पश्चात् अपनी प्रारम्भिक स्थिति में लौट आती है तो उसका ‘शून्य सदिश’ अर्थात् \(\overrightarrow{0}\) होता है।

प्रश्न 2.
कार्तीय निर्देशांक पद्धति में, एक विमीय, द्विविमीय एवं त्रिविमीय सदिशों की व्याख्या कीजिए।
उत्तर:
कार्तीय निर्देशांक पद्धति में एक विमीय, द्विविमीय एवं त्रिविमीय सदिश (One Dimensional, Two Dimensional and Three Dimensional Vectors in Cartesian Coordinate System):
किसी बिन्दु की स्थिति को पूर्णतः व्यक्त करने के लिए मूल बिन्दु एवं तीन परस्पर लम्बवत् अक्षों से निर्मित तन्त्र कार्तीय निर्देशांक तन्त्र कहलाता है। कार्तीय निर्देशांक तन्त्र में क्रमश: धनात्मक एवं Z – अक्ष के अनुदिश एकांक सदिश क्रमश: \(\hat{i}\) \(\hat{j}\) व \(\hat{k}\) X- अक्ष, Y-अक्ष होते हैं। संलग्न

चित्र 4.10 में बिन्दु P (x, y, z) की स्थिति मूल बिन्दु 0 तथा परस्पर लम्बवत् अक्षों X, Y व Z के सापेक्ष बताई गयी है। निर्देश तन्त्र में मूल बिन्दु 0 तथा किसी एक अक्ष का चयन स्वच्छ है, शेष दो अक्षों का निर्धारण क्रमागत वामावर्त (Anticlockwise) दिशा में स्वतः हो जाता है।

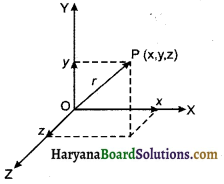
(i) एक विमीय सदिश (One Dimensional Vectors): वह सदिश जिसकी दिशा केवल एक अक्ष (X- अक्ष अथवा Y अक्ष अथवा Z-अक्ष) के अनुदिश हो तो उसे एक विमीय सदिश कहते हैं।
निम्न चित्र 4.11 में तीन दिशाओं में एक विमीय सदिश की स्थितियाँ दर्शायी गई हैं।

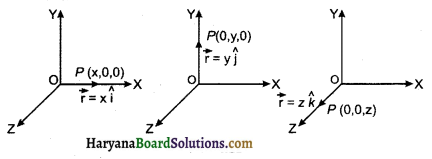
(i) यदि सदिश X- अक्ष की दिशा में है तो \(\vec{r}\) = x\(\hat{i}\)
(ii) यदि सदिश – अक्ष की दिशा में है तो \(\vec{r}\) = y\(\hat{j}\)
(iii) यदि सदिश Z-अक्ष की दिशा में है तो \(\vec{r}\) = z\(\hat{k}\)

(ii) द्विविमीय सदिश (Two Dimensional Vectors): वह सदिश जो एक तल में स्थित होता है, द्विविमीय सदिश कहलाता है। द्विविमीय सदिश का प्रभाव किन्हीं दो दिशाओं अथवा दो अक्षों के अनुदिश होता है। इस प्रकार के सदिश की निम्न तीन स्थितियाँ सम्भव हैं।
(a) यदि कोई सदिश \(\vec{r}\), X-Y तल में स्थित है तो,
\(\vec{r}\) = (x\(\hat{i}\) + y\(\hat{j}\)) चित्र 4.12 (a)
(b) यदि कोई सदिश X-Z तल में है तो,
\(\vec{r}\) = (x\(\hat{i}\) + z\(\hat{k}\)) चित्र 4.12(b)
(c) यदि कोई सदिश Y-Z तल में है तो,
\(\vec{r}\) = (y\(\hat{j}\) + z\(\hat{k}\)) चित्र 4.12(c)

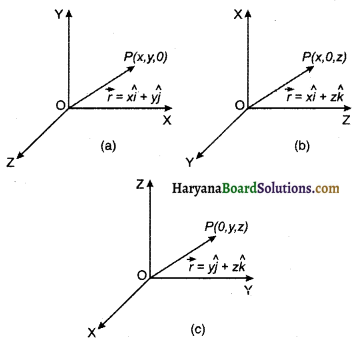
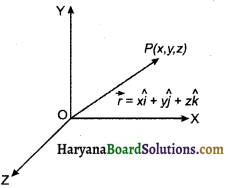
(iii) त्रिविमीय सदिश (Three Dimensional Vector):
वह सदिश जो आकाश (Space) में स्थित हो, त्रिविमीय सदिश कहलाता है। इस सदिश का प्रभाव तीनों अक्षों के अनुदिश होता है। चित्र (4.13) में ऐसा ही एक सदिश प्रदर्शित है जिसका प्रारम्भिक बिन्दु मूलबिन्दु 0 एवं शीर्ष बिन्दु P (x, y, z) है। अतः यह सदिश,

प्रश्न 3.
सदिशों के संयोजन के लिए त्रिभुज नियम क्या है? इस नियम का उपयोग करके परिणामी के परिमाण व दिशा के लिए सूत्र स्थापित कीजिए।
उत्तर:
(i) दो सदिशों के परिणामी सदिश का परिमाण ज्ञात करना (To Determine the Magnitude of Resultant Vector of Two Vectors): त्रिभुज नियम का उपयोग करके यदि दो सदिशों \(\vec{A}\) व \(\vec{B}\) को जोड़ा जाये तो उनका परिणामी \(\vec{R}\) चित्र 4.17(b) की भाँति प्राप्त होगा। माना दोनों सदिशों के बीच कोण है। परिणामी का परिमाण ज्ञात करने के लिए आधार ON आगे बढ़ाते हैं और इस पर Q से OP लम्ब डालते हैं।

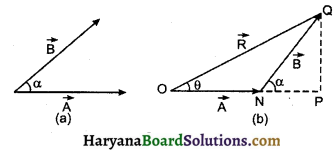
∴ समकोण त्रिभुज NPQ में,
sin α = \(\frac{Q P}{N Q}\)=\(\frac{Q P}{B}\)
QP = B sinα …(1)
तथा
cos α = \(\frac{N P}{N Q}\)=\(\frac{N P}{B}\)
∴NP = Bcosα …(2)
अब त्रिभुज OPQ में,
OP = ON + NP = A + B cosα …(3)
पाइथागोरस प्रमेय से
समकोण ∆OPQ में
या
(OQ)² = (OP)² + (QP)²
(R)² = (A + B cosα)² + (Bsinα)²
या R² = A²+ 2 AB cosα + B² cos²α + B² sin²α
या
R² = A² + B² (cos²α + sin²α ) + 2AB cosα
या
R² = A² + B² + 2ABcosα
या
R = \(\sqrt{A^2+B^2+2 A B \cos \alpha}\) …(4)
उपरोक्त समीकरण को कोज्या का नियम कहते हैं।

प्रश्न 4.
सदिशों के द्विविमीय वियोजन की विस्तार से व्याख्या कीजिए।
उत्तर:
सदिशों का वियोजन (Resolution of Vectors):
व्यापक रूप से एक सदिश को अनेक स्वैच्छ घटकों में वियोजित किया जा सकता है परन्तु यहाँ हम केवल दो या तीन समकोणिक घटकों में वियोजन का अध्ययन करेंगे। इस प्रकार के वियोजन के लिए कार्तीय निर्देशांक पद्धति का उपयोग करेंगे। वियोजन की क्रिया योग की क्रिया की विपरीत क्रिया है। इस क्रिया में एक सदिश को दो या तीन घटकों (Components) में वियोजित किया जाता है। सदिश के घटकों का योग करने पर योगफल के रूप में मूल सदिश ही प्राप्त होता है। सदिश वियोजन की निम्न दो विधियाँ हैं।
(i) द्विविमीय निर्देश तन्त्र में वियोजन (Resolution in Two Dimensions):

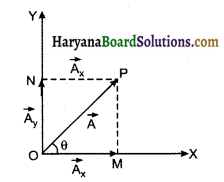
माना X-Y तल में स्थित \(\vec{A}\) जो X- अक्ष के साथ 6 कोण बनाता है, का दो लम्बवत् घटकों में वियोजन करता है। सदिश \(\vec{A}\) के शीर्ष P से X व Y- अक्षों पर लम्ब क्रमश: PM व PN खींचे तो OM सदिश \(\vec{A}\) का X- अक्ष के अनुदिश घटक \(\overrightarrow{A_x}\) होगा और ON, Y-अक्ष के अनुदिश घटक \(\overrightarrow{A_y}\) होगा।
अतः त्रिभुज ∆OPM में त्रिभुज नियम से संयोजन करने पर
\(\overrightarrow{O P}=\overrightarrow{O M}+\overrightarrow{M P}\)
या
\(\vec{A}=\overrightarrow{A_x}+\overrightarrow{A_y}\) …(1)
(क्योंकि \(\overrightarrow{M P}\) = \(\overrightarrow{O N}\) = \(\overrightarrow{A_y}\))
यदि X व Y – अक्षों के अनुदिश एकांक सदिश क्रमशः \(\hat{i}\) व \(\hat{j}\) हों तो,
\(\overrightarrow{A_x}\) = A_x\(\hat{i}\) ……..(2)
एवं
\(\overrightarrow{A_y}\) = A_y\(\hat{j}\) …….(3)
अतः समी० (1) को निम्न प्रकार लिख सकते हैं:
\(\vec{A}\) = A_x\(\hat{i}\) + A_y\(\hat{j}\) ……..(4)

वेक्टर \(\vec{A}\) के घटकों के परिमाण निम्न प्रकार ज्ञात करते हैं:
समकोण त्रिभुज OMP से
cos θ = \(\frac{A_x}{A}\)
अतः
A_x = A.cosθ …(5)
तथा
sin θ = \(\frac{A_Y}{A}\)
अतः
A_y = A sinθ ……(6)
घटकों के पदों में सदिश \(\vec{A}\) का परिमाण
समी० (5) व (6) के वर्गों को जोड़ने पर:
A_xA² + 4 = ( A cosθ)² + (Asinθ)²
= A²cos²θ + A² sin²θ
= A² [cos²θ + sin²θ] = A²
या
A² = A_xA² + A_yA²
∴ A = \(\sqrt{A_x^2+A_y^2}\)
घटकों के पदों में 8 का मान
पुन: समी० (5) व (6) से
\(\frac{A_y}{A_x}=\frac{A \sin \theta}{A \cos \theta}\) = tanθ
या
tanθ = \(\frac{A_y}{A_x}=\frac{A \sin \theta}{A \cos \theta} \)
∴ θ = tan^-1 \(\frac{A_y}{A_x}=\frac{A \sin \theta}{A \cos \theta}\)
स्पष्ट है कि यदि किसी सदिश के घटक ज्ञात हों तो उसका परिमाण समी० (7) की सहायता एवं उसकी दिशा समी० (8) की सहायता से ज्ञात कर सकते हैं।

प्रश्न 5.
सदिशों के सदिश गुणनफल की व्याख्या कीजिए।
उत्तर:
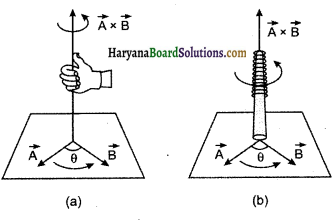
सदिश गुणनफल या क्रॉस गुणनफल (Vector Product or Cross Product): सदिशों का यह गुणनफल सदिश राशि होता है अत: इसे सदिश गुणनफल कहते हैं और इसे व्यक्त करने के लिए क्रॉस (x) चिन्ह का उपयोग किया जाता है, अतः इसे क्रॉस गुणनफल या वज्रीय गुणनफल भी कहते हैं। दो सदिशों का सदिश गुणनफल दोनों सदिशों के परिमाणों व उनके मध्य कोण की ज्या के गुणनफल के बराबर होता है एवं परिणामी सदिश की दिशा उन दोनों सदिशों के तल के लम्बवत् दक्षिणावर्त पेंच नियम द्वारा निर्धारित दिशा में होती है।
दो सदिशों का सदिश गुणनफल निम्न सूत्र से प्राप्त होता है:
\(\vec{A} \). \(\vec{B} \) = A.Bsinθ. \(\hat{n}\) …..(1)
जहाँ
A = | \(\vec{A} \)| = \(\vec{A} \) का परिमाण
B = | \(\vec{B} \) | = \(\vec{B} \) का परिमाण
तथाव के तल के लम्बवत् दिशा में एकांक वेक्टर
सदिश गुणनफल \(\vec{A} \times \vec{B} \) की दिशा निम्न दो नियमों से प्राप्त कर सकते हैं।

(i) दायें हाथ का नियम (Right Hand Rule): इस नियम के अनुसार, यदि हम दाँयें हाथ की अंगुलियों को इस प्रकार मोड़ें कि ये सदिश \(\vec{A} \) से सदिश \(\vec{b} \) की ओर रहे तथा उनके बीच के लघु कोण की ओर घूमने की दिशा को प्रदर्शित करें तो अंगूठा सदिश \(\vec{A} \times \vec{B} \) की दिशा को व्यक्त करेगा [चित्र 4.20 (a)]

(ii) दक्षिणावर्त पेंच का नियम (Right Hand Screw Rule): इस नियम के अनुसार, “यदि हम अपने दाँये हाथ से पेंच को सदिश \(\vec{A} \) से \(\vec{B} \) की ओर उनके बीच के लघु कोण की ओर घुमाएँ तो पेंच की नोंक की गति की दिशा \(\vec{A} \times \vec{B} \) की दिशा होगी [चित्र 4.20 (b)]।

प्रश्न 6.
सिद्ध कीजिए कि प्रक्षेप्य की गति का पथ परवलय होता है।
उत्तर:
प्रक्षेप्य का पथ (Path of Projectile):
माना कोई प्रक्षेप्य क्षैतिज के साथ 6 के कोण पर ऊपर की ओर प्रक्षेपित किया जाता है। प्रक्षेप्य के वेग का क्षैतिज घटक
ux = ucosθ ……(1)

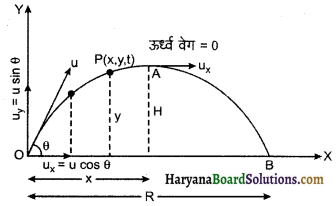
एवं ऊर्ध्व घटक,
uy = usinθ …(2)
गति के दौरान वस्तु पर केवल गुरुत्वीय त्वरण कार्य करता है, जो कि ऊर्ध्वाधर नीचे की ओर होता है, अतः त्वरण के क्षैतिज व ऊर्ध्व घटक, ax = 0 तथा ay = -g होंगे।
माना प्रक्षेप्य पथ पर कोई बिन्दु P (x,y,t) स्थित है तो सूत्र
s = ut + \(\frac{1}{2}\) का प्रयोग करने पर
x = ux.t + 0 = ucosθ.t
x = ucosθ.t …(3)
y = uyt + \(\frac{1}{2}\)ayt²
या
y = usinθ.t – \(\frac{1}{2}\)gt² …(4)
समी० (3) से,
x = \(\frac{x}{u \cos \theta}\)
समय का यह मान समी० (4) में रखने पर
y = usinθ x \(\frac{x}{u \cos \theta}-\frac{1}{2} g \frac{x^2}{u^2 \cos ^2 \theta}\)
या
y = tanθ.x – \(\left(\frac{g}{2 u^2 \cos ^2 \theta}\right) \cdot x^2\)
या
y = ax – bx² …..(5)
जहाँ
a = tanθ एवं b = \(\frac{g}{2 u^2 \cos ^2 \theta}\)
समीकरण (5) एक परवलय का समीकरण है अतः “प्रक्षेप्य पथ परवलयाकार होता है।”

प्रश्न 7.
प्रक्षेप्य की गति हेतु उड्डयन काल (T), प्रक्षेप्य की अधिकतम ऊँचाई (H) व प्रक्षेप्य की क्षैतिज परास (R) हेतु व्यंजक प्राप्त कीजिए।
उत्तर:
प्रक्षेप्य का उड्डयन काल (T) (Time of Flight of Projectile):
प्रक्षेप्य जितने समय तक वायु में रहता है अर्थात् प्रक्षेपण के बाद भूमि से टकराने तक प्रक्षेप्य को जितना समय लगता है, उसे प्रक्षेप्य का उड्डयन काल कहते हैं। इसे 7 से व्यक्त करते हैं।
प्रक्षेप्य जब अपने पथ के उच्च बिन्दु पर पहुँचता है तो ऊर्ध्व वेग घटक uy = 0 हो जाता है; अतः यदि इस आधी यात्रा का समय : मान लें तो ऊर्ध्व वेग घटक के लिए सूत्र
v = u + at
0 = usinθ – gt
या
gt = usinθ
∴ t = \(\frac{u \sin \theta}{g}\)
वायु के प्रतिरोध को यदि नगण्य मान लें तो जितना समय प्रक्षेप्य ऊपर जाने में लेता है ठीक उतना ही समय नीचे आने में लेता है। अतः प्रक्षेप्य का उड्डयन काल
T = t + t = 2t
या
T = \(\frac{2 u \sin \theta}{g}\) …….(6)

प्रक्षेप्य की महत्तम ऊँचाई (H) (Maximum Height of Projectile):
प्रक्षेप्य पथ के उच्चतम बिन्दु के संगत प्रक्षेप्य की ऊँचाई को महत्तम ऊँचाई कहते हैं। इसे H से व्यक्त करते हैं। सूत्र
v² = u² + 2as से के लिए
ऊर्ध्वं वेग घटक uy के लिए,
या
0 = (usinθ)² + 2(-g) H = u²sin²θ – 2gH
2gH = u² sin²θ
H = \(\frac{u^2 \sin ^2 \theta}{2 g}\) ………(7)
प्रक्षेप्य को अधिकतम ऊँचाई प्रदान करने के लिए sin²θ का मान
अधिकतम अर्थात् 1 होना चाहिए। अतः के लिए,
sin²θ = 1 => sinθ = 1
अधिकतम ऊँचाई के लिए,
=> θ = 90°
स्पष्ट है कि अधिकतम ऊँचाई तक फेंकने के लिए प्रक्षेप्य को 90° के प्रक्षेपण कोण पर अर्थात् ऊर्ध्वाधर ऊपर की ओर फेंकना होगा।
Hmax = \(\frac{u^2}{2 g}\) ………(8)

प्रक्षेप्य की क्षैतिज परास (R) (Horizontal Range of a Projectile):
प्रक्षेप्य द्वारा सम्पूर्ण उड्डयन काल के दौरान तय की गई क्षैतिज दूरी को प्रक्षेप्य का परास कहते हैं। इसे R से व्यक्त करते हैं।
यदि वायु के घर्षण को नगण्य मान लें तो प्रक्षेप्य के क्षैतिज वेग में कोई परिवर्तन नहीं होता है अतः प्रक्षेप्य का क्षैतिज परास,
R = क्षैतिज वेग x उड़ान का समय
= ucosθ x T
= ucosθ x \(\frac{2 u \sin \theta}{g}\)
या
R = \(\frac{u^2 \sin ^2 \theta}{2 g}\) ……(9)
(i) अधिकतम क्षैतिज परास के लिए,
sin²θ = 1 ⇒ 2θ = 90°
θ = 45°
अतः अधिकतम परास के लिए प्रक्षेपण कोण 45° होना चाहिए।
Rmax = \(\frac{u^2}{g}\) …….(10)

(ii) θ प्रक्षेपण कोण के लिए परास
R = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
यदि प्रक्षेपण कोण (90° – θ) हो तो परास,
R’ = \(\frac{u^2}{g}\)sin²( 90°- θ)
या R = \(\frac{u^2}{g}\) sin (180° – 2θ) = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
या
R = R
अर्थात् प्रक्षेपण कोण θ हो या (90° – θ) हो; दोनों स्थितियों में परास का मान समान होगा लेकिन महत्तम ऊँचाई भिन्न होगी।

आंकिक प्रश्न:

प्रश्न 1.
यदि \(\vec{a}\) तथा \(\vec{b}\) एकांक सदिश हों तो सिद्ध कीजिए।
उत्तर:
\(\sin \left(\frac{\theta}{2}\right)=\frac{1}{2}|(\vec{a}-\vec{b})\)

प्रश्न 2.
30 N तथा 40 N के दो बल एक ही बिन्दु पर परस्पर 60° के कोण पर कार्य कर रहे हैं। इन बलों का परिणामी बल ज्ञात कीजिए।
उत्तर:
60.83 NJ

प्रश्न 3.
एक कण पर दो बल 5 N तथा 10 N एक साथ कार्यरत् हैं। उनके बीच का कोण 120° है। इन बलों का परिणामी बल ज्ञात कीजिए।
उत्तर:
8.66 N

प्रश्न 4.
क्षैतिज से 30° के कोण पर कार्यरत एक बल का ऊर्ध्व घटक 200 N है। आरोपित बल का मान बताइये।
उत्तर:
400N

प्रश्न 5.
घास के रोलर के हत्थे को 50N के बल से खींचा जाता है। यदि हत्था क्षैतिज से 30° का कोण बनाए तो बल के क्षैतिज एवं ऊर्ध्व घटक बताइये।
उत्तर:
43.3 N; 25 N

प्रश्न 6.
किसी बिन्दु पर बल \(\vec{F}=(2 \hat{i}-3 \hat{j}+4 \hat{k})\) न्यूटन \(\vec{s} = (3 \hat{i}+2 \hat{j}+3 \hat{k})\) मीटर है। इसके बल आघूर्ण की गणना कीजिए।
उत्तर:
\((17 \hat{i}-6 \hat{j}-13 \hat{k})\)N-m

प्रश्न 7,
यदि वेक्टर \(\vec{A}=(2 \hat{i}+2 \hat{j}-2 \hat{k})\) और \(\overrightarrow{\boldsymbol{B}}= \hat{i}-5 \hat{j}+2 \hat{k}\) हों, तो \(\vec{A} \times \vec{B}\) का मान ज्ञात कीजिए।
उत्तर:
\(-6 \hat{i}-18 \hat{j}-24 \hat{k}\)

प्रश्न 8.
यदि \(\vec{A}=(2 \hat{i}+2 \hat{j}-2 \hat{k})\) तथा \(\vec{B}=-5 \hat{i}-5 \hat{j}+5 \hat{k}\) तो \(\vec{A} \times \vec{B}\) का मान ज्ञात कीजिए।
उत्तर:
\((15 \hat{i}-20 \hat{j}-5 \hat{k}\)

प्रश्न 9.
एक मीनार से तीन गोलियाँ A, B व C क्रमश: 0.5 ms^-1; 1ms^-1 तथा 2ms^-1 के क्षैतिज वेग से फेंकी जाती है। सबसे पहले कौन सी गोली पृथ्वी से टकरायेगी? कौन सी गोली मीनार के आधार पर सबसे अधिक दूर टकरायेगी?
उत्तर:
तीनों गोलियाँ एक साथ पृथ्वी से टकरायेंगी C गोली सबसे अधिक दूरी तय करेगी।

प्रश्न 10.
40m ऊँची मीनार की चोटी से एक गोला क्षैतिज में 20ms^-1 के वेग से छोड़ा जाता है। यह कितने समय पश्चात् तथा मीनार से कितनी क्षैतिज दूरी पर पृथ्वी से टकरायेगा ? (g = 9.8ms^-2)
उत्तर:
2.88 s; 57.14m

प्रश्न 11.
एक हवाई जहाज 1960 m की ऊंचाई पर 500/3 ms^-1 के क्षैतिज वेग से उड़ रहा है। जब जहाज पृथ्वी के किसी स्थान 4 के ठीक ऊपर होता है, तो उससे एक बम छोड़ा जाता है जो पृथ्वी तल पर किसी बिन्दु Q पर टकराता है। बम की प्रक्षेपण बिन्दु से टकराने के बिन्दु तक की क्षैतिज दूरी ज्ञात कीजिए।
उत्तर:
3.333km

प्रश्न 12.
एक गेंद 30ms^-1 के वेग से क्षैतिज से 60° का कोण बनाते हुए फेंकी जाती है। ज्ञात कीजिए
1. उड़ान का समय,
2. अधिकतम ऊँचाई,
3. परास,
4. पृथ्वी से टकराने पर गेंद के वेग का परिमाण व दिशा।
उत्तर:

1.  5.2s,
2. 33.75m,
3. 78m,
4. 30ms^-1, क्षैतिज के साथ 60° नीचे की ओर

प्रश्न 13.
एक पुल से एक पत्थर क्षैतिज से नीचे की ओर 30° के कोण पर 20 ms^-1 के वेग से फेंका जाता है। यदि पत्थर 2.0s में जल से टकराता है तो जल के तल से पुल की ऊँचाई क्या है? (g = 9:8 ms^-2)
उत्तर:
39.6m

प्रश्न 14.
0.1 kg द्रव्यमान के एक पत्थर को 1.0m लम्बी डोरी के एक सिरे पर बाँधकर \(\frac{10}{\pi}\) चक्कर प्रति सेकण्ड की दर से एक क्षैतिज वृत्त में घुमाया जाता है। डोरी में तनाव ज्ञात कीजिए।
उत्तर:
40N

प्रश्न 15.
एक डोरी के सिरे पर बँधी हुई 1kg द्रव्यमान की एक वस्तु 0.1m त्रिज्या के क्षैतिज वृत्त में 3 चक्कर प्रति सेकण्ड के वेग से घुमायी जा रही है। गुरुत्व का प्रभाव नंगण्य मानकर
1. वस्तु का रेखीय वेग,
2. अभिकेन्द्रीय त्वरण
3. डोरी में तनाव का परिकलन कीजिए।
4. यदि डोरी टृट जाये तो क्या होगा?
उत्तर:

1. 1.88 ms^-1
2. 35.34ms^-2
3. 35.34N
4. यदि डोरी टूट जाती है तो डोरी टूटने पर तनाव समाप्त हो जायेगा, फलस्वरूप वस्तु स्पर्श रेखा की दिशा में गति करने लगेगी।

प्रश्न 16.
0.10kg द्रव्यमान का पिण्ड 1.0m व्यास के वृत्तीय पथ पर 31.4s में 10 चक्कर की दर से घूम रहा है। पिण्ड पर लगने वाले
उत्तर:
0.2N