HBSE 11th Class Physics Important Questions Chapter 14 दोलन

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 14 दोलन गति Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 14 दोलन

वस्तुनिष्ठ प्रश्न (MCQs Type)

प्रश्न 1.
निम्न में से कौन-सा समीकरण सरल आवर्त गति को व्यक्त नहीं करता है-
(a) y =R sin (ωt + ϕ)
(b) y =R cos (ωt + ϕ)
(c) y = R sin ωt + b cos ωt
(d) y = R sin ωt cos 2 ωt
उत्तर :
(d) y = R sin ωt cos 2ωt

प्रश्न 2.
सरल आवर्त गति करते कण का अधिकतम वेग 4 ms^-1 है तथा अधिकतम त्वरण 16 ms^-2 है तो कण का आयाम व आवर्तकाल क्या होगा-
(a) 1 m, \(\frac{\pi}{2}\)
(b) 2 m, π s
(c) 4 m, 2π s
(d) इनमें से कोई नहीं
उत्तर :
(a) 1 m, \(\frac{\pi}{2}\)

प्रश्न 3.
सरल आवर्त गति करते हुए एक पिण्ड का आवर्तकाल 0.05 s तथा आयाम 4 cm है। पिण्ड का अधिकतम वेग होगा-
(a) 1.6 π ms^-1
(b) 2 π ms^-1
(c) 3.1 π ms^-1
(d) 4 π ms^-1
उत्तर :
(a) 1.6 π ms^-1

प्रश्न 4.
एक सरल लोलक का पृथ्वी पर आवर्तकाल T₁ है, यदि पृथ्वी से R ऊँचाई पर आवर्तकाल T₂ हो, तो \(\frac{T_2}{T_1}\) होगा-
(a) 1
(b) 2
(c) √2
(d) 4
उत्तर :
(b) 2

प्रश्न 5.
सरल आवर्त गति करते कण का अधिकतम विस्थापन की स्थिति में त्वरण होता है-
(a) अधिकतम
(b) न्यूनतम
(c) न अधिकतम न न्यूनतम
(d) शून्य
उत्तर :
(a) अधिकतम

प्रश्न 6.
0.2 किग्रा द्रव्यमान का एक पिण्ड x-अक्ष के अनुदिश 25/π हट्र्ज की आवृत्ति से सरल आवर्त गति कर रह्न है। x = 0.04 मीटर की दूरी पर पिण्ड की गतिज ऊर्जा 0.4 जूल है, दोलन का आयाम है –
(a) 0.12 m
(b) 0.03 m
(c) 0.06 m
(d) इनमें से कोई नहीं
उत्तर :
(c) 0.06 m

प्रश्न 7.
सरल आवर्त गति में क्या स्थिर रहता है-
(a) गतिज ऊर्जा
(b) स्थितिज ऊर्जा
(c) प्रत्यानयन बल
(d) आवर्तकाल
उत्तर :
(d) आवर्तकाल

प्रश्न 8.
यदि एक सेकण्ड लोलक की लम्बाई, जहाँ g = 9.8 ms^-2 है, 1 m है, किसी ग्रहपर, जहाँ g = 4.9 ms^-2 है, सेकण्ड लोलक की लम्बाई होगी-
(a) 1 m
(b) 2 m
(c) 0.5 m
(d) 1.5 m
उत्तर :
(c) 0.5 m

प्रश्न 9.
यदि एक सरल लोलक मुक्त रूप से गुरुत्वाकर्षण बल के अन्तर्गत नीचे गिर रहा है तो उसका आवर्तकाल होगा-
(a) 2 π \(\sqrt{\frac{l}{g}}\)
(b) 2 π
(c) शून्य
(d) अनन्त
उत्तर :
(d) अनन्त

प्रश्न 10.
सरल आवर्त गति करते कण की स्थितिज ऊर्जा अधिकतम होती है-
(a) साम्य स्थिति में
(b) अधिकतम विस्थापन की स्थिति में
(c) आधे विस्थापन पर
(d) एक-चौथाई विस्थापन पर।
उत्तर :
(b) अधिकतम विस्थापन की स्थिति में

प्रश्न 11.
किसी सरल आवर्त गति का आयाम R है तथा आवर्तकाल T है। अधिकतम तात्कालिक वेग होगा-
(a) \(\frac{2 \pi R}{T}\)
(b) \(\frac{2 R}{T}\)
(c) \(\frac{4 \mathrm{R}}{\mathrm{T}}\)
(d) \(2 \pi \sqrt{\frac{R}{T}}\)
उत्तर :
(a) \(\frac{2 \pi R}{T}\)

प्रश्न 12.
सरल आवर्त गति करते हुए कण की साम्य स्थिति से x दूरी पर स्थितिज ऊर्जा होती है-
(a) \(\frac{1}{2} m \omega^2 \mathrm{R}^2\)
(b) \(\frac{1}{2} m \omega^2 x^2\)
(c) \(\frac{1}{2} m \omega^2\left(\mathrm{R}^2-x^2\right)\)
(d) शून्य।
उत्तर :
(b) \(\frac{1}{2} m \omega^2 x^2\)

प्रश्न 13.
एक वस्तु का द्रव्यमान m है तथा \mathrm{F}=-k x बल के अधीन आयाम a से सरल आवर्त गति कर रही है। वस्तु की कुल ऊर्जा निर्भर करती है-
(a) k, x
(b) k, a
(c) k, a, x
(d) k, a, v
उत्तर :
(b) k, a

प्रश्न 14.
सरल आवर्त गति करते हुए किसी कण का आवर्तकाल होता है-
(a) T = \(2 \pi \sqrt{\frac{\text { विस्थापन }}{\text { त्वरण }}}\)
(b) T = \(2 \pi \sqrt{\frac{g}{\text { विस्थापन }}}\)
(c) T = \(2 \pi \sqrt{\frac{\text { वेग }}{\text { विस्थापन }}}\)
(d) T = \(2 \pi \sqrt{g \times \text { विस्थापन }}\)
उत्तर :
(a) T = \(2 \pi \sqrt{\frac{\text { विस्थापन }}{\text { त्वरण }}}\)

प्रश्न 15.
एक कण समीकरण x = 7 cos 0.5 πt के अनुसार दोलन कर रहा है, जहाँ x विस्थापन तथा t समय है। कण अपनी माध्य स्थिति से अधिकतम विस्थापन तक की स्थिति में पहुँचने में समय लेता है-
(a) 4 सेकण्ड
(b) 2 सेकण्ड
(c) 1 सेकण्ड
(d) 0.5 सेकण्ड।
उत्तर :
(c) 1 सेकण्ड

प्रश्न 16.
एक स्प्रिंग से लटके किसी पिण्ड का आवर्तकाल T है, यदि इस स्प्रिंग को बराबर चार भागों में बाँट दिया जाए तथा उसी पिण्ड को किसी एक भाग से लटकाकर दोलन कराएँ तो नया आवर्तकाल होगा-
(a) \(\frac{T}{2}\)
(b) 2 T
(c) \(\frac{T}{4}\)
(d) T
उत्तर :
(a) \(\frac{T}{2}\)

प्रश्न 17.
एक कण का विस्थापन x = 6 cos ωt + 8 sin ωt मीटर है। यह समीकरण एक सरल आवर्त दोलन व्यक्त करता है जिसका आयाम है-
(a) 14 m
(b) 2 m
(c) 10 m
(d) 5 m
उत्तर :
(c) 10 m

प्रश्न 18.
5 cm आयाम की सरल आवर्त गति करने वाले कण की अधिकतम चाल 31.4 cm s^-1 है। इन दोलनों की आवृत्ति है-
(a) 13 Hz
(b) 2 Hz
(c) 4 Hz
(d) 1 Hz
उत्तर :
(d) 1 Hz

प्रश्न 19.
निम्न में से कौन-सा वक्र अवमन्दित दोलन प्रदर्शित करता है-

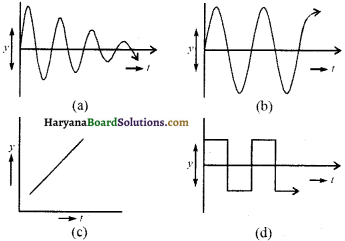
उत्तर :

प्रश्न 20.
m द्रव्यमान का एक पिण्ड मूलबिन्दु के परितः X-अक्ष पर दोलन कर रहा है। इसकी स्थितिज ऊर्जा U_x = k|x|³ है, जहाँ k एक धनात्मक नियतांक है। यदि दोलन का आयाम r है, तब इसका आवर्तकाल T –
(a) \(\frac{1}{\sqrt{r}}\) के अनुक्रमानुपाती है
(b) r पर निर्भर करता है
(c) √r के अनुक्रमानुपाती है
(d) r^3/2 के अनुक्रमानुपाती है।
उत्तर :
(a) \(\frac{1}{\sqrt{r}}\) के अनुक्रमानुपाती है

प्रश्न 21.
अनुनाद एक विशेष अवस्था है-
(a) मुक्त दोलन की
(b) प्रणोदित दोलन की
(c) अवमन्दित दोलनों की
(d) पोषित दोलनों की।
उत्तर :
(b) प्रणोदित दोलन की

प्रश्न 22.
एक कण का विस्थापन x = 3 sin (5 πt) + 4 cos (5 πt) द्वारा व्यक्त है। कण का आयाम होगा-
(a) 3
(b) 4
(c) 5
(d) 7
उत्तर :
(c) 5

प्रश्न 23.
एक लड़की झूले पर बैठी हुई झूल रही है। यदि वह खड़ी हो जाये तो झूलने का दोलन काल-
(a) घट जायेगा
(b) बढ़ जायेगा
(c) अपरिवर्तित रहेगा
(d) दो गुना हो जायेगा
उत्तर :
(a) घट जायेगा

प्रश्न 24.
समान आवर्तकाल किन्तु π/2 कलान्तर वाली दो असमान आयाम वाली परस्पर लम्बवत् सरल आवर्त गतियों का परिणामी है-
(a) वृत्त
(b) दीर्घवृत्त
(c) सरल रेखा
(d) परवलय
उत्तर :
(b) दीर्घवृत्त

प्रश्न 25.
जब समान आयाम तथा समान आवृत्ति वाली दो सरल आवर्त गतियाँ π/2 कलान्तर में एक-दूसरे के ऊपर प्रत्यारोपित हैं तो परिणामी गति है-
(a) दीर्घवृत्ताकार
(b) वृत्ताकार
(c) सरल रेखीय
(d) इनमें से कोई नहीं।
उत्तर :
(b) वृत्ताकार

अति लघु उत्तरीय प्रश्न (Very Short Answer type Questions)

प्रश्न 1.
सरल आवर्त गति का विस्थापन समीकरण लिखिए।
उत्तर :
विस्थापन समीकरण y = R sin ωt
तथा यदि कण की प्रारम्भिक कला ϕ है तो विस्थापन समीकरण y = R sin (ωt + ϕ)

प्रश्न 2.
सरल आवर्त गति करते हुए कण के त्वरण व उसके विस्थापन के बीच सम्बन्ध लिखिए।
उत्तर :
त्वरण a = -ω² y, जहाँ ω² एक नियतांक है। अतः a ∝ -y अतः त्वरण विस्थापन के अनुक्रमानुपातीं तथा विपरीत दिशा में है।

प्रश्न 3.
किसी सरल लोलक को खान में ले जाने पर उसकी आवृत्ति पर क्या प्रभाव पड़ेगा ?
उत्तर :
आवर्तकाल T ∝ \(\frac{1}{\sqrt{g}}\), अतः खान में ले जाने से g का मान कम होने के कारण आवर्तकाल बढ़ जाएगा, अतः आवृत्ति (v=\(\frac{1}{T}\)) घट जाएगी।

प्रश्न 4.
सरल आवर्त गति करते हुए कण के वेग तथा त्वरण के व्यंजक, कण के विस्थापन के पदों में लिखिए।
उत्तर :
कण का वेग u = 0 \(\sqrt{A^2-y^2}\) तथा कण का त्वरण a = -ω² y, जहाँ y विस्थापन, A आयाम तथा ω कोणीय आवृत्ति है।

प्रश्न 5.
सरल आवर्त गति करते हुए कण के आवर्तकाल का सूत्र लिखिए।
उत्तर :
T= 2π \(\sqrt{\frac{\text { विस्थापन }}{\text { त्वरण }}}\)

प्रश्न 6.
सेकण्ड लोलक से क्या तात्पर्य है?
उत्तर :
जिस सरल लोलक का आवर्तकाल 2 सेकण्ड होता है, सेकण्ड लोलक कहलाता है।

प्रश्न 7.
सरल आवर्त गति करते हुए किसी कण के त्वरण, विस्थापन तथा आवृत्ति के बीच सम्बन्ध लिखिए।
उत्तर :
कण का त्वरण
a = -ω² y = -(2πv)² y
या a = -4π²v²y

प्रश्न 8.
सरल आवर्त गति करते हुए किसी कण की गति का समीकरण a = -bx से प्रदर्शित किया जाता है, जिसमें त्वरण है, x मध्यमान स्थिति से विस्थापन है तथा कोई नियतांक है। कण का दोलनकाल क्या होगा ?
उत्तर :
समीकरण a = -bx से,
\(\frac{\text { विस्थापन }(x)}{\text { त्वरण }(a)}=\frac{1}{b}\) (आंकिक रूप से)
अतः कण का दोलनकाल T= 2π \(\sqrt{\frac{\text { विस्थापन }}{\text { त्वरण }}}\)
या
T= 2π \(\sqrt{\frac{1}{b}}\)

प्रश्न 9.
क्या कृत्रिम भू-उपग्रह में कमानी द्वारा नियन्त्रित कलाई घड़ी प्रयुक्त की जा सकती है?
उत्तर :
हाँ, क्योंकि T = 2π \(\sqrt{\frac{m}{k}}\) द्रव्यमान m व बल नियतांक k नियत रहने से T नियत रहा है।

प्रश्न 10.
एक सरल लोलक के आवर्तकाल में प्रतिशत परिवर्तन ज्ञात कीजिए यदि लोलक की लम्बाई 4% बढ़ा दी जाए।
उत्तर :
T ∝ \(\sqrt{l}\)
अतः लोलक की लम्बाई 4% बढ़ा देने पर आवर्तकाल में 2% का परिवर्तन (बढ़) हो जायेगा।

प्रश्न 11.
एक लड़की झूलते झूलते खड़ी हो जाती है ? झूले के आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
लड़की के खड़े होने पर गुरुत्व केन्द्र ऊँचा हो जाएगा। जिससे प्रभावी लम्बाई l घट जाएगी अतः सूत्र T = 2π \(\sqrt{\frac{l}{g}}\) से आवर्तकाल T भी घट जाएगा।

प्रश्न 12.
किसी स्प्रिंग के बल नियतांक का अर्थ समझाइए ।
उत्तर :
स्प्रिंग का बल नियतांक- यदि किसी स्प्रिंग पर F बल लगाने से उसकी लम्बाई में वृद्धि हो जाए, तो
F ∝ -x या F = -kx.
जहाँ = स्प्रिंग का बल नियतांक।
यदि x = 1, तो F (आंकिक रूप से)
अतः किसी स्प्रिंग का बल नियतांक उस बल के बराबर है जो उसकी लम्बाई में एकांक वृद्धि कर दे इसका मात्रक न्यूटन / मीटर होता है।

प्रश्न 13.
सरल आवर्त गति के आवश्यक प्रतिबन्ध लिखिए।
उत्तर :
सरल आवर्त गति के प्रतिबन्ध
(1) कण की गति एक स्थिर बिन्दु (माध्य स्थिति) के इधर-उधर सीधी रेखा में होती है।
(2) कण पर लगने वाला प्रत्यानयन बल (अथवा त्वरण) सदैव उस बिन्दु से कण के विस्थापन के अनुक्रमानुपाती होता है।
(3) बल (अथवा त्वरण) सदैव उस बिन्दु (मध्य बिन्दु) की ओर दिष्ट होता है।

प्रश्न 14.
एक भारहीन स्प्रिंग का बल नियतांक है। इससे लटकते हुए ” द्रव्यमान के कण की सरल आवर्त गति के आवर्त काल का सूत्र लिखिए।
उत्तर :
आवर्तकाल का सूत्र T = 2π \(\sqrt{\frac{m}{k}}\)

प्रश्न 15.
यदि लड़की झूला झूल रही है उसके पास उसके आधे भार का एक बच्चा आकर बैठ जाता है झूले के आवर्तकाल पर क्या प्रभाव पड़ेगा?
उत्तर :
झूले का आवर्तकाल पिण्ड के द्रव्यमान पर निर्भर नहीं करता, अतः आवर्तकाल वही रहेगा।

प्रश्न 16.
सरल आवर्त गति में कौन-सी भौतिक राशि संरक्षित रहती है।
उत्तर :
यांत्रिक ऊर्जा संरक्षित रहती है।

प्रश्न 17.
क्या कोई गायक अपने गाने से काँच की वस्तु के टुकड़े-टुकड़े कर सकता है?
उत्तर :
यदि गायक ऐसा स्वर उत्पन्न करे कि उसकी आवृत्ति काँच की वस्तु की स्वाभाविक आवृत्ति के बराबर हो जाये तो अनुनाद के कारण वस्तु के दोलनों का आयाम बहुत अधिक बढ़ जायेगा और वस्तु के टुकड़े टुकड़े हो जाएँगे।

प्रश्न 18.
तार वाले वाद्य यन्त्र में प्रधान तार के साथ अन्य तार क्यों लगाए जाते हैं?
उत्तर :
स्वर की तीव्रता को बढ़ाने के लिए प्रधान तार के साथ अन्य तार लगाए जाते हैं।

प्रश्न 19.
ध्वनि तथा विद्युत् चुम्बकीय अनुनाद का एक-एक उदाहरण दीजिए।
उत्तर :
(i) ध्वनि – सोनोमीटर।
(ii) विद्युत् चुम्बकीय अनुनाद – रेडियो ।

प्रश्न 20.
सरल आवर्त गति कर रहे किसी लोलक के लिए यह क्यों आवश्यक है कि उसका आयाम लम्बाई की तुलना में कम हो ?
उत्तर :
लोलक की गति सरल आवर्त गति तभी होती है, जबकि उसका कोणीय आयाम 10° से कम हो ।

प्रश्न 21.
वायु में सरल लोलक के दोलन किस प्रकार के होते हैं?
उत्तर :
अवमन्दित दोलन ।

प्रश्न 22.
क्या अवमन्दन में यान्त्रिक ऊर्जा संरक्षित रहती है?
उत्तर :
हाँ

प्रश्न 23.
सरल आवर्त गति किस भौतिक राशि के संरक्षण पर आधारित है ?
उत्तर :
ऊर्जा संरक्षण पर ।

प्रश्न 24.
क्या कृत्रिम उपग्रह पर लोलक घड़ी प्रयुक्त की जा सकती है ?
उत्तर :
नहीं, कृत्रिम उपग्रह में भारहीनता की स्थिति होती है, अतः 8 का प्रभावी मान शून्य होता है।

प्रश्न 25.
निम्न स्थितियों में प्रत्यानयन बल कौन प्रदान करेगा-
(i) यदि स्प्रिंग को दबाकर कम्पन के लिए छोड़ दिया जाये।
(ii) यदि नली में पारे को विस्थापित करके छोड़ दिया जाये।
(iii) यदि सरल लोलक को माध्य स्थिति से विस्थापित कर छोड़ दिया जाये।
हल :
(i) स्प्रिंग के पदार्थ की प्रत्यास्थता के द्वारा
(ii) पारे के भार के द्वारा
(iii) लोलक के भार के द्वारा।

लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
जब लोलक घड़ी को पर्वत चोटी पर ले जाया जाये तो क्या यह समय ग्रहण करेगी या खाएगी ?
उत्तर :
पर्वत की चोटी पर जाने पर गुरुत्वीय त्वरण के मान घट जाने की वजह से आवर्तकाल बढ़ जायेगा, अतः घड़ी सुस्त हो जायेगी और समय ग्रहण करेगी।

प्रश्न 2.
पोषित कम्पन क्या होते हैं?
उत्तर :
यदि कम्पन करने वाली वस्तु को किसी बाह्य अनावर्ती स्रोत से ऊर्जा देकर उसके स्वाभाविक कम्पनों का आयाम समय के साथ नियत रखा जाये तो इन कम्पनों को पोषित कम्पन कहते हैं, जैसे-विद्युत् पोषित स्वरित्र द्विभुज ।

प्रश्न 3.
प्रणोदित दोलनों से क्या तात्पर्य है? उदाहरण देकर समझाइए ।
उत्तर :
प्रणोदित दोलन (Force Oscillation ) :
“जब किसी दोलन करने वाली वस्तु पर कोई बाह्य आवर्ती बल कार्य करता है, तो प्रारम्भ में वस्तु अपनी स्वाभाविक आवृत्ति से दोलन करने का प्रयास करती है, परन्तु कुछ समय पश्चात् वह बाह्य आवर्ती बल की आवृत्ति से दोलन करने लगती है। वस्तु के इन दोलनों को प्रणोदित दोलन कहते हैं।” उदाहरण- जब तने हुए पतले तार से प्रत्यावर्ती धारा प्रवाहित करके को चुम्बक के ध्रुवों के बीच रखते हैं, तो तार प्रत्यावर्ती धारा की आवृत्ति से प्रणोदित कम्पन करने लगता है।

प्रश्न 4.
मुक्त दोलन का अर्थ एक उदाहरण द्वारा समझाइए ।
उत्तर :
मुक्त दोलन (Free Oscillation ) :
जब किसी वस्तु को जो कि दोलन कर सकती हो, उसकी साम्य स्थिति से थोड़ा-सा विस्थापित करके छोड़ दिया जाता है तो वह एक निश्चित आवृत्ति से दोलन करने लगती है। यह आवृत्ति उस वस्तु के आकार व प्रत्यास्थता इत्यादि जैसे निजी गुणों पर निर्भर करती है। इसे वस्तु की ‘स्वाभाविक आवृत्ति’ (Natural Frequency) कहते हैं।
“वस्तु के इस प्रकार के दोलन जिस पर कोई भी बाह्य बल अपना प्रभाव नहीं डाल रहा है, मुक्त दोलन कहलाते हैं। ”
उदाहरणार्थ – स्वरित्र द्विभुज (Tuning Fork) को रबर की गद्दी पर मारने से उसकी भुजाएँ अपनी स्वाभाविक आवृत्ति से कम्पन करने लगती हैं। यह आवृत्ति भुजाओं की लम्बाई, मोटाई तथा उनके पदार्थ की प्रत्यास्थता पर निर्भर करती है।
इस प्रकार स्वरित्र द्विभुज के दोलनमुक्त दोलन हैं।

प्रश्न 5.
एक कण की दोलनी गति का समीकरण \(\frac{d^2 x}{d t^2}=-b x\) है जिसमें x माध्य स्थिति से विस्थापन तथा 6 नियतांक है। कण का दोलन काल क्या होगा ?
उत्तर :

प्रश्न 6.
जब कहीं बम विस्फोट होता है तो दूर-दूर तक बनी इमारतों की खिड़कियों के काँच टूट जाते हैं। समझाइए, क्यों ?
उत्तर :
बम विस्फोट के द्वारा हवा में तरंगें उत्पन्न होती हैं। इन तरंगों से खिड़कियों के काँच में कम्पन उत्पन्न हो जाते हैं। जब इन तरंगों की आवृत्ति खिड़की के काँच की मूल आवृत्ति के बराबर हो जाती है तो कम्पनों का आयाम बहुत अधिक हो जाता है। इस स्थिति में खिड़कियों के काँच टूट जाते हैं।

प्रश्न 7.
क्या कोई कण अपनी चाल को परिवर्तित किये बिना त्वरित गति कर सकता है ?
उत्तर :
हाँ, जब कण नियत चाल से वृत्ताकार पथ पर गति करता है तो यह गति त्वरित होती है, क्योंकि इस गति में दिशा निरन्तर बदलती रहती है।

प्रश्न 8.
क्या स्वतन्त्रतापूर्वक गिरती हुई कलाई घड़ी सही समय का मापन कर सकती है ?
उत्तर :
हाँ, क्योंकि कलाई घड़ी स्प्रिंग के दोलन क्रिया पर आधारित होती है, और स्प्रिंग का आवर्तकाल (T) = 2π \(\sqrt{\frac{m}{k}}\) होता है जिसमें g (गुरुत्वीय त्वरण) का कोई पद नहीं होता है।

प्रश्न 9.
आवर्ती गति एवं दोलन गति को परिभाषित कीजिए ।
उत्तर :
“जब कोई वस्तु एक निश्चित समय में एक निश्चित पथ पर बार-बार अपनी गति को दोहराती है तो उसकी गति को आवर्ती गति कहते हैं और उस निश्चित समय को आवर्तकाल (time period) कहते हैं।” उदाहरण के लिए, पेण्डुलम की गति, घड़ी की सुइयों की गति, ग्रहों एवं उपग्रहों की गति आदि पृथ्वी सूर्य के चारों ओर 3654 दिन में अपनी परिक्रमा पूरी करती है, अतः पृथ्वी की आवर्ती गति का आवर्तकाल 365 दिन हुआ।

दोलनी या कम्पनिक गति (Oscillatory or Vibratory Motion) : जब कोई वस्तु आवर्ती गति में एक ही पथ पर किसी निश्चित बिन्दु के इधर-उधर या आगे-पीछे (to and fro ) गति करती है तो यह गति दोलनी अथवा कम्पनिक गति कहलाती है। जिस निश्चित बिन्दु के दोनों ओर दोलनी गत्ति होती है उसे माध्य स्थिति या साम्य स्थिति (mean position or equilibrium position) कहते हैं। उदाहरण के लिए; लोलक की गति, स्वरित्र द्विभुज की भुजाओं की गति आदि कम्पनिक गति के उदाहरण हैं। दोलन गति में वस्तु एक निश्चित साम्य स्थिति के एक ओर जाती है, फिर वापस उसी स्थिति में लौटकर दूसरी ओर चली जाती है और पुन: लौटकर माध्य स्थिति में आ जाती है।

प्रश्न 10.
l लम्बाई के एक सरल लोलक का गोलक ऋण आवेशित है। यदि गोलक के ठीक नीचे एक धनावेशित धातु की प्लेट रखकर लोलक का दोलन कराया जाये तो बताइए सरल लोलक के आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
ऋण आवेश तथा धन आवेश में आकर्षण बल के कारण g का प्रभावी मान बढ़ जायेगा, अत: दोलन काल घट जायेगा ।

प्रश्न 11.
किसी पुल पर सैनिकों को गुजरते समय कदम से कदम न मिलाकर चलने के निर्देश क्यों दिये जाते हैं।
उत्तर :
जब सेना किसी पुल को पार करती है तब सैनिक कदम मिलाकर नहीं चलते। इसका कारण यह है कि यदि सैनिकों के कदमों की आवृत्ति, पुल की स्वाभाविक आवृत्ति के बराबर हो जाए तो पुल बड़े आयाम के कम्पन होने लगेंगे और पुल के टूटने का खतरा हो जाएगा।

प्रश्न 12.
यदि खोखला पाइप पृथ्वी के व्यास के अनुदिश रखकर उसमें एक पिण्ड गिरा दिया जाये तो इसके वेग और त्वरण में क्या परिवर्तन होगा ?
उत्तर :
यह पिण्ड पाइप में सरल आवर्त गति करेगा, जिसकी माध्य स्थिति पृथ्वी के केन्द्र पर होगी। पृथ्वी के केन्द्र से गुजरते समय वेग अधिकतम होगा तथा पृथ्वी की सतह पर न्यूनतम और त्वरण पृथ्वी की सतह पर अधिकतम होगा तथा पृथ्वी के केन्द्र पर न्यूनतम होता है।

प्रश्न 13.
यदि सरल आवर्त गति करते हुए सरल लोलक को एक लिफ्ट में रख दिया जाये, जो ऊपर की ओर त्वरण (a) से गतिमान हो तो उसके आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
जब लिफ्ट ऊपर की ओर त्वरित होगी तो सरल लोलक पर कार्यकारी बल
R – mg = ma
या R = ma + mg = m (a + g)
या mg = m (a + g)
या g = (a + g)
∵ सरल लोलक का आवर्तकाल (T) = 2π \(\sqrt{\frac{l}{g}}\)
∵ T ∝ \(\frac{l}{\sqrt{g}}\)
∵ g बढ़ जायेगा, अतः आवर्तकाल घट जायेगा।

प्रश्न 14.
सरल आवर्त गति करते हुए किसी सरल लोलक को एक लिफ्ट में रख दिया जाये, यदि लिफ्ट त्वरण से नीचे की दिशा में त्वरित हो तो इसके आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
जब लिफ्ट (a) त्वरण से नीचे की ओर त्वरित होती है तो उसमें रखे लोलक पर प्रभावकारी बल
mg – R = ma
या R = mg – ma = m(g – a)
या mg’ = m(g – a)
या g’ = (g – a)
∵ सरल लोलक का आवर्तकाल (T) = 2π \(\sqrt{\frac{l}{g}}\)
T ∝ \(\frac{l}{\sqrt{g}}\)
∵गुरुत्वीय त्वरण का प्रभावी मान घट जाता है, इसलिए आवर्तकाल का मान बढ़ जाता है।

प्रश्न 15.
क्या दोलन करते सरल लोलक की डोरी में तनाव बल सदैव नियत रहता है ? यदि नहीं तो कब न्यूनतम व कब अधिकतम होता है ?
उत्तर :
जब लोलक माध्य स्थिति में θ कोण से विस्थापित होता है तो तनाव बल T = mg cos θ से होता है, क्योंकि θ का मान विभिन्न स्थानों पर दोलन करते समय भिन्न होगा। अतः तनाव बल का मान भी भिन्न होगा। अधिकतम विस्थापन की स्थिति में θ का मान अधिकतम होगा तथा cos θ का मान न्यूनतम होगा। इस कारण तनाव बल न्यूनतम होगा।
माध्य स्थिति पर θ = 0, cos θ = 1 जो कि cos θ का अधिकतम मान है, अतः तनाव बल अधिकतम होता है।

प्रश्न 16.
एक स्प्रिंग का स्प्रिंग नियतांक (k) है, जिसे तीन बराबर भागों में विभाजित कर दिया जाता है। प्रत्येक भाग का स्प्रिंग नियतांक क्या हो जायेगा ?
उत्तर :
चूँकि हम जानते हैं कि
k = \(\frac{F}{y}\)
जब स्प्रिंग को तीन भागों में काट दिया जाता है तो लम्बाई तीन गुनी कम हो जाती है। जिससे वल नियतांक का मान तीन गुना बढ़ जाता है।
y’ = \(\frac{y}{3}\)
∴ k’ = \(\frac{F}{y/3}=3 \frac{F}{y}\) = 3k

प्रश्न 17.
कभी-कभी भूकम्प बहुत विध्वंसकारी क्यों होता है ?
उत्तर :
जब इमारतों की मूल आवृत्ति भूकम्प के समय उत्पन्न पृथ्वी के कम्पनों की आवृत्ति के बराबर हो जाती है तो अनुनाद के कारण इमारतें बड़े आयाम के साथ कम्पन करना प्रारम्भ कर देती हैं, जिससे वह नीचे गिर जाती हैं।

प्रश्न 18.
एक सरल लोलक के धात्विक गोले का आपेक्षिक घनत्व ρ है। इसका आवर्तकाल T है यदि गोलक को पानी में डुबोया जाये तो सरल लोलक के आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
सरल लोलक का आवर्तकाल
T = 2π \(\sqrt{\frac{l}{g}}\)
यदि लोलक को पानी में डुबो दिया जाता है तो पानी से लगने वाले उछाल के कारण लोलक का आभासी भार कम होगा। अतः आभासी गुरुत्वीय त्वरण g’ का मान g से कम होगा। फलस्वरूप आवर्त काल T का मान बढ़ जायेगा।

प्रश्न 19.
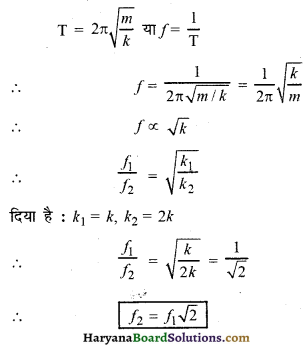
एक द्रव्यमान m एवं k बल नियतांक तथा l लम्बाई वाली स्प्रिंग से लटकाया जाता है। इस द्रव्यमान की दोलन आवृत्ति f₁ है। यदि स्प्रिंग को दो बराबर भागों में काटकर उसी द्रव्यमान को एक भाग से लटका दिया जाए और नयी आवृत्ति f₂ हो तो f₁ तथा f₂ के मध्य क्या सम्बन्ध है ?
उत्तर :
स्प्रिंग को दो बराबर भागों में तोड़ने पर प्रत्येक भाग का बल नियतांक दो गुना हो जाता है।

प्रश्न 20.
सिद्ध कीजिए कि परवलयिक विभव कूप में कण सरल आवर्त गति करता है।
उत्तर :
जब कोई पिण्ड सरल आवर्त गति करता है तो उसकी माध्य स्थिति y दूरी पर स्थितिज ऊर्जा U = \(\frac{1}{2}\) ky² होती है। जब हम स्थितिज ऊर्जा U और विस्थापन में ग्राफ खींचते हैं तो एक परवलय प्राप्त होता है। इसका आकार कूप के समान होता है इस प्रकार के विभव फलन को परवलयिक विभव कूप (parabolic potential well) कहते हैं। सरल आवर्त गति इस प्रकार के कूप में पायी जाती है।
स्थितिज ऊर्जा U = \(\frac{1}{2}\) ky²
कण पर लगने वाला परिणामी बल
F = \(– \frac{d}{dy}\) |U|
या F = \(– \frac{d}{dy}\) (\(\frac{1}{2}\) ky²)
= \(\frac{1}{2}\) k . 2y
या F = -ky
स्पष्ट है कि प्रत्यानयन बल विस्थापन के समानुपाती होता है। जिसकी दिशा माध्य स्थिति की ओर होती है अतः पिण्ड सरल आवर्त गति करेगा।

प्रश्न 21.
यदि आपको एक हल्का स्प्रिंग, एक मीटर स्केल और एक ज्ञात द्रव्यमान दे दिया जाये तो आप घड़ी का उपयोग किये बिना आवर्तकाल कैसे ज्ञात करोगे ?
उत्तर :
हम दिये गये द्रव्यमान को स्प्रिंग से लटका देते हैं और स्केल की सहायता से स्प्रिंग में विस्तार ज्ञात कर लेते हैं। इस प्रकार स्प्रिंग के बल नियतांक की गणना की जा सकती है।
F = k . l लेकिन F = mg
kl = mg
k = \(\frac{mg}{l}\),
जहाँ l = स्प्रिंग की लम्बाई में वृद्धि
स्प्रिंग का आवर्तकाल (T) = 2π\(\sqrt{\frac{m}{k}}\)
k का मान रखने पर,
T = 2π \(\sqrt{\frac{m}{m g / l}}=\sqrt{\frac{l}{g}}\)
l तथा g के मान ज्ञात हैं, अतः T का मान ज्ञात हो सकता है।

प्रश्न 22.
सरल लोलक में लोहे के गोलक के स्थान पर उसी आकार का चाँदी का गोलक लटका कर प्रयोग करने पर आवर्तकाल पर क्या प्रभाव पड़ेगा ?
उत्तर :
अपरिवर्तित रहेगा क्योंकि सरल लोलक का आवर्तकाल द्रव्यमान तथा घनत्व पर निर्भर नहीं करता है।

प्रश्न 23.
सरल आवर्त गति कर रहे कण द्वारा एक सम्पूर्ण दोलन में कितना कार्य करना पड़ेगा ?
उत्तर :
कार्य (W) = बल × विस्थापन
चूँकि सम्पूर्ण दोलन में विस्थापन = 0
∴ W = 0
अतः कार्य शून्य होगा।

प्रश्न 24.
समान द्रव्यमान के दो पिण्ड P तथा Q दो द्रव्यमानहीन स्प्रिंगों से अलग-अलग लटके हैं। स्प्रिंगों के बल नियतांक क्रमशः k₁ तथा k₂ हैं यदि दोनों पिण्ड ऊर्ध्वाधर तल में इस प्रकार कम्पन करते हैं कि उनके अधिकतम वेग समान हों, तब P तथा Q के कम्पन के आयाम में क्या अनुपात होगा ?
उत्तर :
चूँकि दो पिण्ड P तथा Q के अधिकतम वेग समान हैं-
∴ P का अधिकतम वेग = Q का अधिकतम वेग
a₁ω₁ = a₂ω₂
या a₁ × \(\frac{2л}{T_1}\) = a₂ × \(\frac{2л}{T_2}\)
या a₁ × \(\sqrt{\frac{k_1}{m}}\) = a₂ × \(\sqrt{\frac{k_2}{m}}\)
या \(\frac{a_1}{a_2}\) = \(\sqrt{\frac{k_2}{k_1}}\)

प्रश्न 25.
एक सरल लोलक जिसके धागे की लम्बाई (l) तथा गोलक का दव्यमान m है, ऊर्ध्वाधर तल में θ कोण के वृत्तीय चाप पर गति कर रहा है। चाप के अन्तिम सिरे पर m द्रव्यमान का एक अन्य गोलक जो स्थिर स्थिति में रखा है से टकराता है तो गतिशील गोलक द्वारा स्थिर गोलक को कितना संवेग दिया जायेगा ?
उत्तर :
शून्य (0), क्योंकि अन्तिम बिन्दु पर गोलक का वेग शून्य होता है इसी कारण संवेग शून्य होगा।

प्रश्न 26.
l लम्बाई की एक स्प्रिंग का बल नियतांक & है, जब इस पर भार लटकाया जाता है तो इसकी लम्बाई में वृद्धि होती है। यदि स्प्रिंग को दो बराबर टुकड़ों में काटकर तथा उन्हें समान्तर क्रम में रखकर उन पर वही भार » लटकायें तो उसकी लम्बाई पर क्या प्रभाव पड़ेगा ?
उत्तर :
स्प्रिंग को दो बराबर भागों में बाँटने पर उसकी स्प्रिंग का बल नियतांक दो गुना हो जायेगा। चूंकि स्प्रिंग दो स्प्रिंगों में बदल जाती हैं जिन्हें समान्तर क्रम में जोड़ने पर परिणामी बल नियतांक 46 हो जायेगा।
भार समान है इसलिए
∵ x ∝ \(\frac{1}{k}\)
∴ \(\frac{x_1}{x_2}=\frac{k_1}{k_2}=\frac{4k}{k}=4\)
x₂ = \(\frac{x_1}{4}\)

प्रश्न 27.
यदि हम अपने कान के पास एक गिलास रख लें, तो हमें गुन-गुन की ध्वनि सुनाई देती है, क्यों ?
उत्तर :
वातावरण के कणों के कम्पनों की आवृत्ति गिलास में भरी वायु की स्वाभाविक आवृत्ति के बराबर हो जाती है, जिससे अनुनाद की घटना होती है। अतः हमें गुन-गुन की ध्वनि सुनाई देती है।

प्रश्न 28.
ऊँचा सुनने वाला व्यक्ति अपने कान के पीछे हाथ क्यों लगा लेता है ?
उत्तर :
अनुनाद की घटना उत्पन्न करने के लिए, जिससे उसे स्पष्ट ध्वनि सुनाई दे।

प्रश्न 29.
स्प्रिंग का बल नियतांक किन कारकों पर निर्भर करता है ?
उत्तर :
किसी स्प्रिंग का बल नियतांक, स्प्रिंग के पदार्थ की प्रकृति, स्प्रिंग की बनावट एवं उसकी भौतिक अवस्था पर निर्भर करता है, अर्थात् मुलायम स्प्रिंग के लिए k का मान कम तथा कठोर स्प्रिंग के लिए k का मान अधिक होता है।
∴ \(k_{\text {कठोर }}>k_{\text {मुलायम }}\)

दीर्घ उत्तरीय प्रश्न (Long Answer Type Question)

प्रश्न 1.
सरल आवर्त गति के आवश्यक प्रतिबन्ध बताइए तथा सिद्ध कीजिए कि किसी वृत्त की परिधि पर एकसमान कोणीय वेग से गतिमान बिन्दु का वृत्त पर प्रक्षेप सरल आवर्त गति करता है ?
उत्तर :
रैखिक सरल आवर्त गति (Linear Simple Harmonic Motion) :
किसी वस्तु की रैखिक सरल आवर्त गति होने के लिए निम्नलिखित तीन प्रतिंबन्ध हैं–
(i) वस्तु की गति एक स्थिर बिन्दु (साम्य स्थिति) के इधर-उधर सरल रेखा में हो।
(ii) वस्तु पर कार्यरत् प्रत्यानयन बल अर्थात् वस्तु में उत्पन्न त्वरण सदैव माध्य स्थिति से वस्तु के विस्थापन के अनुक्रमानुपाती हो अर्थात् a ∝ (-y) जहाँ (-) चिह्न यह दर्शाता है कि त्वरण a की दिशा सदैव विस्थापन y की दिशा के विपरीत होती है।
(iii) बल अर्थात् त्वरण सदैव साम्य स्थिति की ओर दिष्ट हो।
इस प्रकार सरल आर्वत गति में प्रत्यानयन बल, साम्य स्थिति से विस्थापन के रामानुपाती रंध्या जिपरीत दिशा में होता है। अर्थात्
F ∝ -y
F = -k y …………(1)
यहाँ F प्रत्यानयन बल, y साम्य स्थिति से विस्थापन तथा k प्रत्यानयन बल नियतांक कहलाता है, जिसका मात्रक न्यूटन/मीटर होता है।
प्रत्यानयन बल (F) तथा विस्थापन (y) में वक्र निम्न प्रकार रैखिक प्राप्त होता है-

रैखिक सरल आवर्त गति का अवकल समीकरण :
माना कि किसी वस्तु का द्रव्यमान m है जिस पर F बल आरोपित है।
वस्तु की गति में त्वरण a = \(\frac{F}{m}\)
लेकिन समीकरण (l) से F = -k y

सरल आवर्त गति : एकसमान वृत्तीय गति में प्रक्षेप (Simple Harmonic Motion : Project in Uniform Circular Motion) :
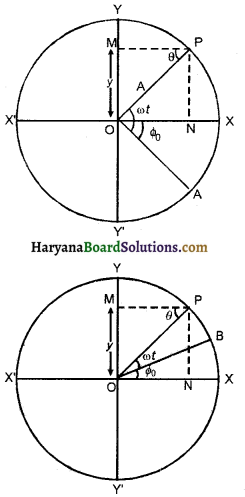
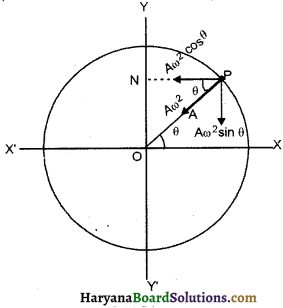
माना कोई कण त्रिज्या (A) के वृत्तीय पथ पर एकसमान कोणीय वेग ω से घूम रहा है। परिभाषा के अनुसार कण की गति आवर्ती गति तो है, परन्तु सरल आवर्त गति नहीं है।

जब कण बिन्दु N पर है, तो बिन्दु N से वृत्त के व्यास YY’ पर डाले गये लम्ब का पाद P बिन्दु पर मिलता है। जब कण Y पर है, तो लम्ब का पाद भी Y पर है। जब कण X’ पर पहुँचता है, तो लम्ब का पाद व्यास पर चलकर Y से O पर आ जाता है। जब कण Y’ पर पहुँचता है, तो पाद भी Y’ पर पहुँच जाता है। जब कण X पर पहुँचता है, तब लम्ब का पाद O पर पहुँच जाता है तथा जब कण लौटकर बिन्दु N तक पहुँचता है तो पुन: लम्ब का पाद P हो जाता है।

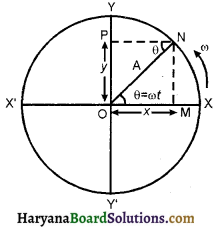
सणष्ट है कि एकसमान वृत्तीय गति पर गतिमान कण की तात्कालिक स्थितियों से किसी व्यास Y.Y’ पर डाले गये लम्ब का पाद बिन्दु O के इधर-उधर एक सरल रेखा में गति करता है। लम्ब के पाद की यह गति दोलनी गति कहलाती है।

जितने समय में कण एक समान वृत्तीय गति पर एक चक्कर पूरा कर लेता है, लम्ब का पाद भी उतने समय में एक कम्पन पूरा कर लेता है। इस समय को दोलन काल कहते हैं।

कण की स्थिति N में लम्ब के पाद P का साम्य स्थिति से विस्थापन = (OP = y) कण पर केन्द्र की ओर बल F = mω²A लगता है जिसमें m कण का द्रव्यमान है। इस बल का y दिशा में घटक F_y = mω²A sin θ, ॠणात्मक चिह्न केवल प्रदर्शित करता है कि बल F_y की दिशा केन्द्र O की ओर है।
∴ त्रिभुज OPN में,
sin θ = \(\frac{OP}{ON}=\frac{y}{a}\)
y = A sin θ
∴ F_y = -mω²A sin θ
sin θ का मान रखने पर,
F_y = -mω²A . \(\frac{y}{a}\) = -mω²y
चूँक कण का द्रव्यमान (m) तथा कोणीय वेग (ω) नियत हैं, अर्थात् कह सकते हैं कि mω² = नियतांक = k
∴ F_y = -ky
F_y ∝ -y
अर्थात् लम्ब के पाद (N) पर कार्य करने वाला बल उसकी माध्य स्थिति से विस्थापन के अनुक्रमानुपाती है तथा इसकी दिशा माध्य स्थिति की ओर ही दिष्ट है। यही सरल आवर्त गति का आवश्यक तथा पर्याप्त त्रतिबन्ध है, अतः हम कह सकते हैं कि लम्ब के पाद की गति सरल आवर्त गति है।

इस प्रकार एकसमान वृत्तीय गति पर गतिमान कण की गति आवर्ती है, परन्तु सरल आवर्त गति नहीं, जबकि एकसमान वृत्तीय ति पर गतिमान कण की तात्कालिक स्थितियों से किसी व्यास पर डाले गये लम्ब के प्रक्षेप या लम्ब पाद की गति सरल आवर्त गति है।
नोट : इस वृत्त को सरल आवर्त गति का निर्देश वृत्त (reference circle) कहते हैं।

प्रश्न 2.
सरल आवर्त गति से क्या अभिप्राय है ? सरल आवर्त गति करते हुए किसी कण के त्वरण एवं विस्थापन में सम्बन्ध स्थापित कीजिए।
उत्तर :
अनुच्छेद संख्या 14.7, 14.10 तथा 14 .12 . 2 देखें।

जब कोई कण अपनी साम्य या माध्य स्थिति के इधर-उधर गति इस प्रकार करे कि इस पर कार्यकारी बल प्रत्येक स्थिति में इसकी साम्य स्थिति की ओर दिष्ट रहे तब कण की गति सरल आवर्त गति (S.H.M.) कहलाती है।

उदाहरण के लिए, सरल लोलक के दोलन, स्प्रिंग में लटके पिण्ड के कम्पन, स्वरित्र द्विभुज की भुजाओं के कम्पन आदि।

एक वृत्त के चाप पर भी कोणीय गति हो सकती है। जैसे मरोड़ी लोलक में। वस्तु को जब माध्य स्थिति से विस्थापित किया जाता है तो उस पर एक प्रत्यानयन बल लगता है तो उसे माध्य स्थिति की ओर लाता है। सरल आवर्त गति, दोलन गति का एक विशेष रूप है, जो सबसे सरल होता है।

सरल आवर्त गति के प्रकार (Types of S.H.M.) :
सरल आवर्त गति निम्नलिखित दो प्रकार की होती हैं-
(i) रैखिक सरल आवर्त गति (Linear Simple Harmonic Motion)
(ii) कोणीय सरल आवर्त गति (Angular Simple Harmonic Motion)

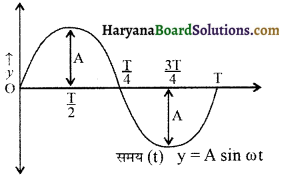
सरल आवर्त गति का विस्थापन समीकरण (Displacement equation of S.H.M.) :
माना एक कण की एकसमान वृत्तीय मार्ग पर प्रारम्भिक स्थिति X है तथा t सेकण्ड में यह कण θ कोण घूम जाता है, तो
कोणीय विस्थापन = कोणीय वेग × समय
θ = ω.t

चित्र से स्पष्ट है कि t समय में लम्ब का पाद O से P तक पहुँचता है तथा इसकी माध्य स्थिति O से विस्थापन
x = OP = ON sin θ = A sin θ

y = A sin ωt ……………(1)

∵ पथ की त्रिज्या A ही सरल आवर्त गति का आयाम है अतः

y = A sin ωt ……………(1)

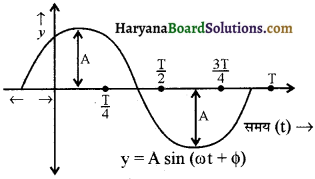
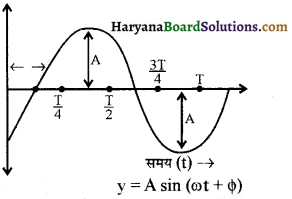
व्यापक रूप में प्रारम्भिक स्थिति को कहीं भी माना जा सकता है। माना कण की प्रारस्भिक स्थिति A पर है एवं ∠AOX = ϕ_o एवं ∠AOP = ωt
θ = ∠XOP = ωt – ϕ₀
अतः y = A sin (ωt – ϕ₀)
एवं x = A cos (ωt – ϕ₀)

– ϕ₀ को प्रारम्भिक कला कहते हैं। अगर कण की प्रारम्भिक स्थिति B पर है

एवं ∠BOX = ϕ₀
तथा ∠BOP = ωt
तब θ = ∠XOP = ωt + ϕ₀
अतः y = A sin (ωt + ϕ₀)
एवं x = A cos (ωt + ϕ₀)
यहाँ + ϕ₀ को प्रारम्भिक कला कहते हैं।

सरल आवर्त गति में विस्थापन-समय आलेख :

विस्थापन व समय में आलेख निम्न प्रकार होगा-
(i) जब ϕ – शून्य हो-

(ii) जब प्रारम्भिक कला कोण +ϕ हो-

(iii) जब प्रारम्भिक कला कोण -ϕ हो-

सरल आवर्त गति में त्वरण के लिए व्यंजक (Expression for Acceleration in S.H.M.) :
हम जानते हैं कि जब कोई वस्तु वृत्तीय गति करती है तो उस पर एक अभिकेन्द्रीय त्वरण लगता है। यदि वस्तु का कोणीय वेग ω एवं पथ की त्रिज्या A हो तो अभिकेन्द्रीय त्वरण का मान Aω² होगा जिसकी दिशा केन्द्र की ओर होगी अर्थात् P बिन्दु OP दिशा में होगी। इस त्वरण का हमें वह घटक चाहिए, जो व्यास YY’ के अनुदिश हो क्योंक सरल आवर्त गति करने वाले लम्बपाद N की गति इसी व्यास के अनुदिश होती है। यदि यह घटक α से व्यक्त करें तो
α = -Aω² sin θ
(यहाँ ऋण चिह्न यह दर्शाता है कि त्वरण एवं विस्थापन की दिशाएँ एक-दूसरे के विपरीत हैं।)
θ = ωt
α = -Aω² sin θ
= -ω² (A sin θ)
या α = -ω²y …………..(1)
क्योंकि y = A sin ωt
कोंणीय वेग ω नियत है अतः
α ∝ -y
अर्थात् त्वरण ∝ -विस्थापन

स्पष्ट है कि सरल आवर्ते गति मे त्वरण वस्तु को साम्य स्थिति से उसके विस्थापन के अनुक्रमानुपाती होता है तथा इसकी दिशा विस्थापन की दिशा के विपरीत होती है।
(i) जब वस्तु माध्य स्थिति में होती है तो
y = 0
अतः त्वरण, α = ω²y = ω² × 0
या α = 0
(ii) जब वस्तु अधिकतम विस्थापन की स्थिति में होती है तो
y = A
अत: α_max = ω²A

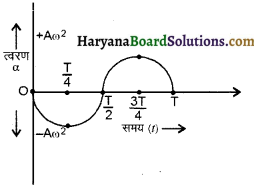
त्वरण-समय वक्र (Time-Acceleration Curve):
सरल आवर्त गति में त्वरण,
α = -Aω² sin θ
या α = -Aω² . sin \(\frac{2π}{T}\).t

इन आँकड़ों के आधार पर खींचा गया समय-त्वरण ग्राफ चित्र में प्रदर्शित है-

प्रश्न 3.
सरल आवर्त गति करते हुए पिण्ड की दोलन गतिज ऊर्जा एवं स्थितिज ऊर्जा के लिए व्यंजक स्थापित कीजिए तथा सिद्ध कीजिए कि सम्पूर्ण ऊर्जा दोलन की आवृत्ति तथा दोलन के आयाम के वर्ग के अनुक्रमानुपाती होती है।
उत्तर :
सरल आवर्त गति में ऊर्जा (Energy in S.H.M.) ;
सरल आवर्त गति करते हुए किसी कण की किसी क्षण कुल ऊर्जा को सरल आवर्त गति की कुल ऊर्जा कहते हैं। सरल आवर्त गति करते हुए कण की ऊर्जा दो प्रकार की होती है-
(i) गतिज ऊर्जा (Kinetic Energy)
(ii) स्थितिज ऊर्जा (Potential Energy)।
इस प्रकार कुल ऊर्जा स्थितिज ऊर्जा तथा गतिज ऊर्जा के योग के बराबर होती है अर्थात्
कुल ऊर्जा = गतिज ऊर्जा + स्थितिज ऊर्जा
E_T = K + U

(i) सरल आवर्त गति करते हुए कण की गतिज ऊर्जा (Kinetic Energy of Particle in S.H.M.) :
सरल आवर्त गति करते हुए कण में उसकी गति के कारण विद्यमान ऊर्जा सरल आवर्त गति की गतिज ऊर्जा कहलाती है।
माना कोई कण जिसका द्रव्यमान (m) तथा चाल u है तो कण की गतिज ऊर्जा

(ii) सरल आवर्त गति में कण की स्थितिज ऊर्जा (Potential Energy of Particle in S.H.M.):
सरल आवर्त गति में कण की स्थिति के कारण निहित ऊर्जा कण की स्थितिज ऊर्जा कहलाती है।
माना दोलन करने वाले m द्रव्यमान के पिण्ड का किसी क्षण साम्य स्थिति से विस्थापन y है, अतः पिण्ड की सरल आवर्त गति का विस्थापन समीकरण,
y = A sin ωt
जहाँ A पिण्ड का दोलन आयाम तथा ω कोणीय वेग है।
अतः पिण्ड का रेखीय वेग,
v = \(\frac{dy}{dt}=\frac{d}{dt}\)(A sin ωt)
= Aω cos ωt
पिण्ड का रेखीय त्वरण
α = \(\frac{dv}{dt}=\frac{d}{dt}\)(Aω cos ωt)
या α = -Aω². sin ωt
या α = -ω².y
क्योंकि y = A sin ωt
पिण्ड पर लगने वाला प्रत्यानयन बल
F = mα = -mω²y …………..(1)

अतः पिण्ड में अत्यन्त सूक्ष्म विस्थापन dy के विपरीत प्रत्यानयन बल द्वारा किया गया कार्य,
dW = F × (-dy) = mω²y dy
या dW = mω².y.dy
अतः पिण्ड को y = 0 से y = y तक विस्थापित करने में कृत कार्य अर्थात् y विस्थापन में पिण्ड y की स्थितिज ऊर्जा

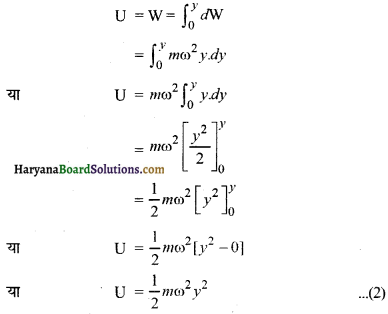
(i) जब पिण्ड का विस्थापन शून्य होता है अर्थात् पिण्ड माध्य स्थिति में होता है तो
y = 0
∴ U_min = 0 ……………(3)
(ii) जब पिण्ड अधिकतम विस्थापन की स्थिति में होता है तो,
y = a
∴ U_max = \(\frac{1}{2}\)mω²A ……………(3)

(iii) सरल आवर्त गति करते हुए कण की कुल ऊर्जा (Total Energy of Particle in S.H.M.) :
सरल आवर्त गति करने वाले कण की गतिज ऊर्जा एवं स्थितिज ऊर्जा का योग कुल ऊर्जा के बराबर होता है अर्थात्
E_T = K + U
या
E_T = \(\frac{1}{2}\)mω²(A² – y²) + \(\frac{1}{2}\)mω²A
= \(\frac{1}{2}\)mω²(A² – y² + y²)
= \(\frac{1}{2}\)mω²A²

स्पष्ट है कि कुल ऊर्जा का समय एवं स्थिति अर्थात् उसके विस्थापन पर निर्भर नहीं करती है। दूसरे शब्दों में कह सकते हैं कि, सरल आवर्त गति में कण की कुल ऊर्जा संरक्षित रहती है। स्पष्ट है कि सरल आवर्त गति में ऊर्जा संरक्षण के नियम का पालन होता है।
ω = 2πn (जहाँ n = आवृत्ति)
∴ E_T = \(\frac{1}{2}\)m(2πn)²A²
= \(\frac{1}{2}\)m.4π²n²A²
या E_T = 2mπ²n²A²
इस प्रकार सरल आवर्त गति में कण की कुल ऊर्जा,
E_T = 2mπ²n²A²
E_T ∝ A² अर्थात् (आयाम)²
तथा
E_T ∝ n² अर्थात् (आवृत्ति)²
सरल आवर्त गति में कण की गतिज ऊर्जा (K), स्थितिज ऊर्जा (U)
तथा कुल ऊर्जा (E_T) को विस्थापन के साथ निम्न चित्र में प्रदर्शित किया गया है-

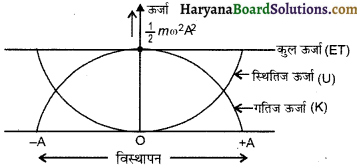
नोट – सरल आवर्त गति में कुल ऊर्जा की आवृत्ति शून्य होती है।

प्रश्न 4.
एक समान परिच्छेद् वाला लकड़ी का बेलन जल में ऊध्र्वाधर तैर रहा है। जब इसे थोड़ा नीचे दबाकर छोड़ देते हैं तो यह दोलन करने लगता है। इसका दोलनकाल जल में डूबी लम्बाई के पदों में ज्ञात कीजिए।
उत्तर :
तैरता हुआ लकड़ी का आयताकार (Oscillations of a Rectangular wooden Block):
माना एक बेलनाकार पिण्ड जिसका द्रव्यमान (m), लम्बाई (L), अनुप्रस्थ काट का क्षेत्रफल (A) तथा घनत्व (ρ) है। ρ₀ घनत्व के द्रव में आंशिक रूप से डूबकर तैर रहा है। यदि बेलन का h भाग द्रव के अन्दर है तो तैरने के सिद्धान्त से,

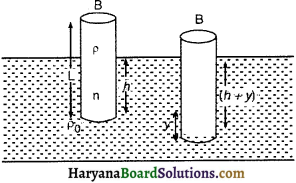
बेलन द्वारा हटाये गये द्रव का भार = बेलन का भार
(A . h) ρ₀ g = mg
m = Ah ρ₀ …………(1)
तैरने की स्थिति में यदि बेलन को थोड़ा नीचे दबाकर छोड़ देते हैं पिण्ड ऊर्ध्व रेखा में दोलन गति करने लगता है।
गति अवस्था में साम्यावस्था से y विस्थापन में प्रत्यानयन बल (F)
F = उत्प्लावन बल = हटाये गये द्रव का भार
F = -(A.y.ρ₀)g …………(2)
ऋणात्मक चिह्न का अर्थ है कि प्रत्यानयन बल, विस्थापन के विपरीत होता है।
यदि पिण्ड का त्वरण (a) हो तो गति के द्वितीय नियम से,

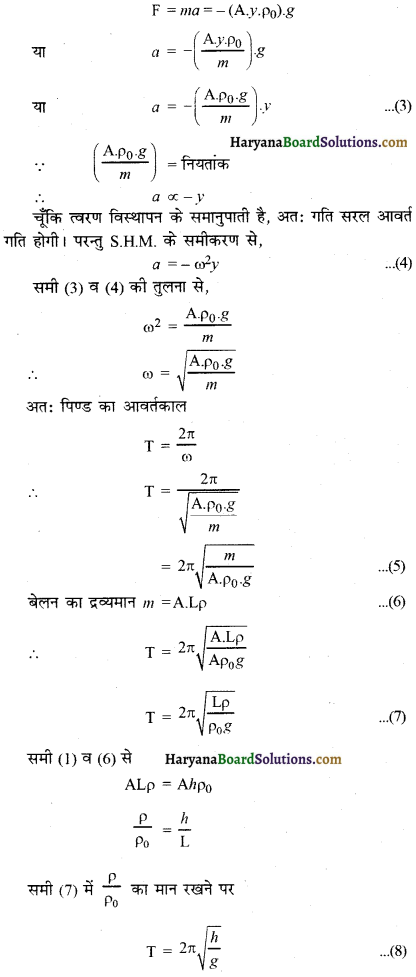
प्रश्न 5.
दोलन के अवमन्दन से क्या अभिप्राय है ? उपयुक्त उदाहरण से स्पष्ट कीजिए।
उत्तर :
अवमंदित सरल आवर्त गति (Undamped Simple Harmonic Motion) :
यदि कम्पित वस्तु का आयाम धीरे-धीरे कम होता जाता है तथा अन्त में शून्य हो जाता है तो ऐसे कम्पन अवमन्दित कम्पन कहलाते हैं। चित्र 14.37 में अवमन्दित कम्पन के आयाम को घटता हुआ दिखाया गया है। इसके उदाहरण निम्नवत् हैं-
(1) सरल लोलक के कम्पनों के आयामों का धीरे-धीरे कम होना।
(2) स्वरित्र द्विभुज के कम्पनों का आयाम भी धीरे-धीरे घटकर शून्य हो जाता है।

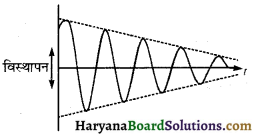
जब कोई वस्तु किसी बाह्य बल के अन्तर्गत, बाह्य बल की आवृत्ति से कम्पन करती है तो वस्तु के कम्पनों को प्रणोदित कम्पन कहते हैं। अवमन्दित कम्पन को प्रणोदित कम्पन में बदला जा सकता है; जैसे-जब कम्पन करते हुए किसी स्वरित्र द्विभुज के दस्ते को हम हाथ में पकड़े रहते हैं तो बहुत मन्द ध्वनि सुनाई पड़ती है। यदि इस दस्ते को मेज पर टिका दें तो ध्वनि तीव्र हो जाती है। इसका कारण यह है कि स्वरित्र द्विभुज को मेज पर टिकाने से स्वरित्र के कम्पन दस्ते के द्वारा मेज तक पहुँच जाते हैं तथा मेज में प्रणोदित कम्पन उत्पन्न हो जाते हैं।

प्रश्न 6.
सिद्ध कीजिए कि किसी स्प्रिंग से लटके किसी पिण्ड को साम्यावस्था में थोड़ा-सा नीचे विस्थापित करके छोड़ दिया जाए तो उसकी गति सरल आवर्त गति होगी। इसके आवर्तकाल का सूत्र भी स्थापित कीजिए।
उत्तर :
कमानी के दोलन (Oscillation of Spring) :
(i) स्प्रिंग से संलग्न द्रव्यमान के क्षैतिज तल में दोलन (Horizontal Vibrations of Mass Attached to a Spring)-माना नगण्य द्रव्यमान की एक स्प्रिंग का एक सिरा दृढ़ सतह से बँधा है और दूसरे सिरे से एक m द्रव्यमान का पिण्ड बँधा है तथा स्प्रिंग एक घर्षणरहित क्षैतिज मेज पर रखी है।
माना पिण्ड पर एक बाह्य बल F लगाकर उसमें x विस्थापन उत्पन्न करके छोड़ दिया जाता है तो द्रव्यमान क्षैतिज तल में दोलन करने लगता है।

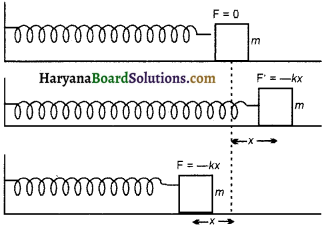
माना स्प्र्रंग का बल नियतांक k है तो x विस्थापन की स्थिति में पिण्ड पर लगने वाला प्रत्यानयन बल,
\(\overrightarrow{\mathrm{F}^{\prime}}=-k \vec{x}\)
यहाँ पर ऋण चिह्न का प्रयोग यह इंगित करता है कि F व x की दिशाएँ परस्पर विपरीत हैं।
यदि पिण्ड का त्वरण α हो तो
F’ = ma
अतः mα = -kx
या α = –\(\frac{k}{m}\)x
या α = -ω²x ……………..(1)
जहाँ ω² = \(\frac{k}{m}\) = नियतांक
∴ ω = \(\sqrt{\frac{k}{m}}\)
∴ समी (1) से α ∝ -x
या त्वरण ∝ -विस्थापन
अतः पिण्ड की गति सरल आवर्त गति होगी। इस गति में पिण्ड का आवर्त काल
\(\mathrm{T}=\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{k}{m}}}\)
\(\mathrm{~T}=2 \pi \sqrt{\frac{m}{k}}\)
स्पष्ट है कि स्प्रिंग से बँधे पिण्ड का दोलन काल पिण्ड के द्रव्यमान एवं स्प्रिंग के बल नियतांक पर निर्भर करता है।
नोट – स्प्रिंग से बँधे पिण्ड का आवर्तकाल गुरुत्वीय त्वरण (g) तथा सरल आवर्त गति के आयाम (A) पर निर्भर नहीं करता है।

प्रश्न 7.
k₁ व k₂ बल नियतांकों की दो स्प्रिंगों को लम्बाई में जोड़कर ऊध्र्वाधर लटका दिया जाता है। स्प्रिंग के निचले सिरे पर m द्रव्यमान का पिण्ड लटका दिया जाये तो पिण्ड के कम्पन का दोलन काल ज्ञात कीजिए।
उत्तर :
भारित स्प्रिंग संयोजन के दोलन (Oscillation of Loaded Spring Combination):
माना k₁ व k₂ बल नियतांकों की दो स्प्रिंगें संयुक्त की जाती हैं। दोनों स्प्रिंगों के निम्न तीन प्रकार के संयोजन हो सकते हैं-

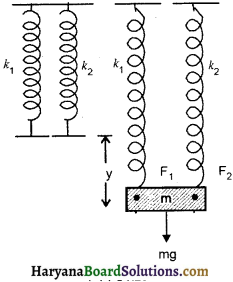
स्थिति I –
माना कि दोनों स्प्रिंगों को चित्र 14.23 की भाँति समान्तर क्रम में एक दृढ़ आधार से लटकाकर संयोजन से m द्रव्यमान का पिण्ड लटकाने पर संयोजन में y विस्थापन उत्पन्न होता है। दोनों स्प्रिंगों में क्रमशः F₁ व F₂ विरोधी बल अर्थात् प्रत्यानयन बल उत्पन्न होते हैं अतः
F₁ = -k₁ y
तथा F₂=-k₂ y
∴ संयोजन द्वारा पिण्ड पर आरोपित परिणामी प्रत्यानयन बल
F = F₁ + F₂
F = -k₁ y + (-k₂ y)
या F = -(k₁ + k₂) y
यदि संयोजन का तुल्य बल नियतांक (Equivalent force constant) k है तो
F = -ky
∴ -ky = -(k₁ + k₂) y
या k = k₁ + k₂
∴ पिण्ड का आवर्तकाल,
\(\mathrm{T}=\frac{2 \pi}{\sqrt{\frac{k}{m}}}\)
\(\mathrm{~T}=\frac{2 \pi}{\sqrt{\frac{k}{k_1+k_2}}}\)

स्थिति II –
इस स्थिति में चित्र की भाँति पिण्ड को दोनों स्प्रिंगों के मध्य बाँधते हैं और स्प्रिंगों के दोनों मुक्त सिरे दो दृढ़ आधारों के मध्य सम्बद्ध कर दिये जाते हैं। पिण्ड में चित्र की भाँति यदि y विस्थापन दिया जाता है तो एक स्प्रिंग में विरलन एवं दूसरी में उतना ही सम्पीडन हो जाता है। इस स्थिति में भी परिणामी प्रत्यानयन बल
F = F₁ + F₂

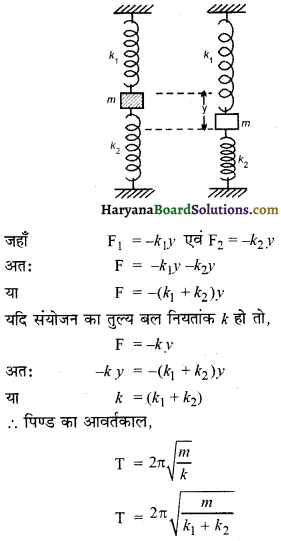
स्थिति III –
इस स्थिति में दोनों स्प्रिंगों को श्रेणी क्रम में जोड़कर संयोजन का एक सिरा दृढ़ आधार से सम्बद्ध करके दूसरे सिरे से m द्रव्यमान का पिण्ड सम्बद्ध कर देते हैं। संयोजन में उत्पन्न विस्थापन y दोनों स्प्रिंगों में उत्पन्न विस्थापनों क्रमशः y₁ व y₂ के योग के बराबर होता है। अतः
y = y₁ + y₂
दोनों स्प्रिंगें श्रेणी क्रम में जुड़ी हैं।
अतः दोनों में समान प्रत्यानयन बल F उत्पन्न होता है।

प्रश्न 8.
किसी सरल लोलक के आवर्त काल के लिए व्यंजक स्थापित कीजिए। सेकण्ड लोलक से क्या तात्पर्य है ?
उत्तर :
सरल लोलक (Simple pendulum) :
“यदि छोटे से पीतल के गोले को किसी हल्के एवं मजबूत धागे की सहायता से किसी दृढ़ आधार से लटका दें तो प्राप्त व्यवस्था को सरल लोलक कहते हैं।’ पीतल के गोले को ‘गोलक’ (bob) कहते हैं। दृढ़ आधार के जिस बिन्दु से लोलक को लटकाया जाता है, उसे ‘निलम्बन बिन्दु (point of suspension) कहते हैं। निलम्बन बिन्दु से गोले के गुरुत्व केन्द्र तक की दूरी को लोलक की प्रभावकारी लम्बाई (effective length) कहते हैं।

सेकण्ड लोलक (Second’s Pendulum) :
ऐसा सरल लोलक जिसका आवर्तकाल 2 सेकण्ड हो तो उसे सेकण्ड लोलक कहते हैं। इस प्रकार का लोलक प्रत्येक 1 सेकण्ड बाद अपनी माध्य स्थिति से गुजरता है।
सेकण्ड लोलक की प्रभावकारी लम्बाई
T = 2 सेकण्ड, g = 9.8

अतः सेकण्ड लोलक की लम्बाई लगभग 100 सेमी होती है।

नोट :
1. लोलक की प्रभावकारी लम्बाई गोलक के गुरुत्व केन्द्र से नापी जाती है। गुरुत्व केन्द्र के परिवर्तित होने पर आवर्तकाल बदल जाता है।

2. यदि खोखली गेंद (जिसमें पारा भरा है) में एक छोटा-सा छेद करने पर उसमें से बूँद-बूँद कर पारा गिरने लगेगा जिस कारण गुरुत्व केन्द्र नीचे खिसक जायेगा और प्रभावकारी लम्बाई बढ़ जायेगी। अतः आवर्तकाल बढ़ जायेगा।

3. यदि सरल लोलक किसी दिये गये घनत्व ρ वाले द्रव के अन्दर दोलन कर रहा है जहाँ ρ₀ (गोलक का घनत्व) तो सरल लोलक का आवर्तकाल बढ़ जायेगा क्योंकि-
गोलक का भार =m g=\mathrm{V} ρ g
गोलक पर कार्यरत् उत्प्लावन बल =V_{ρ0} g
∴ गोलक पर परिणामी बल = V ρ g-V ρ₀ g
F’ = V(ρ – ρ₀) g (नीचे की ओर)
अतः यदि प्रभावी गुरुत्वीय त्वरण g’ हो तो

4. अगर सरल लोलक को किसी तार द्वारा लटकाया जाये तो लोलक की प्रभावी लम्बाई ताप के बढ़ने पर बढ़ जाती है अतः सरल लोलक का आवर्तकाल बढ़ जाता है। माना ताप में परिवर्तन dθ है और α
तार का रेखीय प्रसार गुणांक है, तो तार की प्रभावी लम्बाई

प्रश्न 9.
यदि पृथ्वी के केन्द्र से होकर पृथ्वी के आर-पार एक सुरंग बनाई जाये तथा उस सुरंग में एक कण छोड़ा जाये तो दिखाइए कि कण का त्वरण सदैव सुरंग के मध्य-बिन्दु (अर्थात् पृथ्वी के केन्द्र) से विस्थापन के अनुक्रमानुपाती होता है।
उत्तर :
पृथ्वी के आर-पार एक काल्पनिक सुरंग में पिण्ड की गति (Body moving in a tunnel through The Earth) :
पृथ्वी के आर-पार काल्पनिक सुरंग की निम्न दो स्थितियाँ सम्भव हैं-
(i) जब सुरंग पृथ्वी के केन्द्र से न गुजरे-माना कि O पृथ्वी का केन्द्र है तथा AB एक सुरंग है। यदि इस सुरंग में m द्रव्यमान की एक गोली डाली जाए तो इस पर केन्द्र O की ओर एक बल (गोली का भार) mg लगेगा। बल mg का सुरंग के अनुदिश घटक mg cos θ है जो गोली में सुरंग के अनुदिश त्वरण उत्पन्न करेगा, जिससे गोली का वेग लगातार बढ़ता जाएगा। यह वेग वृद्धि का क्रम सुरंग के मध्य-बिन्दु C तक चलेगा और C पर वेग अधिकतम होगा। जैसे ही गोली बिन्दु को पार करेगी उक्त बल m g cosθ की दिशा उलट जाएगी। अब यह बल गोली की गति का विरोध करेगा, फलस्वरूप C के बाद गोली का वेग घटना प्रार्भम्भ करेगा और बिन्दु B (सुरंग का दूसरा किनारा) पर शून्य हो जाएगा। बिन्दु B पर m g cos θ बल की दिशा बिन्दु A की ओर अर्थात् केन्द्र C की ओर होगी और गोली पूर्व की भाँति गति करके पुन: A तक जाएगी। इसी क्रम की पुनरावृत्ति होती रहेगी और गोली केन्द्र C के दोनों ओर सरल आवर्त गति करती रहेगी।

अधिकतम विस्थापन की स्थिति A में गोली पर कार्यरत प्रत्यानयन

प्रश्न 10.
अनुनाद से क्या तात्पर्य है ? यान्त्रिकी, ध्वनि तथा विद्युत् -चुम्बकीय अनुनाद का एक-एक उदाहरण दीजिए।
उत्तर :
जब किसी दोलन करने वाली वस्तु पर कोई बाह्य आवर्ती बल लगाया जाता है तो वस्तु बल की आवृत्ति से प्रणोदित दोलन करने लगती है। यदि बाह्य बल की आवृत्ति, वस्तु की स्वाभाविक आवृत्ति के बराबर (अथवा इसकी पूर्ण गुणज) हो तो वस्तु के प्रणोदित दोलनों का आयाम बहुत बढ़ जाता है। इस घटना को अनुनाद (resonance) कहते हैं। बाह्य बल और वस्तु की आवृत्ति में थोड़ा सा ही अन्तर होने पर आयाम बहुत कम हो जाता है। स्पष्ट है कि अनुनाद, प्रणोदित दोलनों की ही एक विशेष अवस्था है।

अनुनाद की व्याख्या- जब बाह्य बल की आवृत्ति वस्तु की स्वाभाविक आवृत्ति के बराबर होती है तो दोनों समान कला में कम्पन करते हैं। अतः आवर्ती बल द्वारा लगाये गए उत्तरोत्तर आवेग वस्तु की ऊर्जा लगातार बढ़ाते जाते हैं और वस्तु का आयाम लगातार बढ़ता जाता है। सिद्धान्त रूप से वस्तु का आयाम अनन्त तक बढ़ता रहना चाहिए परन्तु व्यवहार में दोलन करती हुई वस्तु में वायु के घर्षण तथा ध्वनि विकिरण के कारण ऊर्जा क्षय होती रहती है। दोलन- आयाम बढ़ने के साथ-साथ ऊर्जा क्षय भी बढ़ता जाता है और एक ऐसी स्थिति आ जाती है कि बाह्य बल द्वारा प्रति दोलन दी गई ऊर्जा, वस्तु द्वारा प्रति दोलन में ऊर्जा क्षय के बराबर हो जाती है। इस स्थिति में आयाम का बढ़ना रुक जाता है।

उदाहरण- (1) यान्त्रिक अनुनाद सेना का पुल पार करना- जब सेना किसी पुल को पार करती है तब सैनिक कदम मिलाकर नहीं चलते। इसका कारण यह है कि यदि सैनिकों के कदमों की आवृत्ति, पुल की स्वाभाविक आवृत्ति के बराबर हो जाए तो पुल में बड़े आयाम के कम्पन होने लगेंगे और पुल के टूटने का खतरा हो जाएगा।

(2) ध्वनि अनुनाद – डोरियों के कम्पन– यदि समान आवृत्ति की दो डोरियाँ एक ही बोर्ड पर तनी हों तथा उनमें से एक को कम्पित किया जाए तो दूसरी स्वयं कम्पन करने लगती है।

(3) विद्युत् चुम्बकीय दोलन में अनुनाद – रेडियो द्वारा विभिन्न स्टेशनों से प्रेषित प्रोग्राम का सुनना भी अनुनाद के कारण ही सम्भव होता है विभिन्न स्टेशनों द्वारा विभिन्न आवृत्तियों की तरंगें प्रसारित की जाती हैं। रेडियो में एक विद्युत् परिपथ (L-C परिपथ) होता है जिसमें विद्युत् कम्पन उत्पन्न होते हैं। इन विद्युत् कम्पनों की स्वाभाविक आवृत्ति सूत्र T = \(\frac{1}{2π{\sqrt{LC}}}\) से ज्ञात की जाती है। जब रेडियो की ट्यून वाली घुण्डी को घुमाया जाता है तो विद्युत् परिपथ में लगे संधारित्र की धारिता C बदल जाती है जिससे विद्युत् कम्पन की स्वाभाविक आवृत्ति बदल जाती है।

जब यह आवृत्ति किसी स्टेशन द्वारा प्रसारित विद्युत् चुम्बकीय तरंगों की आवृत्ति के ठीक बराबर हो जाती है तो विद्युत् परिपथ उन तरंगों को ग्रहण कर लेता है तथा उस स्टेशन का प्रोग्राम सुनाई देने लगता है।

नोट :
अनुनाद की तीक्ष्णता एवं अवमन्दन- जिस माध्यम में कोई वस्तु दोलन करती है, उस माध्यम के कारण वस्तु पर एक अवमन्दन बल कार्य करता है, जिससे दोलनों का आयाम घटता जाता है। यदि अनुनादित वस्तु की स्वाभाविक आवृत्ति तथा बाह्य आवर्त बल की आवृत्ति में थोड़ा-सा अन्तर आ जाने पर आयाम बहुत कम हो जाता है तो अनुनाद तीक्ष्ण कहलाता है अन्यथा सपाट अनुनाद की तीक्ष्णता अवमन्दन पर निर्भर करती है। अवमन्दन के कम होने पर अनुनाद तीक्ष्ण होता है, जैसा स्वरमापी के तार में देखा जाता है।

प्रश्न 11.
प्रणोदित दोलनों से क्या अभिप्राय है ? उदाहरण देकर समझाइए। मेल्डी का प्रयोग देकर इनकी उत्पत्ति समझाइए।
उत्तर :
प्रणोदित दोलन (Forced Oscillation) ;
जब किसी दोलन करती हुई वस्तु पर कोई बाह्य आवर्त बल आरोपित किया जाता है, जिसकी आवृत्ति का मान वस्तु की स्वाभाविक आवृत्ति से भिन्न होता है तो प्रारम्भ में वस्तु स्वाभाविक आवृत्ति से दोलन करती है, लेकिन बाह्य बल के प्रभाव में वस्तु बाह्य आवर्त बल की आवृत्ति से दोलन करने लगती है। इस प्रकार के दोलन परिचालित दोलन या प्रणोदित दोलन कहलाते हैं।

अतः इस प्रकार जब कोई वस्तु किसी बाह्य आवर्ती बल के प्रभाव में, बाह्य आवृत्ति से दोलन करती है तब वस्तु के दोलन प्रणोदित दोलन कहलाते हैं।

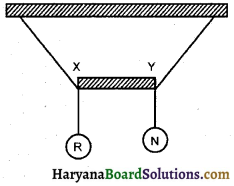
उदाहरण के लिए चित्र में दो भिन्न-भिन्न लम्बाइयों के लोलक R तथा N एक छड़ X-Y द्वारा लटकाये गये हैं। इनकी स्वाभाविक आवृत्तियाँ अलग-अलग है।

जब लोलक R को दोलन कराते हैं तब लोलक N का सम्बन्ध छड़ X-Y से होने के कारण एक आवर्त बल आरोपित होता है जिसकी आवृत्ति लोलक R की आवृत्ति के बराबर होती है उस आवर्त बल के प्रभाव से लोलक N, लोलक R की आवृत्ति से दोलन करता है। लोलक N के दोलन प्रणोदित दोलन कहलाते हैं। यहाँ लोलक Rको चालक (driver) लोलक, और N को चालित (driven) लोलक कहते हैं।

नोट-
1. जब तने हुए तार में प्रत्यावर्ती धारा प्रवाहित करके तार को चुम्बक के ध्रुवों के बीच रखते हैं तो तार प्रत्यावर्ती धारा की आवृत्ति के प्रणोदित कम्पन करने लगता है।
2 सितार वायलिन, स्वरमापी के तार पर जब किसी आवृत्ति का स्वर उत्पन्न किया जाता है तो तार के कम्पन सेतु के द्वारा खोखले ध्वनि बोर्ड में पहुँच जाते हैं। इससे बोर्ड के अन्दर की वायु में प्रणोदित दोलन उत्पन्न हो जाते हैं, जिससे ध्वनि की तीव्रता बढ़ जाती है।

माना अवमन्दित दोलक पर कोई समय के साथ विचरण करने वाले आयाम का आवर्ती बाह्य बल F(1) आरोपित किया जाता है, इसे निम्न प्रकार निरूपित करते हैं-
F (t) = F₀ cos ω_dt ………..(1)
रैखिक प्रत्यानयन बल, अवमन्दक बल तथा कालाश्रित प्रणोदित बल के संयोजी प्रभाव के अन्तर्गत कण की गति का समीकरण निम्नलिखित होगा-
ma = -kx ( t ) – bv (t) + F₀ cos ω_dt ………….(2)
जहाँ F = -kx प्रत्यानयन बल तथा F_d = -bv अवमन्दक बल है।

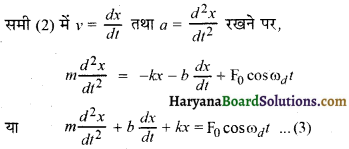
यह m द्रव्यमान वाले दोलित्र, जिस पर ०५ आवृत्ति का बल कार्यरत है, की गति का समीकरण है। दोलित्र प्रारम्भ में अपनी प्राकृतिक आवृत्ति से दोलन करता है। जब इस पर बाह्य आवर्ती वल आरोपित किया जाता है तब आरोपित बाह्य बल की आवृत्ति से दोलन होने लगते हैं। प्राकृतिक दोलन के शान्त होने पर दोलित्र का विस्थापन निम्नवत् होता है-
x (t) = A cos (ω_dt + ϕ) ……….(4)
आयाम A कोणीय आवृत्तियों तथा प्रणोदित आवृत्ति ω का फलन है जिसे हम निम्न प्रकार व्यक्त करते हैं-
A = \(\frac{\mathrm{F}_0}{\left\{m^2\left(\omega^2-\omega_d^2\right)+\omega_d^2 b^2\right\}^{1 / 2}}\) ………..(5)
तथा tan – = \(\frac{v_0}{\omega_d x_0}\) ………(6)
यहाँ m कण का द्रव्यमान ω_d तथा v₀ व x₀ समय t = 0 पर कण के क्रमशः वेग व विस्थापन हैं। इसी क्षण हम आवर्ती बल आरोपित करते हैं। ω_d व ω में अत्यधिक भिन्नता होने और इनके समीप होने की अवस्थाओं में हम दोलित्र का भिन्न-भिन्न व्यवहार देखते हैं। ये दोनों स्थितियाँ निम्नवत् हैं।

प्रश्न 12.
दर्शाइये कि U-नली में भरे एक द्रव की गति सरल आवर्त गति होती है तथा यदि द्रव को n दूरी तक विस्थापित किया जाता है तो दोलन के आवर्तकाल का सूत्र ज्ञात कीजिए।
उत्तर :
U-नली में द्रव का दोलन (Oscillation of Liquid of U-Tube) :
माना कि एक U-नली में h ऊँचाई तक द्रव भरा है। जिसकी अनुप्रस्थ काट का क्षेत्रफल (A) एकसमान है। प्रारम्भिक स्थिति में दोनों भुजाओं में द्रव का तल समान है।

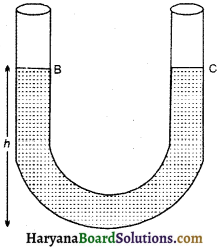
जब तल B को y दूरी नीचे बिन्दु D तक दबाया जाता है तो तल C उतनी ही दूरी y ऊपर चढ़ जाता है। इस प्रकार U-नली में दायीं भुजा में D’E अतिरिक्त द्रव स्तम्भ है। द्रव के दबाये हुए तल छोड़ देने पर सम्पूर्ण द्रव स्तम्भ D’E के भार के कारण उत्पन्न प्रत्यानयन बल के कारण ऊपर-नीचे दोलन करने लगता है।

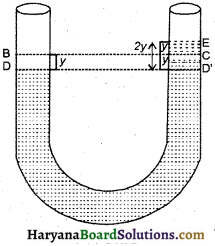
माना नली में एकांक लम्बाई में द्रव का द्रव्यमान = m हो तो द्रव पर कार्य करने वाला प्रत्यानयन बल
F = -(एकांक द्रव्यमान × लम्बाई) × g
F = -(m × 2 y) . g ………..(1)
ऋणात्मक चिह्न केवल यह प्रदर्शित करता है कि बल द्रव के विस्थापन के विपरीत दिशा में है।
अतः नली में सम्पूर्ण द्रव का द्रव्यमान
(M)=m × 2 h ………….(2)

प्रश्न 13.
सरल आवर्त गति करते हुए कण की गतिज ऊर्जा, स्थितिज ऊर्जा एवं कुल ऊर्जा में विस्थापन के साथ होने वाले परिवर्तनों की ग्राफीय विधि द्वारा विवेचना कीजिए।
उत्तर :
सरल आवर्त गति में ऊर्जा (Energy in S.H.M.) ;
सरल आवर्त गति करते हुए किसी कण की किसी क्षण कुल ऊर्जा को सरल आवर्त गति की कुल ऊर्जा कहते हैं। सरल आवर्त गति करते हुए कण की ऊर्जा दो प्रकार की होती है-
(i) गतिज ऊर्जा (Kinetic Energy)
(ii) स्थितिज ऊर्जा (Potential Energy)।
इस प्रकार कुल ऊर्जा स्थितिज ऊर्जा तथा गतिज ऊर्जा के योग के बराबर होती है अर्थात्
कुल ऊर्जा = गतिज ऊर्जा + स्थितिज ऊर्जा
E_T = K + U

(i) सरल आवर्त गति करते हुए कण की गतिज ऊर्जा (Kinetic Energy of Particle in S.H.M.) :
सरल आवर्त गति करते हुए कण में उसकी गति के कारण विद्यमान ऊर्जा सरल आवर्त गति की गतिज ऊर्जा कहलाती है।
माना कोई कण जिसका द्रव्यमान (m) तथा चाल u है तो कण की गतिज ऊर्जा

(ii) सरल आवर्त गति में कण की स्थितिज ऊर्जा (Potential Energy of Particle in S.H.M.):
सरल आवर्त गति में कण की स्थिति के कारण निहित ऊर्जा कण की स्थितिज ऊर्जा कहलाती है।
माना दोलन करने वाले m द्रव्यमान के पिण्ड का किसी क्षण साम्य स्थिति से विस्थापन y है, अतः पिण्ड की सरल आवर्त गति का विस्थापन समीकरण,
y = A sin ωt
जहाँ A पिण्ड का दोलन आयाम तथा ω कोणीय वेग है।
अतः पिण्ड का रेखीय वेग,
v = \(\frac{dy}{dt}=\frac{d}{dt}\)(A sin ωt)
= Aω cos ωt
पिण्ड का रेखीय त्वरण
α = \(\frac{dv}{dt}=\frac{d}{dt}\)(Aω cos ωt)
या α = -Aω². sin ωt
या α = -ω².y
क्योंकि y = A sin ωt
पिण्ड पर लगने वाला प्रत्यानयन बल
F = mα = -mω²y …………..(1)

अतः पिण्ड में अत्यन्त सूक्ष्म विस्थापन dy के विपरीत प्रत्यानयन बल द्वारा किया गया कार्य,
dW = F × (-dy) = mω²y dy
या dW = mω².y.dy
अतः पिण्ड को y = 0 से y = y तक विस्थापित करने में कृत कार्य अर्थात् y विस्थापन में पिण्ड y की स्थितिज ऊर्जा

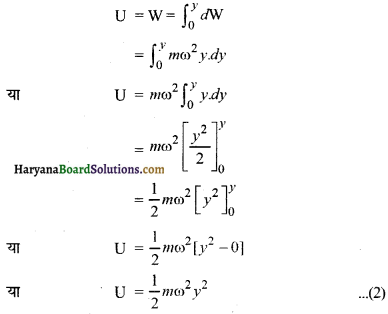
(i) जब पिण्ड का विस्थापन शून्य होता है अर्थात् पिण्ड माध्य स्थिति में होता है तो
y = 0
∴ U_min = 0 ……………(3)
(ii) जब पिण्ड अधिकतम विस्थापन की स्थिति में होता है तो,
y = a
∴ U_max = \(\frac{1}{2}\)mω²A ……………(3)

(iii) सरल आवर्त गति करते हुए कण की कुल ऊर्जा (Total Energy of Particle in S.H.M.) :
सरल आवर्त गति करने वाले कण की गतिज ऊर्जा एवं स्थितिज ऊर्जा का योग कुल ऊर्जा के बराबर होता है अर्थात्
E_T = K + U
या
E_T = \(\frac{1}{2}\)mω²(A² – y²) + \(\frac{1}{2}\)mω²A
= \(\frac{1}{2}\)mω²(A² – y² + y²)
= \(\frac{1}{2}\)mω²A²

स्पष्ट है कि कुल ऊर्जा का समय एवं स्थिति अर्थात् उसके विस्थापन पर निर्भर नहीं करती है। दूसरे शब्दों में कह सकते हैं कि, सरल आवर्त गति में कण की कुल ऊर्जा संरक्षित रहती है। स्पष्ट है कि सरल आवर्त गति में ऊर्जा संरक्षण के नियम का पालन होता है।
ω = 2πn (जहाँ n = आवृत्ति)
∴ E_T = \(\frac{1}{2}\)m(2πn)²A²
= \(\frac{1}{2}\)m.4π²n²A²
या E_T = 2mπ²n²A²
इस प्रकार सरल आवर्त गति में कण की कुल ऊर्जा,
E_T = 2mπ²n²A²
E_T ∝ A² अर्थात् (आयाम)²
तथा
E_T ∝ n² अर्थात् (आवृत्ति)²
सरल आवर्त गति में कण की गतिज ऊर्जा (K), स्थितिज ऊर्जा (U)
तथा कुल ऊर्जा (E_T) को विस्थापन के साथ निम्न चित्र में प्रदर्शित किया गया है-

नोट – सरल आवर्त गति में कुल ऊर्जा की आवृत्ति शून्य होती है।