HBSE 11th Class Physics Important Questions Chapter 13 अणुगति सिद्धांत

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 13 अणुगति सिद्धांत Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 13 अणुगति सिद्धांत

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
एक आदर्श गैस का वर्ग-माध्य-मूल वेग है-
(a) \(\mathrm{C}_{r m s}=\sqrt{3 \mathrm{RTM}}\)
(b) \(\mathrm{C}_{r m s}=\sqrt{\mathrm{RTM}}\)
(c) \(C_{r m s}=\sqrt{\frac{3 R T}{M}}\)
(d) \(\mathrm{C}_{r m s}=\sqrt{\frac{\mathrm{M}}{\mathrm{RT}}}\)
उत्तर:
(c) \(C_{r m s}=\sqrt{\frac{3 R T}{M}}\)

प्रश्न 2.
समान ताप पर हाइड्रोजन व ऑक्सीजन के अणुओं के वर्ग- माध्य-मूल वेगों का अनुपात होगा-
(a) 32:1
(b) 16:1
(c) 8:1
(d) 4:1
उत्तर:
(d) 4:1

प्रश्न 3.
गैस नियतांक का मात्रक है-
(a) कैलोरी / °C
(b) जूल / मोल
(c) जूल / मोल K
(d) जूल / किग्रा
उत्तर:
(c) जूल / मोल K

प्रश्न 4.
किसी बर्तन में P दाब पर गैस है। यदि सभी अणुओं के द्रव्यमान आधे और उनकी चालें दोगुनी कर दी जाएँ तो परिणामी दाब होगा-
(a) 4P₀
(b) P₀
(c) 2P₀
(d) P₀/2
उत्तर:
(c) 2P₀

प्रश्न 5.
यदि कोई गैस बॉयल के नियम का पालन करे तो उसके लिए PV व P के बीच ग्राफ होगा-
(a) अतिपरवलय
(b) PV अक्ष के समान्तर सरल रेखा
(c) P-अक्ष के समान्तर सरल रेखा
(d) मूलबिन्दु से गुजरती P अक्ष से 45° कोण पर सरल रेखा ।
उत्तर:
(d) मूलबिन्दु से गुजरती P अक्ष से 45° कोण पर सरल रेखा ।

प्रश्न 6.
हीलियम गैस के परमाणुओं की वर्ग-माध्य-मूल चाल हाइड्रोजन गैस के अणुओं की वर्ग-माध्य-मूल चाल का \(\frac{5}{7}\) है। यदि हाइड्रोजन गैस का ताप 0°C हो तो हीलियम का ताप लगभग होगा-
(a) 0°C
(b) 0K
(c) 273°C
(d) 100°C
उत्तर:
(a) 0°C

प्रश्न 7.
किसी गैस का परम ताप 9 गुना बढ़ा दिया जाता है। गैस के अणुओं का वर्ग माध्य-मूल वेग हो जाएगा-
(a) 9 गुना
(b) 3 गुना
(c) \(\frac{1}{3}\) गुना
(d) √3 गुना ।
उत्तर:
(b) 3 गुना

प्रश्न 8.
एक ही बर्तन में ऑक्सीजन तथा हाइड्रोजन अणुओं की औसत गतिज ऊर्जाओं का अनुपात होगा-
(a) 1:1
(c) 8:1
(b) 4:1
(d) 16:1
उत्तर:
(a) 1:1

प्रश्न 9.
एक आदर्श गैस का दाब P और इसके एकांक आयतन की गतिज ऊर्जा E में परस्पर सम्बन्ध है-
(a) P = E
(b) P = \(\frac{E}{2}\)
(c) P = \(\frac{2}{3}\) E
(d) P = \(\frac{2}{5}\) E
उत्तर:
(c) P = \(\frac{2}{3}\) E

प्रश्न 10.
यदि किसी गैस के एक ग्राम अणु की गतिज ऊर्जा 27°C पर E है तो 627°C पर यह होगी-
(a) 26
(b) 3E
(c) \(\frac{627}{27}\) E
(d) \(\frac{27}{627}\) E
उत्तर:
(b) 3E

प्रश्न 11.
त्रि-परमाणुक अरेखीय गैस की सामान्य ताप पर स्वातन्त्र्य की कोटियों की कुल संख्या है-
(a) 1
(b) 2
(c) 6
(d) 3.
उत्तर:
(c) 6

प्रश्न 12.
किसी द्वि-परमाणुक अणु की स्थानान्तरीय तथा घूर्णीय स्वातन्त्र्य कोटियों की कुल संख्या होगी-
(a) 2
(b) 3
(c) 4
(d) 5
उत्तर:
(d) 5

प्रश्न 13.
एक गुब्बारे में 4 वायुमण्डलीय दाब तथा 27°C ताप पर 1500 m³ गैस है। -3°C ताप तथा 2 वायुमण्डलीय दाब पर गैस का आयतन हो जाएगा-
(a) 2700 m³
(b) 1900 m³
(c) 1700 m³
(d) 1500 m³
उत्तर:
(a) 2700 m³

प्रश्न 14.
गैस समीकरण PV = RT में V निम्न में से किसका आयतन है-
(a) गैस की किसी मात्रा का
(b) 1 ग्राम गैस का
(c) 1 ग्राम अणु गैस का
(d) 1 लीटर गैस का।
उत्तर:
(c) 1 ग्राम अणु गैस का

प्रश्न 15.
सामान्य ताप तथा दाब (STP) पर वायु में ब्राउनियन गति में 5 × 10^-17 kg द्रव्यमान के धुएँ के कणों की वर्ग-माध्य-मूल
चाल ज्ञात कीजिए-
(a) 1.5mm gl
(b) 1.5 cm st
(c) 1.5 m sl
(d) 1.5 kms l
उत्तर:
(b) 1.5 cm st

प्रश्न 16.
नियत दाब पर 27°C की एक आदर्श गैस को इस प्रकार गर्म लिया जाता है कि उसका आयतन दो गुना हो जाता है। गैस का ताप होगा-
(a) 300°C
(b) 327°C
(c) 600°C
(d) 54°C
उत्तर:
(b) 327°C

प्रश्न 17.
स्थिर दाब पर 300 ml गैस को जो 27°C पर है, 7°C तक ठण्डा किया जाता है, तब इसका अन्तिम आयतन होगा-
(a) 540 ml
(b) 350ml
(c) 280 ml
(d) 135ml
उत्तर:
(c) 280 ml

प्रश्न 18.
किस ताप पर किसी आदर्श गैस का आयतन 0°C के आयतन का तीन गुना हो जाएगा-
(a) 546°C
(b) 182°C
(c) 819°C
(d) 646°C
उत्तर:
(a) 546°C

प्रश्न 19.
हीलियम गैस के अणुओं का वर्ग माध्य-मूल वेग हाइड्रोजन अणुओं के वर्ग माध्य-मूल वेग का वाँ भाग है। यदि हाइड्रोजन गैस का ताप °C है तो हीलियम का ताप लगभग होगा-
(a) 5°C
(b) 0K
(c) 273°C
(d) 100°C
उत्तर:
(a) 5°C

प्रश्न 20.
किसी द्वि- परमाणुक गैस के अणुओं का कमरे के ताप पर वर्ग-माध्य-मूल वेग 1930 m/see पाया गया है। गैस है-
(a) H₂
(b) F₂
(c) O₂
(d) Cl₂
उत्तर:
(b) F₂

प्रश्न 21.
अणु गति सिद्धान्त से परम शून्य ताप पर अणुओं का वेग-
(a) अनन्त होता है
(b) धनात्मक किन्तु नगण्य होता है
(c) शून्य होता है
(d) कुछ निश्चित नहीं होता।
उत्तर:
(c) शून्य होता है

प्रश्न 22.
किसी निश्चित द्रव्यमान की गैस के दाब में कितने प्रतिशत वृद्धि की जाये कि स्थिर ताप पर इसके आयतन में 10% कमी आजाये-
(a) 10%
(b) 11%
(c) 9%
(d) 8%.
उत्तर:
(b) 11%

प्रश्न 23.
चन्द्रमा पर वायुमण्डल की अनुपस्थिति का कारण है कि चन्द्रमा के पृष्ठ पर पलायन वेग का मान-
(a) वायु के अणुओं के C_rms से अधिक होता है
(b) वायु के अणुओं के C_rms से कम होता है
(c) वायु के अणुओं के C_rms से दोगुना होता है।
(d) 11.2 km/sec होता है जो कि वायु के अणुओं के C_rms से अधिक है।
उत्तर:
(d) 11.2 km/sec होता है जो कि वायु के अणुओं के C_rms से अधिक है।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
अणु गति सिद्धान्त के आधार पर किसी गैस के दाब का सूत्र लिखिए। प्रयुक्त संकेतों के अर्थ भी स्पष्ट कीजिए ।
उत्तर:
आदर्श गैस के दाब का सूत्र P = \(\frac{1}{3} \frac{m \mathrm{~N}}{\mathrm{~V}} \bar{v}^2\)
जहाँ
m → गैस के एक अणु का द्रव्यमान
\(\bar{v}\)गैस के अणुओं का वर्ग माध्य वेग
N → गैस के V आयतन में अणुओं की संख्या ।

प्रश्न 2.
सामान्य ताप एवं दाब पर एक मोल गैस का आयतन कितना होता है?
उत्तर:
सामान्य ताप व दाब पर एक मोल गैस का आयतन 22.4 लीटर होता है।

प्रश्न 3.
आदर्श गैस के लिए स्थिर ताप पर दाब P तथा घनत्व d में क्या सम्बन्ध है ?
उत्तर:
\(\frac{P}{d}\) = नियतांक

प्रश्न 4.
गैस नियतांक का मात्रक SI पद्धति में लिखिए।
उत्तर:
जूल / मोल K

प्रश्न 5.
आदर्श गैस समीकरण PV = RT से R का विमीय सूत्र लिखिए।
उत्तर:
PV = RT से,

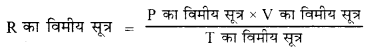
= \(\frac{\mathrm{ML}^{-1} \mathrm{~T}^{-2} \times \mathrm{L}^3}{\mathrm{~K}}\)
= \({\left[\mathrm{ML}^2 \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]}\)

प्रश्न 6.
गैस के अणु गति सिद्धान्त के अनुसार परम शून्य ताप क्या होता है?
उत्तर:
परम शून्य ताप वह ताप है, जिस पर गैस के समस्त अणु गतिहीन हो जाते हैं।

प्रश्न 7.
परम शून्य ताप पर किसी गैस की गतिज ऊर्जा कितनी होगी ?
उत्तर:
परम शून्य ताप पर किसी गैस की गतिज ऊर्जा शून्य होती है, क्योंकि किसी गैस के अणु की गतिज ऊर्जा E, परम ताप T के अनुक्रमानुपाती होती है।

प्रश्न 8.
क्या ताप बढ़ने पर स्वातन्त्र्य कोटियाँ बदल जाती हैं?
उत्तर:
ताप बढ़ने पर गैस के अणु की घूर्णन गति के साथ उसके परमाणुओं की कम्पनिक गति भी प्रारम्भ हो जाती है जिसके कारण स्वातन्त्र्य की कोटियाँ बढ़ जाती हैं।

प्रश्न 9.
किसी गैस की स्वातन्त्र्य कोटियों का क्या अर्थ है?
उत्तर:
किसी कण के पास जितने प्रकार की स्वतन्त्र गतिज ऊर्जाएँ हो सकती हैं, उनकी संख्या उस कण की स्वातन्त्र्य कोटियाँ कहलाती हैं।

प्रश्न 10.
एकपरमाणुक गैस के लिए दो विशिष्ट ऊष्माओं का अनुपात कितना होता है?
उत्तर:
\(\frac{C_P}{C_V}\) = \(\frac{5}{3}\)

प्रश्न 11.
एकपरमाणुक गैस की आन्तरिक ऊर्जा अणुओं की कौन-सी गति के कारण होती है?
उत्तर:
स्थानान्तरीय गति के कारण।

प्रश्न 12.
किसी गैस के परम ताप T तथा उसके एक अणु की औसत ऊर्जा E में क्या सम्बन्ध है?
उत्तर:
एक अणु की औसत गतिज ऊर्जा E = \(\frac{3}{2}\) K_BT,
जहाँ K_B बोल्ट्जमैन नियतांक है।

प्रश्न 13.
बोल्ट्जमैन नियतांक से क्या तात्पर्य है?
उत्तर:
सार्वत्रिक गैस नियतांक R तथा आवोगाद्रो संख्या N_A के अनुपात को बोल्ट्जमैन नियतांक कहते हैं।
K_B = \(\frac{R}{N_A}\)

प्रश्न 14.
एक सिलेण्डर में समान परम ताप T पर हाइड्रोजन तथा ऑक्सीजन गैसें भरी हैं। इनमें से किसके अणुओं की औसत गतिज अधिक होगी ?
उत्तर:
दोनों के अणुओं की औसत गतिज ऊर्जाएं बराबर होंगी-
E ∝ T

प्रश्न 15.
एक चींटी फर्श पर चल रही है। इसकी स्वातन्त्र्य की कोटि कितनी है?
उत्तर:
2 (दो)।

प्रश्न 16.
ऊर्जा के समविभाजन का नियम बताइए ।
उत्तर:
इस नियम के अनुसार किसी गैस की सम्पूर्ण ऊर्जा उसकी सभी स्वातन्त्र्य कोटियों में समान रूप से बँटी रहती है तथा परम ताप T पर प्रत्येक स्वातन्त्र्य कोटि से सम्बद्ध ऊर्जा – ABT होती है, जहाँ बोल्ट्जमैन नियतांक है।

प्रश्न 17.
एक वायुयान हवा में उड़ रहा है। इसके उड़ने की स्वातन्त्र्य कोटि कितनी है?
उत्तर:
वायुयान तीनों दिशाओं में स्वतन्त्रतापूर्वक गति कर सकता है, अतः वायुयान की स्वातन्त्र्य कोटि 3 होगी।

प्रश्न 18.
किसी दृढ़ द्विपरमाणुक गैस के लिए दो विशिष्ट ऊष्माओं का अनुपात कितना होगा?
उत्तर:
∵ γ = \(1+\frac{2}{f}\) = \(1+\frac{2}{5}\)
[∵दृढ द्वि-परमाणुक के लिए /= 5)
∴ γ = \(\frac{7}{5}\)

लघु उत्तरीय प्रश्न

प्रश्न 1.
अणु गति सिद्धान्त के आधार पर आवोगाद्रो के नियम का सत्यापन कीजिए।
उत्तर:
आवोगाद्रो का नियम (Avagadra’s Law):
इस नियम के अनुसार, “समान ताप व दाब पर सभी गैसों के समान आयतनों में अणुओं की संख्या समान होती है।”
गैसों के अणुगति सिद्धान्त से निगमन-अणुगति सिद्धान्त के अनुसार गैस का दाब

अर्थात् नियत दाब तथा ताप पर समान आयतन पर सभी गैसों में अणु की एक नियत संख्या होती है। यही आवोगाद्रो नियम है।

प्रश्न 2.
परम शून्य ताप से क्या अभिप्राय है?
उत्तर;
आदर्श गैस के ताप की अणुगतिक व्याख्या (Molecular Kinetic Interpretation of Temperature of an Ideal Gas):

अर्थात् गैस का परमताप उसकी औसत गतिज ऊर्जा के समानुपाती होता है। इस प्रकार स्पष्ट है कि आदर्श गैस की आन्तरिक ऊर्जा केवल उसके परमताप पर निर्भर करती है, दाब या आयतन पर नहीं। ताप की इस व्याख्या से स्पष्ट है कि आदर्श गैसों का अणुगति सिद्धान्त आदर्श गैस समीकरण और इस पर आधारित विभिन्न गैस नियमों के पूर्णतः संगत है।

प्रश्न 3.
कणों की ब्राउनियन गति से क्या अभिप्राय है? तथा यह किन कारकों पर निर्भर करती है ?
उत्तर:
द्रव्य की आण्विक प्रकृति (Molecular Nature Of Matter):
‘द्रव्य परमाणुओं से मिलकर बना है।’ इस सिद्धान्त को बीसर्वी शताब्दी के वैज्ञानिकों ने महत्वपूर्ण माना है। इनमें से रिचर्ड फिनमेन ने परमाणु परिकल्पना प्रस्तुत की जिसके अनुसार – “सभी वस्तुएँ परमाणुओं से बनी हैं, जो अनवरत गतिमान अत्यन्त सूक्ष्म कण हैं, बीच में अल्प दूरी होने पर ये एक-दूसरे को आकर्षित करते हैं पर एक-दूसरे में निष्पीड़ित किए जाने पर प्रतिकर्षित करने लगते हैं।”

यह विचार कि द्रव्य सतत नहीं हो सकता, कई संस्कृतियों में पहले से ही विद्यमान था। भारत में कणाद ने वैशेषिक दर्शन (छठठी शताब्दी ई.पू.) में परमाण्वीय प्रारूप का विस्तृत विकास किया। उन्होंने परमाणुओं को अविभाज्य, सूक्ष्म तथा द्रव्य को अविभाज्य अंश माना। यह भी तर्क दिया कि यदि द्रव्य को विभाजित करने के क्रम में कोई अन्त हो तो किसी सरसों के दाने तथा मेरु पर्वत में कोई अन्तर नहीं होगा।

प्रश्न 4.
अणुओं के वेग के वर्ग-माध्य-मूल मान एवं परम ताप में सम्बन्ध बताइए।
उत्तर:
गैस के अणुओं का वर्ग माध्य मूल वेग (Root mean square velocity of Gas molecules):
माना 1 ग्राम मोल गैस का आयतन V तथा ताप T है। गैस के 1 ग्राम मोल मे अणुओं की संख्या N_A = 6.02 × 10²³ इस संख्या को आवोगाद्रो संख्या कहते हैं। गैस के अणुगति सिद्धान्त के अनुसार 1 मोल गैस का दाब

समी (5) से स्पष्ट है कि वर्ग माध्य मूल वेग गैस के परम ताप पर निर्भर करता है। परम शून्य ताप पर C_rms = 0 अर्थात् वर्ग माध्य मूल वेग शून्य होने से गतिज ऊर्जा का मान भी शून्य होगा। परम शून्य ताप पर गैस में आण्विक गति समाप्त हो जाती है।

प्रश्न 5.
परम शून्य ताप पर अणु का वेग व गतिज ऊर्जा कितनी होगी ?
उत्तर:
आदर्श गैस का दाब का व्यंजक
(Expression Of Pressure Of Ideal Gas):
जब कोई गैस किसी पात्र में बन्द कर दी जाती है तो बर्तन की दीवार पर दाब लगाती है। गैस के अणुगति मॉडल के अनुसार गैस के गतिमान अणुओं द्वारा बर्तन की दीवारों से टकराने के कारण उत्पन्न होता है। जब भी गैस का कोई अणु पात्र की दीवार से टकराकर लौटता है, तो उनके संवेग में कुछ परिवर्तन होता है। संवेग संरक्षण सिद्धान्त के अनुसार यह परिवर्तन दीवार को हस्तान्तरित हो जाता है। गति के द्वितीय नियम से संवेग परिवर्तन की दर दीवार पर लगने वाले बल के बराबर होती हैं। क्योंकि गैस में असंख्यक अणु निरन्तर एक के बाद एक दीवार से टकसाते हैं। दीवार पर लगा बल स्थायी होता है। दीवार के इकाई क्षेत्रफल पर आरोपित बल ही गैस का दाब होता है।

प्रश्न 6.
हल्की गैस का विसरण भारी गैस की तुलना में आसानी से क्यों होता है ?
उत्तर:
गैस के अन्दर अणुओं का वेग उनके द्रव्यमानों पर निर्भर करता है, इसलिए भारी गैस के अणुओं की गति हल्की गैस की तुलना में कम होती है। इस कारण ही हल्की गैस, भारी गैस में आसानी से विसरित होती है।

प्रश्न 7.
किसी बर्तन में भरी गैस के ताप पर क्या प्रभाव पड़ेगा यदि उसे तीव्र गतिमान ट्रेन में रख दियाजाये ?
उत्तर:
गैस का ताप प्रति अणु स्थानान्तरीय गतिज ऊर्जा के अनुक्रमानुपाती होता है तीव्र गतिमान ट्रेन में रखने पर गैस के अणुओं की द्रव्यमान केन्द्र के सापेक्ष गति अपरिवर्तित रहती है, अतः बर्तन में भरी गैस के ताप में कोई परिवर्तन नहीं होगा।

प्रश्न 8.
यदि अणुओं के मध्य आकर्षण बल अचानक समाप्त हो जाये तो एक पात्र में भरी गैस के दाब में क्या कोई परिवर्तन होगा ?
उत्तर:
गैस के अणुओं के मध्य आकर्षण बल की अनुपस्थिति में, गैस के अणु पात्र की दीवारों से कठोरता से टकराएँगे। इस कारण गैस द्वारा लगाया गया दाब बढ़ जायेगा।

प्रश्न 9.
किसी गैस के परम ताप T तथा गैस के वर्ग माध्य वेग (C) में ग्राफ खींचिए।
उत्तर:
गैस का वर्ग माध्य वेग

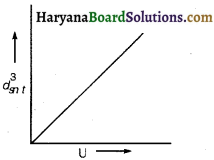
\(C_{r m s}^2=\frac{3 \mathrm{RT}}{\mathrm{M}} \text { या } c_{r m s}^2 \propto \mathrm{T}\)
अर्थात् \(C_{r m s}^2\) व T के बीच खींचा गया ग्राफ सरल रेखीय होगा।

प्रश्न 10.
“ब्राउनियन गति अवलोकनीय होती है चूँकि आवोगाद्रो संख्या निश्चित होती है।” टिप्पणी कीजिए।
उत्तर:
यदि आवोगाद्रो संख्या अनिश्चित हो तो प्रत्येक निलम्बित कण पर बहुत से परमाणुओं द्वारा बमबारी की जायेगी, इस प्रकार निलम्बित कणों को प्रदान किया गया कुल आवेग शून्य होगा। इसलिए कर्णों का गमन नगण्य हो जायेगा और इनको प्रेक्षित नहीं किया जा सकता।

प्रश्न 11.
एक प्रयोग में एक गैस एक अतिरिक्त नियम VP²= नियतांक का पालन करती है। प्रारम्भ में गैस का ताप T तथा आयतन V है। इसके प्रसार के पश्चात् इसका आयतन 2V हो जाता है, तो इसका ताप कितना होगा?
लागू
उत्तर – आदर्श गैस का समीकरण PV = RT सभी प्रक्रमों के लिए होता है।
अतिरिक्त प्रतिबन्ध है-
VP² = नियतांक ……….(1)
समीकरण PV = RT से,
P= \(\frac{RT}{V}\) ……….(2)
यह मान समीकरण (1) में रखने पर,
V(\(\frac{RT}{V}\))² = नियतांक
या \(\frac{T^2}{V}\) = नियतांक (चूँकि R = नियतांक)
यदि अंतिम आयतन V’ तथा ताप T’ हो, तो

प्रश्न 12.
किसी पात्र में P₀ दाब पर गैस भरी है। यदि अणुओं का द्रव्यमान आधा व चाल दोगुनी कर दी जाये तो परिणामी दाब क्या होगा ?
उत्तर:
अणु गति सिद्धान्त के अनुसार,

प्रश्न 13.
एक पिस्टनयुक्त सिलेण्डर में निश्चित ताप व दाब पर गैस भरी है। अणु गति सिद्धान्त से स्पष्ट कीजिए-
(i) ताप बढ़ने पर गैस का दाब बढ़ जाता है।
(ii) पिस्टन को बाहर खींचने पर दाब घट जाता है।
उत्तर:
(i) ताप बढ़ाने से गैस के अणुओं की औसत चाल बढ़ जाती है। इससे सिलेण्डर की दीवार से प्रति सेकण्ड अधिक अणु टकराते हैं तथा प्रत्येक टक्कर में दीवार को अधिक संवेग हस्तान्तरित होता है। इन दोनों ही कारणों से दाब बढ़ जाता है।

(ii) आयतन बढ़ने से अणुओं को गति करने के लिए अधिक स्थान मिलता है, अतः दीवारों से प्रति सेकण्ड कम अणु टकराते हैं। इसके अतिरिक्त ये टक्करें अब दीवारों के बड़े क्षेत्रफल पर होती हैं। इन दोनों ही कारणों से दाब घट जाता है।

प्रश्न 14.
ब्राउनियन गति तापमान के साथ क्यों बढ़ जाती है ?
उत्तर:
क्योंकि ताप बढ़ जाता है, इसलिए अणु अधिक तेज गति करते हैं और इस तरह निलम्बित कण पर अधिक बल लगाते हैं यही कारण है कि ब्राउनियन गति ताप में वृद्धि से बढ़ जाती है।

प्रश्न 15.
किसी आदर्श द्वि-परमाण्विक गैस को नियत दाब पर गर्म किया जाता है प्रदान ऊष्मा का वह भाग ज्ञात कीजिए जो गैस की अन्तिम ऊर्जा में वृद्धि करता है।
उत्तर:
जब किसी गैस को गर्म किया जाता है तो प्रदान ऊष्मा का एक भाग उसकी आन्तरिक ऊर्जा बढ़ाता है, जबकि दूसरा दाब के विरुद्ध कार्य करने में खर्च होता है अर्थात्
(∆Q)_P = ∆U + ∆W
⇒ nC_P∆T = nC_V∆T + P∆V
अतः वह भाग जो आन्तरिक ऊर्जा में वृद्धि करता है
\(\frac{\mathrm{DU}}{(\mathrm{DQ})_{\mathrm{P}}}=\frac{\mathrm{C}_{\mathrm{V}}}{\mathrm{C}_{\mathrm{P}}}=\frac{1}{\gamma}=\frac{5}{7}\)
[क्योंकि y = 3 द्विपरमाण्विक गैस के लिए]

प्रश्न 16.
दो गैसों X व Y के ताप, दाब व आयतन क्रमशः T, P व V हैं। यदि गैसें मिश्रित की जायें तो मिश्रण का ताप व आयतन क्रमशः V व T ही रहते हैं। मिश्रण का दाब व द्रव्यमान ज्ञात कीजिए।
उत्तर:
डाल्टन नियम से,
मिश्रण का दाब = P₁ + P₂ = P + P = 2P
इसी प्रकार द्रव्यमान दोगुना अर्थात् 2M हो जायेगा।

प्रश्न 17.
देर तक स्कूटर चलाते रहने पर टायर में वायुदाब कुछ बढ़ जाता है, क्यों?
उत्तर:
टायर व सड़क के बीच घर्षण के कारण टायर का ताप बढ़ जाने से उसमें भरी वायु का दाव बढ़ जाता है।

प्रश्न 18.
एक बन्द बर्तन में हीलियम व नाइट्रोजन के उच्च समान ताप हैं किस गैस की प्रति अणु कुल गतिज ऊर्जा अधिक होगी ?
उत्तर:
नाइट्रोजन की, क्योंकि दोनों गैसें समान ताप पर होने से दोनों की स्थानान्तरीय गतिज ऊर्जाएँ तो समान होंगी, परन्तु नाइट्रोजन गैस द्विपरमाणुक है, अतः इसके घूर्णन की गतिज ऊर्जा अधिक होगी।

प्रश्न 19.
गैस का अवस्था समीकरण (\(P+\frac{aT^2}{V}\))V^c = (RT + b) द्वारा प्रदर्शित है, जहाँ a, b, c व R नियतांक हैं। समतापी वक्र P = BV^m – NVⁿ द्वारा प्रदर्शित है, जहाँ A व B ताप पर निर्भर हैं तब व के मान ज्ञात कीजिए।
उत्तर:
(\(P+\frac{aT^2}{V}\) )V^c = RT + b
⇒ P + aT²V^-1 = RTV^-c + bV^-c
⇒ P = (RT+ b) V^-c – (aT²) V^-1
इस समीकरण की दिये गये समीकरण P = BV^m – NVⁿ से तुलना करने पर m = -c व n = -1 प्राप्त होता है।

प्रश्न 20.
चित्र में तीन गैसों A, B व C के निश्चित मोलों के दाब (P) के सापेक्ष दाब आयतन (PV) का परिवर्तन स्थिर ताप (T) पर प्रदर्शित है। उचित तर्क देकर बताइए कि इनमें से कौन-सी गैस आदर्श गैस है

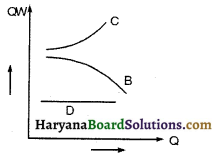
उत्तर:
आदर्श गैस के निश्चित मोलों (i) के लिए समीकरण है = PV – MRT चूँकि मोलों की संख्या व ताप T नियत हैं, अत: PV – नियत रहेगा। अतः ग्राफ C आदर्श गैस को निरूपित करता है

प्रश्न 21.
एक बक्से में हाइड्रोजन तथा ऑक्सीजन के बराबर-बराबर अणु हैं, यदि बक्से में एक सूक्ष्म छिद्र हो तो कौन-सी गैस तेजी से निकलेगी ?
उत्तर:
प्रति सेकण्ड छिद्र से गैस लीक होने का आयतन छिद्र का क्षेत्रफल × गैस की औसत चाल
चूँकि गैस के अणुओं की चाल
अणुभार हाइड्रोजन का अणुभार ऑक्सीजन की तुलना में कम होता है, अतः बक्से में से छिद्र द्वारा हाइड्रोजन गैस तेजी से निकलेगी।

प्रश्न 22.
आदर्श गैस को ठोस या द्रव अवस्था में नहीं परिवर्तित किया जा सकता है?
उत्तर:
आदर्श गैस के अणुओं के मध्य अन्तराण्विक बल शून्य माने जाते हैं। द्रव व ठोस अवस्था में अणु परस्पर बन्धन की अवस्था में होते हैं और यह बन्धन आदर्श गैस के अणुओं में सम्भव नहीं है।

प्रश्न 23.
किस ताप पर गैस के सभी अणु गति विहीन हो जाते हैं?
उत्तर:
गैस के अणु गति सिद्धान्त के अनुसार गैस की प्रति अणु औसत गतिज ऊर्जा परमताप के अनुक्रमानुपाती होती है अर्थात्
\(\frac{1}{2}\)mv_rms² = kT
\(\frac{1}{2}\)mv_rms² ∝ T
∵ v_rms² = 0
∴ T = 0
अतः परम शून्य ताप पर गैस के अणु गतिविहीन हो जाते हैं।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
अणु गति सिद्धान्त की आदर्श गैस के लिए प्रमुख परिकल्पनाएँ लिखिए। उनके आधार पर गैस दाब के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
आदर्श गैसों का अणुगति सिद्धान्त (Molecular Kinetic Theory Of Ideal Gas):
आदर्श गैसों का अणुगति सिद्धान्त निम्नलिखित मुख्य परिकल्पनाओं पर आधारित है-
1. अणु (Molecule): प्रत्येक गैस बहुत छोटे-छोटे अणुओं से मिलकर बनी मानी गई है। ये अणु दृढ़ पूर्णतः प्रत्यास्थ ठोस गोले के रूप में माने गये हैं। ये अणु द्रव्यमान बिन्दु (Mass Point) माने जाते हैं अर्थात् इनका द्रव्यमान तो होता है, परन्तु आकार तथा आयतन प्रायः नगण्य होता है। वास्तव में ऐसा होना असम्भव है क्योंकि अणुओं का आयतन गैस के आयतन की तुलना में कम चाहे जितना हो, लेकिन शून्य कदापि नहीं हो सकता।

2. गति (Motion): अणु अनवरत ( Incessant) यादृच्छिक या अनियमित गति की अवस्था में माना जाता है। ये सभी सम्भव दिशाओं में सभी सम्भव वेगों से निरन्तर गति करते रहते हैं, अतः गैस आण्विक अव्यवस्था की अवस्था में होती है।

3. संघट्ट (Collisions): अणु आपस में तथा वर्तन की दीवारों से निरन्तर टकराते रहते हैं। प्रत्येक टक्कर में अणु की चाल तथा गति की दिशा बदल जाती है, परन्तु सभी अणुओं की कुल गतिज ऊर्जा स्थिर रहती है। टक्कर के कारण आण्विक घनत्व पर कोई प्रभाव नहीं पड़ता है, अतः प्रति इकाई आयतन में अणुओं की संख्या पूरी गैस में समान रहती है।

4. बल (Force): अणुओं की टक्करें पूर्ण प्रत्यास्थ होती हैं, अतः अणुओं के मध्य कोई भी आकर्षण या प्रतिकर्षण बल कार्य नहीं करता है इसका तात्पर्य यह है कि आदर्श गैस की सम्पूर्ण ऊर्जा केवल गतिज ऊर्जा के रूप में ही होती है, आण्विक स्थितिज ऊर्जा शून्य होती है।

5. समय ( Time): टक्कर में अणुओं के सम्पर्क का समय दो उत्तरोत्तर टक्करों के मध्य लगे समय की तुलना में नगण्य होता है।

6. पथ (Path): दो उत्तरोत्तर टक्करों के बीच अणुओं का मार्ग ऋजुरेखीय होता है, इसे मुक्त पथ ( Free Path) कहते हैं। दो उत्तरोत्तर टक्करों के मध्य अणुओं के बीच औसत दूरी माध्य मुक्त पथ (Mean free Path) कहलाती है। सामान्य ताप एवं दाब पर यह 107 मी कोटि का होता है। माध्य मुक्त पथ को तय करने में लगा समय माध्य मुक्मत काल (mean free time) कहलाता है इसका मान 10-10 सेकण्ड कोटि का होता है।

7. अणुओं की गति पर गुरुत्वाकर्षण बल का कोई प्रभाव नहीं होता है क्योंकि अणुओं का द्रव्यमान नगण्य तथा वेग अत्यधिक होता है। इसी कारण पूरे बर्तन में गैस का घनत्व हर जगह समान होता है।

8. गैस के अणु सभी दिशाओं में समान रूप से दाव डालते हैं।

प्रश्न 2.
अणु गति सिद्धान्त के आधार पर ताप की क्या अविधारणा है? इसके आधार पर परम शून्य ताप की व्याख्या कीजिए।
उत्तर:
आदर्श गैस के ताप की अणुगतिक व्याख्या (Molecular Kinetic Interpretation of Temperature of an Ideal Gas):

अर्थात् गैस का परमताप उसकी औसत गतिज ऊर्जा के समानुपाती होता है। इस प्रकार स्पष्ट है कि आदर्श गैस की आन्तरिक ऊर्जा केवल उसके परमताप पर निर्भर करती है, दाब या आयतन पर नहीं। ताप की इस व्याख्या से स्पष्ट है कि आदर्श गैसों का अणुगति सिद्धान्त आदर्श गैस समीकरण और इस पर आधारित विभिन्न गैस नियमों के पूर्णतः संगत है।

प्रश्न 3.
वाण्डर वाल्स समीकरण लिखिए। समझाइए कि सामान्य गैस समीकरण में यह संशोधन किन कारणों से आवश्यक हुए?
उत्तर:
वास्तविक गैसों के लिए अवस्था समीकरण : वाण्डरवाल समीकरण
(Equation Of State For Real Gas : Vanderwaal’s Equation):
बॉयल के नियमानुसार, स्थिर ताप पर किसी गैस के निश्चित द्रव्यमान के लिए दाब P तथा आयतन V का गुणनफल एक नियतांक होता है अर्थात् PV= नियतांक प्रयोगों द्वारा यह पाया जाता है कि कोई भी वास्तविक गैस इस नियम का पूर्णतः पालन नहीं करती। अति निम्न दाब तथा उच्च ताप पर वास्तविक गैसें इस नियम का एक सीमा तक पालन करती है, परन्तु उच्च दाब तथा निम्न ताप पर वास्तविक गैसें इस नियम से बहुत अधिक विचलन दिखाती हैं। बॉयल के नियमानुसार यदि PV व P के बीच ग्राफ खींचा जाए तो P अक्ष के समान्तर एक सरल रेखा आनी चाहिए परन्तु इन ग्राफों से स्पष्ट है कि PV का मान P के बढ़ने पर नियत नहीं रहता है बल्कि हाइड्रोजन के लिए P का मान बढ़ने पर PV का मान बढ़ता है। जबकि नाइट्रोजन के लिए P के बढ़ने पर PV का मान पहले घटता है तथा फिर बढ़ने लगता है। कार्बन डाइ ऑक्साइड जैसी गैसें (अधिक ताप पर द्रवित होने वाली गैसें) तो बॉयल के नियम से और भी अधिक विचलन दिखाती हैं।

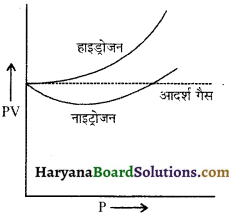
के बढ़ने पर PV का मान बढ़ता है, जबकि नाइट्रोजन के लिए P के बढ़ने पर PV का मान पहले घटता है तथा फिर बढ़ने लगता है। कार्बन डाइ ऑक्साइड जैसी गैसें (अधिक ताप पर द्रवित होने वाली गैसें तो बॉयल के नियम से और भी अधिक विचलन दिखाती हैं।
यह पाया गया है कि वास्तविक गैसों के आदर्श गैस के नियम से विचलन के दो प्रमुख कारण हैं- (i) अणुओं का अशून्य आकार तथा (ii) अन्तराण्विक अन्योन्यक्रिया ।

(i) अणुओं का अशून्य आकार :
आदर्श गैस के लिए अणुओं का आकार नगण्य माना जाता है जिससे अणुओं द्वारा घेरा गया आयतन गैस के कुल आयतन की तुलना में नगण्य होता है, परन्तु वास्तव में अणुओं का आकार नगण्य नहीं माना जा सकता है। एक वास्तविक गैस के लिए अणु का व्यास 10-10 मीटर की कोटि का होता है, जबकि गैस में दो अणुओं के बीच की औसत दूरी 10 मीटर की कोटि की होती है, अतः गैस के अणुओं का आयतन गैस के आयतन की तुलना में नगण्य नहीं माना जा सकता, विशेषकर अधिक दाब की स्थिति में जबकि गैस का स्वयं का आयतन बहुत कम होता है। यदि गैस का आयतन V है तो इस आयतन का कुछ भाग तो स्वयं अणु घेर लेते हैं, अतः अणुओं की गति के लिए उपलब्ध आयतन V से कुछ कम होगा। इसके लिए अणुओं के प्रभावी आयतन को गैस के प्रेक्षित आयतन V में से घटाना होगा। यदि अणुओं का प्रभावी आयतन 6 हो तो अणुओं को अपनी गति के लिए उपलब्ध आयतन (V – b) होगा।
अतः आदर्श गैस का आयतन Vi = V – b
जहाँ b एक नियतांक है।

(ii) अन्तराण्विक अन्योन्यक्रिया : आदर्श गैस के लिए अणुओं के बीच पारस्परिक आकर्षण अथवा प्रतिकर्षण बल को नगण्य माना जाता है, परन्तु वास्तविक गैस के लिए यह मान्यता सही नहीं है। गैस का प्रत्येक अणु दूसरे अणुओं पर एक बल आरोपित करता है, जिसे अन्तराण्विक बल कहते हैं साधारण दाब पर गैस के अणु बहुत दूर-दूर होते हैं, अतः उनके बीच अन्तराण्विक बल का मान नगण्य होता है। इसके अतिरिक्त उच्च ताप पर अणुओं की गतिज ऊर्जा अधिक होती है। जिससे अन्तराण्विक बल का उनकी गति पर प्रभाव नगण्य होता है, अतः निम्न दाब तथा उच्च ताप पर अन्तराण्विक बलों को नगण्य माना जा सकता है परन्तु उच्च दाब पर अणु एक-दूसरे के पास आ जाते हैं तथा वै एक-दूसरे को आकर्षित करने लगते हैं, अतः उच्च दाब तथा निम्न ताप पर आकर्षण बल की उपेक्षा नहीं की जा सकती।

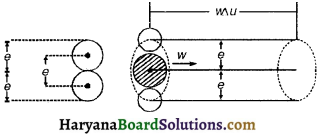
माना कि गैस किसी बर्तन में बन्द है जो अणु पूर्णतः वर्तन के अन्दर हैं, जैसे- अणु A (चित्र 13.8); वे अपने चारों ओर के अणुओं द्वारा समान रूप से आकर्षित होते हैं, अतः ऐसे अणुओं पर परिणामी अन्तराण्विक बल शून्य होता है, परन्तु जो अणु वर्तन की दीवार के समीप हैं, जैसे- अणु B उन पर परिणामी अन्तराण्विक बल अन्दर की ओर कार्य करता है जिससे वे अन्दर की ओर खिंचते हैं। इस खिचाव के कारण दीवार से टकराते समय अणु के संवेग में कुछ कमी आ जाती है। जिससे अणु दीवार पर उतना बल आरोपित नहीं कर पाता जितना कि वह अन्तराण्विक बल की अनुपस्थिति में करता है। अतः गैस का प्रेक्षित दाब उसके वास्तविक दाब से कम होता है। यदि दाब में यह कमी ß हो तो गैस का वास्तविक दाब (P + ß) रखना होगा।

ß का मान दो बातों पर निर्भर करता है- (i) दीवार के समीप अणु को आकर्षित करने वाले अणुओं की प्रति एकांक आयतन में संख्या पर, (ii) दीवार के प्रति एकांक क्षेत्रफल पर प्रति सेकण्ड टकराने वाले अणुओं की संख्या पर ये दोनों कारक प्रति एकांक आयतन में अणुओं की संख्या अर्थात् गैस के घनत्व के अनुक्रमानुपाती होते हैं।
अतः दाब में कमी ß ∝ (घनत्व × घनत्व) ∝ (घनत्व)²
घनत्व ∝ \(\frac{1}{\text { आयतन (V) }}\)
अतः ß ∝ \(\frac{1}{V^2}\) अथवा ß = \(\frac{a}{V^2}\)
जहाँ गैस के 1 ग्राम अणु के लिए नियतांक है।
अतः वास्तविक दाब (P+ ß) = \(P+\frac{a}{V^2}\)
अतः आदर्श गैस समीकरण में P के स्थान पर (\(P+\frac{a}{V^2}\)) रखना होगा।

वाण्डर वाल्स समीकरण : आदर्श गैस समीकरण में अणुओं के अशून्य आकार तथा अणुओं के बीच लगने वाले अन्तराण्विक बल का संशोधन लगाने पर वास्तविक गैस के लिए निम्न समीकरण प्राप्त होता है-
(\(P+\frac{a}{V^2}\))(V – b) = RT
यह वाण्डर वाल गैस समीकरण कहलाता है तथा 6 वाण्डर वाल नियतांक कहलाते हैं। वास्तविक गैसें इस समीकरण का उच्च दाब व निम्न ताप पर भी काफी सीमा तक पालन करती हैं।

प्रश्न 4.
गैसों के अणु गति सिद्धान्त के आधार पर किसी गैस के लिए बॉयल, चार्ल्स, आवोगाद्रो तथा गेलुसाक के नियमों का निगमन कीजिए।
उत्तर:
गैसीय नियम एवं अणुगति सिद्धान्त से निगमन
(Gas Laws and Derivations of its on the Basis of Kinetic Theory)
(i) बॉयल का नियम (Boyle’s Law):
इस नियम के अनुसार, “नियत ताप पर, गैस के किसी दिए गए द्रव्यमान का दाब उसके आयतन के व्युत्क्रमानुपाती होता है।”

यही बॉयल का नियम है अर्थात् नियत ताप पर किसी गैस के निश्चित द्रव्यमान का आयतन उसके दाब के व्युत्क्रमानुपाती है।

(ii) चार्ल्स का नियम (Charle’s Law):
इस नियम के अनुसार, “नियत दाब पर किसी दी गई गैस का आयतन उसके परमताप (T) के अनुक्रमानुपाती होता है।”

(iii) दाब-ताप का नियम या गैलुसॉक का नियम (PressureTemperature law or Gay-Lussac’s Law):
इस नियम के अनुसार, “नियत आयतन पर गैस का दाब परमताप के अनुक्रमानुपाती होता है।”

प्रश्न 5.
स्वतन्त्र्यता की कोटि से क्या अभिप्राय है? ऊर्जा समवितरण से एकपरमाणुक, द्विपरमाणुक एवं त्रिपरमाणुक गैसों की विशिष्ट ऊष्माओं की व्याख्या कीजिए।
उत्तर:
एकल, द्विपरमाणुक व बहुपरमाणुक अणुओं की स्वातंत्र्य कोटियाँ (Degrees Of freedom Of monoatomic Diatomic and Polyatomic Molecules):
(a) गैस के एक-परमाण्विक अणु के लिए,
N = 1 तथा K = 0
f = 3 × 1 – 0 = 3
अर्थात् गैसों के एक परमाण्विक अणु में स्वतन्त्रता की तीन कोटियाँ होती हैं।

(b) गैस के द्वि-परमाण्विक अणु के लिए, द्वि-परमाण्विक अणु में दोनों परमाणु एक निश्चित दूरी पर आण्विक बन्ध द्वारा बँधे रहते हैं, अत:
N = 2 तथा K = 1
f = 3 × 2 – 1 = 5

(c) गैस के त्रि-परमाण्विक अणु के लिए-समतलीय त्रि-परमाण्विक अणु में तीनों परमाणु एक-दूसरे के सापेक्ष निश्चित दूरियों पर तीन आण्विकों द्वारा बद्ध रहते हैं जैसा चित्र 13.9 में प्रदर्शित है। अतः
N = 3 तथा K = 3
f = 3 × 3 – 3 = 6

अर्थात् समतलीय त्रि-परमाण्विक अणु में छः स्वतन्त्रता की कोटियाँ होती हैं।
रेखीय त्रि-परमाण्विक अणु में,
N = 3 तथा K = 2
f = 3 × 3 – 2 = 7

अर्थात् रेखीय त्रि-परमाण्विक अणु में सात स्वतन्त्रता की कोटियाँ होती हैं।
किसी बर्तन में बन्द गैस एक ऊष्मागतिक निकाय है। गैस के परमाणु अथवा अणु अनियमित गति की अवस्था में रहते हैं। उनमें विभिन्न प्रकार की गतियों के कारण गतिज ऊर्जा होती है। गैस के अणुओं की स्वतन्त्रता की कोटियाँ इस बात से भी निर्धारित की जाती हैं कि वे अणु कितने तरीके से ऊर्जा अवशोषित करते हैं। किसी निकाय के कण जितने स्वतन्त्र तरीकों से ऊर्जा अवशोषित कर सकते हैं, वे उसकी स्वतन्त्रता की कोटियाँ कहलाती हैं।

गैसों की विशिष्ट ऊष्माएँ (SPECIFIC HEAT OF A GAS)
हमें ज्ञात है कि 1 मोल गैस की परमताप पर कुल आन्तरिक ऊर्जा
U = \(\frac{1}{2} f \mathrm{RT}\) …….(1)
अवकलन करने पर
\(\frac{d \mathrm{U}}{d \mathrm{~T}}=\frac{1}{2} f \mathrm{R}\) …………..(2)
माना कि गैस को ‘स्थिर आयतन पर’ गर्म करके उसके ताप में dT वृद्धि की जाती है। तब गैस को दी गयी ऊष्मा dQ = C_VdT होगी। चूँकि आयतन स्थिर रहता है, अतः बाह्य कार्य शून्य होगा। अतः ऊष्मागतिकी के प्रथम नियम से,
dU = dQ – dW से,
dU = C_VdT
या C_V = \(\frac{dU}{dT}\) ……………(3)
समी (2) व (3) से
\(\mathrm{C}_{\mathrm{V}}=\frac{1}{2} f \mathrm{R}\)
यह गैस की स्थिर आयतन पर ग्राम-अणुक विशिष्ट ऊष्मा है। स्थिर दाब पर ग्राम-अणुक विशिष्ट ऊष्मा के लिए मेयर सम्बन्ध \(\mathrm{C}_{\mathrm{P}}-\mathrm{C}_{\mathrm{V}}=\mathrm{R}\) से
C_P = C_V + R = \(\frac{1}{2} fR\) + R
C_P = (\(\frac{f}{2}\) + 1)R
गैस की ग्राम अणुक विशिष्ट ऊष्माओं की निष्पत्ति-
\(\gamma=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}=\frac{\left(\frac{f}{2}+1\right) \mathrm{R}}{\frac{f}{2} \mathrm{R}}\)
\(\gamma=1+\frac{2}{f}\)
स्पष्ट है कि स्वातंत्र्य कोटि की संख्या f का मान बढ़ने पर γ घटता है।

प्रश्न 6.
माध्य मुक्त पथ से क्या अभिप्राय है? इसके लिए व्यंजक प्राप्त कीजिए।
उत्तर:
माध्य मुक्त पथ की अवधारणा (Concept Of Mean Free Path):
गैसों के अणुगति सिद्धान्त के अनुसार किसी गैस के अणु विभिन्न चालों से सभी सम्भव दिशाओं में लगातार गति करते रहते हैं। गति करने के दौरान ये एक-दूसरे से संघट्ट करते हैं जिससे उनकी चाल तथा गति की दिशा दोनों बदलते रहते हैं। टक्करों के समय को छोड़कर, अणु एक-दूसरे पर कोई आकर्षण बल नहीं लगाते हैं, अतः दो टक्करों के बीच अणु नियत चालों से सीधी रेखाओं में चलते हैं। यदि किसी एक अणु के पथ को प्रेक्षित किया जाए तब वह टेढ़ी-मेढ़ी सीधी रेखाओं का पथ प्राप्त होता है।

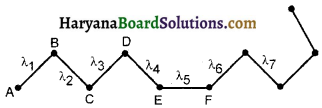
दो उत्तरोत्तर टक्करों के बीच अणु पथ की लम्बाई अणु का मुक्त पथ कहलाती है। एक दीर्घ समयावधि में अणु के सभी मुक्त पथों का औसत अणु का माध्य मुक्त पथ (Mean Free Path) कहलाता है अतः “किसी अणु का माध्य मुक्त पथ वह औसत दूरी है जो कि अणु अन्य अणुओं से दो उत्तरोत्तर टक्करों के बीच तय करता है।” इसे प्रायः λ से प्रदर्शित करते हैं।

यदि गैस के अणु द्वारा N टक्करों में तय की गई दूरियाँ क्रमश: λ₁, λ₂, λ₃ ……… λ_N

औसत मुक्त पथ λ = \(\frac{\lambda_1+\lambda_2+\lambda_3+\ldots \lambda_N}{N}\) ……….(1)
यदि कुल पथ में अणु द्वारा लिया गया समय t हो तथा अणु की औसत चाल हो तो
औसत मुक्त पथ λ = \(\frac{\lambda_1+\lambda_2+\lambda_3+\ldots \lambda_N}{N}\) …….(2)

माध्य मुक्त पथ के लिए व्यंजक (Expressions for Mean Free Path):
माना एक पात्र में गैस भरी है तथा इसके प्रति एकांक आयतन में अणु है। प्रत्येक अणु का व्यास है माना इस गैस का केवल एक अणु 1] वेग से गतिमान है तथा शेष सभी अणु स्थिर हैं। गतिमान अणु उन सभी अणुओं से टकरायेगा, जिनके केन्द्र इसके केन्द्र से दूरी पर है जैसा चित्र 13-15 में प्रदर्शित है 3 समय में अणु द्वारा तय की गई दूरी है। अत: Ar समय में यह अणु उन सभी अणुओं से टकरायेगा जिनकी त्रिज्या है तथा लम्बाई के बेलन में है।

बेलन का आयतन = πd²v.∆t
बेलन में अणुओं की संख्या = आयतन × प्रति एकांक आयतन में उपस्थित अणु
= (πd²v.∆t).n ……..(3)
यदि अणु द्वारा अन्य अणुओं से 3 समय में टक्करों की संख्या है अर्थात्
N = = πd²v.∆t.n …………(4)
औसत मुक्त पशु λ = \(\frac{v.∆t}{N}\)
= \(\frac{v \cdot \Delta t}{\pi d^2 v \cdot \Delta t \cdot n}=\frac{1}{\pi d^2 n}\)
या λ = \(\frac{1}{\pi d^2 n}\) ………..(5)
इस सूत्र को प्राप्त करने में हमने यह कल्पना की कि दूसरे सभी अणु विरामावस्था में है। परन्तु वास्तव में सभी अणु गतिमान है और संघट्ट दर अणुओं के औसत आपेक्षिक वेग द्वारा निर्धारित की जाती है। अन्य अणुओं की गति पर विचार करने पर अणु का माध्य मुक्त पथ निम्नलिखित होगा –
λ = \(\frac{1}{√2 \pi d^2 n}\) ………..(6)
यही अभीष्ट व्यंजक है, इसके अनुसार अणु का माध्य मुक्त पथ प्रति एकांक आयतन में अणुओं की संख्या के अनुक्रमानुपाती है अर्थात् यह गैस के अणु घनत्व के व्युत्क्रमानुपाती है।
आदर्श गैस के लिए
PV = NkT
n = \(\frac{N}{V}\)
P = nkT ⇒ n = \(\frac{P}{kT}\)
समीकरण (6) मैं n का मान रखने पर
λ = \(\frac{kT}{√2 \pi d^2 P}\) ………..(7)
स्पष्ट है कि
λ ∝ \(\frac{T}{P}\)
अर्थात् गैस के अणुओं का औसत मुक्त पथ गैस के परमताप के अनुक्रमानुपाती तथा गैस के दाब के व्युत्क्रमानुपाती होता है।

प्रश्न 7.
अणु गति सिद्धान्त का सम्बन्ध P = \(\frac{1}{3} r \bar{c^2}\) मानते हुए सिद्ध कीजिए कि अणु की औसत गतिज ऊर्जा गैस के परम ताप के समानुपाती होती है।
उत्तर:
आदर्श गैस के ताप की अणुगतिक व्याख्या (Molecular Kinetic Interpretation of Temperature of an Ideal Gas):

अर्थात् गैस का परमताप उसकी औसत गतिज ऊर्जा के समानुपाती होता है। इस प्रकार स्पष्ट है कि आदर्श गैस की आन्तरिक ऊर्जा केवल उसके परमताप पर निर्भर करती है, दाब या आयतन पर नहीं। ताप की इस व्याख्या से स्पष्ट है कि आदर्श गैसों का अणुगति सिद्धान्त आदर्श गैस समीकरण और इस पर आधारित विभिन्न गैस नियमों के पूर्णतः संगत है।

आंकिक प्रश्न (Numerical Questions)

आदर्श गैस समीकरण तथा इसके नियम पर आधारित

प्रश्न 1.
250 सेमी³ आयतन वाले विद्युत् बल्ब को सील करते समय 27°C ताप पारे का 10^-3 मिमी दाब था। बल्ब में अणुओं की संख्या कितनी है?
उत्तर:
8.04 × 10¹⁵

प्रश्न 2.
1 × 10^-6 m³ आयतन के वायु के बुलबुले झील की सतह के नीचे 40 मीटर गहराई पर हैं, जहाँ ताप 283K है। जब बुलबुला जल की संतह पर पहुँचे, तो इसका आयतन बताइए जल की सतह पर ताप 27°C है वायुमण्डलीय दाब = 1.01 × 10⁵ Pa
उत्तर:
4.15 × 10^-6 m³

प्रश्न 3.
किसी गैस का निश्चित आयतन पर दाब 2000 न्यूटन / मी² से परिवर्तित होकर 3000 N/m² हो जाता है। यदि प्रारम्भिक ताप 350 K था तो अन्तिम ताप ज्ञात कीजिए।
उत्तर:
525K

प्रश्न 4.
किसी फ्लास्क में 27°C ताप पर 13 ग्राम आदर्श गैस भरी है ताप बढ़कर 52°C करने पर कितनी गैस फ्लास्क से निकल जायेगी जबकि गैस का तापं 52°C व दाब पूर्ववत् ही रहें?
उत्तर:
1 ग्राम

प्रश्न 5.
अन्तरिक्ष के किसी क्षेत्र के प्रति सेमी³ आयतन में औसतन केवल 5 अणु हैं तथा वहाँ पर ताप 3 K है इतनी विरल गैस का दाब क्या है ? (बोल्ट्जमैन नियतांक (k) = 1.38 × 10^-23 जूल / K)
उत्तर:
20.7 x 10-17N/m²

अणुओं के वेगों पर आधारित

प्रश्न 6.
स्थिर दाब पर 327°C ताप की हाइड्रोजन को किस ताप तक ठण्डा किया जाए कि उसके अणुओं का वर्ग माध्य-मूल वेग पहले का आधा हो जाये ?
उत्तर:
123°C

प्रश्न 7.
तीन अणुओं के वेग क्रमश: 3v, 4v व 5v हैं। इनकी वर्ग-माध्य-मूल चाल ज्ञात कीजिए।
उत्तर:
4.08v

प्रश्न 8.
किसी ताप पर ऑक्सीजन के अणुओं की वर्ग-माध्य मूल चाल 150 मी/से है उसी ताप पर हाइड्रोजन के अणुओं की वर्ग- माध्य-मूल चाल क्या होगी ? (M_o = 32, M_H = 2)
उत्तर:
600 मी/से

प्रश्न 9.
नाइट्रोजन अणु के वर्ग माध्य-मूल वेग का मान 15°C ताप तथा पारे के स्तम्भ के 76 सेमी दाब पर ज्ञात कीजिए।
उत्तर:
5.06 × 10⁴ सेमी / से

अणुओं की ऊर्जा पर आधारित

प्रश्न 10.
27°C ताप पर हाइड्रोजन के लिए ज्ञात कीजिए-
(i) एक ग्राम अणु गैस की गतिज ऊर्जा,
(ii) एक ग्राम गैस की गतिज ऊर्जा [हाइड्रोजन का अणुभार 2, तथा R = 8.31 J mol^-1K^-1]
उत्तर:
(i) 3.74 × 10⁵ जूल
(ii) 1.87 × 10³ जूल

प्रश्न 11.
एक ग्राम अणु गैस की गतिज ऊर्जा सामान्य ताप व दाब पर ज्ञात कीजिए तथा 273°C पर इसका मान क्या होगा ?
उत्तर:
3.40 × 10³ जूल, 6.80 × 10³ जूल

प्रश्न 12.
गैस की गतिज ऊर्जा प्रति मोल, NTP पर ज्ञात कीजिए यदि गैस का घनत्व 0.178 किग्रा / घन मीटर है तथा अणुभार 4 हो ।
उत्तर:
3414 जूल

प्रश्न 13.
किसी गैस का ताप 68°C है इसको किस ताप पर गर्म किया जाये ताकि (i) अणुओं की औसत गतिज ऊर्जा दोगुनी हो जाये, (ii) अणुओं का वर्ग माध्य-मूल वेग दोगुना हो जाये ?
उत्तर:
(i) 137°C
(ii) 547°C

प्रश्न 14.
300 K ताप पर किसी गैस के अणु की माध्य गतिज ऊर्जा क्या है? इस ताप पर हाइड्रोजन गैस के किसी अणु की वर्ग-माध्य-मूल चाल क्या होगी ? (R = 8.31 J mole^-1 K^-1, N = 6.02 × 10²³ प्रति मोल तथा हाइड्रोजन के अणु का द्रव्यमान 3.34 × 10^-27 Kg)
उत्तर:
1.93 × 10³ ms^-1

औसत मुक्त पथ पर आधारित

प्रश्न 15.
100°C तथा I arm दाब पर, जल वाष्य में, जल के अणु के माध्य मुक्त पथ की गणना कीजिए। जल के अणु का व्यास 44 बोल्ट्समैन नियतांक kg = 1.38 × 10-23 JK
उत्तर:
7.2 × 10^-8 मी