HBSE 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.2

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2

प्रश्न 1.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए।
(i) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिल तथा 7 कलमों का कुल मूल्य 50 रु० है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य 46 रु० है। एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए।
हल :
(i) माना पहेली प्रतियोगिता में भाग लेने वाली कक्षा X की लड़कियों की संख्या =x
पहेली प्रतियोगिता में भाग लेने वाले कक्षा X के लड़कों की संख्या =y
प्रश्नानुसार
x+y = 10 ………. (i)
तथा x = y +4 …………. (ii)
अतः ग्राफीय निरूपण के लिए,
x + 1 = 10
y = 10 -x

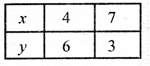
x = y + 4

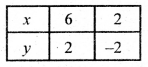
अब हम ग्राफ पेपर पर बिंदु A(4, 6) तथा बिंदु B(7, 3) लेकर उन्हें मिलाकर रेखा AB प्राप्त करेंगे जो समीकरण (i) को निरूपित करेगी तथा बिंदु C(6, 2) तथा बिंदु D(2, -2) लेकर उन्हें मिलाकर CD रेखा प्राप्त करेंगे जो समीकरण (ii) को निरूपित करेगी।

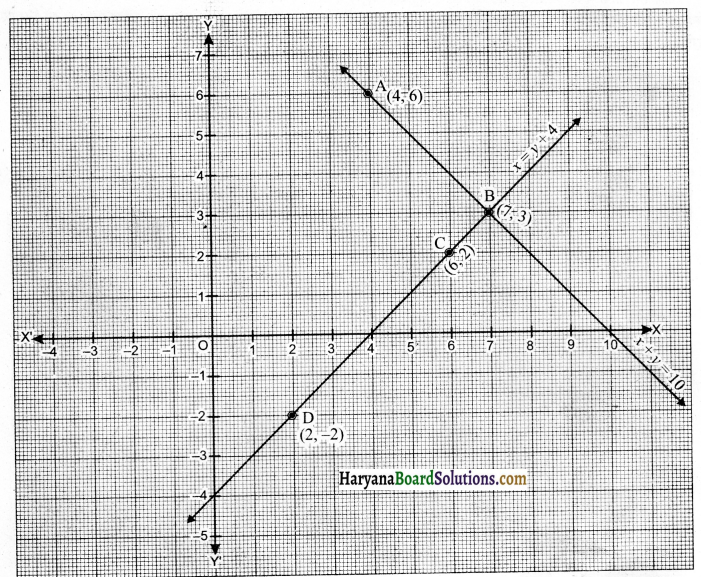
क्योंकि दो रेखाएँ AB और CD परस्पर बिंदु B(7, 3) पर काटती हैं। इसलिए रैखिक युग्म के अभीष्ट हल x = 7 व y= 3 हैं।
अतः
लड़कियों की संख्या = 7
लड़कों की संख्या = 3

(ii) माना 1 पेंसिल का मूल्य = x रु०
तथा 1 कलम का मूल्य = y रु०
प्रश्नानुसार
5x + 7y = 50
तथा 7x + 5y = 46
अतः ग्राफीय निरूपण के लिए,
5x + 7y = 50
y = \(\frac{50-5 x}{7}\)

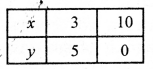
7x + 5y = 46
y = \(\frac{46-7 x}{5}\)

अब हम ग्राफ पेपर पर बिंदु A(3, 5) तथा बिंदु B(10, 0) लेकर उन्हें मिलाकर रेखा AB प्राप्त करेंगे जो समीकरण (i) को निरूपित करेगी तथा बिंदु C(3, 5) तथा बिंदु D(8, -2) लेकर उन्हें मिलाकर CD रेखा प्राप्त करेंगे जो समीकरण (ii) को निरूपित करेगी।

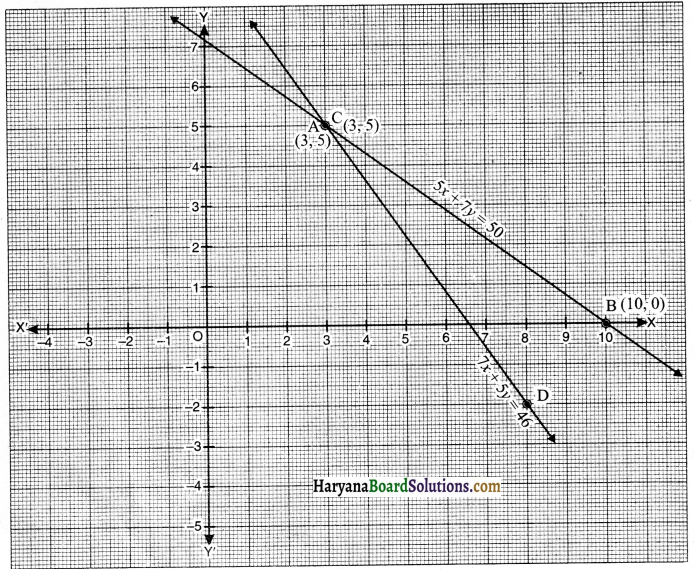
क्योंकि दो रेखाएँ AB और CD परस्पर बिंदु A(3, 5) पर काटती हैं। इसलिए रैखिक युग्म के अभीष्ट हल x = 3 व y = 5 हैं
अतः
1 पेंसिल का मूल्य = 3 रु०
1 कलम का मूल्य = 5 रु०

प्रश्न 2.
अनुपातों \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\)और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं-
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y+ 10 = 0
2x – y + 9 = 0
हल :
(i) दी गई समीकरणें हैं,
5x-4y + 8 = 0 …… (i)
7x + 6y -9 = 0 ……. (ii)
यहाँ पर a₁= 5, b₁ = -4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = -9
\(\frac{a_{1}}{a_{2}}=\frac{5}{7}, \frac{b_{1}}{b_{2}}=\frac{-4}{6}=\frac{-2}{3} \text { व } \frac{c_{1}}{c_{2}}=\frac{8}{-9}=\frac{-8}{9}\)
क्योकि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) ⇒ समीकरण युग्म का अद्वितीय हल है।
इसलिए दिए गए समीकरण युग्म द्वारा निरूपित रेखाएँ परस्पर एक बिंदु पर प्रतिच्छेद करेंगी।

(ii) दी गई समीकरणें हैं,
9x + 3y + 12 = 0 …… (i)
18x+6y+24 = 0 …… (ii)
यहाँ पर a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24
\(\frac{a_{1}}{a_{2}}=\frac{9}{18}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{12}{24}=\frac{1}{2}\)
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) ⇒ समीकरण युग्म के अनंत हल हैं।
इसलिए दिए गए समीकरण युग्म द्वारा निरूपित रेखाएँ संपाती होगी।

(iii) दी गई समीकरणे हैं,
6x – 3y + 10 = 0…… (i)
2x – y + 9 = 0 …… (ii)
यहाँ पर a₁ = 6, b₁ = -3, c₁ = 10
a₂ = 2, b₂ = -1, c₂ = 9
क्योंकि 10
\(\frac{a_{1}}{a_{2}}=\frac{6}{2}=\frac{3}{1}, \frac{b_{1}}{b_{2}}=\frac{-3}{-1}=\frac{3}{1} \text { व } \frac{c_{1}}{c_{2}}=\frac{10}{9}\)
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) ⇒ समीकरण युग्म का कोई हल नहीं है।
इसलिए दिए गए समीकरण युग्म द्वारा निरूपित रेखाएँ परस्पर समांतर होंगी।

प्रश्न 3.
अनुपातों \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगत-
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x-3y = 8; 4x-6y = 9
(iii) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
(iv) 5x-3y = 11; -10x + 6y =-22
(v) \(\frac{4}{3}\)x+2y = 8; 2x +3y = 12
हल :
(i) दी गई समीकरणे हैं, 3x +2y = 5
या 3x + 2y – 5 = 0 ………..(i)
और 2x – 3y = 7
2x – 3y – 7 = 0 ………….(ii)
यहाँ पर a₁ = 3, b₁ = 2, c₁ =-5
a₂ = 2, b₂ = -3, c₂ =-7
\(\frac{a_{1}}{a_{2}}=\frac{3}{2}, \frac{b_{1}}{b_{2}}=\frac{2}{-3}=\frac{-2}{3} \text { व } \frac{c_{1}}{c_{2}}=\frac{-5}{-7}=\frac{5}{7}\)
क्योंकि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।

(ii) दी गई समीकरणे हैं,
2x – 3y = 8
या 2x – 3y – 8 = 0 ………….(i)
और 4x – 6y = 9
या 4x – 6y – 9 = 0 ……. (ii)
यहाँ पर a₁ = 2, b₁ = -3, c₁ = -8
a₂ = 4, b₂ = -6, c₂ = -9
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2} ; \frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{-8}{-9}=\frac{8}{9}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म असंगत है।

(iii) दी गई समीकरणे हैं,
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
या \(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0 ………..(i)
और 9x – 10y = 14
या 9x – 10y – 14 = 0 ………….(ii)
यहाँ पर a₁ = \(\frac{3}{2}\)
b₁ = \(\frac{5}{3}\)
c₁ = -7
a₂ = 9, b₂ = -10, c₂ =-14
\(\frac{a_{1}}{a_{2}}=\frac{3}{2 \times 9}=\frac{1}{6}, \frac{b_{1}}{b_{2}}=\frac{5}{3 \times(-10)}=\frac{-1}{6} \text { व } \frac{c_{1}}{c_{2}}=\frac{-7}{-14}=\frac{1}{2}\)
क्योंकि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।

(iv) दी गई समीकरणें हैं,
5x – 3y = 11
या 5x – 3y – 11 = 0 ____ (i)
और -10x + 6y = -22
या -10x + 6y + 22 = 0 ………….(ii)
यहाँ पर
a₁ = 5, b₁ = -3, c₁ =-11
a₂ = -10, b₂ = 6, C₂ = 22
\(\frac{a_{1}}{a_{2}}=\frac{5}{-10}=\frac{-1}{2}, \frac{b_{1}}{b_{2}}=\frac{-3}{6}=\frac{-1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{-11}{22}=\frac{-1}{2}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।

(v) दी गई समीकरणे हैं,
\(\frac{4}{3}\)x + 2y = 8
\(\frac{4}{3}\)x + 2y – 8 = 0 ………..(i)
2x + 3y = 12 2x +3y- 12 = 0 ……. (ii)
यहाँ पर a₁= 4/3, b₁ = 2, c₁ = -8
a₂ = 2, b₂ = 3, c₂ = -12
\(\frac{a_{1}}{a_{2}}=\frac{4}{3 \times 2}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{2}{3} \text { व } \frac{c_{1}}{c_{2}}=\frac{-8}{-12}=\frac{2}{3}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।

प्रश्न 4.
निम्न रैखिक समीकरणों के युग्मों में से कौन-से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
हल :
(i) यहाँ पर
x+y-5 = 0 ….(i)
2x +2y – 10 = 0……..(ii)
a₁ = 1, b₁ = 1, c₁ = -5
a₂ = 2, b₂ = 2, c₂ = -10
\(\frac{a_{1}}{a_{2}}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।
ग्राफीय विधि से हल करने के लिए,
x + y = 5
y = 5 – x

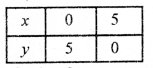
2x +-2y = 10
या y = \(\frac{10-2 x}{2}\)

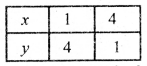
ग्राफ पेपर पर बिंदु A(0, 5) तथा बिंदु B(5, 0) लेकर मिलाने से रेखा AB प्राप्त करें जो समीकरण (i) को निरूपित करेगी तथा बिंदु C(1, 4) तथा बिंदु D(4, 1) लेकर मिलाने से CD प्राप्त करें जो समीकरण (ii) को निरूपित करती है।

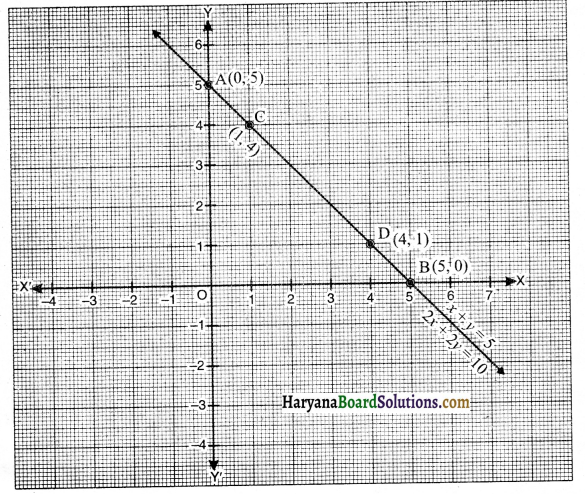
क्योंकि दोनों रेखाएँ AB और CD एक ही हैं। इसलिए रेखा AB पर स्थित प्रत्येक बिंदु रैखिक समीकरण युग्म का अभीष्ट हल है। अतः इस रैखिक समीकरण युग्म के अपरिमित रूप से अनेक हल हैं।

(ii) यहाँ पर
x – y – 8 = 0 ………….(i)
3x – 3y – 16 = 0 ……….(ii)
a₁ = 1, b₁ = -1, c₁ = -8
a₂ = 3, b₂ =-3, c₂=-16
\(\frac{a_{1}}{a_{2}}=\frac{1}{3}, \frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3} \text { व } \frac{c_{1}}{c_{2}}=\frac{-8}{-16}=\frac{1}{2}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म असंगत है।

(iii) यहाँ पर
2x + y-6 = 0 ……………(i)
4x – 2y – 4 = 0 …………(ii)
a₁ = 2, b₁ = 1, c₁ =-6
a₂ = 4, b₂ = -2, c₂ = -4
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{-2}=\frac{-1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{-6}{-4}=\frac{3}{2}\)
क्योंकि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
इसलिए रैखिक समीकरण युग्म संगत है।
ग्राफीय विधि से हल करने के लिए-
2x + y – 6 = 0
y = 6 – 2x

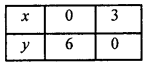
4x-2y-4 = 0
या y = \(\frac{4 x-4}{2}\)

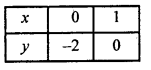
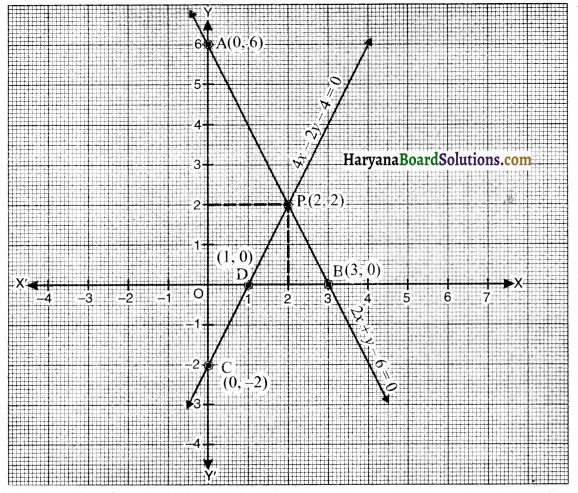
ग्राफ पेपर पर बिंदु A(0, 6) तथा बिंदु B(3, 0) लेकर मिलाने से रेखा AB प्राप्त करें जो समीकरण (1) को निरूपित करती है तथा बिंदु C(0, -2) व D(1,0) लेकर मिलाने से CD प्राप्त करें जो समीकरण (ii) को निरूपित करती है।
ग्राफ से पता चलता है कि दोनों रेखाएँ AB और CD परस्पर बिंदु P(2, 2) पर प्रतिच्छेद करती हैं। इसलिए रैखिक युग्म के अभीष्ट हल x = 2 व y = 2 हैं।

(iv) यहाँ पर
2x -2y -2 = 0 ………(i)
4x -4y-5 = 0 …………(ii)
a₁ = 2, b₁ = -2, c₁ = -2
a₂ = 4, b₂ = -4, c₂ =-5
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2} \text { व } \frac{c_{1}}{c_{2}}=\frac{-2}{-5}=\frac{2}{5}\)
क्योंकि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
इसलिए रैखिक समीकरण युग्म असंगत है।

प्रश्न 5.
एक आयताकार बाग जिसकी लंबाई, चौड़ाई से 4m अधिक है, का अर्धपरिमाप 36m है। बाग की विमाएँ ज्ञात कीजिए।
हल :
माना आयताकार बाग की लंबाई = x m
तथा आयताकार बाग की चौड़ाई = y m
प्रश्नानुसार
x = y +4
x – 1 – 4 = 0 …………(i)
x + y = 36 [∵ अर्धपरिमाप = x +y]
x + y – 36 = 0 ……. (ii)
ग्राफीय विधि से हल करने के लिए,
x – y – 4 = 0
x = y + 4

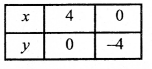
x + y – 36 = 0
y = 36 – x

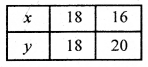
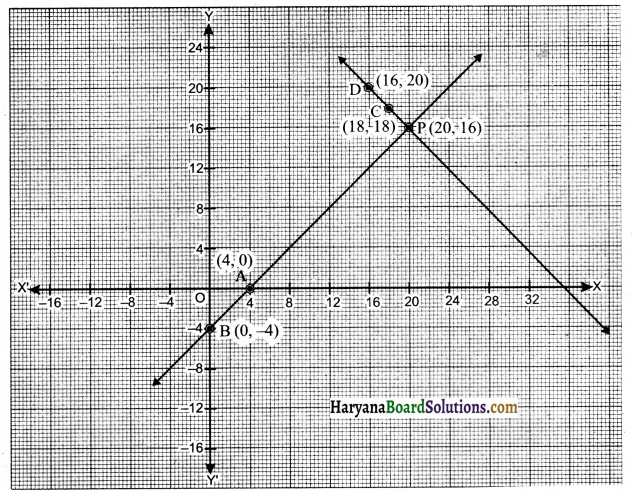
ग्राफ पेपर पर बिंदु A(4,0) तथा बिंदु B(0, -4) लेकर मिलाने से रेखा AB प्राप्त करें जो समीकरण (i) को निरूपित करती है तथा बिंदु C(18, 18) तथा बिंदु D(16, 20) लेकर मिलाने से CD प्राप्त करें जो समीकरण (ii) को निरूपित करती है।
ग्राफ से पता चलता है कि दोनों रेखाएँ AB और CD परस्पर बिंदु P(20, 16) पर प्रतिच्छेद करती हैं। इसलिए रैखिक युग्म के अभीष्ट हल x = 20 व y = 16 हैं।
अतः
आयताकार बाग की लंबाई = 20m
आयताकार बाग की चौड़ाई = 16m

प्रश्न 6.
एक रैखिक समीकरण 2x +3y-8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
(i) प्रतिच्छेद करती रेखाएँ हों।
(ii) समांतर रेखाएँ हों।
(iii) संपाती रेखाएँ हों।
हल :
यहाँ पर दी गई रैखिक समीकरण है, 2x + 3y- 8 = 0
a₁ = 2, b₁ = 3, c₁ = -8

(i) प्रतिच्छेदी रेखाएँ होने के लिए आवश्यक है कि,

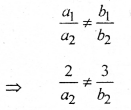
अतः a₂ = 3 व b₂ = 2 हो सकता है।
इस प्रकार प्रतिच्छेदी रेखाओं के लिए द्वितीय रैखिक समीकरण हो सकती है,
3x + 2y-7 = 0

(ii) समांतर रेखाएँ होने के लिए आवश्यक है कि,

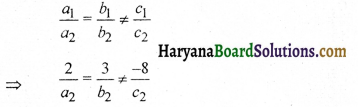
अतः a₂ = 2, b₂ = 3 व c₂ = -12 हो सकते हैं।
इस प्रकार समांतर रेखाएँ होने के लिए द्वितीय रैखिक समीकरण हो सकती है,
2x + 3y – 12 = 0

(iii) संपाती रेखाएँ होने के लिए आवश्यक है कि,

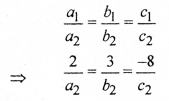
अतः a₂ = 4, b₂ = 6 व c₂ = -16 हो सकते हैं।
इस प्रकार संपाती रेखाएँ होने के लिए द्वितीय रैखिक समीकरण हो सकती है,
4x + 6y – 16 = 0
नोट-इस प्रश्न में अन्य कई संभावित हल हो सकते हैं।

प्रश्न 7.
समीकरणों x – y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ खींचिए। .x-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
हल :
ग्राफीय विधि से हल करने के लिए, x – y + 1 = 0 …………..(i)
y = x +1

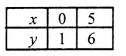
3x +2y- 12 = 0 ___… (ii)
y= \(\frac{12-3 x}{2}\)

ग्राफ पेपर पर बिंदु A (0, 1) तथा बिन्दु B (5, 6) लेकर मिलाने पर प्राप्त रेखा AB समीकरण (i) को निरूपित करेगी तथा बिंदु C (4, 0) तथा बिंदु D (0, 6) लेकर मिलाने पर प्राप्त रेखा CD जो समीकरण (ii) को निरूपित करती है।

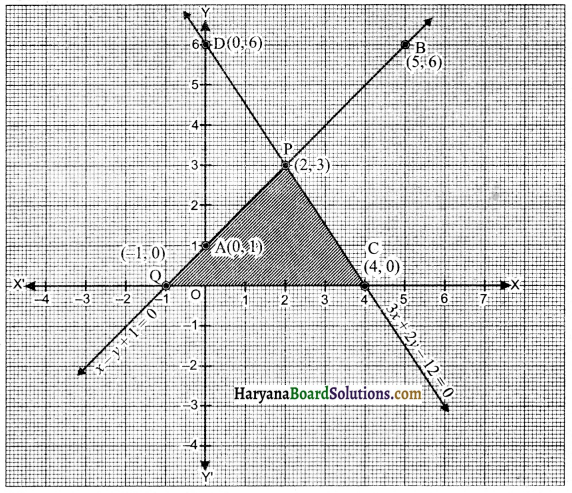
क्योंकि रेखाएँ AB और CD परस्पर बिंदु P (2, 3) पर काटती हैं तथा AB, x-अक्ष को Q(-1, 0) पर तथा CD, x-अक्ष को C(4,0) पर प्रतिच्छेदित करती है। इसलिए त्रिभुज के शीर्ष (2, 3), (-1, 0) व (4,0) हैं।
त्रिभुज PQC का छायांकित भाग ग्राफ में दिखाया गया है।