HBSE 10th Class Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 1 वास्तविक संख्याएँ Exercise 1.1

प्रश्न 1.
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए-
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255
हल :
(i) यूक्लिड विभाजन एल्गोरिथ्म से
= 135 x 1 + 90
135 = 90 x 1 +45
= 45 x 2 + 0

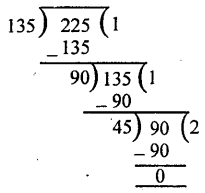
क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 45 है।
इसलिए 135 और 225 का HCF = 45

(ii) यूक्लिड विभाजन एल्गोरिथ्म से-
38220 = 196 x 195 + 0

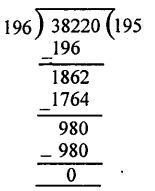
1862 क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 196 है।
इसलिए 196 और 38220 का HCF = 196

(iii) यूक्लिड विभाजन एल्गोरिथम से-
867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0

क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 51 है।
इसलिए 867 और 255 का HCF = 51

प्रश्न 2.
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q +3 या 6q + 5 के रूप का होता है, जहाँ कोई पूर्णांक है।
हल :
माना a एक धनात्मक विषम पूर्णांक तथा b = 6 हो तो यूक्लिड विभाजन एल्गोरिथ्म से-
a = 6q + r
क्योंकि 0 ≤ r < 6 है, इसलिए संभावित शेषफल 0, 1, 2, 3, 4 और 5 हो सकते हैं।
अर्थात् a संख्याओं 6q, 6q+ 1, 6q + 2, 6q + 3, 6q + 4 या 6q +5 के रूप का हो सकता है जहाँ qभागफल है।
अब क्योंकि a एक विषम पूर्णांक है इसलिए यह 6q, 6q + 2 और 6q + 4 के रूप का नहीं हो सकता।
(क्योंकि ये तीनों 2 से विभाज्य अर्थात् सम हैं)।
अतः कोई भी धनात्मक विषम पूर्णांक 6q+ 1,6q + 3 या 6q + 5 के रूप का होगा।

प्रश्न 3.
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं?
हल :
प्रश्नानुसार यहाँ पर हमें 616 और 32 का HCF यूक्लिड एल्गोरिथ्म द्वारा ज्ञात करना है-
616 = 32 x 19 + 8
32 = 8 x 4 + 0

क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 8 है।
इसलिए 616 और 32 का HCF = 8
अतः स्तंभों की अधिकतम संख्या = 8

प्रश्न 4.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के . लिए 3m या 3m + 1 के रूप का होता है।
हल :
माना x एक धनात्मक पूर्णांक है तो यह 3q, 3q + 1 या 3q+ 2 के रूप का होगा।
पहली अवस्था में जब x = 3q
तो x² = (3q)²
= 9q² = 3(3q²)
= 3m जहाँ m = 3q²
दूसरी अवस्था में जब x = 3q + 1
तो x ² = (3q + 1)²x
= 9q² + 2 x 3q x 1 +1
= 9q2 + 6q + 1
= 3q (3q + 2) +1
= 3m + 1 जहाँ m = q(3q+ 2)
तीसरी अवस्था में जब x = 3q + 2
x² = (3q + 2)²
= 9q² + 2 x 3q x 2 +4
= 9q² + 12q + 3 + 1
= 3(3q² + 4q + 1) +1
= 3m + 1 जहाँ m = 3q² + 4q + 1
अतः x धनात्मक पूर्णांक के वर्ग को 3m तथा 3m + 1 के रूप में लिखा जा सकता है, जहाँ m कोई पूर्णांक है।

प्रश्न 5.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
हल :
माना x एक धनात्मक पूर्णांक है तो यह 3q, 3q + 1 या 3q+ 2 के रूप में होगा।
पहली अवस्था में जब x = 3q
x³ = (3q)³
= 27q³ = 9(3q³)
= 9m जहाँ m = 3q³
दूसरी अवस्था में जब x = 3q + 1
x³ = (3q+ 1)³
= (3q)³ + 3 x 3q x 1(3q+ 1) + (1)³
= 27q³ + 27q² + 9q+1
= 9q (3q² + 3q + 1) + 1
= 9m + 1 जहाँ m = q(3q³ + 3q+ 1)
तीसरी अवस्था में जब x = 3q + 2
x³ = (3q+ 2)³
= (3q)³ + 3 x 3q x 2 (3q + 2) + (2)³
= 27q³ + 54q² + 36q + 8
= 9q (3q² + 6q + 4) + 8
= 9m + 8 जहाँ m = q(3q² + 6q+ 4)
अतः x धनात्मक पूर्णांक के घन को 9m, 9m + 1 तथा 9m + 8 के रूप में लिखा जा सकता है।