HBSE 10th Class Maths Notes Chapter 2 Polynomials

Haryana State Board HBSE 10th Class Maths Notes Chapter 2 Polynomials Notes.

Haryana Board 10th Class Maths Notes Chapter 2 Polynomials

Introduction
We have studied about polynomials in one variable and their degrees, factors, multiples etc., in previous classes. Recall that p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial. For example, 4y² – 3y + 8 is a polynomial in y of degree 2: In this chapter we shall extend our knowledge about zeroes of a polynomial, relationship between zeroes and coefficients of a polynomial, division algorithm for polynomials and quadratic polynomials.

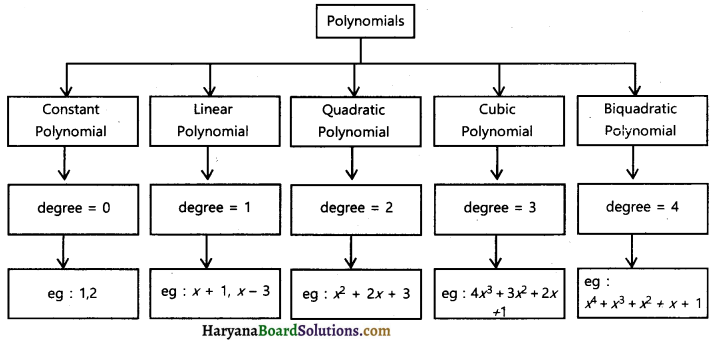
Polynomial
1. Polynomial: An algebraic expression of the form a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ……. + a₁x + a₀ is called a polynomial in x of degree x. Where a₀, a₁……, a_n are real numbers and coefficients of each term of polynomial, n is a non-negative integer and a_n ≠ 0.
For example :
(i) 4x + 9 is a polynomial in x of degree 1.
(ii) 7y² + 5y + 9 is polynomial in y of degree 2.
(iii) 2p³ + 1/2P² + 3P + 8 is a polynomial in P of degree 3.
The expressions like \(\frac{1}{x+2}\), \(\sqrt{x}\) + 1, \(\frac{1}{x^2+2 x+1}\) etc. are not polynomials.
2. Degree of a polynomial: The highest power of the variable in a polynomial is called the degree of the polynomial.
3. Monomials, binomials, trinomials etc. are the classifications of polynomials on the bases of number of terms.
4. Monomials, binomials and trinomials have 1, 2 and 3 terms respectively.
Degrees of linear, quadratic, cubic, biquadratic and constant polynomials are 1, 2, 3, 4 and 0 respectively.
5. Zero of a polynomial: A real number is said to be a zero of the polynomial p(x) if p(k) = 0.
6. The zeroes of polynomial p(x) are the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.
7. A linear polynomial has one and only one zero, a quadratac polynomial can have at most 2 zeroes, a cubic polynomial can have at most 3 zerors and a biquadratic polynomial can have at most 4 zeroes.
8. 0 (zero) is a constant polynomial and is also called zero polynomial. The degree of the zero polynomial is not defined.
9. A non-zero constant polynomial has no zero and every real number is a zero of the zero polynomial.
10. Division algorithm for polynomials: If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then p(x) = g(x) × q(x) + r(x)
where r(x) = 0 or degree of r(x) < degree of g(x).

Types of Polynomial
(a) Constant polynomial: A polynomial of degree zero is called a constant polynomial and it is of the form p(x) = k.
For example:
f(x) = 7, g(x) = 13, p(x) = –\(\frac{7}{3}\)
(b) Linear Polynomial: A polynomial of degree 1, is called linear polynomial.
It is of the form p(x) = ax + b, where a ≠ 0 and a and b are real numbers.
For example:
(i) p(x) = 3x + 9
(ii) f(x) = \(\frac{4}{5}\)x – 5
(c) Quadratic Polynomial: A polynomial of degree 2 is called quadratic polynomial. It is of the form p(x) = ax² + bx + c, where a and a,b,c are real numbers.
For example:
(i) p(x) = 2x² + 4x – 7
(ii) f(x) = x² – 3x + \(\sqrt{5}\)
(iii) g(y) = \(\frac{y}{3}\) – 4y² + 5
(d) Cubic Polynomial: A polynomial of degree 3 is called a cubic polynomial.
It is of the form p(x) = ax³ + bx² + cx + d.
where a ≠ 0. and a, b, c, d are real numbers.
For example:
(i) p(z) = 2z³ + z² – 4 + 9
(ii) f(x) = 4x³ + \(\sqrt{3}\)x² – 8x + 4

(e) Biquadratic polynomial: A polynomial of degree 4 is called a biquadratic polynomial. It is of the form p(x) = ax⁴ + bx³ + cx² + dx + e, where a ≠ 0 and a, b, c, d, e are real number.
For example:
(i) p(y)= y⁴ – 5y³ + 2y² + 9y + 5
(ii) f(x) = 3r⁴ – 5x² + 2.

Value of a Polynomial
In a polynomial p(x), the real number obtained by replacing x by a in p(x), is called the value of p(x) at x = a and it is denoted by p(a).
For example: Find the value of polynomial
p(x) = 4x² – 5x + 6 at
x = -1
Solution:
p(x) = 4x² – 5x + 6
putting x = -1
p(-1) = 4 (-1)² – 5 × (-1) + 6
4 + 5 + 6 = 15.

Graph of the Polynomial
(a) Graph of a linear polynomial is a straight line.
(b) For a quadratic polynomial ax² + bx + c, where a ≠ 0, the graph of the corresponding equation y = zx² + bx + c is a parabola. It has one of the two shapes either opens upward like ∪ (where a > 0) or opens downward linen ∩ (where a < 0).

Number of zeroes of a polynomial in a graph
In a polynomial p(x) of degree, the graph of y = p(x) intersects the x-axis at most points. Therefore, a polynomial p(x) of degree n has at most zeroes.

Relationship between zeroes and coefficients of a polynomial
(A) Relationship between reroes and coefficients of a quadratic polynomial:
Let α and β are zeroes of quadratic polynominl P(x) = ax² + bx + c, where a ≠ 0, then (x – α) and (x – β) are factors of P(x).
Therefore, ax² + bx + c = k(x – α)(x – β), where k is constant
= k[x² – (α + β)x + α × β]
= kx² – k(α + β)x + kαβ
On comparing the coefficients of x², x and constant terms on both sides, we get,
a = k, b = -k(α + β) and c = kαβ.
b = -k(α + β)
b = -a(α + β) [Put k = a]
(α + β) = \(-\frac{b}{a}\)
and c = kαβ
c = aαβ
αβ = \(\frac{c}{a}\)
∴ Sum of zeroes = \(-\frac{b}{a}=-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)
Product of zeroes = \(\frac{c}{a}=\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

(B) Relationship between zeroes and coefficients of cubic polynomial:
If, α, β and γ are zeroes of the cubic polynomial p(x) = ax³ + bx² + cx + d, where a ≠ 0.
Then by factor theorem, x – α, x – β and x – γ are the factors of p(x).
p(x) = k(x – α) (x – β) (x – γ)
ax³ + bx² + cx + d = k(x – α) (x – β) (x – γ)
= k[(x² – xβ – xα + xβ) (x – γ)]
= k[x³ – x²γ – x²β + xβγ – x²α + xαγ + xαβ – αβγ]
= k[x³ – (α + β + γ)x² + (αβ + βγ + αγ)x – αβγ]
= kx³ – k(α + β + γ)x² + k(αβ + βγ + αγ)x – kαβγ
Equating the coefficient of x³, x², x and the constant terms on the both sides, we get
a = k, …..(i)
b = -k(α + β + γ) …….(ii)
c = k(αβ + βγ + αγ) …….(iii)
d = -kαβγ ……..(iv)
From (ii),
– k(α + β + γ) = b
α + β + γ = \(-\frac{b}{k}\)
α + β + γ = \(-\frac{b}{a}\) [a = k from (i)]
from (iii)
k(αβ + βγ + αγ) = c
αβ + βγ + αγ = \(\frac{c}{k}=\frac{c}{a}\) [k = a from (i)]
From (iv),
-kαβγ = d
αβγ = \(\frac{d}{-k}=-\frac{d}{a}\) [k = a from (i)]
Hence,
(1) Sum of zeroes = \(-\frac{b}{a}=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)
(2) Sum of the products of the zeroes taken two at a time = \(\frac{c}{a}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)
(3) Product of zeroes = \(-\frac{d}{a}\)
= \(-\frac{\text { Constant term }}{\text { Coefficient of } x^3}\)

(C) Relationship between Zeroes and Coefficients of Biquadratic Polynomial :
If α, β, γ and δ are zeroes of Biquadratic polynomial p(x) = ax⁴ + bx³ + cx² + dx + e, where a ≠ 0.
(1) α + β + γ + δ = \(-\frac{b}{a}=-\frac{\text { Coefficient of } x^3}{\text { Coefficient of } x^4}\)
(2) αβ + βγ + γδ + δα + δβ + αγ = \(\frac{c}{a}\)
\(=\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^4}\)
(3) αγδ + αβδ + αβγ + βγδ = \(-\frac{d}{a}\) = \(-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^4}\)
(4) αβγδ = \(\frac{e}{a}=\frac{\text { Constant term }}{\text { Coefficient of } x^4}\)

(D) Find a quadratic polynomial when its zeroes a and are given:
p(x) = [x² – (α + β)x + α × β]
or p(x) = [x² – (sum of zeroes)x + product of zeroes]

(E) Find a cubic polynomial when its zeroes, α, β and γ are given:
p(x) = [x³ (α + β + γ)x² + (αβ + βγ + γα)x – αβγ]
or p(x) = [x³ – (sum of zeroes)x² + (sum of products of zeroes taken two at a time) x – product of zeroes]

Division Algorithm for Polynomials
In chapter 1, we have studied Euclid’s division algorithm. Recall when a positive integer is divided by another positive integer we obtain quotient and remainder. It can be expressed in the form
a = bq + r Where 0 ≤ r < b.
Where, a is dividend, is quotient, b is divisor and r is remainder.

Here, we study the division of polynomials where a polynomial f(x) is divided by an another polynomial g(x), we get quotient q(x) and remainder r(x). We can express it in the form of long division as

By Euclid division algorithm it follows that f(x) = g(x) × q(x) + r(x)
Where r(x) = 0 or degree of r(x) < degree of g(x).
This rule is known as the division algorithm for polynomials.
Remarks: (i) If r(x) = 0, then polynomial g(x) is a factor of f(x).
(ii) If α is a zero of the polynomial f(x), then (x – α) is a factor of f(x).

For example : Divide polynomial f(x) = 4x³ – 3x² + 2x – 4 by other polynomial g(x) = -1. Find the quotient and remainder.

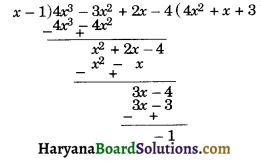
Here, quotient q(x) = 4x² + x + 3
and remainder r(x) = -1
∵ f(x) = g(x) × q(x) + r(x)
∴ 4x³ – 3x² + 2x – 4 = (x – 1)(4x² + x + 3) + (-1)