HBSE 10th Class Maths Important Questions Chapter 4 Quadratic Equations

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 4 Quadratic Equations Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 4 Quadratic Equations

Short/Long Answer Type Questions

Question 1.
If x = 3 is one root of quadratic equation x² – 2kx – 6 = 0, then find the value of k.
Solution :
Since, x = 3 is one root of the quadratic equation x² – 2kx – 6 = 0. So, we put x = 3 in the given equation, we get
(3)² – 2k × 3 – 6 = 0
⇒ 9 – 6k – 6 = 0
⇒ – 6k + 3 = 0
⇒ k = \(\frac {3}{6}\)
⇒ k = \(\frac {1}{2}\)

Question 2.
If one root of the quadratic equation 6x² – x – k = 0 is \(\frac {2}{3}\) then find the value of k.
Solution :
Since, \(\frac {2}{3}\) is one root of the quadratic equation 6x² – x – k = 0.
So, we put x = \(\frac {2}{3}\) in the given equation, we get
6 × (\(\frac {2}{3}\))² – \(\frac {2}{3}\) – k = 0
⇒ 6 × \(\frac{4}{9}-\frac{2}{3}\) – k = 0
⇒ \(\frac{8}{3}-\frac{2}{3}\) – k = 0
⇒ \(\frac {6}{3}\) – k = 0
⇒ 2 – k = 0
⇒ k = 2

Question 3.
Find the possible root of \(\sqrt{3 x^2+6}\) = 9.
Solution :
The given equation is
\(\sqrt{3 x^2+6}\) = 9
Squaring on both sides, we get
3x² + 6 = 81
⇒ 3x² = 81 – 6
⇒ 3x² = 75
⇒ x² = \(\frac {75}{3}\)
⇒ x² = 25
Taking square root both sides, we get
\(\sqrt{x^2}\) = \(\sqrt{25}\)
x = ± 5

Question 4.
Solve : \(\frac{1}{a+b+x}=\frac{1}{a}+\frac{1}{b}=\frac{1}{x}\) where a + b ≠ 0.
Solution :
The given equation is :

⇒ – (a + b) × ab = (a + b)x (a + b + x)
⇒ (a + b)x (a + b + x) + ab (a + b) = 0
⇒ (a + b) [x(a + b + x) + ab] = 0
⇒ x (a + b + x) + ab = 0
⇒ ax + bx + x² + ab = 0
⇒ x² + ax + bx + ab = 0
⇒ x(x + a) + b (x + a) = 0
⇒ (x + a) (x + b) = 0
⇒ (x + a) = 0 and (x + b) = 0
⇒ x = – a and x = – b

Question 5.
A train travels 300 km at a uniform speed. If the speed had been 10 km/hr more, it would have 1 hr less for same journey. Find the speed of train.
Solution :
Let the speed of train be x km/hr
Distance = 300 km (given)
Time taken by train = \(\frac {300}{x}\)hrs.
[∵ Time = Distance / Speed]
If speed had been 10 km/hr more then new speed = (x + 10) km/hr.
Time taken = \(\frac{360}{x+10}\) hrs.
According to question

Question 6.
The diagonal of a rectangular field is 25 metres more than the shorter side. If longer side is 23 metres more than the shorter side, find the sides of the field.
Solution :
Let the shorter side be x m. Then diagonal = (x + 25)m and longer side = (x + 23)m.
We known that each angle of a rectangle is 90°. In a right ΔABC, we have (x + 25)² = (x + 23)² + x².

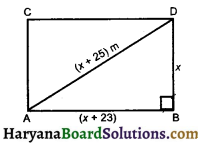
⇒ x² + 50x + 625 = x² + 46x + 529 + x²
⇒ 2x² + 46x + 529 – x² – 50x – 625 = 0
⇒ x² – 4x – 96 = 0
⇒ x² – (12 – 8)x – 96 = 0
⇒ x² – 12x + 8x – 96 = 0
⇒ (x² – 12x) + (8x – 96) = 0
⇒ x(x – 12) + 8 (x – 12) = 0
⇒ (x – 12) (x + 8) = 0
⇒ x – 12 = 0 and x + 8 = 0
⇒ x = 12 and x = – 8 (Reject)
Hence, longer side 12 + 23 i.e., 35 m and shorter side = 12 m.

Question 7.
In a flight of 600 km, an discraft was slowed down due to bad weather. The average speed of the strip was reduced by 200 km/hr and time of flight increased by 30 minutes. Find the duration of flight.
Solution :
Distance = 600 km.
Let the speed of discraft be x km/hr. Time taken by discraft (T₁) = \(\frac {600}{x}\) hrs.
It speed of is craft was slow down by 200 km/ hr then new speed = (x – 200) km/hr.
Time taken by discraft (T₂) = \(\frac{600}{x-200}\) hrs
According to question,

⇒ 2,40,000 = x² – 200x
⇒ x² – 200x – 2,40,000 = 0
⇒ x² – (600 – 400)x – 2,40,000 = 0
⇒ x² – 600x + 400x – 2,40,000 = 0
⇒ x(x – 600) + 400(x – 600) = 0
⇒ (x – 600) (x + 400) = 0
⇒ x – 600 = 0 and x + 400 = 0
⇒ x = 600 and x = – 400 (Reject)
So, speed of discraft = 600 km/hr and duration of flight = \(\frac{600}{600-200}\) hrs
= \(\frac{600}{400}=\frac{3}{2}\) = 1\(\frac {1}{2}\)hrs.

Question 8.
The speed of a boat in still water is 18 km/hr. It takes \(\frac {1}{2}\) an hours extra in going 12 km upstream instread of going the same distance down stream. Find the speed of the stream.
Solution :
Let the speed of stream be x km/hr. Speed of boat in still water = 18 km/hr (given)
Speed of boat in down stream = (18 + x) km/hr
Time taken in going down stream (T₁) = \(\frac{12}{(18+x)}\) hrs
Speed of boat in upstream (18 – x) km/hr.
Time taken in going upstream (T₂) = \(\frac{12}{(18-x)}\) hrs
According to question,

⇒ 48x = – x² + 324
⇒ x² + 48x – 324 = 0
⇒ x² + (54 – 6)x – 324 = 0
⇒ x² + 54x – 6x – 324 = 0
⇒ x(x + 54) – 6(x + 54) = 0
⇒ (x + 54) (x – 6) = 0
⇒ x + 54 = 0 and x – 6 = 0
⇒ x = – 54 (Reject) and x = 6
Hence, speed of stream = 6 km/hr.

Question 9.
I can take 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. How long would it take for each pipe to fill the pool separately ?
Solution :
Let the time taken by larger pipe be x hours and time taken by smaller pipe be y hours
The portion of tank filled by larger pipe in 1 hour = \(\frac {1}{x}\)part
The portion of tank filled by smaller pipe in 1 hour = \(\frac {1}{y}\)part
Two pipe can fill the tank in 12 hours.
∴ The portion of tank filled by both pipe in 1 hr = \(\frac {1}{12}\)part
According to condition 1st
\(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\) ……………(1)
If larger pipe used for 4 hours, then the portion of tank filled by larger pipe in 4 hours = \(\frac {4}{x}\)part
And smaller pipe used for 9 hours, then. Portion of tank filled by smaller pipe in 9 hours = \(\frac {9}{y}\)part
According to condition 2nd
\(\frac{4}{x}+\frac{9}{y}=\frac{1}{2}\) ………..(2)
Let \(\frac{1}{x}\) be a and \(\frac{1}{y}\) be b, from equations (1) and (2) we get
a + b = \(\frac {1}{12}\) ………(3)
4a + 9b = \(\frac {1}{2}\) ………….(4)
By cross-multiplication, we get

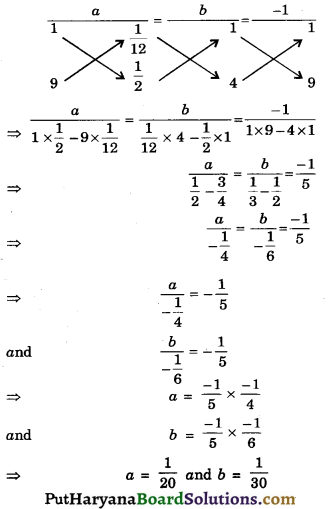
Putting the values of a and b, we get
\(\frac{1}{x}=\frac{1}{20}\) and \(\frac{1}{y}=\frac{1}{30}\)
⇒ x = 20 and y = 30
Hence, time taken by larger pipe is 20 hours and smaller pipe is 30 hours.

Question 10.
Find the value of k for which are roots of the equation 3x² – 10x + k = 0 are reciprocal of each other.
Solution :
The given equation is :
3x² – 10x + k = 0
Let one root of the equation be a since roots are reciprocal each other so, other root is \(\frac {1}{α}\)
Product of two roots = \(\frac {c}{a}\)
⇒ α × \(\frac {1}{α}\) = \(\frac {k}{3}\)
⇒ 1 = \(\frac {k}{3}\)
⇒ k = 3

Question 11.
For what value of k, the given quadratic equation kx² – 6x – 1 = 0 has no real roots ?
Solution :
The given equation is :
kx² – 6x – 1 = 0
The condition for no real roots is :
D < 0
⇒ b² – 4ac < 0
⇒ (-6)² – 4 × k × -1 < 0
⇒ 36 + 4k < 0
⇒ 4k < – 36
⇒ k < –\(\frac {36}{4}\)
⇒ k < – 9
Hence, k should be less than – 9 i.e., (-10, – 11, …..).

Question 12.
For what values of k, the roots of the equation kx² + 4x + k = 0 are real ?
Solution :
The given equation is :
x² + 4x + k = 0
∵ The given equation has real roots
∴ D ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (4)² – 4 × 1 × k ≥ 0
⇒ 16 – 4k ≥ 0
⇒ – 4k ≥ – 16
⇒ k ≤ \(\frac {-16}{-4}\)
⇒ k ≤ + 4
Therefore, k should be ≤ 4 i.e., (4, 3, 2, 1, ….)

Question 13.
Find the k so that the quadratie equation (k + 1)x² – 2 (k + 1)x + 1 = 0 has equal roots.
Solution :
The given equation is :
(k + 1)x² – 2(k + 1) x + 1 = 0
Since, equation has equal roots
∴ D = 0
⇒ b² – 4ac = 0
⇒ [-2(k + 1)]² – 4 × (k + 1) × 1 = 0
⇒ 4(k² + 2k + 1) – 4k – 4 = 0
⇒ 4k² + 8k + 4 – 4k – 4 = 0
⇒ 4k² + 4k = 0
⇒ 4k(k + 1) = 0 and k + 1 = 9
⇒ k = – 1
k = – 1 (Reject since if we put the k = – 1 in the equation (-1 + 1)x will be zero
k = 0

Question 14.
If – 3 is a root of the quadratic equation 2x² + Px – 15 = 0 while the quadratic equation x² – 4Px + k = 0 has equal root. Find the value of k.
Solution :
Since, – 3 is a root of the equation
2x² + Px – 15 = 0.
So, we put x = – 3 in this equation, we get
2(-3)² + P(-3) – 15 = 0
⇒ 18 – 3P – 15 = 0
⇒ 3 – 3P = 0
⇒ P = \(\frac {-3}{-3}\) = 1
Putting the value of P in the equation, we get
x² – 4 × 1 + k = 0
⇒ x² – 4x + k = 0
The equation x² – 4x + k = 0 has equal roots.
So, D = 0
⇒ b² – 4ac = 0
⇒ (-4)² – 4 × 1 × k = 0
⇒ 16 – 4k = 0
⇒ k = \(\frac {-16}{-4}\)
⇒ k = 4

Question 15.
If the roots of the quadratic equation (x – a) (x – b) + (x – b) (x – c) + (x – c)(x – a) = 0 are equal, then show that a = b = c.
Solution :
The given equation is :
(x – a) (x – b) + (x – b) (x – c) + (x – c)(x – a) = 0
x² – ax – bx + ab + x² – bx – xc + bc + x² – cx – ax + ac = 0
⇒ 3x² – 2ax – 2x – 2x + ab + bc + ac = 0
⇒ 3x² – 2 (a + b + c) x + (ab + bc + ac) = 0
Since, roots are equal, then
D = 0
⇒ b² – 4ac = 0
⇒ [- 2 (a + b + c)]² – 4 × 3 × (ab + bc + ac) = 0
⇒ 4(a² + b² + c² + 2ab + 2bc + 2ca) – 12 (ab + bc + ac) = 0
⇒ 4[a² + b² + c² + 2ab + 2bc + 2ca – 3ab – 3bc – 3ac] = 0
⇒ a² + b² + c² – ab – bc – ac = 0
⇒ \(\frac {1}{2}\)[2a² + 2b² + 2c² – 2ab – 2bc – 2ac] = 0
⇒ \(\frac {1}{2}\)[(a² + b² – 2ab) + (b² + c² – 2bc) + (a² + c² – 2ac)] = 0
⇒ (a – b)² + (b – c)² + (a – c)² = 0
⇒ (a – b)² = 0, (b – c)² = 0, (a – c)² = 0
⇒ a = b, b = c, a = c
∴ a = b = c
Hence Proved.

Question 16.
If the root of the quadratic equation (c² – ab)x² – 2 (a² – bc)x + b² – ac = 0 in x are equal, then show that either a = 0 or a³ + b³ + c³ = 3abc.
Solution :
The given equation is:
(c² – ab)x² – 2(a² – bc)x + (b² – ac) = 0
Since, roots are equal, then
D = 0
⇒ b² – 4ac = 0
⇒ [- 2(a² – bc)]² – 4 × (c² – ab) (b² – ac) = 0
⇒ 4(a⁴ + b²c² – 2abc) – 4(b²c² – ac³ – ab³ + a²bc) = 0
⇒ 4[a⁴ + b²c² – 2a²bc – b²c² + ac³ + ab³ – a²bc) = 0
⇒ [a⁴ – 3a²bc + ac³ + ab³] = 0
⇒ a[a³ + b³ + c³ – 3abc] = 0
⇒ a = 0 or a³ + b³ + c³ – 3abc = 0
⇒ a = 0 or a³ + b³ + c³ = 3abc
Hence proved.

Question 17.
A pole has to erected at a point on the boundary of a circular park of diameter 17 metres in such a way that the differences of its distances from two dimetrically opposite fixed gates A and B on the boundary is 7 metres. It is possible to do so? If yes, at what distances from the two gates should the pole be erected ?
Solution :
Let us first draw the diagram. Let P be location of the pole. Let the distance of pole from the gate B be x m ie., BP = x m. Now distances of the pole from the two gates = AP – BP (or BP – AP) = 7 m.
Therefore AP = (x + 7) m.
Now,
AB = 17 m.

∠APB = 90° (angle in a pamicircle is 90°) In a right triangle APB, we have
AB² = AP² + BP²
[By Pythagoaes theorem]
⇒ 17² = (x + 7)² + x²
⇒ 289 = x² + 49 + 14x + x²
⇒ 289 = 2x² + 14x + 49
⇒ 2x² + 14x + 49 – 289 = 0
⇒ x² + 7x – 120 = 0
⇒ x² + (15 – 8) x – 120 = 0
⇒ x² + 15x – 8x – 120 = 0
⇒ x(x + 15) – 8(x + 15) = 0
⇒ (x – 8) (x + 15) = 0
⇒ x – 8 = 0 or x + 15 = 0
⇒ x = 8 or x = – 15 (Reject)
Hence, the pole has to be erected on the boundary of the park at a distance of 8 m from gate Band 8 + 7 i.e., 15 m from gate A.

Fill in the Blanks

Question 1.
A quardratic equation ax² + bx + c = 0 has two………..real roots, if b² – 4ac > 0.
Solution :
Distinct

Question 2.
A quadratic equation ax² + bx + c = 0 has no ………… roots, if b² – 4ac < 0.
Solution :
Real

Question 3.
If we can factorise ax² + bx + c, a ≠ 0, into a product of two linear factors, then the roots of the quadratic equation ax² + bx + c = 0 can be found by equating each ………. to zero.
Solution :
Factor

Question 4.
A quadratic equation can also be solved by the method of completing the …………..
Solution :
Square

Question 5.
ar² + bx + c = 0, a ≠ 0 is called the standard form in a quadratic ………..
Solution :
Equation

Question 6.
A quadratic equation has atmost ……….. roots.
Solution :
Two.

Multiple Choice Questions

Question 1.
The root of the quadratic equation x² – 0.04 = 0 are:
(a) ± 0.2
(b) ± 0.02
(c) 0.4
(d) 2
Solution :
(a) ± 0.2

x² – 0.04 = 0
⇒ x² – (0.2)² = 0
⇒ (x + 0.2) (x – 0.2) = 0
⇒ x + 0.2 = 0
and x – 0.2 = 0
⇒ x = – 0.2
and x = 0.2
⇒ x = ± 0.2

Question 2.
If x² + 2kx + 4 = 0 has a root x = 2, then value of k is:
(a) – 1
(b) – 2
(c) 2
(d) – 4.
Solution :
(b) – 2

x² + 2kx + 4 = 0
one root x = 2 then
(2)² + 2k(2) + 4 = 0
4k + 8 = 0
⇒ k = – 2
So correct choice is (b).

Question 3.
(x² + 1)² – x² = 0 has
[NCERT Exemplar Problems]
(a) four real roots
(b) two real roots
(c) no real roots
(d) one real roots.
Solution :
(c) no real roots

(x² + 1)² – x² = 0 get x² = y, then
(y + 1)² – y = 0
y² + 1 + 2y – y = 0
y² + y + 1 = 0
∵ b² < 4ac
So, no real root.
Hence correct choice is (c).

Question 4.
Which of the following equations has two distinct real roots ?
[NCERT Exemplar Problems]
(a) 2x² – 3\(\sqrt{2}\)x + \(\frac {9}{4}\)
(b) x² + x – 5 = 0
(c) x² + 3x + 2\(\sqrt{2}\) = 0
(d) 5x² – 3x + 1 = 0.
Solution :
(b) x² + x – 5 = 0

(a) 2x² – 3\(\sqrt{2}\)x + \(\frac {9}{4}\) = 0
D = (-3\(\sqrt{2}\))² – 4 × 2 × \(\frac {9}{4}\) = 0

(b) x² + x – 5 = 0
D = (1)² – (4) (1) (-5) = 21
D > 1
Hence correct choice is (b).

Question 5.
The roots of the equation 3x² – 4x + 3 = 0 are :
(a) real and unequal
(b) real and equal
(c) imaginary
(d) none of these.
Solution :
(c) imaginary

3x² – 4x + 3 = 0
a = 3, b = – 4, c = 3
b² = (-4)² = 16
4ac = 4 × 3 × 3 = 36
∵ b² < 4ac
So roots are imaginary Hence correct choice (c).