HBSE 10th Class Maths Important Questions Chapter 6 त्रिभुज

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 6 त्रिभुज Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 6 त्रिभुज

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
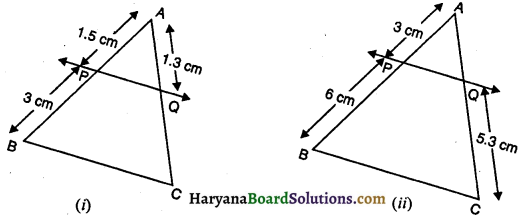
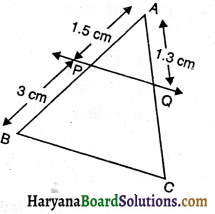
यदि आकृति (i) और (ii) में, PQ || BC हो, तो (i) में QC और (ii) में AQ ज्ञात कीजिए-

हल :
(i) आकृति अनुसार
AP = 1.5 cm, PB = 3 cm, AQ = 1.3 cm, QC = ?
ΔABC में, ∵ PQ || BC (दिया है)
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AQ}}{\mathrm{QC}}\)
⇒ \(\frac{1.5}{3.0}=\frac{1.3}{\mathrm{QC}}\)
या 1.5 × QC = 1.3 × 3.0
या QC = \(\frac{1.3 \times 3.0}{1.5}\) = 2.6 cm
अतः QC = 2.6 cm

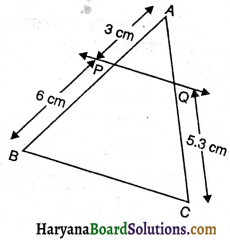
(ii) आकृति अनुसार
AP = 3 cm, PB = 6 cm, AQ = ?, QC = 5.3 cm
ΔABC में, ∵ PQ || BC (दिया है)

प्रश्न 2.
ABCD एक समलंब है जिसमें AB || DC है। असमांतर भुजाओं AD और BC पर क्रमशः बिंदु E और F इसे प्रकार स्थित हैं कि EF भुजा AB के समांतर है (देखिए संलग्न आकृति) । दर्शाइए कि \(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\) है।

सिद्ध कीजिए कि समलंब की समांतर भुजाओं के समांतर कोई रेखा, उन भुजाओं को जो समांतर नहीं हैं, आनुपातिकता (अर्थात् समान अनुपात) में विभाजित करती है।
हल :
दिया है : एक समलंब चतुर्भुज ABCD जिसमें AB || CD तथा EF इनके समांतर खींची गई रेखा है। जो AD और BC को क्रमशः E व F पर मिलती है।

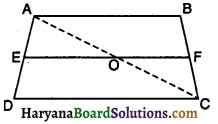
सिद्ध करना है :
\(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\)
रचना : विकर्ण AC खींचिए जो रेखा EF को ‘O’ पर काटता है
प्रमाण : ΔADC में, EO || DC, अतः थेल्स प्रमेय से,
\(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{A O}}{\mathbf{O C}}\) ………..(i)
अब ΔABC में, OF || AB, अतः थेल्स प्रमेय से
\(\frac{\mathbf{A O}}{\mathbf{O C}}=\frac{\mathbf{B F}}{\mathbf{F C}}\) ………..(ii)
समीकरण (i) व (ii) से,
\(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\) [इति सिद्धम]

प्रश्न 3.
यदि तीन या अधिक समांतर रेखाएँ दो तिर्यक रेखाओं से प्रतिच्छेदित होती हों, तो सिद्ध कीजिए कि उनके द्वारा तिर्यक रेखाओं पर काटे गए अंतः खंड (intercepts) आनुपातिक होते हैं ।
[टिप्पणी : इस परिणाम को सामान्यतः आनुपातिकता अंतः खंड गुणधर्म कहते हैं ।]
हल :
दिया है : तीन समांतर रेखाएँ ‘l’, ‘m’ तथा ‘n’ जिनको दो तिर्यक रेखाएँ p तथा q क्रमश: A, B, C, F, E तथा D पर काटती हैं। जैसा कि आकृति में दिखाया गया है।
सिद्ध करना है : \(\frac{\mathbf{A B}}{\mathbf{B C}}=\frac{\mathbf{E F}}{\mathbf{E D}}\)

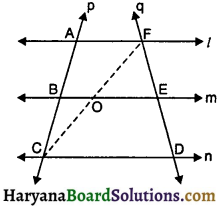
रचना : CF को मिलाइए जो रेखा BE को O पर काटती है ।
प्रमाण : ΔACF में, AF || BO अतः आधारभूत आनुपातिक प्रमेय से,
\(\frac{\mathbf{A B}}{\mathbf{B C}}=\frac{\mathbf{F O}}{\mathbf{O C}}\) ………….(i)
इसी प्रकार ΔFCD में, OE || CD, अतः आधारभूत आनुपातिक प्रमेय से,
\(\frac{\mathbf{F O}}{\mathbf{O C}}=\frac{\mathbf{F E}}{\mathbf{E D}}\) ………….(ii)
समीकरण (i) व (ii) से,
\(\frac{\mathbf{A B}}{\mathbf{B C}}=\frac{\mathbf{F E}}{\mathbf{E D}}\) [इति सिद्धम]

प्रश्न 4.
एक रेखाखंड AB 10 cm लंबाई का खींचिए और उसको 3 : 4 के आंतरिक अनुपात में विभाजित कीजिए ।
हल :
दिया है : एक रेखाखंड AB जिसकी लंबाई 10cm है ।
सिद्ध करना है : AB पर एक बिंदु P ऐसा जो इसे 3 : 4 के आंतरिक अनुपात में विभाजित करता हो ।

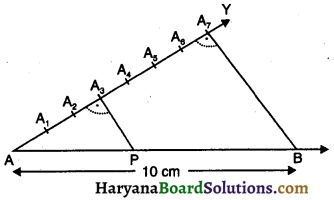
रचना के चरण :

1. 10 cm लंबाई वाला रेखाखंड AB खींचो।
2. A से न्यून कोण ∠BAY बनाते हुए एक रेखा AY खींचो ।
3. AY पर समान दूरी पर सात बिंदु A₁, A₂, A₃, A₄, A₅, A₆ और A₇ अंकित करो अर्थात् AA₁ = A₁A₂ = A₂A₃ = ………………. A₆A₇.
4. A₇B को मिलाओ ।
5. A₃ से A₃P || A₇B खींचो जोकि AB को P पर प्रतिच्छेद करे । अब बिंदु P रेखा AB पर अभीष्ट बिंदु है जो इसे 3 : 4 के आंतरिक अनुपात में विभाजित करता है अर्थात् AP : PB = 3 : 4

प्रश्न 5.
संलग्न आकृति में EF || AB || DC है । सिद्ध कीजिए कि \(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\)
हल :

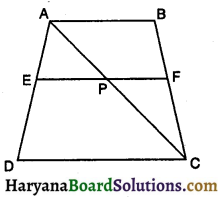
ΔADC से, हम पाते हैं,
EP || DC [∵ EF || DC (दिया है)]
∴ \(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{A P}}{\mathbf{P C}}\) ………(i)
साथ ही ΔCAB से, हमें मिलता है,
FP || BA [∵ EF || AB (दिया है)]
∴ \(\frac{\mathbf{B F}}{\mathbf{F C}}=\frac{\mathbf{A P}}{\mathbf{P C}}\) ………(ii)
समीकरण (i) और (ii) से,
\(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\) [इति सिद्धम]

प्रश्न 6.
संलग्न आकृति में यदि EB = 2 cm; AE = 5cm AF = x; FC = x – 1 तथा EF || BC, तो x का मान ज्ञात कीजिए।
हल :

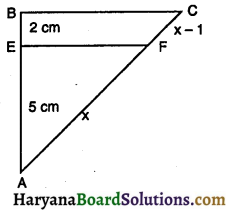
क्योंकि त्रिभुज ABC में EF || BC
∴ \(\frac{\mathbf{A E}}{\mathbf{E B}}=\frac{\mathbf{A F}}{\mathbf{F C}}\)
परंतु, AE = 5 cm, EB = 2 cm
AF = x, FC = x – 1
⇒ \(\frac{5}{2}=\frac{x}{x-1}\)
या 5(x – 1) = 2x
या 5x – 5 = 2x
या 5x – 2x = 5
या 3x = 5
या x = \(\frac {5}{3}\)

प्रश्न 7.
संलग्न आकृति में, ΔEDC ~ ΔEBA, ∠BEC = 115° और ∠EDC = 70° है। ∠DEC, ∠DCE, ∠EAB, ∠AEB और ∠EBA ज्ञात कीजिए ।
हल :

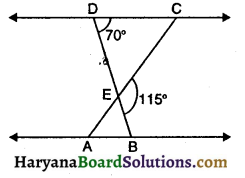
आकृति अनुसार,
∠BEC = 115°, ∠EDC = 70°
∠DEC + ∠BEC = 180° (सरल रैखिक युग्म)
या ∠DEC + 115° = 180° [∵ ∠BEC = 115°]
या ∠DEC = 180° – 115° = 65°
अब ΔDEC में,
∠DEC + ∠EDC + ∠DCE = 180° (त्रिभुज के कोण )
⇒ 65° + 70° + ∠DCE = 180°
या 135° + ∠DCE = 180°
या ∠DCE = 180° – 135° = 45°
परंतु ΔEDC ~ ΔEBA (दिया है)
इसलिए
∠EAB = ∠DCE = 45°
∠AEB = ∠DEC = 65°
∠EBA = ∠EDC = 70°
अतः ∠DEC = 65°, ∠DCE = 45°, ∠EAB = 45°, ∠AEB = 65°, ∠EBA = 70°

प्रश्न 8.
संलग्न आकृति में, यदि PS || QR है, तो सिद्ध कीजिए कि ΔPOS ~ ΔROQ है ।
हल :

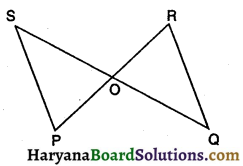
दिया है : आकृति में PS || QR
सिद्ध करना है : ΔPOS ~ ΔROQ
प्रमाण : ΔPOS और ΔROQ में
∠POS = ∠QOR (शीर्षाभिमुख कोण)
∠PSO = ∠RQO (एकांतर कोण)
∠SPO = ∠QRO (एकांतर कोण)
∴ ΔPOS ~ ΔROQ (कोण-कोण समरूपता नियम) [इति सिद्धम]

प्रश्न 9.
दो समरूप त्रिभुजों के परिमाप क्रमशः 30 cm और 20 cm हैं। यदि पहले त्रिभुज की एक भुजा 12 cm हो, तो दूसरे त्रिभुज की संगत भुजा ज्ञात कीजिए ।
हल :

माना ΔDEF और ΔABC अभीष्ट त्रिभुज हैं जिनके परिमाप क्रमशः 30 cm व 20 cm हैं।
माना भुजा EF = 12 cm
तो ΔABC की संगत भुजा BC = ?

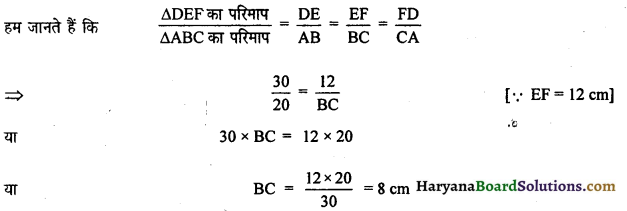
अतः दूसरे त्रिभुज की संगत भुजा = 8 cm

प्रश्न 10.
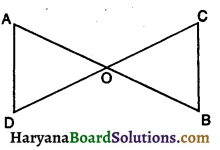
संलग्न आकृति में, \(\frac{O A}{O C}=\frac{O D}{O B}\) है । सिद्ध कीजिए कि ∠A = ∠C और ∠B = ∠D है।

हल :
दिया है : \(\frac{O A}{O C}=\frac{O D}{O B}\)
सिद्ध करना है : ∠A = ∠C और ∠B = ∠D
प्रमाण : ΔAOD और ΔBOC में,
∠AOD = ∠BOC (शीर्षाभिमुख कोण)
एवं \(\frac{O A}{O C}=\frac{O D}{O B}\) (दिया है)
अतः ΔAOD ~ ΔBOC (∴ भुजा – कोण – भुजा समरूपता गुणधर्म से)
अतः ∠A = ∠C
व ∠D = ∠B
(यदि त्रिभुजें समरूप हों, तो संगत कोण समान होते हैं ।) [इति सिद्धम]

प्रश्न 11.
CM और RN क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं यदि ΔABC ~ ΔPQR है, तो सिद्ध कीजिए कि ΔAMC ~ ΔPNR
हल :

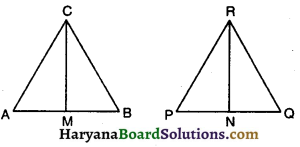
दिया है : CM और RN क्रमशः ΔABC और ΔPQR की
माध्यिकाएँ हैं तथा ΔABC ~ ΔPQR है ।
सिद्ध करना है : ΔAMC ~ ΔPNR
प्रमाण : क्योंकि ΔABC ~ ΔPQR
∴ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C A}{R P}\) …………..(i)
तथा ∠A = ∠P, ∠B = ∠Q व ∠C = ∠R …………..(ii)
परन्तु AB = 2AM तथा PQ = 2PN [∵ CM और RN माध्यिकाएँ हैं] …. (iii)
समीकरण (i) व (iii) की तुलना से
\(\frac{2 A M}{2 P N}=\frac{C A}{R P}\)
⇒ \(\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{CA}}{\mathrm{RP}}\) ………(iv)
तथा ∠MAC = ∠NPR ……… (v)
समीकरण (iv) व (v) से हमें प्राप्त होता है ।
ΔAMC ~ ΔPNR (इति सिद्धम्)

प्रश्न 12.
संलग्न आकृति में, ∠A = ∠B और AD = BE है | सिद्ध कीजिए कि DE || AB है ।
हल :

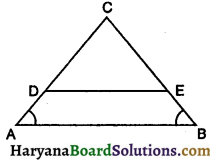
दिया है : ∠A = ∠B और AD = BE
सिद्ध करना है : DE || AB
प्रमाण : ∠A = ∠B ………..(दिया है)
⇒ AC = BC (समान कोणों की सम्मुख भुजाएँ)
या (DC + DA) = (EC + EB) …………(i)
परंतु AD = BE …….. (दिया है) …………..(ii)
समीकरण (i) और (ii) से,
DC + BE = EC + BE
या DC = EC …………..(iii)
समीकरण (iii) को (ii) से भाग करने पर
\(\frac{\mathrm{DC}}{\mathrm{AD}}=\frac{\mathrm{EC}}{\mathrm{BE}}\)
अतः DE || BC (थेल्स प्रमेय के विलोम से) [इति सिद्धम]

प्रश्न 13.
संलग्न आकृति में, XY || AC और XY त्रिभुजीय क्षेत्र ABC को दो बराबर क्षेत्रफल वाले भागों में विभाजित करता है । \(\frac {AX}{AB}\) ज्ञात कीजिए ।
हल :

दिया है : ΔABC में XY || AC
ΔABC का क्षेत्रफल = 2 × ΔBXY का क्षेत्रफल
सिद्ध करना है :
\(\frac {AX}{AB}\) = ?
अब : ΔABC और ΔXBY में,
∠B = ∠B (उभयनिष्ठ)
\(\frac{\mathrm{BA}}{\mathrm{BC}}=\frac{\mathrm{BX}}{\mathrm{BY}}\)
∴ ΔABC ~ ΔXBY
हम जानते हैं कि समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है ।

प्रश्न 14.
एक सीढ़ी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 मी की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 मी की ऊँचाई पर बनी खिड़की तक पहुँचता है। सीढ़ी की लम्बाई ज्ञात कीजिए ।
हल :

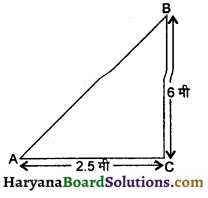
यहाँ पर,
खिड़की की ऊँचाई (BC) = 6 मी
सीढ़ी के निचले सिरे की दीवार से दूरी (AC) = 2.5 मी
माना सीढ़ी की लम्बाई (AB) = x मी
समकोण ΔABC में
AB² = AC² + BC² (पाइथागोरस प्रमेय)
⇒ x² = (2.5)² + (6)²
या x² = 6.25 + 36
या x² = 42.25
या x² = \(\sqrt{42.25}\) = 6.5 मी
अतः सीढ़ी की लम्बाई = 6.5 मी

प्रश्न 15.
पृथ्वी से 15m ऊँचाई पर भवन की एक खिड़की तक 17 m लम्बाई की एक सीढ़ी पहुँचती है। सीढ़ी के पाद से भवन की दूरी ज्ञात कीजिए ।
हल :

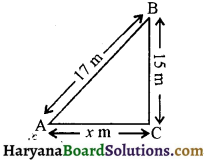
यहाँ पर,
खिड़की की ऊँचाई (BC) = 15m
सीढ़ी की लम्बाई (AB) = 17 m
माना सीढ़ी के निचले सिरे की भवन की दीवार से दूरी (AC) = x m
समकोण ΔABC में पाइथागोरस प्रमेय से
AB² = AC² + BC²
⇒ (17)² = x² + (15)²
⇒ 289 = x² + 225
⇒ x² = 289 – 225
⇒ x = \(\sqrt{64}\) = 8 m
अतः सीढ़ी के निचले सिरे (पाद) की भवन की दीवार से दूरी = 8m

प्रश्न 16.
एक व्यक्ति पूरब की ओर 10m और फिर उत्तर की ओर 30m जाता है। प्रारंभिक बिंदु से उसकी दूरी ज्ञात कीजिए ।
हल :
यहाँ पर व्यक्ति O बिंदु से पूर्व की ओर 10m दूरी तय कर A बिंदु पर पहुँचता तथा वहाँ से उत्तर की ओर 30 m दूरी तय करके B बिंदु पर पहुँचता है । व्यक्ति की दूरी OB ज्ञात करनी है ।
अर्थात्
OA = 10m
AB = 30m
OB = ?

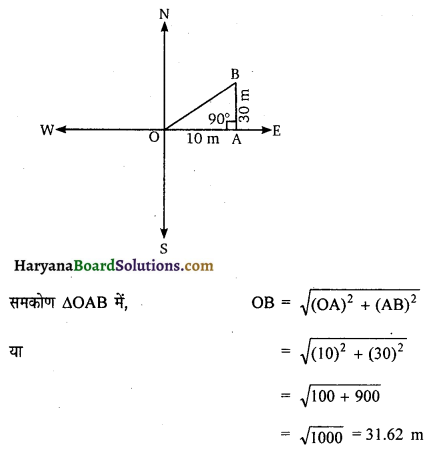
अतः व्यक्ति की प्रारंभिक बिंदु से दूरी = 31.62 m

प्रश्न 17.
90 सें०मी० की लम्बाई वाली एक लड़की बल्ब लगे एक खम्भे के आधार से परे 1.2 मी० / सेकण्ड की चाल से चल रही है। यदि बल्ब भूमि से 3.6 मी० की ऊँचाई पर है, तो 4 सेकण्ड बाद उस लड़की की छाया की लम्बाई ज्ञात कीजिए ।
हल :

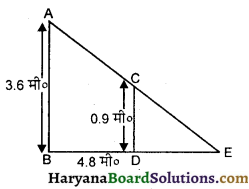
माना आकृति में AB एक खम्भा है जिस पर बल्ब लगा हुआ है तथा CD एक लड़की है जो खम्भे से 4 सेकण्ड चलने के पश्चात् दर्शाई गई है। माना DE लड़की की छाया है जिसे हमें ज्ञात करना है 1
लड़की द्वारा B से D तक 4 सेकण्ड में तय दूरी (BD)
= 1.2 × 4 = 4.8 मी०
समरूप त्रिभुजों ABE और CDE में (∵ ∠E = ∠E, ∠B = ∠D)

प्रश्न 18.
आयत ABCD के अभ्यंतर में कोई बिंदु O है । सिद्ध कीजिए कि OB² + OD² = OC² + OA² है।
हल :

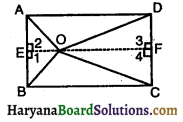
दिया है : एक आयत ABCD, इसके अभ्यंतर में कोई बिंदु O है । OA, OB, OC और OD को मिलाया गया है ।
सिद्ध करना है : OB² + OD² = OC² + OA²
रचना : O से EOF || BC और BC || AD खींचो।
प्रमाण :
∵ EOF || BC और BC || AD है,
∴ AD || EOF || BC
∵ AD ⊥ AB ……….. (ABCD आयत है)
∴ EF ⊥ AB
इसी प्रकार EF ⊥ DF
∴ AEFD भी एक आयत है ⇒ AE = DF ………..(i)
इसी प्रकार, BEFC एक आयत है
⇒ EB = FC ………(ii)
∠1 = ∠2 = ∠3 = ∠4= 90°
समकोण ΔOBE में, OB² = OE² + EB² = OE² + FC² ….[(ii) से] …….(iii)
समकोण ΔODF में,
OD² = OF² + DF² = OF² + AE² ….[(i) से] …….(iv)
समीकरण (iii) और (iv) को जोड़ने पर,
OB² + OD² = OE² + FC² + OF² + AE² ……..(v)
परंतु समकोण ΔOFC में,
OF² + FC² = OC² ………..(vi)
और समकोण ΔOAE में, OE² + AE² = OA² ……….(vii)
(v), (vi) और (vii) से,
OB² + OD² = OC² + OA²

प्रश्न 19.
यदि आकृति में दिए हुए ΔABC में AB = 5 cm, AC = 10 cm, BD = 1.5 cm और CD = 3.5 cm हो तो जाँच कीजिए कि क्या AD, ∠A का समद्विभाजक है ।
हल :

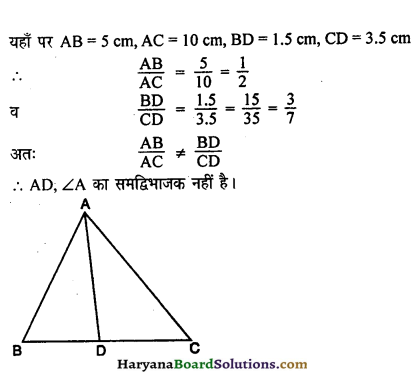
प्रश्न 20.
दो खंभे एक समतल भूमि पर खड़े हैं । निम्नलिखित स्थितियों के लिए खंभों के ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए :
(i) खंभों की ऊँचाई = 6 मी, 12 मी; खंभों के निचले सिरों के बीच की दूरी = 8 मी
(ii) खंभों की ऊँचाई = 7 मी, 12 मी; खंभों के निचले सिरों के बीच की दूरी = 12 मी
हल :

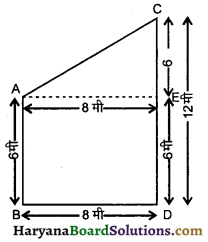
(i) दिया है-दो खंभे AB और CD क्रमशः 6 मी और 12 मी लम्बे हैं तथा उनके निचले सिरों के बीच की दूरी BD = 8 मी है। ज्ञात करना है-खंभों के ऊपरी सिरों के बीच की दूरी (AC) = ?
AB = 6 मी
CD = 12 मी
DE = AB = 6 मी
∴ CE = CD – DE
= (12 – 6) मी = 6 मी
AE = BD = 8 मी
अब समकोण त्रिभुज ACE में,
AC² = AE² + CE²
= (8)² + (6)²
= 64 + 36 = 100
या AC = \(\sqrt{100}\) = 10 मी
अतः दोनों खंभों के ऊपरी सिरों के बीच की दूरी = 10 मी

(ii) दिया है- दो खंभे AB और CD क्रमशः 7 मी और 12 मी लम्बे हैं तथा उनके निचले सिरों के बीच की दूरी BD = 12 मी है।

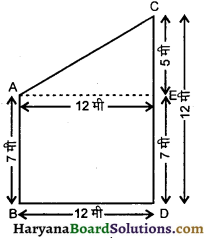
ज्ञात करना है – खंभों के ऊपरी सिरों के बीच की दूरी (AC) = ?
AB = 7 मी
CD = 12 मी
DE = AB = 7 मी
∴ CE = CD – DE
= (12 – 7) मी = 5 मी
AE = BD = 12 मी
अब समकोण त्रिभुज ACE में,
AC² = AE² + CE²
= (12)² + (5)²
= 144 + 25 = 169
या AC = \(\sqrt{169}\) = 13 मी
अतः दोनों खंभों के ऊपरी सिरों के बीच की दूरी = 13 मी

प्रश्न 21.
ΔABC एक समद्विबाहु समकोण त्रिभुज है । यदि ∠ACB = 90° तथा AB = 5\(\sqrt{2}\) cm, तो AC मान ज्ञात कीजिए।
हल :

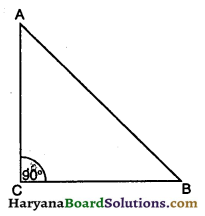
दिया है : ΔABC एक समद्विबाहु समकोण त्रिभुज है ।
जिस कारण AC = BC तथा ∠ACB = 90° व AB = 5\(\sqrt{2}\)cm
ज्ञात करना है : AC = ?
अब : समकोण ΔACB में,
AC² + BC² = AB²
या AC² + AC² = (5\(\sqrt{2}\))² (∵ AC = BC दिया है)
या 2AC² = 50
या AC² = \(\frac {50}{2}\) = 25
या AC = 5 cm

प्रश्न 22.
एक चतुर्भुज ABCD का विकर्ण BD, ∠B और ∠D को समद्विभाजित करता है । सिद्ध कीजिए कि \(\frac{A \mathbf{B}}{B C}=\frac{D A}{C D}\) है ।
हल :

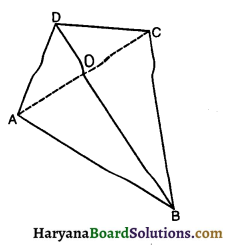
दिया है : एक चतुर्भुज ABCD का विकर्ण BD, ∠B और ∠D को समद्विभाजित करता है।
सिद्ध करना है :
\(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{DA}}{\mathrm{CD}}\)
रचना : A और C को मिलाइए जो BD को O पर मिलाता है ।
प्रमाण : ΔABC में BO, ∠B का समद्विभाजक है।
∴ \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{DA}}{\mathrm{CD}}\) ………(i)
इसी प्रकार ΔADC में ∠O, ∠D का समद्विभाजक है।
∴ \(\frac{\mathrm{AD}}{\mathrm{DC}}=\frac{\mathrm{AO}}{\mathrm{OC}}\) ………(ii)
समीकरण (i) व (ii) की तुलना से,
\(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AD}}{\mathrm{DC}}\) [इति सिद्धम]

प्रश्न 23.
दो समरूप त्रिभुजों ABC और PQR के क्षेत्रफल क्रमशः 36 cm² तथा 64 cm² हैं। यदि BC = 4.2 cm हो तो QR ज्ञात कीजिए ।
हल :

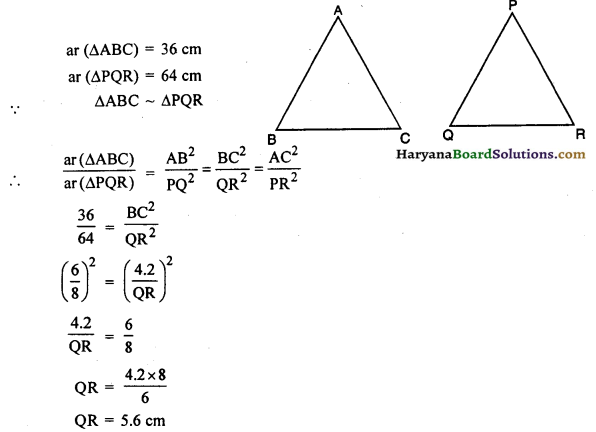
बहुविकल्पीय प्रश्न :

प्रश्न 1.
यदि दो समान संख्या वाली भुजाओं वाले बहुभुजों में संगत कोण बराबर हों तथा उनकी संगत भुजाओं की लम्बाइयाँ समानुपाती हों तो उन्हें कहा जाता है-
(A) समरूप बहुभुज
(B) सर्वांगसम बहुभुज
(C) समान बहुभुज
(D) उपरोक्त में से कोई नहीं
हल :
(A) समरूप बहुभुज

प्रश्न 2.
यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को काटते हुए कोई रेखा खींचे तो वह त्रिभुज की अन्य दोनों भुजाओं को समान अनुपात में विभाजित करती है । इस प्रमेय को कहा जाता है-
(A) पाइथागोरस प्रमेय
(B) आधारभूत समानुपातिकता प्रमेय
(C) पाइथागोरस प्रमेय का विलोम
(D) आधारभूत समानुपातिकता प्रमेय का विलोम
हल :
(B) आधारभूत समानुपातिकता प्रमेय

प्रश्न 3.
यदि कोई रेखा किसी त्रिभुज की किन्हीं दो भुजाओं को समान अनुपात में विभाजित करती हो, तो यह रेखा तीसरी भुजा के समान्तर होती है, इसे कहा जाता है-
(A) पाइथागोरस प्रमेय
(B) आधारभूत समानुपातिकता प्रमेय
(C) पाइथागोरस प्रमेय का विलोम
(D) आधारभूत समानुपातिकता प्रमेय का विलोम
हल :
(D) आधारभूत समानुपातिकता प्रमेय का विलोम

प्रश्न 4.
संलग्न आकृति में यदि ST || QR हो तो PS का मान होगा-

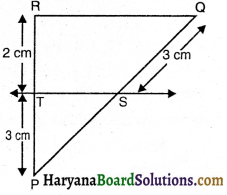
(A) 3.0 cm
(B) 4.0 cm
(C) 4.5 cm
(D) 6.0 cm
हल :
(C) 4.5 cm

प्रश्न 5.
संलग्न आकृति में यदि PQ || BC हो तो QC का मान होगा-

(A) 2.6 cm
(B) 1.3 cm
(C) 3.9 cm
(D) 3.0 cm
हल :
(A) 2.6 cm

प्रश्न 6.
संलग्न आकृति में यदि PQ || BC हो तो AQ का मान होगा-

(A) 5.3 cm
(B) 2.65 cm
(C) 4.5 cm
(D) 1.65 cm
हल :
(B) 2.65 cm

प्रश्न 7.
त्रिभुज की किसी भुजा के मध्य – बिन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को …………. करती है।
(A) त्रिभाजित
(B) चतुर्भाजित
(C) समद्विभाजित
(D) उपरोक्त में से कोई नहीं
हल :
(C) समद्विभाजित

प्रश्न 8.
सभी वृत्त ………….. होते हैं ।
(A) सर्वांगसम
(B) दोनों
(C) (A) व (B) दोनों
(D) उपरोक्त में से कोई नहीं
हल :
(B) समरूप

प्रश्न 9.
ΔABC में, AB तथा AC पर क्रमशः D तथा E बिन्दु इस प्रकार हैं कि DE || BC, यदि AD = 6 सेमी., DB = 9 सेमी. और AE = 8 सेमी., तो निम्न से AC का मान ज्ञात कीजिए-
(A) 12 सेमी.
(B) 16 सेमी.
(C) 20 सेमी.
(D) इनमें से कोई नहीं
हल :
(C) 20 सेमी.

प्रश्न 10.
सभी ……….. त्रिभुज समरूप होते हैं ।
(A) विषमबाहु
(B) समद्विबाहु
(C) समबाहु
(D) समकोण
हल :
(C) समबाहु

प्रश्न 11.
भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं यदि उनके संगत कोण ……………… हों तथा उनकी संगत भुजाएँ ……………… हों ।
(A) बराबर ; समानुपाती
(B) असमान; समानुपाती
(C) समान; विषमपाती
(D) उपरोक्त में से कोई नहीं
हल :
(A) बराबर; समानुपाती

प्रश्न 12.
दी गई आकृति में DE || BC, तो EC का मान है :

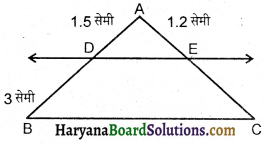
(A) 2.7 सेमी
(B) 1.5 सेमी
(C) 2.4 सेमी
(D) 3 सेमी
हल :
(C) 2.4 सेमी

प्रश्न 13.
दी गई आकृति में DE || BC, तो DB का मान है :

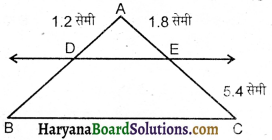
(A) 2.4 सेमी
(B) 4.8 सेमी
(C) 1.8 सेमी
(D) 3.6 सेमी
हल :
(D) 3.6 सेमी

प्रश्न 14.
ΔABC में, AB तथा AC पर क्रमश: D तथा E बिन्दु इस प्रकार हैं कि DE || BC, यदि \(\frac {AD}{DB}\) = \(\frac {3}{4}\) तथा AC = 15 सेमी. निम्नलिखित में से AE का मान ज्ञात कीजिए-
(A) 6.43 सेमी.
(B) 6.34 सेमी.
(C) 4.63 सेमी.
(D) इनमें से कोई नहीं
हल :
(A) 6.43 सेमी.

प्रश्न 15.
किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा होती है-
(A) तीसरी भुजा के लम्बवत्
(B) तीसरी भुजा के समान्तर
(C) तीसरी भुजा के असमान्तर
(D) तीसरी भुजा के बराबर
हल :
(B) तीसरी भुजा के समान्तर

प्रश्न 16.
संलग्न आकृति ΔABC में, DE || BC तथा \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}\) यदि AC = 4.8 cm हो तो AE का मान होगा-

(A) 1.8cm
(B) 2.7 cm
(C) 3.0cm
(D) 3.6 cm
हल :
(A) 1.8.cm

प्रश्न 17.
त्रिभुजों के युग्मों में से कौन-सा युग्म समरूप नहीं है?

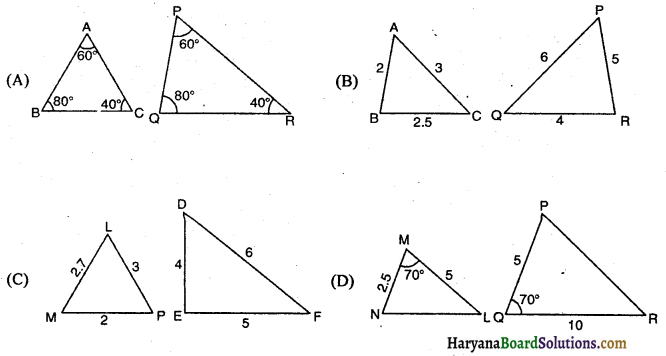
हल :

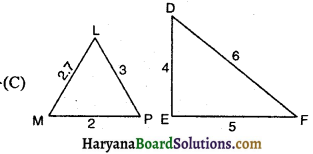
प्रश्न 18.
दी गई आकृति में ΔODC ~ ΔOAB, ∠BOC = 125°, ∠ODC = 70°, तो ∠OAB का मान है :

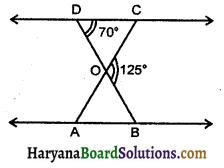
(A) 70°
(B) 35°
(C) 50°
(D) 55°
हल :
(A) 70°

प्रश्न 19.
दो समरूप त्रिभुजों के परिमाप क्रमशः 30 cm और 20 cm हैं। यदि पहले त्रिभुज की एक भुजा 12 cm हो, तो दूसरे त्रिभुज की संगत भुजा होगी-
(A) 12 cm
(B) 10 cm
(C) 8 cm
(D) 6 cm
हल :
(C) 8 cm

प्रश्न 20.
संलग्न आकृति में, यदि EB = 2 cm, AE = 5 cm, AF = x, FC = x – 1 तथा EF || BC, तो x का मान होगा-

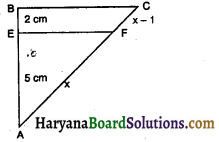
(A) \(\frac {5}{3}\)cm
(B) \(\frac {5}{2}\)cm
(C) \(\frac {5}{4}\)cm
(D) \(\frac {3}{5}\)cm
हल :
(A) \(\frac {5}{3}\)cm

प्रश्न 21.
यदि दो समरूप त्रिभुजों की भुजाओं का अनुपात 3 : 5 है, तो इन त्रिभुजों के क्षेत्रफलों का अनुपात ……………… है ।
(A) 3 : 5
(B) 9 : 25
(C) 5 : 3
(D) इनमें से कोई नहीं
हल :
(B) 9 : 25

प्रश्न 22.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 64 : 121 है, तो उनकी भुजाओं में अनुपात होगा-
(A) 8 : 11
(B) 11 : 8
(C) 64 : 121
(D) इनमें से कोई नहीं
हल :
(A) 8 : 11

प्रश्न 23.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं-
(i) 3 cm, 6 cm, 8 cm
(ii) 5 cm, 12 cm, 13 cm
(iii) 5 cm, 8 cm, 10cm
इनमें से कोई नहीं
इनमें से समकोण त्रिभुज है-
(A) (i)
(B) (ii)
(C) (iii)
(D) इनमें से कोई नहीं
हल :
(B) (ii)

प्रश्न 24.
यदि दो त्रिभुजें ABC और DEF इस प्रकार हैं कि \(\frac{\mathbf{A B}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathbf{C A}}{\mathbf{F D}}=\frac{2}{5}\) हो तो ar (ΔABC) : ar (ΔDEF) होगा-
(A) 4 : 25
(B) 2 : 5
(C) 8 : 125
(D) 4 : 10
हल :
(A) 4 : 25

प्रश्न 25.
यदि दो समरूप त्रिभुजों की भुजाओं का अनुपात 2 : 3 है, तो उनके क्षेत्रफलों का अनुपात है :
(A) \(\sqrt{2}\) : \(\sqrt{3}\)
(B) 2 : 3
(C) 4 : 9
(D) इनमें से कोई नहीं
हल :
(C) 4 : 9

प्रश्न 26.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात बराबर होता है-
(A) संगत भुजाओं के अनुपात के
(B) संगत भुजाओं के वर्गों के अनुपात के
(C) संगत भुजाओं के घनों के अनुपात के
(D) इनमें से कोई नहीं
हल :
(B) संगत भुजाओं के वर्गों के अनुपात के

प्रश्न 27.
किसी वर्ग की एक भुजा पर निर्मित समबाहु त्रिभुज का क्षेत्रफल, उसके विकर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल का ………….. होता है ।
(A) दुगुना
(B) तीन गुना
(C) एक-तिहाई
(D) आधा
हल :
(D) आधा

प्रश्न 28.
मान लीजिए ΔABC ~ ΔDEF है और इनके क्षेत्रफल क्रमशः 64 cm² और 121 cm² हैं । यदि EF = 15.4 cm, तो BC का मान है-
(A) 11.2 cm
(B) 11.4 cm
(C) 12.4 cm
(D) इनमें से कोई नहीं
हल :
(A) 11.2 cm

प्रश्न 29.
यदि दो समरूप त्रिभुजों की भुजाओं का अनुपात 3 : 2 है, तो उनके क्षेत्रफलों का अनुपात है-
(A) \(\sqrt{3}\) : \(\sqrt{2}\)
(B) 2 : 3
(C) 9 : 4
(D) इनमें से कोई नहीं
हल :
(C) 9 : 4

प्रश्न 30.
त्रिभुज ABC और DEF समरूप हैं। यदि ΔABC का क्षेत्रफल = 16 cm², ΔDEF का क्षेत्रफल = 25 cm 2 और BC = 2.3 cm,
तो EF है-
(A) 2.875 cm
(C) 2.578 cm
(B) 2.758cm
(D) इनमें से कोई नहीं
हल :
(A) 2.875 cm

प्रश्न 31.
समकोण त्रिभुज में कर्ण का वर्ग अन्य दोनों भुजाओं के वर्गों के योग के बराबर होता है। इस प्रमेय को कहा जाता है-
(A) आधारभूत समानुपातिकता प्रमेय
(B) पाइथागोरस प्रमेय
(C) आधारभूत समानुपातिकता प्रमेय का विलोम
(D) पाइथागोरस प्रमेय का विलोम
हल :
(B) पाइथागोरस प्रमेय

प्रश्न 32.
किसी त्रिभुज में यदि एक भुजा का वर्ग अन्य दोनों भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा के सामने का कोण समकोण होता है । यह है-
(A) आधारभूत समानुपातिकता प्रमेय
(B) पाइथागोरस प्रमेय
(C) आधारभूत समानुपातिकता प्रमेय का विलोम
(D) पाइथागोरस प्रमेय का विलोम
हल :
(D) पाइथागोरस प्रमेय का विलोम

प्रश्न 33.
त्रिभुज ABC और DEF समरूप हैं। यदि AC = 19cm और DF = 8 cm, तो दोनों त्रिभुजों के क्षेत्रफलों का अनुपात है-
(A) \(\frac {19}{8}\)
(B) \(\frac {361}{64}\)
(C) \(\frac {38}{65}\)
(D) इनमें से कोई नहीं
हल :
(B) \(\frac {361}{64}\)

प्रश्न 34.
एक सीढ़ी इस प्रकार रखी है कि उसका निचला सिरा किसी दीवार से 5m दूर है और उसका ऊपरी सिरा एक खिड़की तक पहुँचता है, जो भूमि से 12m ऊँचाई पर है। सीढ़ी की लंबाई होगी-
(A) 13m
(B) 14m
(C) 15m
(D) 17 m
हल :
(A) 13m

प्रश्न 35.
यदि एक समबाहु त्रिभुज ABC इस प्रकार है कि AD ⊥ BC है तो AD² =
(A) 2 CD²
(B) 3 CD²
(C) 4 CD²
(D) \(\sqrt{3}\) CD²
हल :
(B) 3 CD²

प्रश्न 36.
एक सीढ़ी किसी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 m की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6m की ऊँचाई पर बनी एक खिड़की तक पहुँचता है। सीढ़ी की लंबाई होगी-
(A) 8.5m
(B) 7.5m
(C) 6.5m
(D) 11.0m
हल :
(C) 6.5m

प्रश्न 37.
20m लंबी एक सीढ़ी एक भवन की खिड़की पर पहुँचती है, जो भूमि से 16m की ऊँचाई पर है । भवन से सीढ़ी के निचले सिरे की दूरी होगी-
(A) 13m
(B) 12m
(C) 14m
(D) 15m
हल :
(B) 12 m

प्रश्न 38.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 4 : 5 है, तो उनकी संगत भुजाओं का अनुपात है :
(A) 4 : 5
(B) 16 : 25
(C) 2 : \(\sqrt{5}\)
(D) 5 : 4
हल :
(C) 2 : \(\sqrt{5}\)

प्रश्न 39.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं-
(i) 5 cm, 12 cm, 15 cm
(ii) 5 cm, 6 cm, 8 cm
(iii) 8 cm, 15 cm, 17 cm
इनमें से समकोण त्रिभुज है-
(A) (i)
(B) (ii)
(C) (iii)
(D) इनमें से कोई नहीं
हल :
(C) (iii)

प्रश्न 40.
एक आदमी उत्तर की ओर 7m जाता है और फिर पूर्व की ओर 24m जाता है । बताइए कि वह प्रारंभिक बिंदु से कितनी दूरी पर है ?
(A) 25m
(B) 17m
(C) 31m
(D) 24 m
हल :
(A) 25m

प्रश्न 41.
एक सीढ़ी सड़क के एक ओर 12m ऊँची खिड़की पर पहुँचती है। सीढ़ी के निचले सिरे को हटाए बिना वह सीढ़ी सड़क के दूसरी ओर 9m ऊँची खिड़की तक पहुँचती है। यदि सीढ़ी की लंबाई 15m हो, तो सड़क की चौड़ाई होगी-
(A) 3 m
(B) 21 m
(C) 27 m
(D) 24 m
हल :
(B) 21m

प्रश्न 42.
एक व्यक्ति एक निश्चित बिंदु से प्रथम पूर्व की ओर कुछ दूर चलता है तदोपरांत 12 m उत्तर की ओर जाता है और इस प्रकार वह अपनी प्रथम स्थिति से 13m की दूरी पर पहुँचता है। उसके द्वारा पूर्व दिशा में चली दूरी होगी-
(A) 25m
(B) 1m
(C) 5m
(D) 7m
हल :
(C) 5m

प्रश्न 43.
6m और 11 m लंबे दो खंभे समतल मैदान में गड़े हैं। यदि उनके निचले सिरों की दूरी 12m हो तो उनके ऊपरी सिरों के बीच की दूरी होगी-
(A) 17m
(B) 11m
(C) 12 m
(D) 13m
हल :
(D) 13m

प्रश्न 44.
5 m तथा 8 m ऊँचाई के दो खंभे एक समान तल पर खड़े हुए हैं। यदि उनके निचले सिरों के मध्य की दूरी 4 m हो तो उनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए ।
(A) 5m
(B) 4m
(C) 3m
(D) 8m
हल :
(A) 5m

प्रश्न 45.
ΔABC एक समद्विबाहु समकोण त्रिभुज है । यदि ∠ACB = 90° तथा AB = 5 √2 cm हो तो AC का मान होगा-
(A) 4 cm
(B) 5 cm
(C) 10 cm
(D) 7.5 cm
हल :
(B) 5 cm

प्रश्न 46.
किसी समबाहु त्रिभुज में उसकी एक भुजा के वर्ग का तीन गुना उसके शीर्षलम्ब के वर्ग के …………….. गुने के बराबर होता है ।
(A) दुगुने
(B) तीन
(C) चार
(D) पाँच
हल :
(C) चार

प्रश्न 47.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है । त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है-
(A) 1 : 4
(B) 1 : 2
(C) 2 : 1
(D) 4 : 1
हल :
(D) 4 : 1

प्रश्न 48.
ΔABC में AD, ∠BAC का समद्विभाजक है। यदि AB = 6 cm, AC = 5 cm व BD = 3 cm हो तो DC का मान होगा-
(A) 11.3 cm
(B) 2.5 cm
(C) 3.0 cm
(D) 5.5 cm
हल :
(B) 2.5 cm

प्रश्न 49.
यदि आकृति में AD, ∠A को समद्विभाजित करता है तथा AB = 12 cm, AC = 20 cm और BD = 5 cm हो, तो CD का मान होगा-
(A) 5.33 cm,
(B) 6.33 cm
(C) 7.33 cm
(D) 8.33 cm
हल :
(D) 8.33 cm

प्रश्न 50.
निम्नांकित आकृति में AD, ∠A का अर्द्धक है। यदि BD = 4 cm, DC = 3 cm और AB = 6 cm हो, तो AC का मान होगा-

(A) 4.5 cm
(B) 6.0 cm
(C) 9.0 cm
(D) 3.0 cm
हल :
(A) 4.5 cm

प्रश्न 51.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 5:3 है, तो उनकी संगत भुजाओं का अनुपात है : [ 2018 (Set-A)]
(A) 5 : 3
(B) 3 : 5
(C) \(\sqrt{5}\) : \(\sqrt{3}\)
(D) \(\sqrt{3}\) : \(\sqrt{5}\)
हल :
(C) \(\sqrt{5}\) : \(\sqrt{3}\)

प्रश्न 52.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं-
(i) 3 cm, 4 cm, 6 cm
(ii) 5 cm, 12 cm, 16 cm
(iii) 8 cm, 15 cm, 17 cm
इनमें से समकोण त्रिभुज है-
(A) (i)
(B) (ii)
(C) (iii)
(D) इनमें से कोई नहीं
हल :
(C) (iii)

प्रश्न 53.
ΔABC में AD, ∠BAC का समद्विभाजक है। यदि AB = 10cm, AC = 14 cm व BD = 2.5 cm हो तो DC की लंबाई होगी-
(A) 7.0 cm
(B) 14.0 cm
(C) 3.5 cm
(D) 28.0 cm
हल :
(C) 3.5 cm

प्रश्न 54.
दो समरूप त्रिभुजों की संगत माध्यिकाओं का अनुपात 4 : 9 है, तो त्रिभुजों के क्षेत्रफलों का अनुपात है-

(A) 2 : 3
(B) 4 : 9
(C) 16 : 81
(D) 81 : 16
हल :
(C) 16 : 81