HBSE 10th Class Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण युग्म

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण युग्म Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण युग्म

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
जसलीन ने एक पेंसिल और एक रबड़ 3 रु० में खरीदी। ऐसी ही दो पेंसिल व 5 रबड़ के लिए जतिन ने 12 रु० दिए। इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए ।
हल :
माना 1 पेंसिल का मूल्य x रु० तथा एक रबड़ का मूल्य ५ रु० हो तो रैखिक समीकरण-युग्म होगा-
x + y = 3 ……….(i)
2x + 5y = 12 ………….(ii)

ग्राफीय निरूपण के लिए,
x + y = 3
2x + 5y = 12

⇒ x = 3 – y

x	0	3
y	3	0

⇒ x = \(\frac{12-5 y}{2}\)

x	6	1
y	0	2

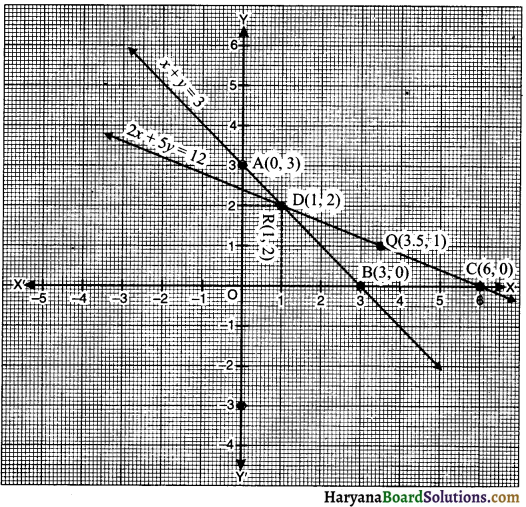
ग्राफ पेपर पर बिंदु A (0, 3) व B (3, 0) लेकर उन्हें मिलाकर रेखा AB प्राप्त करें जो समीकरण (i) को निरूपित करेगी तथा बिंदु C (6, 0) तथा बिंदु D (1, 2) लेकर मिलाकर रेखा CD प्राप्त करें जो समीकरण (ii) को निरूपित करेगी।
दोनों रेखाएँ AB और CD परस्पर बिंदु R (1, 2) पर प्रतिच्छेद करती हैं । अतः 1 पेंसिल का मूल्य 1 रु० व 1 रबड़ का मूल्य 2 रु०

प्रश्न 2.
निम्नलिखित समीकरणों को हल कीजिए :
\(\frac{2 x}{3}+\frac{y}{2}\) = 3
\(\frac{x}{2}-\frac{2 y}{3}=\frac{1}{6}\)
हल :
यहाँ पर,
\(\frac{2 x}{3}+\frac{y}{2}\) = 3
⇒ 4x + 3y = 18 (दोनों ओर 6 से गुणा करने पर) …………(i)
तथा \(\frac{x}{2}-\frac{2 y}{3}=\frac{1}{6}\)
⇒ 3x – 4y = 1 (दोनों ओर 6 से गुणा करने पर) …………(ii)
समीकरण (i) को 4 से तथा समीकरण (ii) को 3 से गुणा करने पर व जोड़ने पर,
16x + 12y = 72
9x – 12y = 3
या 25x = 75
या x = \(\frac {75}{25}\) = 3
x का मान समीकरण (i) में रखने पर,
4(3) + 3y = 18
या 3y = 18 – 12
या y = \(\frac {6}{3}\) = 2
अतः x = 3 व y = 2

प्रश्न 3.
समीकरणों 2x + y = 6 और 2x – y + 2 = 0 को आलेखित कीजिए। अक्ष के साथ इन समीकरणों को निरूपित करने वाली रेखाएँ जो त्रिभुज बनाती हैं उसके शीर्ष ज्ञात कीजिए। इस प्रकार बने त्रिभुजाकार क्षेत्र को छायांकित कीजिए ।
हल :
यहाँ पर
2x + y = 6 ……….. (i)
2x – y + 2 = 0 ……….. (ii)
समीकरण (i) से,
y = 6 – 2x

x	0	3
y	3	0

बिंदुओं A (0, 6) और B(3, 0) को आलेखित कर रेखा AB प्राप्त कीजिए जो समीकरण (i) को निरूपित करती है।
समीकरण (ii) से
y = 2x + 2

x	0	3
y	3	0

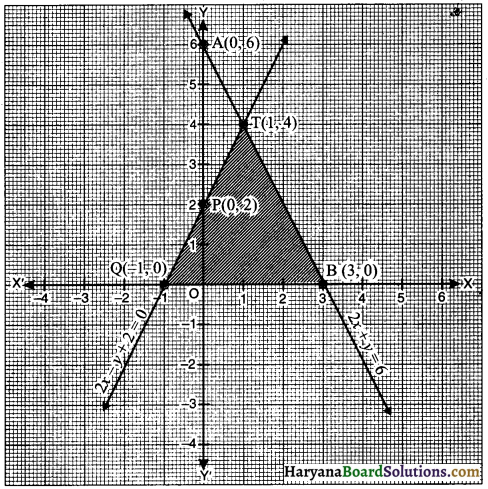
बिंदुओं P(0, 2) और Q (- 1, 0) को आलेखित कर रेखा PQ प्राप्त कीजिए
जो समीकरण (ii) को निरूपित करती है ।
अब (i) रेखा AB और PQ का प्रतिच्छेदन बिंदु T(1, 4) है।
(ii) रेखा AB, x- अक्ष को B (3, 0) पर काटती है ।
(iii) रेखा PQ, x – अक्ष को Q (-1, 0) पर काटती है ।
इस प्रकार, त्रिभुज के शीर्ष (1, 4), (3, 0) तथा (- 1, 0) हैं । अभीष्ट
छायांकित क्षेत्र आकृति में दर्शाया गया है।

प्रश्न 4.
निम्नलिखित समीकरणों को हल कीजिए :
\(\frac{x}{2}+\frac{2 y}{3}\) = – 1
\(\frac{x}{3}-\frac{y}{2}=\frac{13}{6}\)
हल :
यहाँ पर
\(\frac{x}{2}+\frac{2 y}{3}\) = – 1
⇒ 3x + 4y = – 6 (दोनों ओर 6 से गुणा करने पर ) …………… (i)
तथा \(\frac{x}{3}-\frac{y}{2}=\frac{13}{6}\)
⇒ 2x – 3y = 13 (दोनों ओर 6 से गुणा करने पर ) … (ii)
समीकरण (i) को 3 से तथा समीकरण (ii) को 4 से गुणा करने पर,
9x + 12y = – 18 … (iii)
8x – 12y = 52 … (iv)
समीकरण (iii) व (iv) को जोड़ने पर,
17x = 34
या x = \(\frac {34}{17}\) = 2
x का मान समीकरण (i) में रखने पर,
3 (2) + 4y = – 6
या 4y = – 6 – 6
या y = \(\frac {- 12}{4}\) = – 3
अतः x = 2 व y = -3

प्रश्न 5.
निम्नलिखित समीकरणों को हल कीजिए :
\(\frac{2 x}{3}-\frac{3 y}{2}\) = – 2
\(\frac{x}{2}+\frac{4 y}{3}=\frac{25}{3}\)
हल :
यहाँ पर,
\(\frac{2 x}{3}-\frac{3 y}{2}\) = – 2
⇒ 4x – 9y = – 12 (दोनों ओर 6 से गुणा करने पर ) …………(i)
तथा \(\frac{x}{2}+\frac{4 y}{3}=\frac{25}{3}\)
⇒ 3x + 8y = 50 (दोनों ओर 6 से गुणा करने पर ) …………(ii)
समीकरण (i) को 8 से तथा समीकरण (ii) को 9 से गुणा करने पर,
32x – 72y = – 96 …………….(iii)
27x + 72y = 450 ………….. (iv)
समीकरण (iii) व (iv) को जोड़ने पर प्राप्त होगा,
59x = 354
या x = \(\frac {354}{59}\) = 6
x का मान समीकरण (i) में प्रतिस्थापित करने पर,
4(6) – 9y = -12
या – 9y = – 12 – 24
या y = \(\frac {-36}{-9}\) = 4
अतः अभीष्ट हल x = 6 व y = 4

प्रश्न 6.
निम्नलिखित रैखिक समीकरण-युग्म को विलोपन विधि से हल कीजिए-
– 6x + 5y = 2 और 5x + 6y = 9
हल :
यहाँ पर
– 6x + 5y = 2 …………(i)
– 5x + 6y = 9 …………..(ii)
समीकरण (i) को 6 से तथा समीकरण (ii) को 5 से गुणा करने पर,
– 36x + 30y = 12 ………….(iii)
– 25x + 30y = 45 ………….(iv)
घटाने पर

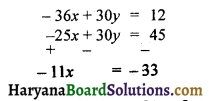
x = \(\frac {-33}{11}\) = 3
या x = 3 को समीकरण (i) में रखने पर,
या – 6 (3) + 5y = 2
या – 18 + 5y = 2
या 5y = 2 + 18
या 5y = 20
या y = \(\frac {20}{5}\) = 4
अतः अभीष्ट हल x = 3 व y = 4

प्रश्न 7.
रैखिक समीकरण – युग्म 2x + 3y = 7 और 6x – 5y = 11 को वज्र-गुणन विधि से हल कीजिए ।
हल :
यहाँ पर
2x + 3y – 7 = 0 ….(i)
व 6x – 5y – 11 = 0
वज्र – गुणन विधि से हल करने के लिए

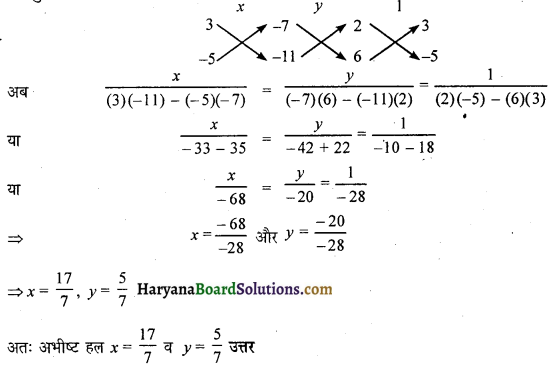
प्रश्न 8.
हल कीजिए :
\(\frac{2}{x}+\frac{3}{y}\) और \(\frac{5}{x}-\frac{4}{y}\) = – 2
हल :
यहाँ पर,
2(\(\frac {1}{x}\)) + 3(\(\frac {1}{y}\)) = 13 ………….(i)
5(\(\frac {1}{x}\)) – 4(\(\frac {1}{y}\)) = – 2 ………….(ii)
समीकरण (i) व (ii) में \(\frac {1}{x}\) = p व \(\frac {1}{y}\) = q प्रतिस्थापित करने पर प्राप्त होता है-
2p + 3q = 13 ………….(iii)
5p – 4q = -2 ………….(iv)
समीकरण (iii) को 4 से व (iv) को 3 से गुणा करने व जोड़ने पर प्राप्त होता है-

या p = \(\frac {46}{23}\) = 2
p का मान समीकरण (iii) में प्रतिस्थापित करने पर
2 (2) + 3q = 13
या 3q = 13 – 4
या q = \(\frac {9}{3}\) = 3
p और q का मान पुनः प्रतिस्थापित करने पर \(\frac {1}{x}\) = p और \(\frac {1}{y}\) = q
\(\frac {1}{x}\) = 2 और \(\frac {1}{y}\) = 3
⇒ x = \(\frac {1}{2}\) व y = \(\frac {1}{3}\).

प्रश्न 9.
समीकरण – युग्म 2x – 3y = 1 और kx + 5y= 7 में k का वह मान ज्ञात कीजिए जिसके लिए युग्म का अद्वितीय हल हो ।
हल :
यहाँ पर
2x – 3y = 1 ……………(i)
kx + 5y = 7 ……………(ii)
a₁ = 2, b₁ = – 3
a₂ = k, b₂ = 5
अद्वितीय हल होने के लिए आवश्यक है,
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{2}{k} \neq \frac{-3}{5}\)
या k ≠ \(\frac {10}{-3}\)
अतः \(\frac {10}{-3}\) के अतिरिक्त k के सभी मानों के लिए दिए गए समीकरण – युग्म का एक अद्वितीय हल होगा।

प्रश्न 10.
k का ऐसा मान ज्ञात कीजिए जिसके लिए समीकरण – युग्म 2x + ky = 1 और 3x – 5y = 7 का कोई हल न हो।
हल :
यहाँ पर
2x + ky – 1 = 0 ……..(i)
3x – 5y – 7 = 0 ………(ii)
a₁ = 2, b₁ = k, c₁ = – 1
a₂ = 3, b₂ = – 5, c₂ = – 7
समीकरण-युग्म का कोई हल न होने के लिए आवश्यक है कि,
\(\frac{a_1}{a_2}:=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
⇒ \(\frac {2}{3}\) = \(\frac {k}{- 5}\)
या 3k = – 10
या k = \(\frac {-10}{3}\)
अतः k = \(\frac {-10}{3}\) के लिए समीकरण -युग्म का कोई हल नहीं होगा ।

प्रश्न 11.
k के किस मान के लिए समीकरण – युग्म x + 2y + 7 = 0 व 2x + ky + 14 = 0 संपाती रेखाएँ प्रदर्शित करेगी?
हल :
यहाँ पर
x + 2y + 7 = 0 …………(i)
2x + ky + 14 = 0 ………….(ii)
⇒ a₁ = 1, b₁ = 2, c₁ = 7, a₂ = 2, b₂ = k, c₂ = 14
संपाती रेखाएँ अर्थात् अनंत अनेक हल होने के लिए आवश्यक है

अतः k = 4 के लिए समीकरण-युग्म की रेखाएँ संपाती होंगी।

प्रश्न 12.
पाँच वर्ष पहले नीता की आयु, गीता की आयु की तीन गुनी थी। दस वर्ष पश्चात् नीता की आयु, गीता की आयु की दुगुनी होगी। इस समय नीता और गीता की आयु क्या है ?
हल :
माना गीता की वर्तमान आयु = x वर्ष
तथा नीता की वर्तमान आयु = y वर्ष
प्रश्नानुसार पाँच वर्ष पहले, y – 5 = 3(x – 5)
या y – 5 = 3x – 15
या y – 3x = – 15 + 5
या y – 3x = – 10 ………….(i)
प्रश्नानुसार दस वर्ष बाद,
y + 10 = 2 (x + 10)
या y + 10 = 2x + 20
या y = 2x + 20 – 10
या y = 2x + 10 ………….(ii)
y का मान समीकरण (i) में रखने पर,
2x + 10 – 3x = – 10
या 2x – 3x = – 10 – 10
– x = – 20
या x = 20
∴ गीता की वर्तमान आयु = 20 वर्ष
तथा नीता की वर्तमान आयु = 2 × 20 + 10 = 50 वर्ष

प्रश्न 13.
किसी भिन्न के अंश और हर दोनों में से प्रत्येक में यदि 1 जोड़ दें, तो वह \(\frac {4}{5}\) बन जाती है। परंतु यदि प्रत्येक में से 5 घटा दें, तो वह \(\frac {1}{2}\) हो जाती है । वह भिन्न ज्ञात कीजिए ।
हल :
माना भिन्न का अंश = x
तथा भिन्न का हर = y
∴ भिन्न = \(\frac {x}{y}\)
पहली शर्त के अनुसार, \(\frac{x+1}{y+1}=\frac{4}{5}\)
या 5x + 5 = 4y + 4
या 5x – 4y = 4 – 5
या 5x – 4y = – 1 ………….(i)
दूसरी शर्त के अनुसार, \(\frac{x-5}{y-5}=\frac{1}{2}\)
या 2x – 10 = y – 5
या 2x – y = – 5 + 10
या 2x – y = 5 ………….(ii)
समीकरण (i) को 1 से तथा समीकरण (ii) को 4 से गुणा करने पर,

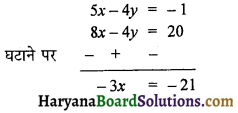
या x = \(\frac {-21}{-3}\) = 7
x = 7 को समीकरण (i) में रखने पर,
5 (7) – 4y = – 1
या 35 – 4y = – 1
या – 4y = – 1 – 35
या – 4y = – 36
या y = \(\frac {-36}{-4}\) = 9
अतः अभीष्ट भिन्न = \(\frac {7}{9}\)

प्रश्न 14.
दो अंकों वाली एक संख्या के अंकों का योग 8 है । अंकों को पलटने पर प्राप्त होने वाली संख्या दी गई संख्या से 36 अधिक है । वह संख्या ज्ञात कीजिए ।
हल :
माना संख्या की इकाई का अंक = x और दहाई का अंक = y
तो संख्या = 10y + x
∴ अंकों को पलटने पर प्राप्त संख्या = 10x + y
पहली शर्त के अनुसार,
x + y = 8 …….. (i)
दूसरी शर्त के अनुसार,
(10x + y) – (10y + x) = 36
या 10x + y – 10y – x = 36
या 9x – 9y = 36
x – y = 4 ………… (ii) (दोनों ओर 9 से भाग करने पर)
समीकरण (i) और (ii) को जोड़ने पर,
x – y = 4 …….. (ii)
x + y = 8 …….. (i)
2x = 12 ⇒ x = \(\frac {12}{2}\) = 6
x का मान समीकरण (i) में रखने पर,
या y = 8 – 6 = 2
अतः अभीष्ट संख्या = 10 × 2 + 6 = 26

प्रश्न 15.
तीन कुर्सियों और दो मेजों का मूल्य 1850 रु० है । पाँच कुर्सियों और तीन मेजों का मूल्य 2850 रु० है । दो कुर्सियों और दो मेजों का मूल्य ज्ञात कीजिए ।
हल :
माना कि एक कुर्सी का मूल्य = x रुपए
और एक मेज का मूल्य = y रुपए
पहली शर्त के अनुसार,
3x + 2y = 1850 ……. (i)
दूसरी शर्त के अनुसार,
5x + 3y = 2850 ……. (ii)
समीकरण (i) को 3 से तथा समीकरण (ii) को 2 से गुणा करने पर,

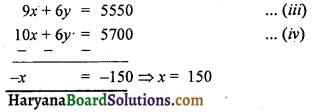
x का मान समीकरण (i) में रखने पर,
3 × 150 + 2y = 1850
या 450 + 2y = 1850
या 2y = 1850 – 450
या 2y = 1400
y = \(\frac {1400}{2}\) = 700
∴ 2 कुर्सियों और 2 मेजों का मूल्य = 2x + 2y
= 2 × 150 + 2 × 700
= 300 + 1400 = 1700 रुपए

प्रश्न 16.
स्टेशन A से स्टेशन B के 2 टिकटों और स्टेशन A से स्टेशन C के 3 टिकटों के लिए 795 रु० देने पड़ते हैं। परंतु स्टेशन A से B के 3 और A से C के 5 टिकटों के लिए कुल 1300 रु० देने पड़ते हैं। स्टेशन A से B का और स्टेशन A से C तक का किराया ज्ञात कीजिए ।
हल :
माना, स्टेशन A से स्टेशन B तक किराया = x रु०
तथा स्टेशन A से स्टेशन C तक किराया = y रु०
प्रश्नानुसार,
2x + 3y = 795 ……….(i)
3x + 5y = 1300 ……….(ii)
समीकरण (i) को 3 से तथा समीकरण (ii) को 2 से गुणा कर घटाने पर,

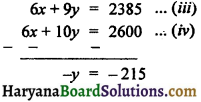
या y = 215
y का मान समीकरण (i) में रखने पर,
2x + 3 × 215 = 795
या 2x = 795 – 3 × 215
x = \(\frac{795-645}{2}=\frac{150}{2}\) = 75
अतः स्टेशन A से स्टेशन B तक किराया = 75 रु०
और स्टेशन A से स्टेशन C तक किराया = 215 रु०

प्रश्न 17.
यदि एक आयत की लंबाई को 2 मात्रक बढ़ा दें और उसकी चौड़ाई को 2 मात्रक घटा दें, तो उसका क्षेत्रफल 28 वर्ग मात्रक घट जाता है । यदि लंबाई को 1 मात्रक कम कर दें और चौड़ाई को 2 मात्रक बढ़ा दें, तो क्षेत्रफल 33 वर्ग मात्रक बढ़ जाता है । आयत की विमाएँ (dimensions) ज्ञात कीजिए ।
हल :
माना आयत की लम्बाई = x मात्रक
तथा आयत की चौड़ाई = y मात्रक
तो आयत का क्षेत्रफल = xy वर्ग मात्रक
पहली शर्त के अनुसार,
(x + 2) (y – 2) = xy – 28
या xy – 2x + 2y – 4 = xy – 28
या – 2x + 2y = xy – 28 – xy + 4
या – 2x + 2y = – 24
या x – y = 12 ……………(i)
दूसरी शर्त के अनुसार,
या (x – 1) (y + 2) = xy + 33
या xy + 2x – y – 2 = xy + 33
या 2x – y = xy + 33 – xy + 2
या 2x – y = 35 ……………(ii)
समीकरण (ii) को समीकरण (i) में से घटाने पर,

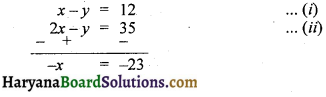
या x = 23
x का मान समीकरण (i) में रखने पर,.
23 – y = 12
या – y = 12 – 23
या – y = – 11
या y = 11
अतः आयत की लंबाई = 23 मात्रक
तथा आयत की चौड़ाई = 11 मात्रक

प्रश्न 18.
हल कीजिए :
\(\frac{5}{x}-\frac{4}{y}\) = – 2 और \(\frac{2}{x}+\frac{3}{y}\) = 13
हल :
यहाँ पर
5(\(\frac {1}{x}\)) – 4(\(\frac {1}{y}\)) = – 2 …………..(i)
2(\(\frac {1}{x}\)) + 3(\(\frac {1}{y}\)) = 13 …………..(ii)
माना \(\frac {1}{x}\) = p व \(\frac {1}{y}\) = q समीकरण (i) व (ii) में प्रतिस्थापित करने पर प्राप्त होता है-
5p – 4q = – 2 …………..(iii)
2p + 3q = 13 …………..(iv)
समीकरण (iii) को 3 से तथा (iv) को 4 से गुणा करके जोड़ने पर प्राप्त होता है-

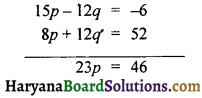
या p = \(\frac {46}{23}\) = 2
p का मान समीकरण (iii) में रखने पर
5 (2) – 4q = – 2
⇒ – 4q = – 2 – 10
⇒ q = \(\frac {-12}{-4}\) = 3
p और q का मान पुनः प्रतिस्थापित करने पर
\(\frac {1}{x}\) = p और \(\frac {1}{y}\) = q
\(\frac {1}{x}\) = 2 और \(\frac {1}{y}\) = 3
⇒ x = \(\frac {1}{2}\) और y = \(\frac {1}{3}\)

प्रश्न 19.
एक व्यक्ति नदी की धारा की दिशा में 2 घंटे में 20 कि०मी० और धारा के विरुद्ध 2 घंटे में 4 कि०मी० नाव चला सकता है। स्थिर जल में इस व्यक्ति की नाव चलाने की चाल और धारा की चाल ज्ञात कीजिए ।
हल :
माना स्थिर जल में नाव की चाल = x कि०मी० / घंटा
और धारा की चाल = y कि०मी० / घंटा
अतः जल के बहाव की ओर नाव की चाल = (x + y) कि०मी० / घंटा
और जल के बहाव के विपरीत नाव की चाल = (x – y) कि०मी० / घंटा
पहली शर्त के अनुसार, 20 = (x + y) × 2
या x + y = 10 ………..(i)
दूसरी शर्त के अनुसार, 4 = (x – y) × 2
या x – y = 2 ………..(ii)
समीकरण (i) और समीकरण (ii) को जोड़ने पर,
2x = 12 ⇒ x = \(\frac {12}{2}\) = 6
x का मान समीकरण (i) में रखने पर,
6 + y = 10
या y = 10 – 6 = 4
अतः स्थिर जल में नाव की चाल = 6 कि०मी० / घंटा
और धारा की चाल = 4 कि०मी० / घंटा

प्रश्न 20.
हल कीजिए : \(\frac{1}{2 x}-\frac{1}{y}\) = – 1, \(\frac{1}{x}+\frac{1}{2y}\) = 8
हल :
यहाँ पर,
\(\frac {1}{2}\)(\(\frac {1}{x}\)) – \(\frac {1}{y}\) = – 1 …………(i)
\(\frac {1}{x}\) + \(\frac {1}{2}\)(\(\frac {1}{y}\)) = 8 …………(ii)
समीकरण (i) व (ii) में \(\frac {1}{x}\) = p व \(\frac {1}{y}\) = q प्रतिस्थापित करने पर प्राप्त होता है ।
\(\frac {1}{2}\)p – q = – 1
या p – 2q = – 2 …………(iii)
p + \(\frac {1}{2}\)q = 8
या 2p + q = 16 …………(iv)
समीकरण (iv) को 2 से गुणा करके समीकरण (iii) में जोड़ने पर प्राप्त होता है ।

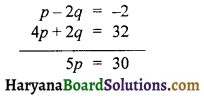
या p = \(\frac {30}{5}\) = 6
p का मान समीकरण (iii) में रखने पर
6 – 2q = – 2
⇒ – 2q = – 2 – 6
⇒ q = \(\frac {-8}{-2}\) = 4
p और q का मान पुनः प्रतिस्थापित करने पर – \(\frac {1}{x}\) = p और \(\frac {1}{y}\) = q
\(\frac {1}{x}\) = 6 और \(\frac {1}{y}\) = 4
⇒ x = \(\frac {1}{6}\) और y = \(\frac {1}{4}\)

बहुविकल्पीय प्रश्न

प्रश्न 1.
यदि दो चरों वाले रैखिक समीकरण के ग्राफ में l और m रेखाएँ एक-दूसरे को प्रतिच्छेद करें तो-
(A) समीकरण -युग्म के अनेक हल होते हैं
(B) समीकरण-युग्म का अद्वितीय हल होता है
(C) समीकरण -युग्म का कोई हल नहीं होता
(D) समीकरण-युग्म के दो हल होते हैं
हल :
(B) समीकरण-युग्म का अद्वितीय हल होता है

प्रश्न 2.
यदि दो चरों वाले रैखिक समीकरण के ग्राफ में p और q रेखाएँ एक-दूसरे के समांतर हों तो ………………………
(A) समीकरण -युग्म के अनेक हल होते हैं
(B) समीकरण-युग्म का अद्वितीय हल होता है
(C) समीकरण -युग्म का कोई हल नहीं होगा
(D) समीकरण -युग्म के दो हल होते हैं।
हल :
(C) समीकरण-युग्म का कोई हल नहीं होगा

प्रश्न 3.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\), तो निम्नलिखित में कौन-सा सत्य है?
(A) समांतर रेखाएँ
(B) प्रतिच्छेदित रेखाएँ
(C) संपाती रेखाएँ
(D) इनमें से कोई नहीं
हल :
(B) प्रतिच्छेदित रेखाएँ

प्रश्न 4.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) तो निम्नलिखित में कौन-सा सत्य है ?
(A) प्रतिच्छेदित रेखाएँ
(B) संपाती रेखाएँ
(C) समांतर रेखाएँ
(D) इनमें से कोई नहीं
हल :
(B) संपाती रेखाएँ

प्रश्न 5.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), तो निम्नलिखित में कौन-सा सत्य है ?
(A) प्रतिच्छेद करती हुई रेखाएँ
(B) संपाती रेखाएँ
(C) समांतर रेखाएँ
(D) इनमें से कोई नहीं
हल :
(C) समांतर रेखाएँ

प्रश्न 6.
समीकरणों x + y = 5, x – y = 5 और x = 0 को आलेखित करने पर बनने वाले त्रिभुज का x – अक्ष पर स्थित शीर्ष होगा-
(A) (0, 5)
(B) (5, 0)
(C) (0, – 5)
(D) (0, 0)
हल :
(B) (5, 0)

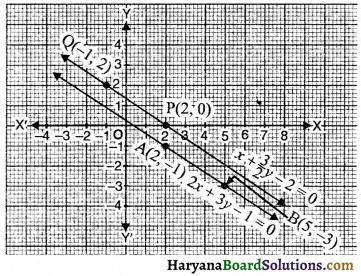
प्रश्न 7.
ग्राफ में दर्शाए गए रैखिक युग्म के कितने हल होंगे?
(A) कोई नहीं
(B) एक
(C) दो
(D) अपरिमित रूप से अनेक
हल :
(A) कोई नहीं

प्रश्न 8.

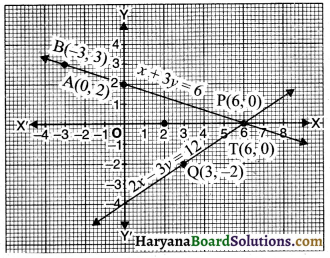
(A) (0, 2)
(B) (0, – 4)
(C) (6, 0)
(D) (0, 6)
हल :
(C) (6, 0)

प्रश्न 9.
संलग्न ग्राफ में दर्शाए गए रैखिक युग्म 2x – 4y – 10 = 0 व x – 2y = 5 के अभीष्ट हलों की संख्या होगी-

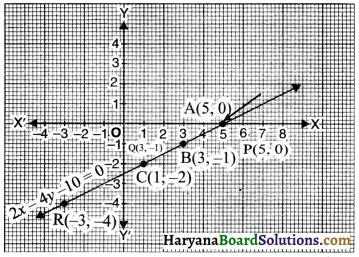
(A) कोई नहीं
(B) केवल एक
(C) दो
(D) अपरिमित रूप से अनेक
हल :
(D) अपरिमित रूप से अनेक

प्रश्न 10.
राम की आयु श्याम की आयु से 8 वर्ष अधिक है। दोनों की आयु का योगफल 28 वर्ष है तो राम की आयु होगी-
(A) 18 वर्ष
(B) 10 वर्ष
(C) 8 वर्ष
(D) 16 वर्ष
हल :
(A) 18 वर्ष

प्रश्न 11.
एक संख्या दूसरी संख्या से दोगुनी है और इनका योगफल 150 है, तो बड़ी संख्या होगी-
(A) 25
(B) 50
(C) 75
(D) 100
हल :
(D) 100

प्रश्न 12.
एक संख्या को 2 से गुणा करके 6 जोड़ने पर 28 प्राप्त होता है । इसका रैखिक समीकरण होगा-
(A) 2x + 28 = 6
(B) 2x + 6 = 28
(c) \(\frac {x}{2}\) + 6 = 28
(D) \(\frac{x+6}{2}\) = 28
हल :
(B) 2x + 6 = 28

प्रश्न 13.
रैखिक समीकरणों के युग्म 2x – ky + 3 = 0 तथा 3x + 2y – 1 = 0 का कोई हल नहीं है, के लिए k का मान ………………. है ।
(A) \(\frac {-4}{3}\)
(B) \(\frac {4}{3}\)
(C) 6
(D) – 6
हल :
(A) \(\frac {-4}{3}\)

प्रश्न 14.
समीकरणों x – 2y – 3 = 0 तथा 3x + ky – 1 = 0 के अद्वितीय हल के लिए k का मान होगा-
(A) k ≠ 6
(B) k ≠ 3
(C) k ≠ – 6
(D) इनमें से कोई नहीं
हल :
(C) k ≠ – 6

प्रश्न 15.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\),
(A) कोई हल नहीं
(C) अद्वितीय हल
हल :
(C) अद्वितीय हल

प्रश्न 16.
k के किस मान के लिए, निम्नलिखित रैखिक समीकरणों के युग्म के एक अद्वितीय (unique) हल है ?
4x + ky + 8 = 0
2x + 2y + 5 = 0
(A) k ≠ 4
(B) k ≠ 2
(C) k = 4
(D) इनमें से कोई नहीं
हल :
(A) k ≠ 4

प्रश्न 17.
k के किस मान के लिए, निम्नलिखित रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल हैं?
kx + 4y + 6 = 0
3x + 8y + 12 = 0
(A) k = 6
(B) k = 3
(C) k = 2
(D) k = 1.5
हल :
(D) k = 1.5

प्रश्न 18.
k के किस मान के लिए, निम्नलिखित रैखिक समीकरणों का कोई हल नहीं है ?
6x + 4y + k = 0
3x + 2y + 5 = 0
(A) k = 10
(B) k ≠ 10
(C) k = 5
(D) k = 2.5
हल :
(B) k ≠ 10

प्रश्न 19.
समीकरण – युग्म 5x + 2y = 16 और 7x – 4y = 2 में ……………………. होंगे।
(A) अनेक हल
(B) कोई हल नहीं
(C) अद्वितीय हल
(D) दो हल
हल :
(C) अद्वितीय हल

प्रश्न 20.
समीकरण – युग्म \(\sqrt{2}\)x – \(\sqrt{3}\)y = 0 और \(\sqrt{5}\)x + \(\sqrt{2}\)y = 0 का हल होगा-
(A) (0, 0)
(B) (1, 1)
(C) (-1, – 1)
(D) \(\sqrt{2}\), \(\sqrt{3}\)
हल :
(A) (0, 0)

प्रश्न 21.
समीकरण-युग्म x + y = 7 और 2x – 3y = 11 में से x का निराकरण करने पर y का मान …………………. होगा।
(A) \(\frac {32}{5}\)
(B) \(\frac {3}{5}\)
(C) \(\frac {5}{3}\)
(D) \(\frac {5}{32}\)
हल :
(B) \(\frac {3}{5}\)

प्रश्न 22.
समीकरण ax + by – c = 0 जहाँ x – अक्ष पर मिलता है, वह बिंदु होगा-
(A) (\(\frac {-c}{a}\), 0)
(B) (0, \(\frac {c}{b}\))
(C) (0, \(\frac {c}{a}\))
(D) (\(\frac {c}{a}\), 0)
हल :
(D) (\(\frac {c}{a}\), 0)

प्रश्न 23.
समीकरण-युग्म 3x – 5y = 1 और 5x + 2y = 19 को हल करने पर x का मान होगा
(A) \(\frac {97}{31}\)
(B) \(\frac {52}{31}\)
(C) \(\frac {31}{97}\)
(D) \(\frac {31}{52}\)
हल :
(A) \(\frac {97}{31}\)

प्रश्न 24.
समीकरणों 2x + 3y – 5 = 0 तथा kx – 6y – 8 = 0 के एक अद्वितीय हल के लिए, k का मान होगा-
(A) k ≠ 4
(B) k ≠ – 4
(C) k ≠ – 6
(D) इनमें से कोई नहीं
हल :
(B) k ≠ – 4

प्रश्न 25.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\), तो निम्नलिखित में कौन-सा सत्य है ?
(A) अद्वितीय हल
(B) कोई हल नहीं
(C) अपरिमित हल
(D) इनमें से कोई नहीं
हल :
(C) अपरिमित हल

प्रश्न 26.
‘K’ का वह मान, जिनके लिए रैखिक समीकरणों kx + 3y + (3 – k) = 0 तथा 12x + ky – k = 0 के युग्म के अपरिमित रूप से अनेक हल हैं,
(A) – 6
(C) 12
(B) – 12
(D) + 6
हल :
(A) – 6

प्रश्न 27.
समीकरणों a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), तो निम्नलिखित में कौन-सा सत्य है ?
(A) अद्वितीय हल
(B) कोई हल नहीं
(C) अपरिमित हल
(D) इनमें से कोई नहीं
हल :
(B) कोई हल नहीं

प्रश्न 28.
किसी भिन्न के अंश में 1 जोड़ने और उसके हर में से 1 घटाने पर 1 प्राप्त होता है। यदि यह भी ज्ञात हो कि उसके हर में 1 जोड़ने पर \(\frac {1}{2}\) प्राप्त होता है, तो भिन्न होगी –
(A) \(\frac {2}{5}\)
(B) \(\frac {5}{2}\)
(C) \(\frac {3}{5}\)
(D) \(\frac {5}{3}\)
हल :
(C) \(\frac {3}{5}\)

प्रश्न 29.
किसी भिन्न के हर में 5 जोड़ने और उसके अंश में से 5 घटाने पर \(\frac {1}{7}\) प्राप्त होता है। यदि उसके अंश में से 3 घटाया जाए और उसके हर में 3 जोड़ा जाए, तो \(\frac {1}{3}\) प्राप्त होता है, तो भिन्न होगी-
(A) \(\frac {7}{9}\)
(B) \(\frac {9}{7}\)
(C) \(\frac {5}{9}\)
(D) \(\frac {2}{9}\)
हल :
(A) \(\frac {7}{9}\)

प्रश्न 30.
दो अंकों वाली एक संख्या के अंकों का योग 8 है। अंकों को पलटने पर प्राप्त होने वाली संख्या दी गई संख्या से 36 अधिक है । वह संख्या होगी-
(A) 62
(B) 26
(C) 35
(D) 53
हल :
(B) 26

प्रश्न 31.
एक परिमेय संख्या का हर अंश से 5 अधिक है । यदि हर और अंश में से 2-2 घटा दिए जाएं तो संख्या \(\frac {2}{7}\) बन जाती है । परिमेय संख्या होगी-
(A) \(\frac {1}{6}\)
(B) \(\frac {4}{9}\)
(C) \(\frac {2}{7}\)
(D) \(\frac {3}{8}\)
हल :
(B) \(\frac {4}{9}\)

प्रश्न 32.
एक संख्या दो अंकों की बनी है, जिसके अंकों का योग 8 है। यदि संख्या में 18 जोड़ दिया जाए तो अंक अपना स्थान बदल लेते हैं । संख्या होगी-
(A) 26
(B) 62
(C) 35
(D) 44
हल :
(C) 35

प्रश्न 33.
दो अंकों वाली एक संख्या के अंकों का योग 9 है। अंकों का परस्पर क्रम बदलने पर प्राप्त संख्या दी गई संख्या से 27 अधिक है । दी गई संख्या होगी-
(A) 63
(B) 36
(C) 27
(D) 72
हल :
(B) 36

प्रश्न 34.
एक व्यक्ति कुछ मासिक वेतन पर नौकरी शुरू करता है और प्रत्येक वर्ष उसके वेतन में एक नियत वृद्धि होती रहती है । यदि 4 वर्ष के बाद उसका वेतन 1800 रु० हो तो उसका आरंभिक वेतन ……………….. होगा ।
(A) 1300 रु०
(B) 50 रु०
(C) 1000 रु०
(D) 1200 रु०
हल :
(A) 1300 रु०

प्रश्न 35.
चक्रीय चतुर्भुज के सम्मुख कोणों का योग होता है-
(A) 90°
(B) 180°
(C) 360°
(D) 270°
हल :
(B) 180°

प्रश्न 36.
1500 रु० हो और 10 वर्ष के बाद उसका वेतन होगा ।
(A) 26 मी०, 10 मी०
(B) 20 मी०, 16 मी०
(C) 22 मी०, 14 मी०
(D) इनमें से कोई नहीं
हल :
(B) 20 मी०, 16 मी०

प्रश्न 37.
राम ने 5 कुर्सियाँ और 2 मेजें 1625 रु० की खरीदीं। श्याम ने 1 मेज और 2 कुर्सियाँ 750 रु० की खरीदीं। प्रति कुर्सी और प्रति मेज, मूल्य क्रमशः होगा-
(A) 125 रु०; 500 रु०
(B) 500 रु०; 125 रु०
(C) 175 रु०; 400 रु०
(D) 400 रु०; 175 रु०
हल :
(A) 125 रु०; 500 रु०

प्रश्न 38.
3 कुर्सियाँ और 2 मेजों का मूल्य 700 रु० है और 5 कुर्सियों और 3 मेजों का मूल्य 1100 रु० है । 2 कुर्सियों और 2 मेजों का मूल्य होगा-
(A) 400 रु०
(B) 500 रु०
(C) 1800 रु०
(D) 600 रु०
हल :
(D) 600 रु०

प्रश्न 39.
एक संख्या दूसरी से 5 अधिक है, संख्याओं का योगफल 75 हो तो छोटी संख्या होगी-
(A) 35
(B) 40
(C) 45
(D) 30
हल :
(A) 35

प्रश्न 40.
दो संख्याओं का अनुपात 5 : 7 है और योगफल 360 है तो बड़ी संख्या होगी –
(A) 150
(B) 180
(C) 210
(D) 240
हल :
(C) 210

प्रश्न 41.
दो संख्याओं का अनुपात 5 : 4 है और यदि प्रत्येक संख्या में 10 जोड़ दिया जाए तो अनुपात 6 : 5 बन जाता है । संख्याएँ होंगी-
(A) 50, 40
(B) 40, 30
(C) 60, 50
(D) 45, 35
हल :
(A) 50, 40

प्रश्न 42.
दो संख्याओं का अनुपात 3 : 4 है, यदि प्रत्येक संख्या में से 7 घटा दिया जाए तो अनुपात 2 : 3 बन जाता है । संख्याएँ होंगी-
(A) 22, 29
(B) 21, 28
(C) 23, 31
(D) 28, 35
हल :
(B) 21,28

प्रश्न 43.
दो धनात्मक पूर्णांकों का अंतर 36 है। इन पूर्णांकों में 4 : 3 का अनुपात है। ये पूर्णांक होंगे-
(A) 144, 108
(B) 108, 72
(C) 180, 144
(D) 216, 180
हल :
(A) 144, 108