Class 9

Haryana State Board HBSE 9th Class Maths Notes Chapter 8 चतुर्भुज Notes.

Haryana Board 9th Class Maths Notes Chapter 8 चतुर्भुज

→ चार रेखाखंडों से बनी बंद आकृति को चतुर्भुज कहते हैं। एक चतुर्भुज की चार भुजाएं, चार कोण व चार शीर्ष होते हैं।

→ चतुर्भुज के कोणों का योग 360° होता है।

→ प्रत्येक समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वागसम त्रिभुजों में विभाजित करता है।

→ किसी समांतर चतुर्भुज में,

• सम्मुख भुजाएं बराबर होती हैं।
• सम्मुख कोण बराबर होते हैं।
• विकर्ण परस्पर समद्विभाजित करते हैं।

→ एक चतुर्भुज समांतर चतुर्भुज होता है, यदि-

• सम्मुख भुजाएं बराबर हों।
• सम्मुख कोण बराबर हों।
• विकर्ण परस्पर समद्विभाजित करते हों ।
• सम्मुख भुजाओं का एक युग्म बराबर और समांतर हो ।

→ यदि चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD का एक युग्म समांतर हो तो उसे समलंब कहते हैं।

→ आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। आयत का प्रत्येक कोण 90° का होता है।

→ समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इसकी सभी भुजाएं समान होती हैं।

→ वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं और बराबर होते हैं। वर्ग का प्रत्येक कोण 90° का होता है तथा सभी भुजाएं समान होती हैं।

→ किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर और उसका आधा होता है।

→ किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।

→ किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को एक क्रम से मिलाने वाले रेखाखंडों द्वारा बना चतुर्भुज एक समांतर चतुर्भुज होता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 7 त्रिभुज Notes.

Haryana Board 9th Class Maths Notes Chapter 7 त्रिभुज

→ त्रिभुज- तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई बंद आकृति को त्रिभुज कहते हैं। इसकी तीन भुजाएँ व तीन कोण होते हैं।

→ सर्वांगसम- दो आकृतियाँ सर्वांगसम कहलाती हैं, यदि उनका एक ही आकार व एक ही माप हो।

→ भुजा-कोण-भुजा सर्वांगसमता- दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।

→ कोण-भुजा-कोण सर्वांगसमता- दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हों।

→ एक त्रिभुज जिसकी दो भुजाएँ बराबर हों, उसे समद्विबाहु त्रिभुज कहते हैं।

→ एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।

→ किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।

→ भुजा-भुजा-भुजा सर्वांगसमता- यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।

→ समकोण-कर्ण-भुजा सर्वांगसमता- यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।

→ यदि किसी त्रिभुज की दो भुजाएँ असमान हों, तो बड़ी भुजा के सामने का सम्मुख कोण बड़ा होता है।

→ किसी त्रिभुज में बड़े कोण की सम्मुख भुजा बड़ी होती है।

→ त्रिभुज की किन्हीं दो भुजाओं का योग सदा तीसरी भुजा से बड़ा होता है।

→ किसी समबाहु त्रिभुज का प्रत्येक कोण 60° का होता है।

→ समान त्रिज्याओं वाले दो वृत्त सर्वांगसम होते हैं।

Haryana State Board HBSE 9th Class Maths Notes Chapter 6 रेखाएँ और कोण Notes.

Haryana Board 9th Class Maths Notes Chapter 6 रेखाएँ और कोण

→ रेखाखंड- एक रेखा का वह भाग जिसके दो अंत बिंदु हों, उसे एक रेखाखंड कहते हैं।

→ किरण- रेखा का वह भाग जिसका एक अंत बिंदु हो, उसे एक किरण कहते हैं ।

→ सरेख बिंदु- यदि तीन या अधिक बिंदु एक ही रेखा पर स्थित हों तो उन्हें संरेख बिंदु (Collinear Points) कहते हैं।

→ असरेख बिंदु- यदि तीन या अधिक बिंदु एक ही रेखा पर स्थित न हों तो उन्हें असरेख बिंदु (Non-Collinear Points) कहते हैं।

→ कोण- जब दो किरणें एक ही अंत बिंदु से प्रारंभ होती हों तो एक कोण बनता है। कोण को बनाने वाली दोनों किरणें कोण की भुजाएँ कहलाती हैं तथा वह उभयनिष्ठ अंत बिंदु कोण का शीर्ष कहलाता है।

→ न्यून कोण- 0° से 90° के बीच के कोण को न्यून कोण कहा जाता है।

→ समकोण- 90° के कोण को समकोण कहा जाता है।

→ अधिक कोण- 90° से 180° के बीच के कोण को अधिक कोण कहा जाता है।

→ ऋजु कोण- 180° के कोण को ऋजु कोण या सरल कोण कहा जाता है।

→ प्रतिवर्ती कोण- 180° से अधिक परंतु 360° से कम माप के कोण को प्रतिवर्ती कोण कहा जाता है।

→ पूरक कोण यदि दो कोणों का योग एक समकोण के बराबर हो तो ऐसे कोण पूरक कोण कहलाते हैं ।

→ संपूरक कोण यदि दो कोणों का योग 180° हो तो ऐसे कोण संपूरक कोण कहलाते हैं।

→ आसन्न कोण- ऐसे दो कोण जिनमें एक उभयनिष्ठ शीर्ष हो, एक उभयनिष्ठ भुजा हो, अन्य दो भुजाएँ उभयनिष्ठ भुजा के विपरीत दिशा में हों, उन्हें आसन्न कोण कहते हैं; जैसे आकृति में ∠ABD और ∠DBC आसन्न कोण हैं।

आकृति

→ रैखिक युग्म- यदि दो आसन्न कोणों का योग 180° हो तो उन्हें रैखिक युग्म कहा जाता है; जैसे ∠ABD और ∠DBC रैखिक युग्म हैं।

आकृति

→ शीर्षाभिमुख कोण- दो सरल रेखाओं के परस्पर काटने से आमने-सामने बने कोण शीर्षाभिमुख कोण कहलाते हैं तथा ये समान होते हैं; जैसे ∠AOD और ∠COB शीर्षाभिमुख कोण हैं।

आकृति

→ यदि दो आसन्न कोणों का योग 180° हो तो उनकी उभयनिष्ठ भुजाएँ एक रेखा बनाती हैं।

→ महत्त्वपूर्ण प्रमेय-

• यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हों तो शीर्षाभिमुख कोण बराबर होते हैं।
• यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो एकांतर अंतः कोणों का प्रत्येक युग्म बराबर होता है।
• यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि एकांतर अंतः कोणों का एक युग्म बराबर है, तो दोनों रेखाएँ परस्पर समांतर होती हैं।
• यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो तिर्यक रेखा के एक ही ओर के अंतः कोणों का प्रत्येक युग्म संपूरक होता है।
• यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि तिर्यक रेखा के एक ही ओर के अंतः कोणों का एक युग्म संपूरक है, तो दोनों रेखाएँ परस्पर समांतर होती हैं।
• वे रेखाएँ जो एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं।
• किसी त्रिभुज के कोणों का योग 180° होता है।
• यदि एक त्रिभुज की एक भुजा बढ़ाई जाए तो इस प्रकार बना बहिष्कोण दोनों अंतः अभिमुख (विपरीत) कोणों के योग के बराबर होता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 5 युक्लिड के ज्यामिति का परिचय Notes.

Haryana Board 9th Class Maths Notes Chapter 5 युक्लिड के ज्यामिति का परिचय

→ बिंदु – एक बिंदु (Point) वह है, जिसका कोई भाग नहीं होता।

→ एक रेखा (Line) चौड़ाई रहित लंबाई होती है।

→ एक रेखा के सिरे बिंदु होते हैं ।

→ एक सीधी रेखा ऐसी रेखा है, जो स्वयं पर बिंदुओं के साथ सपाट रूप से स्थित होती है।

→ एक पृष्ठ (Surface) ऐसा पृष्ठ है, जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।

→ पृष्ठ के किनारे (Edges) रेखाएँ होती हैं।

→ एक समतल पृष्ठ (Plane surface) ऐसा पृष्ठ है, जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।

→ यूक्लिड के कुछ अभिगृहीत हैं-

• वे वस्तुएँ जो एक ही वस्तु के बराबर हों, एक-दूसरे के बराबर होती हैं।
• यदि बराबरों को बराबरों में जोड़ा जाए, तो पूर्ण भी बराबर होते हैं।
• यदि बराबरों को बराबरों में से घटाया जाए, तो शेषफल भी बराबर होते हैं।
• वे वस्तुएँ जो परस्पर संपाती हों एक-दूसरे के बराबर होती हैं।
• पूर्ण अपने भाग से बड़ा होता है।
• एक ही वस्तुओं के दुगुने परस्पर बराबर होते हैं।
• एक ही वस्तुओं के आधे परस्पर बराबर होते हैं।

→ यूक्लिड की अभिधारणाएँ निम्नलिखित थीं-

• एक बिंदु से एक अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।
• एक सांत रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।
• किसी बिंदु को केंद्र मानकर और किसी त्रिज्या से एक वृत्त खींचा जा सकता है।
• सभी समकोण एक-दूसरे के बराबर होते हैं।
• यदि एक सीधी रेखा दो सीधी रेखाओं पर गिरकर अपने एक ही ओर दो अंतः कोण इस प्रकार बनाए कि इन दोनों कोणों का योग मिलकर दो समकोणों से कम हो, तो वे दोनों सीधी रेखाएँ अनिश्चित रूप से बढ़ाए जाने पर उसी ओर मिलती हैं, जिस ओर यह योग दो समकोणों से कम होता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 4 दो चरों वाले रैखिक समीकरण Notes.

Haryana Board 9th Class Maths Notes Chapter 4 दो चरों वाले रैखिक समीकरण

→ वह समीकरण जो ax + by + c = 0 के रूप में व्यक्त की जा सकती हो, जहां, a, b और c वास्तविक संख्याएं हैं। a व b दोनों शून्य नहीं हैं, उसे दो चरों वाला रैखिक समीकरण कहा जाता है।

→ दो चरों वाले रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं।

→ दो चरों वाले प्रत्येक रैखिक समीकरण का आलेख एक सरल रेखा होता है।

→ एक समीकरण को हल करते समय निम्नलिखित बातों को ध्यान में रखना होता है। एक रैखिक समीकरण पर तब कोई प्रभाव नहीं पड़ता जबकि :

• समीकरण के दोनों पक्षों में समान संख्या जोड़ी या घटाई जाती है।
• समीकरण के दोनों पक्षों को समान शून्येतर संख्या से गुणा या भाग किया जाता है।

→ x = 0, y-अक्ष का और y = 0, x-अक्ष का समीकरण है।

→ x = a का आलेख y-अक्ष के समांतर एक सरल रेखा होता है।

→ y = a का आलेख x-अक्ष के समांतर एक सरल रेखा होता है।

→ y = mx के प्रकार का समीकरण मूल बिंदु से होकर जाने वाली एक रेखा को निरूपित करता है ।

→ दो चरों वाले रैखिक समीकरण के आलेख पर स्थित प्रत्येक बिंदु रैखिक समीकरण का एक हल होता है। विलोमतः रैखिक समीकरण का प्रत्येक हल रैखिक समीकरण के आलेख पर स्थित एक बिंदु होता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 3 निर्देशांक ज्यामिति Notes.

Haryana Board 9th Class Maths Notes Chapter 3 निर्देशांक ज्यामिति

→ एक तल में किसी वस्तु या बिंदु का स्थान निर्धारण करने के लिए हमें दो लांबिक रेखाओं की आवश्यकता होती है, जिनमें से एक क्षैतिज तथा दूसरी ऊर्ध्वाधर होती है ।

→ तल को कार्तीय या निर्देशांक तल कहा जाता है और रेखाओं को निर्देशांक अक्ष कहा जाता है।

→ एक तल पर एक बिंदु की स्थिति का निर्धारण करने में प्रयुक्त पद्धति को दकार्ते के सम्मान में कार्तीय पद्धति कहा जाता है ।

→ क्षैतिज रेखा x अक्ष तथा ऊर्ध्वाधर रेखा y-अक्ष कहलाती है।

→ x-अक्ष व y-अक्ष के प्रतिच्छेद बिंदु को मूलबिंदु (origin) कहा जाता है।

→ y-अक्ष से किसी बिंदु की दूरी को उसका x-निर्देशांक या भुज कहते हैं ।

→ x-अक्ष से किसी बिंदु की दूरी को उसका y-निर्देशांक या कोटि कहते हैं।

→ निर्देशांक तल में एक बिंदु के निर्देशांक लिखते समय पहले x-निर्देशांक लिखते हैं और उसके बाद y-निर्देशांक लिखते हैं। हम निर्देशांकों को कोष्ठक के अंदर लिखते हैं।

→ मूलबिंदु के निर्देशांक (0, 0), x-अक्ष पर किसी बिंदु के निर्देशांक (x, 0) व y-अक्ष पर किसी बिंदु के निर्देशांक (0, y) होते हैं।

→ ध्यान रहे-

(i) यदि बिंदु पहले चतुर्थांश में है, तो बिंदु (+, +) के रूप का होगा, क्योंकि पहला चतुर्थांश धनात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(ii) यदि बिंदु दूसरे चतुर्थाश में है, तो बिंदु (-, +) के रूप का होगा, क्योंकि दूसरा चतुर्थांश ऋणात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(iii) यदि बिंदु तीसरे चतुर्थांश में है, तो बिंदु (-, -) के रूप में होगा, क्योंकि तीसरा चतुर्थांश ऋणात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है।
(iv) यदि बिंदु चौथे चतुर्थांश में है तो बिंदु (+, -) के रूप में होगा, क्योंकि चौथा चतुर्थांश धनात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 2 बहुपद Notes.

Haryana Board 9th Class Maths Notes Chapter 2 बहुपद

→ बहुपद – बहुपद एक ऐसा व्यंजक होता है, जिसमें एक या एक से अधिक पद होते हैं। सामान्यतः चर x में एक बहुपद को निम्नलिखित प्रकार से लिखा जा सकता है-
p(x) = a₀xⁿ + a₁x^n-1 + ……. + a_n-1x + a_n
जिसमें a₀, a₁, a₂, …………., a_n आदि सभी गुणांक वास्तविक संख्याएँ हैं तथा a_n ≠ 0 और n एक ऋणोतर पूर्णांक है।

→ बहुपद की घात- बहुपद की अधिकतम घात वाले पद के घातांक को उस बहुपद की घात कहते हैं; जैसे x⁴ + x³ – x में बहुपद की घात 4 है।

→ एक घात वाले बहुपद को रैखिक बहुपद कहा जाता है।

→ दो घात वाले बहुपद को द्विघाती या द्विघात बहुपद कहा जाता है।

→ तीन घात वाले बहुपद को त्रिघाती बहुपद कहा जाता है।

→ एक शून्येतर अचर बहुपद की घात शून्य होती है अर्थात अचर बहुपद 0 को शून्य बहुपद कहा जाता है।

→ केवल एक पद वाले बहुपद को एकपदी (monomial), दो पदों वाले बहुपद को द्विपद (binomial) तथा तीन पदों वाले बहुपद को त्रिपद (trinomial) कहा जाता है।

→ भाग के किसी प्रश्न के लिए-
भाज्य = (भाजक × भागफल) + शेषफल

→ p(x) = 3x² + x – 1 को (x + 1) से भाग देने पर जो शेषफल प्राप्त होता है, यह वही होता है जोकि बहुपद (x + 1) के शून्यक अर्थात -1 पर बहुपद p(x) का मान होता है।

→ शेषफल प्रमेय- मान लीजिए p(x) एक से अधिक या एक के बराबर घात वाला एक बहुपद है और मान लीजिए a कोई वास्तविक संख्या है। यदि p(x) को रैखिक बहुपद (x – a) से भाग दिया जाए तो शेषफल p(a) होता है।

→ गुणनखंड प्रमेय- यदि p(x) घात n ≥ 1 वाला एक बहुपद हो और कोई वास्तविक संख्या हो तो-
(i) x – a, p(x) का एक गुणनखंड होता है, यदि p(a) = 0 हो और (ii) p(a) = 0 होता है, यदि (x – a), p(x) का एक गुणनखंड हो ।

→ बीजीय सर्वसमिकाएँ-
(i) (x + y)² = x² + 2xy + y²
(ii) (x – y)² = x² – 2xy + y²
(iii) x² – y² = (x + y)(x – y)
(iv) (x + a)(x + b) = x² + (a + b)x + ab
(v) (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
(vi) (x + y)³ = x³ + y³ + 3xy(x + y)
(vii) (x – y)³ = x³ – y³ – 3xy(x – y)
(viii) x + y + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)

Haryana State Board HBSE 9th Class Maths Notes Chapter 1 संख्या पद्धति Notes.

Haryana Board 9th Class Maths Notes Chapter 1 संख्या पद्धति

→ प्राकृत संख्याएँ (N) = 1, 2, 3, 4, 5, …………..

→ सबसे छोटी प्राकृत संख्या 1 है।

→ पूर्ण संख्याएँ = 0, 1, 2, 3, 4, ………….

→ सबसे छोटी पूर्ण संख्या 0 (शून्य) है।

→ पूर्णांक (Z) = …………, -3, -2, -1, 0, 1, 2, 3, …………….

→ परिमेय संख्या – संख्या r को परिमेय संख्या कहा जाता है, यदि इसेद \(\frac{p}{q}\) के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।

→ किन्हीं दो दी हुई परिमेय संख्याओं के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं।

→ अपरिमेय संख्या – संख्या ‘s’ को अपरिमेय संख्या कहा जाता है यदि इसे \(\frac{p}{q}\) के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है; जैसे \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{15}\), π आदि ।

→ वास्तविक संख्याएँ – परिमेय संख्याओं और अपरिमेय संख्याओं के संग्रह को वास्तविक संख्याएँ कहा जाता है।

→ सांत दशमलव संख्या – यदि किसी संख्या के अंश को हर से भाग करने पर शेष शून्य हो जाता है तो ऐसी संख्या के दशमलव प्रसार को सांत दशमलव कहते हैं।

→ असांत दशमलव या अनवसानी आवर्ती संख्या – यदि किसी संख्या के अंश को हर से भाग करने पर शेष कभी भी शून्य नहीं होता तो ऐसी संख्या के दशमलव प्रसार को असांत दशमलव या अनवसानी आवर्ती संख्या कहते हैं।

→ एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार सांत या अनवसानी आवर्तीीं है, परिमेय होती है।

→ एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती है, अपरिमेय होती है।

→ एक परिमेय संख्या और एक अपरिमेय संख्या का जोड़ या घटाना, अपरिमेय होता है।

→ एक अपरिमेय संख्या के साथ एक शून्येतर (non-zero) परिमेय संख्या का गुणनफल या भागफल अपरिमेय होता है।

→ यदि हम दो अपरिमेय संख्याओं को जोड़े, घटाएँ, गुणा करें या एक अपरिमेय संख्या को दूसरी अपरिमेय संख्या से भाग दें, तो परिणाम परिमेय या अपरिमेय कुछ भी हो सकता है।

→ यदि a और b धनात्मक वास्तविक संख्याएँ हों तो-
(i) \(\sqrt{a b}=\sqrt{a} \cdot \sqrt{b}\)
(ii) \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)
(iii) \((\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b\)
(iv) \((a+\sqrt{b})(a-\sqrt{b})=a^2-b\)
(v) \((\sqrt{a}+b)(\sqrt{a}-b)=a-b^2\)
(vi) \((\sqrt{a}+\sqrt{b})^2=a+2 \sqrt{a b}+b\)

→ घातांक के नियम परिमेय संख्याओं पर भी लागू होते हैं अर्थात यदि a > 0, एक वास्तविक संख्या हो और p तथा q परिमेय संख्याएँ हों तो-
(i) a^p · a^q = a^p+q
(ii) \(\left(a^p\right)^q=a^{p q}\)
(iii) \(\frac{a^p}{a^q}=a^{p-q}\)
(iv) a^p · b^p = (ab)^p

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 15 प्रायिकता

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
टायर बनाने वाली एक कंपनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए हैं।

यदि आप इस कंपनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 कि०मी० की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(ii) यह 9000 कि०मी० से भी अधिक दूरी तक चलेगा?
(iii) 4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?
हल :
संभाव्य परिणामों की कुल संख्या = 20 + 210 + 325 + 445 = 100
(i) उस टायर की बारंबारता, जिसे 4000 कि०मी० की दूरी तय करने से पहले बदलना आवश्यक हो, 20 है।
अतः, P (4000 कि०मी० की दूरी तय करने से पहले टायर बदलना आवश्यक हो)
= \(\frac{20}{1000}\) = 0.02

(ii) उस टायर की बारंबारता जो 9000 कि०मी० से भी अधिक दूरी तय करेगा = 325 + 445 = 770
अतः,P (टायर 9000 कि०मी० से भी अधिक दूरी तक चलेगा) = \(\frac{770}{1000}\) = 0.77

(iii) उस टायर की बारंबारता जिसे 4000 कि०मी० और 14000 कि०मी० के बीच की दूरी तय कर लेने के बाद बदलना आवश्यक होगा = 210 + 325 = 535
अतः, P (4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद टायर को बदलना आवश्यक हो)
= \(\frac{535}{1000}\) = 0.535.

प्रश्न 2.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यादृच्छया निकाली गई। निकाली गई गेंद के
(i) सफेद?
(ii) लाल?
(iii) काली? होने की प्रायिकता क्या है?
हल :
(i) थैले में 4 सफेद गेंद हैं। तो सफेद गेंद निकलने की 4 संभावनाएं हैं और थैले में से एक गेंद की संभावित परिणाम की संभावना 12 है।

∴ P (सफेद गेंद निकालना) = \(\frac{4}{12}=\frac{1}{3}\)

(ii) P (लाल गेंद निकालना) = \(\frac{3}{12}=\frac{1}{4}\)

(iii) P (काली गेंद निकालना) = \(\frac{5}{12}\)

प्रश्न 3.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यादृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता क्या है?
हल :
गोली को यादृच्छिक रूप से निकालने का अर्थ है कि परिणाम सम-संभावी हैं।
परिणामों की कुल संख्या = 3 + 2 = 5
चूंकि थैले में 2 नीली गोलियां हैं, अतः कुल 5 परिणाम में ।
से, अनुकूल परिणाम = 2
इसलिए, P (एक नीली गोली) = \(\frac{2}{5}\)

प्रश्न 4.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। प्रायिकता (probability) ज्ञात कीजिए, जबकि टिकट पर अंकित अंक
(i) अभाज्य संख्या हो,
(ii) सम पूर्ण वर्ग हो,
(iii) 7 से भाज्य संख्या हो।
हल :
संभाव्य परिणामों की कुल संख्या = 30
(i) 1 से 30 तक अंकित टिकटों में अभाज्य संख्या वाले टिकट = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
अतः अनुकूल परिणामों की कुल संख्या = 10
∴ अभाज्य संख्या वाला टिकट निकलने की प्रायिकता = \(\frac{10}{30}=\frac{1}{3}\)

(ii) संपूर्ण वर्ग वाले टिकट = 4, 16
अतः अनुकूल परिणामों की संख्या = 2
∴ सम पूर्ण वर्ग वाले टिकट निकलने की प्रायिकता = \(\frac{2}{30}=\frac{1}{15}\)

(iii) 7 से भाज्य संख्या वाले टिकट = 7, 14, 21, 28
अतः अनुकूल परिणामों की संख्या = 4
∴ 7 से भाज्य संख्या वाले टिकट निकलने की प्रायिकता = \(\frac{4}{30}=\frac{2}{15}\)

प्रश्न 5.
रिक्त स्थानों की पूर्ति कीजिए :
(i) निश्चित घटना की प्रायिकता ___________ होती है।
(ii) असंभव घटना की प्रायिकता ___________ होती है।
(iii) किसी घटना (निश्चित और असंभव के अतिरिक्त) की प्रायिकता ___________ के बीच में होती है।
(iv) एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता ___________ है।
हल :
(i) 1
(ii) 0
(iii) 0 और 1
(iv) \(\frac{1}{2}\)

प्रश्न 6.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-

इन आंकड़ों के आधार पर इस बात की प्रायिकता ज्ञात कीजिए कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है।
हल :
यहाँ पर,
कुल संभाव्य परिणामों की संख्या = यूनिट (I + II + III + IV + V) = 5
70% से अधिक अंक प्राप्त करने के अनुकूल परिणामों की संख्या = यूनिट (II + III + V) = 3
∴ P (70% से अधिक प्राप्त करना) = \(\frac{3}{5}\) = 0.6

प्रश्न 7.
52 पत्तों की ताश की गड्डी से चिड़ी के बादशाह, बेगम और गुलाम को अलग करके शेष को अच्छी तरह से फेंट दिया गया है। शेष पत्तों में से एक पत्ता निकाला जाता है। निम्न की प्राप्ति की प्रायिकता ज्ञात कीजिए :
(i) पान
(ii) बादशाह।
हल :
(i) बादशाह, बेगम और गुलाम को अलग करके शेष बचे पत्तों की संख्या = 52 – 3 = 49 पत्ते
अब 49 पत्तों में 13 पान के पत्ते हैं।
अर्थात अनुकूल परिणामों की संख्या = 13
तथा संभाव्य परिणामों की कुल संख्या = 49
अब, P (पान) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{13}{49}\)

(ii) 49 पत्तों में 3 बादशाह हैं क्योंकि 1 बादशाह को निकाल दिया गया है।
∴ अनुकूल परिणामों की संख्या = 3
अब, P (बादशाह) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{3}{49}\)

Multiple Choice Questions with Answers:

प्रश्न 1.
किसी घटना के घटने की प्रायिकता होती है-
(A) 0 से 0.5 के बीच
(B) 0 से 1 के बीच
(C) 0 से 2 के बीच
(D) 0 से 5 के बीच
उत्तर-
(B) 0 से 1 के बीच

प्रश्न 2.
एक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त हुईं- चित – 455; पट – 545. इसमें पट प्राप्ति की प्रायिकता होगी-
(A) \(\frac{91}{200}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{109}{200}\)
(D) 0
उत्तर-
(C) \(\frac{109}{200}\)

प्रश्न 3.
उपरोक्त प्रश्न नं० 2 में एक चित के आने की घटना की प्रायिकता है-
(A) 0.455
(B) 4.55
(C) 5.45
(D) 0.545
उत्तर-
(A) 0.455

प्रश्न 4.
दो सिक्कों को एक साथ 500 वार उछालने पर हमें प्राप्त होता है। दो चितः 105 बार; एक चित :275 वार; कोई भी चित नहीं-120 बार। इसमें एक चित के आने की घटना की प्रायिकता है-
(A) 0.275
(B) 2.75
(C) 0.55
(D) 0.21
उत्तर-
(C) 0.55

प्रश्न 5.
उपरोक्त प्रश्न नं0 4 में दो चित के आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.105
(C) 0.55
(D) 0.24
उत्तर-
(A) 0.21

प्रश्न 6.
उपरोक्त प्रश्न नं० 4 में कोई भी चित नहीं आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.12
(C) 0.55
(D) 0.24
उत्तर-
(D) 0.24

प्रश्न 7.
एक क्रिकेट मैच में एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है, चौका मारे जाने की प्रायिकता
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(C) \(\frac{1}{5}\)

प्रश्न 8.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता होगी-
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(A) \(\frac{4}{5}\)

प्रश्न 9.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारम्बारताएँ हैं :

28 यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता होगी
(A) \(\frac{23}{200}\)
(B) \(\frac{9}{25}\)
(C) \(\frac{77}{200}\)
(D) \(\frac{7}{50}\)
उत्तर-
(B) \(\frac{9}{25}\)

प्रश्न 10.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के सफेद होने की प्रायिकता होगी-
(A) \(\frac{5}{12}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{2}\)
उत्तर-
(C) \(\frac{1}{3}\)

प्रश्न 11.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के लाल होने की प्रायिकता होगी-
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(B) \(\frac{3}{5}\)

प्रश्न 12.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यदृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता होगी
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(D) \(\frac{2}{5}\)

प्रश्न 13.
सारणी-

इस सारणी में एक विद्यार्थी द्वारा 20 से कम अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{7}{90}\)
(B) \(\frac{17}{90}\)
(C) \(\frac{7}{10}\)
(D) \(\frac{27}{90}\)
उत्तर-
(A) \(\frac{7}{90}\)

प्रश्न 14.
प्रश्न नं0 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 60 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{67}{90}\)
उत्तर-
(B) \(\frac{23}{90}\)

प्रश्न 15.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 70 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{82}{90}\)
उत्तर-
(C) \(\frac{8}{90}\)

प्रश्न 16.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 30 से कम अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{7}{90}\)
(B) \(\frac{10}{90}\)
(C) \(\frac{3}{90}\)
(D) \(\frac{17}{90}\)
उत्तर-
(D) \(\frac{17}{90}\)

प्रश्न 17.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आंकड़ों को नीचे दी गई सारणी में लिख लिया गया है-

प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी सांख्यिकी पसंद करता है
(A) \(\frac{27}{40}\)
(B) \(\frac{13}{40}\)
(C) 1
(D) शून्य
उत्तर-
(A) \(\frac{27}{40}\)

प्रश्न 18.
अच्छी प्रकार से फेंटी गई, 52 पत्तों की ताश की गड्डी में से एक पत्ता खींचा गया है। एक इक्के की प्राप्ति की प्रायिकता होगी-
(A) \(\frac{1}{52}\)
(B) \(\frac{2}{26}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
उत्तर-
(C) \(\frac{1}{13}\)

प्रश्न 19.
एक मौसम केंद्र के रिकॉर्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में किए गए मौसम पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं। एक दिए हुए दिन पर पूर्वानुमान के सही होने की प्रायिकता होगी-
(A) 0.3
(B) 0.7
(C) 0.5
(D) 0.4
उत्तर-
(B) 0.7

प्रश्न 20.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-

इन आंकड़ों के आधार पर इस बात की प्रायिकता क्या होगी कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है-
(A) 0.6
(B) 0.4
(C) 0.5
(D) 0.2
उत्तर-
(A) 0.6

प्रश्न 21.
निश्चित घटना की प्रायिकता _____________ होती है।
(A) शून्य
(B) शून्य से 1 के बीच
(C) \(\frac{1}{2}\)
(D) 1
उत्तर-
(D) 1

प्रश्न 22.
असम्भव घटना की प्रायिकता _____________ होती है।
(A) एक
(B) \(\frac{1}{2}\)
(C) शून्य
(D) \(\frac{3}{2}\)
उत्तर-
(C) शून्य

प्रश्न 23.
एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता होगी
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)

प्रश्न 24.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। निकाली गई टिकट पर अंकित अंक 7 से भाज्य संख्या होने की प्रायिकता होगी-
(A) \(\frac{1}{30}\)
(B) \(\frac{1}{15}\)
(C) \(\frac{2}{15}\)
(D) \(\frac{1}{10}\)
उत्तर-
(C) \(\frac{2}{15}\)

प्रश्न 25.
आटे की उन ग्यारह थैलियों में, जिन पर 5 कि०ग्रा० अंकित है, वास्तव में आटे के निम्नलिखित भार (कि०ग्रा० में) हैं:
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
यादृच्छया चुनी गई एक थैली में 5 कि०ग्रा० से अधिक आटा होने की प्रायिकता होगी-
(A) \(\frac{7}{11}\)
(B) \(\frac{6}{11}\)
(C) \(\frac{5}{11}\)
(D) \(\frac{10}{11}\)
उत्तर-
(A) \(\frac{7}{11}\)

प्रश्न 26.
एक सिक्के को एक बार उछालने पर पट प्राप्त करने की प्रायिकता होती है-
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 14 सांख्यिकी

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
वन महोत्सव के दौरान 100 विद्यालयों में से प्रत्येक में 100 पौधे लगाए गए। एक महीने बाद लगाए गए पौधों में से बच गए पौधों की संख्याएं निम्न थीं:
हल :
95 67 28 32 65 65 69 33 98 96
76 42 32 38 42 40 40 69 95 92
75 83 76 83 85 62. 37 65 63 42
89 65 73 81 49 52 64 76 83 92
93 68 52 79 81 83 59 82 75 82
86 90 44 62 31 36 38 42 39 83
87 56 58 23 35 76 83 85 30 68
69 83 86 43 45 39 83 75 66 83
92 75 89 66 9 1 27 88 89 93 42
53 69 90 55 66 49 52 83 34 36
इन आंकड़ों से वर्ग अंतराल 20-29 लेकर एक वर्गीकृत बारंबारता सारणी बनाइए।
हल :
दिए गए वर्ग अंतराल के अनुसार दिए गए आंकड़ों की बारंबारता सारणी निम्न होगी-

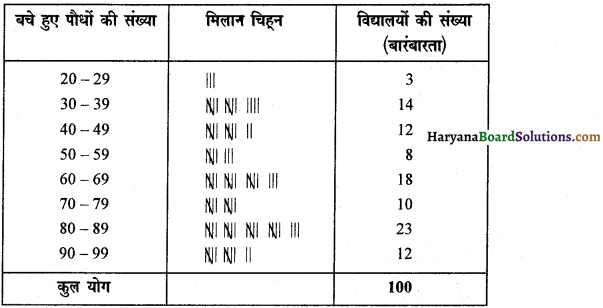
बचे हुए पौधों की संख्या मिलान चिह्न विद्यालयों की संख्या.

प्रश्न 2.
निम्नलिखित आंकड़ों का दंड आलेख खींचिए-

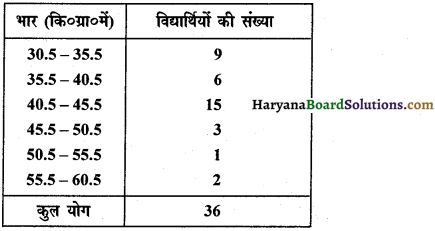
हल :
दिए गए आंकड़ों का दंड आलेख निम्न है-

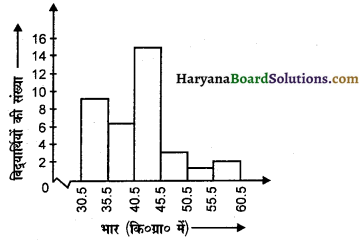
प्रश्न 3.
एक परिवार द्वारा भिन्न-भिन्न मदों पर किया गया मासिक खर्च निम्न अनुसार है। इनको दर्शाने के लिए एक दंड आलेख (Bar-graph) बनाइए-

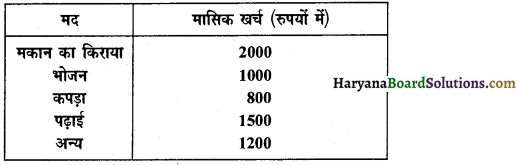
हल :
दिए गए आंकड़ों का दंड आलेख निम्न होगा –

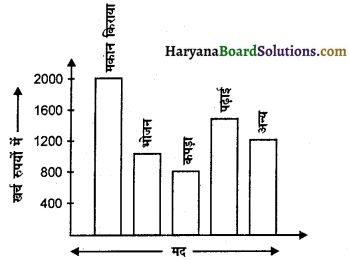
प्रश्न 4.
निम्नलिखित आंकड़ों के लिए एक ही आलेख पर आयतचित्र तथा बारंबारता बहुभुज बनाएं-

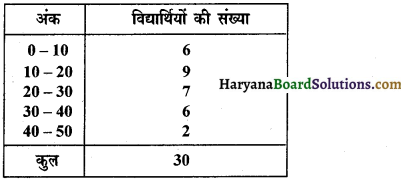
हल :
30 विद्यार्थियों के अंकों की बंटन सारणी को दर्शाने के लिए आयतचित्र तथा बारंबारता बहुभुज अग्रांकित होगा-

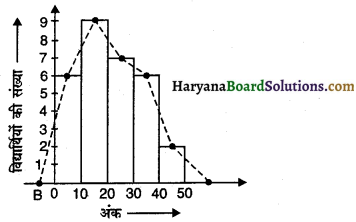
प्रश्न 5.
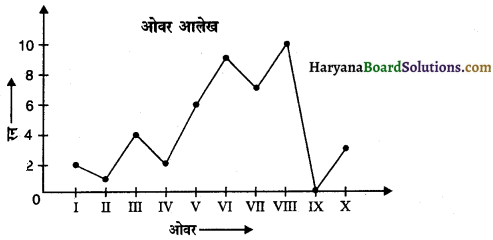
एक क्रिकेट टीम ने पहले 10 ओवर्स में जो रन बनाए वह निम्न अनुसार हैं। इनके लिए एक आलेख बनाएं।

हल :
दिए गए आंकड़ों का आलेख संलग्न है-

प्रश्न 6.
यदि प्रेक्षणों 9, 13, 18, 15, p तथा 17 का मध्यमान 15 हो तो p का मान ज्ञात करें।
हल :
मध्यमान = \(\frac{9+13+18+15+p+17}{6}\)
⇒ 15 = \(\frac{72+p}{6}\)
15 × 6 = 72 + p
90 = 72 + p
p = 90 – 72 = 18

प्रश्न 7.
निम्नलिखित आंकड़ों का बहुलक ज्ञात करें।
30, 50, 35, 30, 42, 70, 55, 50, 60, 65, 61, 60, 60, 50, 50, 55
हल :
उपरोक्त आंकड़ों से निम्नलिखित सारणी बनती हैं-

यहां हम देखते हैं कि प्रेक्षण 50 की बारंबारता (4) सबसे अधिक है। इसलिए बहुलक (mode) = 50 है।

प्रश्न 8.
हॉकी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये हैं-
24, 10, 8, 14, 5, 48, 10, 8, 7, 18, 28, 15, 27, 10, 2, 7
टीम द्वारा प्राप्त किए गए अंकों का माध्य, माध्यक व बहुलक ज्ञात कीजिए।
हल :
(i) माध्य \((\bar{x})=\frac{24+10+8+14+5+48+10+8+7+18+28+15+27+10+2+7}{16}\)
= \(\frac{241}{16}\)
= 15.06

(ii) आंकड़ों का आरोही क्रम = 2, 5, 7, 7, 8, 8, 10, 10, 10, 14, 15, 18, 24, 27, 28, 48
माध्यक = (आठवां आंकड़ा + नौवां आंकड़ा) / 2
= \(\frac{10+10}{2}=\frac{20}{2}\) = 10

(iii) बहुलक = 10 [∵ 10 सबसे अधिक बार आता है।]

Multiple Choice Questions with Answers:

प्रश्न 1.
अध्ययन का वह क्षेत्र जिसमें आँकड़ों के प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है, उसे कहा जाता है-
(A) सांख्यिकी
(B) क्षेत्रमिति
(C) त्रिकोणमिति
(D) ज्यामिति
उत्तर-
(A) सांख्यिकी

प्रश्न 2.
अन्वेषक द्वारा स्वयं एकत्रित किए गए आँकड़ों को कहा जाता है-
(A) गौण आँकड़े
(B) प्राथमिक आँकड़े
(C) द्वितीयक आँकड़े
(D) माध्यक आँकड़े
उत्तर-
(B) प्राथमिक आँकड़े

प्रश्न 3.
दिए गए आँकड़ों के अधिकतम और न्यूनतम मानों के अन्तर को आँकड़ों का कहा जाता है-
(A) माध्यक
(B) बहुलक
(C) परिसर
(D) माध्य
उत्तर-
(C) परिसर

प्रश्न 4.
गणित की परीक्षा में 10 विद्यार्थियों द्वारा प्राप्त किए गए निम्न अंकों का परिसर होगा-
18, 12, 36, 24, 40, 60, 23, 09, 70, 62
(A) 23
(B) 61
(C) 09
(D) 70
उत्तर-
(B) 61

प्रश्न 5.
सबसे अधिक बार आने वाले प्रेक्षण का मान कहलाता है-
(A) बहुलक
(B) माध्यक
(C) माध्य
(D) उपरोक्त में से कोई नहीं
उत्तर-
(A) बहुलक

प्रश्न 6.
रक्त समूह विद्यार्थियों की संख्या-

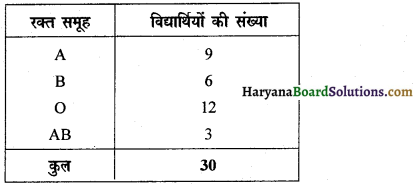
इस सारणी में सामान्य रक्त समूह हैं-
(A) AB
(B) A
(C) B
(D) 0
उत्तर-
(D) 0

प्रश्न 7.
प्रश्न नं0 6 की सारणी में विरलतम रक्त समूह है-
(A) A
(B) AB
(C) B
(D) 0
उत्तर-
(B) AB

प्रश्न 8.
प्रश्न नं० 6 की सारणी में कुल कितने विद्यार्थियों के रक्त की जाँच हुई ?
(A) 12
(B) 18
(C) 27
(D) 30
उत्तर-
(D) 30

प्रश्न 9.
प्रश्न नं० 6 की सारणी में 0 रक्त समूह वाले विद्यार्थियों की संख्या B रक्त समूह वाले विद्यार्थियों की संख्या से जितनी अधिक है-
(A) 6
(B) 3
(C) 9
(D) 12
उत्तर-
(A) 6

प्रश्न 10.

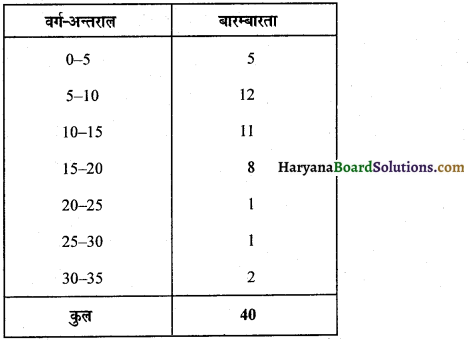
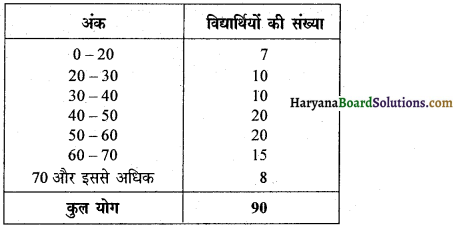
प्रत्येक वर्ग-अन्तराल की माप है-
(A) 10
(B) 5
(C) 35
(D) 12
उत्तर-
(B) 5

प्रश्न 11.
प्रश्न नं० 10 की सारणी में चौथे वर्ग-अन्तराल की निम्न वर्ग सीमा है-
(A) 15
(B) 20
(C) 17.5
(D) 8
उत्तर-
(A) 15

प्रश्न 12.
प्रश्न नं0 10 की सारणी में अन्तिम वर्ग-अन्तराल की उच्च वर्ग सीमा है-
(A) 30
(B) 32.5
(C) 35
(D) 2
उत्तर-
(C) 35

प्रश्न 13.
प्रश्न नं0 10 की सारणी में तीसरे वर्ग-अन्तराल का वर्ग-चिह्न है-
(A) 10
(B) 15
(C) 11
(D) 12.5
उत्तर-
(D) 12.5

प्रश्न 14.
प्रश्न नं0 10 की सारणी में अधिकतम बारम्बारता वाला वर्ग-अन्तराल है-
(A) 0 – 5
(B) 5 – 10
(C) 10 – 15
(D) 15 – 20
उत्तर-
(B) 5 – 10

प्रश्न 15.
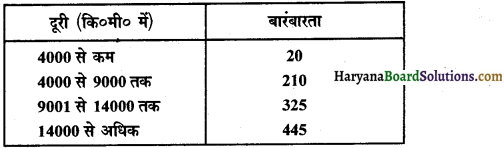
नीचे की सारणी में 400 नियॉन लैंपों के जीवन काल दिए गए हैं :

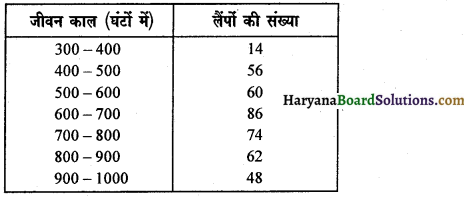
उपरोक्त सारणी में 700 घण्टों से अधिक जीवन काल वाले लैंपों की संख्या है-
(A) 74
(B) 136
(C) 184
(D) 110
उत्तर-
(C) 184

प्रश्न 16.
प्रश्न नं० 15 की सारणी में 500 घण्टों से कम जीवन काल वाले लैंपों की संख्या है-
(A) 14
(B) 70
(C) 56
(D) 42
उत्तर-
(B) 70

प्रश्न 17.
प्रश्न नं 15 की सारणी में अधिकतम लैंपों का जीवन काल कितना है ?
(A) 700 – 800 घण्टे
(B) 800 – 900 घण्टे
(C) 500 – 600 घण्टे
(D) 600 – 700 घण्टे
उत्तर-
(D) 600 – 700 घण्टे

प्रश्न 18.
प्रश्न नं० 15 की सारणी में 800 घण्टों से अधिक जीवन काल वाले लैंपों की संख्या है-
(A) 74
(B) 136
(C) 184
(D) 110
उत्तर-
(D) 110

प्रश्न 19.
नौवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आंकड़ों से निम्नलिखित आलेख बनाया गया-

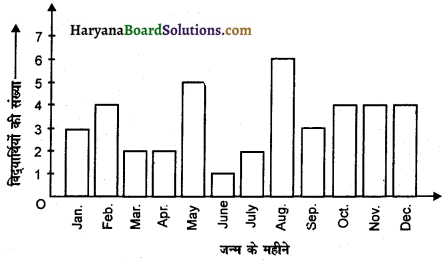
उपरोक्त आलेख से बताइए कि नवम्बर के महीने में कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 5
(C) 6
(D) 12
उत्तर-
(A) 4

प्रश्न 20.
प्रश्न नं0 19 के आलेख में किस महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ ?
(A) फरवरी
(B) मई
(C) अगस्त
(D) अक्तूबर
उत्तर-
(C) अगस्त

प्रश्न 21.
प्रश्न नं० 19 के आलेख में किस महीने में सबसे कम विद्यार्थियों का जन्म हुआ ?
(A) मार्च
(B) अप्रैल
(C) सितम्बर
(D) जून
उत्तर-
(D) जून

प्रश्न 22.
प्रश्न नं० 19 के आलेख में जनवरी से अप्रैल के बीच कितने विद्यार्थियों का जन्म हुआ ?
(A) 11
(B) 9
(C) 7
(D) 16
उत्तर-
(A) 11

प्रश्न 23.
प्रश्न नं० 19 के आलेख में मई के महीने में कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 5
(C) 6
(D) 3
उत्तर-
(B) 5

प्रश्न 24.
प्रश्न नं0 19 के आलेख में अक्तूबर से दिसम्बर के बीच कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 8
(C) 12
(D) 16
उत्तर-
(C) 12

प्रश्न 25.
10, 7, 13, 20 और 15 का माध्य होगा-
(A) 13
(B) 13.5
(C) 14
(D) 14.5
उत्तर-
(A) 13

प्रश्न 26.
दिए गए सभी प्रेक्षणों के योग को प्रेक्षणों की कुल संख्या से भाग करने पर प्राप्त परिणाम को कहा जाता है-
(A) माध्यक
(B) बहुलक
(C) वर्ग-चिह्न
(D) माध्य
उत्तर-
(D) माध्य

प्रश्न 27.
आँकड़ों 2, 3, 4, 5, 0, 1, 3, 3, 4, 3 का माध्य होगा-
(A) 2.5
(B) 2.6
(C) 2.8
(D) 2.9
उत्तर-
(C) 2.8

प्रश्न 28.
प्रथम पाँच प्राकृतिक संख्याओं का माध्य होगा-
(A) 3.0
(B) 3.5
(C) 2.5
(D) 4.0
उत्तर-
(A) 3.0

प्रश्न 29.
15, 2, 7, 9, 3, 11, 12, 19 का माध्यक होगा-
(A) 9
(B) 10
(C) 11
(D) 19
उत्तर-
(B) 10

प्रश्न 30.
किसी वर्ग अन्तराल 150-160 का वर्ग-चिह्न होगा-
(A) 150
(B) 160
(C) 310
(D) 155
उत्तर-
(D) 155

प्रश्न 31.
प्रथम छः विषम संख्याओं का माध्य होगा-
(A) 4
(B) 5
(C) 5.5
(D) 6
उत्तर-
(D)6

प्रश्न 32.
एक कक्षा के 9 विद्यार्थियों की (सेंटीमीटरों में) लंबाइयाँ ये हैं-
155, 160 145 149 150 147 152 144 148 इन आँकड़ों का माध्यक होगा-
(A) 149
(B) 148.5
(C) 148
(D) 147
उत्तर-
(A) 149

प्रश्न 33.
कबड्डी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये हैं- 17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28 टीम द्वारा प्राप्त किए गए अंकों का माध्यक होगा-
(A) 10
(B) 12
(C) 14
(D) 13
उत्तर-
(B) 12

प्रश्न 34.
20 विद्यार्थियों द्वारा (10 में से) प्राप्त किए गए निम्नलिखित अंकों का बहुलक ज्ञात कीजिए-
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
(A) 7
(B) 6
(C) 9
(D) 10
उत्तर-
(C) 9

प्रश्न 35.
निम्नलिखित आँकड़ों का बहुलक होगा-
5, 7, 19, 12, 12, 9, 17, 13, 12, 15, 15, 17, 13, 12, 9
(A) 12
(B) 15
(C) 9
(D) 17
उत्तर-
(A) 12

प्रश्न 36.
यदि प्रेक्षणों 9, 13, 18, 15, p तथा 17 का मध्यमान 15 हो तो p का मान होगा-
(A) 16
(B) 18
(C) 17
(D) 15
उत्तर-
(B) 18

प्रश्न 37.
निम्नलिखित आँकड़ों का माध्यक होगा-
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
(A) 48
(B) 50
(C) 52
(D) 53
उत्तर-
(C) 52

प्रश्न 38.
एक फैक्टरी की एक छोटी इकाई लीजिए जहाँ 5 व्यक्ति काम करते हैं, जिनमें एक सुपरवाइजर है और चार मजदूर हैं। प्रत्येक मजदूर को प्रति माह ₹ 5000 वेतन मिलता है, जबकि सुपरवाइजर को प्रति माह ₹ 15000 वेतन मिलता है। फैक्टरी की इस इकाई के वेतनों का माध्य होगा-
(A) ₹ 5000
(B) ₹ 5500
(C) ₹ 6000
(D) ₹ 7000
उत्तर-
(D) ₹ 7000

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
हमीद ने अपने घर के लिए, ढक्कन वाली एक घनाकार (cubical) पानी की टंकी बनवाई है, जिसका प्रत्येक बाहरी किनारा 1.5 मी० लंबा है। वह इस टंकी के बाहरी पृष्ठ पर, तली को छोड़ते हुए, 25 सें०मी० भुजा वाली वर्गाकार टाइलें (tiles) लगवाता है (देखिए आकृति)। यदि टाइलों की लागत ₹ 360 प्रति दर्जन है, तो उसे टाइल लगवाने में कितना व्यय करना पड़ेगा?

हल :
यहां पर
घनाकार टंकी की भुजा (a) = 1.5 मी० = 150 सें०मी०
घनाकार टंकी के उस पृष्ठीय तल का क्षेत्रफल जिस पर टाइलें लगवानी हैं = 5 × (a)²
= 5 × 150 × 150 सें०मी०²
= 112500 सें०मी०²
1 वर्गाकार टाइल की भुजा = 25 सें०मी०
1 वर्गाकार टाइल का क्षेत्रफल = ( भुजा )²
= 25 × 25 = 625 सें०मी०²
वांछित टाइलों की संख्या = टंकी का पृष्ठीय क्षेत्रफल / एक टाइल का क्षेत्रफल
= \(\frac{112500}{625}\) = 180
12 टाइलों का व्यय = ₹ 360
1 टाइल का व्यय = ₹ \(\frac{360}{12}\)
180 टाइलों का व्यय = \(\frac{360}{12}\) × 180 = ₹ 5400.

प्रश्न 2.
एक संदूक के माप 48 सें०मी०, 36 सें०मी० व 28 सें०मी० है। संदूक का आयतन ज्ञात कीजिए। इस संदूक का कवर बनाने के लिए कितने कपड़े की आवश्यकता होगी ?
हल :
यहां पर
l = 48 सें०मी०
b = 36 सेंव्मी०
h = 28 सें०मी०
(i) संदूक का आयतन (V) = l × b × h = 48 × 36 × 28 सें०मी०
= 48384 सें०मी०³

(ii) संदूक का कवर बनाने के लिए आवश्यक कपड़े का क्षेत्रफल = 2 [lb + bh + hl]
= 2 [48 × 36 + 36 × 28 + 28 × 48 ] सें०मी०²
= 2 × 48 × [ 1 × 36 + 3 × 7 +28 × 1] सें०मी०²
= 96 × 85 सें०मी०²
= 8160 सें०मी०²

प्रश्न 3.
सावित्री को अपने विज्ञान के प्रोजेक्ट के लिए एक बेलनाकार केलिडोस्कोप (kaleidoscope) का मॉडल बनाना था। वह इस केलिडोस्कोप की वक्र पृष्ठ बनाने के लिए चार्ट कागज (chart paper) का प्रयोग करना चाहती थी (देखिए आकृति)। यदि वह 25 सें०मी० लंबाई और 3.5 सें०मी० त्रिज्या का केलिडोस्कोप बनाना चाहती है, तो उसे चार्ट कागज के कितने क्षेत्रफल की आवश्यकता होगी ? (π = \(\frac{22}{7}\) लीजिए।)

हल :
यहां पर
बेलनाकार केलिडोस्कोप की त्रिज्या (r) = 3.5 सें०मी०
केलिडोस्कोप की ऊंचाई (लंबाई) (h) = 25 सें०मी०
अतः, आवश्यक चार्ट कागज का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 25 सें०मी०²
= 550 सें०मी०²

प्रश्न 4.
किसी भवन का ऊपरी भाग अर्धगोलाकार है और इस पर पेंट किया जाना है (देखिए आकृति)। यदि इस अर्धगोले के आधार की परिधि 17.6 मी० है, तो 5 रुपए प्रति 100 सें०मी० की दर से इसे पेंट कराने का व्यय ज्ञात कीजिए।
हल :

यहां पर,
आधार की परिधि = 17.6 मी०
2πr = 17.6
2 × \(\frac{22}{7}\) × r = 17.6
r = \(\frac{17.6 \times 7}{2 \times 22}\) मी०
= 2.8 मी०
इसीलिए, भवन का वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7}\) × 2.8 × 2.8 मी०²
= 49.28 मी०²
100 सें०मी०- पेंटिग की लागत = ₹ 5
1 मी०- पेंटिग की लागत = ₹ 500 [∵ 1 मी०² = 10000 सें०मी०²]
अतः, 49.28 मी०² पेंटिग की लागत = ₹ (500 × 49.28) = ₹ 24640

प्रश्न 5.
एक खुले मैदान में 10 मी० लंबी एक दीवार का निर्माण किया जाना था। दीवार की ऊंचाई 4 मी० है और उसकी मोटाई 24 सें०मी० है। यदि इस दीवार को 24 सें०मी० x 12 सें०मी० x 8 सें०मी० विमाओं वाली ईंटों से बनाया जाना है, तो इसके लिए कितनी ईंटों की आवश्यकता होगी ?
हल :
यहां पर,
दीवार की लंबाई (l) = 10 मी० = 1000 सें०मी०
दीवार की चौड़ाई (b) = 24 सें०मी०.
दीवार की ऊंचाई (h) = 4 मी० = 400 सें०मी०
दीवार का आयतन (V) = lbh
= 1000 × 24 × 400 सें०मी०³
= 9600000 सें०मी०
1 ईंट का आयतन = 24 × 12 × 8 सें०मी०³
= 2304 सें०मी०³
वांछित ईंटों की संख्या = दीवार का आयतन / 1 ईट का आयतन
= \(\frac{9600000}{2304}\)
= 4166.6 2304
= 4167.

प्रश्न 6.
रमजान के एक मेले में, भोज्य पदार्थों के एक स्टॉल पर दुकानदार के पास आधार त्रिज्या 15 सें०मी० वाला एक बर्तन था जो 32 सें०मी० की ऊंचाई तक संतरे के जूस से भरा हुआ था। जूस को 3 सें०मी० त्रिज्या वाले बेलनाकार गिलासों में 8 सें०मी० ऊंचाई तक भरकर 3 रुपए प्रति गिलास की दर से बेचा जाता है (देखिए आकृति)। जूस को पूरा बेचने पर दुकानदार को कुल कितनी राशि प्राप्त हुई ?
हल :

यहां पर,
बड़े बर्तन की त्रिज्या (R) = 15 सें०मी०
बड़े बर्तन की ऊंचाई (H) = 32 सें०मी०
बड़े बर्तन में जूस का आयतन = बेलनाकार बर्तन का आयतन
= πR²H
= π × 15 × 15 × 32 सें०मी०³
एक गिलास की त्रिज्या (r) = 3 सें०मी०
एक गिलास की ऊंचाई (h) = 8 सें०मी०
एक गिलास जूस का आयतन = πr²h
= π × 3 × 3 × 8 सें०मी०³
अतः जूस के बेचे गए गिलासों की संख्या = बर्तन का आयतन / एक गिलास का आयतन
= \(\frac{\pi \times 15 \times 15 \times 32}{\pi \times 3 \times 3 \times 8}\)
= 100
अतः, दुकानदार द्वारा प्राप्त की गई राशि = ₹ 3 × 100 = ₹ 300

प्रश्न 7.
सीसे के एक ठोस गोले, जिसकी त्रिज्या 8 सें०मी० है, से 1 सें०मी० त्रिज्या वाली कितनी गोलियां बनाई जा सकती हैं?
हल :
यहां पर,
ठोस गोले की त्रिज्या (R) = 8 सें०मी०
ठोस गोले का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × π × 8 × 8 × 8 सें०मी०³
एक गोली की त्रिज्या (r) = 1 सें०मी०
एक गोली का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π × 1 × 1 × 1 सें०मी०³
गोलियों की संख्या = ठोस गोले का आयतन / एक गोली का आयतन
= \(\frac{\frac{4}{3} \times \pi \times 8 \times 8 \times 8}{\frac{4}{3} \times \pi \times 1 \times 1 \times 1}\) = 512

Multiple Choice Questions with Answers:

प्रश्न 1.
लम्बाई 1, चौड़ाई b तथा ऊँचाई h वाले घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) lbh
(B) 2lbh
(C) 1b + bh + hl
(D) 2(lb + bh + hl)
उत्तर-
(D) 2(lb + bh + hl)

प्रश्न 2.
क्षेत्रफल का मात्रक होता है-
(A) वर्ग इकाई
(B) घन इकाई
(C) इकाई
(D) (इकाई)⁴
उत्तर-
(A) वर्ग इकाई

प्रश्न 3.
घन का कुल पृष्ठीय क्षेत्रफल क्या होगा, यदि भुजा 6 सेमी है?
(A) 36 सेमी
(B) 144 सेमी
(C) 1296 सेमी²
(D) 216 सेमी²
उत्तर-
(D) 216 सेमी²

प्रश्न 4.
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र है-
(A) 2 (l + b) × h
(B) 2 × (l + b + h) × h
(C) 2 × lbh
(D) 2 × (h + l) × b
उत्तर-
(A) 2 (l + b) × h

प्रश्न 5.
किनारे a वाले एक घन का पार्श्व पृष्ठीय क्षेत्रफल होगा-
(A) 6a²
(B) 5a²
(C) 3a²
(D) 4a²
उत्तर-
(D) 4a²

प्रश्न 6.
एक बॉक्स की लम्बाई 8 cm, चौड़ाई 4 cm तथा ऊँचाई 2 cm है; इसका सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 112 cm²
(B) 56 cm²
(C) 64 cm²
(D) 112 cm³
उत्तर-
(A) 112 cm²

प्रश्न 7.
एक घनाकार टंकी को बनाने में 180 टाइलें लगनी हैं। यदि एक टाइल का मूल्य ₹ 30 हो तो टंकी बनाने पर कुल खर्च आएगा-
(A) ₹ 540
(B) ₹ 5400
(C) ₹ 54
(D) ₹ 54000
उत्तर-
(B) ₹ 5400

प्रश्न 8.
10 cm भुजा वाले धन के आकार के डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल होगा-
(A) 600 cm²
(B) 600 cm³
(C) 400 cm²
(D) 400 cm²
उत्तर-
(D) 400 cm²

प्रश्न 9.
त्रिज्या तथा ॥ ऊँचाई वाले बेलन का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) πrh
(B) 2πrh
(C) πr²h
(D) 2πr (r + h)
उत्तर-
(B) 2πrh

प्रश्न 10.
r त्रिज्या तथा h ऊँचाई वाले बेलन का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πrh
(B) 2πrh
(C) πr²h
(D) 2πr (r + h)
उत्तर-
(D) 2πr (r + h)

प्रश्न 11.
3.5 cm त्रिज्या तथा 25 cm लम्बाई वाले बेलनाकार केलिडोस्कोप का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 550 cm²
(B) 550 cm³
(C) 627 cm²
(D) 627 cm³
उत्तर-
(A) 550 cm²

प्रश्न 12.
14 cm ऊँचाई वाले एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm हो तो इसके आधार की त्रिज्या-
(A) 4 cm
(B) 2 cm
(C) 1 cm
(D) 3 cm
उत्तर-
(C) 1 cm

प्रश्न 13.
4 cm आन्तरिक व्यास वाले 77 cm लम्बे बेलनाकार धातु के पाइप का आन्तरिक वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 968 cm²
(B) 968 cm³
(C) 96.8 cm²
(D) 1936 cm²
उत्तर-
(A) 968 cm²

प्रश्न 14.
एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है यदि इसके आधार की त्रिज्या 0.7 m हो तो इसकी ऊँचाई होगी-
(A) 2 m
(B) 1 m
(C) 3 m
(D) 4 m
उत्तर-
(B) 1 m

प्रश्न 15.
3.5 m व्यास वाले तथा 10 m गहरे बेलनाकार कुएँ का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 330 m²
(B) 220 m²
(C) 110 m²
(D) 55 m²
उत्तर-
(C) 110 m²

प्रश्न 16.
₹ 40 प्रति वर्ग मी० की दर से 110 वर्ग मी० क्षेत्रफल पर प्लास्टर कराने का व्यय होगा-
(A) ₹ 44000
(B) ₹ 44
(C) ₹ 440
(D) ₹ 4400
उत्तर-
(D) ₹ 4400

प्रश्न 17.
एक लम्ब वृत्तीय बेलन के आधार का व्यास 10 cm है और ऊँचाई 15 cm है। यदि π = 3.14 हो तो बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 628 cm²
(B) 628 cm³
(C) 471 cm²
(D) 471 cm³
उत्तर-
(A) 628 cm²

प्रश्न 18.
r त्रिज्या तथा l तिर्यक ऊँचाई वाले लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 2πrl
(B) πrl
(C) πr(l + r)
(D) 2πr(l + r)
उत्तर-
(B) πrl

प्रश्न 19.
r त्रिज्या तथा l तिर्यक ऊँचाई वाले लम्ब वृत्तीय शंकु का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πrl
(B) 2πrl
(C) πr(l + r)
(D) 2πr(l + r)
उत्तर-
(C) πr(l + r)

प्रश्न 20.
आधार की त्रिज्या 7 cm तथा तिर्यक ऊँचाई 10 cm वाले लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 748 cm²
(B) 374 cm²
(C) 440 cm²
(D) 220 cm²
उत्तर-
(D) 220 cm²

प्रश्न 21.
एक शंकु की ऊँचाई 16 cm तथा आधार की त्रिज्या 12 cm है, इसकी तिर्यक ऊँचाई होगी-
(A) 28 cm
(B) 4 cm
(C) 20 cm
(D) 14 cm
उत्तर-
(C) 20 cm

प्रश्न 22.
r त्रिज्या तथा h ऊँचाई वाले लम्ब वृत्तीय शंकु की तिर्यक ऊँचाई (l) होगी-
(A) \(\sqrt{r^2+h^2}\)
(B) \(\sqrt{r^2-h^2}\)
(C) \(\sqrt{h^2-r^2}\)
(D) \(\sqrt[3]{r^2+h^2}\)
उत्तर-
(A) \(\sqrt{r^2+h^2}\)

प्रश्न 23.
एक शंकु के आधार की त्रिज्या \(\frac{21}{4}\) cm तथा तिर्यक ऊँचाई 10 cm है, इसका वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 251.6 cm²
(B) 866.25 cm²
(C) 230 cm²
(D) 165 cm²
उत्तर-
(D) 165 cm²

प्रश्न 24.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm- तथा तिर्यक ऊँचाई 14 cm है। इसके आधार की त्रिज्या होगी-
(A) 7 cm
(B) 3.5 cm
(C) 10.5 cm
(D) 14 cm
उत्तर-
(A) 7 cm

प्रश्न 25.
आधार की त्रिज्या 7 cm तथा तिर्यक ऊँचाई 14 cm वाले लम्ब वृत्तीय शंकु का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 924 cm²
(B) 462 cm²
(C) 308 cm²
(D) 616 cm²
उत्तर-
(B) 462 cm²

प्रश्न 26.
26 m तिर्यक ऊँचाई तथा 10 m आधार की त्रिज्या वाले लम्ब वृत्तीय शंकु की ऊँचाई होगी-
(A) 16 m
(B) 10 m
(C) 24 m
(D) 26 m
उत्तर-
(C) 24 m

प्रश्न 27.
आधार की त्रिज्या 6 m तथा ऊँचाई 8 m वाले शंकु के आकार के तम्बू की तिर्यक ऊँचाई होगी-
(A) 14 m
(B) 2 m
(C) 20 m
(D) 10 m
उत्तर-
(D) 10 m

प्रश्न 28.
आधार की त्रिज्या 7 m तथा तिर्यक ऊँचाई 25 m वाले शंकु के आकार के गुम्बद का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 550 m²
(B) 275 m²
(C) 1100 m²
(D) 704 m²
उत्तर-
(A) 550 m²

प्रश्न 29.
r त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल होगा-
(A) 2πr²
(B) 3πr²
(C) 4πr²
(D) πr²
उत्तर-
(C) 4πr²

प्रश्न 30.
r त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 3πr²
(B) 2πr²
(C) 4πr²
(D) πr²
उत्तर-
(B) 2πr²

प्रश्न 31.
त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πr²
(B) 2πr²
(C) 4πr²
(D) 3πr²
उत्तर-
(D) 3πr²

प्रश्न 32.
7 cm त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल होगा-
(A) 616 cm²
(B) 1232 cm²
(C) 308 cm²
(D) 924 cm²
उत्तर-
(A) 616 cm²

प्रश्न 33.
21 cm त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 4158 cm²
(B) 2772 cm²
(C) 5544 cm²
(D) 1386 cm²
उत्तर-
(B) 2772 cm²

प्रश्न 34.
21 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 2772 cm²
(B) 5544 cm²
(C) 1386 cm²
(D) 4158 cm²
उत्तर-
(D) 4158 cm²

प्रश्न 35.
14 cm व्यास वाले गोले का पृष्टीय क्षेत्रफल होगा-
(A) 28 cm
(B) 28 cm²
(C) 42 cm²
(D) 616 cm²
उत्तर-
(D) 616 cm²

प्रश्न 36.
14 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 616 cm²
(B) 1232 cm²
(C) 1848 cm²
(D) 2464 cm²
उत्तर-
(C) 1848 cm²

प्रश्न 37.
यदि π = 3.14 हो तो 10 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 314 cm²
(B) 628 cm²
(C) 1256 cm²
(D) 942 cm²
उत्तर-
(D) 942 cm²

प्रश्न 38.
घनाभ का आयतन ज्ञात करने का सूत्र है-
(A) l × b × h
(B) 2 × l × b × h
(C) 2 × (1+ b) × h
(D) 2 × (lb + bh + hl)
उत्तर-
(A) l × b × h

प्रश्न 39.
किसी ठोस वस्तु द्वारा घेरे गए स्थान की माप को कहा जाता है-
(A) परिमाप
(B) क्षेत्रफल
(C) आयतन
(D) वक्र पृष्ठीय क्षेत्रफल
उत्तर-
(C) आयतन

प्रश्न 40.
एक घन की भुजा 4 cm है। उसका पृष्ठीय क्षेत्रफल होगा-
(A) 16 cm²
(B) 96 cm²
(C) 64 cm²
(D) 12 cm²
उत्तर-
(B) 96 cm²

प्रश्न 41.
एक घन का किनारा 12 cm है, तो इसका आयतन होगा- .
(A) 1728 cm³
(B) 1728 cm²
(C) 36 cm³
(D) 36 cm²
उत्तर-
(A) 1728 cm³

प्रश्न 42.
एक ईंट की लम्बाई 24 cm, चौड़ाई 12 cm तथा ऊँचाई 8 cm है, इसका आयतन होगा-
(A) 2304 cm³
(B) 2304 cm²
(C) 4608 cm²
(D) 1152 cm³
उत्तर-
(A) 2304 cm³

प्रश्न 43.
माचिस की डिब्बी के माप 4 सें०मी० × 2.5 सें०मी० × 1.5 सें०मी० हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा ?
(A) 15 cm³
(B) 90 cm³
(C) 135 cm³
(D) 180 cm³
उत्तर-
(D) 180 cm³

प्रश्न 44.
एक घनाभाकार पानी की टंकी 6 मी० लंबी, 5 मी० चौड़ी और 4.5 मी० गहरी है। इसमें कितने लीटर पानी आ सकता है ? (1 मी०³ = 10001)
(A) 135 लीटर
(B) 135000 लीटर
(C) 1350 लीटर
(D) 13500 लीटर
उत्तर-
(B) 135000 लीटर

प्रश्न 45.
एक घनाभाकार वर्तन 10 मी० लंबा और 8 मी० चौड़ा है। इसको कितना ऊंचा बनाया जाए कि इसमें 320 घन मीटर द्रव आ सके ?
(A) 4 m
(B) 5 m
(C) 6 m
(D) 4.5 m
उत्तर-
(A) 4 m

प्रश्न 46.
r त्रिज्या तथा h ऊँचाई वाले वेलनाकार वर्तन का आयतन होगा-
(A) 2πrh
(B) πr²h
(C) 2πrh
(D) 2πr(h + r)
उत्तर-
(B) πr²h

प्रश्न 47.
आधार की त्रिज्या 21 cm तथा ऊँचाई 25 cm वाले वेलनाकार बर्तन का आयतन होगा-
(A) 34650 cm³
(B) 3465 cm³
(C) 346.50 cm³
(D) 34.650 cm³
उत्तर-
(A) 34650 cm³

प्रश्न 48.
एक लम्ब वृत्तीय बेलन के आधार का व्यास 7 cm तथा ऊँचाई 40 cm है, इसका आयतन होगा-
(A) 770 cm³
(B) 1155 cm³
(C) 1540 cm³
(D) 2310 cm³
उत्तर-
(C) 1540 cm³

प्रश्न 49.
7 cm त्रिज्या तथा 15 cm ऊँचाई वाले लम्ब वृत्तीय बेलन का आयतन होगा-
(A) 770 cm³
(B) 1155 cm³
(C) 1540 cm³
(D) 2310 cm³
उत्तर-
(D) 2310 cm³

प्रश्न 50.
r त्रिज्या तथा h ऊँचाई वाले शंकु का आयतन होगा-
(A) πr²h
(B) \(\frac{1}{2}\) πr²h
(C) \(\frac{1}{3}\) πr²h
(D) 3πr²h
उत्तर-
(C) \(\frac{1}{3}\) πr³h

प्रश्न 51.
6 cm त्रिज्या तथा 7 cm ऊँचाई वाले लम्ब वृत्तीय शंकु का आयतन होगा-
(A) 264 cm³
(B) 132 cm³
(C) 396 cm³
(D) 528 cm³
उत्तर-
(A) 264 cm³

प्रश्न 52.
9 cm ऊँचाई वाले एक लम्ब वृत्तीय शंकु का आयतन 48 π cm³ है, इसके आधार की त्रिज्या होगी-
(A) 8 cm
(B) 6 cm
(C) 4 cm
(D) 2 cm
उत्तर-
(C)4 cm

प्रश्न 53.
r त्रिज्या वाले गोले का आयतन होगा-
(A) 4πr²
(B) \(\frac{2}{3}\) πr³
(C) πr³
(D) \(\frac{4}{3}\) πr³
उत्तर-
(D) \(\frac{4}{3}\) πr³

प्रश्न 54.
r त्रिज्या वाले अर्धगोले का आयतन होगा-
(A) \(\frac{2}{3}\) πr³
(B) \(\frac{4}{3}\) πr³
(C) \(\frac{1}{3}\) πr³
(D) πr³
उत्तर-
(A) \(\frac{2}{3}\) πr³

प्रश्न 55.
7 cm त्रिज्या वाले गोले का आयतन होगा-
(A) \(\frac{4312}{6}\) cm³
(B) \(\frac{4312}{5}\) cm³
(C) \(\frac{4312}{4}\) cm³
(D) \(\frac{4312}{3}\) cm³
उत्तर-
(D) \(\frac{4312}{3}\) cm³

प्रश्न 56.
एक अर्धगोलाकार कटोरे की त्रिज्या 3.5 cm है। इसका आयतन होगा-
(A) 89.6 cm³
(B) 89.8 cm³
(C) 89.5 cm³
(D) 89.2 cm³
उत्तर-
(B) 89.8 cm³