HBSE 9th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
हमीद ने अपने घर के लिए, ढक्कन वाली एक घनाकार (cubical) पानी की टंकी बनवाई है, जिसका प्रत्येक बाहरी किनारा 1.5 मी० लंबा है। वह इस टंकी के बाहरी पृष्ठ पर, तली को छोड़ते हुए, 25 सें०मी० भुजा वाली वर्गाकार टाइलें (tiles) लगवाता है (देखिए आकृति)। यदि टाइलों की लागत ₹ 360 प्रति दर्जन है, तो उसे टाइल लगवाने में कितना व्यय करना पड़ेगा?

हल :
यहां पर
घनाकार टंकी की भुजा (a) = 1.5 मी० = 150 सें०मी०
घनाकार टंकी के उस पृष्ठीय तल का क्षेत्रफल जिस पर टाइलें लगवानी हैं = 5 × (a)²
= 5 × 150 × 150 सें०मी०²
= 112500 सें०मी०²
1 वर्गाकार टाइल की भुजा = 25 सें०मी०
1 वर्गाकार टाइल का क्षेत्रफल = ( भुजा )²
= 25 × 25 = 625 सें०मी०²
वांछित टाइलों की संख्या = टंकी का पृष्ठीय क्षेत्रफल / एक टाइल का क्षेत्रफल
= \(\frac{112500}{625}\) = 180
12 टाइलों का व्यय = ₹ 360
1 टाइल का व्यय = ₹ \(\frac{360}{12}\)
180 टाइलों का व्यय = \(\frac{360}{12}\) × 180 = ₹ 5400.

प्रश्न 2.
एक संदूक के माप 48 सें०मी०, 36 सें०मी० व 28 सें०मी० है। संदूक का आयतन ज्ञात कीजिए। इस संदूक का कवर बनाने के लिए कितने कपड़े की आवश्यकता होगी ?
हल :
यहां पर
l = 48 सें०मी०
b = 36 सेंव्मी०
h = 28 सें०मी०
(i) संदूक का आयतन (V) = l × b × h = 48 × 36 × 28 सें०मी०
= 48384 सें०मी०³

(ii) संदूक का कवर बनाने के लिए आवश्यक कपड़े का क्षेत्रफल = 2 [lb + bh + hl]
= 2 [48 × 36 + 36 × 28 + 28 × 48 ] सें०मी०²
= 2 × 48 × [ 1 × 36 + 3 × 7 +28 × 1] सें०मी०²
= 96 × 85 सें०मी०²
= 8160 सें०मी०²

प्रश्न 3.
सावित्री को अपने विज्ञान के प्रोजेक्ट के लिए एक बेलनाकार केलिडोस्कोप (kaleidoscope) का मॉडल बनाना था। वह इस केलिडोस्कोप की वक्र पृष्ठ बनाने के लिए चार्ट कागज (chart paper) का प्रयोग करना चाहती थी (देखिए आकृति)। यदि वह 25 सें०मी० लंबाई और 3.5 सें०मी० त्रिज्या का केलिडोस्कोप बनाना चाहती है, तो उसे चार्ट कागज के कितने क्षेत्रफल की आवश्यकता होगी ? (π = \(\frac{22}{7}\) लीजिए।)

हल :
यहां पर
बेलनाकार केलिडोस्कोप की त्रिज्या (r) = 3.5 सें०मी०
केलिडोस्कोप की ऊंचाई (लंबाई) (h) = 25 सें०मी०
अतः, आवश्यक चार्ट कागज का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 25 सें०मी०²
= 550 सें०मी०²

प्रश्न 4.
किसी भवन का ऊपरी भाग अर्धगोलाकार है और इस पर पेंट किया जाना है (देखिए आकृति)। यदि इस अर्धगोले के आधार की परिधि 17.6 मी० है, तो 5 रुपए प्रति 100 सें०मी० की दर से इसे पेंट कराने का व्यय ज्ञात कीजिए।
हल :

यहां पर,
आधार की परिधि = 17.6 मी०
2πr = 17.6
2 × \(\frac{22}{7}\) × r = 17.6
r = \(\frac{17.6 \times 7}{2 \times 22}\) मी०
= 2.8 मी०
इसीलिए, भवन का वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7}\) × 2.8 × 2.8 मी०²
= 49.28 मी०²
100 सें०मी०- पेंटिग की लागत = ₹ 5
1 मी०- पेंटिग की लागत = ₹ 500 [∵ 1 मी०² = 10000 सें०मी०²]
अतः, 49.28 मी०² पेंटिग की लागत = ₹ (500 × 49.28) = ₹ 24640

प्रश्न 5.
एक खुले मैदान में 10 मी० लंबी एक दीवार का निर्माण किया जाना था। दीवार की ऊंचाई 4 मी० है और उसकी मोटाई 24 सें०मी० है। यदि इस दीवार को 24 सें०मी० x 12 सें०मी० x 8 सें०मी० विमाओं वाली ईंटों से बनाया जाना है, तो इसके लिए कितनी ईंटों की आवश्यकता होगी ?
हल :
यहां पर,
दीवार की लंबाई (l) = 10 मी० = 1000 सें०मी०
दीवार की चौड़ाई (b) = 24 सें०मी०.
दीवार की ऊंचाई (h) = 4 मी० = 400 सें०मी०
दीवार का आयतन (V) = lbh
= 1000 × 24 × 400 सें०मी०³
= 9600000 सें०मी०
1 ईंट का आयतन = 24 × 12 × 8 सें०मी०³
= 2304 सें०मी०³
वांछित ईंटों की संख्या = दीवार का आयतन / 1 ईट का आयतन
= \(\frac{9600000}{2304}\)
= 4166.6 2304
= 4167.

प्रश्न 6.
रमजान के एक मेले में, भोज्य पदार्थों के एक स्टॉल पर दुकानदार के पास आधार त्रिज्या 15 सें०मी० वाला एक बर्तन था जो 32 सें०मी० की ऊंचाई तक संतरे के जूस से भरा हुआ था। जूस को 3 सें०मी० त्रिज्या वाले बेलनाकार गिलासों में 8 सें०मी० ऊंचाई तक भरकर 3 रुपए प्रति गिलास की दर से बेचा जाता है (देखिए आकृति)। जूस को पूरा बेचने पर दुकानदार को कुल कितनी राशि प्राप्त हुई ?
हल :

यहां पर,
बड़े बर्तन की त्रिज्या (R) = 15 सें०मी०
बड़े बर्तन की ऊंचाई (H) = 32 सें०मी०
बड़े बर्तन में जूस का आयतन = बेलनाकार बर्तन का आयतन
= πR²H
= π × 15 × 15 × 32 सें०मी०³
एक गिलास की त्रिज्या (r) = 3 सें०मी०
एक गिलास की ऊंचाई (h) = 8 सें०मी०
एक गिलास जूस का आयतन = πr²h
= π × 3 × 3 × 8 सें०मी०³
अतः जूस के बेचे गए गिलासों की संख्या = बर्तन का आयतन / एक गिलास का आयतन
= \(\frac{\pi \times 15 \times 15 \times 32}{\pi \times 3 \times 3 \times 8}\)
= 100
अतः, दुकानदार द्वारा प्राप्त की गई राशि = ₹ 3 × 100 = ₹ 300

प्रश्न 7.
सीसे के एक ठोस गोले, जिसकी त्रिज्या 8 सें०मी० है, से 1 सें०मी० त्रिज्या वाली कितनी गोलियां बनाई जा सकती हैं?
हल :
यहां पर,
ठोस गोले की त्रिज्या (R) = 8 सें०मी०
ठोस गोले का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × π × 8 × 8 × 8 सें०मी०³
एक गोली की त्रिज्या (r) = 1 सें०मी०
एक गोली का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π × 1 × 1 × 1 सें०मी०³
गोलियों की संख्या = ठोस गोले का आयतन / एक गोली का आयतन
= \(\frac{\frac{4}{3} \times \pi \times 8 \times 8 \times 8}{\frac{4}{3} \times \pi \times 1 \times 1 \times 1}\) = 512

Multiple Choice Questions with Answers:

प्रश्न 1.
लम्बाई 1, चौड़ाई b तथा ऊँचाई h वाले घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) lbh
(B) 2lbh
(C) 1b + bh + hl
(D) 2(lb + bh + hl)
उत्तर-
(D) 2(lb + bh + hl)

प्रश्न 2.
क्षेत्रफल का मात्रक होता है-
(A) वर्ग इकाई
(B) घन इकाई
(C) इकाई
(D) (इकाई)⁴
उत्तर-
(A) वर्ग इकाई

प्रश्न 3.
घन का कुल पृष्ठीय क्षेत्रफल क्या होगा, यदि भुजा 6 सेमी है?
(A) 36 सेमी
(B) 144 सेमी
(C) 1296 सेमी²
(D) 216 सेमी²
उत्तर-
(D) 216 सेमी²

प्रश्न 4.
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र है-
(A) 2 (l + b) × h
(B) 2 × (l + b + h) × h
(C) 2 × lbh
(D) 2 × (h + l) × b
उत्तर-
(A) 2 (l + b) × h

प्रश्न 5.
किनारे a वाले एक घन का पार्श्व पृष्ठीय क्षेत्रफल होगा-
(A) 6a²
(B) 5a²
(C) 3a²
(D) 4a²
उत्तर-
(D) 4a²

प्रश्न 6.
एक बॉक्स की लम्बाई 8 cm, चौड़ाई 4 cm तथा ऊँचाई 2 cm है; इसका सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 112 cm²
(B) 56 cm²
(C) 64 cm²
(D) 112 cm³
उत्तर-
(A) 112 cm²

प्रश्न 7.
एक घनाकार टंकी को बनाने में 180 टाइलें लगनी हैं। यदि एक टाइल का मूल्य ₹ 30 हो तो टंकी बनाने पर कुल खर्च आएगा-
(A) ₹ 540
(B) ₹ 5400
(C) ₹ 54
(D) ₹ 54000
उत्तर-
(B) ₹ 5400

प्रश्न 8.
10 cm भुजा वाले धन के आकार के डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल होगा-
(A) 600 cm²
(B) 600 cm³
(C) 400 cm²
(D) 400 cm²
उत्तर-
(D) 400 cm²

प्रश्न 9.
त्रिज्या तथा ॥ ऊँचाई वाले बेलन का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) πrh
(B) 2πrh
(C) πr²h
(D) 2πr (r + h)
उत्तर-
(B) 2πrh

प्रश्न 10.
r त्रिज्या तथा h ऊँचाई वाले बेलन का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πrh
(B) 2πrh
(C) πr²h
(D) 2πr (r + h)
उत्तर-
(D) 2πr (r + h)

प्रश्न 11.
3.5 cm त्रिज्या तथा 25 cm लम्बाई वाले बेलनाकार केलिडोस्कोप का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 550 cm²
(B) 550 cm³
(C) 627 cm²
(D) 627 cm³
उत्तर-
(A) 550 cm²

प्रश्न 12.
14 cm ऊँचाई वाले एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm हो तो इसके आधार की त्रिज्या-
(A) 4 cm
(B) 2 cm
(C) 1 cm
(D) 3 cm
उत्तर-
(C) 1 cm

प्रश्न 13.
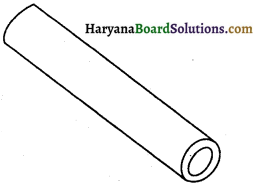
4 cm आन्तरिक व्यास वाले 77 cm लम्बे बेलनाकार धातु के पाइप का आन्तरिक वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 968 cm²
(B) 968 cm³
(C) 96.8 cm²
(D) 1936 cm²
उत्तर-
(A) 968 cm²

प्रश्न 14.
एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है यदि इसके आधार की त्रिज्या 0.7 m हो तो इसकी ऊँचाई होगी-
(A) 2 m
(B) 1 m
(C) 3 m
(D) 4 m
उत्तर-
(B) 1 m

प्रश्न 15.
3.5 m व्यास वाले तथा 10 m गहरे बेलनाकार कुएँ का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 330 m²
(B) 220 m²
(C) 110 m²
(D) 55 m²
उत्तर-
(C) 110 m²

प्रश्न 16.
₹ 40 प्रति वर्ग मी० की दर से 110 वर्ग मी० क्षेत्रफल पर प्लास्टर कराने का व्यय होगा-
(A) ₹ 44000
(B) ₹ 44
(C) ₹ 440
(D) ₹ 4400
उत्तर-
(D) ₹ 4400

प्रश्न 17.
एक लम्ब वृत्तीय बेलन के आधार का व्यास 10 cm है और ऊँचाई 15 cm है। यदि π = 3.14 हो तो बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 628 cm²
(B) 628 cm³
(C) 471 cm²
(D) 471 cm³
उत्तर-
(A) 628 cm²

प्रश्न 18.
r त्रिज्या तथा l तिर्यक ऊँचाई वाले लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 2πrl
(B) πrl
(C) πr(l + r)
(D) 2πr(l + r)
उत्तर-
(B) πrl

प्रश्न 19.
r त्रिज्या तथा l तिर्यक ऊँचाई वाले लम्ब वृत्तीय शंकु का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πrl
(B) 2πrl
(C) πr(l + r)
(D) 2πr(l + r)
उत्तर-
(C) πr(l + r)

प्रश्न 20.
आधार की त्रिज्या 7 cm तथा तिर्यक ऊँचाई 10 cm वाले लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 748 cm²
(B) 374 cm²
(C) 440 cm²
(D) 220 cm²
उत्तर-
(D) 220 cm²

प्रश्न 21.
एक शंकु की ऊँचाई 16 cm तथा आधार की त्रिज्या 12 cm है, इसकी तिर्यक ऊँचाई होगी-
(A) 28 cm
(B) 4 cm
(C) 20 cm
(D) 14 cm
उत्तर-
(C) 20 cm

प्रश्न 22.
r त्रिज्या तथा h ऊँचाई वाले लम्ब वृत्तीय शंकु की तिर्यक ऊँचाई (l) होगी-
(A) \(\sqrt{r^2+h^2}\)
(B) \(\sqrt{r^2-h^2}\)
(C) \(\sqrt{h^2-r^2}\)
(D) \(\sqrt[3]{r^2+h^2}\)
उत्तर-
(A) \(\sqrt{r^2+h^2}\)

प्रश्न 23.
एक शंकु के आधार की त्रिज्या \(\frac{21}{4}\) cm तथा तिर्यक ऊँचाई 10 cm है, इसका वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 251.6 cm²
(B) 866.25 cm²
(C) 230 cm²
(D) 165 cm²
उत्तर-
(D) 165 cm²

प्रश्न 24.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm- तथा तिर्यक ऊँचाई 14 cm है। इसके आधार की त्रिज्या होगी-
(A) 7 cm
(B) 3.5 cm
(C) 10.5 cm
(D) 14 cm
उत्तर-
(A) 7 cm

प्रश्न 25.
आधार की त्रिज्या 7 cm तथा तिर्यक ऊँचाई 14 cm वाले लम्ब वृत्तीय शंकु का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 924 cm²
(B) 462 cm²
(C) 308 cm²
(D) 616 cm²
उत्तर-
(B) 462 cm²

प्रश्न 26.
26 m तिर्यक ऊँचाई तथा 10 m आधार की त्रिज्या वाले लम्ब वृत्तीय शंकु की ऊँचाई होगी-
(A) 16 m
(B) 10 m
(C) 24 m
(D) 26 m
उत्तर-
(C) 24 m

प्रश्न 27.
आधार की त्रिज्या 6 m तथा ऊँचाई 8 m वाले शंकु के आकार के तम्बू की तिर्यक ऊँचाई होगी-
(A) 14 m
(B) 2 m
(C) 20 m
(D) 10 m
उत्तर-
(D) 10 m

प्रश्न 28.
आधार की त्रिज्या 7 m तथा तिर्यक ऊँचाई 25 m वाले शंकु के आकार के गुम्बद का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 550 m²
(B) 275 m²
(C) 1100 m²
(D) 704 m²
उत्तर-
(A) 550 m²

प्रश्न 29.
r त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल होगा-
(A) 2πr²
(B) 3πr²
(C) 4πr²
(D) πr²
उत्तर-
(C) 4πr²

प्रश्न 30.
r त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 3πr²
(B) 2πr²
(C) 4πr²
(D) πr²
उत्तर-
(B) 2πr²

प्रश्न 31.
त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) πr²
(B) 2πr²
(C) 4πr²
(D) 3πr²
उत्तर-
(D) 3πr²

प्रश्न 32.
7 cm त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल होगा-
(A) 616 cm²
(B) 1232 cm²
(C) 308 cm²
(D) 924 cm²
उत्तर-
(A) 616 cm²

प्रश्न 33.
21 cm त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 4158 cm²
(B) 2772 cm²
(C) 5544 cm²
(D) 1386 cm²
उत्तर-
(B) 2772 cm²

प्रश्न 34.
21 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 2772 cm²
(B) 5544 cm²
(C) 1386 cm²
(D) 4158 cm²
उत्तर-
(D) 4158 cm²

प्रश्न 35.
14 cm व्यास वाले गोले का पृष्टीय क्षेत्रफल होगा-
(A) 28 cm
(B) 28 cm²
(C) 42 cm²
(D) 616 cm²
उत्तर-
(D) 616 cm²

प्रश्न 36.
14 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 616 cm²
(B) 1232 cm²
(C) 1848 cm²
(D) 2464 cm²
उत्तर-
(C) 1848 cm²

प्रश्न 37.
यदि π = 3.14 हो तो 10 cm त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा-
(A) 314 cm²
(B) 628 cm²
(C) 1256 cm²
(D) 942 cm²
उत्तर-
(D) 942 cm²

प्रश्न 38.
घनाभ का आयतन ज्ञात करने का सूत्र है-
(A) l × b × h
(B) 2 × l × b × h
(C) 2 × (1+ b) × h
(D) 2 × (lb + bh + hl)
उत्तर-
(A) l × b × h

प्रश्न 39.
किसी ठोस वस्तु द्वारा घेरे गए स्थान की माप को कहा जाता है-
(A) परिमाप
(B) क्षेत्रफल
(C) आयतन
(D) वक्र पृष्ठीय क्षेत्रफल
उत्तर-
(C) आयतन

प्रश्न 40.
एक घन की भुजा 4 cm है। उसका पृष्ठीय क्षेत्रफल होगा-
(A) 16 cm²
(B) 96 cm²
(C) 64 cm²
(D) 12 cm²
उत्तर-
(B) 96 cm²

प्रश्न 41.
एक घन का किनारा 12 cm है, तो इसका आयतन होगा- .
(A) 1728 cm³
(B) 1728 cm²
(C) 36 cm³
(D) 36 cm²
उत्तर-
(A) 1728 cm³

प्रश्न 42.
एक ईंट की लम्बाई 24 cm, चौड़ाई 12 cm तथा ऊँचाई 8 cm है, इसका आयतन होगा-
(A) 2304 cm³
(B) 2304 cm²
(C) 4608 cm²
(D) 1152 cm³
उत्तर-
(A) 2304 cm³

प्रश्न 43.
माचिस की डिब्बी के माप 4 सें०मी० × 2.5 सें०मी० × 1.5 सें०मी० हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा ?
(A) 15 cm³
(B) 90 cm³
(C) 135 cm³
(D) 180 cm³
उत्तर-
(D) 180 cm³

प्रश्न 44.
एक घनाभाकार पानी की टंकी 6 मी० लंबी, 5 मी० चौड़ी और 4.5 मी० गहरी है। इसमें कितने लीटर पानी आ सकता है ? (1 मी०³ = 10001)
(A) 135 लीटर
(B) 135000 लीटर
(C) 1350 लीटर
(D) 13500 लीटर
उत्तर-
(B) 135000 लीटर

प्रश्न 45.
एक घनाभाकार वर्तन 10 मी० लंबा और 8 मी० चौड़ा है। इसको कितना ऊंचा बनाया जाए कि इसमें 320 घन मीटर द्रव आ सके ?
(A) 4 m
(B) 5 m
(C) 6 m
(D) 4.5 m
उत्तर-
(A) 4 m

प्रश्न 46.
r त्रिज्या तथा h ऊँचाई वाले वेलनाकार वर्तन का आयतन होगा-
(A) 2πrh
(B) πr²h
(C) 2πrh
(D) 2πr(h + r)
उत्तर-
(B) πr²h

प्रश्न 47.
आधार की त्रिज्या 21 cm तथा ऊँचाई 25 cm वाले वेलनाकार बर्तन का आयतन होगा-
(A) 34650 cm³
(B) 3465 cm³
(C) 346.50 cm³
(D) 34.650 cm³
उत्तर-
(A) 34650 cm³

प्रश्न 48.
एक लम्ब वृत्तीय बेलन के आधार का व्यास 7 cm तथा ऊँचाई 40 cm है, इसका आयतन होगा-
(A) 770 cm³
(B) 1155 cm³
(C) 1540 cm³
(D) 2310 cm³
उत्तर-
(C) 1540 cm³

प्रश्न 49.
7 cm त्रिज्या तथा 15 cm ऊँचाई वाले लम्ब वृत्तीय बेलन का आयतन होगा-
(A) 770 cm³
(B) 1155 cm³
(C) 1540 cm³
(D) 2310 cm³
उत्तर-
(D) 2310 cm³

प्रश्न 50.
r त्रिज्या तथा h ऊँचाई वाले शंकु का आयतन होगा-
(A) πr²h
(B) \(\frac{1}{2}\) πr²h
(C) \(\frac{1}{3}\) πr²h
(D) 3πr²h
उत्तर-
(C) \(\frac{1}{3}\) πr³h

प्रश्न 51.
6 cm त्रिज्या तथा 7 cm ऊँचाई वाले लम्ब वृत्तीय शंकु का आयतन होगा-
(A) 264 cm³
(B) 132 cm³
(C) 396 cm³
(D) 528 cm³
उत्तर-
(A) 264 cm³

प्रश्न 52.
9 cm ऊँचाई वाले एक लम्ब वृत्तीय शंकु का आयतन 48 π cm³ है, इसके आधार की त्रिज्या होगी-
(A) 8 cm
(B) 6 cm
(C) 4 cm
(D) 2 cm
उत्तर-
(C)4 cm

प्रश्न 53.
r त्रिज्या वाले गोले का आयतन होगा-
(A) 4πr²
(B) \(\frac{2}{3}\) πr³
(C) πr³
(D) \(\frac{4}{3}\) πr³
उत्तर-
(D) \(\frac{4}{3}\) πr³

प्रश्न 54.
r त्रिज्या वाले अर्धगोले का आयतन होगा-
(A) \(\frac{2}{3}\) πr³
(B) \(\frac{4}{3}\) πr³
(C) \(\frac{1}{3}\) πr³
(D) πr³
उत्तर-
(A) \(\frac{2}{3}\) πr³

प्रश्न 55.
7 cm त्रिज्या वाले गोले का आयतन होगा-
(A) \(\frac{4312}{6}\) cm³
(B) \(\frac{4312}{5}\) cm³
(C) \(\frac{4312}{4}\) cm³
(D) \(\frac{4312}{3}\) cm³
उत्तर-
(D) \(\frac{4312}{3}\) cm³

प्रश्न 56.
एक अर्धगोलाकार कटोरे की त्रिज्या 3.5 cm है। इसका आयतन होगा-
(A) 89.6 cm³
(B) 89.8 cm³
(C) 89.5 cm³
(D) 89.2 cm³
उत्तर-
(B) 89.8 cm³