Class 9

Haryana State Board HBSE 9th Class Maths Notes Chapter 5 Introduction to Euclid’s Geometry Notes.

Haryana Board 9th Class Maths Notes Chapter 5 Introduction to Euclid’s Geometry

Introduction
The word ‘geometry’ is derived from the Greek words ‘geo’, means the ‘earth’, and ‘metrein’, means ‘to measure’. So, it appears to have originated from the need for measuring land. Many ancient civilization of Egypt, Babylonia, India, Greece, China have studied the ‘geometry’ in various forms. They short out the several practical problems which required the development of geometry in various ways.

In Indus Valley Civilization, the ratio length : breadth : thickness of the bricks was taken as 4 : 2 : 1.

Construction of altars (or vedis) and fireplaces for performing Vedic rites were originated in Vedic period. Square and circular altars were used for household rituals, while shape of altars were the combination of rectangles, triangles and trapeziums. They are used for public worship. The ‘sriyantra’ consists of nine interwoven isosceles triangles which are arranged in such a way that they produce 43 subsidiary triangles. A Greek mathematician, Thales, (640 BC) gave the first known proof of the statement that a circle is bisected (cut into two equal parts) by its diameter.

Pythagoras (572 BC) was the most famous pupil of Thales discovered many geometric properties and developed the theory of geometry to a great extent. This process continued till 300 BC. His important theorem is; In right triangle, the square of hypotenuse is equal the sum of the square of base and square of perpendicular.

Euclid (300 BC) was a mathematics teacher who was born in Alexandria in Greece introduced the method of proving mathematical results by using deductive logical reasoning and the previously proved results. The geometry of plane figure is known as “Euclidean Geomery.”

The Indian Mathematician, Aryabhatta (born 476 AD) worked out the area of an isosceles triangle, the volume of a pyramid and approximate value of π.

Brahmagupta (born 598 AD) discovered the formula for finding the area of cyclic quadrilateral.

Bhaskara II (born 1114 AD) gave a dissection proof of Pythagoras’ theorem.

In this chapter, we shall study the Euclid’s approach to geometry.

Key Words
→ Version – Translation.

→ Altars – Raised plateform used for sacrifice or religious offering.

→ Rituals – Way of performing religious services.

→ Rite – Religious ceremony.

→ Subsidiary – Accessory.

→ Allied – Related.

→ Extent – Large space or tract size.

→ Volume – Space occupied, mass.

→ Cyclic Quadrilateral – A quadrilateral whose four vertices lie on a circle.

→ Proof – The course of reasoning which establishes the truth of a statement.

→ Logic – The science or art of reasoning.

→ Physical – Belonging to physics.

→ Universal – Belonging to all.

→ Fact – A thing known to be true.

→ Coincide – To occupy the same space.

→ Proposition – A statement of something to be done.

→ Interpreted – To exposed the meaning of.

→ Demonstrate – To prove with certainly.

→ Consequence – result.

→ Superposed – To put or place over or above.

→ Assumption – A supposition, thing assumed.

Basic Concepts
Euclid’s Definitions, Axioms and Postulates:
(a) Euclid summarised the work of ‘geometry’ as definitions. He listed 23 definitions in Book 1 of ‘Elements’. A few of them are given below:

• A point is that which has no part.
• A line is breadthless length.
• The ends of a line are points.
• A straight line is a line which lies evenly with the points on itself.
• A surface is that which has length and breadth only.
• The edges of surface are lines.
• A plane surface is a surface which lies evenly with the straight lines on itself.

In these definitions, we observe that, point, line, breadth, length, plane etc. are undefined terms. The only thing is that we can represent them intuitively or explain them with the help of ‘physical models.’

Starting with these definitions, Euclid assumed certain properties, which were not to be proved. These assumptions are actually “obvious universal truths”. He divided them into two types: axioms and postulates. He used term ‘postulate’ for the assumptions that were specific to geometry. Common notions (often called axioms), on the other hand, were. assumption used throughout mathematics and not specifically linked to geometry.

(b) Axioms: The basic facts which are taken for granted, without proof, are called axioms.
Some of the Euclid’s axioms (not in order) are given below:
(i) Things which are equal to the same thing are equal to one another.
i.e., If p = q and r = q, then p = r.
(ii) If equals are added to equals, the wholes are equal.
i.e., If p = q, then p + r = q + r.
(iii) If equals are subtracted from equals, the remainders are equal.
i.e., If p = q, then p – r = q – r.
(iv) Things which coincide with one. another are equal to one another.
(v) The whole is greater than the part ie., If p>q, then there exists r(r ≠ 0) such that
P = q + r.
(vi) Things which are double of the same things are equal to one another. i.e., If p = q, then 2p = 2q.
(vii) Things which are halves of the same things are equal to one another.
Le. If p = q, then \(\frac{p}{2}=\frac{q}{2}\)

(c) Postulate: A statement whose validity is accepted without proof, is called a postulate.
Euclid gave five postulates stated as below:
Postulate 1: A straight line may be drawn from any one point to any other point.
This postulate tells us that at least one straight line passes through two distinct points which is shown in the figure below:

Axiom 5.1. Given two distinct points, there is a unique line that passes through them.

In the given figure, P and Q are two distinct points. Out of all lines passing through the point P, there is exactly one line ‘l’ which also passes through Q. Also out of all lines passing through the point Q, there is exactly one line l which also passes through the point P. Hence, we find there is a unique line l which passes through the points P and Q.

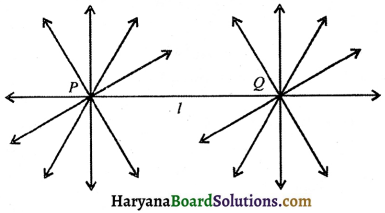
Postulate 2: A terminated line can be produced indefinitely.

Postulate 3: A circle can be drawn with any centre and any radius.
Postulate 4: All right angles are equal to one another.
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

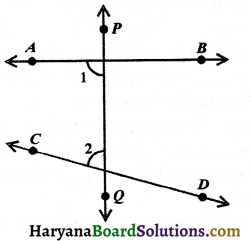
For example, in the figure line PQ falls on the lines AB and CD such that ∠1 + ∠2 < 180° on the left side of PQ. Therefore, the lines AB and CD will eventually intersect on the left side of PQ.

(d) Statement: A sentence which can be judged either true or false is called a statement.
For example:
(i) The sum of the angles to a quadrilateral is 360°, is a true statement.
(ii) The sum of the angles of a triangle is 90°, is a false statement.
(iii) y + 5 > 9 is a sentence but not a statement.

Theorem: In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems and previously accepted statements, such as axioms. The derivation of a theorem is often interpreted as a proof of the truth of the resulting expression, but different deductive systems can yield other interpretations, depending on the meanings of the derivation rules. The proof of a mathematical theorem is logical argument demonstrating that the conclusion.

For example:
(i) The area of a triangle is equal to half its base, multiplied by its attitude.
(ii) An exterior angle of a triangle is equal to sum of its opposite interior angles.
Corollary: A proposition, whose truth can easily be deducted from a preceeding theorem, is called its corollary.

(e) Some terms allied to Geometry:
(i) Point: A point is a mark of position, which has no length, no breadth and no thickness. We represent a point by a capital letters A, B, C, P, Q etc., as shown in the figure.

(ii) Plane: A plane is a every surface such that point of the line joining any two points on it, lies on it.
The surface of the top of the table, surface of the smooth blackboard and surface of a sheet of paper are the some close examples of a plane surfaces are limited in extent but geometrical plane extends endlessly in all directions.

(iii) Line: A line has length but no breadth or thickness. A line has no ends points. A line has no definite length. It can be extended infinitely in both the directions. The given figure shows line \(\bar{AB}\).

Some times we shall denote lines by small letters such as l, m, n, p etc.

(iv) Ray: It is a straight line which starts from a fixed point and moves in the same direction. A ray has one endpoint and it has no definite length.
The given figure shows a ray \(\overrightarrow{A B}\).

(v) Line segment: It is a straight line with its both ends fixed. The given figure shows a line segment \(\bar{AB}\), with fixed ends A and B. A line has a definite length.

So, a line segment is the shortest distance between two fixed points.

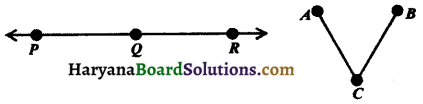
(vi) Collinear points: Three or more than three points are said to be collinear, if they lie on the straight line.
The given figure shows the collinear points P, Q, R while A, B, C are non-collinear.

(vii) Parallel lines: The straight lines which lie in the same plane and do not meet at any point on producing on either side, are called parallel lines.
If l and m are parallel lines in a plane, we write l || m.

The distance between the two parallel lines always remains same.

(viii) Intersecting lines: Two lines having a common point are known as intersecting lines.
The common point (O, in figure 5.18) is known as the point of intersection.

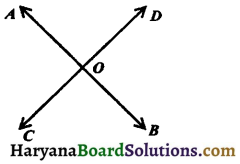
(ix) Concurrent lines: In the figure 5.19, the lines pass through the same point. In this case, lines are called concurrent lines.

(x) Congruence of line segment: If the given two line segments are of the same size, they are said to be ‘congruent. Two lines AB and CD are congruent, if the trace copy of one can be superposed on the other so as to cover it completely and exactly.
Symbolically, \(\bar{AB}\) ≅ \(\bar{CD}\) or line segment AB ≅ line segment CD.

Congruence relation in the set of all line segments:
(i) AB ≅ AB
(ii) AB ≅ CD ⇒ CD ≅ AB
(iii) AB ≅ CD and CD ≅ EF, then AB ≅ EF.

Theorem 5.1.
Two distinct lines cannot have more than one point in common.
Proof. Here, we are given two lines I and m. We need to prove that they have only one point in common. If possible, let P and Q two points common to the given lines l and m. Then the line I passes through the points P and Q and line m passes through the points P and Q. But this assumption clashes with the axiom that one and only one line can pass through two distinct points. So, our supposition that two lines pass through two distinct points is wrong.
Hence, two distinct lines cannot have more than one point in common.

Equivalent Versions of Euclid’s Fifth Postulate:
There are several equivalent versions of fifth postulate of Euclid. One of them is ‘Playfair’s Axiom’ (given by Scottish mathematician John Playfair in 1729), as stated below:

Playfair’s Axiom: “For every line l and for every point P not lying on l, there exists a unique line m passing through P and parallel to l.”
From figure 5.52, we observe that all the lines passing through the point P, only line m is parallel to line l.

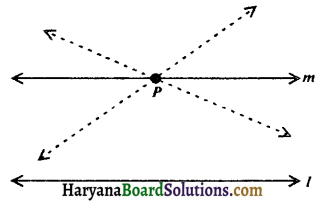
This result can also be stated as: Two distinct intersecting lines cannot be parallel to the same line.

Haryana State Board HBSE 9th Class Maths Notes Chapter 3 Coordinate Geometry Notes.

Haryana Board 9th Class Maths Notes Chapter 3 Coordinate Geometry

Introduction
In previous class, we have studied how to locate a point on a real number line. We also know how to describe the position of a point on the line.
In this chapter, we shall study to locate the coordinates of a point in a plane. We shall also learn about the plotting the points in the plane (Cartesian plane).

In the seventeenth century, French mathematician Rene Descartes developed the idea of describing the position of a point in a plane. His method was a development of the older idea of latitude and longitude. In honour of Descartes, the system used for describing the position of a point in a plane is also known as the cartesian system.

Key Words
→ Coordinates: A set of numbers which locate a point. In general, two numbers are needed to locate a point in a plane and is written as (x, y).

→ Quadrant : (\(\frac{1}{4}\))^th part of a plane divided by coordinate axes is known as a quadrant.

→ Abscissa: The first coordinate x, of a pair (x, y) of cartesian coordinates in the plane.

→ Ordinate: The second coordinate y, of a pair (x, y) of cartesian coordinates in the plane.

Basic Concepts
Cartesian System: We have studied the number line. On the number line, distance from a fixed point is marked in equal units positively in one direction and negatively in the other. The point from which the distances are marked is called the origin. A cartesian (or coordinate) plane consists of two mutually perpendicular number lines intersecting each other at their zeroes.

The adjoining figure shows a cartesian plane consisting of two mutually perpendicular number lines XOX’ and YOY’ intersecting each other at O.
1. The horizontal number line XOX’ is called the x-axis.
2. The vertical number line YOY’ is called the y-axis.
3. The point of intersection ‘O’ is called the origin which is zero for both the axes.

The system consisting of the x-axis, the y-axis and the origin is also called cartesian coordinate system. The x-axis and y-axis together are called coordinate axes.
(a) Coordinates of points in a plane: The position of each point in a coordinate plane is determined by means of an ordered pair (a pair of numbers) with reference of the coordinates axes; as stated below:
(i) The distance of the point along x-axis from the origin O is called x-coordinate or abscissa of the point.
(ii) The distance of the point along y-axis from the origin O is called y-coordinate or ordinate of the point.
Thus, coordinates of the point = Position of the point reference to coordinates axes = (abscissa, ordinate)
If the abscissa of a point is x and its ordinate is y, then its coordiantes = (x, y).

(b) Quadrants: The coordinate plane is divided by axes into four parts which are known as quadrants. Each point is located either in one of the quadrants or on one of the axes.
Starting from OX in the anticlockwise direction :
(i) XOY is called the first quadrant.
(ii) YOX’ is called the second quadrant.
(iii) X’OY’ is called the third quadrant.
(iv) Y’OX is called the fourth quadrant which are shown in the adjoining figure.

(c) Rules for signs of coordinates:
(i) In the first quadrant, the abscissa and ordinate both are positive.
(ii) In the second quadrant, the abscissa is negative and ordinate is positive.
(iii) In the third quadrant, the abscissa and ordinate both are negative.
(iv) In the fourth quadrant, the abscissa is positive and ordinate is negative.
Using the convention of signs, we have the signs of the coordinates in quadrants as given below :

(d) Coordinates of a point on the x-axis: The distance of every point on the x-axis from x-axis is 0 unit. So, its ordinate is 0.
So, the coordinates of a point on the x-axis is of the form (x, 0).
e.g., (5, 0), (3, 0), (-5, 0) etc.

(e) Coordinates of a point on the y-axis: The distance of every point on the y-axis from the y-axis is 0 unit. So, its abscissa is zero.
So, the coordinates of a point on the y-axis is of the form (0, y).
e.g., (0,5), (0, 2), (0, -7) etc.

(f) The coordinates of the origin are (0, 0).

Plotting of a point in the plane if its coordinates are given: In this section, we will learn about to locate a point in the cartesian plane if co-rdinates of the points are given. This process is known as the plotting of the point with given coordinates. In this process, we use a graph paper as the coordinates plane. We draw x-axis and y-axis on it which intersect each other at origin O. Any point P in the xy-plane can be located by using an ordered pair (x, y) of real numbers. Let x denote the signed distance of P from the y-axis (signed in the sence that, if x > 0, then P is to the right of the y-axis and if x < 0, then P is to the left of the y-axis); and let y denote the signed distance of P from the x-axis. The ordered pair (x, y) is called the coordinates of P, that gives us enough information to locate the point P in the cartesian plane.

If (a, b) are the coordinates of a point P, then ‘a’ is called the x-coordinate or abscissa of P and ‘b’ is called the y-coordinate or ordinate of P as shown in fig 3.11.

For example, to locate the point (-3, 5), go 3 units along x-axis to the left of O(origin) and then go up straight 5 units and to locate the point (5, -3), go 5 units along the x-axis to the right of O and then go down 3 units. We plot these points by placing a dot at this location. See figure 3.12 in which the points(-4, -7) and (2, 2) are also located.

Any point on the x-axis has coordinates of the form (x, 0) and any point on the y-axis has coordinates of the form (0, y).

Haryana State Board HBSE 9th Class Maths Notes Chapter 2 Polynomials Notes.

Haryana Board 9th Class Maths Notes Chapter 2 Polynomials

Introduction
In previous classes, we have learnt about algebraic expressions and various operations on them such as addition, subtraction, multiplication and division. We have also studied the factorization of algebraic expressions. In this chapter, we shall review these concepts and extent them to particular types of expressions known as polynomials. We shall also study the Remainder Theorem and Factor Theorem and their use in the factorization of polynomials.

Key Words
→ Polynomial: A polynomial is a algebraic expression in which the variables involved have only non negative integral powers.

→ TermEach individual part of an expression or sum which stands alone or is connected to other parts of an expression by a plus (+) or minus (-) sign e.g., in expression 3x² + 4x + 9, there are three terms, 3x², 4x and 9.

→ Coefficients of polynomial: Refers to a multiplying factor e.g., in 5x and 7xy; 5 and 7y are the coefficients of x.

→ Algebraic expression: An algebraic expression is a collection of one or more terms, which are seperated from each other by addition (+) or subtraction signs.

→ Standard form of a polynomial: A polynomial is said to be in standard form, if the powers of x are either in increasing or in decreasing order.

→ Remainder theorem: If p(x) is any polynomial of degree greater than or equal to 1 and p(x) is divided by the linear polynomial (x – a) then remainder is p(a).

→ Factor theorem: (x – a) is a factor of the polynomial p(x), if p(a) = 0.

→ Zero of a polynomial: A real number ‘a’ is a zero of a polynomial p(x), if p(a) = 0.

→ Algebraic equation: An algebraic equation is a statement which states that the two expressions are equal.

→ Factors of the polynomial: When a polynomial (an algebraic expression) is expressed as the product of two or more expressions, then each of these expressions is called a factor of the polynomial.

→ Linear factors: If a factors contains no higher power of the variable quantity than the first power is called linear factor e.g., 4x + 5 is a linear factor.

Basic Concepts
Polynomial in One Variable:
(a) Polynomial: An expression of the form a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ….. + a₂xⁿ + a₁x + a₀ is called polynomial, where n is a whole number, a₀, a₁, a₂, a₃,…, a_n, are real numbers and coefficients of the polynomial.
e.g., (i) 4x³ + 9x² – 3x + 4 is a polynomial in one variable x.
(ii) y⁴ + 6y³ – 4y² + 2y + 7 is a polynomial in one variable y.

(b) Terms and their Coefficients: (i) The polynomial 5x³ + 9x² – 3x – 5 has four terms, namely 5x³, 9x², -3x and -5, and 5, 9, -3 are coefficients of x, x and x respectively.
(ii) The polynomial x² + 3x – 7 has three terms, namely x², 3x and -7 and 1, 3 are coefficients of x² and x respectively.

(c) Degree of a Polynomial: The highest power of the variable is called the degree of polynomial.
(i) f(x) = 3x³ + 4x² – 8x + 10.
Here, highest power term of given polynomial is 3x³, so it’s degree is 3.
(ii) g(x) = 5x² – 4x + 8.
Here, highest power term of given polynomial is 5x², so it’s degree is 2.

(d) Types of Polynomial (according to degree):
1. Constant Polynomial: A polynomial of degree zero is called a constant polynomial.
eg., 3, -7, \(\frac{5}{9}\), etc. are all constant polynomials.
2. Linear Polynomial: A polynomial of degree 1 is called a linear polynomial.
e.g., (i) 3x + 7 is a linear polynomial in one variable x.
(ii) 4y – 8 is a linear polynomial in one variable y.
(iii) ax + b, a ≠ 0 is a linear polynomial in one variable x.
3. Quadratic Polynomial: A polynomial of degree 2 is called a quadratic polynomial.
e.g., (i) 11x² + 6x – \(\frac{3}{2}\) is a quadratic polynomial in x.
(ii) y² + 6y – 8 is a quadratic polynomial in y.
(iii) ax² + bx + c, a ≠ 0 is a quadratic polynomial in x.

4. Cubic Polynomial: A polynomial of degree 3 is called a cubic polynomial.
e.g., (i) 7x³ + 5x² + 6 is a cubic polynomial in x.
(ii) 3x² – 4xy² + 7 is a cubic polynomial in x and y.
(iii) ax³ + bx² + cx + d, a ≠ 0 is a cubic polynomial in x.
5. Biquadratic Polynomial: A polynomial of degree 4 is called a biquadratic polynomial.
e.g., (i) x⁴ – 5x³ + 3x² – 6x + 4 is a biquadratic polynomial in x.
(ii) ax⁴ + bx³ + cx² + dx + e, a ≠ 0 is a biquadratic polynomial in x.

(e) Types of Polynomial (According to terms):
(i) Monomial: A polynomial having one term is called a monomial.
e.g., 5, 2x, 4xy, 3x² are all monomials.
(ii) Binomial: A polynomial having two terms is called a binomial.
eg., 4x + 3, 5x² + 9, 7x² + 7x are all binomials.
(iii) Trinomial: A polynomial having three terms is called a trinomial.
e.g., 7x³ + 4x² + 5, x² + 5x + 3 are all trinomials.
(iv) Zero Polynomial: A polynomial consisting of one term, namely zero only, is called a zero polynomial.
The degree of a zero polynomial is not defined.

Zeroes of a Polynomial: Consider the polynomial:
p(x) = 2x³ – 3x² + 4x + 5.
If we replace x by 1 everywhere in p(x), we get
p(1) = 2 × (1)³ – 3 × (1)² + 4 × 1 + 5
= 2 – 3 + 4 + 5
= 11 – 3 = 8.
So, we can say that the value of p(x) at x = 1 is 8.
Similarly,
P(0) = 2 × (0)³ – 3 × (0)² + 4 × 0 + 5
= 0 – 0 + 0 + 5 = 5.
So, we can say that the value of p(x) at x = 0 is 5 and
p(-2) = 2 × (-2)³ – 3 × (-2)² + 4 × (-2) + 5
= -16 – 12 – 8 + 5
= -31.
So, we can say that the value of p(x) at x = -2 is -31. Now, consider another polynomial
f(x) = x² – 4
f(2) = (2)² – 4 = 4 – 4 = 0
f(-2) = (-2)² – 4 = 4 – 4 = 0.
We can say, that 2 and -2 are the zeroes of the polynomial.
In general, a real number ‘a’ is said to be a zero of a polynomial p(x), if the value of the polynomial p(x) at x = a is 0 i.e., p(a) = 0.
Now, consider general linear polynomial p(x) = ax + b, a ≠ 0.
For zero of the polynomial p(x) = 0.
0 = ax + b
⇒ ax = -b
⇒ x = \(\frac{-b}{a}\)
∴ \(\frac{-b}{a}\) is the zero of the polynomial.
(v) A zero of polynomial need not to be zero.
(vi) Number of zeroes is equal to the degree of polynomial.

1. Remainder Theorem: Let p(x) be any polynomial of degree ≥ 1 and let a be any real number. If the polynomial p(x) is divided by linear polynomial (x – a), then the remainder is p(a).
Proof:
Suppose that when p(x) is divided by (x – a), then the quotient is q(x) and the remainder is r(x), then we have
p(x) = (x – a).q(x) + r(x)
where degree of r(x) < degree (x – a) or r(x) = 0. Since, degree of (x – a) = 1, degree of r(x) = 0 i.e., constant.
Let r(x) = r, then we have
p(x) = (x – a).q(x) + r ……..(i)
Putting x = a in (i), we get
p(a) = (a – a).q(a) + r
p(a) = 0·q(a) + r
p(a) = 0 + r
p(a) = r
Hence, the remainder is p(a) when p(x) is divided by (x – a).
Hence proved.

Corollary I. When a polynomial p(x) of degree ≥ 1 is divided by a linear polynomial ax + b, a ≠ 0, then remainder is equal to p\(\left(\frac{-b}{a}\right)\).
Corollary II. If a polynomial p(x) vanishes when x = a and also x = b, then p(x) is divisible by (x – a) (x – b).

2. Factor Theorem: If p(x) is a polynomial of degree ≥ 1 and a is any real number, then:
(i) (x – a) is a factor of p(x), if p(a) = 0 and
(ii) p(a) = 0, if (x – a) is a factor of p(x).
Proof:
When a polynomial p(x) is divided by (x – a), then
p(x) = (x – a).q(x) + r(x)…….(i)
where q(x) is the quotient and r(x) is the remainder.
By Remainder theorem, we have
remainder = p(a).
Putting r(x) = p(a) in (i), we get
p(x) = (x – a).q(x) + p(a).
(i) If p(a) = 0, then p(x) = (x – a).q(x)
⇒ (x – a) is a factor of p(x).
(ii) If (x – a) is a factor of p(x) (given), then p(x) = (x – a).g(x), for some polynomial g(x)
In this case, when p(x) is divided by (x – a), the remainder is
p(a) = (a – a).g(a)
⇒ p(a) = 0 × g(a)
⇒ p(a) = 0. Hence proved.

Factorisation of Polynomials:
(a) Factorisation of a quadratic polynomial by splitting the middle term : Quadratic polynomial ax² + bx + c, where a, b, c ≠ 0 divided into two classes:
(i) When a = 1 i.e., x² + bx + c.
(ii) When a ≠ 1 i.e., ax² + bx + c.
Resolution of x² + bx + c into two factors: Examine the following example:
(x + 3)(x + 4) = x² + (3 + 4)x + 3 × 4 = x² + 7x + 12
Here, we obtain product 12 by multiplying together 3 × 4 and 7 is obtain by adding together (+3) and (+4).
Hence, in order to find out factors of x² + 7x + 12, we must find two numbers whose product is 12 and sum is 7.
Since, (x + p) (x + q) = x² + (p + q)x + pq
∴ x² + (p + q)x + pq = (x + p) (x + q)
We observe that, the product pq is obtained by multiplying together p and q, and (p + q) is the sum of the coefficient of the two second terms. Conversely, to find the factors, we have to find two numbers whose sum is (p + q) and product is pq.
We have the following procedure for factorising the quadratic polynomial x² + bx +c:
Step 1: Rewrite the quadratic polynomial in standard form (x² + bx + c), if not already in this form.
Step 2: Factorise constant term e into two factors p and q such that p × q = c and p + q = b.
Step 3: Split the middle term i.e., the term x into two terms with the coefficients p and q.
Step 4: By using grouping factorisation method, factorise the obtained four terms.

(b) Factorisation of a quadratic polynomial by splitting the middle term (continued): For factors of the quadratic polynomial of the form ax² + bx + c, where a ≠ 1 and a, b, c ≠ 0. We have the following procedure for factorising the quadratic polynomial ax² + bx + c.
Step 1: Rewrite the quadratic polynomial in standard form (ax² + bx + c), if not already in this form.
Step 2: Find the product of constant term and the coefficient of x² i.e., a × c = ac.
Step 3: (i) Observe that, if ac is positive (+ve), then find two factors p and q of ac such that p + q = b.
(ii) If ac is negative (-ve), then find two factors p and q of ac such that p – q = b.
Step 4: Split the middle term into two terms with coefficients p and q.
Step 5: Factorize the four terms by grouping.

(c) Factorisation of cubic polynomials by factor theorem: In this section, we have studied how to factorize cubic polynomials. The idea is to find out a linear factor (x – a) of the given polynomial p(x) and write it as p(x) = (x – a).q(x).
The degree of q(x) is one less than that of p(x). Therefore, q(x) is a quadratic polynomial which can be factorised by the method of splitting the middle term or we may again try to find a linear factor (x – b) of q(x). Thus, we have p(x) = (x – a).(x – b) g(x).
Here, the degree of g(x) is one less than q(x) i.e., the degree of g(x) is 1. Thus p(x) = (x – a).(x – b) g(x), which is product of linear factors.

For example: Factorise x³ – 2x² – 5x + 6 by factor theorem.
Solution:
First Method: Let
p(x) = x³ – 2x² – 5x + 6.
Step 1. First check at which value, the given polynomial p(x) becomes zero. These values can be any one of the factors of constant term.
The factors of constant term (6) are ±1, ±2, ±3, ±6.
p(1) = p(1)³ – 2 × (1)² – 5 × 1 + 6
= 1 – 2 – 5 + 6
= 7 – 7 = 0.
∴ By factor theorem (x – 1) is a factor of p(x).
Step 2. Now, divide x³ – 2x² – 5x + 6 by x – 1

The other factor of p(x) is x² – x – 6.
Step 3. Now, p(x) = (x – 1) (x² – x – 6)
= (x – 1)[x² – (3 – 2)x – 6)
[∵ -6 = -(3 × 2), 3 – 2 = 1]
= (x – 1)[x² – 3x + 2x – 6[
= (x – 1)[x(x – 3) + 2(x – 3)]
= (x – 1)(x – 3)(x + 2)
Hence, x³ – 2x² – 5x + 6 = (x – 1)
(x – 3)(x + 2).

Second method: Let
p(x) = x³ – 2x² – 5x + 6
First check at which value, the given p(x) becomes zero. These values can be any one of the factors of constant term. Factors of constant term 6 are ±1, ± 2, ± 3, ±6.
Put x = 1,
p(1) = (1)³ – 2 × (1)² – 5 × 1 + 6
= 1 – 2 – 5 + 6
= 7 – 7 = 0
⇒ (x – 1) is a factor of x³ – 2x² – 5x + 6.
Put x = -2,
p(-2) = (-2)³ – 2 × (-2)² – 5 × (-2) + 6
= – 8 – 8 + 10 + 6
= -16 + 16 = 0
⇒ (x + 2) is a factor of p(x).
Put x = 3,
p(3) = (3)³ – 2 × (3)² – 5 × 3 + 6
= 27 – 18 – 15 + 6
= 33 – 33 = 0
⇒ (x – 3) is a factor of p(x).
Since, the given expression is a cubic polynomial.
So, it will have three factors of first degree.
∴ x³ – 2x² – 5x + 6 = k(x – 1)(x + 2)(x – 3) ……(i)
Here, k is the numerical coefficient yet to be found. Now putting x = 0 (value other than 1, 2, 3) on both sides of equation (i),
we get
6 = k(0 – 1) (0 + 2) (0 – 3)
⇒ 6 = 6k ⇒ k = \(\frac{6}{6}\) ⇒ k = 1
Putting the value of k in (i), we get
x³ – 2x² – 5x + 6 = (x – 1)(x + 2)(x – 3).

Algebraic Identities: In previous classes, we have learnt about some algebraic identities.
An algebraic identity is an algebraic equation that is true for all values of the variables present in the equation.
Identity I: (x + y)² = x² + 2xy + y².
Identity II: (x – y)² = x² – 2xy + y².
Identity III: x² – y² = (x + y) (x – y).
Identity IV: (x + a)(x + b) = x² + (a + b)x + ab.
(a) Algebraic Identities for Cubes of Binomials
Identity V: (x + y)³ = x³ + y³ + 3xy(x + y)
= x³ + y³ + 3x²y + 3xy².
Identity VI: (x – y)³ = x³ – y³ – 3xy(x – y)
= x³ – y³ – 3x²y + 3xy².

(b) Algebraic Identities Relating to Trinomials
Identity VII: (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.
Identity VIII: x³ + y³ + z³ – 3xyz
= (x + y + z) (x² + y² + z² – xy – yz – zx)
Note: If x + y + z = 0, then
x³ + y³ + z³ – 3xyz = 0(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3xyz = 0
x³ + y³ + z³ = 3xyz.

(c) Sum and Difference of Cubes
We will use the following identity for factorisation of sum and difference of two cubes.
Identity IX: x³ + y³ = (x + y)(x² – xy + y²).
Identity X: x³ – y³ = (x – y)(x² + xy + y²).

Haryana State Board HBSE 9th Class Maths Notes Chapter 1 Number Systems Notes.

Haryana Board 9th Class Maths Notes Chapter 1 Number Systems

Introduction
In our previous classes, we have learnt about various types of numbers such as natural numbers, whole numbers, integers, rational numbers etc. and their representation on the number line. In this chapter, we shall study rational numbers, irrational numbers and their representation on number line and laws of exponents for real numbers. Let us review the various types of numbers.
(a) Natural Numbers: The counting numbers 1, 2, 3, 4, 5, … are called natural numbers. The smallest natural number is 1 but there is no largest as it goes up to infinity. The set of natural numbers is denoted by N.
N = {1, 2, 3, 4, 5, ………}.
(b) Whole Numbers: In the set of natural numbers, if we include the number 0, the resulting set is known as the set of whole numbers. The set of whole numbers is denoted by W.
W = {0, 1, 2, 3, 4,……}.
(c) Integers: Natural numbers along with zero and their negative are called integers. The set of integers is denoted by Z.
Z = {…….., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ………}.
The set of integers contains negative numbers, zero and positive numbers. Z comes from the German word “Zahlen’ which means “to count”.

In order to represent integers on the number line we draw a straight line and mark origin (O) in the middle of the line. The numbers may be represented by dots along a straight line as shown in below figure. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin.

(d) Rational Numbers: A rational number is a number which can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Thus, Q = {\(\frac{p}{q}\) : q ≠ 0, p, q ∈ Z}

A rational number may be positive, negative or zero. The rational number is positive if p and q have like signs and negative if p and q have unlike signs.
For example: 5 = \(\frac{5}{1}\), -11 = \(\frac{-11}{1}, \frac{-2}{3}, \frac{4}{7}, \frac{32}{96}, \frac{3}{-5}\)
In above examples 5, \(\frac{4}{7}\), \(\frac{32}{96}\), are positive rational numbers and -11, \(\frac{-2}{3}\), \(\frac{3}{-5}\) are negative rational numbers.
For representing rational numbers on the number line, we draw a line and mark origin (O) in the middle of line. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin. If we mark a point P on the line to the right of O to represent 1, then OP = 1 unit and mark a point Q on the line to the left of O to represent -1, then OQ = -1 unit.

For representing the rational numbers \(\frac{1}{3}\), \(\frac{2}{3}\) on the number line, we divide the segment OP into three equal parts such that OA = AB = BP = \(\frac{1}{3}\). So, A and B represent \(\frac{1}{3}\) and \(\frac{2}{3}\) respectively as shown in the figure 1.2.

For representing rational numbers \(\frac{1}{2}\) on the number line, we divide the segment OQ into four equal parts such that OR = RS = ST = TQ = \(\frac{1}{4}\). So R, S and T represent \(\frac{-1}{4}, \frac{-2}{4}\) and \(\frac{-3}{4}\) respectively.

(e) To find out rational numbers between two rationals: 1. If x and y are two rational numbers such that x < y.
Then a rational number lying between x and y is \(\left(\frac{x+y}{2}\right)\).

2. If a and b are two rational numbers, such that a < b.
Then a rational numbers lying between a and b are

Key Words
→ Numbers: The natural numbers or whole numbers are known as numbers. e.g., 0, 1, 2, 3,…, etc.

→ Even number: A number which is divisible by 2 is called an even number. e.g., 2, 4, 6, 8,…, etc.

→ Odd number: A number which cannot divisible by 2 is called an odd number. e.g., 1, 3, 5, 7,…, etc.

→ Prime number: A natural number which is divisible by 1 and itself, is called a prime number. e.g., 2, 3, 5, 7,…, etc.

→ Composite number: A whole number that can be divided evenly by numbers other than 1 or itself is called composite numbers e.g., 4, 6, 8, 9 …, etc.

→ Coprime numbers: Two numbers are said to be coprime, if their H.C.F. is 1. eg., (4, 5), (8, 9), (15, 16), etc.

→ Number line: Refers to a straight horizontal line on which each point represents a real number.

→ Terminating decimal: A number which divides completly in decimal or whole number is called terminating decimal.
e.g., \(\frac{3}{5}\) = 0.6, \(\frac{20}{4}\) = 5, etc.

→ Non terminating decimal: A number which cannot divide completly in decimal or whole number i.e., process of division will never end, is called non terminating decimal. eg., \(\frac{1}{11}\) = 0.090909…, \(\frac{1}{7}\) = 0.142857…, etc.

→ Recurring (or repeating) decimal: A non terminating decimal, in which a digit or set of digits repeats continually, is called a recurring or repeating decimal.
e.g., \(\frac{4}{9}\) = 0.444….., \(\frac{2}{11}\) = 0.181818…, \(\frac{1}{3}\) = 0.076923076923… etc.

→ Exponent or Index or Power: Suppose that ‘a’ is a real number, when the product a × a × a × a × a is written as a⁵, the number 5 is called the exponent of a.

Basic Concepts
1. Irrational Numbers: In previous section, we observe that some numbers are not rational. These numbers can not write in the form of \(\frac{p}{q}\), where p and q are intergers and q ≠ 0.
For example: 0.141441444…., 0.232332333…..
In 400 B.C., the famous Mathematician Pythagoras was the first to discover the number which were not rational. These numbers are called irrational numbers.
Let us define these numbers as an irrational is a non-terminating and non-recurring decimal, that is, it cannot be written in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.

Examples of Irrational Numbers:
(i) 0.2020020002……, 0.313311333111……., 0.535535553… are irrational numbers.
(ii) \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), \(\sqrt{10}\), \(\sqrt{11}\), \(\sqrt{12}\), \(\sqrt{15}\), \(\sqrt{16}\) etc. all are irrational numbers.
(iii) \(\sqrt[3]{2}, \sqrt[3]{3}, \sqrt[3]{4}, \sqrt[3]{5}, \sqrt[3]{6}, \sqrt[3]{7}, \sqrt[3]{9}, \sqrt[3]{10}\) etc. all are irrational numbers.
(iv) π is irrational, while \(\frac{22}{7}\) is rational.

2. Properties of Irrational Numbers:
A. (a) Sum of a rational number and an irrational number is an irrational number.
(b) Difference of a rational number and an irrational number is an irrational number.
(c) Product of a rational number and an irrational number is an irrational number.
(d) Quotient of a rational number and an irrational number is an irrational number.
For example: (5 + \(\sqrt{2}\)), (5 – \(\sqrt{3}\)), 3\(\sqrt{2}\) and \(\frac{7}{\sqrt{3}}\) all are irrational numbers.

B. (a) It is not necessary that sum of two irrational numbers may be an irrational number.
For example:(4 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) both are irrational number. But (4 + \(\sqrt{5}\))+(3 – \(\sqrt{5}\)) = 7, which is rational number.
(b) It is not necessary that difference of two irrational numbers may be an irrational number.
For example: (4 + \(\sqrt{3}\)) and (3 + \(\sqrt{3}\)) both are irrational numbers. But (4 + \(\sqrt{3}\)) – (3 + \(\sqrt{3}\)) = 1, which is rational number.

(c) It is not necessary that product of two irrational numbers may be an irrational number.
For example: \(\sqrt{2}\) is an irrational number. But \(\sqrt{2}\) × \(\sqrt{2}\) = 2, which is rational number.
(d) It is not necessary that quotient of two irrational numbers may be an irrational number.
For example: 6\(\sqrt{2}\) and 3\(\sqrt{2}\) both are irrational numbers. But \(\frac{6 \sqrt{2}}{3 \sqrt{2}}\) = 2, which is rational number.

3. Representation of Irrational Numbers on the Number Line: We show the representation of irrational numbers on the number line by help of some examples given below:

(a) Real Numbers: Rational numbers and irrational numbers form the collection of all real numbers.
Every real number is either rational or irrational number.
For example: -3\(\frac{1}{2}\), \(\sqrt{3}\), π, 1.596. etc.
(i) Rational Number: A number whose decimal expension is either terminating or non-terminating recurring is called a rational number.
For example: \(\frac{3}{4}\), 2.1, \(\frac{1}{3}\) etc.
(ii) Irrational Number: A number whose decimal expension is non-terminating non recurring is called an irrational number.
For example: \(\sqrt{2}\), \(\sqrt{3}\), 2010010001…., π, etc.

(b) Decimal Expansions of Rational Numbers: A rational number can be expressed as a decimal. For example, if we divide 3 by 5, we will get 0.6, a terminating decimal.

Similarly, if we divide 2 by 8, we will get 0.25, a terminating decimal.

Similarly,
\(\frac{3}{4}\) = 0.75
\(\frac{7}{16}\) = 0.4375
\(\frac{-2}{5}\) = -0.4 etc.
are rational numbers expressed as decimals. Now let us divide 3 by 11

We observe that the continued process of division by 11, in the quotient digits 2, 7 will repreat from the stage marked (→) onwards. Thus
\(\frac{3}{11}\) = 0.2727…..
= \(0 . \overline{27}\)
The process of division, in this case the decimal expressions are known as non-terminating repeating (recurring) decimals.
Similarly,

A repeating decimal such as 0.6666… is often written as \(0.\overline{6}\), where over bar indicates the number that repeats. Hence,
\(\frac{2}{3}\) = \(0.\overline{6}\)
So, we say that every terminating or repeating decimal represents a rational number.

Representing Real Numbers on the Number Line: In the previous section, we have learn about the decimal expansions of real numbers. This help us to represent it on the number line. In this section, we will learn how to visualise the position of real numbers in decimal form.

Suppose we want to visualise the representation of 2.665 on the number line. We observe that 2.665 is located between 2 and 3. So let us look closely at the portion of the number line 2 and 3. We divide it into 10 equal parts and mark each point of division as shown in figure 1.10. Then the first mark to the right of 2 will represent 2.1, the second 2.2 and so on. To see this clearly we may take a magnifying glass and look at the portion between 2 and 3. Now, we observe that 2.665 lies between 2.6 and 2.7. To get more accurate visualization of the representation, we divide this portion of real line into 10 equal parts. The first mark will represent 2.61, the second 2.62 and so on.

Again, 2.665 lies between 2.66 and 2.67, so let us focus on this portion of the number line. We magnify the portion of line between 2.66 and 2.67 and divide it into 10 equal parts. The first mark represents 2.661, the next one represents 2.662 and so on. So 2.665 is the 5th mark in these subdivisions. We call this process of visualisation of representation of numbers on the number line through a magnifying glass, as the process of successive magnification.

1. Operations on Real Numbers: In the previous classes, we have learnt about that rational numbers satisfied the associative, commutative and distributive properties for addition and multiplication. The sum, difference, product and quotient of two rational numbers will be a rational number. Irrational numbers also satisfied the commutative, associative and distributive properties for addition and multiplication. However the sum, difference, quotients and products of irrational numbers are not always irrational.

The facts related to operations on real numbers are given below:

• The sum or difference of a rational number and an irrational number is an irrational number.
• The product or quotient of a non-zero rational number with an irrational number is an irrational number.
• If we, add, subtract, multiply or divide two irrational numbers, the result may be a rational or irrational number.

2. Existence of Square Root of a given Positive Real Number:
To find \(\sqrt{x}\) geometrically, where x is any positive real number.
Construction: Draw a line AB of length x units extend AB to point C such that BC = 1 unit. Find the midpoint of AC and marked that point O. Draw a semicircle with centre O and radius OA. Draw a line perpendicular to AC passing through B and intersecting the semicircle at D, then BD = \(\sqrt{x}\).

Proof:
We have AB = x units, BC = 1 unit
⇒ AC = x + 1 units
OA = OD = OC = \(\frac{x+1}{2}\),
(∵ O is the mid-point of AC)
Now,
OB = x – \(\frac{(x+1)}{2}\)
⇒ OB = \(\frac{2 x-x-1}{2}=\frac{x-1}{2}\)
In right ΔOBD,
OD² = OB² + BD²,
(By Pythagoras theorem)
⇒ BD² = OD² – OB²
⇒ BD² = \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)
⇒ BD² = \(\frac{x^2+1+2 x}{4}-\frac{x^2+1-2 x}{4}\)
⇒ BD² = \(\frac{1}{4}\)[x² + 1 + 2x – x² – 1 + 2x]
⇒ BD² = \(\frac{1}{4}\) × 4x
⇒ BD² = x
⇒ BD = \(\sqrt{x}\)

3. Rationalisation of Irrational Number:
The process of multiplying a given irrational number by its rationalising factor to get a rational number as product is called rationalisation of the given irrational number.
When the product of two irrational numbers is a rational number, each is called the Rationalising Factors (R.F.) of the other.

For Example:
(i) Since 5\(\sqrt{2}\) × 3\(\sqrt{2}\) = 15 × 2 = 30; which is a rational number. Therefore, 5\(\sqrt{2}\) and 3\(\sqrt{2}\) are rationalising factors of each other.
(ii) (\(\sqrt{3}\) + \(\sqrt{2}\)) (\(\sqrt{3}\) – \(\sqrt{2}\)) = (\(\sqrt{3}\))² – (\(\sqrt{2}\))²
= 3 – 2 = 1
(\(\sqrt{3}\) + \(\sqrt{2}\)) and (\(\sqrt{3}\) – \(\sqrt{2}\)) are the
rationalising factors of each other.
(iii) (3 + \(\sqrt{5}\)) (3 – \(\sqrt{5}\)) = 3² – (\(\sqrt{5}\))²
= 9 – 5 = 4
(3 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) are rationalising factors of each other.

In the same way:
(i) R.F. of \(\sqrt{5}\) – 2 is \(\sqrt{5}\) + 2.
(ii) R.F. of 4 + 3\(\sqrt{5}\) is 4 – 3\(\sqrt{5}\).

Laws of Exponents for Real Numbers:
Let a be real number and m, n be rational numbers, then we have

Note: Here a is called base and m, n are called exponents.

Haryana State Board HBSE 9th Class Maths Notes Chapter 15 प्रायिकता Notes.

Haryana Board 9th Class Maths Notes Chapter 15 प्रायिकता

→ गणित की एक शाखा, जिसे ‘प्रायिकता का सिद्धांत’ (Theory of Probability) कहते हैं, में अनिश्चितता के मापन का प्रावधान है। इस सिद्धांत में हम ऐसी स्थितियों (या प्रयोगों या घटनाओं पर ध्यान देते हैं जिनमें कोई विशेष परिणाम निश्चित नहीं होता है, किंतु वह अनेक संभाव्य परिणामों में से एक हो सकता है।

→ किसी घटना E की प्रायिकता, जिसे P (E) से दर्शाते हैं, निम्न सूत्र से प्राप्त होती है :

→ किसी घटना के घटने की प्रायिकता 0 से 1 के बीच (जिसमें 0 व 1 सम्मिलित हैं) होती है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 14 सांख्यिकी Notes.

Haryana Board 9th Class Maths Notes Chapter 14 सांख्यिकी

→ आंकड़े एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को आंकड़े कहा जाता है।

→ सांख्यिकी : सांख्यिकी अध्ययन का वह क्षेत्र है जिसमें आंकड़ों के प्रति प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है।

→ सांख्यिकी आंकड़ों का निरूपण सांख्यिकी आंकड़ों को निरूपित करने के लिए निम्नलिखित प्रकार के आलेखों या आरेखों का उपयोग किया जाता है-

• आयत-चित्र,
• बारंबारता बहुभुज,
• बारंबारता वक्र,
• दंड आरेख,
• चित्रालेख,
• पाइ चार्ट या वृत्तीय आरेख ।

→ अवर्गीकृत आंकड़ों का माध्य (समांतर माध्य) : सांख्यिकी आंकड़ों का आदर्श मापक ‘माध्य’ होता है क्योंकि माध्य अथवा औसत ज्ञात करने के लिए सभी आंकड़ों को निरूपित किया जाता है। इसे द्वारा प्रकट किया जाता है तथा प्राप्त आंकड़ों का माध्य सभी प्रेक्षणों के योग को प्रेक्षणों की संख्या से भाग देकर ज्ञात किया जाता है। यदि n प्रेक्षण x₁, x₂, x₃,…… x_n हो तो
माध्य (\(\bar{x}\)) = \(\frac{x_1+x_2+x_3+\ldots \ldots \ldots+x_n}{n}=\frac{1}{n} \sum_{i=1}^n x_i\)

→ अवर्गीकृत आंकड़ों के माध्य का परिकलन : इसकी निम्नलिखित दो विधियां हैं-
(a) प्रत्यक्ष विधि : यदि चर x के x₁, x₂, x₃, ……….. x_n अलग-अलग मान हों तथा इनकी संगत बारंबारता f₁, f₂, f₃, ………f_n हो तो
माध्य (\(\bar{x}\)) = \(=\frac{f_1 x_1+f_2 x_2+f_3 x_3+\ldots \ldots \ldots}{f_1+f_2+f_3+\ldots \ldots \ldots}=\frac{\sum_{i=1}^n f_i x_i}{\sum_{i=1}^n f_i}\)

(b) कल्पित माध्य विधि : यदि बारंबारताएं अधिक हों तो गणना कठिन हो जाती है, और तब इस विधि का प्रयोग करते हैं। इस विधि में हम एक स्वेच्छ अचर मान ‘a’ को लेते हैं । (ध्यान रहे कि ‘a’ का मान x का वह मान लेना चाहिए, जो बंटन के मध्य भाग में हो।) ‘a’ के मान को x में से घटाते जाते हैं। घटाने पर प्राप्त मान (x – a) को विचलन मान ‘d’ कहते हैं अर्थात d_i = x_i – a
तो माध्य \(\bar{x}\) = a + \(\bar{d}\), जहां \(\bar{d}=\frac{\sum f_i d_i}{\sum f_i}\)
कभी-कभी प्राप्त विचलनों d_i को एक अचर h से भाग देते हैं तथा मान u_i प्राप्त होता है।

→ माध्यक : सबसे मध्य वाले प्रेक्षण का मान माध्यक कहलाता है। यदि n विषम संख्या है, तो माध्यक = \(\left(\frac{n+1}{2}\right)\) वें प्रेक्षण का मान यदि ” सम संख्या है, तो माध्यक = \(\left(\frac{n}{2}\right)\) वें और \(\left(\frac{n}{2}+1\right)\) वें प्रेक्षणों के मानों का माध्य।

→ बहुलक सबसे अधिक बार आने वाले प्रेक्षण का मान बहुलक कहलाता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Notes.

Haryana Board 9th Class Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

यदि लंबाई = l, चौड़ाई = b, ऊंचाई = h, त्रिज्या = r, भुजा = a, तिर्यक ऊंचाई = l से लिखे जाएं तो-

→ घनाभ का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)

→ घन का पृष्ठीय क्षेत्रफल = 6a² [अर्थात् 6 (भुजा)2]

→ बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh

→ बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr(r + h)

→ शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl

→ शंकु का कुल पृष्ठीय क्षेत्रफल = πr(l + r)

→ गोले का पृष्ठीय क्षेत्रफल = 4πr²

→ अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²

→ अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr²

→ कमरे के फर्श या छत का क्षेत्रफल = b

→ कमरे की चार दीवारों का क्षेत्रफल = 2(l + b) × h

→ आयत का परिमाप = 2 (l + b)

→ घनाभ का आयतन = l × b × h

→ घन का आयतन = a³ अर्थात् [(भुजा)3]

→ बेलन का आयतन = πr²h

→ शंकु का आयतन = \(\frac{1}{3}\)πr²h

→ गोले का आयतन = \(\frac{4}{3}\)πr³

→ अर्धगोले का आयतन = \(\frac{2}{3}\)πr³

Haryana State Board HBSE 9th Class Maths Notes Chapter 12 हीरोन सूत्र Notes.

Haryana Board 9th Class Maths Notes Chapter 12 हीरोन सूत्र

→ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

→ त्रिभुज का क्षेत्रफल निकालने का हीरोन का सूत्र = \(\sqrt{s(s-a)(s-b)(s-c)}\)
जहाँ s = त्रिभुज का अर्धपरिमाप = \(\frac{a+b+c}{2}\) तथा a, b, c, त्रिभुज की भुजाएँ हैं।

→

→

→ वर्ग का क्षेत्रफल = भुजा × भुजा

→ आयत का क्षेत्रफल = लंबाई × चौड़ाई

→ 1 हेक्टेयर = 10,000m²

→ एक चतुर्भुज जिसकी भुजाएँ तथा एक विकर्ण दिए हों तो उसका क्षेत्रफल उसे दो त्रिभुजों में विभाजित करके और फिर हीरोन के सूत्र का प्रयोग करके ज्ञात किया जा सकता है।

→ किसी समकोण त्रिभुज में- (कर्ण)² = (आधार)² + (लंब)²

→ समांतर चतुर्भुज का क्षेत्रफल- आधार × ऊँचाई

Haryana State Board HBSE 9th Class Maths Notes Chapter 11 रचनाएँ Notes.

Haryana Board 9th Class Maths Notes Chapter 11 रचनाएँ

→ अंशाकित पटरी (Ruler)- जिसके एक ओर सेंटीमीटर तथा मिलीमीटर चिह्नित होते हैं तथा दूसरी ओर इंच और उसके भाग चिह्नित होते हैं ।

→ सेट-स्क्वायर- सेट-स्क्वायर का एक युग्म जिसमें एक के कोण 90°, 60° तथा 30° तथा दूसरे के कोण 90°, 45° तथा 45° होते हैं।

→ डिवाइडर- डिवाइडर जिसकी दोनों भुजाओं में दो नुकीले सिरे होते हैं। इसकी भुजाओं को समायोजित किया जा सकता है।

→ परकार- परकार, जिसमें पेंसिल लगाने का विधान होता है, जिससे कोण बनाए जाते हैं ।

Haryana State Board HBSE 9th Class Maths Notes Chapter 10 वृत्त Notes.

Haryana Board 9th Class Maths Notes Chapter 10 वृत्त

→ वृत्त वृत्त किसी तल के उन सभी बिंदुओं का समूह होता है, जो तल के एक स्थिर बिंदु से समान दूरी पर हों।

→ एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएं केंद्र (या संगत केंद्रों) पर बराबर कोण बनाती हैं।

→ यदि किसी वृत्त की (या सर्वांगसम वृत्तों की) दो जीवाएं केंद्र पर (या संगत केंद्रों पर) बराबर कोण बनाएं, तो जीवाएं बराबर होती हैं।

→ किसी वृत्त के केंद्र से किसी जीवा पर डाला गया लंब उसे समद्विभाजित करता है।

→ केंद्र से होकर जाने वाली और किसी जीवा को समद्विभाजित करने वाली रेखा जीवा पर लंब होती है।

→ चाप : वृत्त की परिधि के किसी भाग को चाप कहते हैं।

→ तीन असरेखीय बिंदुओं से होकर जाने वाला एक ओर केवल एक वृत्त होता है।

→ एक वृत्त की बराबर जीवाएं केंद्र से समान दूरी पर होती हैं।

→ एक वृत्त के केंद्र से समान दूरी पर स्थित जीवाएं बराबर होती हैं।

→ यदि किसी वृत्त के दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएं बराबर होती हैं।

→ यदि किसी वृत्त की दो जीवाएं बराबर हों, तो उनके संगत चाप (लघु, दीर्घ) सर्वांगसम होते हैं।

→ किसी वृत्त की सर्वांगसम चाप केंद्र पर बराबर कोण बनाती हैं।

→ किसी चाप द्वारा केंद्र पर अंतरित कोण उसके द्वारा वृत्त के शेष भाग के किसी बिंदु पर अंतरित कोण का दोगुना होता है।

→ एक वृत्तखंड में बने कोण बराबर होते हैं।

→ अर्द्धवृत्त का कोण समकोण होता है।

→ यदि दो बिंदुओं को मिलाने वाला रेखाखंड उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिंदुओं पर समान कोण अंतरित करे, तो चारों बिंदु एक वृत्त पर स्थित होते हैं।

→ चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग 180° होता है।

→ यदि किसी चतुर्भुज के सम्मुख कोणों के किसी एक युग्म का योग 180° हो, तो वह चक्रीय चतुर्भुज होता है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Notes.

Haryana Board 9th Class Maths Notes Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

→ एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध ( किसी मात्रक में) एक संख्या होती है।

→ दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं, परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।

→ समांतर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्षलंब

→ दो आकृतियां एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।

→ एक ही आधार वाले और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।

→ एक ही आधार वाले और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।

→ यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।

→ एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।

→ त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलंब के गुणनफल का आधा होता है।

→ एक ही आधार वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।

→ त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
अर्थात ar (ΔABD) = ar (ΔACD)