Haryana State Board HBSE 9th Class Maths Notes Chapter 3 Coordinate Geometry Notes.
Haryana Board 9th Class Maths Notes Chapter 3 Coordinate Geometry
Introduction
In previous class, we have studied how to locate a point on a real number line. We also know how to describe the position of a point on the line.
In this chapter, we shall study to locate the coordinates of a point in a plane. We shall also learn about the plotting the points in the plane (Cartesian plane).
In the seventeenth century, French mathematician Rene Descartes developed the idea of describing the position of a point in a plane. His method was a development of the older idea of latitude and longitude. In honour of Descartes, the system used for describing the position of a point in a plane is also known as the cartesian system.
Key Words
→ Coordinates: A set of numbers which locate a point. In general, two numbers are needed to locate a point in a plane and is written as (x, y).
→ Quadrant : (\(\frac{1}{4}\))th part of a plane divided by coordinate axes is known as a quadrant.
→ Abscissa: The first coordinate x, of a pair (x, y) of cartesian coordinates in the plane.
→ Ordinate: The second coordinate y, of a pair (x, y) of cartesian coordinates in the plane.
![]()
Basic Concepts
Cartesian System: We have studied the number line. On the number line, distance from a fixed point is marked in equal units positively in one direction and negatively in the other. The point from which the distances are marked is called the origin. A cartesian (or coordinate) plane consists of two mutually perpendicular number lines intersecting each other at their zeroes.
The adjoining figure shows a cartesian plane consisting of two mutually perpendicular number lines XOX’ and YOY’ intersecting each other at O.
1. The horizontal number line XOX’ is called the x-axis.
2. The vertical number line YOY’ is called the y-axis.
3. The point of intersection ‘O’ is called the origin which is zero for both the axes.
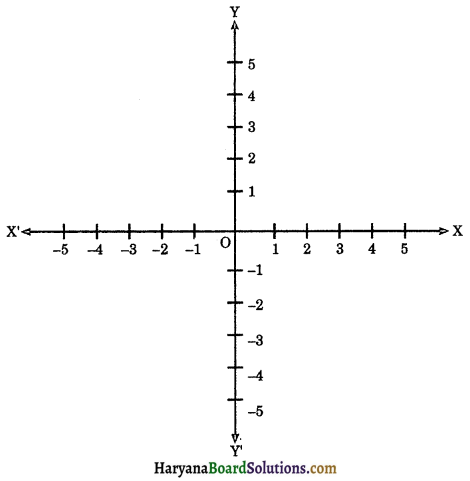
The system consisting of the x-axis, the y-axis and the origin is also called cartesian coordinate system. The x-axis and y-axis together are called coordinate axes.
(a) Coordinates of points in a plane: The position of each point in a coordinate plane is determined by means of an ordered pair (a pair of numbers) with reference of the coordinates axes; as stated below:
(i) The distance of the point along x-axis from the origin O is called x-coordinate or abscissa of the point.
(ii) The distance of the point along y-axis from the origin O is called y-coordinate or ordinate of the point.
Thus, coordinates of the point = Position of the point reference to coordinates axes = (abscissa, ordinate)
If the abscissa of a point is x and its ordinate is y, then its coordiantes = (x, y).
(b) Quadrants: The coordinate plane is divided by axes into four parts which are known as quadrants. Each point is located either in one of the quadrants or on one of the axes.
Starting from OX in the anticlockwise direction :
(i) XOY is called the first quadrant.
(ii) YOX’ is called the second quadrant.
(iii) X’OY’ is called the third quadrant.
(iv) Y’OX is called the fourth quadrant which are shown in the adjoining figure.
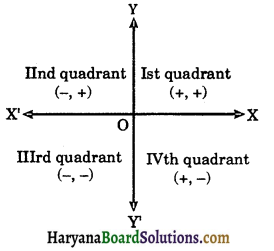
(c) Rules for signs of coordinates:
(i) In the first quadrant, the abscissa and ordinate both are positive.
(ii) In the second quadrant, the abscissa is negative and ordinate is positive.
(iii) In the third quadrant, the abscissa and ordinate both are negative.
(iv) In the fourth quadrant, the abscissa is positive and ordinate is negative.
Using the convention of signs, we have the signs of the coordinates in quadrants as given below :
| Quadrant | x-coordinate | y-coordinate | Point |
| Ist (XOY) | + | + | (+, +) |
| IInd (YOX’) | – | + | (-, +) |
| IIIrd (XOY’) | – | – | (-, -) |
| IVth (Y’OX) | + | – | (+, -) |
(d) Coordinates of a point on the x-axis: The distance of every point on the x-axis from x-axis is 0 unit. So, its ordinate is 0.
So, the coordinates of a point on the x-axis is of the form (x, 0).
e.g., (5, 0), (3, 0), (-5, 0) etc.
(e) Coordinates of a point on the y-axis: The distance of every point on the y-axis from the y-axis is 0 unit. So, its abscissa is zero.
So, the coordinates of a point on the y-axis is of the form (0, y).
e.g., (0,5), (0, 2), (0, -7) etc.
(f) The coordinates of the origin are (0, 0).
![]()
Plotting of a point in the plane if its coordinates are given: In this section, we will learn about to locate a point in the cartesian plane if co-rdinates of the points are given. This process is known as the plotting of the point with given coordinates. In this process, we use a graph paper as the coordinates plane. We draw x-axis and y-axis on it which intersect each other at origin O. Any point P in the xy-plane can be located by using an ordered pair (x, y) of real numbers. Let x denote the signed distance of P from the y-axis (signed in the sence that, if x > 0, then P is to the right of the y-axis and if x < 0, then P is to the left of the y-axis); and let y denote the signed distance of P from the x-axis. The ordered pair (x, y) is called the coordinates of P, that gives us enough information to locate the point P in the cartesian plane.
If (a, b) are the coordinates of a point P, then ‘a’ is called the x-coordinate or abscissa of P and ‘b’ is called the y-coordinate or ordinate of P as shown in fig 3.11.

For example, to locate the point (-3, 5), go 3 units along x-axis to the left of O(origin) and then go up straight 5 units and to locate the point (5, -3), go 5 units along the x-axis to the right of O and then go down 3 units. We plot these points by placing a dot at this location. See figure 3.12 in which the points(-4, -7) and (2, 2) are also located.

Any point on the x-axis has coordinates of the form (x, 0) and any point on the y-axis has coordinates of the form (0, y).