Haryana State Board HBSE 9th Class Maths Notes Chapter 1 Number Systems Notes.
Haryana Board 9th Class Maths Notes Chapter 1 Number Systems
Introduction
In our previous classes, we have learnt about various types of numbers such as natural numbers, whole numbers, integers, rational numbers etc. and their representation on the number line. In this chapter, we shall study rational numbers, irrational numbers and their representation on number line and laws of exponents for real numbers. Let us review the various types of numbers.
(a) Natural Numbers: The counting numbers 1, 2, 3, 4, 5, … are called natural numbers. The smallest natural number is 1 but there is no largest as it goes up to infinity. The set of natural numbers is denoted by N.
N = {1, 2, 3, 4, 5, ………}.
(b) Whole Numbers: In the set of natural numbers, if we include the number 0, the resulting set is known as the set of whole numbers. The set of whole numbers is denoted by W.
W = {0, 1, 2, 3, 4,……}.
(c) Integers: Natural numbers along with zero and their negative are called integers. The set of integers is denoted by Z.
Z = {…….., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ………}.
The set of integers contains negative numbers, zero and positive numbers. Z comes from the German word “Zahlen’ which means “to count”.
In order to represent integers on the number line we draw a straight line and mark origin (O) in the middle of the line. The numbers may be represented by dots along a straight line as shown in below figure. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin.
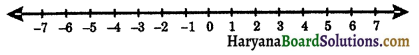
(d) Rational Numbers: A rational number is a number which can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Thus, Q = {\(\frac{p}{q}\) : q ≠ 0, p, q ∈ Z}
A rational number may be positive, negative or zero. The rational number is positive if p and q have like signs and negative if p and q have unlike signs.
For example: 5 = \(\frac{5}{1}\), -11 = \(\frac{-11}{1}, \frac{-2}{3}, \frac{4}{7}, \frac{32}{96}, \frac{3}{-5}\)
In above examples 5, \(\frac{4}{7}\), \(\frac{32}{96}\), are positive rational numbers and -11, \(\frac{-2}{3}\), \(\frac{3}{-5}\) are negative rational numbers.
For representing rational numbers on the number line, we draw a line and mark origin (O) in the middle of line. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin. If we mark a point P on the line to the right of O to represent 1, then OP = 1 unit and mark a point Q on the line to the left of O to represent -1, then OQ = -1 unit.
For representing the rational numbers \(\frac{1}{3}\), \(\frac{2}{3}\) on the number line, we divide the segment OP into three equal parts such that OA = AB = BP = \(\frac{1}{3}\). So, A and B represent \(\frac{1}{3}\) and \(\frac{2}{3}\) respectively as shown in the figure 1.2.
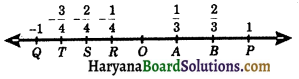
For representing rational numbers \(\frac{1}{2}\) on the number line, we divide the segment OQ into four equal parts such that OR = RS = ST = TQ = \(\frac{1}{4}\). So R, S and T represent \(\frac{-1}{4}, \frac{-2}{4}\) and \(\frac{-3}{4}\) respectively.
(e) To find out rational numbers between two rationals: 1. If x and y are two rational numbers such that x < y.
Then a rational number lying between x and y is \(\left(\frac{x+y}{2}\right)\).
2. If a and b are two rational numbers, such that a < b.
Then a rational numbers lying between a and b are

![]()
Key Words
→ Numbers: The natural numbers or whole numbers are known as numbers. e.g., 0, 1, 2, 3,…, etc.
→ Even number: A number which is divisible by 2 is called an even number. e.g., 2, 4, 6, 8,…, etc.
→ Odd number: A number which cannot divisible by 2 is called an odd number. e.g., 1, 3, 5, 7,…, etc.
→ Prime number: A natural number which is divisible by 1 and itself, is called a prime number. e.g., 2, 3, 5, 7,…, etc.
→ Composite number: A whole number that can be divided evenly by numbers other than 1 or itself is called composite numbers e.g., 4, 6, 8, 9 …, etc.
→ Coprime numbers: Two numbers are said to be coprime, if their H.C.F. is 1. eg., (4, 5), (8, 9), (15, 16), etc.
→ Number line: Refers to a straight horizontal line on which each point represents a real number.
→ Terminating decimal: A number which divides completly in decimal or whole number is called terminating decimal.
e.g., \(\frac{3}{5}\) = 0.6, \(\frac{20}{4}\) = 5, etc.
→ Non terminating decimal: A number which cannot divide completly in decimal or whole number i.e., process of division will never end, is called non terminating decimal. eg., \(\frac{1}{11}\) = 0.090909…, \(\frac{1}{7}\) = 0.142857…, etc.
→ Recurring (or repeating) decimal: A non terminating decimal, in which a digit or set of digits repeats continually, is called a recurring or repeating decimal.
e.g., \(\frac{4}{9}\) = 0.444….., \(\frac{2}{11}\) = 0.181818…, \(\frac{1}{3}\) = 0.076923076923… etc.
→ Exponent or Index or Power: Suppose that ‘a’ is a real number, when the product a × a × a × a × a is written as a5, the number 5 is called the exponent of a.
![]()
Basic Concepts
1. Irrational Numbers: In previous section, we observe that some numbers are not rational. These numbers can not write in the form of \(\frac{p}{q}\), where p and q are intergers and q ≠ 0.
For example: 0.141441444…., 0.232332333…..
In 400 B.C., the famous Mathematician Pythagoras was the first to discover the number which were not rational. These numbers are called irrational numbers.
Let us define these numbers as an irrational is a non-terminating and non-recurring decimal, that is, it cannot be written in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Examples of Irrational Numbers:
(i) 0.2020020002……, 0.313311333111……., 0.535535553… are irrational numbers.
(ii) \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), \(\sqrt{10}\), \(\sqrt{11}\), \(\sqrt{12}\), \(\sqrt{15}\), \(\sqrt{16}\) etc. all are irrational numbers.
(iii) \(\sqrt[3]{2}, \sqrt[3]{3}, \sqrt[3]{4}, \sqrt[3]{5}, \sqrt[3]{6}, \sqrt[3]{7}, \sqrt[3]{9}, \sqrt[3]{10}\) etc. all are irrational numbers.
(iv) π is irrational, while \(\frac{22}{7}\) is rational.
2. Properties of Irrational Numbers:
A. (a) Sum of a rational number and an irrational number is an irrational number.
(b) Difference of a rational number and an irrational number is an irrational number.
(c) Product of a rational number and an irrational number is an irrational number.
(d) Quotient of a rational number and an irrational number is an irrational number.
For example: (5 + \(\sqrt{2}\)), (5 – \(\sqrt{3}\)), 3\(\sqrt{2}\) and \(\frac{7}{\sqrt{3}}\) all are irrational numbers.
B. (a) It is not necessary that sum of two irrational numbers may be an irrational number.
For example:(4 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) both are irrational number. But (4 + \(\sqrt{5}\))+(3 – \(\sqrt{5}\)) = 7, which is rational number.
(b) It is not necessary that difference of two irrational numbers may be an irrational number.
For example: (4 + \(\sqrt{3}\)) and (3 + \(\sqrt{3}\)) both are irrational numbers. But (4 + \(\sqrt{3}\)) – (3 + \(\sqrt{3}\)) = 1, which is rational number.
(c) It is not necessary that product of two irrational numbers may be an irrational number.
For example: \(\sqrt{2}\) is an irrational number. But \(\sqrt{2}\) × \(\sqrt{2}\) = 2, which is rational number.
(d) It is not necessary that quotient of two irrational numbers may be an irrational number.
For example: 6\(\sqrt{2}\) and 3\(\sqrt{2}\) both are irrational numbers. But \(\frac{6 \sqrt{2}}{3 \sqrt{2}}\) = 2, which is rational number.
3. Representation of Irrational Numbers on the Number Line: We show the representation of irrational numbers on the number line by help of some examples given below:
(a) Real Numbers: Rational numbers and irrational numbers form the collection of all real numbers.
Every real number is either rational or irrational number.
For example: -3\(\frac{1}{2}\), \(\sqrt{3}\), π, 1.596. etc.
(i) Rational Number: A number whose decimal expension is either terminating or non-terminating recurring is called a rational number.
For example: \(\frac{3}{4}\), 2.1, \(\frac{1}{3}\) etc.
(ii) Irrational Number: A number whose decimal expension is non-terminating non recurring is called an irrational number.
For example: \(\sqrt{2}\), \(\sqrt{3}\), 2010010001…., π, etc.
(b) Decimal Expansions of Rational Numbers: A rational number can be expressed as a decimal. For example, if we divide 3 by 5, we will get 0.6, a terminating decimal.

Similarly, if we divide 2 by 8, we will get 0.25, a terminating decimal.

Similarly,
\(\frac{3}{4}\) = 0.75
\(\frac{7}{16}\) = 0.4375
\(\frac{-2}{5}\) = -0.4 etc.
are rational numbers expressed as decimals. Now let us divide 3 by 11

We observe that the continued process of division by 11, in the quotient digits 2, 7 will repreat from the stage marked (→) onwards. Thus
\(\frac{3}{11}\) = 0.2727…..
= \(0 . \overline{27}\)
The process of division, in this case the decimal expressions are known as non-terminating repeating (recurring) decimals.
Similarly,

A repeating decimal such as 0.6666… is often written as \(0.\overline{6}\), where over bar indicates the number that repeats. Hence,
\(\frac{2}{3}\) = \(0.\overline{6}\)
So, we say that every terminating or repeating decimal represents a rational number.
![]()
Representing Real Numbers on the Number Line: In the previous section, we have learn about the decimal expansions of real numbers. This help us to represent it on the number line. In this section, we will learn how to visualise the position of real numbers in decimal form.
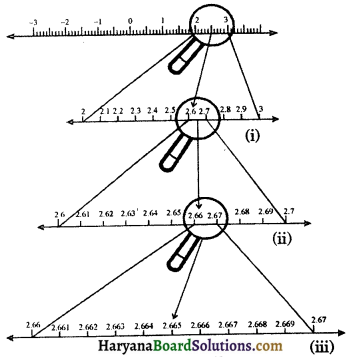
Suppose we want to visualise the representation of 2.665 on the number line. We observe that 2.665 is located between 2 and 3. So let us look closely at the portion of the number line 2 and 3. We divide it into 10 equal parts and mark each point of division as shown in figure 1.10. Then the first mark to the right of 2 will represent 2.1, the second 2.2 and so on. To see this clearly we may take a magnifying glass and look at the portion between 2 and 3. Now, we observe that 2.665 lies between 2.6 and 2.7. To get more accurate visualization of the representation, we divide this portion of real line into 10 equal parts. The first mark will represent 2.61, the second 2.62 and so on.
Again, 2.665 lies between 2.66 and 2.67, so let us focus on this portion of the number line. We magnify the portion of line between 2.66 and 2.67 and divide it into 10 equal parts. The first mark represents 2.661, the next one represents 2.662 and so on. So 2.665 is the 5th mark in these subdivisions. We call this process of visualisation of representation of numbers on the number line through a magnifying glass, as the process of successive magnification.
1. Operations on Real Numbers: In the previous classes, we have learnt about that rational numbers satisfied the associative, commutative and distributive properties for addition and multiplication. The sum, difference, product and quotient of two rational numbers will be a rational number. Irrational numbers also satisfied the commutative, associative and distributive properties for addition and multiplication. However the sum, difference, quotients and products of irrational numbers are not always irrational.
The facts related to operations on real numbers are given below:
- The sum or difference of a rational number and an irrational number is an irrational number.
- The product or quotient of a non-zero rational number with an irrational number is an irrational number.
- If we, add, subtract, multiply or divide two irrational numbers, the result may be a rational or irrational number.
2. Existence of Square Root of a given Positive Real Number:
To find \(\sqrt{x}\) geometrically, where x is any positive real number.
Construction: Draw a line AB of length x units extend AB to point C such that BC = 1 unit. Find the midpoint of AC and marked that point O. Draw a semicircle with centre O and radius OA. Draw a line perpendicular to AC passing through B and intersecting the semicircle at D, then BD = \(\sqrt{x}\).
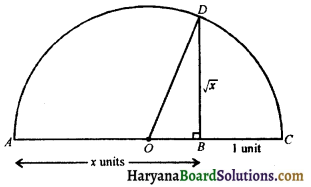
Proof:
We have AB = x units, BC = 1 unit
⇒ AC = x + 1 units
OA = OD = OC = \(\frac{x+1}{2}\),
(∵ O is the mid-point of AC)
Now,
OB = x – \(\frac{(x+1)}{2}\)
⇒ OB = \(\frac{2 x-x-1}{2}=\frac{x-1}{2}\)
In right ΔOBD,
OD2 = OB2 + BD2,
(By Pythagoras theorem)
⇒ BD2 = OD2 – OB2
⇒ BD2 = \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)
⇒ BD2 = \(\frac{x^2+1+2 x}{4}-\frac{x^2+1-2 x}{4}\)
⇒ BD2 = \(\frac{1}{4}\)[x2 + 1 + 2x – x2 – 1 + 2x]
⇒ BD2 = \(\frac{1}{4}\) × 4x
⇒ BD2 = x
⇒ BD = \(\sqrt{x}\)
3. Rationalisation of Irrational Number:
The process of multiplying a given irrational number by its rationalising factor to get a rational number as product is called rationalisation of the given irrational number.
When the product of two irrational numbers is a rational number, each is called the Rationalising Factors (R.F.) of the other.
For Example:
(i) Since 5\(\sqrt{2}\) × 3\(\sqrt{2}\) = 15 × 2 = 30; which is a rational number. Therefore, 5\(\sqrt{2}\) and 3\(\sqrt{2}\) are rationalising factors of each other.
(ii) (\(\sqrt{3}\) + \(\sqrt{2}\)) (\(\sqrt{3}\) – \(\sqrt{2}\)) = (\(\sqrt{3}\))2 – (\(\sqrt{2}\))2
= 3 – 2 = 1
(\(\sqrt{3}\) + \(\sqrt{2}\)) and (\(\sqrt{3}\) – \(\sqrt{2}\)) are the
rationalising factors of each other.
(iii) (3 + \(\sqrt{5}\)) (3 – \(\sqrt{5}\)) = 32 – (\(\sqrt{5}\))2
= 9 – 5 = 4
(3 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) are rationalising factors of each other.
In the same way:
(i) R.F. of \(\sqrt{5}\) – 2 is \(\sqrt{5}\) + 2.
(ii) R.F. of 4 + 3\(\sqrt{5}\) is 4 – 3\(\sqrt{5}\).
![]()
Laws of Exponents for Real Numbers:
Let a be real number and m, n be rational numbers, then we have
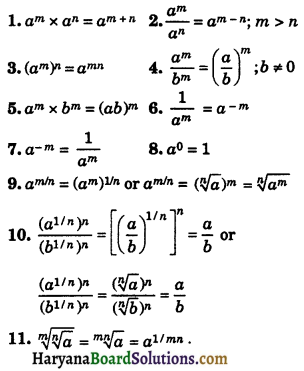
Note: Here a is called base and m, n are called exponents.