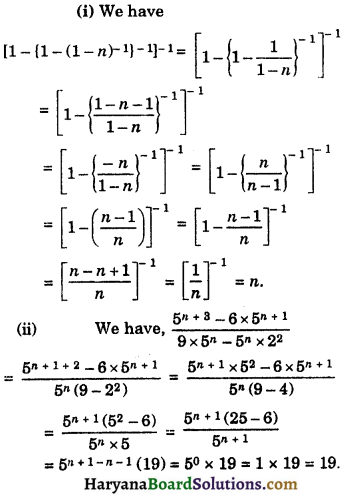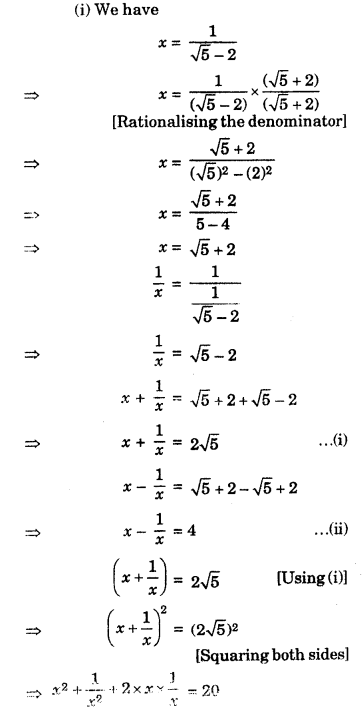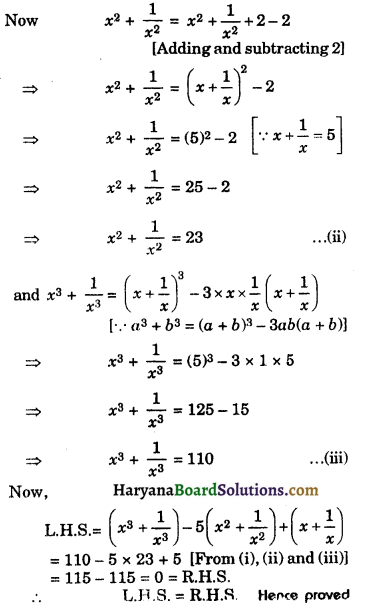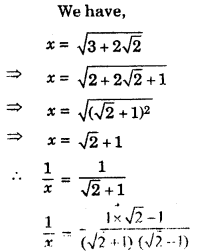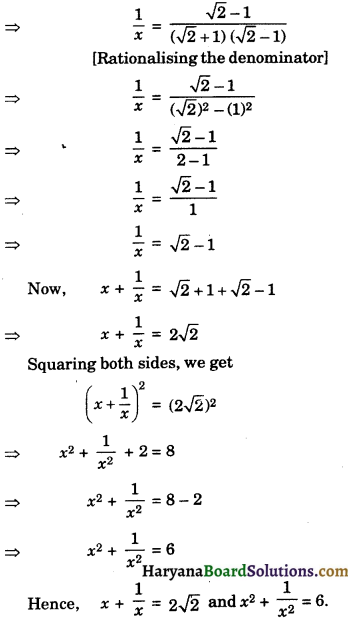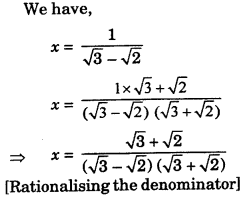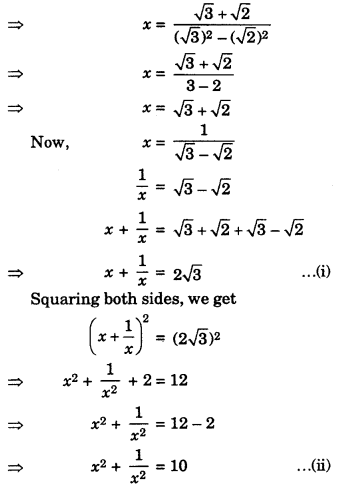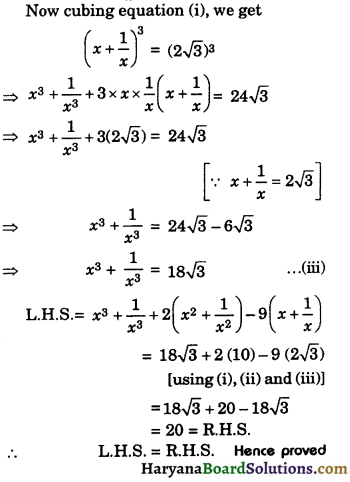Class 9

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 2 Polynomials Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 2 Polynomials

Very Short Answer Type Questions

Question 1.
Write the coefficients of x³ in each of the following :
(i) 4x³ – 3x + 9
(i) 14 – 5x³ + 7x + 2x²
(iii) \(\frac {3}{4}\)x³ + 7x – 9
(iv) 5x² + \(\sqrt{3}\)x + 1
(v) \(\sqrt{5}\)x³ + x² + 7
(vi) x – x³
Solution :
(i) The coefficient of x³ in 4x³ – 3x + 9 is 4.
(ii) The coefficient of x³ in 14 – 5x³ + 7x + 2x² is – 5.
(iii) The coefficient of x³ in \(\frac {3}{4}\)x³ + 7x – 9 is \(\frac {3}{4}\).
(iv) The coefficient of x³ in 5x² + \(\sqrt{3}\)x + 1 is 0.
(v) The coefficient of x³ in \(\sqrt{5}\)x³ + x² + 7 is
(vi) The coefficient of x3 in 1 – 13 is – 1.

Question 2.
Write a monomial of degree 30, a binomial of degree 50 and a trinomial of degree 60.
Solution:
Monomial of degree 30 = x³⁰
Binomial of degree 50 = 3x⁵⁰ + 5
Trinomial of degree 60 = 5x⁶⁰ + x + 7.

Question 3.
Classify the following as linear, quadratic, cubic and biquadratic polynomials:
(i) 3x² + 4x + 7
(ii) x² – x³
(iii) 1 + t
(iv) 5x⁴ + 2x³ + x + 5
(v) y³ + 3y² – 5
(vi) y² + 7y
(vii) t²
Solution:
(i) Degree of the given polynomial is 2. So it is the quadratic polynomial.
(ii) Degree of the given polynomial is 3. So, it is the cubic polynomial.
(iii) Degree of the given polynomial is 1. So, it is a linear polynomial.
(iv) Degree of the given polynomial is 4. So, it is a biquadratic polynomial.
(v) Degree of the given polynomial is 3. So, it is a cubic polynomial.
(vi) Degree of the given polynomial is 2. So, it is a quadratic polynomial.
(vii) Degree of the given polynomial is 2. So, it is a quadratic polynomial.

Question 4.
Find the values of the polynomial x³ – 2x² + 3x + 5 at:
(i) x = 0
(ii) x = 1
(iii) x = – 2.
Solution:
Let p(x) = x³ – 2x² + 3x + 5
(i) At x = 0, the value of the polynomial p(x) is given by
p(0) = (0)³ – 2 × (0)² + 3 × 0 + 5
= 0 – 0 + 0 + 5 = 5
Hence, p(0) = 5.

(ii) At x = 1, the value of the polynomial p(x) is given by
p(1) = (1)³ – 2 × (1)² + 3 × 1 + 5
= 1 – 2 + 3 + 5 = 7
Hence, p(1) = 7.

(iii) At x = – 2, the value of the polynomial p(x) is given by
p(-2) = (-2)³ – 2 × (-2)² + 3 × (-2) + 5
= – 8 – 8 – 6 + 5
= – 22 + 5 = – 17
Hence, p(-2) = – 17.

Question 5.
Find the remainder when x⁴ – x³ – 2x² + 4x – 10 is divided by x + 2.
Solution :
Let
p(x) = x⁴ – x³ – 2x² + 4x – 10
We know that when p(x) is divided by (x + 2), the remainder is p(-2).
(By Remainder Theorem)
So, p(-2) = (-2)⁴ – (-2)³ – 2 × (2)² + 4 × (-2) – 10
= 16 + 8 – 8 – 8 – 10
= 16 – 18 = – 2
Hence, the required remainder = – 2.

Question 6.
Find the remainder when x³ – 2x² – 11x + 15 is divided by x + 3.
Solution:
Let
p(x) = x³ – 2x² – 11x + 15
We know that when p(x) is divided by (x + 3) the remainder is p(-3).
[By Remainder Theorem]
So, p(-3) = (-3)³ – 2 × (- 3)² – 11 × (-3) + 15
= – 27 – 18 + 33 + 15
= 48 – 45 = 3.
Hence, the required remainder = 3.

Question 7.
Determine the value of k, such that (x + 3) is a factor of the polynomial f(x) = 2x³ + 11x² + kx + 6.
Solution :
We have,
f(x) = 2x³ + 11x² + kx + 6
If (x + 3) is a factor of f(x), then by factor theorem, the remainder f(-3) should be zero.
⇒ f(-3) = 0
⇒ 2x(-3)³ + 11 × (-3)² + k × (-3) + 6 = 0
⇒ – 54 + 99 – 3k + 6= 0
⇒ – 3k + 105 – 54 = 0
⇒ – 3k + 51 = 0
⇒ -3k = – 51
⇒ k = \(\frac {-51}{-3}\) = 17
Hence, k = 17.

Question 8.
Find the value of a, if x – a is a factor of x³ – ax² + 2x + a – 1. [NCEAT Exemplar Problems]
Solution :
Let p(x) = x³ – ax² + 2x + a – 1
If (x – a) is a factor of p(x), then by factor theorem, the remainder p(a) should be zero.
⇒ p(a) = 0
⇒ (a)³ – a × (a)² + 2 × a + a – 1 = 0
⇒ a³ – a³ + 2a + a – 1 = 0
⇒ 3a – 1 = 0
⇒ 3a = 1
⇒ a = \(\frac {1}{3}\)

Question 9.
If (x – 2) is a factor of the polyomial x⁵ – 3x⁴ – kx³ + 3kx² + 2kx + 4, find the value of k.
Solution :
Let p(x) = x⁵ – 3x⁴ – kx³ + 3kx² + 2kx + 4
If (x – 2) is a factor of p(x), then by factor theorem, the remainder p(2) should be zero
⇒ p(2) = 0
⇒ (2)⁵ – 3 × (2)⁴ – k × (2)³ + 3k × (2)² + 2k × 2 + 4 = 0
⇒ 32 – 48 – 8k + 12k + 4k + 4 = 0
⇒ 36 – 48 – 8k + 16k = 0
⇒ – 12 + 8k = 0
⇒ 8k = 12
⇒ k = \(\frac{12}{8}=\frac{3}{2}\)
Hence, k = \(\frac {3}{2}\)

Question 10.
Find the value of x³ + y³ – 12xy + 64, when x + y = – 4. [NCERT Exemplar Problems]
Solution :
We have,
x + y = – 4
⇒ x + y + 4 = 0
We know that, if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Here,
x + y + 4 = 0
⇒ x³ + y³ + (4)³ = 3 × x × y × 4
⇒ x³ + y³ + 64 = 12xy
⇒ x³ + y³ – 12xy + 64 = 0.
Hence, x³ + y³ – 12xy + 64 = 0.

Question 11.
Find the value of x³ – 8y³ – 36xy – 216, when x = 2y + 6. [NCERT Exemplar Problems] Solution:
We have x = 2y + 6
⇒ x – 2y – 6 = 0
We known that, it x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Here x – 2y – 6 = 0
x³ + (-2y)³ + (-6)³ = 3 × x × (-2y) × (-6)
x³ – 8y³ – 216 = 36xy
x³ – 8y³ – 36xy – 216 = 0
Hence, x³ – 8y³ – 36xy – 216 = 0.

Question 12.
If ab + bc + ca = 25 and a + b + c = 9, find a² + b² + c².
Solution :
We have, a + b + c = 9
⇒ (a + b + c)² = (9)²
⇒ a² + b² + c² + 2ab + 2bc + 2ca = 81
⇒ a² + b² + c² + 2(ab + bc + ca) = 81
⇒ a² + b² + c² + 2 × 26 = 81 [∵ ab + bc + ca = 26]
⇒ a² + b² + c² + 52 = 81
⇒ a² + b² + c² = 81 – 52
⇒ a² + b² + c² = 29.
Hence, a² + b² + c² = 29.

Question 13.
If a² + b² + c = 64 and ab + bc + ca = 18, find a + b + c.
Solution :
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
⇒ (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
⇒ (a + b + c)² = 64 + 2 × 18 [∵ a² + b² + c² = 64 and ab + bc + ca = 18]
⇒ (a + b + c)² = 64 + 36 = 100
⇒ (a + b + c)² = (10)²
⇒ a + b + c = 10
Hence, a + b + c = 10.

Question 14.
If x – y = 5 and xy = 7, find the value of x³ – y³
Solution :
We have, xy = 7
and x – y = 5
⇒ (x – y)³ = (5)³
(Cubing on both sides)
⇒ x³ – y³ – 3xy(x – y) = 125 [Using the identity,
(x – y)³ = x³ – y³ – 3xy(x – y)]
⇒ x³ – y³ – 3 × 7(5) = 125 [∵ xy = 7, x – y = 5]
⇒ x³ – y³ – 105 = 125
⇒ x³ – y³ = 125 + 105
⇒ x³ – y³ = 230.
Hence, x³ – y³ = 230.

Question 15.
Factorise the following quadratic polynomials by splitting the middle term :
(i) x² – 18x + 77
(ii) x² – 25x + 144
Solution :
(i) x² – 18x + 77 = x² – (11 + 7)x + 77
= x² – 11x – 7x + 77
= (x² – 11x) – (7x – 77)
= x(x – 11) – 7(x – 11)
= (x – 11) (x – 7).
Hence,
x² – 18x + 77 = (x – 11) (x – 7)

(ii) x² – 25x + 144 = x² – (16 + 9)x + 144
= x² – 16x – 9x + 144
= (x² – 16x) – (9x – 144)
= x(x – 16) – 9 (x – 16)
= (x – 16) (x – 9).
Hence,
x² – 25x + 144 = (x – 16) (x – 9).

Question 16.
Factorize \(\frac {1}{3}\)x² + 5x + 12
Solution :
(i) Ist method : \(\frac {1}{3}\)x² + 5x + 12 = \(\frac {1}{3}\)(x² + 15x + 36)
= \(\frac {1}{3}\)(x² + (12 + 3)x + 36]
= \(\frac {1}{3}\)(x² + 12x + 3x + 36]
= \(\frac {1}{3}\)(x² + 12x) + (3x + 36)]
= \(\frac {1}{3}\)[x(x + 12) + 3(x + 12)]
= \(\frac {1}{3}\)(x + 12) (x + 3)
= (x + 12) (\(\frac {x}{3}\) + 1)
Hence,
\(\frac {1}{3}\)x² + 5x + 12 = (x + 12) (\(\frac {x}{3}\) + 1)

Short Answer Type Questions

Question 1.
Verify, whether the following are zeroes of the polynomial indicated against them :
(i) p(x) = 4x² + 3x – 7; x = 1, – 2
(ii) p(y) = y² + y – 6; y = 2, – 3
Solution:
(i) We have,
p(x) = 4x² + 3x – 7
The value of the polynomial p(x) at x = 1, is given by
p(1) = 4 × (1)² + 3 × 1 – 7
= 4 + 3 – 7 = 0.
The value of the polynomial p(x) at x = – 2, is given by
p(-2) = 4 × (-2)² + 3 × (-2) – 7
= 16 – 6 – 7 = 3 ≠ 0.
Hence, 1 is zero of the polynomial p(x) but – 2 is not

(ii) We have, p(y) = y² + y – 6
The value of the polynomial p(y) at y = 2, is given by
p(2) = (2)² + 2 – 6
= 4 + 2 – 6 = 0.
The value of the polynomial p(y) at y = – 3, is given by
p(-3) = (-3)² – 3 – 6
= 9 – 3 – 6 = 0.
Hence, 2, – 3 are the zeroes of the polynomial p(y).

Question 2.
Find the zero of the polynomial in each of the following cases:
(i) p(x) = 2x – 3
(ii) p(y) = ay – b, a ≠ 0
(iii) q(x) = 4πx + 3
(iv) g(t) = (t + 1)² – (t – 1)².
Solution :
(i) We have,
p(x) = 2x – 3
For zero of the polynomial, p(x) = 0
⇒ 0 = 2x – 3
⇒ 2x = 3
⇒ x = \(\frac {3}{2}\)
Hence, \(\frac {3}{2}\) is the zero of the polynomial p(x).

(ii) We have, p(y) = ay – b, a ≠ 0
For zero of the polynomial, p(y) = 0
⇒ 0 = ay – b
⇒ ay = b
⇒ y = \(\frac {b}{a}\)
Hence, \(\frac {b}{a}\) is the zero of the polynomial p(y).

(iii) We have, q(x) = 4πx + 3
For zero of the polynomial, q(x) = 0
⇒ 0 = 4πx + 3
⇒ 4πx = – 3
⇒ x = \(\frac {-3}{4π}\)
Hence, \(\frac {-3}{4π}\) is the zero of the polynomial q(x).

(iv) We have, g(t) = (t + 1)² – (t – 1)²
⇒ g(t) = t² + 1 + 2t – t² – 1 + 2t
⇒ q(t) = 4t
For zero of the polynomial,
q(t) = 0
⇒ 0 = 4t
⇒ t = \(\frac {0}{4}\) = 0
Hence, 0 is the zero of the polynomial q(t).

Question 3.
Divide the polynomial 2x² + 7x³ + 4x² – 7x – 9 by x + 1.
Solution :
By Long Division, we have

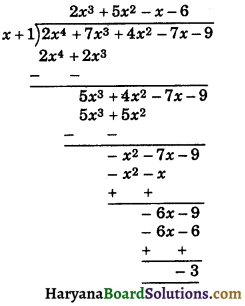
Hence, remainder = – 3.

Question 4.
Divide the polynomial x⁴ + 1 by – 1.
[NCERT Exemplar Problems]
Solution :
By long division, we have

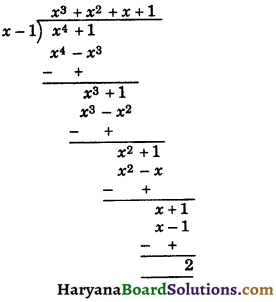
Hence, remainder = 2.

Question 5.
If p(x) = 4x³ – 12x² + 14x – 3, find the remainder when p(x) is divided by 2x – 1. Also, verify the result by actual division.
[NCERT Exemplar Problems]
Solution :
We have,
p(x) = 4x³ – 12x² + 14x – 3
We know that when p(x) is divided by (2x – 1), the remainder is p(\(\frac {1}{2}\))
[By Remainder Theorem]
So,

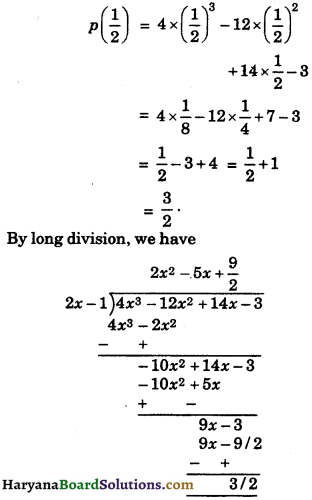
Remainder by actual division method is also \(\frac {3}{2}\)
Hence, the remainder in both cases is same.

Question 6.
When 4x³ + 18x² + 14x + k is divided by 2x + 5, the remainder is 0. Find the value of k.
Solution :
Let p(x) = 4x³ + 18x² + 14x + k is divided by (2x + 5), the remainder is 0.
By Remainder Theorem, remainder = p(\(\frac {-5}{2}\))

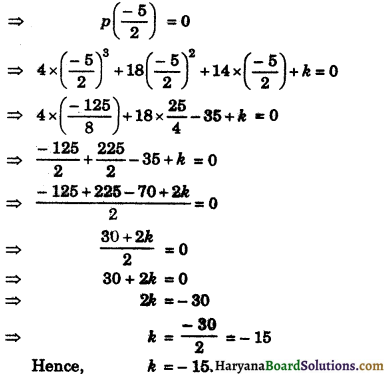
Question 7.
If the polynomials ax³ + 4z² + 3z – 4 and z³ – 4z + a leave the same remainder when divided by z – 3, find the value of a.
Solution :
Let p(x) = az³ + 4z² + 3z – 4
When p(z) is divided by (z – 3), the remainder is p(3)
∴ p(3) = a × (3)³ + 4 × (3)² + 3 × 3 – 4
= 27a + 36 + 9 – 4
= 27a + 41
Let q(z) = z³ – 4z + a
When q(z) is divided by (z – 3), the remainder is q(3).
∴ q(3) = (3)³ – 4 × 3 + a
= 27 – 12 + a
= 15 + a
According to question, the remainders in both cases are equal.
⇒ p(3) = q(3)
⇒ 27a + 41 = 15 + a
⇒ 27 – a = 15 – 41
⇒ 26a = – 26
⇒ a = – \(\frac {26}{26}\)
⇒ a = – 1
Hence a = – 1

Question 8.
If the polynomial f(x) = x³ + px² + qx – 10 is divided by (x – 3) and (x – 2) leaves the remainders 8 and – 12 respectively. Find the values of p and q.
Solution :
We have,
f(x) = x³ + px² + qx – 10
When the given polynomial f(x) is divided by (x – 3), the remainder is 8.
By Remainder Theorem, the remainder = f(3)
⇒ f(3) = 8
⇒ (3)³ + p × (3)² + q × 3 – 10 = 8
⇒ 27 + 9p + 3q – 10 = 8
⇒ 17 + 9p + 3q = 8
⇒ 9p + 3q = 8 – 17
⇒ 9p + 3q = – 9
⇒ 3p + q = – 3 …(i)
And when the given polynomial f(x) is divided by (x – 2), the remainder is – 12.
By Remainder Theorem, the remainder = f(2)
⇒ f(2) = – 12
⇒ (2)³ + p × (2)² + q × 2 – 10 = – 12
⇒ 8 + 4p + 2q – 10 = – 12
⇒ 4p + 2q – 2 = – 12
⇒ 4p + 2q = – 12 + 2
⇒ 4p + 2q = – 10
⇒ 2p + q = – 5 ……..(ii)
Subtracting the equation (ii) from (i), we get

Putting the value of p in equation (ii), we get
2 × 2 + q = – 5
⇒ 4 + 9 = – 5
⇒ q = – 5 – 4
⇒ q = – 9
Hence, P = 2 and q = – 9.

Question 9.
Let R₁ and R₂ be the remainders when the polynomials kx³ + 3x² – 14x + 5 and x³ – 5x² + kx + 12 are divided by (x + 3) and (x – 2) respectively. If R₁ – R₂ = 16, then find the value of k.
Solution :
Let p(x) = kx³ + 3x² – 14x + 5
When p(x) is divided by (x + 3), the remainder (R₁) is p(-3).
[By Remainder Theorem]
R₁ = p(-3)
R₁ = k(-3)³ + 3(-3)² – 14 × (- 3) + 5
R₁ = – 27k + 27 + 42 + 5
R₁ = – 27k + 74
And let q(x) = x³ – 5x² + kx + 12
When q(x) is divided by (x – 2), the remainder (R₂) is q(2).
(By Remainder Theorem)
⇒ R₂ = q(2)
⇒ R₂ = (2)³ – 5 × (2)² + k × 2 + 12
⇒ R₂ = 8 – 20 + 2k +12
⇒ R₂ = 20 – 20 + 2k
⇒ R₂ = 2k
According to question,
R₁ – R₂ = 16
⇒ – 27k + 74 – 2k = 16
⇒ – 29k = 16 – 74
⇒ – 29k = – 58
⇒ k = \(\frac {-58}{-29}\)
Hence, k = 2.

Question 10.
If both (x – 2) and (x – \(\frac {1}{2}\)) are factors of px² + 5x + r, then show that p = r. (NCERT Exemplar Problems)
Solution :
Let f(x) = px² + 5x + r
If (x – 2) is a factor of f(x), then by factor theorem, the remainder f(2) should be zero.
⇒ f(2) = 0
⇒ p × (2)² + 5 × 2 + r = 0
⇒ 4p + 10 + r = 0 ……(i)
If (x – \(\frac {1}{2}\)) is a factor of f(x), then by factor theorem, the remainder f(\(\frac {1}{2}\)) should be zero.
⇒ f(\(\frac {1}{2}\)) = 0
⇒ p × (\(\frac {1}{2}\))² + 5 × \(\frac {1}{2}\) + r = 0
⇒ \(\frac{p}{4}+\frac{5}{2}\) + r =0
⇒ p + 10 + 4r = 0 ……….(ii)
From equations (i) and (ii), we get
4p + 10 + r = P + 10 + 4r
⇒ 4p + r = p + 4r
⇒ 4p – p = 4r
⇒ 3p = 3r
⇒ p = \(\frac {3r}{3}\) = r
Hence, P = r. Hence Proved.

Question 11.
What must be subtracted from 3x³ – 11x² + 11x – 10 to obtain a polynomial which is exactly divisible by (x – 3).
Solution :
Let f(x) = 3x³ – 11x² + 11x – 10
Let k be subtracted from f(x), so that it may be exactly divisible by (x – 3).
∴ p(x) = 3x³ – 11x² + 11x – 10 – k
If p(x) is exactly divisible by (x – 3), then by factor theorem, the remainder p(3) should be zero.
⇒ p(3) = 0
⇒ 3 × (3)³ – 11 × (3)² + 11 × 3 – 10 – k = 0
⇒ 81 – 99 +33 – 10 – k = 0
⇒ 114 – 109 – k = 0
⇒ 5 – k = 0
⇒ k = 5
Hence, 5 must be subtracted from the given polynomial.

Question 12.
If x + \(\frac {1}{x}\) = 5, find the values of each of the following:
(i) x² + \(\frac{1}{x^2}\)
(ii) x⁴ + \(\frac{1}{x^4}\)
Solution :

Question 13.
If x² + \(\frac{1}{x^2}\) = 34, find the values of each of the following :
(i) x + \(\frac {1}{x}\)
(ii) x³ + \(\frac{1}{x^3}\)
Solution :
(i) We have,
x² + \(\frac{1}{x^2}\) = 34
⇒ x² + \(\frac{1}{x^2}\) + 2 = 34 + 2 [Adding 2 on both sides]
⇒ x² + \(\frac{1}{x^2}\) + 2 × x × \(\frac {1}{x}\) = 36
⇒ (x + \(\frac {1}{x}\))² = (6)²
[Using the identity, x² + y² + 2xy = (x+y)²]
⇒ x + \(\frac {1}{x}\) = ± 6
[Taking square root on both sides]
Hence, x + \(\frac {1}{x}\) = ± 6.

(ii) From (i), we have

Question 14.
If x + y = 7 and x² + y² = 25, find the value of x³ + y³.
Solution :
We have,
x + y = 7
⇒ (x + y)² = (7)²
[Squaring on both sides]
⇒ x² + y² + 2xy = 49
⇒ 25 + 2xy = 49, [∵ x² + y² = 25]
⇒ 2xy = 49 – 25
⇒ 2xy = 24
⇒ xy = \(\frac {24}{2}\) = 12.
Now, we have(x + y) = 7
⇒ (x + y)³ = (7)³
(Cubing on both sides)
⇒ x³ + y³ + 3xy(x + y) = 343
[Using the identity, (x + y)³ = x³ + y³ + 3xy(x + y)]
⇒ x³ + y³ + 3 × 12(7) = 343,
[∵ x + y = 7 and xy = 12]
⇒ x³ + y³ + 252 = 343
⇒ x³ + y³ = 343 – 252
⇒ x³ + y³ = 91.
Hence, x³ + y³ = 91.

Question 15.
If a² + b² + c² = 14 and a + b + c = 6, find ab + bc + ca.
Solution :
We have,
a + b + c = 6
⇒ (a + b + c)² = (6)²
(Squaring on both sides)
⇒ a² + b² + c² + 2ab + 2bc + 2ca
⇒ 14 + 2(ab + bc + ca) = 36,
[∵ a² + b² + c² = 14]
⇒ 2(ab + bc + ca) = 36 – 14
⇒ 2(ab + bc + ca) = 22
⇒ ab + bc + ca = \(\frac {22}{2}\)
⇒ ab + bc + ca = 11
Hence, ab + bc + ca = 11.

Question 16.
Evaluate each of the following by using suitable identity :
(i) \(\frac{0.94 \times 0.94 \times 0.94+0.06 \times 0.06 \times 0.06}{0.94 \times 0.94-0.94 \times 0.06+0.06 \times 0.06}\)
(ii) \(\frac{2.05 \times 2.05 \times 2.05-0.05 \times 0.05 \times 0.05}{2.05 \times 2.05+2.05 \times 0.05+0.05 \times 0.05}\)
(iii) 105³ + 95³
Solution :
We use the identity in each of the following [(i) to (iv)] :
(i) x³ + y³ = (x + y) (x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)

Question 17.
If 3x + 4y = 18 and xy = 6, then find the value of 27x³ + 64y³.
Solution :
We have,
3x + 4y = 18
⇒ (3x + 4y)³ = (18)³ (Cubing on both sides)
⇒ 27x³ + 64y³ + 3 × 3x × 4y(3x + 4y) = 5832
[Using the identity, (x + y)³ = x³ + y³ + 3xy(x + y)] +
⇒ 27x³ + 64y³ + 36xy(18) = 5832, (∵ 3x + 4y = 18)
⇒ 27x³ + 64y³ + 36 × 6 × 18 = 5832
⇒ (∵ xy = 6)
⇒ 27x³ + 64y³ + 3888 = 5832
⇒ 27x³ + 64y³ = 5832 – 3888
⇒ 27x³ + 64y³ = 1944.
Hence, 27x³ + 64y³ = 1944.

Question 18.
If a + b + c = 3, abc = – 12 and ab + bc + ca = – 4, find the value of a³ + b³ + c³.
Solution :
We have, a + b + c = 3 …(i)
⇒ (a + b + c)² = (3)²
(Squaring on both sides)
⇒ a² + b² + c² + 2ab + 2bc + 2ca = 9
⇒ a² + b² + c² + 2(ab + bc + ca) = 9
⇒ a² + b² + c² + 2 × (- 4) = 9
[∵ ab + bc + ca = – 4]
⇒ a² + b² + c² – 8 = 9
⇒ a² + b² + c² = 9 + 8 = 17 ………(ii)
We know that,
a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)
⇒ a³ + b³ + c³ – 3 × (- 12) = 3 × [17 – (ab + bc + ca)],
[∵ From (ii), a² + b² + c² = 17, abc = – 12 and a + b + c = 3 (given)]
⇒ a³ + b³ + c³ + 36 = 3 × [17 – (-4)]
⇒ [∵ ab + bc + ca = – 4]
⇒ a³ + b³ + c³ + 36 = 3 x 21
⇒ a³ + b³ + c³ + 36 = 63
⇒ a³ + b³ + c³ = 63 – 36
⇒ a³ + b³ + c³ = 27.
Hence, a³ + b³ + c³ = 27.

Question 19.
Factorise : x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
Solution :
= x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
= x² + \(\frac{1}{x^2}\) + 2 + 1 – 2x – \(\frac {2}{x}\)
= (x + \(\frac {1}{x}\))² + 1 – 2(x + \(\frac {1}{x}\))
[Using the identity, x² + y² + 2xy = (x + y)²
= a² + 1 – 2a, where a = x + \(\frac {1}{x}\)
= (a – 1)²
= (a – 1) (a – 1)
= (x + \(\frac {1}{x}\) – 1) (x + \(\frac {1}{x}\) – 1)
Hence, x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
= (x + \(\frac {1}{x}\) – 1) (x + \(\frac {1}{x}\) – 1)

Question 20.
If a + b + c = 3x, then prove that: (x – a)³ + (x – b)³ + (x – c)³ – 3(x – a) (x – b) (x – c) = 0.
Solution :
We have,
a + b + c = 3x
⇒ a + b + c = x + x + x
⇒ (x – a) + (x – b) + (x – c) = 0
We know that, if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Since,(x – a) + (x – b) + (x – c) = 0
Therefore, (x – a)³ + (x – b)³ + (x – c)³
= 3(x – a)(x – b)(x – c)
⇒ (x – a)³ + (x – b)³ + (x – c)³ – 3(x – a)(x – b)(x – c) = 0.
Hence proved

Question 21.
Factorise : x¹² – y¹²
Solution :
x¹² – y¹² = (x⁶)² – (y⁶)²
= (x⁶ + y⁶) (x⁶ – y⁶)
[Using the identity, x² – y² = (x + y)(x – y)]
= [(x²)³ + (y²)³] [(x³)² + (y³)²]
= (x² + y²) [(x²)² – x²y² + (y²)²] (x³ + y³) (x³ – y³)
[Using the identity,
x³ + y³ = (x + y) (x² – xy + y²)]
= (x² + y²) (x⁴ – x²y² + y⁴)(x + y) (x² – xy + y²) (x – y)(x² + xy + y²)
= (x + y) (x – y) (x² + y²) (x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴)
Hence, x¹² – y¹² = (x + y) (x – y) (x² + y²)
(x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴).

Question 22.
If x = y = 333 and z = 334, find the value of x³ + y³ + z³ – 3xyz, without actually calcuting cubes.
Solution :
We know that,
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
= \(\frac {1}{2}\) (x + y + z) [2(x² + y² + z² – xy – yz – zx)]
= \(\frac {1}{2}\) (x + y + z) (2x² + 2y² + 2z² – 2xy – 2yz – 2zx)
= \(\frac {1}{2}\) (x + y + z) (x² + y² – 2xy + y² + z² – 2yz + z² + x² – 2zx]
= \(\frac {1}{2}\) (x + y + z) [(x – y)² + (y – z)² + (z – x)²]
= \(\frac {1}{2}\) (333 + 333 + 334) [(333 – 333)² + (333 – 334)² + (334 – 333)²]
[it is given that x = 333, y = 333 and z = 334)
= \(\frac {1}{2}\) (1000) (0 + 1 + 1)
= \(\frac {1}{2}\) (1000) × 2 = 1000
Hence,
x³ + y³ + z³ – 3xyz = 1000.

Question 23.
Find the remainder when 6x³ + 12x² – 9x – 3 is divided by x + \(\frac {2}{3}\)
Solution :
Let p(x) = 6x³ + 12x² – 9x – 3
We know that when p(x) is divided by (x + \(\frac {2}{3}\)) the remainder is p(\(\frac {-2}{3}\))
[By Remainder Theorem]

Question 24.
Find p(0),p(-1) and p(-2) for each of the following polynomials :
(i) p(x) = 2x³ – 7x + 9
(ii) p(y) = 4y² + 3y – 2
Solution :
(i) We have,
p(x) = 2x³ – 7x + 9
p(0) = 2 × (0)³ – 7 × 0 + 9
= 0 – 0 + 9 = 9.
p(-1) = 2 × (-1)³ – 7 × (-1) + 9
= 2 × (-1) + 7 + 9
= – 2 + 7 + 9
= 14.
and p(-2) = 2 × (-2)³ – 7 × (-2) + 9
= – 16 + 14 + 9 = 7
Hence, p(0) = 9, p(-1)= 14 and p(-2) = 7.

(ii) We have,
p(y) = 4y² + 3y – 2
p(0) = 4 × (0)² + 3 × 0 – 2
= 0 + 0 – 2 = – 2.
p(-1) = 4 × (-1)² + 3 × (-1) – 2
= 4 – 3 – 2 = – 1.
and p(-2) = 4 × (-2)² + 3 × (-2) – 2
= 16 – 6 – 2
= 16 – 8 = 8.
Hence, p(0) = – 2, p(-1) = – 1
and p(-2) = 8.

Long Answer Type Questions

Question 1.
If the polynomial p(x) = x⁴ – 3x³ + x² + ax + b is divided by (x – 1) and (x + 1) leaves the remainders 13 and 9 respectively, find the values of a and b. Hence, find the remainder when p(x) is divided by (x – 2).
Solution :
We have,
p(x) = x⁴ – 3x³ + x² + ax + b
When the given polynomial p(x) is divided by (x – 1), the remainder is 13.
By Remainder Theorem, the remainder = p(1)
⇒ P(1) = 13
⇒ (1)⁴ – 3 × (1)³ + (1)² + a × 1 + b = 13
⇒ 1 – 3 + 1 + a + b = 13
⇒ – 1 + a + b = 13
⇒ a + b = 13 + 1
⇒ a + b = 14 …(i)
And when the given polynomial p(x) is divided by (x + 1), the remainder is 9.
By Remainder Theorem, the remainder = P(-1)
⇒ p(-1) = 9
⇒ (-1)⁴ – 3 × (-1)³ + (-1)² + a × (-1) + b = 9
⇒ 1 + 3 + 1 – a + b = 9
⇒ 5 – a + b = 9
⇒ – a + b = 9 – 5
⇒ – a + b = 4 …(ii)
Adding the equations (i) and (ii), we get
a + b = 14 …(i)
– a + b = 4 …(ii)
2b = 18
⇒ b = \(\frac {18}{2}\) = 9
Putting the value of b in equation (i), we get
a + 9 = 14
⇒ a = 14 – 9 = 5
Now, putting the values of a and b in the given polynomial p(x), we get
p(x) = x⁴ – 3x³ + x² + 5x + 9
Now, p(x) is divided by (x – 2).
By Remainder Theorem,
the remainder = p(2).
So, p(2) = (2)⁴ – 3 × (2)³ + (2)² + 5 × 2 + 9
= 16 – 24 + 4 + 10 + 9
= 39 – 24
= 15.
Hence, a = 5, b = 9 and p(2) = 15.

Question 2.
Find the values of p and q so that (x – 2) and (x + 3) are the factors of the polynomial
f(x) = 5x³ + 6x² – px + q.
Solution :
We have,
f(x) = 5x³ + 6x² – px + q
If (x – 2) is a factor of f(x), then by factor theorem, the remainder f(2) should be zero
⇒ f(2) = 0
⇒ 5 × (2)³ + 6 × (2)³ – p × 2 + q = 0
⇒ 40 + 24 – 2p + q = 0
⇒ 64 – 2p + q = 0
⇒ – 2p + q = – 64 …(i)
If (x + 3) is a factor of f(x), then by factor theorem, the remainder f(-3) should be zero.
⇒ f(-3) = 0
⇒ 5 × (-3)³ + 6 × (-3) -p × (-3) + q = 0
⇒ – 135 + 54 + 3p + q = 0
⇒ – 81 + 3p + q = 0
⇒ 3p + q = 81 …(ii)
Subtracting the equation (ii) from (i), we get

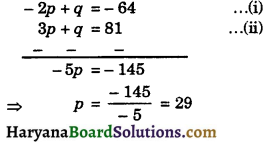
Putting the value of p in equation (ii), we get
3 × 29 + 9 = 81
⇒ 87 + q = 81
⇒ q = 81 – 87 = – 6
Hence, p = 29 and q = – 6.

Question 3.
Determine the values of h and k such that (x² – 2x – 3) is a factor of the polynomial x³ – 3x² + hx + k.
Solution :
Let p(x) = x³ – 3x² + hx + k
Now, x² – 2x – 3 = x² – (3 – 1)x – 3
⇒ x² – 2x – 3 = x² – 3x + x – 3
⇒ x² – 2x – 3 = x(x – 3) + 1(x – 3)
⇒ x² – 2x – 3 = (x – 3)(x + 1)
If (x² – 2x – 3) is a factor of p(x), then (x – 3) and (x + 1) are also the factors of p(x).
Now, (x – 3) is a factor of p(x), then by factor theorem, the remainder p(3) should be zero.
⇒ p(3) = 0
⇒ (3)³ – 3 × (3)² + h × 3 + k = 0
⇒ 27 – 27 + 3h + k = 0
⇒ 3h + k = 0 ….(i)
And if (x + 1) is a factor of p(x), then by factor theorem, the remainder p(- 1) should be zero.
⇒ p(-1) = 0
⇒ (-1)³ – 3 x (-1)² + h x (-1) + k = 0
⇒ – 1 – 3 – h + k = 0
⇒ – 4 – h + k = 0
⇒ – h + k = 4
⇒ h – k = – 4 ….(ii)
Adding equations (i) and (ii), we get

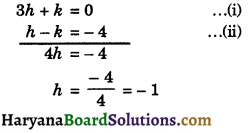
Putting the value of h in equation (ii), we get
– 1 – k = – 4
⇒ – k = – 4 + 1 = – 3
⇒ k = 3
Hence, k = 3 and h = – 1.

Question 4.
Without actual division, prove that x⁴ – 5x³ + 7x² – 5x + 6 is exactly divisible by x² – 5x + 6.
Solution :
Let p(x) = x⁴ – 5x³ + 7x² – 5x + 6
And let
g(x) = x² – 5x + 6
= x² – (3 + 2)x + 6
= x² – 3x – 2x + 6
= x(x – 3) – 2(x- 3)
= (x – 3)(x – 2)
If p(x) is exactly divisible by g(x), then p(x) is exactly divisible by (x – 3) and (x – 2) also.
Now, if p(x) is divisible by (x – 3), then by factor theorem, the remainder p(3) should be zero.
So, p(3) = (3)⁴ – 5 × (3)³ + 7 × (3)² – 5 × 3 + 6
= 81 – 135 + 63 – 15 + 6
= 150 – 150 = 0
Therefore, p(x) is divisible by (x – 3).
⇒ (x – 3) is a factor of p(x). …(i)
And if p(x) is divisible by (x – 2), then by factor theorem, the remainder p(2) should be zero.
So, p(2) = (2)⁴ – 5 × (2)³ + 7 × (2)² – 5 × 2 + 6
= 16 – 40 + 28 – 10 + 6
= 50 – 50 = 0
Therefore, p(x) is divisible by (x – 2).
⇒ (x – 2) is a factor of p(x). …(ii)
From (i) and (ii), we get
(x – 3)(x – 2) is a factor of p(x).
i.e., (x² – 5x + 6) is a factor of p(x).
Hence, p(x) is exactly divisible by (x² – 5x + 6). Proved

Question 5.
Factorise the following polynomials:
x⁴ + x³ – 7x² – x + 6
Solution :
Ist method: Let
p(x) = x⁴ + x³ – 7x² – x + 6
Factors of 6 are ±1, ±2, ±3, ±6.
Put x = 1
∴ p(1) = (1)⁴ + (1)³ – 7 × (1)² – 1 + 6
= 1 + 1 – 7 – 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Now, divide x⁴ + x³ – 7x² – x + 6 by (x – 1),
we get

So, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x³ + 2x² – 5x – 6)
Other factor of p(x) is x³ + 2x² – 5x – 6.
Factors of – 6 are ± 1, ± 2, ± 3, ± 6.
Again, put x = – 1
∴ p(-1) = (-1)³ + 2 × (-1)² – 5 × (-1) – 6
= – 1 + 2 + 5 – 6
= 7 – 7 = 0.
∴ By factor theorem, (x + 1) is a factor of x³ + 2x² – 5x – 6.
Again, divide x³ + 2x² – 5x – 6 by (x + 1), we get

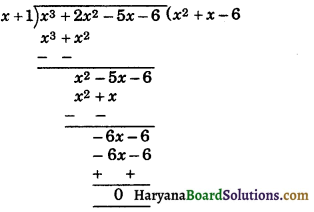
So, x³ + 2x² – 5x – 6 = (x + 1) (x² + x – 6)
And
x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1)(x² + x – 6)
= (x – 1)(x + 1) [x² + (3 – 2)x – 6]
= (x – 1)(x + 1)[x² + 3x – 2x – 6]
= (x – 1)(x + 1) [(x² + 3x) – (2x + 6)]
= (x – 1)(x + 1) (x(x + 3) – 2(x + 3)]
= (x – 1)(x + 1) (x + 3)(x – 2).
Hence, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1) (x + 3)(x – 2).

IInd method: Let
p(x) = x⁴ + x³ – 7x² – x + 6
Factors of 6 are = ± 1, ± 2, ± 3, ± 6
Put
x = 1
∴ p(1) = (1)⁴ + (1)³ – 7 × (1)² – 1 + 6
= 1 + 1 – 7 – 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Again put x = – 1
∴ p(-1) = (-1)⁴ + (-1)³ – 7 × (-1)² – (-1) + 6
= 1 – 1 – 7 + 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x + 1) is a factor of p(x).
Again put x = 2
∴ p(2) = (2)⁴ + (2)³ – 7 × (2)² – 2 + 6
= 16 + 8 – 28 – 2 + 6
= 30 – 30 = 0.
∴ By factor theorem, (x – 2) is a factor of p(x).
And put x = – 3 .
∴ p(-3) = (-3)⁴ + (-3)³ – 7 × (-3)² – (-3) + 6
= 81 – 27 – 63 + 3 + 6
= 90 – 90 = 0.
∴ By factor theorem, (x + 3) is a factor of p(x). Now, since the given expression is of 4th degree, so it will have only four factors of first degree.
∴ x⁴ + x³ – 7x² – x + 6 = k(x – 1) (x + 1) (x – 2) (x + 3) ……….(i)
Putting x = 0 (value of other than – 1, 1, 2, + 3) on both sides of equation (i), we get
+ 6 = k(-1)(1)(-2)(+3)
⇒ + 6 = 6k
⇒ k = \(\frac {6}{6}\) = 1
Putting the value of k in equation (i), we get
x⁴ + x³ – 7x² – x + 6 = (x – 1) (x + 1) (x – 2) (x + 3)
Hence, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1) (x – 2)(x + 3).

Question 6.
Factorise the following polynomials:
x⁴ – 4x³ – x² + 16x – 12.
Solution :
Let
p(x) = x⁴ – 4x³ – x² + 16x – 12
Factors of – 12 are ±1, ±2, ±3, ±4, ±6, ±12.
Put x = 1
∴ p(1) = (1)⁴ – 4 × (1)³ – (1)² + 16 × 1 – 12 .
= 1 – 4 – 1 + 16 – 12
= 17 – 17 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Now, divide x⁴ – 4x³ – x² + 16x – 12. by (x – 1), we get

So,
x⁴ – 4x³ – x² + 16x – 12 = (x – 1)(x³ – 3x² – 4x + 12).
Other factor of p(x) is x³ – 3x² – 4x + 12.
Factors of 12 are ±1, ±2, ±3, ±4, ±6, ±12
Again, put x = 2
∴ p(2) = (2)³ – 3 × (2)² – 4 × 2 + 12
= 8 – 12 – 8 + 12
= 20 – 20 = 0.
∴ By factor theorem, (x – 2) is a factor of x³ – 3x² – 4x + 12.
Now, divide x³ – 3x² – 4x + 12 by (x – 2), we get

So,
x³ – 3x² – 4x + 12 = (x – 2) (x² – x – 6)
And x⁴ – 4x³ – x² + 16x – 12 = (x – 1)(x – 2)(x² – x – 6)
= (x – 1) (x – 2)[x² – (3 – 2)x – 6]
= (x – 1) (x – 2)[x² – 3x + 2x – 6]
= (x – 1) (x – 2)[(x² – 3x) + (2x – 6)]
= (x – 1) (x – 2)[x(x – 3) + 2(x – 3)]
= (x – 1) (x – 2)(x – 3) (x + 2).
Hence, x⁴ – 4x³ – x² + 16x – 12
= (x – 1)(x – 2)(x – 3)(x + 2).

Question 7.
If (x + 2) be a factor of the polynomial p(x) = kx³ + x² – 12x – 4, then find the value of k and hence factorise the polynomial p(x).
Solution :
We have p(x) = kx³ + x² – 12x – 4
If (x + 2) is a factor of p(x), then by factor theorem, p(-2) should be zero.
⇒ p(-2) = 0
⇒ k(-2)³ + (-2)² – 12 × (-2) – 4 = 0
⇒ – 8k + 4 + 24 – 4 = 0
⇒ – 8k + 24 = 0
⇒ – 8k = – 24
⇒ k = \(\frac {- 24}{- 8}\) = 3
Putting the value of k in p(x), we get
p(x) = 3x³ + x² – 12x – 4
According to question, (x + 2) is a factor of p(x).
Dividing 3x³ + x² – 12x – 4 by (x + 2), we get

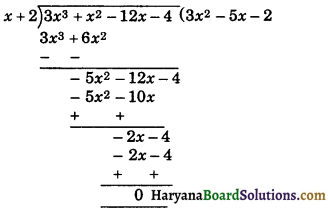
So, 3x³ + x² – 12x – 4= (x + 2) (3x² – 5x – 2)
= (x + 2) [3x² – (6 – 1)x – 2]
= (x + 2) [3x² – 6x + x – 2]
= (x + 2) [(3x² – 6x) + (x – 2)]
= (x + 2) (3x(x – 2) + 1(x – 2)]
= (x + 2)(x – 2)(3x + 1).
Hence, k = 3 and 3x³ + x² – 12x – 4 = (x + 2)(x – 2)(3x + 1).

Question 8.
If a⁴ + \(\frac{1}{a^4}\) = 322, find the value of a³ – \(\frac{1}{a^3}\).
Solution :
We have

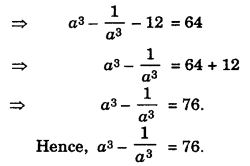
Question 9.
If a⁴ + \(\frac{1}{a^4}\) = 47, find the value of a³ + \(\frac{1}{a^3}\)
Solution :
We have,
a⁴ + \(\frac{1}{a^4}\) = 47

Question 10.
Factorise each of the following :
(i) (a – b)³ + (b – c)³ + (c – a)³
(ii)\(\frac{\left(p^2-q^2\right)^3+\left(q^2-r^2\right)^3+\left(r^2-p^2\right)^3}{(p-q)^3+(q-r)^3+(r-p)^3}\)
Solution :
We have,
(a – b)³ + (b – c)³ + (c – a)³
We know that if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Since, a – b + b – c + c – a = 0
Therefore, (a – b)³ + (b – c)³ + (c – a)³
= 3(a – b)(b – c) (c – a).

(ii) We have, \(\frac{\left(p^2-q^2\right)^3+\left(q^2-r^2\right)^3+\left(r^2-p^2\right)^3}{(p-q)^3+(q-r)^3+(r-p)^3}\)
We know that, if x + y + z = 0, then x³ + y³ + z³ = 3xyz
Since, p² – q² + q² – r² + r² – p² = 0
Therefore, (p² – q²)³ + (q² – r²)³ + (r² – p²)³
= 3(p² – q²) (q² – r²) (r² – p²) and p – q + q – r + r – p = 0

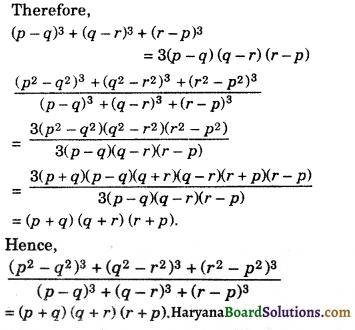
Question 11.
If \(\frac{x}{(b-c)(b+c-2 a)}=\frac{y}{(c-a)(c+a-2 b)}\) = \(\frac{z}{(a-b)(a+b-2 c)}\) then find the value of x + y + z.
Solution :
Let
\(\frac{x}{(b-c)(b+c-2 a)}=\frac{y}{(c-a)(c+a-2 b)}\) = \(\frac{z}{(a-b)(a+b-2 c)}\) = k
∴ x = k(b – c)(b + c – 2a),
y = k(c – a) (c + a – 26)
And z = k(a – b)(a + b – 2c)
Now, x + y + z = (b – c)(b + c – 2a) + k(c – a) (c + a – 2b) + k(a – b)(a + b – 2c)
= k[(b – c)(b + c – 2a) + (c – a)(c + a – 2b) + (a – b)(a + b – 2c)]
= k[b² + bc – 2ab – bc – c² + 2ac + c² + ac – 2bc – ac – a² + 2ab + a² + ab – 2ac – ab – b² + 2bc]
= k[b² – c² + c² – a² + a² – b² + bc – bc – 2ab + 2ab + 2ac – 2ac + ac – ac – 2bc + 2bc + ab – ab]
= k(0) = 0
Hence, x + y + z = 0.

Question 12.
Prove that : (a + b)³ + (b + c)³ + (c + a)³ – 3(a + b)(b + c) (c + a) = 2(a³ + b³ + c³ – 3abc).
Solution :
We have,
L.H.S. = (a + b)³ + (b + c)³ + (c + a)³ – 3(a + b)(b + c)(c + a)
Let, a + b = x, b + c = y, c + a = z, we get
L.H.S. = x³ + y³ + z³ – 3xyz
= (x + y + z)(x² + y² + z² – xy – yz – zx)
= (a + b + b + c + c + a) [(a + b)² + (b + c)² + (c + a)² – (a + b)(b + c) – (b + c)(c + a) – (c + a)(a + b)]
= 2(a + b + c) (a² + b² + 2ab + b² + c² + 2bc + c² + a² + 2ac – ab – ac – b² – bc – bc – ab – c² – ac – ac – bc – a² – ab)
= 2(a + b + c) (2a² + 2b² + 2c² – a² – b² – c² + 2ab + 2bc + 2ca – 3ab – 3bc – 3ca]
= 2(a + b + c)(a² + b² + c² – ab – bc – ca)
= 2(a³ + b³ + c³ – 3abc)
= R.H.S.
Hence, L.H.S. = R.H.S. Proved

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
Which of the following is a polynomial in variable x?
(a) x + \(\frac {1}{x}\)
(b) \(\sqrt{x^2}+\frac{1}{\sqrt{x^2}}\)
(c) x2 + \(\frac{x^{3 / 2}}{\sqrt{x}}\)
(d) x3/2 + \(\frac{1}{\sqrt{x^2}}\)
Solution :
(c) x2 + \(\frac{x^{3 / 2}}{\sqrt{x}}\)

Question 2.
\(\sqrt{2}\) is a polynomial of degree: [NCERT Exemplar Problems]
(a) 2
(b) 0
(c) 1
(d) \(\frac {1}{2}\)
Solution :
(b) 0

Question 3.
Which of the following is binomial in y:
(a) y2 + 5
(b) y2 + 5y + 6
(c) y2 + \(\frac{1}{y^2}\) + 2
(d) y\(\sqrt{y}\) + 7
Solution :
(a) y2 + 5

Question 4.
Which of the following is trinomial in x:
(a) x3 + 1
(b) x3 + 3x
(c) x\(\sqrt{x^2}\) + \(\sqrt{x^2}\) + 7
(d) x3 + x2
Solution :
(c) x\(\sqrt{x^2}\) + \(\sqrt{x^2}\) + 7

Question 5.
Degree of a zero polynomial is [NCERT Exemplar Problems]
(a) 2
(b) 0
(c) 1
(d) not defined
Solution :
(d) not defined

Question 6.
Which of the following polynomial’s degree is zero?
(a) x2
(b) x + \(\frac {1}{x}\)
(c) 7
(d) x.
Solution :
(c) 7

Question 7.
Degree of the polynomial 27 + y2 – 3y3 + 5y5 is :
(a) 5
(b) 3
(c) 2
(d) o
Solution :
(a) 5

Question 8.
Zero of the polynomial p(x) = 2x + 5 is : [NCERT Exemplar Problems]
(a) –\(\frac {2}{5}\)
(b) – \(\frac {5}{2}\)
(c) \(\frac {2}{5}\)
(d) \(\frac {5}{2}\)
Solution :
(b) – \(\frac {5}{2}\)

Question 9.
If (x – 2) is a factor of x3 – 6×2 + 12x – k, then value of k is :
(a) 4
(b) 8
(c) 6
(d) 10
Solution :
(b) 8

Question 10.
If x120 + 4×143 + k is divisible by x + 1, then value of k is :
(a) 2
(b) – 2
(c) 3
(d) – 3
Solution :
(c) 3

Question 11.
(x + 1) is a factor of xn + 1, only if :
(a) n is a positive integer
(b) n is a negative integer
(c) n is an odd integer
(d) n is an even integer
Solution :
(c) n is an odd integer

Question 12.
If x51 + 51 is divided by x + 1, the remainder is: [NCERT Exemplar Problems]
(a) o
(b) 1
(c) 49
(d) 50
Solution :
(d) 50

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 3 Coordinate Geometry Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 3 Coordinate Geometry

Very Short Answer Type Questions

Question 1.
Write the coordinates of each of the points A, B, C, D, E in figure.

Solution :
(i) Distance of the point A from the y-axis is 6 units and that of from x-axis is 4 units.
Hence, the coordinates of point A are (6, 4).
(ii) Distance of the point B from the y-axis is -5 units and that of from x-axis is 3 units.
Hence, the coordinates of point B are (- 5, 3).
(iii) Distance of the point C from the y-axis is – 3 units and that of from x-axis is 4 units.
Hence, the coordinates of point C are (- 3, – 4).
(iv) Distance of the point D from the y-axis is – 5 units and that of from x-axis is – 6 units.
Hence, the coordinates of point D are (- 5, – 6).
(v) Distance of the point E from the y-axis is 4 units and that of from x-axis is – 5 units.
Hence, the coordinates of point E are (4, – 5).

Question 2.
Write down the abscissa, ordinate and coordinates of the point P as given in the figure.

Solution :
Abscissa of the point P = – PR = – OQ = – a
Ordinate of the point P = PQ = OR = b
Coordinates of the point P = (abscissa, ordinate) = (- a, b).

Question 3.
Plot the points (-2, 0), (2, 0), (2, 2), (0, 4) and (-2, 2) and join them in order. What figure do you get?
Solution :
Plotting the points A(-2, 0), B(2, 0), C(2, 2), D(0, 4) and E(-2, 2). Join A to B, B to C, C to D, D to E and E to A. The figure so formed is a pentagon as shown in the figure.

Short Answer Type Questions

Question 1.
Locate the points (3,0), (-3.5, 2.5), (5.5, – 3.5), (-3.5, – 4.5) and (0, – 5.5) in the Cartesian plane.
Solution :
We draw x-axis and y-axis on the graph paper. Using the scale 1 cm = 1 unit, the given points are plotted in the figure.

Question 2.
Plot the points (x, y) given in the following table on the plane, choosing a suitable scale 1 cm = 0.5 unit on the axes.

Solution :
The pairs of the numbers given in the table can be represented by the points (3.5, 1.5), (- 0.5, 1.25), (-1.5, – 1.75), (1.0, – 2.25), (- 2.75, 0.75). Scale is given that 1 cm = 0.5 unit. The locations of the points are shown by dots in the figure.

Question 3.
Draw the triangle ABC, whose vertices are A(6, 2), B(3, – 1) and C(- 2, 4).
Solution :

With the axes, plot the points A(6, 2), B(3, – 1) and C(- 2, 4).
Joining the points A to B, B to C and C to A, then ΔABC is formed.

Question 4.
Three vertices of a rectangle are (3, 2), (- 4, 2) and (-4, 5). Plot these points and find the coordinates of the fourth vertex. [NCERT Exemplar Problems]
Solution :
Plot the three vertices of the rectangle as A(3, 2), B(-4, 2), C(-4, 5).

Join A to B, B to Ć. Since sides of rectanges are equal and parallel, so through point C draw CD || AB and CD equal to AB and joing DA. Hence, coordinate of the point D are (3, 5).

Question 5.
The three vertices of a square ABCD taken in order are A(7, – 3), B(4, 1) and C(8, 4). Find the coordinates of the fourth vertex.
Solution :
Plotting the three vertices A(7, – 3), B(4, 1) and C(8, 4) of a square ABCD on the graph paper. Join A to B, B to C and complete the square as shown in the figure.

So, fourth vertex Dis (11, 0).

Question 6.
The length and breadth of a rectangle are a units and 6 units respectively, one vertex at origin. The length runs along positive x-axis and breadth on positive y-axis. Find the coordinates of the vertices of the rectangle.
Solution :
One vertex of a rectangle is origin. So its coordinates are A(0,0). Since, length runs along positive x-axis and breadth runs along positive y-axis. As length is a units and breadth is b units. So, the coordinates of IInd, IVth vertices are B(a, 0) and D(0, b) respectively. Distance of third vertex C from y-axis is a units and distance of third vertex C from x-axis is b units. So the coordinates of vertex Care (a, b). See in figure.

Hence, the coordinates of the vertices of a rectangle are A(0,0), B(a,0), C(a,b) and D(0,b).

Long Answer Type Questions

Question 1.
See the figure and write the following:

(i) Coordinates of the point P.
(ii) Coordinates of the point R.
(iii) Abscissa of the point Q.
(iv) Ordinate of the point S.
(v) The point identified by the coordinates (0, – 4).
(vi) The point identified by the coordinates (4, – 2).
Solution:
(i) Distance of the point P from the y-axis is 3 units and that of from x-axis is 0 unit. Hence, the coordinates of point P are (3, 0).
(ii) Distance of the point R from the y-axis is – 4 units and that of from x-axis is 0 unit. Hence, the coordinates of point Rare (-4, 0).
(iii) Distance of the ponit Q from the y-axis is – 3 units. Hence, abscissa of the point Q is – 3
(iv) Distance of the point S from the x-axis is – 3 units. Hence, ordinate of the point S is – 3.
(v) The point identified by the coordinates (0, – 4) is ‘T’.
(vi) The point identified by the coordinates (4, – 2) is ‘U’.

Question 2.
Write down the abscissa, ordinate and coordinates of the points A, B, C, D, E and F as given in the figure.

Solution :
(i) Point A: Distance of the point A from the y-axis is 5 units. So, abscissa of the point A is 5. Distance of the point A from the x-axis is – 2 units. So, ordinate of the point A is – 2 units. Hence, coordinate of the point A are (5, – 2).
(ii) Point B: Abscissa of the point B is 3 units. Ordinate of the point B is 4 units. Hence, coordinates of the point B are (3, 4).
(iii) Point C: Abscissa of the point C is – 5 units. Ordinate of the point C is 0 unit. Hence, coordinates of the point C are (-5, 0).
(iv) Point D: Abscissa of the point D is – 2 units. Ordinate of the point D is 5 units. Hence, coordinates of the point D are (-2, 5).
(v) Point E: Abscissa of the point E is – 6 units. Ordinate of the point E is – 4 units. Hence, coordinates of the point E are (-6, – 4).
(vi) Point F: Abscissa of the point Fis 0. Ordinate of the point F is 3. Hence, coordinates of the point F are (0, 3).

Question 3.
Plot the following points and state whether they are collinear or not?
(i) A(-1, 2), B(2, 0) and C(5, – 2).
(ii) K(3, 2), L(- 2, – 2) and M(2, – 1).
(iii) O(0, 0), P(2, 2) and Q(5, 5).
[NCERT Exemplar Problems]
Solution :
(i) With the axes, plot the given points A(-1, 2), B(2, 0) and C(5, – 2).

Joining the points A to B and B to C, we get a straight line. Hence, the given points are collinear.

(ii) With the axes, plot the given points K(3, 2), L(-2, – 2) and M(2, – 1).

Joining the points K to L and L to M, we do not get a straight line. Hence, the given points are not collinear.

(iii) With the axes, plot the given points 0(0,0), P(2, 2) and Q(5,5). Joining the points O to P and P to Q, we get a straight line. Hence, the given points are collinear.

Question 4.
Plot the following points and write the name of the quadrilateral so formed in each case :
(i) A(1, 1), B(6, 2), C(7, 6) and D(2, 5).
(ii) A(1, 1), B(2, 4), C(8, 4) and D(10, 1).
(iii) A(-2, – 2), B(-4, 2), C(-6, – 2) and D(-4, – 6).
Solution :
(i) With the axes, plot the given points A(1, 1), B(6, 2), C(7, 6) and D(2, 5).

Join A to B, B to C, C to D and D to A. The quadrilateral so formed is a parallelogram.

(ii) With the axes, plot the points A(1, 1), B(2,4), C(8,4) and D(10, 1).

Join A to B, B to C, C to D and D to A. The quadrilateral so formed is a trapezium.

(iii) With the axes, plot the given points A(-2, – 2), B(-4, 2), C(-6, – 2) and D(-4, – 6).

Join A to B, B to C, C to D and D to A. The quadrilateral so formed is a rhombus.

Multiple Choice Questions

Choose the correct option in each of the following :

Question 1.
The point at which the x-axis and y-axis meet is called : [NCERT Exemplar Problems]
(a) the ordinate
(b) the abscissa
(c) the origin
(d) quadrant
Solution :
(c) the origin

Question 2.
The signs of abscissa and ordinate of a point in the quadrant IVth are :
(a) (+,+)
(b) (+, -)
(c) (-, +)
(d) (-, -)
Solution :
(b) (+, -)

Question 3.
The signs of abscissa and ordinate of a point in the quadrant II are:
[NCERT Exemplar Problems]
(a) (+, -)
(b) (-, -)
(c) (+, +)
(d) (-, +)
Solution :
(d) (-, +)

Question 4.
Ordinate of all points on the x-axis is :
[NCERT Exemplar Problems]
(a) – 1
(b) 1
(c) 0
(d) none of these
Solution :
(c) 0

Question 5.
Abscissa of all points on the x-axis is :
[NCERT Exemplar Problems]
(a) 0
(b) – 1
(c) 1
(d) any number
Solution :
(d) any number

Question 6.
Abscissa of a point is negative in :
(a) only IIIrd quadrant
(b) only IInd quadrant
(c) IInd and IIIrd quadrants
(d) IInd and IVth quarrants
Solution :
(c) IInd and IIIrd quadrants

Question 7.
Ordinate of a point is positive in :
(a) Ist and IInd quadrants
(b) only Ist quadrant
(c) only IInd quadrant
(d) IInd and IV quadrants
Solution :
(a) Ist and IInd quadrants

Question 8.
The coordinates of the point lying on the negative side of y-axis at a distance of 7 units from the origin are :
(a) (0, 7)
(b) (0, – 7)
(c) (7, 0)
(d) (- 7, 0)
Solution :
(b) (0, – 7)

Question 9.
The coordinates of the point lying on the negative side of x-axis at a distance of 3 units from the origin are :
(a) (0, 3)
(b) (0, – 3)
(c) (3, 0)
(d) (- 3, 0)
Solution :
(d) (- 3, 0)

Question 10.
The coordinates of the point lying on the positive side of y-axis at a distance of 5 units from the origin are :
(a) (5, 0)
(b) (- 5, 0)
(c) (0, 5)
(d) (0, – 5)
Solution :
(c) (0, 5)

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 13 Surface Areas and Volumes

Very Short Answer Type Questions

Question 1.
Three cubes each with 7 cm edge are joined end to end. Find the total surface area of the resulting cuboid.
Solution:
Since three cubes each with 7 cm edge are joined end to end.

∴ Dimensions of resulting cuboid are
l = 7 + 7 + 7 = 21 cm
b = 7 cm and h = 7 cm
Total surface area of the resulting cuboid
= 2(lb + bh + hl)
= 2(21 × 7 + 7 × 7 + 7 × 21)
= 2(147 + 49 + 147)
= 2 × 343
= 686 cm²
Hence, total surface area of resulting cuboid = 686 cm².

Question 2.
Find the length of longest pole that can be put in a room of dimensions 12 m × 9 m × 8 m.
Solution:
Dimensions of the room are
l = 12 m, b = 9 m and h = 8 m
Length of a diagonal of a room
= \(\sqrt{l^2+b^2+h^2}\)
= \(\sqrt{12^2+9^2+8^2}\)
= \(\sqrt{144+81+64}\)
= \(\sqrt{289}\) = 17 m
Hence,length of a diagonal of a room = 17 m.

Question 3.
The length and breadth of a hall are 16 m and 10 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the total surface area.
Solution:
We have,
The length and breadth of a hall are 16 m and 10 m.
Let the height of the hall be h m.
Area of floor and flat roof = 2 × l × b
= 2 × 16 × 10
= 320 m²
Area of four walls of a hall = 2(l + b) × h
= 2(16 + 10) × h = 52h
According to question,
Area of floor and flat roof = Area of four walls
⇒ 320 = 52h
⇒ h = \(\frac{320}{52}\)
⇒ h = 6.15 m (approx.)
The total surface of the hall
= 2(lb + bh + hl)
= 2(16 × 10 + 10 × 6.15 + 6.15 × 16)
= 2(160 + 61.5 + 98.4)
= 2(319.9) = 639.8 m²
Hence, total surface area of a hall = 639.8 m².

Question 4.
A well is 7.2 m deep. The cost of cementing its inner surface at 75 paise per dm² is Rs. 11880. Determine the radius of the well.
Solution:
We have,
Depth of well (h) = 7.2 m
Rate of cementing of inner surface of well 75 paise/dm² = Rs. 0.75 per dm²
Total cost of cementing the well = Rs. 11880
C.S.A. of the well = \(\frac{\text { Total cost }}{1 \mathrm{dm}^2 \cos t}\) = \(\frac{11880}{0.75}\)
= 15840 dm² = 158.4 m² …….(i)
Let the radius of the well be r m.
C.S.A. of the well = 2πrh
⇒ 158.4 = 2 × \(\frac{22}{7}\) × r × 7.2
⇒ 158.4 = \(\frac{316.8}{7}\)r
⇒ r = \(\frac{158.4 \times 7}{316.8}\)
⇒ r = 3.5 m
Hence,radius of the well = 3.5 m.

Question 5.
A rectangular sheet of paper 44 cm by 20 cm is rolled along its length and a cylinder is formed. Find the total surface area of cylinder.
Solution:
We have,
Length of rectangular sheet (l) = 44 cm
Breadth of rectangular sheet (b) = 20 cm
Since, rectangular sheet of paper is rolled along its length.
Height of the cylinder (h) = 20 cm
and base circumference of cylinder of radius r cm = 44 cm
⇒ 2πr = 44
⇒ 2 × \(\frac{22}{7}\) × r = 44
⇒ \(\frac{44}{7}\) × r = 44
⇒ r = \(\frac{44 \times 7}{44}\) = 7 cm
Total surface area of the cylinder
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 7(20 + 7)
= 44 × 27 = 1188 cm²
Hence, total surface area of the cylinder = 1188 cm².

Question 6.
The radii of the two cylinders are in the ratio 3 : 4 and their heights are in the ratio 4 : 5. Determine the ratio of their curved surface areas.
Solution:
We have,
Ratio of radii of two cylinders = 3 : 4
Let radii of two cylinders be 3x and 4x and ratio of heights of two cylinders = 4 : 5
Let heights of two cylinders be 4h and 5h.
C.S.A. of the Ist cylinder = 2 × π × 3x × 4h …(i)
C.S.A. of the IInd cylinder = 2 × π × 4x × 5h …(ii)
Dividing (i) by (ii), we get
⇒ \(\frac{\text { C.S.A. of the Ist cylinder }}{\text { C.S.A. of the IInd cylinder }}=\frac{2 \times \pi \times 3 x \times 4 h}{2 \times \pi \times 4 x \times 5 h}\)
⇒ \(\frac{\text { C.S.A. of the Ist cylinder }}{\text { C.S.A. of the IInd cylinder }}=\frac{3}{5}\)
⇒ C.S.A. of the Ist cylinder : C.S.A. of the IInd cylinder = 3 : 5
Hence, required ratio of two cylinders = 3 : 5.

Question 7.
The curved surface area of the cylinder is \(\frac{2}{3}\) of the total surface area of a cylinder whose length is 27 cm. Find the radius of the cylinder.
Solution:
We have,
Length of the cylinder (h) = 27 cm
Let radius of the cylinder be r cm.
∴ Curved surface area of the cylinder = 2лrh
= 2πr × 27 = 54πr
and total surface area of the cylinder
= 2πr(h+r) = 2πr(27 + r)
According to question,
Curved surface area of cylinder = \(\frac{2}{3}\) of total surface area of cylinder
54πr = \(\frac{2}{3}\) of 2πr(27 + r)
⇒ 54πr = \(\frac{4 \pi r}{3}\)(27 + r)
⇒ \(\frac{3 \times 54 \pi r}{4 \pi r}\) = 27 + r
⇒ 40.5 = 27+ r
⇒ r = 40.5 – 27
⇒ r = 13.5 cm
Hence, radius of the cylinder = 13.5 cm.

Question 8.
A cylindrical roller 2.5 m in length, 1.75 m in radius when rolled on a road was found to cover the area of 5500 m². How many revolutions did it make?
Solution:
We have,
Length of the roller (h) = 2.5 m
Radius of the roller (r) = 1.75 m
and total area covered by roller = 5500 m²
Area covered by roller in one revolution
= C.S.A. of the roller
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.5
= 44 × 0.25 × 2.5
= 27.5 m²
No. of revolutions = \(\frac{\text { Total area }}{\text { Area covered in one revolution }}\)
= \(\frac{5500}{27.5}\)
= 200
Hence, no. of revolutions makes by roller = 200.

Question 9.
Find the ratio of the curved surface areas of two cones, if the diameters of their bases are equal and slant heights are in the ratio 3 : 5.
Solution:
We have,
Diameters of bases of two cones are equal.
Therefore radius of their bases are also equal.
Slant height of Ist cone (l₁) : Slant height of IInd cone (l₂) = 3 : 5
Let slant height of Ist cone be 3x, second cone be 5x and same radius of their bases be r
\(\frac{\text { Curved surface area of Ist cone }}{\text { Curved surface area of IInd cone }}=\frac{\pi r l_1}{\pi r l_2}\)
\(\frac{\pi r \times 3 x}{\pi r \times 5 x}\) = 3 : 5
Hence,required ratio = 3 : 5.

Question 10.
Radii of two spheres are in the ratio 2 : 3. Find the ratio of their surface areas.
Solution:
We have, Ratio of radii of two spheres = 2 : 3
Let radii of two spheres be 2 and 3x, then
Surface area of Ist sphere = 4π(2x)²
= 4π × 4x² = 16πx²
Surface area of IInd sphere = 4π(3x)²
= 4π × 9x² = 36x²
Now, \(\frac{\text { Surface area of Ist sphere }}{\text { Surface area of IInd sphere }}\)
= \(\frac{16 \pi x^2}{36 \pi x^2}\)
⇒ \(\frac{\text { Surface area of Ist sphere }}{\text { Surface area of IInd sphere }}=\frac{4}{9}\)
⇒ Surface area of Ist sphere : Surface of IInd sphere = 4 : 9
Hence, required ratio of two spheres = 4 : 9.

Question 11.
The volume of a cuboid is 720 m³. Its length is 12 m and its breadth and height are in the ratio 5 : 3. Find the breadth and height of the cuboid.
Solution:
We have, Length of a cuboid = 12 m
Ratio of breadth and height = 5 : 3
Let the breadth of a cuboid be 5x and height be 3x
and volume of a cuboid = 720 m³
l × b × h = 720
12 × 5x × 3x = 720
180x² = 720
x² = \(\frac{720}{180}\)
x² = 4
x = \(\sqrt{4}\) = 2
∴ breadth of a cuboid = 5 × 2 = 10 m
and height of a cuboid = 3 × 2 = 6 m
Hence, breadth and height of a cuboid are 10 m and 6 m respectively.

Question 12.
The dimensions of a metallic cuboid are 54 cm × 36 cm × 24 cm. It is melted and recast into a cube. Find the surface area of the cube.
Solution:
We have,
Dimensions of the metallic cuboid = 54 cm × 36 cm × 24 cm
∴ Volume of the cuboid = 54 × 36 × 24
= 46656 cm³
Since cuboid is melted and recast into a cube.
Let the edge of new cube be a cm.
∴ Volume of a cube = Volume of cuboid
⇒ a³ = 46656
⇒ a = \(\sqrt[3]{46656}\)
⇒ a = 36 cm
Surface area of the cube = 6a²
= 6 × (36)²
= 7776 cm²
Hence,surface area of the cube = 7776 cm².

Question 13.
A cone and a cylinder have same heights and same volumes. Find the ratio of their bases radii.
Solution:
Let the radii of bases of cone and cylinder be r₁ and r₂.
Let their heights be h.
According to question,
Volume of the cone = Volume of the cylinder
⇒ \(\frac{1}{3} \pi r_1{ }^2 h=\pi r_2{ }^2 h\)
⇒ \(\frac{r_1^2}{r_2^2}=\frac{3 \pi h}{\pi h}\)
⇒ \(\frac{r_1{ }^2}{r_2{ }^2}=3\)
⇒ \(\frac{r_1}{r_2}=\frac{\sqrt{3}}{1}\)
⇒ r₁ : r₂ = \(\sqrt{3}\) : 1
Hence, required ratio of radii of bases of cone and cylinder = \(\sqrt{3}\) : 1.

Question 14.
Find the volume of the largest right circular cone that can be cut out from a cube whose edge is 21 cm.
Solution:
The base of the cone will the circle inscribed in a face of the cube and its height will be equal to the an edge of cube.
Edge of the cube = 21 cm

∴ Radius of base of the cone (r) = \(\frac{21}{2}\)
= 10.5 cm
Height of the cone (h) = 21 cm
Volume of the cone cut out = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × (10.5)² × 21
= 22 × 110.25
= 2425.5 cm³
Hence,volume of the cone cut out = 2425.5 cm³.

Question 15.
If h, c and V are respectively the height, the curved surface area and volume of a cone, then prove that :
3πVh³ – c²h² + 9V² = 0.
Solution:
Let r be radius and h be the height of a cone.
∴ Slant height (l) = \(\sqrt{h^2+r^2}\)
Volume of a cone (V) = \(\frac{1}{3}\)πr²h
and curved surface area (c) = πrl
⇒ c = πr(\(\sqrt{h^2+r^2}\))
⇒ c² = π²r² (h² + r²)
Now, L.H.S. = 3πVh³ – c²h² + 9V²
= 3π × \(\frac{1}{3}\)πr²h × h³ – π²r² × (h² + r²) × h² + 9 × \(\left(\frac{1}{3} \pi r^2 h\right)^2\)
= π²r²h⁴ – π²r²h⁴ – π²r⁴h² + 9 × \(\frac{1}{9}\)π²r⁴h²
= -π²r⁴h² + πr⁴h²
= 0 = R.H.S.
∴ L.H.S. = R.H.S. Hence proved.

Question 16.
The diameter of copper sphere is 6 cm. The sphere is melted and is drawn into a long wire of uniform circular section. If the length of wire is 36 cm, find its radius.
Solution:
We have,
Diameter of copper sphere = 6 cm
∴ Radius of copper sphere (R) = \(\frac{6}{2}\) = 3 cm
Length of wire (h) = 36 cm
Let radius of wire be r сm.
Since, copper sphere is melted and is drawn into a circular wire.
∴ Volume of circular wire = Volume of sphere
∴ πr²h = \(\frac{4}{3}\)πR³
⇒ π × r² × 36 = \(\frac{4}{3}\)π × (3)³
⇒ r² = \(\frac{4 \pi \times 3 \times 3 \times 3}{3 \times \pi \times 36}\)
⇒ r² = 1
⇒ r = 1 cm
Hence, radius of wire = 1 cm.

Short Answer Type Questions

Question 1.
An open box is made of wood 5 cm thick. Its external length is 1.50 m, breadth 1.30 m and height 0.90 m. Find the cost of painting the inner surface of the box at 75 paise per 100 cm².
Solution:
External dimensions of the box are
l = 1.50 m = 150 cm
b = 1.30 m = 130 cm
h = 0.90 m = 90 cm
Thickness of the wood = 5 cm. Therefore inner dimensions of the box are
l = 150 cm – 2 × 5 cm
= 140 cm
b = 130 cm – 2 × 5 cm
= 120 cm
h = 90 cm – 2 × 5 cm
= 80 cm
Inner surface area of the box = 2(lb + bh + hl)
= 2(140 × 120 + 120 × 80 + 80 × 140)
= 2(16800 + 9600 + 11200)
= 2(37600) = 75200 cm²
∵ 100 cm² painting cost of box = 75 paise
i.e., Rs. \(\frac{75}{100}\)
∴ 1 cm² painting cost of box = Rs. \(\frac{75}{100 \times 100}\)
∴ 75200 cm² painting cost of box = Rs. \(\frac{75 \times 75200}{100 \times 100}\)
= Rs. 564
Hence, painting cost of inner surface area of the box = Rs. 564.

Question 2.
A class room is 8 m long, 6 m wide and 4 m high. It has two doors 2.5 m by 1.5 m and three windows 1.5 m by 80 cm.
Find:
(i) Area of the walls excluding doors and windows.
(ii) The cost of distempering at the rate of Rs. 5.40 per m².
Solution:
Dimensions of the class room are
l = 8 m, b = 6 m and h = 4 m
(i) Surface area of walls of the class room
= 2(l + b) × h = 2(8 + 6) × 4
= 2 × 14 × 4 = 112 m²
Area of 1 door = 2.5 × 1.5 = 3.75 m²
Area of 2 doors = 2 × 3.75 = 7.5 m²
Area of 1 window = 1.5 m × 80 cm
= 1.5 m × 0·80 m
= 1.2 m²
Area of 3 windows = 3 × 1.2 = 3.6 m²
Area of 2 doors + Area of 3 windows = 7.5 + 3.6 = 11.1 m²
Area of the walls of the class room excluding doors and windows
= 112 – 11.1 = 100.9 m².

(ii) ∵ 1 m² distempering cost of walls = Rs. 5.40
∴ 100.9 m² distempering cost of walls
= Rs. 5.40 × 100.9
= Rs. 544.86
= Rs. 544.80 (approx.)
Hence, (i) Area of the walls excluding doors and windows is 100.9 m².
(ii) cost of distempering of walls of a class room = Rs. 544.80 (approx.)

Question 3.
Lateral surface area of a cuboid is 486 m². Its breadth is 12 m and length and height are in the ratio 5 : 3. Find the length and height of the cuboid.
Solution:
We have,
Lateral surface area of cuboid = 486 m²
Breadth of a cuboid = 12 m
Ratio of length : height = 5 : 3
Let the length and height of the cuboid be 5x and 3x respectively.
Lateral surface area of a cuboid = 2(l + b) × h
⇒ 486 = 2(5x + 12) × 3x
⇒ 486 = 30x² + 72x
⇒ 30x² + 72x – 486 = 0
⇒ 5x² + 12x – 81 = 0
⇒ 5x² + (27 – 15)x – 81 = 0
⇒ 5x² + 27x – 15x – 81 = 0
⇒ x(5x + 27) – 3(5x + 27) = 0
⇒ (5x + 27) (x – 3)= 0
⇒ 5x + 27 = 0 or x – 3 = 0
⇒ x = \(\frac{-27}{5}\) or x = 3
Since, length and height are not negative,
so we neglect x = \(\frac{-27}{5}\)
∴ x = 3
Length of cuboid = 5 × 3 = 15 m
height of cuboid = 3 × 3 = 9 m
Hence, length and height of the cuboid = 15 m and 9 m.

Question 4.
The dimensions of the cuboid are in the ratio 5 : 3 : 2 and the lateral surface area is 288 m². The outer surface area of the cuboid is painted with colour enamel at the rate of Rs. 6 per m². Find the total cost of painting.
Solution:
We have,
Ratio of the dimensions of the cuboid = 5 : 3 : 2
Let the dimensions of the cuboid as l = 5x m, b = 3x m and h = 2x m
Lateral surface area of the cuboid = 288 m² (given)
⇒ 2(5x + 3x) × 2x = 288
⇒ 32x² = 288
⇒ x² = \(\frac{288}{32}\)
⇒ x² =9
⇒ x = \(\sqrt{9}\) = 3 m
∴ 15 × 3 = 15 m, b = 3 × 3 = 9 m and h = 2 × 3 = 6 m
Outer surface area of the cuboid = 2(lb + bh + hl)
= 2(15 × 9 + 9 × 6 + 6 × 15)
= 2(135 + 54 + 90)
= 2 × 279 = 558 m²
∵ 1 m² colour painted cost = Rs. 6
∴ 558 m² colour painted cost= Rs. (558 × 6)
= Rs. 3348
Hence,
total cost of painting = Rs. 3348.

Question 5.
The cost of papering of four walls of a room at Rs. 1.5 per square metre is Rs. 324. The height of the room is 4.5 m. If ratio of length and breadth of a room is 5 : 3, find them.
Solution:
We have,
height of a room 4.5 m
Ratio of length and breadth of a room = 5 : 3
Let the length and breadth of a room be 5x m and 3x m.
Area of four walls of a room = 2(l + b) × h
= 2(5x + 3x) × 4.5
= 2 × 8x × 4.5 = 72x ……(1)
Rate of papering of four walls of a room = 1.5 per m²
Total cost of papering = Rs. 324
Area of four walls of a room = \(\frac{\text { Total cost }}{1 \mathrm{~m}^2 \cos t}\)
Area of four walls of a room = \(\frac{324}{1.5}\)
Area of four walls of a room = 216 m² …….(2)
From (1) and (2), we get
72x = 216
⇒ x = \(\frac{216}{72}\)
⇒ x = 3 m
Length of a room= 5 × 3 = 15 m
Breadth of a room= 3 × 3 = 9 m
Hence, length and breadth of a room= 15m, 9 m.

Question 6.
A cylindrical metallic pipe is 20 cm long. The difference between the total surface area and inner surface area is 1232 cm². Find the radius of the pipe.
Solution:
We have,
Length of metallic pipe (h) = 20 cm
Let the radius of the metallic pipe be r cm.
Then,total surface area of metallic pipe
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × r(20 + r)
and lateral surface area = 2πrh
22 × \(\frac{22}{7}\) × r × 20
According to question,
Total surface area – Lateral surface area
= 1232

Since, radius of the pipe cannot be negative, therefore, we neglect r = – 14 cm.
∴ r = 14 cm

Question 7.
The total surface area of a hollow metallic cylinder open both ends of external radius 10 cm and height 14 cm is 576π cm². Taking r to be inner radius. find the thickness of the metal in the cylinder.
Solution:
We have,
External radius of the hollow metallic cylinder (R) = 10 cm
Height of the hollow metallic cylinder (h) = 14 cm
Let inner radius of the hollow metallic cylinder be r cm.
and total surface area of the hollow metallic cylinder open both ends
= 1408 cm²
⇒ 2πRh + 2πrh + 2π(R² – r²) = 576 π
⇒ 2πh(R + r) + 2π (R + r) (R – r) = 576 π
⇒ 2π(R + r) [h + R – r] = 576 π
⇒ (10 + r) (14 + 10 – r) = \(\frac{576 \pi}{2 \pi}\)
⇒ (10 + r) (24 – r) = 288
⇒ 240 – 10r + 24r – r² = 288
⇒ 240 + 14r – r² = 288
⇒ r² – 14r + 288 – 240 = 0
⇒ r² – 14r + 48 = 0
⇒ r² – (8 + 6)r + 48 = 0
⇒ r² – 8r – 6r + 48 = 0
⇒ r(r – 8) -6 (r – 8) = 0
⇒ (r – 8)(r – 6) = 0
⇒ r – 8 = 0 or r – 6 = 0
⇒ r = 8 or r = 6
When r = 8, then thickness of the metal in the cylinder = 10 – 8 = 2 cm.
When r = 6, then thickness of the metal in the cylinder = 10 – 6 = 4 cm.
Hence, thickness of the metal in the cylinder = 2 cm or 4 cm.

Question 8.
60 two rupees coins are placed one above the other to form a right circular cylinder. If each coin has radius 1.6 cm and thickness 0.3 cm, find its total surface area.

Solution:
We have,
Radius of each circular 2 rupees coin (r) = 1.6 cm
Number of 2 rupees coins = 60
and thickness of the 2 rupees coin= 0.3 cm
Since, two rupees coins are placed one above the other.
Therefore, radius of the new formed. cylinder (R) = radius of the 2 rupees coin
= 1.6 cm
and height of the new cylinder (h) = Thickness × no. of coins
= 0·3 × 60 = 18 cm
∴ Total surface area of the new cylinder
= 2πR(h + R)
= 2 × \(\frac{22}{7}\) × 1.6(18 + 1.6)
= \(\frac{70.4 \times 19.6}{7}\)
= 197.12 cm²
Hence, total suface area of the new cylinder 197.12 cm².

Question 9.
A rectangular box 40 cm long, 30 cm wide and 25 cm deep had the same total surface area as that of a cylindrical tin of radius 18 cm. Calculate the height of the cylindrical tin correct to 2 decimal places.
Solution:
We have,
Length, breadth and height of a rectangular box are 40 cm, 30 cm and 25 cm respectively.
Total surface area of the box = 2(lb + bh + hl)
= 2(40 × 30 + 30 × 25 + 25 × 40)
= 2(2950) = 5900 cm²
Now,radius of the cylindrical tin (r) = 18 cm
Let height of the cylindrical tin be h cm.
∴ Total surface area of cylindrical tin
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 18(h + 18)
= \(\frac{792}{7}\)(h + 18)
According to question
T.S.A. of rectangular box = T.S.A. of the cylindrical tin
⇒ 5900 = \(\frac{792}{7}\)(h + 18)
⇒ \(\frac{5900 \times 7}{792}\) = h + 18
⇒ 52.15 (approx.) = h + 18.
⇒ h = 52.15 – 18
⇒ h = 34.15 cm (approx.)
Hence, height of the cylindrical tin = 34.15 cm (approx.).

Question 10.
The circumference of the base of a 14 m high conical tent is 66 metres. Calculate the length of canvas used in making the tent if width of canvas is 2.5 m. [User π = \(\frac{22}{7}\)]
Solution:
We have,
Height of the conical tent (h) = 14 m
Circumference of base of the conical tent = 66 m
⇒ 2πr = 66
⇒ 2× \(\frac{22}{7}\) × r = 66
⇒ \(\frac{44}{7}\) × r = 66
⇒ r = \(\frac{66 \times 7}{44}\)
⇒ r = 10.5 m
⇒ \(\sqrt{h^2+r^2}\)
⇒ \(\sqrt{14^2+(10.5)^2}\)
⇒ \(\sqrt{196+110.25}\)
⇒ \(\sqrt{306.25}\)
⇒ l = ± 17.5 m
⇒ l = 17.5 m
Area of canvas used in making the tent = C.S.A. of the conical tent
= πrl
= \(\frac{22}{7}\) × 10.5 × 17.5
= 577.5 m²
Width of the canvas = 2.5 m, (given)
Length of the canvas = \(\frac{\text { C.S.A. of the canvas }}{\text { Width of the canvas }}=\frac{577.5}{2.5}\)
= 231 metres
Hence, required length of the canvas = 231 metres.

Question 11.
A tent of height 8.25 m is in the form of a right circular cylinder with radius of base 15 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of canvas of the tent at the rate of Rs. 40 per m².

Solution:
We have, Total height of the tent = 8.25 m
Height of the cylindrical portion (h) = 5.5 m
∴ Height of the conical portion = 8.25 – 5.5
= 2.75 m
and radius of base of cylinder and base of cone (r) = 15 m
⇒ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{2.75^2+15^2}\)
⇒ l = \(\sqrt{7.5625+225}\)
⇒ l = \(\sqrt{232.5625}\)
⇒ l = 15.25 m
Required area of canvas of tent = C.S.A. of cylindrical portion + C.S.A. of conical portion
= 2πrh + πrl = πr(2h + l)
= \(\frac{22}{7}\) × 15(2 × 5.5 + 15.25)
= \(\frac{330}{7}\) × 26.25
= 1237.5 m²
∵ 1 m² canvas cost = Rs. 40
∴ 1237.5 m² canvas cost = Rs. 40 × 1237.5 = Rs. 49500
Hence,cost of canvas = Rs. 49500.

Question 12.
A cone and a hemisphere have equal bases and have equal total surface areas. Find the ratio of their heights.
Solution:
We have,
A cone and a hemisphere have equal bases
i.e., they have equal base radius.
∴ Let radius of a cone and a hemisphere be r.

Let heights of a cone and hemisphere be h₁ and h₂ respectively, then
slant height of a cone (l₁) = \(\sqrt{h_1^2+r^2}\)
According to question,
Total surface area of a cone = Total surface area of a hemisphere
⇒ πrl + πr²= 3πr²
⇒ πr(l + r) = 3πг²

[∵ height of a hemisphere = radius of hemisphere]
⇒ h₁ : h₂ = \(\sqrt{3}\) : 1
Hence, required ratio of heights of cone and a hemisphere = \(\sqrt{3}\) : 1.

Question 13.
Curved surface area of a cone having base radius as 60 cm and height as 45 cm is same as the surface area of the sphere. Find the radius of the sphere.
Solution:
We have, Base radius of a cone (r₁) = 60 cm
Height of the cone (h) = 45 cm
Slant height of the cone (l) = \(\sqrt{h^2+r_1^2}\)
= \(\sqrt{45^2+60^2}\)
= \(\sqrt{2025+3600}\)
= \(\sqrt{5625}\) = 75 cm
Let radius of the sphere be r² cm.
According to question,
Curved surface area of a cone = Surface area of a sphere
⇒ πr₁l = 4πr₂²
⇒ π × 60 × 75 = 4 × π × r₂²
⇒ 60 × 75 = 4 × r₂²
⇒ \(\sqrt{2025+3600}\) = r₂²
⇒ 15 × 75 = r₂²
⇒ r² = \(\sqrt{15 \times 75}\)
⇒ r² = \(\sqrt{15 \times 15 \times 5}\)
⇒ r² = 15\(\sqrt{5}\) cm
Hence,radius of the sphere = 15\(\sqrt{5}\) cm.

Question 14.
A solid is the form of a right circular cylinder with hemispherical ends whose total length is 2.7 mand diameter of each hemispherical end is 0.7m. Find the total surface area of the solid.

Solution:
We have,
Radius of each end of hemispherical end (r) = \(\frac{0.7}{2}\) = 0.35 m
Total length of the solid = 2.7 m
∴ Length of the cylinder (h) = 2.7 – 2 × 0.35
= 2.7 – 0.7 = 2.0 m
Total surface area of the solid = Curved surface area of the cylindrical portion + 2 × curved surface area of hemispherical end
= 2πrh + 2 × 2πr²
= 2πr(h + 2r)
= 2 × \(\frac{22}{7}\) × 0.35(2 + 2 × 0.35)
= 2.2 × 2.7 = 5.94 m²
Hence, total surface area of the solid = 5.94 m².

Question 15.
The edges of three metallic cubes are in the ratio of 3 : 4 : 5. These cubes are melted and recast into a single cube whose diagonal is 12\(\sqrt{3}\) cm. Find the edges of three cubes.
Solution:
We have,
Ratio of the edges of three metallic cubes = 3 : 4 : 5
Let the edges of three metallic cubes be 3x cm, 4x cm and 5x cm.
Sum of the volumes of three cubes = (3x)³ + (4x)³ + (5x)³ = 27x³ + 64x³ + 125x³
= (27 + 64 + 125)x³
= 216x³
Let the edge of single new cube be a cm.
Diagonal of a single new cube= 12\(\sqrt{3}\) cm (given)
a\(\sqrt{3}\) = 12\(\sqrt{3}\)
a = \(\frac{12 \sqrt{3}}{\sqrt{3}}\)
a = 12 cm
Volume of a single new case = a³
= (12)³ = 1728 cm³
Since, three cubes are melted and recast into a single cube.
∴ Sum of the volumes of three cubes = Volume of a single new cube
⇒ 216x³ = 1728
⇒ x³ = \(\frac{1728}{216}\)
⇒ x³ = 8
⇒ x = \(\sqrt{3}{8}\) = 2 cm
∴ Edges of three metallic cubes are 3 × 2 cm, 4 × 2 cm and 5 × 2 cm
= 6 cm, 8 cm and 10 cm
Hence, edges of the three metallic cubes = 6 cm, 8 cm and 10 cm.

Question 16.
A solid cube is cut into three cuboids of equal volumes. Find the ratio of the total surface area of cube to one of the cuboid.
Solution:
Let the edge of the solid cube be a units.
Since, cube is cut into three cuboids of equal volumes.
Dimensions of each of the cuboid are length = a units, breadth = a units
and height = \(\frac{a}{3}\) units
Total surface area of the cube = 6a²
and total surface area of the one cuboid.

Hence, ratio of the total surface area of cube to one of the cuboid = 9 : 5.

Question 17.
A cone of radius 8 cm is filled with water. If the water is poured into a cylinder of radius 12 cm, the height of the water rises 1.8 cm, find the height of the cone.
Solution:
We have,
Radius of a cone (r) = 8 cm
Radius of a cylinder (R) = 12 cm
Water level in the cylinder (H) = 1.8 cm
Let the height of the cone be h cm.

Since, water of cone poured into a cylinder.
∴ Volume of water in cone = Volume of water in cylinder upto height 1.8 cm

Hence,height of the cone = 12.15 cm.

Question 18.
Find the number of coins having 2.8 cm as diameter and 0.25 cm as thickness, to be melted to form a right circular cylinder of height 10 cm and diameter 5.6 cm.
Solution:
We have, Diameter of a coin (d) = 2.8 cm
∴ Radius of a coin (r) = \(\frac{2.8}{2}\) = 1.4 cm
Thickness of a coin (h) = 0.25 cm
Let the number of coins be x.
Volume of 1 coin = πr²h
\(\frac{22}{7}\) × 1.4 × 1.4 × 0.25
Volume of x coins = x × \(\frac{22}{7}\) × 1.4 × 1.4 × 0.25
Diameter of recast cylinder (D) = 5.6 cm, (given)
∴ Radius of recast cylinder (R) = \(\frac{5.6}{2}\)
= 2.8 cm.
And height of recast cylinder (H) = 10 cm, (given)
∴ Volume of recast cylinder = πR²H
= \(\frac{22}{7}\) × 2.8 × 2.8 × 10
Since x coins melted and recast a cylinder.
∴ Volume of x coins = Volume of recast cylinder
⇒ x × \(\frac{22}{7}\) × 1.4 × 1.4 × 0.25 = \(\frac{22}{7}\) × 2.8 × 2.8 × 10
⇒ x × 1.4 × 1.4 × 0.25 = 2.8 × 2.8 × 10
⇒ x = \(\frac{2.8 \times 2.8 \times 10}{1.4 \times 1.4 \times 0.25}\)
⇒ x = 160
Hence, number of coins = 160.

Question 19.
Water is being pumped out through a circular pipe whose internal diameter is 7 cm. If the speed of water is 72 cm per sec. how many litres of water are being pumped out in 2 hours?
Solution:
We have,
Diameter of circular pipe (d) = 7 cm
∴ Radius of circular pipe (r) = \(\frac{7}{2}\) = 3.5 cm
= 0.035 m3
Speed of water flow through a pipe = 72 cm/sec
= \(\frac{\frac{72}{100}}{\frac{1}{60 \times 60}}\) m/hr
= \(\frac{72}{100}\) × 60 × 60 m/hr
= 2592 m/hr
∴ In 2 hrs. length of water that flows through a pipe (h) = 2592 × 2 m = 5184 m
Volume of water in 2 hrs. that flows through a pipe = πr²h
\(\frac{22}{7}\) × (0.035)² × 5184
= 19.9584 m³
= 19958.4 litres
Hence, volume of water in 2 hrs. that flows through a pipe = 19958.4 litres.

Question 20.
Cost of painting the total surface area of a cylinder at the rate of Rs. 5 per m² is Rs. 1540. The height of the cylinder is 3 times its radius of the base. Find the volume of the cylinder.
Solution:
Let the radius of the base of a cylinder be x m, then
Height of the cylinder = 3x m
Rate of painting= Rs. 5 per m², (given)
Total cost of painting = Rs. 1540, (given)

So, radius of cylinder = 3.5 m and height of the cylinder = 3 × 3.5 = 10.5 m
∴ Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × (3.5)² × 10.5
= 404.25 m³
Hence,volume of the cylinder = 404.25 m³.

Long Answer Type Questions

Question 1.
Ratio of length and breadth of a room is 4 : 3. The cost of papering the walls at Rs. 1.5 per m² is Rs. 265.5 and cost of carpeting the floor of a room is at Rs. 140 per m² is Rs. 15120. If 1 door and 2 windows occupy 12 m², then find the dimensions of the room.
Solution:
We have,
Ratio of length : breadth = 4 : 3
Let length and breadth of a room be 4x m and 3x m respectively.
Rate of carpeting the floor = Rs. 140 per m²
Total cost of carpeting the floor = Rs. 15120
Floor area of the room = \(\frac{\text { Total cost }}{1 \mathrm{~m}^2 \cos t}\)
\(\frac{15120}{140}\) = 108 m² …(i)
Again,floor area of the room = 4x × 3x
⇒ Floor area of the room = 12x² …(ii)
From (i) and (ii), we get
⇒ 12x² = 108
⇒ x² = \(\frac{108}{12}\)
⇒ x² = 9
⇒ x = \(\sqrt{9}\) = ±3
So, length of room = 4 × 3 = 12 m and
breadth of the room = 3 × 3 = 9 m.
Let the height of the room be h m.
Area of four walls of a room = 2(l + b) × h
= 2(12 + 9) × h
= 2 × 21 × h = 42h m².
Area of four walls of a room excluding 1 door and 2 windows = (42h – 12) m² …(iii)
Rate of the papering the walls = Rs. 1.5 per m²
Total cost of the papering of the walls = Rs. 265.5
Area of four walls of a room excluding 1 door 2 windows
\(\frac{\text { Total cost }}{1 m^2 \cos t}=\frac{265.5}{1.5}\)
= 177 m² ……(iv)
From (iii) and (iv), we get
42h – 12 = 177
⇒ 42h = 177 + 12
⇒ 42h = 189
⇒ h = \(\frac{189}{42}\)
h = 4.5 m
Hence, dimensions of a room are 12 m × 9 m × 4.5 m.

Question 2.
A solid cylinder has total surface area of 180π. Its curved surface area is \(\frac{3}{5}\) of its total surface area. Find the radius and height of the cylinder.
Solution:
We have,
Total surface area of a cylinder = 180π
2πrh + 2πr² = 180π ……(i)
According to question,
Curved surface area of a cylinder = \(\frac{3}{5}\) of its total surface area
⇒ 2πrh = \(\frac{3}{5}\) of 180π
⇒ 2πrh = 108π ……(ii)
Subtracting (ii) from (i), we get
Total surface area – curved surface area
= 180π – 108π
⇒ 2πrh + 2πr² – 2πrh = 72π
⇒ 2πr² = 72π
⇒ r² = \(\frac{72 \pi}{2 \pi}\)
⇒ r² = 36
⇒ r = \(\sqrt{36}\)
⇒ r = ±6 cm
Since, radius of the cylinder cannot be negative.
Therefore, we neglect r = -6 cm
∴ r = 6 cm
Putting the value of r in (ii), we get
2π × 6 × h = 108π
⇒ 12πh = 108π
⇒ h = \(\frac{108 \pi}{12 \pi}\)
⇒ h = 9 cm
Hence, radius and height of a cylinder are 6 cm and 9 cm respectively.

Question 3.
A conical tent has the area of its base as 154 m and that of its curved surface area Rs 550 m². Find the height of the tent.
Solution:
We have,
Base area of a conical tent = 154 m²
⇒ πr² = 154
⇒ r² = \(\frac{154}{\pi}\)
⇒ r² = \(\frac{154 \times 7}{22}\)
⇒ r² = 7 × 7
⇒ r = \(\sqrt{7 \times 7}\) = 7 m
and curved surface area of a conical tent = 550 m²
⇒ πrl = 550
⇒ \(\frac{22}{7}\) × 7 × l = 550
⇒ 22 × l = 550
⇒ l = \(\frac{550}{22}\)
⇒ l = 25 m
Now l² = h² + r²
⇒ h² = l² – r²
⇒ h² = (25)² – (7)²
⇒ h² = (25 + 7) (25 – 7)
⇒ h² = 32 × 18
⇒ h = \(\sqrt{32 \times 18}\)
⇒ h = \(\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3}\)
⇒ h = 2 × 2 × 2 × 3
⇒ h = 24 m
Hence height of the tent = 24 metres.

Question 4.
A semicircular thin sheet of metal of diameter 28 cm is bent and an open conical cup is made. Find the height and surface area of the cup.
Solution:
We have, Diameter of the semicircular sheet (d) = 28 cm
∴ Radius of the semicircular sheet (r) = \(\frac{28}{2}\)
= 14 cm
Perimeter of the semicircular sheet = πr
= π × 14 = 14π
Let r₁ be the base radius, h be the height of conical cup.
Circumference of the circular top of the conical cup = Perimeter of the semicircular sheet
2πr₁ = 14π
r₁ = \(\frac{14 \pi}{2 \pi}\)
r₁ = 7 cm

and slant height of the conical cup (l) = 14 cm
l² = h² + r₁²
⇒ h² = l² – r₁²,
⇒ h² = 14² – 7²
⇒ h² = (14 + 7)(14 – 7)
⇒ h² = 21 × 7
⇒ h = \(\sqrt{21 \times 7}\)
⇒ h = \(\sqrt{3 \times 7 \times 7}\)
⇒ h = 7\(\sqrt{3}\) cm
Curved surface area of the conical cup
= πr₁l
= \(\frac{22}{7}\) × 7 × 14
= 308 cm²
Hence, height of the conical cup is 7\(\sqrt{3}\) cm and curved surface area of the conical cup is 308 cm².

Question 5.
A right triangle whose sides are 12 cm and 16 cm is made to revolve about its hypotenuse. Find the surface area of the double cone so formed.
Solution:
Let ABC be right triangle, right angled at A whose sides AB and AC measure 12 cm and 16 cm respectively, then
Hypotenuse (BC) length = \(\sqrt{12^2+16^2}\)
= \(\sqrt{144+256}\)
= \(\sqrt{400}\) = 20 cm

By revolving ΔABC around its hypotenuse BC, the double cone solid is generated. This solid consists of two cones (BAA’) and (CAA’).
AO or A’O is the radius of the common base of the double cone.
Let BO = x and AO = y, then
OC = 20 – x
OC and OB are the heights of the double cones (CAA’) and (BAA’) respectively.
In right ΔAOB, we have
AB² = AO² + OB²
(By Pythagoras theorem)
⇒ 12² = y² + x²
⇒ x² + y² = 144 … (1)
In right ΔAOC, we have
AC² = AO² + OC²
⇒ 16² = y² + (20 – x)²
⇒ 256 = y² + 400 + x² – 40x
⇒ 256 = 144 + 400 – 40x [using (1)]
⇒ 256 = 544 – 40x
⇒ 40x = 544 – 256
⇒ 40x = 288 ⇒ x = \(\frac{288}{40}\) = 7.2 cm
Putting the value of x in (1), we get
(7.2)² + y² = 144
⇒ 51.84 + y² = 144
⇒ y² = 144 – 51.84
⇒ y² = 92.16
⇒ y = \(\sqrt{92.16}\) = 9.6 cm
Thus radius of double cone so formed is 9.6 cm and slant heights of cone (CAA’) is 16 cm and cone (BAA’) is 12 cm.
Surface area of double cone is generated = C.S.A. of the cone (CAA’) + C.S.A. of the cone (BAA’)
= π × AO × AC + π × AO × AB
= π[9.6 × 16 + 9.6 × 12]
= π[153.6 + 115.2]
= \(\frac{22}{7}\) × 268.8 = 844.8 cm²
Hence, surface area of double cone so formed = 844.8 cm².

Question 6.
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 7 cm and heights of the cylindrical and conical portions are 12 cm and 8.4 cm respectively. Find the total surface area of the solid toy.
Solution:
We have,
Common diameter of the cylinder, a hemisphere and a cone (d) = \(\frac{7}{2}\) 7 cm
∴ Common radius of the cylinder, a hemisphere and a cone (r) = 3.5 cm
Height of the cylinder (H) = 12 cm
and height of the cone (h) = 8.4 cm

∴ Slant height of the cone (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(8.4)^2+(3.5)^2}\)
= \(\sqrt{70.56+12.25}\)
= \(\sqrt{82.81}\)
= 9.1 cm
Total surface area of the solid toy = C.S.A. of the hemispherical portion + C.S.A. of the cylindrical portion + C.S.A. of the conical portion
= 2πr² + 2πrH + πrl = πr(2r + 2H + l)
= \(\frac{22}{7}\) × 3.5(2 × 3.5 + 2 × 12 + 9.1)
= 11 × (7 + 24 + 9.1) = 11 × 40.1
= 441.1 cm²
Hence, total surface area of the solid toy = 441.1 cm².

Question 7.
Rain water which falls on a flat rectangular surface of length 6 m and breadth, 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if the rain fall is 1 cm? Give your answer to the nearest integer. (use π = 3.14)
Solution:
We have Length of rectangular surface (l) = 6 m = 600 cm
Breadth of rectangular surface (b) = 4 m = 400 cm
Height of rain fall on rectangular surface (h) = 1 cm
∴ Volume of water of rain fall = l × b × h
= 600 × 400 × 1
and internal radius of cylindrical vessel (r) = 20 cm
Let the height of water in the cylindrical vessel be h’ cm.
Volume of water in the cylindrical vessel
= πr²h’
= 3.14 × 20² × h’
According to question,
Rain water which falls on a flat rectangular surface is transferred into a cylindrical vessel.
Therefore,volume of water of rain fall = volume of water in the cylindrical vessel
⇒ 600 × 400 × 1 = 3.14 × 20² × h’
⇒ \(\frac{600 \times 400}{3 \cdot 14 \times 20^2}\) = h’
⇒ \(\frac{600 \times 400}{3.14 \times 400}\) = h’
⇒ h’ = \(\frac{600}{3.14}\)
⇒ h’ = 191.082 cm = 191 cm
Hence, height of water in the cylindrical vessel = 191 cm.

Question 8.
A cylindrical water tank of diameter 3.0 m and height 2.4 m is being fed by a pipe of diameter 4.8 cm through which water flows at the rate of 5 m/sec. Calculate the time taken by pipe to fill the tank.
Solution:
We have,
Diameter of the cylindrical tank (D) = 3 m
∴ Radius of the cylindrical tank (R) = \(\frac{3}{2}\) = 1.5 m = 150 cm
Height of the cylindrical tank (H) = 2.4 m = 240 cm
Diameter of the pipe (d) = 4.8 cm
∴ Radius of the pipe (r) = \(\frac{4.8}{2}\) = 2.4 cm

Speed of the water that flows through the pipe = 5 m/sec
Length of water that flows through the pipe in 1 sec (h) = 5 m = 500 cm
Volume of water that flows in 1 second
= πr²h = \(\frac{22}{7}\) × (2.4)² × 500
Let the time taken by pipe to fill the tank be x seconds.
Volume of water that flows in x seconds
= x × \(\frac{22}{7}\) × (2.4)² × 500
Volume of the water of cylindrical water tank = πR²H
= π × (150)² × 240
= \(\frac{22}{7}\) × 150 × 150 × 240
Since, cylindrical water tank is being fed by a pipe.
∴ Volume of water that flows in x seconds = Volume of the water of cylindrical water tank
⇒ x × \(\frac{22}{7}\) × (2.4)2 × 500
= \(\frac{22}{7}\) × 150 × 150 × 240
⇒ x × 2.4 × 2.4 × 500 = 150 × 150 × 240
⇒ x × 2880 = 5400000
⇒ x = \(\frac{5400000}{2880}\)
⇒ x = 1875 seconds
⇒ x = 31 minutes 15 seconds
Hence,time taken by the pipe = 31 min 15 sec.

Question 9.
The diameter of the cylinder is increased by 25%, then how many percent its height must be decreased so that its volume may remain same.
Solution:
Let the diameter of the cylinder be 2x and its height be h
Radius of the cyļinder = \(\frac{2 x}{2}\) = x
∴ Volume of the cylinder = πx²h
Since, diameter is increased by 25%. Then Increased diameter = 2x + 25% of 2x
= 2x + \(\frac{25}{100}\) × 2x
= 2x + \(\frac{x}{2}=\frac{5 x}{2}\)
New radius = \(\frac{5 x}{4}\)
Let new height be h’.

Hence,decrease % in height = 36%.

Question 10.
A solid metal sphere, 6 cm in diameter, is formed into a cylindrical tube 10 cm in external diameter and 4 cm in length. Find the thickness of the tube.
Solution:
We have,
Diameter of solid sphere = 6 cm
∴ Radius of solid sphere (r) = \(\frac{6}{2}\) = 3 cm
Length of cylindrical tube (h) = 4 cm
External diameter of the cylindrical tube = 10 cm
∴ External radius of the cylindrical tube (r₁) = \(\frac{10}{2}\) = 5 cm
Let the internal radius of cylindrical tube be r₂ cm.
Since, cylindrical tube formed from metal sphere.
∴ Volume of metal of cylindrical tube = Volume of metal sphere
⇒ π[r₁² – r₂²] × h = \(\frac{4}{3}\)πr³
⇒ π[5² – r₂²] × 4 = \(\frac{4}{3}\)π × (3)³
⇒ (25 – r₂²) × 4 = \(\frac{4}{3}\) × 3 × 3 × 3
⇒ 25 – r₂² = 3 × 3
⇒ r₂² = 25 – 9
⇒ r₂² = 16
⇒ r₂² = 4²
⇒ r₂ = 4 cm
∴ Thickness of the tube = r₁ – r₂
= 5 – 4 = 1 cm
Hence, thickness of the tube = 1 cm.

Question 11.
A cylindrical container is filled with ice cream whose diameter is 12 cm and height 15 cm. Whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is four times the radius of its base, find the height of the ice-cone.
Solution:
We have,
Diameter of cylindrical container = 12 cm
∴ Radius of cylindrical container (R) = \(\frac{12}{2}\) = 6 cm
Height of the cylindrical container (H) = 15 cm
∴ Volume of ice-cream in cylindrical container = πR²H
= π × 6² × 15 = 540π cm3

Let radius of base of cone ice-cream be x cm, then height of the conical portion = 4x cm
∴ Volume of 1 ice-cream cone = Volume of conical portion + Volume of hemispherical portion
= \(\frac{1}{3}\)πx² × 4x + \(\frac{2}{3}\)πx³
= \(\frac{1}{3}\)π[4x³ + 2x³]
= \(\frac{1}{3}\)π × 6x³ = 2πx³
Volume of 10 ice-cream cones = 10 × 2πx³ = 20πx³ cm³
Since, ice-cream of cylindrical container is distributed to 10 children in equal ice-cream cones.
∴ Volume of 10 ice-cream cones = Volume of ice cream in cylindrical container
⇒ 20πx³ = 540π
⇒ x³ = \(\frac{540 \pi}{20 \pi}\)
⇒ x³ = 27
⇒ x³ = 33
⇒ x = 3 cm
∴ Radius of ice-cream cone = 3 cm
and height of the conical portion = 4 × 3 = 12 cm
∴ Height of the ice-cream cone = 12 + 3 = 15 cm
Hence, height of the ice-cream cone = 15 cm.

Question 12.
The radius of a right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Solution:
Let the radius of cylinder be r and its height be h, then
Volume of cylinder (V₁) = πr²h
After increasing radius by 20%.
New radius = r + 20% of r
= r + \(\frac{20}{100}\) × r
= r + \(\frac{r}{5}=\frac{6 r}{5}\)
After decreasing height by 20%.

Hence, volume of cylinder increases by 15.2%.

Question 13.
The total surface area of a hollow metal cylinder, open both tops, is 3168 cm². Length of cylinder is 21 cm and volume of metal used in making the cylinder is 4158 cm³. Find the thickness of the metal.

Solution:
Let the external radius of hollow cylinder be R cm and internal radius of hollow cylinder be r сm.
We have,
Length of hollow cylinder (h) = 21 cm
Volume of metal used in making the hollow cylinder = 4158 cm³
⇒ π(R² – r²) × h = 4158
⇒ π(R + r) (R – r) × 21 = 4158
⇒ π(R + r) (R – r) = \(\frac{4158}{21}\) = 198 …(1)
and total surface area = 3168 cm²
⇒ 2πRh + 2πrh + 2π(R² – r²) = 3168
⇒ 2πh(R + r) + 2π(R + r) (R – r) = 3168
⇒ 2π(R + r) [h + R – r] = 3168
⇒ π(R + r) [21 + R – r] = \(\frac{3168}{2}\) = 1584 ……(2)
Dividing (1) by (2), we get
\(\frac{\pi(R+r)(R-r)}{\pi(R+r)[21+R-r]}=\frac{198}{1584}\)
⇒ \(\frac{R-r}{21+R-r}=\frac{1}{8}\)
⇒ 8R – 8r = 21 +R – r
⇒ 7R – 7r = 21
⇒ 7(R – r) = 21
⇒ R – r = \(\frac{21}{7}\) = 3 ……(3)
Putting this value in (1), we get
⇒ π(R + r) × 3 = 198
⇒ \(\frac{22}{7}\) × 3(R + r) = 198
⇒ \(\frac{66}{7}\)(R + r) = 198
⇒ R + r = \(\frac{198 \times 7}{66}\)
⇒ R + r = 21 …….(4)
On adding (3) and (4), we get
R – r = 3
R + r = 21
2R = 24
⇒ R = \(\frac{24}{2}\) = 12 cm
Putting the value of R in (4), we get
12 + r = 21
⇒ r = 21 – 12 = 9 cm
Thickness of the metal
= R – r = 12 – 9 = 3 cm
Hence, thickness of the metal = 3 cm.

Question 14.
6 Tennis balls, diameter 70 mm each are placed in cylindrical card tube. Prove that volume of unfilled space in the tube is 33.33% of volume of the tube.

Solution:
We have,
Diameter of each tennis ball = 70 mm
∴ Radius of each tennis ball (r) = \(\frac{70}{2}\) = 35cm
Volume of 1 tennis balls = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(35)^3\)
= \(\frac{539000}{3} \mathrm{~mm}^3=\frac{539}{3} \mathrm{~cm}^3\)
Volume of 6 tennis ball = \(\frac{539}{3}\) × 6
= 1078 cm³
Radius of the cylindrical card tube (r) = 35 mm = 3.5 cm
Height of the cylindrical card tube
(h) = 6 × diameter of 1 tennis ball
= 6 × 70 = 420 mm
= 42 cm
∴ Volume of the cylindrical card tube
= πr²h = \(\frac{22}{7}\) × (3.5)² × 42
= 1617 cm³
Volume of unfilled space in the tube = Volume of the cylindrical card tube – Volume of 6 tennis balls
= 1617 – 1078
= 539 cm³
Volume of unfilled space % in the tube
= \(\frac{539}{1617}\) × 100%
= \(\frac{100}{3}\)% = 33.33%
Hence, volume of unfilled space is 33.33% of tube.
Hence proved.

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
The length, breadth and height of cuboid are 12 cm, 10 cm and 7 cm. Its total surface area is :
(a) 274 cm²
(b) 548 cm²
(c) 840 cm²
(d) 308 cm²
Answer:
(b) 548 cm²

Question 2.
The total surface area of a cube is 150 cm, then its volume is :
(a) 125 cm³
(b) 120 cm³
(c) 110 cm³
(d) 100 cm³
Answer:
(a) 125 cm³

Question 3.
If total surface area of a cube is equal to its volume. Edge of cube is :
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
Answer:
(b) 6 cm

Question 4.
Length of the longest pole that can be put in a room of demensions (10 m × 10 m × 5 m) is :
(a) 15 m
(b) 16 m
(c) 10 m
(d) 12 m
Answer:
(a) 15 m

Question 5.
The maximum length of pencil that can be placed in a rectangular box of dimensions (6 cm × 4 cm × 2\(\sqrt{3}\) cm) is :
(a) 8 cm
(b) 6\(\sqrt{3}\) cm
(c) 5\(\sqrt{3}\) cm
(d) 4\(\sqrt{3}\) cm
Answer:
(a) 8 cm

Question 6.
A 4 cm cube cut into 1 cm cubes. The total surface area of all the small cubes is :
(a) 96 cm²
(b) 64 cm²
(c) 24 cm²
(d) 384 cm²
Answer:
(d) 384 cm²

Question 7.
Two cubes each with 5 cm edge are joined end to end. The volume of resulting cuboid is :
(a) 125 cm³
(b) 150 cm³
(c) 250 cm³
(d) 300 cm³
Answer:
(c) 250 cm³

Question 8.
If three cubes of metal whose edges are 9 cm, 12 cm and 15 cm made into a single cube, then edge of the new cube so formed is :
(a) 15 cm
(b) 16 cm
(c) 18 cm
(d) 21 cm
Answer:
(c) 18 cm

Question 9.
The perimeter of one face of a cube is 32 cm. The lateral surface area of cube is :
(a) 256 cm²
(b) 384 cm²
(c) 216 cm²
(d) 300 cm²
Answer:
(a) 256 cm²

Question 10.
The length of a diagonal of a cube is 6\(\sqrt{3}\) cm. Surface area of the cube is :
(a) 648 cm²
(b) 432 cm²
(c) 216 cm²
(d) 144 cm²
Answer:
(c) 216 cm²

Haryana State Board HBSE 9th Class Science Important Questions Chapter 10 गुरुत्वाकर्षण Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 10 गुरुत्वाकर्षण

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
गुरुत्वाकर्षण से क्या अभिप्राय है?
उत्तर:
पृथ्वी की सभी वस्तुएँ एक-दूसरे को आकर्षित करती हैं, वस्तुओं के बीच इस आकर्षण बल को गुरुत्वाकर्षण कहते हैं।

प्रश्न 2.
गुरुत्वाकर्षण बल को सबसे पहले किसने बताया?
उत्तर:
सर आइजक न्यूटन ने।

प्रश्न 3.
दो वस्तुओं के बीच का गुरुत्वाकर्षण बल किस दिशा में कार्य करता है?
उत्तर:
दो वस्तुओं के बीच का गुरुत्वाकर्षण बल उनके द्रव्यमान केंद्रों को मिलाने वाली रेखा की दिशा में कार्य करता है।

प्रश्न 4.
हमारे सौरमंडल के अस्तित्व के लिए कौन-सा बल उत्तरदायी है?
उत्तर:
गुरुत्वाकर्षण बल सौरमंडल के लिए उत्तरदायी है।

प्रश्न 5.
‘G’ किसे व्यक्त करता है?
उत्तर:
‘G’ गुरुत्वाकर्षण स्थिरांक (नियतांक) को व्यक्त करता है।

प्रश्न 6.
‘G’ का मान कितना है?
उत्तर:
‘G’ का मान 6.673 x 10^-11 Nm²/kg² है।

प्रश्न 7.
पृथ्वी का द्रव्यमान कितना है?
उत्तर:
पृथ्वी का द्रव्यमान (Me) = 6 x 10²⁴ kg (लगभग)।

प्रश्न 8.
पृथ्वी का अर्द्धव्यास कितना है?
उत्तर:
पृथ्वी का अर्द्धव्यास (Re) = 6.4 x 10⁶ m है।

प्रश्न 9.
पृथ्वी के किस भाग पर ‘g’ का मान अधिक तथा किस भाग पर कम होता है?
उत्तर:
‘g’ का मान पृथ्वी के ध्रुवों पर अधिक तथा भूमध्य रेखा पर कम होता है।

प्रश्न 10.
R दूरी पर रखी क्रमशः m₁ तथा m₂ द्रव्यमान वाली दो वस्तुओं के बीच आकर्षण बल का सूत्र लिखें।
उत्तर:
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{R}^2}\)

प्रश्न 11.
गुरुत्वीय त्वरण (g) किसे कहते हैं?
उत्तर:
वह त्वरण जिसके द्वारा पृथ्वी किसी वस्तु को अपने केंद्र की ओर आकर्षित करती है, ‘गुरुत्वीय त्वरण’ कहलाता है।

प्रश्न 12.
क्या पृथ्वी की ओर गिरते हुए पिंड का त्वरण उसके द्रव्यमान पर निर्भर करता है?
उत्तर:
नहीं, पृथ्वी की ओर गिरते हुए पिंड का त्वरण उसके द्रव्यमान पर निर्भर नहीं करता।

प्रश्न 13.
दो वस्तुओं के बीच की दूरी दुगुनी कर देने पर उनके बीच लगने वाला आकर्षण बल कितना होगा?
उत्तर:
आकर्षण बल एक-चौथाई रह जाएगा।

प्रश्न 14.
चंद्रमा पर किसी वस्तु का भार पृथ्वी की तुलना में कितना होता है?
उत्तर:
1/6 गुना।

प्रश्न 15.
अभिकेंद्र त्वरण क्या है?
उत्तर:
जब कोई वस्तु वृत्ताकार पथ पर गति करती है तो उसमें वेग परिवर्तन के कारण त्वरण उत्पन्न होता है जिसे अभिकेंद्र त्वरण कहते हैं।

प्रश्न 16.
अभिकेंद्र बल किसे कहते हैं?
उत्तर:
अभिकेंद्र त्वरण को उत्पन्न करने वाले बल को अभिकेंद्र बल कहते हैं। यह सदैव केंद्र के अनुदिश होता है।
अर्थात् F = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\)

प्रश्न 17.
‘g’ किसको व्यक्त करता है?
उत्तर:
‘g’ गुरुत्वीय त्वरण को व्यक्त करता है।

प्रश्न 18.
‘g’ का मान पृथ्वी तल के निकट कितना है?
उत्तर:
‘g’ (गुरुत्वीय त्वरण) का मान पृथ्वी तल के निकट 9.8 m/s² है।

प्रश्न 19.
किस स्थान पर ‘g’ का मान शून्य होता है?
उत्तर:
पृथ्वी के केंद्र पर ‘g’ का मान शून्य होता है।

प्रश्न 20.
‘g’ तथा ‘G’ का संबंध सूत्र लिखें।
उत्तर:
g = \(\frac{\mathrm{G} \times \mathrm{M}_{\mathrm{e}}}{\mathrm{R}^2}\)

प्रश्न 21.
गुरुत्वाकर्षण बल किन बातों पर निर्भर करता है?
उत्तर:

• वस्तुओं के द्रव्यमान पर।
• वस्तुओं के बीच की दूरी पर।

प्रश्न 22.
पृथ्वी से चंद्रमा की दूरी कितनी है?
उत्तर:
पृथ्वी की त्रिज्या का 60 गुना = 384000 km

प्रश्न 23.
यदि कोई वस्तु किसी ऊँचाई से शून्य वेग से छोड़ी जाए तो t सेकंड में वह कितनी दूरी तय करती है?
उत्तर:
तय की गई दूरी h = \(\frac { 1 }{ 2 }\) gt²

प्रश्न 24.
‘g’ तथा G में से किसका मान स्थिर रहता है और किसका मान स्थिर नहीं रहता है?
उत्तर:
G का मान पृथ्वी के सभी स्थानों पर स्थिर रहता है, परंतु ‘g’ का मान ध्रुवों पर अधिक तथा भूमध्य रेखा पर कम हो जाता है।

प्रश्न 25.
पृथ्वी सूर्य की परिक्रमा करने में कितना समय लेती है?
उत्तर:
पृथ्वी सूर्य की परिक्रमा करने में 365\(\frac { 1 }{ 4 }\) दिन लेती है।

प्रश्न 26.
चंद्रमा पृथ्वी की परिक्रमा करने में कितना समय लेता है?
उत्तर:
चंद्रमा पृथ्वी की परिक्रमा करने में 27 दिन, 8 घंटे लेता है।

प्रश्न 27.
द्रव्यमान से क्या अभिप्राय है? इसकी इकाई भी लिखें।
उत्तर:
वस्तु में विद्यमान पदार्थ की मात्रा को द्रव्यमान कहते हैं, इसकी इकाई किलोग्राम है।

प्रश्न 28.
किसी वस्तु के भार से क्या अभिप्राय है? इसकी मानक इकाई क्या है?
उत्तर:
पृथ्वी जिस बल से किसी वस्तु को अपनी ओर खींचती है, उस बल को वस्तु का भार कहते हैं। इसकी मानक इकाई न्यूटन है।

प्रश्न 29.
भारहीनता से क्या अभिप्राय है?
उत्तर:
यह वस्तु की वह अवस्था है जब किसी ग्रह (पृथ्वी) का गुरुत्व क्रिया करना बंद कर देता है तो अंतरिक्षयान में बैठा व्यक्ति भारहीनता की स्थिति में होता है।

प्रश्न 30.
द्रव्यमान केंद्र से क्या अभिप्राय है?
उत्तर:
किसी वस्तु का द्रव्यमान केंद्र वह बिंदु है जिस पर वस्तु का समस्त द्रव्यमान आपेक्षित है।

प्रश्न 31.
गुरुत्व केंद्र से क्या अभिप्राय है?
उत्तर:
किसी वस्तु का गुरुत्व केंद्र वह बिंदु है जिस पर समस्त गुरुत्व बल कार्य करता है।

प्रश्न 32.
नियमित आकार की वस्तुओं का गुरुत्व केंद्र कहाँ होता है?
उत्तर:
नियमित आकार व एक समान घनत्व वाली वस्तुओं का गुरुत्व केंद्र उनके ज्यामितीय केंद्र पर होता है।

प्रश्न 33.
क्या होगा यदि दो वस्तुओं के द्रव्यमान और त्वरण दोनों बराबर हो जाएँ?
उत्तर:
यदि दो वस्तुओं के द्रव्यमान और त्वरण दोनों बराबर हो जाएँ तो वे एक-दूसरे की ओर चलती हुई दिखाई देंगी।

प्रश्न 34.
गुरुत्व बल से क्या अभिप्राय है?
उत्तर:
पृथ्वी और किसी वस्तु के बीच के आकर्षण बल को गुरुत्व बल कहते हैं।

प्रश्न 35.
भार को मापने के लिए किस तुला का प्रयोग किया जाता है?
उत्तर:
भार को मापने के लिए कमानीदार तुला का प्रयोग किया जाता है।

प्रश्न 36.
द्रव्यमान को मापने के लिए किस तुला का प्रयोग किया जाता है?
उत्तर:
द्रव्यमान को मापने के लिए भौतिक तुला का प्रयोग किया जाता है।

प्रश्न 37.
वस्तु का भार चंद्रमा पर पृथ्वी की तुलना में कम क्यों होता है?
उत्तर:
क्योंकि चंद्रमा पर गुरुत्वीय त्वरण पृथ्वी की तुलना में कम होता है।

प्रश्न 38.
25 kg द्रव्यमान तथा 2 kg द्रव्यमान के दो पत्थरों को एक मीनार की चोटी से एक साथ नीचे गिराने पर कौन-सा पत्थर पहले जमीन पर पहुंचेगा?
उत्तर:
गुरुत्वीय त्वरण वस्तु के द्रव्यमान पर निर्भर न होने के कारण दोनों पत्थर एक-साथ पृथ्वी पर पहुंचेंगे।

प्रश्न 39.
मेज पर रखी हुई दो वस्तुओं के बीच गुरुत्वाकर्षण बल होता है। इस बल के होते हुए भी वे एक-दूसरे की ओर गति क्यों नहीं करते?
उत्तर:
दोनों वस्तुओं के बीच गुरुत्वाकर्षण बल इतना क्षीण होता है जिससे वस्तुएँ गति नहीं कर पातीं।

प्रश्न 40.
पृथ्वी एक लौह पिन को गुरुत्वाकर्षण बल से नीचे की ओर आकर्षित करती है तो भी चुंबक लौह पिन को पृथ्वी के आकर्षण की दिशा के विपरीत ऊपर की ओर उठा लेता है। क्यों?
उत्तर:
क्योंकि चुंबक द्वारा लौह पिन पर लगाया गया आकर्षण बल, पिन पर लगे गुरुत्वाकर्षण बल की अपेक्षा अधिक होता है।

प्रश्न 41.
पृथ्वी पर उपस्थित दो वस्तुओं के बीच गुरुत्वाकर्षण बल अधिक होता है या वस्तु और पृथ्वी के बीच लगा गुरुत्वाकर्षण बल?
उत्तर:
वस्तु और पृथ्वी के बीच लगा गुरुत्वाकर्षण बल अधिक होता है।

प्रश्न 42.
किसी वस्तु का भार शून्य कहाँ होता है?
उत्तर:
पृथ्वी के केंद्र पर वस्तु का भार शून्य होता है।

प्रश्न 43.
u, v, g तथा t में क्या संबंध है?
उत्तर:
v = u + gt

प्रश्न 44.
कार्तीय (कार्टीजियन) निर्देश तंत्र की परिपाटी के अनुसार ‘g’ का चिहन क्या होता है?
उत्तर:
g सदैव ऋणात्मक लिया जाता है।

प्रश्न 45.
प्रक्षेप्य परास से क्या अभिप्राय है?
उत्तर:
किसी प्रक्षेप्य द्वारा तय की गई अधिकरण क्षैतिज दूरी को प्रक्षेप्य परास कहते हैं।

प्रश्न 46.
प्रक्षेप्य के उच्चतम बिंदु पर वेग तथा त्वरण के बीच कितना कोण होता है?
उत्तर:
समकोण (90°)।

प्रश्न 47.
पृथ्वी की सूर्य से दूरी कितनी है?
उत्तर:
1.5 x 10¹¹ मीटर।

प्रश्न 48.
प्रणोद किसे कहते हैं?
उत्तर:
किसी वस्तु की सतह के लंबवत् लगने वाले बल को प्रणोद कहते हैं।

प्रश्न 49.
प्रणोद बल का दैनिक जीवन में एक उदाहरण दीजिए।
उत्तर:
ड्राईंग बोर्ड पर पिन लगाते समय हमारे हाथ के अंगूठे द्वारा लगाया गया बल बोर्ड पर लंबवत् दिशा में कार्य करता है। अतः यह प्रणोद बल होता है।

प्रश्न 50.
दाब किसे कहते हैं? इसका S. I मात्रक क्या है?
उत्तर:
एकांक क्षेत्रफल पर लगने वाले प्रणोद को दाब कहते हैं ।

इसका S.I. मात्रक पास्कल (Pa) है।

प्रश्न 51.
प्रणोद का S. I. मात्रक क्या है ?
उत्तर:
न्यूटन (N)।

प्रश्न 52.
दाब का SI मात्रक पास्कल (Pa) किस वैज्ञानिक के सम्मान में रखा गया?
उत्तर:
वैज्ञानिक ब्लैस पास्कल के सम्मान में।

प्रश्न 53.
दाब के बड़े मात्रक को क्या कहते हैं ?
उत्तर:
किलो पास्कल (kPa)।

प्रश्न 54.
काटने, चीरने और सुराख निकालने वाले यंत्र हमेशा नुकीले क्यों रखे जाते हैं?
उत्तर:
काटने, चीरने और सुराख निकालने वाले यंत्र हमेशा नुकीले रखे जाते हैं ताकि प्रणोद कम-से-कम क्षेत्रफल को प्रभावित करे जिससे दाब बढ़ जाए और वस्तु आसानी से काटी, चीरी या सुराखी जा सके।

प्रश्न 55.
मनुष्य का दाब जमीन पर बैठे हुए अधिक पड़ता है अथवा एक जगह खड़े रहने पर, क्यों?
उत्तर:
मनुष्य का दाब एक जगह खड़े रहने पर अधिक पड़ता है, क्योंकि एक जगह खड़े रहने पर क्षेत्रफल बैठे हुए की अपेक्षा कम होता है।

प्रश्न 56.
गहराई का द्रव – दाब पर क्या प्रभाव पड़ता है?
उत्तर:
गहराई के साथ- साथ द्रव – दाब बढ़ता जाता है।

प्रश्न 57.
नमकीन पानी में अंडा क्यों तैरता है?
उत्तर:
पानी में नमक मिलाने से पानी का घनत्व बढ़ जाता है जिससे पानी का उत्प्लावन बल अधिक हो जाता है और अंडा तैरता रहता है।

प्रश्न 58.
वस्तु किस अवस्था में तैरती है?
उत्तर:
यदि वस्तु द्वारा हटाए गए द्रव का भार वस्तु के भार के बराबर होता है तो वस्तु द्रव की सतह पर तैरती रहती है।

प्रश्न 59.
आर्किमिडीज के सिद्धांत पर बनने वाले दो यंत्रों के नाम लिखो।
उत्तर:

• जलयान
• पनडुब्बी।

प्रश्न 60.
दूध की शुद्धता मापने के लिए किस यंत्र का प्रयोग किया जाता है और उसका सिद्धांत क्या है?
उत्तर:
दूध की शुद्धता मापने के लिए लैक्टोमीटर का प्रयोग किया जाता है जोकि आर्किमिडीज के सिद्धांत पर कार्य करता है।

प्रश्न 61.
द्रवों के घनत्व को मापने के लिए यंत्र का नाम और उसका सिद्धांत लिखो।
उत्तर:
हाइड्रोमीटर, जोकि आर्किमिडीज़ के सिद्धांत पर कार्य करता है।

प्रश्न 62.
एकांक आयतन के द्रव्यमान को क्या कहा जाता है?
उत्तर:
घनत्व

प्रश्न 63.
घनत्व का SI मात्रक क्या है?
उत्तर:
किलोग्राम प्रति घनमीटर (kg/m³)।

लघुत्तरात्मक प्रश्न

प्रश्न 1.
यदि किसी पत्थर के टुकड़े को किसी निश्चित ऊँचाई से स्वतंत्र अवस्था में गिरने दिया जाए तो उसके वेग में कौन-कौन से परिवर्तन आएँगे?
उत्तर:
किसी पत्थर के टुकड़े को किसी निश्चित ऊँचाई से स्वतंत्र अवस्था में गिरने देने पर निम्नलिखित वेग परिवर्तन होंगे

• पत्थर का प्रारंभिक वेग शून्य होता है तथा नीचे की ओर आते समय बढ़ता चला जाता है।
• पृथ्वी के निकटतम पत्थर का वेग अधिकतम होता है।
• पृथ्वी पर गिर जाने के बाद पत्थर का वेग शून्य हो जाता है।

प्रश्न 2.
गुरुत्वाकर्षण क्या है? यह किस दिशा में कार्य करता है?
उत्तर:
ब्रह्मांड की प्रत्येक वस्तु दूसरी वस्तु को अपनी ओर आकर्षित करती है। किन्हीं दो वस्तुओं के बीच इस आकर्षण को गुरुत्वाकर्षण कहते हैं। दो वस्तुओं के बीच यह आकर्षण उनके केंद्रों को मिलाने वाली सरल रेखा के अनुदिश कार्य करता है।

प्रश्न 3.
सिद्ध करें कि पृथ्वी की ओर गिराई गई वस्तु में उत्पन्न त्वरण उसके द्रव्यमान पर निर्भर नहीं करता।
उत्तर:
यदि m द्रव्यमान की किसी वस्तु को पृथ्वी के केंद्र से ‘R’ दूरी से गिराएँ तो वस्तु पर पृथ्वी द्वारा लगाया गया बल
F = \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}^2}\)
जिसमें M_e = पृथ्वी का द्रव्यमान, G = गुरुत्वाकर्षण स्थिरांक है।
अतः वस्तु में उत्पन्न त्वरण = F/m (F = ma; a = \(\frac { F }{ m }\))
= \(\frac{\frac{\mathrm{Gm}_{\mathrm{e}^{\mathrm{m}}}}{\mathrm{R}^2}}{\mathrm{~m}}\)
= \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}^2} \times \frac{1}{\mathrm{~m}}=\frac{\mathrm{GM}_{\mathrm{e}}}{\mathrm{R}^2}\)
अतः किसी वस्तु में उत्पन्न त्वरण गिराई गई वस्तु के द्रव्यमान पर निर्भर नहीं करता।

प्रश्न 4.
न्यूटन की गति का तीसरा नियम क्या है? क्या यह नियम गुरुत्वाकर्षण बल पर भी लागू होता है? व्याख्या करो।
उत्तर:
इस नियम के अनुसार, “प्रत्येक क्रिया के समान तथा विपरीत प्रतिक्रिया होती है।” उदाहरणतया गेंद को दीवार पर मारते समय हम गेंद पर क्रिया करते हैं तथा दीवार की प्रतिक्रिया के कारण गेंद वापस आती है अर्थात् यदि कोई वस्तु A किसी दूसरी वस्तु B पर बल लगाती है, तो वस्तु B भी वस्तु A पर बराबर तथा विपरीत बल लगाती है। यह तथ्य गुरुत्वाकर्षण बल के लिए भी सत्य है।

जब कोई पत्थर का टुकड़ा पृथ्वी पर गिरता है तो ऐसा पृथ्वी द्वारा पत्थर के टुकड़े पर लगे गुरुत्व बल के कारण होता है। वास्तव में पत्थर का टुकड़ा भी पृथ्वी को अपनी ओर उतने ही गुरुत्व बल से आकर्षित करता है, परंतु पृथ्वी की तुलना में पत्थर का द्रव्यमान कम होने के कारण, पत्थर द्वारा पृथ्वी पर लगाया गया बल कम होता है। अतः पत्थर पृथ्वी की ओर खिंचता दिखाई देता है।

प्रश्न 5.
एक ऊपर की ओर फेंकी गई वस्तु की गति पर विचार कीजिए।
उत्तर:
जब कोई वस्तु ऊपर की ओर फेंकी जाती है तो पृथ्वी उसे लगातार अपनी ओर आकर्षित करती रहती है, इसलिए गुरुत्वाकर्षण बल गति की दिशा के विपरीत लगता है, इसलिए वस्तु धीमी गति से चलने लगती है। चाल 9.8 ms^-2 की दर से कम होती जाती है अर्थात् हर प्रति सेकंड के लिए चाल 9.8 m/s कम हो जाती है और अंत में जब वस्तु सबसे ऊँची स्थिति में पहुँच जाती है तो चाल शून्य हो जाती है। वह वस्तु फिर से पृथ्वी की ओर नीचे 9.8 ms^-2 के त्वरण से गिरती है।

प्रश्न 6.
‘G’ का मात्रक ज्ञात कीजिए।
उत्तर:
‘G’ बल (F) तथा \(\frac{\mathrm{M}_1 \mathrm{M}_2}{\mathrm{R}_2}\) का अनुपात है, इसलिए इसका मात्रक बल, द्रव्यमान तथा दूरी के मात्रकों पर निर्भर करता है। यदि द्रव्यमान को किलोग्राम में, दूरी को मीटर में तथा समय को सेकंड में मापा जाए तो बल का मात्रक न्यूटन (N) होता है, इसलिए

प्रश्न 7.
G को सार्वत्रिक स्थिरांक क्यों कहा जाता है?
उत्तर:
हम जानते हैं कि F = G\(\frac{\mathrm{m}_1 \mathrm{m}_2}{\mathrm{R}_2}\)
इसमें ‘G’ स्थिरांक है। ‘G’ का मान m₁, m₂ या R के मान पर निर्भर नहीं करता। इसका मान इस बात पर भी निर्भर नहीं करता कि F को किसने मापा, कब मापा और कहाँ मापा। ब्रह्मांड में स्थित किन्हीं भी दो वस्तुओं के लिए G का मान स्थिर रहता है। F तथा \(\frac{\mathrm{m}_1 \mathrm{m}_2}{\mathrm{R}_2}\) का अनुपात जोकि G के बराबर होता है किन्हीं दो वस्तुओं के लिए समान होता है, इसलिए ‘G’ को सार्वत्रिक स्थिरांक कहा जाता है।

प्रश्न 8.
‘g’ तथा ‘G’ में क्या अंतर है?
उत्तर:
‘g’ तथा ‘G’ में निम्नलिखित अंतर हैं-

प्रश्न 9.
विभिन्न द्रव्यमानों की वस्तुएँ एक ही ऊँचाई से साथ-साथ नीचे गिराए जाने पर एक साथ नीचे गिरती हैं, सिद्ध करें। (यदि वायु का प्रतिरोध नगण्य मान लिया जाए)
हल:
माना दो विभिन्न द्रव्यमानों की वस्तुएँ ‘h’ ऊँचाई से साथ-साथ गिराई गईं
इस स्थिति में s = h, u = 0
सूत्रानुसार
s = ut + \(\frac { 1 }{ 2 }\) gt²
⇒ h = 0 x t + \(\frac { 1 }{ 2 }\) gt²
या h = \(\frac { 1 }{ 2 }\) gt²
या 2h = gt²
या gt² = 2h
या t² = \(\frac { 2h }{ g }\)
या t = \(\sqrt{\frac{2 h}{g}}\)
समीकरण से स्पष्ट है कि वस्तुओं द्वारा लिया गया समय द्रव्यमानों पर निर्भर नहीं करता अर्थात् दोनों वस्तुएँ समान समय में पृथ्वी पर गिरती हैं। उत्तर

प्रश्न 10.
पृथ्वी की ऊर्ध्वाधर दिशा से क्या अभिप्राय है?
उत्तर:

यदि हम पृथ्वी को एकसमान घनत्व का गोला मान लें तो इसका ऊर्ध्वाधर दिशा द्रव्यमान केंद्र इसके केंद्र पर होगा। अतः किसी वस्तु पर पृथ्वी का आकर्षण बल उसके (पृथ्वी के) केंद्र की दिशा में लगता है। यही वह दिशा है जिसे हम ‘ऊर्ध्वाधर दिशा’ कहते हैं।

प्रश्न 11.
स्वतंत्रतापूर्वक गिरती हुई वस्तुओं से संबंधित समीकरण कौन-कौन से हैं?
हल:
(i) v = u+ gt
(ii) v² – u² = 2gs
(iii) s = ut + \(\frac { 1 }{ 2 }\) gt²
यहाँ पर
u = प्रारंभिक वेग
v = अंतिम वेग
g = गुरुत्वीय त्वरण
s = दूरी या ऊँचाई; t = समय उत्तर

प्रश्न 12.
भार से क्या तात्पर्य है? भार का सूत्र लिखें।
उत्तर:
किसी वस्तु पर, पृथ्वी द्वारा लगाया गया आकर्षण बल उसका भार कहलाता है।
यदि m द्रव्यमान की वस्तु पर पृथ्वी ‘g’ त्वरण उत्पन्न करे तो पृथ्वी द्वारा वस्तु पर लगाया गया आकर्षण बल
F = mg
परंतु पृथ्वी द्वारा वस्तु पर लगाया गया आकर्षण बल (F) = वस्तु का भार (W)
∵ W = mg

प्रश्न 13.
पृथ्वी पर वस्तु का भार तथा किसी अन्य आकाशीय पिंड पर वस्तु के भार की तुलना करने के लिए सूत्र ज्ञात करें।
हल:
माना वस्तु का द्रव्यमान = m
पृथ्वी का द्रव्यमान = Me
पृथ्वी की त्रिज्या = Re
पृथ्वी द्वारा वस्तु पर लगा आकर्षण बल (भार) Fe = \(\frac{\text { GMe m }}{R^2}\) … (i)
माना आकाशीय पिंड का द्रव्यमान = Mm
आकाशीय पिंड की त्रिज्या = Rm
अन्य आकाशीय पिंड द्वारा वस्तु पर लगाया गया आकर्षण बल (भार)
Fm = \(\frac{\mathrm{G} \times \mathrm{Mm} \times \mathrm{m}}{\mathrm{Rm}^2}\) … (ii)
समीकरण (ii) को (i) से भाग देने पर
\(\frac{\mathrm{Fm}}{\mathrm{Fe}}=\frac{\mathrm{Mm}}{\mathrm{Me}} \times\left(\frac{\mathrm{Re}}{\mathrm{Rm}}\right)^2\)

प्रश्न 14.
गुरुत्वीय त्वरण (g) तथा सार्वत्रिक गुरुत्वीय स्थिरांक (G) में संबंध ज्ञात करो।
हल:
माना m द्रव्यमान की एक वस्तु पृथ्वी के केंद्र से ‘R’ दूरी पर रखी है। यदि ‘M’ पृथ्वी का द्रव्यमान हो तो पृथ्वी द्वारा उस वस्तु पर लगाया गया बल
F = G \(\frac{\mathrm{Mm}}{\mathrm{R}^2}\) … (i)
पृथ्वी जिस बल से वस्तु को अपने केंद्र की ओर खींचती है, वह उसका भार होता है । इसे भी ‘F’ द्वारा व्यक्त किया जाता है।
F = द्रव्यमान (m) x गुरुत्वीय त्वरण (g) … (ii)
अर्थात् F = mg
समीकरण (i) और (ii) से
mg = G \(\frac{\mathrm{Mm}}{\mathrm{R}^2}\)
यही अभीष्ट संबंध है। इसकी सहायता से ‘g’ का मान भी ज्ञात किया जा सकता है। उत्तर

प्रश्न 15.
द्रव्यमान किसे कहते हैं? इसको मापने की इकाई क्या है? द्रव्यमान मापने का नियम लिखो।
उत्तर:
द्रव्यमान-किसी वस्तु में पदार्थ का परिमाण उसका द्रव्यमान कहलाता है। यह एक अदिश तथा अचर राशि है। द्रव्यमान को मापने की इकाई किलोग्राम है। इसको भौतिक तुला द्वारा ज्ञात किया जाता है।

द्रव्यमान मापने का नियम – मान लीजिए हमारे पास दो वस्तुएँ हैं जिनके द्रव्यमान m₁ तथा m₂ हैं। मान लो, हम उन्हें पृथ्वी के केंद्र से समान दूरी पर रखते हैं तो पृथ्वी तथा m₁ के बीच आकर्षण बल
F₁ = \(\frac{\mathrm{GMem}_1}{\mathrm{R}^2}\)
यहाँ Me = पृथ्वी का द्रव्यमान तथा R = पृथ्वी के केंद्र से m₁ द्रव्यमान की दूरी
इसी प्रकार पृथ्वी तथा m₂ के बीच आकर्षण बल F₂ = \(\frac{\mathrm{GMem}_2}{\mathrm{R}^2}\)
यदि ये दोनों बल समान हों तो F₁ = F₂
⇒ \(\frac{\mathrm{GMem}_1}{\mathrm{R}^2}\) = \(\frac{\mathrm{GMem}_2}{\mathrm{R}^2}\)
m₁ = m₂
अर्थात् यदि दोनों बल बराबर हों तो दोनों वस्तुओं के द्रव्यमान भी बराबर होंगे तथा भौतिक तुला के पलड़े बराबर दिखाई देंगे।

प्रश्न 16.
प्रक्षेप्य तथा प्रक्षेपण पथ को परिभाषित करें तथा प्रक्षेप्य गति के उदाहरण दें।
उत्तर:
प्रक्षेप्य क्षैतिज दिशा में फेंकी गई वस्तु को प्रक्षेप्य कहते हैं।
प्रक्षेपण पथ-प्रक्षेप्य के द्वारा चले गए वक्र पथ को प्रक्षेपण पथ कहते हैं।

प्रक्षेप्य गति के उदाहरण निम्नलिखित हैं-

• वायुयान से गिराई गई वस्तु का पथ। जैसे की चित्र में 80 m की ऊँची मीनार से गिरती गेंद दिखाई गई है।
• बंदूक से निकली गोली का पथ।
• खिलाड़ी द्वारा फेंके गए गोले का पथ।

प्रश्न 17.
अंतरिक्ष यात्री अंतरिक्ष में भारहीनता क्यों अनुभव करते हैं?
उत्तर:
जब अंतरिक्ष यात्री अंतरिक्ष में बैठकर पृथ्वी के गिर्द चक्कर लगाते हैं तो पृथ्वी और अंतरिक्षयान के बीच लगने वाला गुरुत्वाकर्षण बल पृथ्वी के गिर्द चक्कर लगाने में प्रयुक्त बल के संतुलित हो जाता है जिससे अंतरिक्षयान में बैठे यात्रियों को भारहीनता अनुभव होती है। अंतरिक्षयान में गुरुत्वीय त्वरण का मान शून्य हो जाता है।

प्रश्न 18.
सामान्यतः यदि रुई की गेंद तथा समान आकार के पत्थर को किसी निश्चित ऊँचाई से छोड़कर नीचे गिरने दें तो पृथ्वी के तल पर कौन पहले गिरता है? गैलीलियो ने इस विषय में क्या बताया?
उत्तर:
सामान्यतः रुई की अपेक्षा पत्थर का टुकड़ा पृथ्वी के तल पर पहले पहुँचता है, परंतु सर्वप्रथम गैलीलियो ने यह बताया कि यदि वायु का प्रतिरोध शून्य कर दिया जाए तो रुई की गेंद तथा पत्थर का टुकड़ा दोनों ही समान त्वरण से पृथ्वी के तल पर पहुँचेंगे। गैलीलियो के मतानुसार, “पृथ्वी पर गिरती हुई वस्तुओं के त्वरण उनके द्रव्यमान पर निर्भर नहीं करते।”

प्रश्न 19.
किसी स्थान पर गुरुत्वी प्रवेग कैसे बदलता है-
(1) ऊँचाई के कारण
(2) पृथ्वी के आकार के कारण।
उत्तर:
किसी स्थान पर गुरुत्वी प्रवेग निम्नलिखित प्रकार से बदलता है-
(1) ऊँचाई के कारण – पृथ्वी के तल पर ऊँचाई पर स्थित पहाड़ों पर ‘g’ का मूल्य कम होता है, जबकि मैदानों में यह कुछ अधिक होता है
∴ \(\frac{\mathrm{W}_{\mathrm{h}}}{\mathrm{W}}=\frac{\mathrm{g}_{\mathrm{h}}}{\mathrm{g}}=\frac{\mathrm{R}^2}{(\mathrm{R}+\mathrm{h})^2}\)
इसी प्रकार ऊँचाई बढ़ने के साथ-साथ ‘g’ का मान कम होता जाता है।

(2) पृथ्वी के आकार के कारण – पृथ्वी गेंद की तरह पूरी गोल नहीं है बल्कि यह भूमध्य रेखा के पास उभरी तथा ध्रुवों के पास पिचकी हुई है। पृथ्वी की भूमध्य रेखा और ध्रुवीय रेखा की त्रिज्या में लगभग 22 कि०मी० का अंतर है जिस कारण ‘g’ का मूल्य ध्रुवों पर अधिक तथा भूमध्य रेखा पर कम होता है। क्योंकि
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
(जहाँ G तथा M स्थिरांक हैं) g ∝ \(\frac{\mathrm{1}}{\mathrm{R}^2}\)

प्रश्न 20.
‘चंद्रमा पृथ्वी की ओर गिरता रहता है’, इसका तात्पर्य क्या है? यह पृथ्वी तल पर क्यों नहीं गिर जाता?
उत्तर:
चंद्रमा, पृथ्वी की ओर गिरता रहता है, इसका तात्पर्य यह है कि पृथ्वी गुरुत्वाकर्षण बल के कारण चंद्रमा को अपनी ओर आकर्षित करती है।

परंतु चंद्रमा पृथ्वी के चारों ओर वृत्ताकार पथ में गति करने के कारण पृथ्वी तल पर नहीं गिरता, क्योंकि वृत्ताकार पथ पर घूमते हुए किसी पिंड का वेग प्रत्येक बिंदु पर बदलता है। वेग अथवा त्वरण में यह परिवर्तन पिंड की गति की दिशा में परिवर्तन के कारण होता है। इस त्वरण को उत्पन्न करने वाला अभिकेंद्र बल पिंड को वृत्तीय गति में बनाए रखता है, जो सदैव केंद्र के अनुदिश होता है।

प्रश्न 21.
पृथ्वी सेब को आकर्षित करती है तो क्या सेब भी पृथ्वी को आकर्षित करता है? यदि हाँ, तो पृथ्वी सेब की ओर गति क्यों नहीं करती ?
उत्तर:
निश्चित रूप से सेब भी पृथ्वी को अपनी ओर आकर्षित करता है, परंतु सेब का द्रव्यमान पृथ्वी की तुलना में नगण्य होने के कारण यह (पृथ्वी) सेब की ओर गति नहीं करती।

प्रश्न 22.
केप्लर के गति के तीन नियम कौन-से हैं?
उत्तर:
केप्लर की गति के तीन नियम निम्नलिखित हैं-
(1) प्रत्येक ग्रह की कक्षा से एक दीर्घवृत्त होती है और सूर्य इस दीर्घवृत्त के एक फोकस पर होता है। जैसा कि चित्र में सूर्य की स्थिति को 0 से दर्शाया गया है।

(2) सूर्य तथा ग्रह को मिलाने वाली रेखा समान समय में समान क्षेत्रफल तय करती है। इस प्रकार यदि A से B तक गति करने में लगा समय C से D तक गति करने में लगे समय के बराबर हो तो क्षेत्रफल OAB तथा क्षेत्रफल OCD बराबर होंगे।

(3) सूर्य से किसी भी ग्रह की औसत दूरी (r) का घन उस ग्रह के परिक्रमण काल T के वर्ग के समानुपाती होता है। अथवा r³/T² = स्थिरांक यह जानना बहुत महत्त्वपूर्ण है कि ग्रहों की गति की व्याख्या करने के लिए केप्लर कोई सिद्धांत प्रस्तुत नहीं कर सके। न्यूटन ने ही यह दिखाया कि ग्रहों की गति का कारण गुरुत्वाकर्षण का वह बल है जो सूर्य उन पर लगाता है।

प्रश्न 23.
कारों की अपेक्षा बसों या ट्रकों के टायर चौड़े क्यों रखे जाते हैं?
उत्तर:
बसों या ट्रकों में प्रणोद बल कारों की अपेक्षा अधिक होता है। यदि उनके टायर कारों के टायरों की तरह कम चौड़े रखे जाएँ तो उनका दबाव अधिक हो जाएगा और वे धरती में धंस जाएँगे। इसलिए बसों या ट्रकों के टायर अधिक चौड़े रखे जाते हैं ताकि प्रभावित क्षेत्रफल बढ़ जाए और धरती पर दबाव कम पड़े।

प्रश्न 24.
क्या कारण है कि मरुस्थल में ऊँट आसानी से चल सकता है, जबकि घोड़े के लिए चलना सुगम नहीं है?
उत्तर:
घोड़े के पैरों की अपेक्षा ऊँट के पैरों का क्षेत्रफल अधिक होता है जिससे प्रभावित क्षेत्रफल अधिक होता है और दाब कम हो जाता है। दाब कम होने के कारण ऊँट मरुस्थल से आसानी से चल पाता है। इसके विपरीत घोड़े के पैरों का क्षेत्रफल कम होता है जिससे दाब अधिक होता है। दाब अधिक होने से घोड़े द्वारा मरुस्थल में चलना कठिन हो जाता है।

प्रश्न 25.
उत्प्लावन बल किसे कहते हैं? यह कैसे मापा जाता है?
उत्तर:
जब किसी वस्तु को द्रव में डुबोया जाता है तो वस्तु पर ऊपर की ओर एक बल लगता है, जिसे उत्प्लावन बल कहते हैं।

उत्प्लावन बल का मापन-
एक ठोस बेलन लो। उसे कमानीदार तुला से लटकाओ तथा उसका भार नोट करो। मान लो उसका भार W₁ ग्राम है। अब एक बीकर में पानी डालो और बेलन को बीकर में रखे पानी में धीरे-धीरे ले जाओ। आप देखोगे कि पानी में धीरे-धीरे रखने से बेलन का भार कम प्रतीत होने लगता है जो कि कमानीदार तुला के सूचक से प्रकट होता है। जब ठोस बेलन पूरी तरह से पानी में डूब जाए तो कमानीदार तुला के सूचक का पाठ्यांक नोट करो। मान लो यह पाठ्यांक
W₂ ग्राम है अर्थात् पानी में ठोस बेलन का भार W₂ ग्राम है।
दोनों भारों का अंतर ठोस बेलन के लिए पानी का उत्प्लावन बल होगा।
उत्प्लावन बल = बेलन का वायु में भार-बेलन का पानी में भार = (W₁ – W₂) ग्राम।

प्रश्न 26.
क्या कारण है कि लोहे की सूई पानी में डूब जाती है, परंतु लोहे का बना जलयान पानी में तैरता रहता है?
उत्तर:
लोहे की सूई पानी में डूब जाती है, परंतु लोहे का बना हुआ जलयान पानी में तैरता रहता है। इसका कारण यह है कि सूई जितना पानी हटाती है उस पानी का भार सूई के भार से कम होता है। भारी होने के कारण सूई पानी में डूब जाती है। इसके विपरीत लोहे का बना जलयान जितना पानी हटाता है उसका भार जलयान के भार से अधिक होता है। जलयान का भार हटाए गए पानी के भार से कम होने के कारण वह पानी में तैरता रहता है।

प्रश्न 27.
नदी की अपेक्षा समुद्र के पानी में तैरना आसान क्यों होता है?
उत्तर:
नदी की अपेक्षा समुद्र के पानी में तैरना आसान इसलिए होता है, क्योंकि समुद्र के पानी का घनत्व नदी के पानी की अपेक्षा अधिक होता है। अतः समुद्री जल अधिक भारी होने के कारण मनुष्य के शरीर पर अधिक उत्प्लावन बल लगाता है। इसी कारण समुद्र में तैरने में आसानी होती है।

प्रश्न 28.
घनत्व किसे कहते हैं? इसका SI मात्रक क्या है? इसकी क्या महत्ता है?
उत्तर:
घनत्व-किसी वस्तु का घनत्व उसके एकांक आयतन के द्रव्यमान को कहते हैं। इसका SI मात्रक किलोग्राम प्रति घनमीटर (kg/m³) है। विशिष्ट परिस्थितियों में किसी पदार्थ का घनत्व सदैव समान रहता है। जैसे सोने का घनत्व 19300 kg/m³ तथा पानी का घनत्व 1000 kg/m³ है।

महत्त्व-किसी पदार्थ के नमूने का घनत्व, उस पदार्थ की शुद्धता की जाँच में सहायता करता है।

प्रश्न 29.
आपेक्षिक घनत्व से क्या अभिप्राय है? इसके आधार पर पानी में डूबने व तैरने की क्या शर्त है?
उत्तर:
आपेक्षिक घनत्व-किसी पदार्थ का आपेक्षिक घनत्व उस पदार्थ का घनत्व व पानी के घनत्व का अनुपात है। अर्थात्

क्योंकि, आपेक्षिक घनत्व एक अनुपात है, अतः इसका कोई मात्रक नहीं होता। सोने का आपेक्षिक घनत्व 19.3 है। यदि किसी ठोस या द्रव का आपेक्षिक घनत्व 1 से अधिक हो तो वह पानी में डूब जाएगा। यदि पदार्थ का आपेक्षिक घनत्व 1 से कम है तो इसका तात्पर्य है कि वह पदार्थ पानी में तैरेगा।

प्रश्न 30.
बर्फ पानी पर क्यों तैरती है?
उत्तर:
बर्फ पानी पर इसलिए तैरती है, क्योंकि बर्फ का घनत्व पानी के घनत्व से कम होता है। जब बर्फ का टुकड़ा पानी में डाला जाता है तो उसका भार उसके द्वारा हटाए गए पानी के भार से कम होता है।

प्रश्न 31.
आर्किमिडीज के सिद्धांत की परिभाषा लिखो तथा इसकी व्याख्या करो। इस नियम के कौन-कौन से उपयोग हैं?
अथवा
आर्किमिडीज का सिद्धांत लिखिए। आर्किमिडीज के सिद्धांत के दो अनुपयोग लिखिए।
उत्तर:
सिद्धांत की परिभाषा-जब किसी वस्तु को किसी द्रव में पूर्ण या आंशिक रूप से डुबोया जाता है तो इस वस्तु के भार में कमी आ जाती है। यह कमी वस्तु द्वारा हटाए गए द्रव के भार के बराबर होती है।

व्याख्या-जब कोई ठोस द्रव में डुबोया जाता है तो द्रव अपने उत्प्लावन बल द्वारा उसे ऊपर की ओर उठाता है जिससे उसका भार कम हो जाता है, क्योंकि उत्प्लावन बल ठोस द्वारा विस्थापित द्रव के भार के बराबर होता है। इसलिए द्रव में डुबोने पर ठोस के भार में कमी उसके द्वारा हटाए गए द्रव के भार के बराबर होती है।

आर्किमिडीज के सिद्धांत के दैनिक जीवन में निम्नलिखित अनुपयोग हैं-

• इस सिद्धांत पर जलयान व पनडुब्बियों के डिज़ाइन बनाए जाते हैं।
• दूध की शुद्धता मापने के लिए लैक्टोमीटर भी इसी सिद्धांत पर तैयार किया गया है।
• हाइड्रोमीटर इसी सिद्धांत पर कार्य करता है जो द्रवों का घनत्व मापने के काम आता है।

प्रश्न 32.
दो वस्तुओं के बीच लगने वाले गुरुत्वाकर्षण बल का क्या होगा, यदिः
(1) वस्तुओं के बीच की दूरी एक तिहाई (1/3) कर दी जाए?
(2) दोनों वस्तुओं के द्रव्यमान आधे (1/2) कर दिए जाएँ?
उत्तर:
(1) हम जानते हैं कि दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। इसलिए वस्तुओं के बीच की दूरी एक-तिहाई (1/3) हो जाने पर उनके बीच लगने वाला गुरुत्वाकर्षण बल नौ गुना हो जाएगा।

(2) हम जानते हैं कि दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल उनके द्रव्यमानों के गुणनफल के समानुपाती होता है इसलिए दोनों वस्तुओं के द्रव्यमान आधे (1/2) कर देने पर उनके बीच लगने वाला गुरुत्वाकर्षण बल एक-चौथाई (1/4) रह जाएगा।

गणनात्मक प्रश्न

महत्त्वपूर्ण सूत्र एवं तथ्य:
1. स्वतंत्रतापूर्वक पृथ्वी की ओर गिर रही वस्तुओं के गति समीकरण
(1) v = u + gt, (2) s = ut + \(\frac { 1 }{ 2 }\)gt², (3) v² – u² = 2gh

2. m₁ तथा m₂ द्रव्यमानों वाली r दूरी पर स्थित दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल
(F) = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{R}^2}\)

3. भार (W) = द्रव्यमान (m) x गुरुत्वीय त्वरण (g)

4. गुरुत्वीय त्वरण (g) =

5. गुरुत्वीय त्वरण (g) = 9.8 m/s² ≈10 m/s²
गुरुत्वीय स्थिरांक (G) = 6.673 x 10^-11 Nm²/kg²

प्रश्न 1.
एक गोली क्षैतिज दिशा में 25 m/s से छोड़ी गई। पहले दो सेकंड में यह कितनी दूरी तक नीचे गिरेगी?
हल:
ऊर्ध्वाधर दूरी क्षैतिज वेग से स्वतंत्र होती है।
अतः प्रारंभिक वेग (u) = 0
गुरुत्वीय त्वरण (g) = 9.8 m/s²
समय (t) = 2s
दूरी (s) = ?
हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 }\)gt²
= 0 x 2 + \(\frac { 1 }{ 2 }\) x 9.8 x (2)²
= 19.6 m उत्तर

प्रश्न 2.
5 kg द्रव्यमान वाले पिंड का भार ज्ञात कीजिए।
हल:
पिंड का द्रव्यमान (m) = 5 kg
गुरुत्वीय त्वरण (g) = 9.8 m/s²
पिंड का भार (W) = ?
हम जानते हैं कि
w = m x g
= 5 x 9.8 = 49 N उत्तर

प्रश्न 3.
यदि आप और आपके मित्र का द्रव्यमान 35 kg हो और आपके बीच की दूरी एक मीटर हो तो आप दोनों के बीच लगने वाला आकर्षण बल क्या होगा?
हल:
यहाँ पर
द्रव्यमान (m₁) = 35 kg
द्रव्यमान (m₂) = 35 kg
दूरी (r) = 1 m
गुरुत्वीय स्थिरांक (G) = 6.67 x 10^-11 Nm²/kg²
आकर्षण बल (F) = ?
हम जानते हैं कि आकर्षण बल (F) = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{R}^2}\)
= \(\frac{6.67 \times 10^{-11} \times 35 \times 35}{(1)^2}\)
= 8.17 x 10^-8 N उत्तर

प्रश्न 4.
यदि कोई ऐसा ग्रह हो जिसका द्रव्यमान पृथ्वी से दो गुना तथा अर्द्धव्यास तीन गुना हो तो उस ग्रह की सतह 10 kg द्रव्यमान की वस्तु का भार ज्ञात करो।
हल:
क्योंकि ग्रह के लिए M = 2Me, R = 3 Re
∴ g₁ = \(\frac{\mathrm{G}(2 \mathrm{Me})}{(3 \mathrm{Re})^2}=\frac{2 \mathrm{GMe}}{9 \mathrm{Re}^2}\)
= \(\frac { 2 }{ 9 }\)g
= \(\frac { 2 }{ 9 }\) x 9.8 = \(\frac { 19.6 }{ 9 }\) m/s² [∵ g = 9.8 m/s²]
अतः ग्रह पर 10 kg द्रव्यमान की वस्तु का भार (W) = m x g₁
= 10 x \(\frac { 19.6 }{ 9 }\)
= \(\frac { 196 }{ 9 }\)
= 21.78N उत्तर

प्रश्न 5.
यदि किसी वस्तु का भार 49 N है तो उसका द्रव्यमान क्या होगा?
हल:
वस्तु का भार (W) = 49 N
गुरुत्वीय त्वरण (g) = 9.8 m/s²
भार = द्रव्यमान x गुरुत्वीय त्वरण
या W = mg
⇒ 49 = m x 9.8
या m = \(\frac { 49 }{ 9.8 }\) = 5 kg उत्तर

प्रश्न 6.
एक कार किसी कगार से गिर कर 0.5 s में धरती पर आ गिरती है। g = 10 ms^-2 लीजिए।
(1) धरती पर टकराते समय कार की चाल क्या होगी?
(2) 1/2 सेकंड के दौरान इसकी औसत चाल क्या होगी?
(3) धरती से कगार कितनी ऊँचाई पर है?
हल:
समय (t) = 1/2 s
प्रारंभिक वेग (u) = 0 ms^-1
गुरुत्वीय त्वरण (g) = 10 ms^-2
कार का त्वरण (a) = + 10 ms^-2
(अधोमुखी)
(1) चाल (v) = at
v = 10 ms^-2 x 1/2 s
= 5 ms^-1

(2) औसत चाल =\(\frac { u+v }{ 2 }\)
= (0 ms^-1 + 5 ms^-1)/2
= 2.5 ms^-1

(3) चली गई दूरी (s) = 1/2 at²
= 1/2 x 10 ms^-2 x (1/2 s)²
= 1/2 x 10 ms^-2 x 1/4 s²
= 1.25 m

अतः

• धरती पर टकराते समय इसकी चाल = 5 ms^-1 उत्तर
• 1/2 सेकंड के दौरान इसकी औसत चाल = 2.5 ms^-1 उत्तर
• धरती से कगार की ऊँचाई = 1.25 m उत्तर

प्रश्न 7.
किसी पत्थर को किसी भवन की छत के किनारे से गिराया गया-
(1) 4.9 m दूरी तक गिरने में उसे कितना समय लगेगा?
(2) उस समय उसकी चाल क्या थी?
(3) 7.9 m दूरी तक गिरने के बाद उसकी चाल क्या थी?
(4) गिरने के 1 सेकंड तथा 2 सेकंड पश्चात् पत्थर का त्वरण कितना था?
हल:
(1) पत्थर का प्रारंभिक वेग (u) = 0
पत्थर के द्वारा तय की गई दूरी (s) = 4.9 m
g = 9.8 m/s² तथा t = ?
अब s = ut + \(\frac { 1 }{ 2 }\) gt²
4.9 = 0 x t + \(\frac { 1 }{ 2 }\) x 9.8 x t²
या 4.9 = 0 + 4.9 t²
या 4.9 t² = 4.9
या t² = \(\frac { 4.9 }{ 4.9 }\) = 1 s
अतः t = \(\sqrt{1}\) = 1 सेकंड उत्तर

(2) माना उस समय पत्थर की चाल = v
अब v = u + gt
v = 0+ 9.8 x 1
v = 0 + 9.8 = 9.8 m/s उत्तर

(3) पत्थर का प्रारंभिक वेग (u) = 0
पत्थर के द्वारा तय की गई दूरी (s) = 7.9 मीटर
g = 9.8 m/s² तथा
v = ?
अब v² – u² = 2gs
या v² – (0)² = 2 x 9.8 x 7.9
या v² – 0 = 154.84
या v² = 154.84
या v = \(\sqrt{154.84}\) = 12.44 सेकंड उत्तर

(4) क्योंकि वस्तु गुरुत्व के प्रभाव अधीन स्वतंत्र रूप से नीचे गिर रही है।
∴ 1 सेकंड के बाद वस्तु का त्वरण = 9.8 m/s²
2 सेकंड के बाद वस्तु का त्वरण = 9.8 m/s² उत्तर

प्रश्न 8.
यदि ऊपर की ओर फेंकने पर कोई गेंद 100 m की ऊँचाई तक जाए तो उसकी प्रारंभिक चाल ज्ञात कीजिए।
हल:
यहाँ पर
प्रारंभिक चाल (u) = ?
अंतिम चाल (v) = 0
दूरी (s) = 100m
गुरुत्वीय त्वरण (g) = – 9.8 m/s²
हम जानते हैं कि v² – u² = 2gs
⇒ 0² – u² = 2 x (- 9.8) x 100
या – u² = – 1960
या u = \(\sqrt{1960}\) = 44.2m/s उत्तर

प्रश्न 9.
यदि पत्थर के किसी टुकड़े को किसी भवन की छत से मुक्त रूप से गिरते हुए जमीन पर पहुँचने में 4s का समय लगता हो तो भवन की ऊँचाई क्या होगी?
हल:
यहाँ पर
प्रारंभिक चाल (u) = 0
समय (t) = 4 sec
ऊँचाई या दूरी (s) = ?
गुरुत्वीय त्वरण (g) = 9.8 m/s²
हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 }\) gt²
= 0 x 4 + \(\frac { 1 }{ 2 }\) x 9.8 x (4)²
= \(\frac { 1 }{ 2 }\) x 9.8 x 4 x 4
= 78.4 m उत्तर

प्रश्न 10.
किसी 500g के सील किए हुए टिन (या डिब्बे) का आयतन 350 cm है। इस सील किए टिन का घनत्व कितना है? यह पानी में डूबेगा या तैरेगा? इस टिन के द्वारा हटाए गए पानी का भार कितना होगा?
हल:
टिन का द्रव्यमान (m) = 500g
= \(\frac { 500 }{ 1000 }\) kg
= 0.5 kg
टिन का आयतन = 350 cm³ = \(\frac{350}{100 \times 100 \times 100} \mathrm{~m}^3\)
= 35 x 10^-5 m³

क्योंकि टिन का आपेक्षिक घनत्व 1 से अधिक है इसलिए टिन पानी में डूब जाएगा। अतः टिन द्वारा हटाए पानी का भार टिन के भार से कम होगा। उत्तर

प्रश्न 11.
एक लोहे के टुकड़े का आयतन 20 घन सें०मी० और द्रव्यमान 156 ग्राम है। उसका घनत्व बताओ।
हल:
लोहे का द्रव्यमान = 156
ग्राम लोहे का आयतन = 20 घन सें०मी०
घनत्व = \(\frac {संहति }{ आयतन}\)
= \(\frac {156}{ 20}\)
= 7.8 ग्राम/घन सें०मी० उत्तर

निबंधात्मक प्रश्न

प्रश्न 1.
सार्वत्रिक गुरुत्वाकर्षण स्थिरांक ‘G’ की परिभाषा ज्ञात करो। एस० आई० मानक इकाइयों में ‘G’ के मात्रक लिखो।
उत्तर:
न्यूटन के गुरुत्वाकर्षण के सार्वत्रिक नियम के अनुसार,
F = G\(\mathrm{G} \frac{\mathrm{M}_1 \mathrm{M}_2}{\mathrm{R}^2}\) या \(\frac{\mathrm{FR}^2}{\mathrm{M}_1 \mathrm{M}_2}\)
यदि M₁ = M₂ = 1 इकाई तथा R = 1 इकाई हो तो
\(\mathrm{G}=\frac{\mathrm{F} \times 1^2}{1 \times 1}=\frac{\mathrm{F} \times 1}{1 \times 1}=\mathrm{F}\)
अतः सार्वत्रिक गुरुत्वाकर्षण स्थिरांक वह आकर्षण बल है जो इकाई द्रव्यमान वाली ऐसी दो वस्तुओं के बीच आरोपित होता है जो एक-दूसरे से इकाई दूरी पर स्थित हों।
G का एस० आई० मात्रक-
G = \(\frac{\mathrm{FR}^2}{\mathrm{M}_1 \mathrm{M}_2}\)
क्योंकि G बल F तथा M₁M₂/R² का अनुपात है। इसलिए इसका मात्रक बल, द्रव्यमान तथा दूरी के मात्रकों पर निर्भर करता है। यदि द्रव्यमान को किलोग्राम में, दूरी को मीटर में तथा समय को सेकंड में मापा जाए तो बल का मात्रक न्यूटन (N) होता है, इसलिए G का मात्रक Nm²/kg² होगा। सोने की गेंदों द्वारा किए गए प्रयोगों से G का निम्नलिखित मान प्राप्त हुआ
G = 0.000,000,000,066,734 Nm²/kg²
= 6.673 x 10^-11 Nm²/kg²

प्रश्न 2.
गुरुत्वाकर्षण का सार्वत्रिक नियम बताइए। M तथा m द्रव्यमान के दो पिण्ड A व B जो कि d दूरी पर स्थित हैं, के मध्य लगने वाले गुरुत्वाकर्षण बल के लिए समीकरण स्थापित कीजिए। 1\(\frac { 1 }{ 2 }\) + 2\(\frac { 1 }{ 2 }\) = 4
उत्तर:
गुरुत्वाकर्षण का सार्वत्रिक नियम-विश्व का प्रत्येक पिंड अन्य पिंड को एक बल से आकर्षित करता है, जो दोनों पिंडों के द्रव्यमानों के गुणनफल के समानुपाती तथा उनकी बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों पिंडों को मिलाने वाली रेखा की दिशा में लगता है।

मान लीजिए M तथा m द्रव्यमान के दो पिंड A तथा B एक-दूसरे से d दूरी पर स्थित हैं जैसा कि चित्र में दिखाया गया है। मान लीजिए दोनों पिंडों के बीच आकर्षण बल F है। गुरुत्वाकर्षण के सार्वत्रिक नियम के अनुसार, दोनों पिंडों के बीच लगने वाला बल उनके द्रव्यमानों के गुणनफल के समानुपाती है। अर्थात्
F ∝ M x m …………. (i)
तथा दोनों पिंडों के बीच लगने वाला बल उनकी बीच की दूरी के वर्ग के व्युत्क्रमानुपाती है, अर्थात्
F ∝ \(\frac{1}{\mathrm{~d}^2}\) ……….. (ii)
समीकरणों (i) तथा (ii) से हमें प्राप्त होगा
F ∝ \(\frac{\mathrm{M} \times \mathrm{m}}{\mathrm{d}^2}\) ………… (iii)
या F = G\(\frac{\mathrm{M} \times \mathrm{m}}{\mathrm{d}^2}\) …………. (iv)
जहाँ G एक आनुपातिकता स्थिरांक है और इसे सार्वत्रिक गुरुत्वीय स्थिरांक कहते हैं।

प्रश्न 3.
किसी वस्तु के भारों में तुलना करो यदि उसको पृथ्वी तथा चंद्रमा पर तोला जाए।
उत्तर:
प्रत्येक ग्रह पर गुरुत्वीय त्वरण (g) का मान उसके द्रव्यमान तथा उसके अर्द्धव्यास पर निर्भर करता है। इसी कारण से चंद्रमा पर किसी वस्तु का भार, उसके पृथ्वी के भार का \(\frac { 1 }{ 6 }\) गुना होता है।
माना वस्तु का द्रव्यमान ‘m’ है। यदि M_e पृथ्वी का द्रव्यमान तथा R_e पृथ्वी की त्रिज्या हो तो पृथ्वी पर वस्तु का भार (F_e) होगा
F_e = \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}_{\mathrm{e}}{ }^2}\)
इसी प्रकार यदि M_m चंद्रमा का द्रव्यमान तथा R_mचंद्रमा की त्रिज्या हो तो चंद्रमा पर वस्तु का भार (F_m) होगा-

∴ पृथ्वी का द्रव्यमान चंद्रमा के द्रव्यमान से लगभग 100 गुना अधिक है तथा अर्द्धव्यास चार गुणा अधिक है।

अतः यह स्पष्ट हो गया है कि चंद्रमा पर वस्तु का द्रव्यमान ‘m’ ही रहता है, परंतु उसका भार चंद्रमा की अपेक्षा पृथ्वी पर 6 गुना अधिक होता है।

प्रश्न 4.
निम्नलिखित में अंतर लिखो-
(1) गुरुत्वाकर्षण बल तथा गुरुत्व बल, (2) द्रव्यमान केंद्र तथा गुरुत्व केंद्र।
उत्तर:
(1) गुरुत्वाकर्षण बल तथा गुरुत्व बल में अग्रलिखित अंतर हैं-

(2) द्रव्यमान केंद्र तथा गुरुत्व केंद्र-
किसी विस्तृत आकार की वस्तु को हम बहुत-से कणों से मिलकर बना हुआ मान सकते हैं। तब, हमारे लिए वस्तु में उस बिंदु को परिभाषित करना संभव हो जाता है, जहाँ पर वस्तु का सम्पूर्ण द्रव्यमान केंद्रित माना जा सकता है। इस बिंदु को ‘द्रव्यमान केंद्र’ कहा जाता है। पृथ्वी की सतह पर अथवा इसके पास, जहाँ गुरुत्वीय बल स्थिर है, द्रव्यमान केंद्र ही, वह बिंदु हो जाता है, जहाँ सम्पूर्ण वस्तु पर लगे गुरुत्वीय बल को अनुभव किया जा सकता है।

इस स्थिति में द्रव्यमान केंद्र को ‘गुरुत्व केंद्र’ कहते हैं। अतः किसी वस्तु का ‘गुरुत्व केंद्र’ वह बिंदु है जहाँ सम्पूर्ण वस्तु पर लगा गुरुत्वीय बल, क्रिया करता हुआ माना जा सकता है। (चित्रानुसार) नियमित आकार व एकसमान घनत्व वाली वस्तुओं का गुरुत्व केंद्र उनके ज्यामितीय केंद्र पर होता है। इसकी पुष्टि किसी ऐसी वस्तु को, उसके ज्यामितीय केंद्र पर, एक सूई के ऊपर संतुलित करके की जा सकती है। जैसे कि, गोलाकार गेंद या आयताकार लकड़ी के टुकड़े या वृत्ताकार धातु की डिस्क (चक्रिका) का गुरुत्व केंद्र उसके केंद्र पर होता है।

प्रयोगात्मक कार्य

क्रियाकलाप 1.
चंद्रमा की पृथ्वी से चोर गति को समझने के लिए एक क्रियाकलाप का वर्णन करें। कार्य-विधि-
(1) धागे का एक टुकड़ा लीजिए। इसके एक सिरे पर एक छोटा सा पत्थर बांधिए।
(2) धागे के दूसरे सिर को पकड़िए और पत्थर को वृत्ताकार भाग में घुमाइए। जैसे चित्र में दिखाया गया है।
(3) पत्यर की गति की दिशा एक वृत्ताकार गति होगी।
(4) अब धागे को पकड़िए।
(5) फिर से पत्थर की गति की दिशा को देखिए।

धागे को छोड़ने से पहले पत्थर एक निश्चित चाल से वृत्ताकार मार्ग में गति करता है तथा प्रत्येक बिंदु पर उसकी गति की दिशा बदलती है। दिशा में परिवर्तन में वेग-परिवर्तन या त्वरण सम्मिलित है। जिस बल के कारण यह त्वरण होता है तथा जो वस्तु को वृत्ताकार पथ में गतिशील रखता है, वह बल केंद्र की ओर लगता है। इस बल को अभिकेंद्र बल कहते हैं।

क्रियाकलाप 2.
वस्तुओं के मुक्त पतन को समझने के लिए एक क्रियाकलाप का वर्णन करें।

कार्य-विधि-एक पत्थर लीजिए। इसे ऊपर की ओर फेंकिए। यह एक निश्चित ऊँचाई पर पहुँचकर है नीचे गिरने लगता है।
हम जानते हैं कि पृथ्वी वस्तुओं को अपनी ओर आकर्षित करती है। पृथ्वी के इस आकर्षण बल को गुरुत्वीय बल कहते हैं। अतः जब भी वस्तुएँ पृथ्वी की ओर गिरती हैं, हम कहते हैं कि वस्तुएँ मुक्त पतन में है।

क्रियाकलाप 3.
प्रयोग द्वारा सिद्ध करो कि सामान्य द्रव्यमानों की दो वस्तुओं के बीच गुरुत्वाकर्षण बल का मान क्षीण होता है।

कार्य-विधि-एक चुंबक लो। उसे पत्थर के टुकड़े के समीप रखे लोहे के पिन के पास ले जाओ। आप देखोगे कि लोहे की पिन पत्थर के टुकड़े की ओर तो नहीं खिंचती, परंतु चुंबक की ओर खिंच जाती है। इससे सिद्ध होता है कि पत्थर तथा लोहे की पिन के बीच गुरुत्वाकर्षण बल बहुत ही क्षीण है, इसलिए लोहे की पिन पत्थर की ओर नहीं खिंचती है। वास्तव में, पत्थर के टुकड़े तथा लोहे की पिन के बीच का गुरुत्वाकर्षण बल चुंबकीय बल से भी बहुत कम होता है, इसलिए लोहे की पिन चुंबक की ओर तो खिंच जाती है, परंतु पत्थर के टुकड़े की ओर नहीं। इससे यह निष्कर्ष निकलता है कि सामान्य द्रव्यमानों की दो वस्तुओं के बीच गुरुत्वाकर्षण बल बहुत क्षीण होता है।

क्रियाकलाप 4.
एक क्रियाकलाप द्वारा समझाएँ कि लोहा पानी में क्यों डूब जाता है जबकि कार्क तैरता रहता है?
कार्य-विधि-
(1) पानी से भरा बीकर लीजिए।
(2) एक कील तथा समान द्रव्यमान का एक कार्क का टुकड़ा लीजिए।
(3) इन्हें पानी की सतह पर रखिए। आप देखेंगे कि
(4) कार्क तैरती है जबकि कील डूब जाती है। ऐसा उनके घनत्वों में अंतर के कारण होता है। किसी पदार्थ का घनत्व, उसके एकांक आयतन के द्रव्यमान को कहते हैं। कार्क का घनत्व पानी के घनत्व से कम है। इसका अर्थ है कि कार्क पर लोहे पर पानी का उत्प्लावन बल, कार्क के भार से अधिक है। इसीलिए यह तैरती है।

अध्याय का तीव्र अध्ययन

1. पृथ्वी द्वारा किसी वस्तु पर लगाए जाने वाले बल को कहा जाता है-
(A) गुरुत्व बल
(B) गुरुत्वाकर्षण बल
(C) अभिकेंद्र बल
(D) चुंबकीय बल
उत्तर:
(A) गुरुत्व बल

2. विश्व का प्रत्येक पिंड अन्य पिंड को एक बल से आकर्षित करता है जो दोनों पिंडों के द्रव्यमानों के गुणनफल के समानुपाती व उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। इस नियम को कहा जाता है-
(A) गुरुत्वाकर्षण का सार्वत्रिक नियम
(B) गुरुत्व का नियम
(C) अभिकेंद्र का सार्वत्रिक नियम
(D) आर्किमिडीज का नियम
उत्तर:
(A) गुरुत्वाकर्षण का सार्वत्रिक नियम

3. दो वस्तुओं के बीच की दूरी दुगुनी कर दी जाए, तो उनके मध्य लगने वाला गुरुत्वाकर्षण बल हो जाएगा-
(A) एक-चौथाई
(B) आधा
(C) दुगुना
(D) प्रभावित नहीं होगा
उत्तर:
(A) एक-चौथाई

4. G का मान होता है-
(A) 6.673 x 10^-11 Nm²
(B) 6.673 x 10¹¹ Nm²kg^-2
(C) 6.673 x 10^-11 Nm²kg^-2
(D) 6.673 x 10¹¹ Nm²
उत्तर:
(C) 6.673 x 10^-11 Nm²kg^-2

5. पृथ्वी का अर्द्धव्यास लगभग लिया जाता है-
(A) 6.4 × 10⁵ m
(B) 6.4 × 10⁶ m
(C) 6.4 × 10⁷ m
(D) 6.4 × 10⁸ m
उत्तर:
(A) 6.4 × 10⁵ m

6. पृथ्वी के किस भाग पर गुरुत्वीय त्वरण (g) का मान अधिकतम होता है?
(A) ध्रुवों पर
(B) भूमध्य रेखा पर
(C) केंद्र पर
(D) उपर्युक्त सभी
उत्तर:
(A) ध्रुवों पर

7. पृथ्वी के किस भाग पर गुरुत्वीय त्वरण (g) का मान कम होता है?
(A) ध्रुवों पर
(B) भूमध्य रेखा पर
(A) गुरुत्वाकर्षण त्वरण
(D) गुरुत्वीय त्वरण
उत्तर:
(A) ध्रुवों पर

8. चन्द्रमा पर किसी वस्तु का भार पृथ्वी पर उसके भार की अपेक्षा कितना होता है?
(A) 6 गुना
(B) 3 गुना
(C) \(\frac { 1 }{ 2 }\) गुना
(D) \(\frac { 1 }{ 3 }\) गुना
उत्तर:
(C) \(\frac { 1 }{ 2 }\) गुना

9. वह त्वरण जिसके द्वारा पृथ्वी किसी वस्तु को अपने केंद्र की ओर आकर्षित करती है, उसे कहा जाता है-
(A) गुरुत्वाकर्षण त्वरण
(B) अभिकेंद्री त्वरण
(C) गुरुत्वीय त्वरण
(D) इनमें से कोई नहीं
उत्तर:
(C) गुरुत्वीय त्वरण

10. किसी व्यक्ति का पृथ्वी पर द्रव्यमान 60kg है, उसका द्रव्यमान चंद्रमा पर होगा-
(A) 60kg
(B) 30 kg
(C) 10 kg
(D) 360 kg
उत्तर:
(A) 60kg

11. किसी व्यक्ति का पृथ्वी पर भार 24 N हो तो चन्द्रमा पर उसका भार होगा
(A) 6 N
(B) 8 N
(C) 4 N
(D) 96 N
उत्तर:
(C) 4 N

12. जब कोई वस्तु वृत्ताकार पथ पर गति करती है तो उसमें वेग परिवर्तन के कारण उत्पन्न त्वरण कहलाता है-
(A) गुरुत्वाकर्षण त्वरण
(B) गुरुत्वीय त्वरण
(C) अभिकेंद्री त्वरण
(D) इनमें से कोई नहीं
उत्तर:
(C) अभिकेंद्री त्वरण

14. पृथ्वी से चंद्रमा की दूरी है
(A) 384000m
(B) 384000km
(C) 38400km
(D) 38400m
उत्तर:
(B) 384000km

15. पृथ्वी जिस बल से किसी वस्तु को अपनी ओर आकर्षित करती है, उसे वस्तु का कहा जाता है-
(A) द्रव्यमान
(B) दाब
(C) प्रणोद
(D) भार
उत्तर:
(D) भार

16. भार को मापने के लिए किस तुला का प्रयोग होता है?
(A) भौतिक तुला
(B) कमानीदार तुला
(C) तराजू
(D) इनमें से कोई नहीं
उत्तर:
(B) कमानीदार तुला

17. यदि पृथ्वी का द्रव्यमान तथा अर्द्धव्यास दोनों आधे कर दिए जाएँ तो गुरुत्वीय त्वरण (g) का मान होगा-
(A) 4.9 m/s²
(B) 9.8 m/s²
(C) 19.6 m/s²
(D) 19.6 m/s²
उत्तर:
(C) 19.6 m/s²

18. u,v, g तथा t में संबंध होता है-
(A) v = u + gt
(B) v + u = gt
(C) v + gt = u
(D) \(\frac { v }{ g }\) = u + t
उत्तर:
(A) v = u + gt

19. कोई खिलाड़ी गेंद को क्षितिज के साथ किस कोण पर फेंके कि गेंद अधिकतम दूरी पर जा गिरे?
(A) 90°
(B) 0°
(C) 450
(D) 60°
उत्तर:
(C) 45°

20. निम्नलिखित में से कौन-सी सदिश राशि है?
(A) द्रव्यमान
(B) भार
(C) द्रव्यमान व भार दोनों
(D) इनमें से कोई नहीं
उत्तर:
(B) भार

21. पास्कल को किस संकेत के रूप में व्यक्त किया जाता है?
(A) Pa
(B) Ps
(C) Pcl
(D) P
उत्तर:
(A) Pa

22. दाब का SI मात्रक क्या है?
(A) N
(B) Pa
(C) kg
(D) kpa
उत्तर:
(B) Pa

23. यदि 300 N के बल को 20m- क्षेत्रफल पर लगाया जाए तो उत्पन्न दाब क्या होगा?
(A) 6000 Pa
(B) 30 Pa
(C) 15 Pa
(D) 7.5 Pa
उत्तर:
(C) 15 Pa

24. किसी वस्तु की सतह के लंबवत् लगने वाले बल को कहा जाता है-
(A) प्रणोद
(B) दाब
(C) उत्प्लावन
(D) गुरुत्व
उत्तर:
(A) प्रणोद

25. प्रणोद का S.I. मात्रक है-
(A) न्यूटन
(B) पास्कल
(C) किलो पास्कल
(D) किलोग्राम
उत्तर:
(A) न्यूटन

26. किसी पतली तथा मजबूत डोरी से बने बैग को पकड़ना कठिन होता है क्योंकि प्रणोद प्रभावित करता है-
(A) बड़े क्षेत्रफल को
(B) अधिक क्षेत्रफल को
(C) छोटे क्षेत्रफल को
(D) लंबे क्षेत्रफल को
उत्तर:
(C) छोटे क्षेत्रफल को

27. काटने, चीरने और सुराख करने वाले यंत्र हमेशा नुकीले रखे जाते हैं ताकि-
(A) दाब कम हो जाए
(B) दाब बढ़ जाए
(C) दाब सामान्य रहे
(D) क्षेत्रफल बढ़ जाए
उत्तर:
(B) दाब बढ़ जाए

28. पानी के घनत्व से ………………. घनत्व की वस्तुएँ पानी पर तैरती हैं।
(A) समान
(B) कम
(C) अधिक
(D) अत्यधिक
उत्तर:
(B) कम

29. यदि दो वस्तुओं के बीच की दूरी को आधा कर दिया जाए तो उनके बीच गुरुत्वाकर्षण बल हो जाएगा-
(A) चार गुना
(B) दो गुना
(C) गुना
(D) गुना
उत्तर:
(A) चार गुना

30. पृथ्वी तथा उसकी सतह पर रखी किसी 1kg की वस्तु के बीच लगने वाले गुरुत्वीय बल का परिमाण होगा-
(A) 4.9 N
(B) 9.8 N
(C) 19.6 N
(D) 29.4N
उत्तर:
(B) 9.8 N

31. यदि दो वस्तुओं के बीच की दूरी को तीन गुना कर दिया जाए तो गुरुत्वाकर्षण बल हो जाएगा-
(A) तीन गुना
(B) 9 गुना
(C) \(\frac { 1 }{ 3 }\)गुना
(D) \(\frac { 1 }{ 9 }\)गुना
उत्तर:
(D) \(\frac { 1 }{ 9 }\) गुना

32. यदि दोनों वस्तुओं के द्रव्यमान दुगुने कर दिए जाएँ तो उनके बीच लगने वाला गुरुत्वाकर्षण बल हो जाता है-
(A) 2 गुना
(B) 3 गुना
(C) 4 गुना
(D) 1 गुना
उत्तर:
(C) 4 गुना

33. एक गेंद ऊर्ध्वाधर दिशा में ऊपर की ओर 49m/s के वेग से फेंकी जाती है, तो अधिकतम ऊँचाई जहाँ तक वह पहुँचती है-
(A) 12.25 m
(B) 122.5 m
(C) 1225 m
(D) 1.225 m
उत्तर:
(B) 122.5 m

34. 100 N भार की एक वस्तु किसी द्रव पर तैर रही है, इस पर कार्यरत उत्प्लावक बल होगा-
(A) 10 N
(B) 20 N
(C) 100 N
(D) 50 N
उत्तर:
(C) 100 N

35. 19.6 m ऊँची मीनार की चोटी से छोड़े गए पत्थर का अंतिम वेग होगा-
(A) 19.6 m/s
(B) 9.8 m/s
(C) 4.9 m/s
(D) 98.0 m/s
उत्तर:
(A) 19.6 m/s

36. जल का आपेक्षिक घनत्व कितना होता है?
(A) 1 kg m^-3
(B) 1
(C) 1000 kg m^-3
(D) 1000
उत्तर:
(B) 1

37. ऊर्ध्वाधर दिशा में ऊपर की ओर फेंकी गई एक गेंद 6s के पश्चात् फेंकने वाले के पास लौट आती है, तो गेंद किस वेग से ऊपर फेंकी जाती है?
(A) 29.4 m/s
(B) 9.8 m/s
(C) 19.6 m/s
(D) 4.9 m/s
उत्तर:
(A) 29.4 m/s

38. 50g के किसी पदार्थ का आयतन 20 cm है तो पदार्थ का घनत्व होगा-
(A) 1000 g/cm³
(B) 5.2 g/cm³
(C) 2.5 g/cm³
(D) 2.5 kg/m³
उत्तर:
(C) 2.5 g/cm³

39. द्रवों के घनत्व को मापने वाले यंत्र का नाम है-
(A) हाइड्रोमीटर
(B) लैक्टोमीटर
(C) ओडोमीटर
(D) वोल्टामीटर
उत्तर:
(A) हाइड्रोमीटर

40. आपेक्षिक घनत्व का मात्रक होता है-
(A) kg/m³
(B) g/cm³
(C) m/s
(D) कोई मात्रक नहीं
उत्तर:
(D) कोई मात्रक नहीं

41. बर्फ पानी में तैरती है क्योंकि-
(A) बर्फ का घनत्व पानी के घनत्व से कम होता है
(B) बर्फ का घनत्व पानी के घनत्व से अधिक होता है
(C) बर्फ का घनत्व पानी के घनत्व के समान होता है
(D) बर्फ का द्रव्यमान पानी के द्रव्यमान से अधिक होता है
उत्तर:
(A) बर्फ का घनत्व पानी के घनत्व से कम होता है।

42. 5 kg द्रव्यमान वाले पिंड का पृथ्वी पर भार होगा-
(A) 4.9N
(B) 49N
(C) 5N
(D) 50 N
उत्तर:
(B) 49N

Haryana State Board HBSE 9th Class Science Important Questions Chapter 11 कार्य तथा ऊर्जा Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 11 कार्य तथा ऊर्जा

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
कार्य किसे कहते हैं?
उत्तर:
यदि किसी वस्तु पर बल लगाया जाए और वस्तु बल की दिशा में गति करे तो हम कहेंगे कि कार्य हुआ है।

प्रश्न 2.
कार्य की मात्रा किस पर निर्भर करती है?
उत्तर:
कार्य की मात्रा लगाए गए बल तथा तय की गई दूरी पर निर्भर करती है।

प्रश्न 3.
कार्य का सूत्र क्या है?
उत्तर:
कार्य = बल x विस्थापन।

प्रश्न 4.
कार्य का मात्रक क्या है?
उत्तर:
कार्य का मात्रक न्यूटन मीटर (जूल) है।

प्रश्न 5.
ऊर्जा किसे कहते हैं?
उत्तर:
कार्य करने की क्षमता को ऊर्जा कहते हैं।

प्रश्न 6.
यांत्रिक ऊर्जा कितने प्रकार की होती है?
उत्तर:
यांत्रिक ऊर्जा दो प्रकार की होती है-

• गतिज ऊर्जा
• स्थितिज ऊर्जा।

प्रश्न 7.
स्थितिज ऊर्जा किसे कहते हैं?
उत्तर:
किसी वस्तु में उसकी स्थिति अथवा आकार में परिवर्तन के कारण ऊर्जा उत्पन्न होती है, जिसे स्थितिज ऊर्जा कहते हैं।

प्रश्न 8.
ऊँचाई पर उड़ते हुए वायुयान में किस प्रकार की ऊर्जा होती है?
उत्तर:
स्थितिज तथा गतिज-दोनों प्रकार की ऊर्जा।

प्रश्न 9.
पहाड़ी की चोटी पर रखे पत्थर में किस प्रकार की ऊर्जा होती है?
उत्तर:
स्थितिज ऊर्जा।

प्रश्न 10.
यांत्रिक ऊर्जा किसे कहते हैं?
उत्तर:
किसी वस्तु की स्थितिज तथा गतिज ऊर्जा के योग को यांत्रिक ऊर्जा कहते हैं।

प्रश्न 11.
बंदूक से निकली गोली में किस प्रकार की ऊर्जा होती है?
उत्तर:
गतिज ऊर्जा।

प्रश्न 12.
गतिज ऊर्जा का सूत्र लिखो।
उत्तर:
गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv² [जहाँ m → द्रव्यमान तथा v → वेग]

प्रश्न 13.
स्थितिज ऊर्जा का सूत्र लिखो।
उत्तर:
स्थितिज ऊर्जा = mgh [जहाँ m → द्रव्यमान तथा g→ गुरुत्वीय त्वरण तथा h → ऊँचाई]

प्रश्न 14.
ऊर्जा संरक्षण का नियम क्या है?
उत्तर:
इस नियम के अनुसार किसी भी प्रकार की ऊर्जा को न उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है। उसका केवल रूप परिवर्तित किया जा सकता है या किसी एक वस्तु से दूसरी वस्तु में स्थानांतरित किया जा सकता है।

प्रश्न 15.
कार्य करने से वस्तु की ऊर्जा पर क्या प्रभाव पड़ता है?
उत्तर:
जब कोई वस्तु कार्य करती है तो उसकी ऊर्जा में कुछ कमी हो जाती है।

प्रश्न 16.
जब कोई व्यक्ति अपने सिर पर 10 kg बोझ उठाकर क्षैतिज सड़क पर 50 मीटर चलता है तो उसके द्वारा किया गया कार्य कितना होगा?
उत्तर:
शून्य।

प्रश्न 17.
हमारे शरीर को ऊर्जा कहाँ से मिलती है?
उत्तर:
हमारे द्वारा खाए गए भोजन से।

प्रश्न 18.
हरे पौधे किस ऊर्जा का उपयोग करते हैं?
उत्तर:
सौर ऊर्जा का।

प्रश्न 19.
वायु ऊर्जा का कोई एक महत्त्वपूर्ण उपयोग लिखो।
उत्तर:
वायु ऊर्जा का उपयोग पवन चक्कियों द्वारा आटा पीसने में किया जाता है।

प्रश्न 20.
ऊर्जा के किन्हीं दो प्राकृतिक स्रोतों के नाम लिखो।
उत्तर:

1. सूर्य
2. पानी।

प्रश्न 21.
ऊर्जा के किन्हीं चार रूपों के नाम लिखो।
उत्तर:

1. यांत्रिक ऊर्जा
2. रासायनिक ऊर्जा
3. प्रकाश ऊर्जा
4. ध्वनि ऊर्जा।

प्रश्न 22.
गुरुत्वीय स्थितिज ऊर्जा से क्या अभिप्राय है?
उत्तर:
गुरुत्वीय बल के विरुद्ध किए गए कार्य के कारण वस्तु में संचित ऊर्जा को गुरुत्वीय स्थितिज ऊर्जा कहते हैं।

प्रश्न 23.
प्रत्यास्थ स्थितिज ऊर्जा से क्या अभिप्राय है?
उत्तर:
किसी वस्तु में उसकी आकृति में परिवर्तन के कारण संचित ऊर्जा प्रत्यास्थ स्थितिज ऊर्जा कहलाती है; जैसे खिंचे हुए रबड़ बैंड में।

प्रश्न 24.
जब दो पत्थर आपस में टकराते हैं तो चिंगारी क्यों उत्पन्न होती है?
उत्तर:
क्योंकि पत्थरों की गतिज ऊर्जा, प्रकाश ऊर्जा में रूपांतरित हो जाती है।

प्रश्न 25.
तीर अपनी गतिज ऊर्जा किस प्रकार प्राप्त करता है?
उत्तर:
तीर कमान में संचित स्थितिज ऊर्जा को गतिज ऊर्जा में रूपांतरित कर लेता है।

प्रश्न 26.
ऊर्जा तथा त्वरण में से कौन-सी राशि सदिश है?
उत्तर:
त्वरण सदिश राशि है।

प्रश्न 27.
एक पिंड ऊपर की ओर ऊर्ध्वाधर दिशा में फेंका जाता है, स्पष्टतः इसकी गति घटती रहती है। इसकी गतिज ऊर्जा कम होगी तो उच्चतम बिंदु पर पहुँचकर इसकी गति क्या होगी?
उत्तर:
शून्य।

प्रश्न 28.
उस संयंत्र का नाम लिखो जो विद्युत् ऊर्जा को यांत्रिक ऊर्जा में बदलता है।
उत्तर:
विद्युत् मोटर।

प्रश्न 29.
जल विद्युत् शक्ति केंद्र में किस प्रकार की ऊर्जा का किस प्रकार की ऊर्जा में परिवर्तन होता है?
उत्तर:
जल की गतिज ऊर्जा का विद्युत् ऊर्जा में परिवर्तन होता है।

प्रश्न 30.
शक्ति किसे कहते हैं? इसकी इकाई क्या है?
उत्तर:
कार्य करने की दर को शक्ति कहते हैं। इसकी इकाई वाट है।

प्रश्न 31.
यदि किसी वस्तु का वेग तीन गुना कर दिया जाए तो उसकी गतिज ऊर्जा पर क्या प्रभाव पड़ेगा?
उत्तर:
वस्तु की गतिज ऊर्जा नौ गुना बढ़ जाएगी।

प्रश्न 32.
तने हुए स्प्रिंग में किस प्रकार की ऊर्जा होती है?
उत्तर:
स्थितिज ऊर्जा।

प्रश्न 33.
बांध के जलाशय में एकत्रित हुए पानी में कौन-सी ऊर्जा होती है?
उत्तर:
स्थितिज ऊर्जा।

प्रश्न 34.
घड़ी के स्प्रिंग में कैसी ऊर्जा समाहित होती है?
उत्तर:
स्थितिज ऊर्जा जो घड़ी की सुइयों को गतिज ऊर्जा प्रदान करती है।

प्रश्न 35.
दौड़ रही गाड़ी में कौन-सी ऊर्जा होती है?
उत्तर:
गतिज ऊर्जा।

प्रश्न 36.
यदि किसी वस्तु की ऊँचाई को दुगुना कर दिया जाए तो उसकी स्थितिज ऊर्जा पर क्या प्रभाव पड़ेगा?
उत्तर:
इसकी स्थितिज ऊर्जा दुगुनी हो जाएगी।

प्रश्न 37.
एक किलोवाट तथा वाट में क्या संबंध है?
उत्तर:
1 किलोवाट = 1000 वाट।

प्रश्न 38.
हथेलियों को परस्पर रगड़ने से वे गर्म क्यों हो जाती हैं?
उत्तर:
क्योंकि हथेलियों की गतिज ऊर्जा, ऊष्मीय ऊर्जा में रूपांतरित हो जाती है।

प्रश्न 39.
एक किलोग्राम पत्थर के किसी टुकड़े को एक मीटर ऊँचाई तक उठाने के लिए कितनी ऊर्जा की आवश्यकता होगी?
उत्तर:
9.8 जूल [∵ W = m.g.h = 1 x 9.8 x 1 = 9.8 जूल]

प्रश्न 40.
एक आदमी और उसका बेटा एक समान वेग से दौड़ रहे हैं। अगर आदमी का द्रव्यमान बेटे से दुगुना हो तो उन दोनों की गतिज ऊर्जा में क्या अनुपात होगा?
उत्तर:
2 : 1 [∵ गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv² तथा V समान हैं]

प्रश्न 41.
पाल नाव किस प्रकार की ऊर्जा से चलती है?
उत्तर:
पाल नाव वायु की गतिज ऊर्जा से चलती है।

प्रश्न 42.
जब किसी वस्तु में 10 जूल कार्य करने की क्षमता हो तो उसकी ऊर्जा क्या होगी?
उत्तर:
10 जूल।

प्रश्न 43.
दैनिक जीवन में शक्ति के कौन-से अपवर्त्य मात्रक प्रयोग होते हैं?
उत्तर:
किलोवाट तथा मैगावाट।

प्रश्न 44.
एक अश्व शक्ति में कितने वाट होते हैं?
उत्तर:
एक अश्व शक्ति में 746 वाट होते हैं।

प्रश्न 45.
एक किलोवाट घंटा ऊर्जा से क्या अभिप्राय है?
उत्तर:
एक किलोवाट शक्ति के स्रोत द्वारा 1 घंटे में खर्च की गई ऊर्जा एक किलोवाट घंटा कहलाती है।

प्रश्न 46.
एक किलोवाट घंटा का जूल से क्या संबंध है?
उत्तर:
1 किलोवाट घंटा = 36,00,000 जूल।

प्रश्न 47.
मनुष्य सीढ़ियाँ चढ़ते समय किस ऊर्जा का उपयोग करता है?
उत्तर:
पेशीय ऊर्जा का।।

प्रश्न 48.
हमारे शरीर में भंडारित ऊर्जा का क्या रूप है?
उत्तर:
रासायनिक ऊर्जा।

प्रश्न 49.
निम्नलिखित में से किस गतिविधि में मनुष्य को सबसे कम ऊर्जा की आवश्यकता होती है?
(1) तैरने में
(2) चलने में
(3) सोने में
(4) तेज दौड़ने में।
उत्तर:
(3) सोने में।

प्रश्न 50.
सरल लोलक क्या है?
उत्तर:
सरल लोलक धातु का बना एक गोला होता है, जिसे भारहीन डोरी की सहायता से लटकाया जाता है।

प्रश्न 51.
सरल लोलक जब अपने चरम-बिंदु पर होता है तो उसमें कौन-सी ऊर्जा होती है?
उत्तर:
स्थितिज ऊर्जा।

प्रश्न 52.
मध्य स्थिति में लोलक में कौन-सी ऊर्जा होती है?
उत्तर:
गतिज ऊर्जा।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
कार्य से आप क्या समझते हैं? इसे कैसे मापा जाता है? कार्य का मात्रक क्या है?
उत्तर:
किसी वस्तु पर बल लगाने से बल के क्रिया-बिंदु का गति करना कार्य कहलाता है। कार्य को बल तथा बल दिशा में वस्तु द्वारा चली गई दूरी के गुणनफल द्वारा मापा जाता है।

अर्थात् किया गया कार्य = बल x बल की दिशा में चली गई दूरी
या W = F x s
कार्य एक सदिश राशि है। कार्य की इकाई न्यूटन मीटर अथवा जूल (J) है।

प्रश्न 2.
ऊर्जा किसे कहते हैं? इसके मात्रक का नाम तथा परिभाषा लिखो। इसके विभिन्न रूप कौन-कौन से हैं?
उत्तर:
कार्य करने की क्षमता को ऊर्जा कहते हैं। इसके मात्रक का नाम भी जूल है।

जूल-एक न्यूटन बल लगाने पर यदि कोई वस्तु बल की दिशा में एक मीटर तक विस्थापित हो जाए तो किया गया कार्य एक जूल कहलाता है।

ऊर्जा के विभिन्न रूप-

• यांत्रिक ऊर्जा
• ऊष्मीय ऊर्जा
• रासायनिक ऊर्जा
• विद्युत् ऊर्जा
• नाभिकीय ऊर्जा
• प्रकाशीय ऊर्जा
• परमाणु ऊर्जा
• चुंबकीय ऊर्जा
• ध्वनि ऊर्जा
• सौर ऊर्जा।

प्रश्न 3.
उदाहरण देकर बताएँ कि गतिशील वस्तुओं में कार्य करने की क्षमता होती है।
उत्तर:

• गतिशील कंचे में स्थिर कंचे को विस्थापित करने (कार्य करने) की क्षमता होती है।
• गतिशील वायु पवन चक्की की पंखुड़ियों को घुमाकर कार्य कर सकती है।
• गतिशील पानी भी कई प्रकार की वस्तुओं को एक स्थान से दूसरे स्थान तक बहाकर ले जाता है।
• गतिशील वायु पाल नाव को चलाने में सहायक होती है। अतः हम कह सकते हैं कि गतिशील वस्तुओं में कार्य करने की क्षमता होती है।

प्रश्न 4.
स्थितिज ऊर्जा तथा गतिज ऊर्जा से क्या तात्पर्य है? प्रत्येक के दो-दो उदाहरण दीजिए।
उत्तर:
स्थितिज ऊर्जा-किसी वस्तु में उसकी स्थिति अथवा आकृति में परिवर्तन के कारण उत्पन्न ऊर्जा को स्थितिज ऊर्जा कहते हैं।
उदाहरण-

• मेज पर पड़ी पुस्तक में उसकी स्थिति के कारण स्थितिज ऊर्जा होती है।
• चाबी भरी हुई घड़ी की कमानी में संरूपण के कारण स्थितिज ऊर्जा होती है। गतिज ऊर्जा-किसी वस्तु में उसकी गति के कारण उत्पन्न ऊर्जा को गतिज ऊर्जा कहते हैं।

उदाहरण-

• चलती हुई वायु में गतिज ऊर्जा होती है।
• बहते हुए पानी में गतिज ऊर्जा होती है।

प्रश्न 5.
क्या निम्नलिखित पदार्थों में ऊर्जा है? यदि हाँ, तो वह स्थितिज ऊर्जा है या गतिज ऊर्जा है या दोनों प्रकार की ऊर्जा है?

• छत का वह पंखा जिसका स्विच बंद कर दिया गया हो।
• पहाड़ पर चढ़ता हुआ मनुष्य।
• उड़ता हुआ पक्षी।
• बांध के जलाशय में भरा पानी।
• अपनी समान आकृति से अधिक खींची हुई कमानी।
• किसी मेज पर रखा हुआ रबड़ का कोई छल्ला।
• खिंचा हुआ रबड़ का छल्ला।

उत्तर:
जी हाँ, इन सभी पदार्थों में ऊर्जा है।

•  छत से लटके हुए पंखे में, जिसका स्विच बंद कर दिया गया हो, केवल स्थितिज ऊर्जा ही होती है।
• पहाड़ पर चढ़ते हुए मनुष्य में स्थितिज और गतिज दोनों प्रकार की ऊर्जा होती है।
• उड़ते हुए पक्षी में गतिज तथा स्थितिज ऊर्जा होती है।
• बांध के जलाशय में भरे पानी में स्थितिज ऊर्जा होती है।
• खिंची हुई कमानी में भी स्थितिज ऊर्जा होती है।
• मेज पर पड़े हुए रबड़ के छल्ले में स्थितिज ऊर्जा होती है।
• खिंचे हुए रबड़ के छल्ले में भी स्थितिज ऊर्जा होती है।

प्रश्न 6.
स्थितिज ऊर्जा तथा गतिज ऊर्जा में अंतर लिखो।
उत्तर:
स्थितिज ऊर्जा तथा गतिज ऊर्जा में निम्नलिखित अंतर हैं-

प्रश्न 7.
निम्नलिखित में कौन-सी ऊर्जा होती है?
(1) चाबी भरी घड़ी की कमानी में
(2) भागती हुई भैंस
(3) कमान से छोड़ा गया तीर
(4) छत पर पड़ी मेज
(5) संपीडित वायु
(6) वृक्ष से लगा आम।
उत्तर:
(1) स्थितिज ऊर्जा
(2) गतिज ऊर्जा
(3) गतिज ऊर्जा
(4) स्थितिज ऊर्जा
(5) स्थितिज ऊर्जा
(6) स्थितिज ऊर्जा।

प्रश्न 8.
मानव शरीर की कार्य करने की क्षमता किन परिस्थितियों में कम हो जाती है?
उत्तर:
मानव शरीर की कार्य करने की क्षमता निम्नलिखित परिस्थितियों में कम हो जाती है-

• जब मनुष्य बीमार हो जाता है।
• जब मनुष्य की आयु बढ़ने के कारण बुढ़ापा आ जाता है।
• जब मनुष्य आवश्यकता से कम भोजन करने लगता है तो उसकी मांसपेशियों की ऊर्जा कम हो जाती है।

प्रश्न 9.
कार्य और ऊर्जा में क्या संबंध है? इनके मात्रक लिखो।
उत्तर:
कार्य करने की क्षमता को ऊर्जा कहते हैं। ऊर्जा का परिमाण हमेशा उस कार्य के बराबर होता है, जो वह करने की क्षमता रखती है। ऊर्जा को जूल में मापा जाता है तथा कार्य का मात्रक भी जूल ही है।

उदाहरण के लिए, एक किलोग्राम पत्थर के किसी टुकड़े को एक मीटर ऊँचाई तक उठाने के लिए 9.8 जूल ऊर्जा की आवश्यकता पड़ती है। इसके विपरीत एक मीटर ऊँचाई से गिराए जाने पर पत्थर का यह टुकड़ा उसी परिमाण का कार्य (9.8 जूल) हमें वापस कर सकता है। अतः यदि किसी वस्तु में 100 जूल ऊर्जा हो तो उसमें 100 जूल कार्य करने की क्षमता होती है।

प्रश्न 10.
चाबी वाले खिलौने में किस प्रकार ऊर्जा का रूपांतरण होता है?
उत्तर:
चाबी वाले खिलौने या चाबी वाली घड़ी में एक स्प्रिंग होता है जो चाबी भरने की स्थिति में कस जाता है और उसमें स्थितिज ऊर्जा भर जाती है। कुछ क्षणों बाद स्प्रिंग धीरे-धीरे ढीला होता जाता है और खिलौना गति में आ जाता है अर्थात् स्थितिज ऊर्जा, गतिज ऊर्जा में रूपांतरित हो जाती है।

प्रश्न 11.
एक गेंद को ऊपर की ओर फेंका जाता है और यह फेंकने वाले के पास वापस आ जाती है। गेंद की गतिज और स्थितिज ऊर्जा में किस प्रकार परिवर्तन होता है? वर्णन करो।
उत्तर:
जब गेंद ऊपर की ओर जाती है तो इसकी गतिज ऊर्जा लगातार स्थितिज ऊर्जा में परिवर्तित होती जाती है। अधिकतम ऊँचाई पर जाकर इसकी पूरी-की-पूरी गतिज ऊर्जा स्थितिज ऊर्जा में बदल जाती है। जब गेंद नीचे की ओर आती है तो इसकी स्थितिज ऊर्जा लगातार गतिज ऊर्जा में बदलती जाती है तथा पृथ्वी के नजदीक इसकी सारी स्थितिज ऊर्जा गतिज ऊर्जा में बदल जाती है, परंतु पृथ्वी पर गिरते ही सारी गतिज ऊर्जा स्थितिज ऊर्जा में परिवर्तित हो जाती है।

प्रश्न 12.
एक लड़का अपने फैले हुए एक हाथ में कोई भार रखकर खड़ा है। इस अवस्था में लड़के तथा भार दोनों की स्थिति में कोई परिवर्तन होता दिखाई नहीं देता। क्या वह कोई कार्य कर रहा है? यदि हाँ, तो स्पष्ट करें।
उत्तर:
यद्यपि लड़के तथा भार की स्थिति में बाह्य रूप से हमें कोई परिवर्तन होता दिखाई नहीं देता, परंतु आंतरिक रूप से वही लड़का कार्य कर रहा होता है। हथेली पर रखे भार के कारण उस लड़के की मांसपेशियाँ खिंच जाती हैं, अर्थात् उनका आकार बदल जाता है। उसके हृदय को मांसपेशियों में अधिक रक्त भेजना पड़ता है। इन सभी रासायनिक क्रियाओं में लड़के की ऊर्जा व्यय होती है और वह जल्दी थक जाता है। इसी स्थिति में यदि लड़का काफी देर तक खड़ा रहे लोहे का तो पसीने के रूप में बाह्य परिवर्तन भी दिखाई देने लगता है।

प्रश्न 13.
किसी कृत्रिम उपग्रह द्वारा पृथ्वी के इर्द-गिर्द गति के दौरान गुटका (भार) किया गया कार्य कितना होता है? संक्षेप में समझाइए।
उत्तर:
कृत्रिम उपग्रह पृथ्वी के इर्द-गिर्द लगभग गोलाकार मार्ग में घूमता है। पृथ्वी और कृत्रिम उपग्रह के बीच गुरुत्वाकर्षण बल F पृथ्वी तथा उपग्रह को मिलाने वाली रेखा के अनुदिश (वृत्ताकार पथ की त्रिज्या के अनुरूप) कार्य करता है और उपग्रह गुरुत्व बल की दिशा के लंबवत् गति करता है। अतः बल की दिशा में उपग्रह के विस्थापन का प्रक्षेप शून्य होगा तथा पृथ्वी द्वारा उपग्रह पर किया गया कार्य भी शून्य होगा।

प्रश्न 14.
पवन की गतिज ऊर्जा कैसे प्रयुक्त की जाती है? इसके मुख्य उपयोग बताओ।
उत्तर:
बहती हुई पवन में उपस्थित ऊर्जा से विद्युत् ऊर्जा पैदा की जा सकती है। इसमें बहुत व्यय होता है। अतः पवन चक्की का उपयोग साधारणतः आटा पीसने तथा जलाशयों में से जल निकालने के लिए किया जाता है। पवन चक्की से बहुत कम विद्युत् ऊर्जा पैदा की जा सकती है। ऐसे स्थानों पर जहाँ पवन बहुत तीव्र वेग से वर्ष भर बहती रहती है, पवन संयंत्रों से अधिक मात्रा में आटा पीसने तथा पानी निकालने का काम किया जा सकता है।

पवन की यांत्रिक ऊर्जा के मुख्य उपयोग-इसके मुख्य उपयोग निम्नलिखित हैं-

• इससे जलाशयों से पानी निकालकर खेतों की सिंचाई की जा सकती है।
• इससे आटा पीसने की चक्कियाँ चलाई जा सकती हैं।
• बहुत-से पवन-चक्रों को परस्पर संयुक्त करके पवन की यांत्रिक ऊर्जा को विद्युत् ऊर्जा में परिवर्तित किया जा सकता है।

प्रश्न 15.
जल ऊर्जा किसे कहते हैं? इसके मुख्य उपयोग लिखो।
उत्तर:
बहते हुए जल में गतिज ऊर्जा के कारण इसमें कार्य करने की क्षमता होती है, जिसे जल ऊर्जा कहते हैं। जल ऊर्जा के उपयोग-जल ऊर्जा के उपयोग निम्नलिखित हैं-

• जल ऊर्जा को विद्युत् ऊर्जा में रूपांतरित कर घरों तथा कल-कारखानों में प्रयोग किया जाता है।
• जल ऊर्जा से पनचक्कियाँ चलाकर आटा पीसने का कार्य लिया जाता है।
• जल ऊर्जा के कारण लकड़ी के बड़े-बड़े लट्टे पानी के साथ बहकर एक स्थान से दूसरे स्थान पर जाते हैं।

प्रश्न 16.
जल ऊर्जा का प्रयोग विद्युत् उत्पादन में किस प्रकार किया जाता है?
उत्तर:
बहते पानी की गतिज ऊर्जा बांध बनाकर स्थितिज ऊर्जा के रूप में संचित कर ली जाती है। संचित जल को जलटरबाइन के बड़े-बड़े ब्लेडों पर गिराया जाता है। घूमती हुई टरबाइन के साथ जुड़ी शाफ्ट जनरेटर या डायनमो को तेज़ी से घुमाती है। डायनमो की कुंडली घूमती हुई विद्युत् पैदा करती है। इसे ‘जल विद्युत् शक्ति’ कहते हैं। भाखड़ा डैम पर इसी विधि से जल विद्युत् पैदा की जाती है। यही पन-बिजली घर का सिद्धांत भी कहलाता है।

प्रश्न 17.
जब हम लकड़ी के किसी तख्ते में हथौड़े से कील गाड़ते हैं तो कील गर्म हो जाती है, क्यों?
उत्तर:
जब हम लकड़ी के किसी तख्ते में हथौड़े से कील गाड़ते हैं तो कील गर्म हो जाती है क्योंकि ऊपर उठाए हुए हथौड़े में अपनी स्थिति के कारण कुछ स्थितिज ऊर्जा होती है। जब हथौड़ा कील पर गिरता है तो हथौड़ा तो स्थिर अवस्था में आ जाता है, परंतु अपनी समस्त ऊर्जा कील में स्थानांतरित कर देता है।

इसके फलस्वरूप कील को कुछ गतिज ऊर्जा प्राप्त होती है जिसके कारण वह लकड़ी के अंदर धंस जाती है। जब कील पूर्ण रूप से लकड़ी के अंदर जा चुकी हो, उसके बाद यदि हम हथौड़ा मारते ही चले जाएँ तो हम देखेंगे कि कील गर्म हो गई है क्योंकि हथौड़े की यांत्रिक ऊर्जा कील में स्थानांतरित होकर ऊष्मीय ऊर्जा में परिवर्तित हो जाती है।

प्रश्न 18.
सौर ऊर्जा के क्या लाभ हैं?
उत्तर:
सौर ऊर्जा के लाभ निम्नलिखित हैं-

• सौर ऊर्जा का प्रयोग सोलर कुकर में भोजन बनाने के लिए किया जाता है।
• सौर ऊर्जा का प्रयोग होटलों, अस्पतालों तथा औद्योगिक प्रतिष्ठानों की छतों पर सौर जल ऊष्मक लगाकर पानी गर्म करने के लिए किया जाता है।
• सौर ऊर्जा का प्रयोग विद्युत उत्पन्न करने के लिए किया जाता है।
• सौर भट्ठी में इस ऊर्जा का प्रयोग धातुओं को पिघलाने के लिए किया जाता है।

प्रश्न 19.
कार्य, ऊर्जा व शक्ति में अंतर स्पष्ट कीजिए। इनमें प्रत्येक का S.I. मात्रक लिखिए। अथवा शक्ति किसे कहते हैं? शक्ति का S.I. मात्रक लिखिए।
उत्तर:
कार्य-यदि किसी वस्तु पर बल लगाया जाए और वस्तु बल की दिशा में गति करे तो कार्य हुआ माना जाता है। अर्थात्
कार्य (W) = बल (F) x दूरी (s)
कार्य का S.I. मात्रक जूल है।
ऊर्जा-कार्य करने की क्षमता को ऊर्जा कहते हैं। ऊर्जा का S.I. मात्रक जूल है।
शक्ति कार्य करने की दर को शक्ति कहते हैं। अर्थात्

शक्ति का S.I. मात्रक वाट है।

प्रश्न 20.
ऊर्जा रूपांतरण से तुम क्या समझते हो? ऊर्जा रूपांतरण के कोई दो उदाहरण लिखें।
उत्तर:
ऊर्जा सरंक्षण के नियमानुसार ऊर्जा को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है। इसे केवल एक रूप से दूसरे रूप में रूपांतरित किया जा सकता है। इसे ऊर्जा रूपांतरण कहते हैं। अतः ऊर्जा का कुल परिमाण कभी नहीं बदलता।

उदाहरण-

• पहाड़ों पर पड़ी बर्फ पिघलकर पानी का रूप धारण कर लेती है। यह स्थितिज ऊर्जा का गतिज ऊर्जा में रूपांतरण है।
• विद्युत बल्ब में विद्युत ऊर्जा प्रकाशीय ऊर्जा में बदलकर प्रकाश देने लगती है।

गणनात्मक प्रश्न

महत्त्वपूर्ण सूत्र एवं तथ्य:
यदि m → वस्तु का द्रव्यमान, v → वेग, W → कार्य, s → दूरी, h → ऊँचाई, F → बल, t → समय तथा g → गुरुत्वीय त्वरण हो तो
(1) गतिज ऊर्जा (K.E.) = \(\frac { 1 }{ 2 }\) mv²
(2) स्थितिज ऊर्जा (P.E.) = m.g.h.
(3) कार्य = बल – विस्थापन या बल – दूरी (W = F x s)

(7) 1 अश्व शक्ति (हॉर्स पॉवर) = 746 वाट
(8) 1 कैलौरी = 4.186 जूल
(9) 1 किलोवाट घंटा (kWh) = 36,00,000 जूल = 3.6 x 10⁶ जूल
(10) एक वाट घंटा = 3600 जूल (1 किलोवाट = 1000 वाट) (11) गुरुत्वीय त्वरण (g) = 9.8 मी०/से2

प्रश्न 1.
एक लड़का जिसका द्रव्यमान 40 कि०ग्रा० है। वह 0.5 मीटर प्रति सेकंड के वेग से दौड़ रहा है। इसकी गतिज ऊर्जा क्या होगी?
हल:
यहाँ पर
m = 40 kg
v = 0.5 m/s
हम जानते हैं कि
गतिज ऊर्जा (K.E.) = \(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x 40 x 0.5 x 0.5
= 5 जूल उत्तर

प्रश्न 2.
15 Kg द्रव्यमान की एक वस्तु 4 ms^-1 के एकसमान वेग से गतिशील है। वस्तु की गतिज ऊर्जा कितनी होगी?
हल:
यहाँ पर
वस्तु का द्रव्यमान (m) = 15 kg
वस्तु का वेग (v) = 4 m/s
हम जानते हैं कि
गतिज ऊर्जा (K.E.) = \(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x 15 x (4)²
= \(\frac { 1 }{ 2 }\) x 15 x 16
= 120 जूल उत्तर

प्रश्न 3.
100 ग्राम द्रव्यमान वाले पत्थर को 5 मीटर की ऊँचाई पर रखा हुआ है। बताओ इसमें कौन-सी ऊर्जा है और ऊर्जा की मात्रा भी ज्ञात करो।
हल:
ऊँचाई के कारण पत्थर में स्थितिज ऊर्जा है।
यहाँ पर
m = 100 g = \(\frac { 100 }{ 1000 }\) = 0.1 kg
g = 9.8 m/s²
h = 5m
हम जानते हैं कि
स्थितिज ऊर्जा (P.E.) = m x g x h
= 0.1 x 9.8 x 5
= 4.9 जूल उत्तर

प्रश्न 4.
1 kg द्रव्यमान की वस्तु को 980 J ऊर्जा देकर पृथ्वी तल से कितना ऊपर उठाया जा सकता है?
हल:
यहाँ पर
m = 1 kg
g = 9.8 m/s²
h = ?
स्थितिज ऊर्जा (P.E.) = 980 J
हम जानते हैं कि
स्थितिज ऊर्जा = m.g.h.
या 980 = 1 x 9.8 x h
या h = \(\frac { 980 }{ 1×9.8 }\)
= 100 m उत्तर

प्रश्न 5.
किसी कण की चाल चार गुना बढ़ा दी जाए तो उसकी गतिज ऊर्जा कितने गुना बढ़ जाएगी?
हल:
माना कण की प्रारंभिक चाल = v
तो कण की अंतिम चाल = 4v
माना कण का द्रव्यमान = m
∴ कण की प्रारंभिक गतिज ऊर्जा (K₁) = \(\frac { 1 }{ 2 }\) mv² … (i)
कण की अंतिम गतिज ऊर्जा (K₂) = \(\frac { 1 }{ 2 }\) m(4v)²
= \(\frac { 1 }{ 2 }\) m x 16v² … (ii)
समीकरण (i) और (ii) से
\(\frac{\mathrm{K}_{\mathrm{i}}}{\mathrm{K}_2}=\frac{\frac{1}{2} \mathrm{mv}^2}{\frac{1}{2} \mathrm{~m} \times 16 \mathrm{v}^2}=\frac{1}{16}\)
या K₂ = 16 K₁
अतः कण की गतिज ऊर्जा पहले से 16 गुना बढ़ जाएगी। उत्तर

प्रश्न 6.
100 ग्राम द्रव्यमान की किसी गेंद की गतिज ऊर्जा 20 जूल है। गेंद की चाल का परिकलन कीजिए।
हल:
यहाँ पर
m = 100 ग्राम = \(\frac { 100 }{ 1000 }\) kg = 0.1 kg
v = ?
गतिज ऊर्जा (K.E.) = 20 जूल
हम जानते हैं कि
गतिज ऊर्जा (K.E) = \(\frac { 1 }{ 2 }\) mv²
या 20 = \(\frac { 1 }{ 2 }\) x 0.1 x v²
या v² = \(\frac { 20×2 }{ 0.1 }\) = 400
या v = \(\sqrt{400}\) = 20 m/s उत्तर

प्रश्न 7.
एक कुली 20 kg का बोझ धरती से 1.5 m ऊपर उठाकर अपने सिर पर रखता है। उसके द्वारा बोझे पर किए गए कार्य का परिकलन कीजिए।
हल:
यहाँ पर
बोझ का द्रव्यमान (m) = 20kg
विस्थापन (s) = 1.5m
किया गया कार्य (W) = F x s = mg x s
= 20 kg x 10 ms^-2 x 1.5m
= 300 kgms^-2m
= 300 Nm
= 300 J
कुली द्वारा बोझे पर किया गया कार्य 300 J है। उत्तर

प्रश्न 8.
50 कि०ग्रा० द्रव्यमान का कोई व्यक्ति 1.2 मीटर की ऊँचाई तक कूदता है। अधिकतम ऊँचाई के बिंदु पर उसकी स्थितिज ऊर्जा कितनी होगी?
हल:
यहाँ पर
m = 50 kg
g = 9.8 m/s²
h = 1.2 m
हम जानते हैं कि
स्थितिज ऊर्जा (P.E.) = m x g x h
= 50 × 9.8 × 1.2
= 588 J
अतः अधिकतम ऊँचाई पर व्यक्ति की स्थितिज ऊर्जा = 588 जूल उत्तर

प्रश्न 9.
50 कि०ग्रा० पुंज का कोई व्यक्ति कितने वेग से दौड़े कि उसकी गतिज ऊर्जा 625 जूल हो जाए?
हल:
यहाँ पर
m = 50 kg
v = ?
गतिज ऊर्जा (KE.) = 625 J
हम जानते हैं कि
गतिज ऊर्जा (K.E) = \(\frac { 1 }{ 2 }\) mv²
या 625 =\(\frac { 1 }{ 2 }\) x 50 x v²
या v² = \(\frac { 625×2 }{ 50 }\) = 25
या v = \(\sqrt{25}\) = 5 m/s

प्रश्न 10.
कोई मनुष्य 10 kg के पत्थर को 5m की सीढ़ी के ऊपर से गिराता है। जब वह पृथ्वी पर पहुँचेगा तो उसकी गतिज ऊर्जा क्या होगी? पृथ्वी के अत्यंत निकट पत्थर की चाल क्या होगी?
हल:
यहाँ पर
m = 10 kg
h = 5 m
v = ?
गतिज ऊर्जा (KE.) = ?
हम जानते हैं कि
गतिज ऊर्जा (K.E) = पत्थर के गिरने से खोई स्थितिज ऊर्जा
= mgh
= 10 kg x 9.8 m/s² x 5 m = 490 J …. (i)
क्योंकि गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv² … (ii)
समीकरण (i) और (ii) से
\(\frac { 1 }{ 2 }\)mv² = 490 J
या \(\frac { 1 }{ 2 }\) x 10 kg x v² = 490 J
या v² = \(\frac { 490×2 }{ 10 }\)
= \(\frac { 98 }{ 10 }\)
= 98
या v = \(\sqrt{98}\) = 9.9 m/s (लगभग) उत्तर

प्रश्न 11.
1000 kg की 30 m/s की चाल से चल रही कार ब्रेक लगाने पर एक समान त्वरण से 50 मीटर की दूरी पर रुक जाती है। ब्रेक द्वारा कार पर लगे बल तथा कृत कार्य को ज्ञात कीजिए।
हल:
यहाँ पर
m = 1000 kg
u = 30 m/s
v = 0 m/s
s = 50 m
F = ?
W = ?
हम जानते हैं कि
v² – u² = 2as
a = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{~s}}=\frac{(0)^2-(30)^2}{2 \times 50}=\frac{-900}{100} \mathrm{~m} / \mathrm{s}^2\)
= – 9 m/s², अतः मंदन = 9 m/s²
F = m.a. = 1000 kg x 9 m/s² = 9000 N
ब्रेक द्वारा कार पर लगा बल (F) = 9000 N
किया गया कार्य (W) = F x s = 9000 N x 50 m = 450000 J = 450 kJ उत्तर

प्रश्न 12.
एक मनुष्य का भार 50 किलोग्राम है। वह 20 सेकंड में एक पहाड़ी पर ऊर्ध्वाधरतः 10 मीटर चढ़ जाता है। उसकी शक्ति मालूम करो। (दिया है g = 9.8 मी०/से०²)
हल:
यहाँ पर
F = m x g
= 50 x 9.8 = 490 N
अब W = F x s
= 490 N x 10m
= 4,900 Nm
समय (t) = 20 सेकंड
शक्ति (P) = \(\frac { कार्य }{ समय }\)
= \(\frac { 4,900 }{ 20 }\)
= 245 वाट

प्रश्न 13.
40kg द्रव्यमान का एक लड़का एक जीने पर दौड़कर 45 सीढ़ियाँ 95 में चढ़ता है। यदि प्रत्येक सीढ़ी की ऊँचाई 15cm हो तो उसकी शक्ति का परिकलन कीजिए।g का मान 10ms^-2 लीजिए
हल:
लड़के का भार mg = 40 kg x 10 ms^-2 = 400N
सीढ़ी की ऊँचाई (h) = 45 x 15/100m = 6.75m
चढ़ने में लगा समय t = 9s

लड़के की शक्ति 300W है। उत्तर

प्रश्न 14.
50 kg द्रव्यमान का कोई व्यक्ति 30 सीढ़ियाँ 30 सेकंड में चढ़ जाता है। यदि प्रत्येक सीढ़ी 20 cm ऊँची है तो कुल सीढ़ियाँ चढ़ने में उसके द्वारा प्रयुक्त शक्ति का परिकलन कीजिए।
हल:
व्यक्ति का द्रव्यमान (m) = 50 kg
सीढ़ियों की संख्या = 30
प्रत्येक सीढ़ी की ऊँचाई = 20 cm
= \(\frac { 20 }{ 100 }\) m = 0.2m
व्यक्ति द्वारा तय की गई कुल ऊँचाई = 30 x 0.2 m = 6m
गुरुत्वीय त्वरण (g) = 10 m/s²
अतः व्यक्ति द्वारा किया गया कार्य = m.g.h
= 50 x 10 x 6J
= 3000J
सीढ़ियाँ चढ़ने में लिया गया समय = 30s

प्रश्न 15.
100 वाट के एक बल्ब को 2 घंटे तक जलाया जाता है, कितनी विद्युत् ऊर्जा व्यय होगी?
हल:
बल्ब की शक्ति = 100 वाट
समय = 2 घंटे = 2 x 3600 = 7200 सेकंड
व्यय ऊर्जा = शक्ति x समय
= 100 x 7200 वाट-सेकंड
= 720000 जूल उत्तर

प्रश्न 16.
किसी रॉकेट का द्रव्यमान 3 x 10 kg है; एक km/s वेग से 25 km ऊँचाई पर गतिमान इसकी (a) स्थितिज ऊर्जा, (b) गतिज ऊर्जा का परिकलन कीजिए। (g का मान 10 m/s लीजिए)
हल:
यहाँ पर
रॉकेट का द्रव्यमान (m) = 3x 10⁶ kg
रॉकेट का वेग (v) = 1 km/s
= 1000 m/s
रॉकेट की ऊँचाई (h) = 25 km
= 25000 m
(a) गुरुत्वीय त्वरण (g) = 10 m/s²
स्थितिज ऊर्जा = m.g.h.
= 3 x 10⁶ x 10 x 25000 J
= 7.5 x 10¹¹

(b) गतिज ऊर्जा =\(\frac { 1 }{ 2 }\) mv²
= \(\frac { 1 }{ 2 }\) x 3 x 10⁶ x (1000)² J
= 1.5 x 10¹² J उत्तर

प्रश्न 17.
18 km/h वेग से गतिमान किसी गाड़ी को कोई घोड़ा समतल सड़क पर 300 N बल से खींच रहा है। घोड़े की शक्ति वाट में ज्ञात कीजिए। यह शक्ति कितने हॉर्सपावर के तुल्य है?
हल:
यहाँ पर
गाड़ी का वेग (V) = 18 km/h
= \(\frac { 18×1000 }{ 360 }\) m/s = 5 m/s
घोड़े द्वारा गाड़ी पर लगाया गया बल (F) = 300 N
⇒ m.g. = 300 N
किया गया कार्य = m.g.h
= 300 x 5 = 1500J

हम जानते हैं कि 746 वाट = 1 अश्व शक्ति
1 वाट = \(\frac { 1 }{ 746 }\) अश्व शक्ति
1500 वाट =\(\frac { 1 }{ 746 }\) x 1500 अश्व शक्ति
= 2 अश्व शक्ति (हॉर्सपावर) उत्तर

निबंधात्मक प्रश्न

प्रश्न 1.
स्थितिज ऊर्जा से क्या अभिप्राय है? किसी वस्तु की स्थितिज ऊर्जा का व्यंजक प्राप्त करें।
उत्तर:
स्थितिज ऊर्जा-किसी वस्तु में उसकी स्थिति अथवा आकार में परिवर्तन के कारण जो ऊर्जा उत्पन्न होती है उसे स्थितिज ऊर्जा कहते हैं।
व्यंजक-माना m द्रव्यमान की कोई वस्तु पृथ्वी की सतह पर A बिंदु पर रखी है। उसे F बल लगाकर B बिंदु तक उठाया गया। A व B के मध्य दूरी h है।

जैसा कि हम जानते हैं कि वस्तु को उठाने में लगने वाला बल F, वस्तु पर लगे गुरुत्वाकर्षण बल के बराबर व विपरीत होता है
F = \(\frac{\mathrm{GM}_{\mathrm{e}} \cdot \mathrm{m}}{\mathrm{R}_{\mathrm{e}}{ }^2}\) … (i)
जहाँ M_e = पृथ्वी का द्रव्यमान
R_e = पृथ्वी की त्रिज्या
लेकिन g = \(\frac{\mathrm{GM}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^2}\) (g = गुरुत्वीय त्वरण) …(ii)
समीकरण (i) व (ii) से
F = mg
वस्तु को h ऊँचाई तक ले जाने में किया गया कार्य
W = F x s (∵ s = h)
= mgh
क्योंकि किया गया कार्य और ऊर्जा समान ही है। अतः h ऊँचाई पर वस्तु की
स्थितिज ऊर्जा (PE.) = mgh

प्रश्न 2.
गतिज ऊर्जा से आप क्या समझते हैं? किसी वस्तु की गतिज ऊर्जा का व्यंजक प्राप्त करें।
उत्तर:
गतिज ऊर्जा-गति के आधार पर कार्य करने की क्षमता को गतिज ऊर्जा कहते हैं।
व्यंजक-माना ‘m’ पुंज की एक वस्तु को ‘h’ ऊँचाई से विराम अवस्था में छोड़ा जाता है और पृथ्वी तल पर पहुँचते-पहुंचते उसका वेग v हो जाता है तो
वस्तु का प्रारंभिक वेग (u) = 0
त्वरण (a) = (g) गुरुत्वीय त्वरण
अंतिम वेग = v
दूरी (s) = ऊँचाई = h
हम जानते हैं कि v² – u² = 2as
v² – 0 = 2gh
या v² = 2gh
या h = \(\frac{\mathrm{v}^2}{2 \mathrm{~g}}\) … (i)
ज्यों-ज्यों वस्तु नीचे आती जाती है इसकी स्थितिज ऊर्जा कम होती जाती है और गतिज ऊर्जा बढ़ती जाती है। जब वस्तु पृथ्वी तल पर पहुंचती है तो उसकी सारी स्थितिज ऊर्जा गतिज ऊर्जा में बदल चुकी होती है। ऊर्जा संरक्षण के नियम के अनुसार वस्तु की कुल ऊर्जा न घटती है न बढ़ती है। अतः पृथ्वी तल पर गतिज ऊर्जा = h ऊँचाई पर स्थितिज ऊर्जा
गतिज ऊर्जा = mgh
या गतिज ऊर्जा = mg x \(\frac{\mathrm{v}^2}{2 \mathrm{~g}}\) (∵ h = \(\frac{\mathrm{v}^2}{2 \mathrm{~g}}\) )
या गतिज ऊर्जा = \(\frac { 1 }{ 2 }\) mv²

प्रश्न 3.
ऊर्जा संरक्षण के नियम से क्या अभिप्राय है? ऊर्जा संरक्षण का कोई एक उदाहरण दें।
उत्तर:
ऊर्जा संरक्षण नियम-ऊर्जा संरक्षण नियम के अनुसार ऊर्जा न तो उत्पन्न की जा सकती है और न ही नष्ट की जा सकती है। ऊर्जा केवल एक रूप से दूसरे रूप में परिवर्तित की जा सकती है। जब भी ऊर्जा किसी रूप में मुक्त होती है तो ठीक उतनी ही ऊर्जा अन्य रूपों में प्रकट हो जाती है। अतः विश्व की संपूर्ण ऊर्जा का परिणाम स्थिर रहता है।

माना m द्रव्यमान की कोई वस्तु पृथ्वी तल से h ऊँचाई से नीचे की ओर गिरना आरंभ करती है।

(1) A बिंदु पर ऊर्जा स्थितिज ऊर्जा = mgh
गतिज ऊर्जा = 0
इसलिए कुल ऊर्जा = mgh + 0
= mgh … (i)

(2) B बिंदु पर ऊर्जा माना वस्तु A से B तक s दूरी तक गिरती है तो उसकी पृथ्वी तल से ऊँचाई (h-s) होगी।
∴ स्थितिज ऊर्जा = mg (h – s)
तथा v² – u² = 2gs
या v² = 2gs [∵ u = 0]
गतिज ऊर्जा = \(\frac { 1 }{ 2 }\)mv² = \(\frac { 1 }{ 2 }\)m x 2gs = mgs
कुल ऊर्जा = mg (h-s) + mgs = mgh – mgs + mgs
= mgh … (ii)

(3) C बिंदु पर ऊर्जा
v² – u² = 2gh
v² = 2gh [∵ u = 0]
गतिज ऊर्जा = \(\frac { 1 }{ 2 }\)mv² = \(\frac { 1 }{ 2 }\)m x 2gh = mgh
तथा स्थितिज ऊर्जा = 0
कुल ऊर्जा = mgh + 0 = mgh … (iii)
इस प्रकार हम देखते हैं कि समीकरण (i), (ii) व (iii) में वस्तु की ऊर्जा प्रत्येक स्थान पर स्थिर रहती है। सबसे उच्च बिंदु पर वस्तु में समस्त स्थितिज ऊर्जा होती है। थोड़ा नीचे गिरने पर स्थितिज ऊर्जा का कुछ भाग गतिज ऊर्जा में बदल जाता है तथा पृथ्वी तल पर पहुँचकर समस्त स्थितिज ऊर्जा, गतिज ऊर्जा में बदल जाती है।

प्रयोगात्मक कार्य

क्रियाकलाप 1.
एक प्रयोग द्वारा समझाइए कि किसी बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक दोनों में से कोई एक हो सकता है।

कार्य-विधि-एक बच्चा किसी खिलौना कार को चित्र के अनुसार धरती के समांतर खींच रहा है। बच्चे ने कार के विस्थापन की दिशा में बल लगाया है। इस स्थिति में किया गया कार्य बल तथा विस्थापन के गुणनफल के बराबर होगा। इस स्थिति में बल द्वारा किया गया कार्य धनात्मक माना जाता है।

अब एक स्थिति पर विचार करें कि जिसमें बलों के प्रभाव से एक वस्तु विस्थापित होती है और हम पाते हैं कि इनमें से बल F, विस्थापन s की दिशा के विपरीत दिशा में लग रहा है अर्थात् दोनों दिशाओं के मध्य 180° का कोण बन रहा है। ऐसी स्थिति में बल (F) द्वारा किया गया कार्य ऋणात्मक माना जाता है और इसे ऋण चिह्न द्वारा निर्दिष्ट किया जाता है। बल द्वारा किया गया कार्य F x (-s) या (-F x s) है।

जब बल विस्थापन की दिशा के विपरीत दिशा में लगता है तो किया गया कार्य ऋणात्मक होता है। जब बल विस्थापन की दिशा में लगता है तो किया गया कार्य धनात्मक होता है।

क्रियाकलाप 2.
एक ऐसे क्रियाकलाप का वर्णन करें जिसमें धनात्मक व ऋणात्मक दोनों बल कार्य कर रहे हों।

कार्य-विधि-किसी वस्तु को ऊपर उठाते समय धनात्मक व ऋणात्मक दोनों बल कार्य करते हैं क्योंकि जो बल हम लगाते हैं वह वस्तु को ऊपर की ओर विस्थापित करता है जो धनात्मक बल कहलाता है। जबकि पृथ्वी द्वारा लगाया गया गुरुत्वीय बल वस्तु को नीचे की ओर खींचता है जो ऋणात्मक बल कहलाता है।

क्रियाकलाप 3.
एक प्रयोग द्वारा समझाइए कि अधिक ऊँचाई पर वस्तु में अधिक ऊर्जा होती है।

कार्य-विधि-एक भारी गेंद लीजिए। इसे रेत की मोटी परत (क्यारी) पर गिराइए। गीला रेत अच्छा कार्य करेगा। गेंद को रेत पर लगभग 25cm की ऊँचाई से गिराइए। गेंद रेत में एक गर्त (गड्डा) बना देती है। इस क्रियाकलाप को 50 cm, 1 m तथा 1.5 m की ऊँचाइयों से गेंद को गिराकर दोहराइए। सुनिश्चित कीजिए कि सभी गर्त सुस्पष्ट दिखाई दें। गेंद को गिराने की ऊँचाई के अनुसार सभी गर्मों पर निशान लगाएँ। उनकी गहराइयों की तुलना करें। आप देखेंगे कि 1.5m की ऊँचाई से गेंद को गिराने पर बना गर्त सबसे गहरा होगा जिससे सिद्ध होता है कि अधिक ऊँचाई पर वस्तु में अधिक ऊर्जा होती है जिससे अधिक गहरा गर्त (गड्डा) बनता है।

क्रियाकलाप 4.
एक प्रयोग द्वारा समझाइए कि द्रव्यमान बढ़ने से वस्तु की गतिज ऊर्जा बढ़ जाती है।
कार्य-विधि
(1) चित्र के अनुसार उपकरण फिट कीजिए।

(2) एक ज्ञात द्रव्यमान के लकड़ी के गुटके को ट्रॉली के सामने किसी सुविधाजनक निश्चित दूरी पर रखिए।

(3) पलड़े पर एक ज्ञात द्रव्यमान रखिए जिससे ट्रॉली गतिमान हो जाए।

(4) ट्रॉली आगे चलती है तथा लकड़ी के गुटके से टकराती है तथा गुटका विस्थापित हो जाता है।

(5) अब गुटके के विस्थापन को मापिए। इससे यह स्पष्ट हुआ कि जैसे ही गुटके ने ऊर्जा ग्रहण की ट्रॉली द्वारा गुटके पर कार्य किया गया।

(6) पलड़े पर रखे द्रव्यमान को बढ़ाकर इस प्रयोग को दोहराइए। आप देखेंगे कि द्रव्यमान बढ़ाने पर विस्थापन बढ़ जाएगा जिससे सिद्ध होता है कि द्रव्यमान बढ़ने के साथ-साथ गतिज ऊर्जा बढ़ जाती है।

अध्याय का तीव्र अध्ययन

1. कार्य करने के लिए आवश्यक है-
(A) वस्तु में विस्थापन
(B) वस्तु पर बल आरोपित किया जाए
(C) (A) और (B) दोनों
(D) वस्तु में विस्थापन न हो
उत्तर:
(C) (A) और (B) दोनों

2. ऊँचाई पर रखे किसी पिंड में कौन-सी ऊर्जा होती है?
(A) स्थितिज
(B) गति
(C) (A) और (B) दोनों
(D) ऊर्जा से कोई संबंध नहीं
उत्तर:
(A) स्थितिज

3. विद्युत ऊर्जा को ऊष्मा ऊर्जा में रूपान्तरित करने वाला यन्त्र है-
(A) विद्युत इस्त्री
(B) विद्युत बल्ब
(C) रेडियो
(D) विद्युत मोटर
उत्तर:
(A) विद्युत इस्त्री

4. रेडियो विद्युत ऊर्जा को किस ऊर्जा में रूपान्तरित करता है?
(A) प्रकाश
(B) ध्वनि
(C) यान्त्रिक
(D) ऊष्मा
उत्तर:
(B) ध्वनि

5. उड़ते पक्षी में कौन-सी ऊर्जा होती है?
(A) स्थितिज
(B) गतिज
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों ही नहीं
उत्तर:
(C) (A) और (B) दोनों

6. कार्य के लिए कौन-सा सूत्र उचित है?
(A) W = F
(B) w = \(\frac { s }{ F }\)
(C) W = Fs
(D) w = \(\frac { 1 }{ Fs }\)
उत्तर:
(C) W = Fs

7. बल का मात्रक है-
(A) न्यूटन
(B) न्यूटन मीटर
(C) जूल
(D) (B) और (C) दोनों
उत्तर:
(D) (B) और (C) दोनों

8. किसी वस्तु पर 5 N बल लगाने से 2m विस्थापन होता है, कार्य कितना होगा?
(A) 10 Nm
(B) 10 J
(C) 10 Jm
(D) (A) और (B) दोनों
उत्तर:
(D) (A) और (B) दोनों

9. कुली 15 kg भार धरती से 1.5m ऊपर उठाकर सिर पर रखता है। कुली द्वारा किए कार्य का परिकलन कीजिए।
(A) 22.5J
(B) 2.25J
(C) 225J
(D) 225 N
उत्तर:
(C) 225J

10. 2m की ऊँचाई पर रखी 1kg द्रव्यमान की वस्तु की स्थितिज ऊर्जा होगी-
(A) 9.8J
(B) 19.6J
(C) 29.4J
(D) 39.2J
उत्तर:
(B) 19.6J

11. कितने वाट से एक किलोवाट बनता है?
(A) 10³
(B) 10⁴
(C) 10⁵
(D) 10⁶
उत्तर:
(A) 10³

12. कितने जूल से एक किलोवाट घण्टा बनता है?
(A) 36 लाख
(B) 36 हजार
(C) 36 सौ
(D) 36 करोड़
उत्तर:
(A) 36 लाख

13. 100 वाट के पाँच विद्युत पंखे 4 घण्टे में कितनी ऊर्जा व्यय करेंगे?
(A) 20 kwh
(B) 10 kwh
(C) 2 kwh
(D) 1 kwh
उत्तर:
(C) 2 kwh

14. कार्य करने की दर क्या कहलाती है?
(A) शक्ति
(B) बल
(C) ऊर्जा
(D) इनमें से कोई नहीं
उत्तर:
(A) शक्ति

15. न्यूटन मीटर (Nm) किसका मात्रक है?
(A) कार्य
(B) बल
(C) त्वरण
(D) शक्ति
उत्तर:
(A) कार्य

16. न्यूटन मीटर का दूसरा नाम क्या है?
(A) अर्ग
(B) कूलम्ब
(C) जूल
(D) हज़
उत्तर:
(C) जूल

17. जब बल विस्थापन की दिशा में लगता तो किया गया कार्य होता है-
(A) ऋणात्मक
(B) धनात्मक
(C) शून्य
(D) इनमें से कोई नहीं
उत्तर:
(B) धनात्मक

18. एक व्यक्ति 20 kg का बोझ 10 मिनट तक सिर पर लेकर खड़ा रहता है, किया गया कार्य होगा-
(A) 200 जूल
(B) एक जूल
(C) शून्य
(D) 400 जूल
उत्तर:
(C) शून्य

19. ऊर्जा का मात्रक होता है-
(A) Nm
(B) जूल
(C) (A) व (B) दोनों ही
(D) कोई मात्रक नहीं होता
उत्तर:
(C) (A) व (B) दोनों ही

20. गतिज ऊर्जा का उदाहरण नहीं है-
(A) पहाड़ पर रखा पत्थर
(B) घूमता पहिया
(C) चलती हवा
(D) बंदूक से निकली गोली
उत्तर:
(A) पहाड़ पर रखा पत्थर

21. स्थितिज ऊर्जा का उदाहरण नहीं है-
(A) कमान में रखा तीर
(B) पहाड़ पर रखा पत्थर
(C) गिरता हुआ नारियल
(D) बंदूक में रखी गोली
उत्तर:
(C) गिरता हुआ नारियल

22. 10 kg द्रव्यमान की एक वस्तु को धरती से 6 m ऊँचाई तक उठाया गया। वस्तु की ऊर्जा का परिकलन कीजिए। (g = 9.8 ms^-2)
(A) 98 J
(B) 58.8 J
(C) 588 J
(D) 5880 J
उत्तर:
(C) 588 J

23. ऊर्जा संरक्षण का नियम है-
(A) सभी कार्यों में ऊर्जा की आवश्यकता होती है
(B) ऊर्जा उत्पन्न की जा सकती है
(C) ऊर्जा नष्ट की जा सकती है।
(D) न तो ऊर्जा उत्पन्न की जा सकती है और न ही नष्ट
उत्तर:
(D) न तो ऊर्जा उत्पन्न की जा सकती है और न ही नष्ट

24. कौन-सा कथन सत्य नहीं है?
(A) स्थितिज ऊर्जा + गतिज ऊर्जा = अचर
(B) गतिज ऊर्जा + स्थितिज ऊर्जा = यांत्रिक ऊर्जा
(C) किसी बिंदु पर स्थितिज ऊर्जा में जितनी कमी होती है उतनी ही कमी गतिज ऊर्जा में हो जाती है
(D) किसी बिंदु पर स्थितिज ऊर्जा में जितनी कमी होती है उतनी ही गतिज ऊर्जा में वृद्धि हो जाती है
उत्तर:
(C) किसी बिंदु पर स्थितिज ऊर्जा में जितनी कमी होती है उतनी ही कमी गतिज ऊर्जा में हो जाती है

25. कौन-सा सूत्र ठीक है?
(A) P = W x t
(B) P = \(\frac { W }{ t }\)
(C) P = \(\frac { t }{ w }\)
(D) P = \(\frac { 1 }{ W×t }\)
उत्तर:
(B) P = \(\frac { W }{ t }\)

26. शक्ति का मात्रक क्या है?
(A) जूल
(B) Nm
(C) अर्ग
(D) वाट
उत्तर:
(D) वाट

27. 600 न्यूटन भार वाला व्यक्ति 10 मीटर ऊँचाई तक चढ़ने के लिए कितनी ऊर्जा की खपत करेगा?
(A) 60 जूल
(B) 600 जूल
(C) 6000 जूल
(D) 588 जूल
उत्तर:
(C) 6000 जूल

28. आपके शरीर में स्थितिज ऊर्जा की न्यूनतम मात्रा कब होगी? जब आप-
(A) खड़े हों
(B) कुर्सी पर बैठे हों
(C) धरती पर लेटे हों
(D) धरती पर बैठे हों
उत्तर:
(C) धरती पर लेटे हों

29. कब कार्य नहीं होता-
(A) लकड़ी में कील ठोकने पर
(B) बक्से को फर्श पर खिसकाने पर
(C) गति की दिशा में समानांतर बल का घटक न होने पर
(D) खूटी पर लटकाया एक भार
उत्तर:
(C) गति की दिशा में समानांतर बल का घटक न होने पर

30. 10m कुएँ की गहराई से 5kg द्रव्यमान की एक बाल्टी को ऊपर खींचने में 10 सेकंड का समय लगता है। कार्य में प्रयुक्त शक्ति होगी-
(A) 50 Nm
(B) 50J
(C) 50 W
(D) 500 w
उत्तर:
(C) 50w

31. किसी m द्रव्यमान की वस्तु जिसका वेग ७ है, का संवेग क्या होगा?
(A) (mv)²
(B) mv²
(C) \(\frac { 1 }{ 2 }\) mv²
(D) mv
उत्तर:
(C) \(\frac { 1 }{ 2 }\) mv²

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 1 Number Systems Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 1 Number Systems

Very Short Answer Type Questions

Question 1.
Convert the following decimal number in the form
(i) 0.24
(ii) 8.03
(iii) 6.025
(iv) 0.4640.
Solution :

Question 2.
Give an example of each, two irrational numbers whose :
(i) difference is an irrational number.
(ii) sum is an irrational number.
(iii) product is an irrational number.
(iv) quotient is an irrational number
Solution:
(i) Let 5\(\sqrt{3}\) and 3\(\sqrt{3}\) be two irrational numbers.
∴ Difference = 5\(\sqrt{3}\) – 3\(\sqrt{3}\) = 2\(\sqrt{3}\),
which is an irrational number.
Hence, two irrational numbers are 5\(\sqrt{3}\) and 3\(\sqrt{3}\).

(ii) Let \(\sqrt{2}\) and \(\sqrt{3}\) be two irrational numbers.
∴ Sum = \(\sqrt{2}\) + \(\sqrt{3}\), which is an irrational number.
Hence, two irrational numbers are \(\sqrt{2}\) and \(\sqrt{3}\)

(iii) Let \(\sqrt{2}\) and \(\sqrt{5}\) be two irrational numbers.
∴ Their product = \(\sqrt{2}\) × \(\sqrt{5}\) = \(\sqrt{10}\).
which is an irrational number. Hence, two irrational numbers are \(\sqrt{2}\) and \(\sqrt{5}\).

(iv) Let \(\sqrt{6}\) and \(\sqrt{2}\) be two irrational numbers.
Their quotient \(\frac{\sqrt{6}}{\sqrt{2}}=\sqrt{\frac{6}{2}}=\sqrt{3}\), which is an irrational number. Hence, two irrational numbers are \(\sqrt{6}\) and \(\sqrt{2}\).

Question 3.
Find a rational and irrational number between two positive numbers x and y.
Solution:
A rational number between x and y = \(\frac{x+y}{2}\)
Since, product of x and y i.e., xy cannot be a perfect square.
Therefore, an irrational number between x and y = \(\sqrt{xy}\)
Hence, a rational number between x and y = \(\frac{x+y}{2}\) and an irrational number between x and y = \(\sqrt{xy}\).

Question 4.
Prove that 3 + \(\sqrt{5}\) is an irrational number.
Solution :
Let 3 + \(\sqrt{5}\) be a rational number, say x, then
3 + \(\sqrt{5}\) = x
⇒ x – 3 = \(\sqrt{5}\)
x – 3 is a rational number. [∵ difference of two ratinoal numbers is a rational number]
⇒ \(\sqrt{5}\) is a rational number.
But \(\sqrt{5}\) is an irrational number. So, our assumption is wrong.
Hence, 3 + \(\sqrt{5}\) is an irrational number.
Hence Proved

Question 5.
Add each of the following:
(i) (5\(\sqrt{3}\) – 7\(\sqrt{2}\)) and (2\(\sqrt{3}\) + 4\(\sqrt{2}\))
(ii) (6\(\sqrt{3}\) + 5\(\sqrt{5}\) – 4\(\sqrt{7}\)) and (\(\sqrt{3}\) – 4\(\sqrt{5}\) + 3\(\sqrt{7}\))
Solution:
(i) We have, (5\(\sqrt{3}\) – 7\(\sqrt{2}\)) + (2\(\sqrt{3}\) + 4\(\sqrt{2}\))
= 5\(\sqrt{3}\) – 7\(\sqrt{3}\) + 2\(\sqrt{3}\) + 4\(\sqrt{3}\)
= (5\(\sqrt{3}\) + 2\(\sqrt{3}\)) + (- 7\(\sqrt{2}\) + 4\(\sqrt{2}\))
= 7\(\sqrt{3}\) – 3\(\sqrt{2}\).

(ii) We have,
(6\(\sqrt{3}\) + 5\(\sqrt{5}\) – 4\(\sqrt{7}\)) + (\(\sqrt{3}\) – 4\(\sqrt{5}\) + 3\(\sqrt{7}\))
= 6\(\sqrt{3}\) + 5\(\sqrt{5}\) – 4\(\sqrt{7}\) + \(\sqrt{3}\) – 4\(\sqrt{5}\) + 3\(\sqrt{7}\)
= (6\(\sqrt{3}\) + \(\sqrt{3}\)) + (5\(\sqrt{5}\) – 4\(\sqrt{5}\)) + (- 4\(\sqrt{7}\) + 3\(\sqrt{7}\))
= 7\(\sqrt{3}\) + \(\sqrt{5}\) – \(\sqrt{7}\).

Question 6.
Multiply each of the following :
(i) 3\(\sqrt{2}\) by 5\(\sqrt{3}\)
(ii) 6\(\sqrt{5}\) by 2\(\sqrt{7}\)
(iii) \(\sqrt{10}\) by \(\sqrt{30}\)
Solution :
We have,
(i) 3\(\sqrt{2}\) × 5\(\sqrt{3}\) = 3 × 5 × \(\sqrt{2}\) × \(\sqrt{3}\) = 15\(\sqrt{6}\).

(ii) 6\(\sqrt{5}\) × 2\(\sqrt{7}\) = 6 × 2 × \(\sqrt{5}\) × \(\sqrt{7}\)
= 12\(\sqrt{35}\).

(iii) \(\sqrt{10}\) × \(\sqrt{30}\)
= \(\sqrt{10 \times 30}\)
= \(\sqrt{10 \times 10 \times 3}\)
= 10\(\sqrt{3}\).

Question 7.
Simplify each of the following expressions:
(i) (5 + \(\sqrt{5}\))(2 + \(\sqrt{3}\))
(ii) (\(\sqrt{5}\) – \(\sqrt{3}\)) (\(\sqrt{5}\) + \(\sqrt{3}\))
(iii) 3\(\sqrt{3}\) + 2\(\sqrt{27}\) + \(\frac{7}{\sqrt{3}}\)
[NCERT Exemplar Problems]
Solution :
(i) We have (5 + \(\sqrt{5}\))(2 + \(\sqrt{3}\)) = 10 + 5\(\sqrt{3}\) + 2\(\sqrt{5}\) + \(\sqrt{15}\).

(ii) (\(\sqrt{5}\) – \(\sqrt{3}\)) (\(\sqrt{5}\) + \(\sqrt{3}\)) = (\(\sqrt{5}\))² – (\(\sqrt{3}\))²
= 5 – 3 = 2.

(iii) 3\(\sqrt{3}\) + 2\(\sqrt{27}\) + \(\frac{7}{\sqrt{3}}\)
= 3\(\sqrt{3}\) + 2 × 3\(\sqrt{3}\) + \(\frac{7 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
= 3\(\sqrt{3}\) + 6\(\sqrt{3}\) + \(\frac{7 \sqrt{3}}{3}\) = 9\(\sqrt{3}\) + \(\frac{7 \sqrt{3}}{3}\)
= \(\frac{27 \sqrt{3}+7 \sqrt{3}}{3}=\frac{34 \sqrt{3}}{3}\)

Question 8.
Evaluate :
(i) (64)^{– 1/2}
(ii) (32)^3/5.
Solution:
We have
(i) (64)^{– 1/2} = (8²)^{– 1/2}
= 8^{2 × (- 1/2)} = 8^{– 1} = \(\frac {1}{8}\)

(ii) (32)^3/5 = (2⁵)^3/5
= 2^{5 × 3/5} = 2³ = 8.

Question 9.
Simplify:

[NCERT Exemplar Problems]
Solution:
We have
(i) 3^2/3. 3^1/5
= 3^2/3+1/5 =
= 3^{(10 + 3)/15}
= 3^13/15

(ii) We have,
(\(\frac{1}{4^3}\))^-2/3
= (4³)^2/3 = 4^{3 × 2/3} = 4² = 16.

(iii) We have,
\(\frac{10^{1 / 3}}{10^{1 / 5}}\) = 10^{1/3 – 1/5} = 10^(5-3)/15 = 10^2/15

(iv) We have,
\(\left(-\frac{1}{64}\right)^{-2 / 3}\)
= (-64)^2/3 = [(-4)³]^2/3
= (- 4)^{3 × 2/3} = (-4)² = 16.

(v) We have,
\(\frac{1}{3^{-2}} \cdot \frac{1}{5^{-2}}\) = 3² . 5² = (3 × 5)²
= 15² = 225.

Question 10.
Find the value of x^x, if it is given that 2^x – 2^{x – 1} = 4.
Solution:
We have,
2^x – 2^x-1 = 4
⇒ 2^x – 2^x.2^-1 = 4
⇒ 2^x (1 – 2^-1) = 4
⇒ 2^x(1 – \(\frac {1}{2}\)) = 4
⇒ 2^x × \(\frac {1}{2}\) = 4
⇒ 2^x = 8
⇒ 2^x = 2³
⇒ x = 3 [∵ bases are equal, ∴ exponents are equal]
∴ x^x = 3³
Hence, x^x = 27.

Question 11.
If a =(l – m), b = (m – n) and c =(n – l), then prove that (x^a)ⁿ . (x^b)^l . (x^c)^m = 0.
Solution :
We have, a = (l – m), b = (m – n) and c = (n – l)
L.H.S. = (x^a)ⁿ . (x^b)^l . (x^c)^m
= (x^{l – m})ⁿ . (x^{m – n})^l . (x^{n – l})^m
= x^{(ln – mn)} . x^{(ml – nl)} . x^{(mn – ml)}
= x^{ln – mn + ml – nl + mn – ml
= x0 = 1 = R.H.S.
∴ L.H.S. = R.H.S. Hence proved}

Question 12.
Prove that:
\(\left(\frac{x^a}{x^b}\right)^{(a+b)} \times\left(\frac{x^b}{x^c}\right)^{(b+c)} \times\left(\frac{x^c}{x^a}\right)^{(c+a)}\) = 1
Solution :

Short Answer Type Questions

Question 1.
Represent \(\frac {4}{3}\) and –\(\frac {4}{3}\) on the number line.
Solution:
For representing \(\frac {4}{3}\) and –\(\frac {4}{3}\) on the number line, we draw a number line and mark a point O on it to represent zero. Now we find the points A, B, C on the number line representing the positive integers 1, 2, 3 and the points P, Q, R on the number line representing negative integers – 1, – 2, – 3 respectively as shown in figure 1.3.

\(\frac {4}{3}\) lies between the positive integers 1 and 2. Similarly –\(\frac {4}{3}\) lies between the negative integers – 1 and – 2. So, we divide the AB and PQ in three equal parts such that AM = MN = NB and PX = XY = YQ. So the points M and X represents \(\frac {4}{3}\) and –\(\frac {4}{3}\) respectively on the number line.

Question 2.
Find five rational numbers between \(\frac {3}{5}\) and \(\frac {3}{4}\).
Solution :
Let a = \(\frac {3}{5}\) and b = \(\frac {3}{4}\) and
n = 5

Question 3.
Express the following in the form where p and q are integers and
(i) \(5 \cdot \overline{2}\)
(ii) \(12 \cdot \overline{48}\)
[NCERT Exemplar Problems]
Solution:
(i) Let
x = \(5 \cdot \overline{2}\) = 5.2222 ……..(i)
Multiplying equation (i) by 10, we get
10x = \(52 \cdot \overline{2}\) ……..(ii)
Subtracting the equation (i) from (ii), we get

⇒ x = \(\frac {47}{9}\)
Hence, \(5 \cdot \overline{2}\) = \(\frac {47}{9}\)

(ii) Let x = \(12 \cdot \overline{48}\) = 12.484848 ……… (i)
Multiplying equation (i) by 100, we get
100x = \(1248 \cdot \overline{48}\) ……… (ii)
Subtracting equation (i) from (ii), we get

Question 4.
Write the following in decimal form and say what kind of decimal expansion each has: \(\frac {5}{13}\)
Solution:
(i) By long division, we have

Hence, \(\frac {5}{3}\) = 0.384615384615…. = \(0 \cdot \overline{384615}\)
It has non-terminating and repeating decimal expansion.

Question 5.
Express the rational number \(\frac {1}{13}\) in decimal form and hence find the decimal expansions of \(\frac {1}{13}\) , \(\frac {2}{13}\) and \(\frac {3}{13}\).
Solution :
By long division, we have

We observe that remainder repeat after six digit. So, it has repeating block of six digits. The given rational numbers \(\frac {2}{13}\), \(\frac {3}{13}\) and \(\frac {4}{13}\) will also have repeating block of six digits in the decimal expansion.

So, to obtain the decimal expansion of given rational numbers mutliplying \(0 \cdot \overline{076923}\) successively by 2, 3 and 4 as follows :
\(\frac {2}{13}\) = 2 × \(\frac {1}{13}\) = 2 × \( \cdot \overline{76923}\) = \(0 \cdot \overline{153846}\)
\(\frac {3}{13}\) =3 × \(\frac {1}{13}\) = 3 × \(0 \cdot \overline{076923}\) = \(0 \cdot \overline{230769}\)
and \(\frac {4}{13}\) = 4 × \(\frac {1}{13}\) = 4 × \(0 \cdot \overline{076923}\) = \(0 \cdot \overline{307692}\)

Question 6.
Prove that 3\(\sqrt{2}\) is an irrational number.
Solution :
Let 3\(\sqrt{2}\) be a rational number, say x, then
3\(\sqrt{2}\) = x
⇒ \(\sqrt{2}\) = \(\frac {x}{3}\)
Since x is a rational number and 3 is nonzero rational number.
∴ \(\frac {x}{3}\) being the quotient of two rational numbers, is a rational number.
⇒ \(\sqrt{2}\) is a rational number.
But \(\sqrt{2}\) is an irrational number. So, our assumption is wrong.
Hence, 3\(\sqrt{2}\) is an irrational number.
Proved

Question 7.
Prove that \(\sqrt{3}\) – \(\sqrt{2}\) is not a rational number.
Solution :
Let \(\sqrt{3}\) – \(\sqrt{2}\) be a rational number, say x.
∴ \(\sqrt{3}\) – \(\sqrt{2}\) = x
Squaring both sides, we get
(\(\sqrt{3}\) – \(\sqrt{2}\))² = x²
⇒ 3 + 2 – 2 × \(\sqrt{3}\) × \(\sqrt{2}\) = x²
⇒ 5 – 2\(\sqrt{6}\) = x²
⇒ 5 – x² = 2\(\sqrt{6}\)
⇒ \(\frac{5-x^2}{2}\) = \(\sqrt{6}\)
∵ x is a rational number.
∴ \(\frac{5-x^2}{2}\), is a rational number.
⇒ \(\sqrt{6}\) is a rational number
But \(\sqrt{6}\) is an irrational number
So our assumption is wrong.
⇒ \(\sqrt{3}\) – \(\sqrt{2}\) is not a rational number.
Hence, \(\sqrt{3}\) – \(\sqrt{2}\) is not a rational number.
Proved

Question 8.
Represent \(\sqrt{5.6}\) geometrically on the number line. [NCERT Exemplar Problems]
Solution :
Draw a line AB of length 5.6 units, produce AB to a point C such that BC = 1 unit. Find the mid-point of AC and marked that point 0. Draw a semicircle with centre O and radius OA. Draw a line perpendicular to AC passing through Band intersecting the semicircle at D, then BD = \(\sqrt{5.6}\) units.

Now B as centre and BD as radius, draw an arc meeting AC produced at E, then BE = BD = \(\sqrt{5.6}\) units.

Question 9.
Simplify \(\frac{1}{\sqrt{6}+\sqrt{5}+\sqrt{11}}\)
Solution :
R.F. of the denominator
[(\(\sqrt{6}\) + \(\sqrt{5}\)) + \(\sqrt{11}\)] is [(\(\sqrt{6}\) + \(\sqrt{5}\)) – \(\sqrt{11}\)].
Therefore, multiplying numerator and denominator by [(\(\sqrt{6}\) + \(\sqrt{5}\)) – \(\sqrt{11}\)], we get

Question 10.
Simplify \(\frac{3 \sqrt{2}-2 \sqrt{3}}{3 \sqrt{2}+2 \sqrt{3}}+\frac{2 \sqrt{3}}{\sqrt{3}-\sqrt{2}}\) by rationalising the denominator.
Solution :
We have

Question 11.
It is given that \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732, \(\sqrt{5}\) = 2.236 and \(\sqrt{6}\) = 2.449. Find the value of each of the following upto three places of decimal :
(i) \(\frac{7}{\sqrt{10}}\)
(ii) \(\frac{\sqrt{6}+2 \sqrt{2}}{\sqrt{3}}\)
Solution:
We have

Question 12.
Prove that:
\(\frac{1}{3-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-2}\) = 5
Solution:
Rationalizing the denominator of each term, we get

Question 13.
Simplify :
\(\frac{2^{1 / 2} \times 3^{1 / 3} \times 4^{1 / 4}}{10^{-1 / 5} \times 5^{3 / 5}} \div \frac{3^{4 / 3} \times 5^{-7 / 5}}{4^{-3 / 5} \times 6}\).
Solution:
We have

Question 14.
If x, y, z are positive real numbers, then prove that :
\(\sqrt{x y-1} \cdot \sqrt{y z-1} \cdot \sqrt{z x-1}\) = 1
Solution :

Question 15.
If 2^x+4 – 2^x+2 = 3, then find the value of x.
Solution :
We have
2^x+4 – 2^x+2 = 3
⇒ 2^x+2+2 – 2^x+2 = 3
⇒ 2² . 2^x+2 – 2^x+2 = 3
⇒ 2^x+2(2² – 1) = 3
⇒ 2^x+2(4 – 1) = 3
⇒ 2^x+2 × 3 = 3
⇒ 2^x+2 = \(\frac {3}{3}\)
⇒ 2^x+2 = 1
⇒ 2^x+2 = 2⁰
⇒ x + 2 = 0
[if bases are equal, then exponents are also equal]
Hence x = – 2

Question 16.
If 3^x = 5^y = (75)^z, show that z = \(\frac{x y}{2 x+y}\).
Solution :
Let 3^x = 5^y = (75)^z = k
Then, 3^x = k
⇒ 3 = k^1/x …..(i)
5^y = k
⇒ 5 = k^1/y …..(ii)
and (75)^z = k
⇒ 75 = k^1/z
⇒ 3 × 5² = k^1/z
⇒ k^1/x × k^2/y = k^1/z [From (i) and (ii)]
⇒ k^1/x+2/y = k^1/z
⇒ \(\frac{1}{x}+\frac{2}{y}=\frac{1}{z}\) [On comparing]
⇒ \(\frac{y+2 x}{x y}=\frac{1}{z}\) = \(\frac {1}{z}\)
⇒ z(y + 2x) = xy
⇒ z = \(\frac{x y}{2 x+y}\).
Hence proved

Question 17.
If \(\frac{9^{n+2} \times\left(3^{-n / 2}\right)-2-27^n}{3^{3 m} \times 2^3 \times 10}\) = \(\frac {1}{27}\), Prove that m – n = 1.
Solution :
We have

Question 18.
Prove that:
\(\frac{1}{1+x^{(b-a)}+x^{(c-a)}}+\frac{1}{1+x^{(a-b)}+x^{(c-b)}}\) + \(\frac{1}{1+x^{(b-c)}+x^{(a-c)}}\) = 1
Solution :

Question 19.
If a^x = b^y = c^z and b² = ac, then prove that y = \(\frac{2 x z}{x+z}\).
Solution:
Let a^x = b^y = c^z = k
Then, a = k^1/x, b = k^1/y and c = k^1/z
Now, b² = ac, (given)
⇒ (k^1/y)² = k^1/x × k^1/z
⇒ k^2/y = k^{1/x + 1/z}
⇒ k^2/y = k^{(z + x)/xz}
⇒ \(\frac{2}{y}=\frac{z+x}{x z}\) [On Comparing]
⇒ \(\frac{1}{y}=\frac{x+z}{2 x z}\)
⇒ y = \(\frac{2 x z}{x+z}\). Hence proved.

Question 20.
Prove that:
\(\left(\frac{x^a}{x^b}\right)^{a^2+a b+b^2} \times\left(\frac{x^b}{x^c}\right)^{b^2+b c+c^2} \times\left(\frac{x^c}{x^a}\right)^{c^2+a b+a^2}\) = 1
Solution :

Question 21.
Simplify each of the following :
(i) [1 – {1 – (1 – n)^-1}^-1]^-1
(ii) \(\frac{5^{n+3}-6 \times 5^{n+1}}{9 \times 5^n-5^n \times 2^2}\)
Solution :

Question 22.
If \(\sqrt{57+12 \sqrt{15}}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\), then find the values of a and b.
Solution :
We have,
\(\sqrt{57+12 \sqrt{15}}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\)
⇒ \(\sqrt{12+45+12 \times \sqrt{3 \times 5}}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\)
⇒ \(\sqrt{(2 \sqrt{3})^2+(3 \sqrt{5})^2+2 \times 2 \sqrt{3} \times 3 \sqrt{5}}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\)
⇒ \(\sqrt{(2 \sqrt{3}+3 \sqrt{5})^2}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\)
⇒ 2\(\sqrt{3}\) + 3\(\sqrt{5}\) = a\(\sqrt{3}\) + b\(\sqrt{5}\)
⇒ a = 2, b = 3
[Equating the rational and irrational parts]
Hence, a = 2, b = 3.

Question 23.
If x = 2^2/3 – 2^1/3 – 2, then prove that x³ + 6x² + 18x + 18 = 0.
Solution :
We have
x = 2^2/3 – 2^1/3 – 2
⇒ x + 2 = 2^2/3 – 2^1/3
Cubing both sides, we get
(x + 2)³ = (2^2/3 – 2^1/3)³
⇒ x³ + 8 + 3 × x × 2(x + 2)
= (2^2/3)³ – (2^1/3)³ – 3 × 2^2/3 × 2^1/3 (2^2/3 – 2^1/3)
⇒ x³ + 8 + 6x(x + 2) = 2^{2/3 × 3} – 2^{1/3 × 3} – 3 × 2^{2/3 + 1/3} (x + 2)
⇒ x³ + 8 + 6x² + 12x = 2² – 2¹ – 3 × 2(x + 2)
⇒ x³ + 8 + 6x² + 12x = 4 – 2 – 6x – 12
⇒ x³ + 6x² + 12x + 8 = – 6x – 10
⇒ x³ + 6x² + 18x + 18 = 0. Hence proved

Question 24.
Which of the variables P, Q, R and T given by the following equations, represent rational or irrational numbers:
(i) P² = 25
(ii) Q² = 0.16
(iii) R² = 7
(iv) T² = 0.4
(v) P³ = 125
(vi) R² = 0.84.
Solution :
(i) We have,
P² = 25
⇒ P = \(\sqrt{25}\) = 5
It is a rational number.

(ii) We have, Q² = 0.16
⇒ Q = \(\sqrt{0.16}\) = 0.4
It is a rational number.

(iii) We have, R² = 7
⇒ R = \(\sqrt{7}\) = 2.6457513…
It is an irrational number.

(iv) We have, T² = 0.4
⇒ T = \(\sqrt{0.4}\) = 0.63245…
It is an irrational number.

(v) We have, P³ = 125
⇒ P = \(\sqrt[3]{125}\) = 5
It is a rational number.

(vi) We have, R² = 0.84
⇒ R = \(\sqrt{0.84}\) = 0.916515…
It is an irrational number.

Long Answer Type Questions

Question 1.
Find three different irrational numbers between :
(i) \(\frac {1}{7}\) and \(\frac {4}{11}\)
(ii) \(\frac {3}{11}\) and \(\frac {5}{13}\)
(iii) 3 and 4.
(iv) \(\sqrt{2}\) and \(\sqrt{7}\).
Solution :
(i) \(\frac {1}{7}\) = 0.142857142857…
\(\frac {4}{11}\) = 0.3636363636…
Three different irrational numbers are 0.17010010001….0.262020020002… and 0.3010020040002…

(ii) \(\frac {3}{11}\) = 0.2727272727…
\(\frac {5}{13}\) = 0.384615384…
Three different irrational numbers are 0.28030100131004…, 0.3011001110023001… and 0.32032003200032…

(iii) Three different irrational numbers between 3 and 4 are 3.15013001500014000016…, 3.202002000204… and 3.35035003500035…

(iv) Consider the squares of \(\sqrt{2}\) and \(\sqrt{7}\).
(\(\sqrt{2}\))² = 2 and (\(\sqrt{7}\))² = 7
Choose any three numbers say 3, 5, 6 which lie between 2 and 7.

Since, these numbers lie between 2 and 7, therefore the numbers \(\sqrt{3}\), \(\sqrt{5}\) and \(\sqrt{6}\) lie between \(\sqrt{2}\) and \(\sqrt{7}\). Hence, three irrational numbers between \(\sqrt{2}\) and \(\sqrt{7}\) are \(\sqrt{3}\), \(\sqrt{5}\) and \(\sqrt{6}\).

Question 2.
Simplify each of the following by rationalising the denominators:
(i) \(\frac{1}{2-\sqrt{3}}+\frac{5}{3-\sqrt{2}}-\frac{1}{\sqrt{3}+\sqrt{2}}\)
(ii) \(\frac{4 \sqrt{3}}{2-\sqrt{2}}-\frac{30}{4 \sqrt{3}-3 \sqrt{2}}-\frac{3 \sqrt{2}}{3+2 \sqrt{3}}\)
Solution :
(i) We have


= 0.

Question 3.
If both a and b are rational numbers, then find the values of a and b in each of the following equations:
(i) \(\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}\) = a – b\(\sqrt{15}\)
(ii) \(\frac{\sqrt{2}+\sqrt{3}}{3 \sqrt{2}-2 \sqrt{3}}\) = a + b\(\sqrt{6}\)
(iii) \(\frac{7+\sqrt{5}}{7-\sqrt{5}}-\frac{7-\sqrt{5}}{7+\sqrt{5}}\) = a + \(\frac {7}{11}\)\(\sqrt{5}\)b
Solution:

Question 4.
If x = \(\frac{\sqrt{2}-1}{\sqrt{2}+1}\) and \(\frac{\sqrt{2}+1}{\sqrt{2}-1}\), then find x² + y² .
Solution :

Question 5.
If a = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) and b = \(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\), then find a³ + b³.
Solution :
We have,

⇒ b = 5 – 2\(\sqrt{6}\)
a + b = 5 + 2\(\sqrt{6}\) + 5 – 2\(\sqrt{6}\)
⇒ a + b = 10
ab = \(\left(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\right) \times\left(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\right)\)
⇒ ab = 1
Now, a³ + b³ = (a + b)³ – 3ab(a + b)
⇒ a³ + b³ = (10)³ – 3 × 1 × (10)
[∵ a + b = 10 and ab = 1]
⇒ a³ + b³ = 1000 – 30
⇒ a³ + b³ = 970
Hence, a³ + b³ = 970

Question 6.
If a = \(\frac{1}{2-\sqrt{3}}\) and b = \(\frac{1}{2+\sqrt{3}}\), then find a² + ab + b²
Solution :

⇒ a × b = 4 – 3
⇒ ab = 1
Now, a² + ab + b² = a² + 2ab + b² – ab
[Adding and subtracting ab]
⇒ a² + ab + b² = (a + b)² – ab
⇒ a² + ab + b² = (4)² – 1
[∵ a + b = 4, ab = 1]
⇒ a² + ab + b² = 16 – 1
Hence, a² + ab + b² = 15

Question 7.
If x = \(\frac{1}{\sqrt{5}-2}\), then find the values of :
(i) x² + \(\frac{1}{x^2}\)
(ii) x² – \(\frac{1}{x^2}\)
Solution :

Question 8.
If x = \(\frac{5-\sqrt{21}}{2}\), then prove that \(\left(x^3+\frac{1}{x^3}\right)-5\left(x^2+\frac{1}{x^2}\right)+\left(x+\frac{1}{x}\right)\) = 0
Solution :

Question 9.
If x = \(\sqrt{3+2 \sqrt{2}}\), then find the value of x + \(\frac {1}{x}\) and x² + \(\frac{1}{x^2}\).
Solution :

Question 10.
If x = \(\frac{1}{\sqrt{3}-\sqrt{2}}\), prove that x³ + \(\frac{1}{x^3}\) + 2(x² + \(\frac{1}{x^2}\)) – 9(x + \(\frac {1}{x}\)) = 20
Solution :

Question 11.
If x = \(\frac{\sqrt{a+2 b}+\sqrt{a-2 b}}{\sqrt{a+2 b}-\sqrt{a-2 b}}\), then prove that b²x² – abx + b² = 0.
Solution :
We have,

Question 12.
If x = \(\frac{\sqrt{3}}{2}\), then show that \(\frac{1+x}{1+\sqrt{1+x}}+\frac{1-x}{1-\sqrt{1-x}}\) = 1
Solution :

Question 13.
If \(\sqrt{2}\) = 1.4142 , \(\sqrt{3}\) = 1.7320 and \(\sqrt{6}\) = 2.4495, find correct to three places of decimal, the value of:
(i) \(\sqrt{5+2 \sqrt{6}}+\sqrt{5-2 \sqrt{6}}\)
(ii) \(\frac{1}{\sqrt{3}-\sqrt{2}-1}\)
Solution :

Question 14.
Express the following with rational denominator \(\frac{1}{\sqrt{10}+\sqrt{14}+\sqrt{15}+\sqrt{21}}\).
Solution :

Multiple Choice Questions :

Choose the correct alternative each of the following :

Question 1.
Every rational number is : [NCERT Exemplar Problems]
(a) a natural number
(b) an integer
(c) a real number
(d) a whole number
Solution :
(c) a real number

Question 2.
Between any two rational numbers there:
[NCEAT Exemplar Problems]
(a) is no rational number
(b) is exactly one rational number
(c) are infinitely many rational numbers
(d) there are only rational numbers and no irrational numbers
Solution :
(c) are infinitely many rational numbers

Question 3.
Quotient of any two irrational numbers is :
(a) always an irrational number
(b) always a rational number
(c) always an integer
(d) some times rational number, some times irrational number
Solution :
(d) some times rational number, some times irrational number

Question 4.
Product of any two irrational numbers is : [NCERT Exemplar Problems]
(a) always an irrational number
(b) may be rational or irrational number
(c) always an integer
(d) always a rational number
Solution :
(b) may be rational or irrational number

Question 5.
Decimal representation of rational number cannot be : [NCERT Exemplar Problems]
(a) non-terminating but recurring
(b) terminating
(c) non-terminating non-recurring
(d) non-terminating
Solution :
(c) non-terminating non-recurring

Question 6.
Which of the following is rational :
(a) 0.3010010010001….
(b) π
(c) \(\sqrt{2}\)
(d) \(0 . \overline{142857}\)
Solution :
(d) \(0 . \overline{142857}\)

Question 7.
Which of the following is an irrational :
(a) 0.090909……..
(b) 0.25
(c) \(\frac {22}{7}\)
(d) \(\sqrt{0.4}\)
Solution :
(d) \(\sqrt{0.4}\)

Question 8.
A rational number between \(\sqrt{2}\) and \(\sqrt{3}\) is : [NCERT Exemplar Problems]
(a) \(\frac{\sqrt{2}+\sqrt{3}}{2}\)
(b) \(\frac{\sqrt{2} \times \sqrt{3}}{2}\)
(c) 1.5
(d) 1.8
Solution :
(c) 1.5

Question 9.
An irrational number between \(\sqrt{2}\) and \(\sqrt{3}\) is :
(a) 5^1/4
(b) \(\sqrt{2}\) + \(\sqrt{3}\)
(c) \(\frac{\sqrt{2}+\sqrt{3}}{2}\)
(d) \(\sqrt{\sqrt{2}} \times \sqrt{3}\).
Solution :
(d) \(\sqrt{\sqrt{2}} \times \sqrt{3}\).

Question 10.
\(\sqrt[4]{(81)^{-2}}\) is equal to : [NCERT Exemplar Problems]
(a) \(\frac {1}{9}\)
(b) 9
(c) \(\frac {1}{3}\)
(d) \(\frac {1}{81}\)
Solution :
(a) \(\frac {1}{9}\)

Question 11.
If , then x = \(\frac{1}{2+\sqrt{3}}\), is equal to :
(a) 2\(\sqrt{3}\)
(b) 4
(c) – 2\(\sqrt{3}\)
(d) 4 – 2\(\sqrt{3}\)
Solution :
(b) 4

Question 12.
The value of 1.999 in the form \(\frac {p}{q}\), where p and q are integers and q ≠ 0, is : [NCERT Exemplar Problems]
(a) \(\frac {19}{10}\)
(b) \(\frac {1999}{1000}\)
(c) 2
(d) \(\frac {1}{9}\)
Solution :
(c) 2

Haryana State Board HBSE 9th Class Science Important Questions Chapter 9 बल तथा गति के नियम Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 9 बल तथा गति के नियम

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
बल को परिभाषित करें।
उत्तर:
बल वह बाह्य कारक है, जो किसी वस्तु की विराम की अवस्था या गतिमान वस्तु की चाल तथा दिशा को बदल दे या बदलने की प्रवृत्ति रखे।

प्रश्न 2.
संतुलित बल किसे कहते हैं?
उत्तर:
यदि वस्तु पर लगने वाले सभी बलों का परिणामी बल शून्य हो तो वस्तु पर लगने वाले सभी बल, संतुलित बल कहलाते हैं।

प्रश्न 3.
असंतुलित बल किसे कहते हैं?
उत्तर:
यदि किसी वस्तु पर लगने वाले सभी बलों का परिणामी बल शून्य न हो, तो वे बल असंतुलित बल कहलाते हैं।

प्रश्न 4.
एक ट्रक और एक कार υ वेग से गतिशील हैं, दोनों एक-दूसरे से आमने-सामने संघट्ट करते हैं तथा कुछ समय बाद दोनों रुक जाते हैं। अगर संघट्ट का समयांतराल 1s है, तो-

1. कौन-सी गाड़ी पर बल का सबसे अधिक प्रभाव पड़ेगा?
2. किस गाड़ी के संवेग में सबसे अधिक परिवर्तन होगा?
3. किस गाड़ी का त्वरण सबसे अधिक होगा?
4. ट्रक की अपेक्षा कार को अधिक नुकसान क्यों होगा?

उत्तर:

1. कार पर बल का सबसे अधिक प्रभाव पड़ेगा क्योंकि उसका द्रव्यमान कम है।
2. ट्रक के संवेग में सबसे अधिक परिवर्तन होगा।
3. कार का त्वरण सबसे अधिक होगा।
4. ट्रक का द्रव्यमान अधिक होने के कारण कार को अधिक नुकसान होगा।

प्रश्न 5.
वस्तुओं की गति को नियंत्रित करने वाले नियमों को सबसे पहले किस वैज्ञानिक ने स्थापित किया?
उत्तर:
सर आइजक न्यूटन ने।

प्रश्न 6.
आनति कोण किसे कहते हैं?
उत्तर:
आनत तल द्वारा क्षैतिज से बना कोण आनति कोण कहलाता है।

प्रश्न 7.
घर्षण बल की परिभाषा लिखें।
उत्तर:
जब एक वस्तु किसी अन्य वस्तु के संपर्क में रहते हुए गति करती है तो उस गति की दिशा के विपरीत एक बल कार्य करता है जिसे घर्षण बल या घर्षण कहते हैं।

प्रश्न 8.
घर्षण बल का प्रभाव लिखें।
उत्तर:
घर्षण बल वस्तु की गति को कम कर देता है।

प्रश्न 9.
जब हम साइकिल के पैडल को चलाना बंद कर देते हैं तो साइकिल रुक जाती है, क्यों?
उत्तर:
साइकिल के टायर और सड़क के बीच लगने वाला घर्षण बल उसकी गति को धीरे-धीरे कम करके साइकिल को रोक देता है।

प्रश्न 10.
कैरम के खेल में बोर्ड पर पाऊडर क्यों डाला जाता है?
उत्तर:
कैरम के खेल में कैरम बोर्ड और गोट के बीच घर्षण बल को कम करने के लिए बार-बार पाऊडर डालते हैं।

प्रश्न 11.
संवेग संरक्षण नियम क्या है?
उत्तर:
संवेग संरक्षण नियम के अनुसार किसी बाह्य बल की अनुपस्थिति में किसी निकाय का कुल संवेग संरक्षित रहता है।

प्रश्न 12.
न्यूटन की गति का दूसरा नियम लिखें।
उत्तर:
किसी वस्तु के संवेग परिवर्तन की दर उस पर आरोपित बल के समानुपाती होती है और उसी दिशा में होती है, जिसमें बल लगाया जाता है। (F = ma)

प्रश्न 13.
संवेग से क्या अभिप्राय है?
उत्तर:
किसी वस्तु का संवेग उसके द्रव्यमान व वेग के गुणनफल से परिभाषित किया जाता है। इसें p से प्रकट किया जाता है। अर्थात p= m.v.

प्रश्न 14.
संवेग का S.I. मात्रक क्या है?
उत्तर:
किलोग्राम मीटर प्रति सेकंड (kg m/s)।

प्रश्न 15.
संवेग अदिश राशि है या सदिश।
उत्तर:
संवेग एक सदिश राशि है, क्योंकि इसमें परिमाण व दिशा दोनों होते हैं।

प्रश्न 16.
संवेग किस दिशा में कार्य करता है?
उत्तर:
संवेग, वेग की दिशा में कार्य करता है।

प्रश्न 17.
बल, द्रव्यमान व त्वरण में क्या संबंध है?
उत्तर:
बल = द्रव्यमान – त्वरण (F = ma)।

प्रश्न 18.
बल का S.I. मात्रक क्या है?
उत्तर:
बल का S.I. मात्रक न्यूटन है।

प्रश्न 19.
एक न्यूटन बल को परिभाषित करें।
उत्तर:
वह बल जो एक किलोग्राम संहति की वस्तु पर 1 m/s² का त्वरण उत्पन्न कर दे उसे एक न्यूटन बल कहते हैं।

प्रश्न 20.
अन्योन्य क्रिया किसे कहते हैं?
उत्तर:
जब कोई वस्तु किसी दूसरी वस्तु पर बल लगाकर उसे प्रभावित करती है तो हम कहते हैं पहली तथा दूसरी वस्तु के बीच अन्योन्य क्रिया हुई।

प्रश्न 21.
जड़त्व कितने प्रकार का होता है?
उत्तर:
जड़त्व दो प्रकार का होता है-

• स्थिर जड़त्व
• गतिमान जड़त्व।

प्रश्न 22.
संवेग के आधार पर बल का सूत्र लिखें।
उत्तर:
F = \(\frac{\mathrm{p}_2-\mathrm{p}_1}{\mathrm{t}_2-\mathrm{t}_1}\)

प्रश्न 23.
6 kg द्रव्यमान की किसी वस्तु में 2 m/s² का त्वरण उत्पन्न करने के लिए कितने बल की आवश्यकता होगी?
हल:
बल (F) = द्रव्यमान (m) x त्वरण (a)
= 6 x 2 = 12 न्यूटन

प्रश्न 24.
कोई व्यक्ति 40 kg द्रव्यमान के बॉक्स को 80 N बल लगाकर धकेलता है। बॉक्स का त्वरण कितना होगा?
हल:

प्रश्न 25.
न्यूटन की गति का तीसरा नियम लिखें।
उत्तर:
न्यूटन की गति के तीसरे नियमानुसार “क्रिया तथा प्रतिक्रिया सदैव समान तथा विपरीत दिशा में होती है।”

प्रश्न 26.
जड़त्व किसे कहते हैं?
उत्तर:
वस्तुओं का वह गुण जो उसकी गति या विराम की अवस्था में परिवर्तन होने से रोकता है, जड़त्व कहलाता है।

प्रश्न 27.
क्या किसी एकल बल का अस्तित्व संभव है?
उत्तर:
नहीं, एकल बल का अस्तित्व संभव नहीं है। बल सदैव युगल रूप में होता है।

प्रश्न 28.
कौन-सा बल हमें इच्छित दिशा में गति प्रदान करता है?
उत्तर:
वस्तुओं का वह गुण जो उसकी गति या विराम की अवस्था में परिवर्तन होने से रोकता है, जड़त्व कहलाता है।

प्रश्न 27.
क्या किसी एकल बल का अस्तित्व संभव है?
उत्तर:
नहीं, एकल बल का अस्तित्व संभव नहीं है। बल सदैव युगल रूप में होता है।

प्रश्न 28.
कौन-सा बल हमें इच्छित दिशा में गति प्रदान करता है?
उत्तर:
वह बल जो हमें इच्छित दिशा में गति प्रदान करता है, हमारे शरीर द्वारा लगाए गए बल के प्रति भूमि की प्रतिक्रिया है।

प्रश्न 29.
क्या क्रिया तथा प्रतिक्रिया एक वस्तु पर आरोपित होते हैं?
उत्तर:
नहीं, क्रिया तथा प्रतिक्रिया (बल) दो भिन्न-भिन्न वस्तुओं पर आरोपित होते हैं।

प्रश्न 30.
दो वस्तुओं के संपर्क में हुए बिना लगने वाले दो बलों के नाम बताओ।
उत्तर:

• चुंबकीय बल
• गुरुत्व बल।

प्रश्न 31.
पेड़ से टूटा फल किस बल के कारण पृथ्वी पर गिरता है?
उत्तर:
गुरुत्व बल के कारण।

प्रश्न 32.
चिकने खंभे पर चढ़ना कठिन होता है, क्यों?
उत्तर:
कम प्रतिक्रिया होने के कारण।

प्रश्न 33.
मशीनों में तेल का उपयोग क्यों करते हैं?
उत्तर:
घर्षण को कम करने के लिए।

प्रश्न 34.
रेत पर चलना कठिन क्यों होता है?
उत्तर:
पैरों और रेत के बीच अधिक घर्षण होने के कारण।

प्रश्न 35.
द्रवों तथा ठोसों की सतहों के बीच घर्षण बल की तुलना करो।
उत्तर:
द्रवों की सतहों के बीच घर्षण बल, ठोसों की सतहों के बीच घर्षण बल की तुलना में बहुत कम होता है।

प्रश्न 36.
एक कंकड़ व एक ट्रक समान गति से चल रहे हैं। दोनों को रोकने के लिए किस पर अधिक बल लगाना पड़ेगा?
उत्तर:
ट्रक को रोकने के लिए अधिक बल लगाना पड़ेगा, क्योंकि उसका संवेग अधिक होगा।

प्रश्न 37.
किस बल के कारण हम सड़क पर बिना फिसले चल सकते हैं?
उत्तर:
घर्षण बल के कारण हम सड़क पर बिना फिसले चल सकते हैं।

प्रश्न 38.
वर्षा ऋतु में किसी हरी काई युक्त सड़क पर चलना कठिन हो जाता है, क्यों?
उत्तर:
काई युक्त सड़क पर घर्षण बल कम हो जाता है, इसलिए ऐसी सड़क पर चलना कठिन हो जाता है।

प्रश्न 39.
न्यूटन का कौन-सा गति का नियम बल को मापने में हमारी सहायता करता है?
उत्तर:
न्यूटन का दूसरा गति नियम बल को मापने में हमारी सहायता करता है।

प्रश्न 40.
जैट हवाई जहाज न्यूटन की गति के कौन-से नियम के अनुसार उड़ते हैं?
उत्तर:
न्यूटन की गति के तीसरे नियम के अनुसार उड़ते हैं।

प्रश्न 41.
खिलाड़ी कूदने से पहले क्यों दौड़ता है?
उत्तर:
संवेग बढ़ाने के लिए ताकि अधिक ऊँची कूद लगाई जा सके।

प्रश्न 42.
बल एक सदिश राशि है या अदिश।
उत्तर:
बल एक सदिश राशि है।

प्रश्न 43.
बंदूक से गोली चलने के बाद बंदूक तथा गोली का कुल संवेग कितना होता है?
उत्तर:
शून्य।

प्रश्न 44.
यदि किसी 1kg द्रव्यमान की वस्तु पर 1 न्यूटन (N) बल लगाया जाए तो उसमें कितना त्वरण उत्पन्न होगा?
उत्तर:
1 m/sec²

लघत्तरात्मक प्रश्न

प्रश्न 1.
बल से क्या अभिप्राय है? किसी वस्तु पर बल लगाने से उस पर क्या प्रभाव पड़ सकते हैं?
उत्तर:
बल वह बाह्य कारक है, जो किसी वस्तु की स्थिर अथवा गतिमान अवस्था की चाल तथा दिशा को बदल दे या बदलने की प्रवृत्ति रखे।

प्रभाव-किसी वस्तु पर बल लगाने से उस पर निम्नलिखित प्रभाव पड़ सकते हैं-

• वस्तु की चाल बदल सकती है, जिससे वस्तु तेज अथवा धीमी चलने लगती है।
• वस्तु की गति की दिशा बदल सकती है तथा स्थिर वस्तु को चला सकता है।
• इससे वस्तु का आकार बदल सकता है।

प्रश्न 2.
दैनिक जीवन में बल के पाँच उदाहरण दीजिए।
उत्तर:
दैनिक जीवन में बल के पाँच उदाहरण निम्नलिखित हैं-

• जब रबड़ की गेंद पर बल लगाया जाता है तो वह पिचक जाती है। ऐसा बल के कारण होता है।
• जब किसी स्प्रिंग को खींचा जाता है तो माँसपेशियों के बल के कारण स्प्रिंग की लंबाई बढ़ जाती है।
• भाप अपनी ऊर्जा भाप इंजन को देती है, जिसके कारण भाप इंजन आगे की ओर चलता है।
• लुढ़क रही गेंद को माँसपेशियों के बल द्वारा रोका जा सकता है।
• पेट्रोल अपनी ऊर्जा देकर यांत्रिक बल प्रदान करता है, जिसके कारण बस या कार आदि परिचालित होते हैं।

प्रश्न 3.
आनत-समतल किसे कहते हैं? इसके क्या-क्या उपयोग हैं?
उत्तर:
ऐसा सपाट तल, जो क्षैतिज तल के साथ कोई कोण बनाता है, आनत-समतल कहलाता है; जैसे चाकू, कुल्हाड़ी, छैनी, पेच, पहाड़ी सड़कें, नत-तल वाली सीढ़ियाँ आदि। चित्र में मनुष्य को लकड़ी के तने के बने हुए आनत-समतल की सहायता से भारी बोझ उठाते हुए दिखाया गया है।

आनत-समतल के उपयोग-आनत-समतल के उपयोग निम्नलिखित हैं-

• आनत-समतल का प्रयोग करने से थोड़ा बल लगाकर अधिक भार उठाया जा सकता है।
• इसके उपयोग द्वारा ट्रकों में भारी बोझ चढ़ाया तथा उतारा जाता है।
• पेच भी आनत-समतल के सिद्धांत पर कार्य करता है।

प्रश्न 4.
संतुलित तथा असंतुलित बलों में मुख्य अंतर बताओ।
उत्तर:
संतुलित तथा असंतुलित बलों में मुख्य अंतर निम्नलिखित हैं-

प्रश्न 5.
जड़त्व से क्या अभिप्राय है? उदाहरण सहित स्पष्ट करें।
उत्तर:
वस्तुओं का वह गुण जो वस्तु की गति या विराम की अवस्था में परिवर्तन होने का विरोध करता है, ‘जड़त्व’ कहलाता है।

प्रयोग-एक खाली गिलास लो, उस पर एक गत्ते का टुकड़ा रखो। गत्ते के टुकड़े पर एक सिक्का रखो। इसके पश्चात् गत्ते के टुकड़े को चित्रानुसार झटके से क्षैतिज दिशा में गतिमान करो। आप देखोगे कि गत्ता आगे निकल जाएगा, परंतु सिक्का गिलास में गिर जाएगा। जब गत्ते को गतिमान किया जाता है, तो जड़त्व के गुण के कारण सिक्का विरामावस्था में रहने का प्रयत्न करता है। इस प्रकार गत्ते के गतिमान होने पर सिक्का गिलास में गिर जाता है।

प्रश्न 6.
जड़त्व कितने प्रकार का होता है? उदाहरण सहित वर्णन करें।
उत्तर:
जड़त्व दो प्रकार का होता है-
1. स्थिर जड़त्व-यह पदार्थ का वह गुण है, जिसके कारण पदार्थ अपनी स्थिरता तब तक बनाए रखता है, जब तक कि उस पर बाह्य बल न लगाया जाए।
उदाहरण-मेज़ पर रखी पुस्तक अपने स्थिर जड़त्व गुण के कारण ही अपने आप गति नहीं करती।

2. गति जड़त्व-यह पदार्थ का वह गुण है, जिसके कारण उसकी गति में तब तक परिवर्तन नहीं आता जब तक कि उस पर बाह्य बल न लगाया जाए।
उदाहरण-चल रही बस या गाड़ी में आराम से बैठा व्यक्ति बस या गाड़ी के एकदम रुकने पर आगे की ओर गिरता है। ऐसी अवस्था में यात्री के शरीर का निचला भाग तो गाड़ी के रुकते ही विरामावस्था में आ जाता है, किंतु उसके शरीर का ऊपरी भाग गति की दिशा में गतिशील रहने की कोशिश करता है, जिस कारण व्यक्ति आगे की ओर गिरता है।

प्रश्न 7.
क्या होता है जब आप किसी गीले कपड़े को झटकते हैं? अपने प्रेक्षण को स्पष्ट कीजिए।
उत्तर:
जब हम किसी गीले कपड़े को झटकते हैं तो झटके के कारण कपड़ा अपने स्थान से हट जाता है तथा जल-कण जड़त्व के कारण अपनी स्थिति बनाए रखने की चेष्टा करते हैं, जिस कारण वे कपड़े से अलग होकर वायुमंडल में मिल जाते हैं। अतः कपड़ा जल्दी सूख जाता है।

प्रश्न 8.
जैवलिन थ्रो (भाला फेंकने) में यदि खिलाड़ी किसी निश्चित रेखा को पार कर लेता है तो यह फाउल माना जाता है, किंतु खिलाड़ी इस रेखा पर रुकने में प्रायः असफल रहते हैं। स्पष्ट कीजिए, क्यों?
उत्तर:
जब कोई खिलाड़ी जैवलिन थ्रो (भाला फेंक) प्रतियोगिता में भागता हुआ निश्चित रेखा के पास पहुँचता है तो उसका सारा शरीर गति में होता है। जब वह अपने पैरों को निश्चित रेखा पर रोकने की चेष्टा करता है, तो गति जड़त्व के कारण उसका ऊपरी भाग गति करना चाहता है, जिस कारण खिलाड़ी निश्चित रेखा पार कर लेता है और फाउल हो जाता है।

प्रश्न 9.
किसी घोड़े के अचानक चल पड़ने पर उस पर बैठा सवार पीछे की ओर क्यों गिर पड़ता है?
उत्तर:
किसी घोड़े के अचानक चल पड़ने पर उस पर बैठा सवार पीछे की ओर इसलिए गिर पड़ता है, क्योंकि घोड़े के अचानक चल पड़ने के कारण घोड़ा गति अवस्था में आ जाता है, परंतु उस पर बैठा व्यक्ति स्थिर जड़त्व के कारण विराम अवस्था में रहने की चेष्टा करता है, जिससे वह पीछे की ओर गिर जाता है।

प्रश्न 10.
जब दौड़ता हुआ घोड़ा अचानक रुकता है तो सवार आगे की ओर क्यों गिरता है?
उत्तर:
जब दौड़ता हुआ घोड़ा अचानक रुकता है तो सवार आगे की ओर इसलिए गिरता है, क्योंकि दौड़ते समय घोड़ा और सवार दोनों गति अवस्था में होते हैं, परंतु जब घोड़ा रुकता है तो वह विराम अवस्था में आ जाता है और सवार जड़त्व के अनुसार गति करने की चेष्टा करता है, जिससे वह आगे की ओर गिर पड़ता है।

प्रश्न 11.
वाहनों के टायर खुरदरे तथा लहरीदार क्यों बनाए जाते हैं?
उत्तर:
वाहनों का चलना वाहनों के टायरों तथा सड़क के बीच घर्षण बल के कारण होता है। यदि टायर चिकने होंगे तो सड़क और टायर के बीच घर्षण बल कम होगा, जिससे वाहन को नियंत्रित करना कठिन होगा। वाहनों को नियंत्रित करने के लिए टायर खुरदरे तथा लहरीदार बनाए जाते हैं ताकि टायर और सड़क के बीच घर्षण बढ़ सके, जिससे टायर की सड़क के साथ पकड़ अच्छी बन सके।

प्रश्न 12.
न्यूटन के पहले गति नियम की परिभाषा लिखो तथा इसकी व्याख्या करो।
उत्तर:
न्यूटन का गति का पहला नियम-यदि कोई वस्तु स्थिर हो या एकसमान गति से चल रही हो तो वह उस समय तक एकसमान गति से चलती रहेगी, जब तक कि उस पर कोई असंतुलित बल न लगे। इस नियम को ‘गैलीलियो का जड़त्व का नियम’ भी कहते हैं।

जैसे कि फर्श पर लुढ़कती गेंद घर्षण कम होने पर अधिक दूर तक जा सकती है। यदि किसी साधन से घर्षण शून्य कर दिया जाए तो गेंद निश्चित काल तक अपने प्रारंभिक वेग से गतिशील रहेगी।

प्रश्न 13.
सिद्ध करो कि न्यूटन के पहले गति नियम को जड़त्व का नियम कहा जा सकता है।
उत्तर:
गति के पहले नियम के अनुसार जो वस्तु विराम अवस्था में है, उसकी विराम में ही बने रहने की प्रवृत्ति होती है तथा जो वस्तु गति में होती है, वह सरल रेखा में गति करते रहना चाहती है, जब तक उस पर कोई बाह्य बल न लगे। दूसरे शब्दों में, सभी वस्तुएँ अपनी गति की अवस्था में किसी भी परिवर्तन का विरोध करती हैं। वस्तुओं की अपनी गति की अवस्था में परिवर्तन का विरोध करने की प्रवृत्ति को जड़त्व कहा जाता है। अतः गति-विषयक न्यूटन के प्रथम नियम को जड़त्व का नियम भी कहते हैं।

प्रश्न 14.
सिद्ध करो कि किसी वस्तु का द्रव्यमान उसकी जड़त्व का माप होता है।
उत्तर:
किसी वस्तु में द्रव्य की राशि उस वस्तु का द्रव्यमान कहलाती है। इस प्रकार द्रव्यमान वस्तु के जड़त्व की मापक है, जिस वस्तु का द्रव्यमान जितना अधिक होगा, उसका जड़त्व भी उतना ही अधिक होगा।

व्याख्या – यदि हम किसी फुटबॉल को ठोकर मारते हैं तो वह बहुत दूर चली जाती है, परंतु यदि हम उसी आकार के एक पत्थर को ठोकर मारें तो पत्थर अपने स्थान से नहीं हिलता और हमारे पाँव में चोट भी लगती है, क्योंकि फुटबॉल की अपेक्षा पत्थर में अपनी गति के परिवर्तन को रोकने की क्षमता अधिक होती है इसका कारण उसकी संहति का अधिक होना है, परन्तु किसी वस्तु की संहति ही उसके जड़त्व की माप होती है, अर्थात् पत्थर का जड़त्व अधिक होता है।

प्रश्न 15.
न्यूटन के दूसरे गति नियम की परिभाषा दो तथा इसकी व्याख्या करो। इस नियम की सहायता से बल का समीकरण प्राप्त करें।
उत्तर:
न्यूटन का गति का दूसरा नियम-किसी वस्तु पर लगा बल वस्तु की संहति और उसके त्वरण के गुणनफल के समानुपाती होता है। जिस प्रकार यदि किसी गेंद को जितनी अधिक तेजी के साथ ठोकर मारते हैं, वह उतनी ही तेज गतिशील हो जाती है, क्योंकि उसका त्वरण उतना ही अधिक होता है।

इसी प्रकार क्रिकेट का खिलाड़ी गतिमान गेंद को धीरे-धीरे रोकता है, जिससे गेंद की गति के समान परिवर्तन अधिक समय में होता है। वह अपने हाथों को गेंद की दिशा में गतिशील कर लेता है, जिससे गेंद का त्वरण पहले की अपेक्षा कम हो जाता है और उसे गेंद रोकने के लिए कम बल लगाना पड़ता है।

माना किसी वस्तु का द्रव्यमान ‘m’ है तथा ‘F’ बल के कारण उसमें ‘a’ त्वरण उत्पन्न हो जाता है। गति के दूसरे नियम के अनुसार,
F ∝ m x a
या F = Kma
यहाँ K एक स्थिरांक है, जिसका मान, द्रव्यमान, बल और त्वरण के मात्रकों पर निर्भर करता है।
माना m = 1 kg तथा a = 1 m/s² तथा F = 1 N
तो F = Kma में F, m तथा a का मान रखने पर
1 = K x 1 x 1
या K = 1
इस प्रकार,
F = 1 x ma
बल = द्रव्यमान x त्वरण

प्रश्न 16.
न्यूटन के गति के तीसरे नियम की परिभाषा दो तथा इसकी व्याख्या करो।
उत्तर:
न्यूटन का गति का तीसरा नियम-इस नियम के अनुसार, पहली वस्तु द्वारा दूसरी वस्तु पर लगाया गया बल दूसरी वस्तु द्वारा पहली वस्तु पर लगाए गए बल के बराबर और विपरीत दिशा में होता है।
अथवा
क्रिया और उसकी प्रतिक्रिया बराबर तथा विपरीत दिशा में होते हैं। जैसे-

• पृथ्वी पर पड़ी गेंद जितने बल के द्वारा पृथ्वी को दबाती है, पृथ्वी उसे उतने ही बल के द्वारा ऊपर की ओर उछालती है।
• पानी में तैरते समय मनुष्य पानी को पीछे की ओर धकेलता है, इस प्रतिक्रिया के कारण ही वह आगे की ओर जाने लगता है।

प्रश्न 17.
क्रिकेट की गेंद को पकड़ते समय खिलाड़ी अपने हाथों को पीछे की ओर क्यों खींचता है?
उत्तर:
गति से आ रही गेंद का संवेग अधिक होता है। जब खिलाड़ी गेंद को पकड़ता है तो वह अपने हाथों को पीछे की ओर खींचता है ताकि गेंद के संवेग को शुन्य होने में कुछ समय लगे। इस प्रकार गेंद के संवेग, परिवर्तन की दर तथा गेंद द्वारा हाथों पर लगाया गया बल कम हो जाएगा और चोट नहीं लगेगी।

प्रश्न 18.
समुद्री जहाज को रोकने के लिए सड़क पर चलती कार की अपेक्षा अधिक बल लगाना पड़ता है, क्यों?
उत्तर:
कार के टायरों और सड़क के बीच घर्षण बल अधिक होता है, इसलिए थोड़ा-सा बल लगाकर भी कार शीघ्र रुक जाती है। इसके विपरीत द्रव की सतहों के बीच घर्षण बल ठोसों की सतहों के बीच घर्षण बल की अपेक्षा बहुत कम होता है। इस कारण से समुद्री जहाज को पानी में कम घर्षण बल का सामना करना पड़ता है। अतः जहाज को रोकने के लिए कार की अपेक्षा अधिक बल लगाना पड़ता है।

प्रश्न 19.
जब दो वस्तुओं के बीच अन्योन्य क्रिया होती है तो गतिशील वस्तओं में टकराव के बाद उनकी दिशा में परिवर्तन किस प्रकार होता है? चित्र सहित स्पष्ट करो।
उत्तर:
दो वस्तुओं के बीच अन्योन्य क्रिया में एक वस्तु दूसरी वस्तु पर बल लगाकर प्रभावित करती है। दो कंचों के बीच टकराहट अन्योन्य क्रिया के उदाहरण हैं। चित्र में दो कंचे एक-दूसरे की ओर आते हुए दिखाए गए हैं। उनकी गति की दिशा उन पर लगे तीर के निशान द्वारा दिखाई गई है। चित्र से स्पष्ट है कि आपस में टकराने के बाद कंचों की गति की दिशा बदल जाती है। इस क्रिया में दो बल कार्य करते हैं। एक तो वह जिसने एक कंचे को त्वरित किया और दूसरे वह जिसने दूसरे कंचे को

प्रश्न 20.
क्रिया और प्रतिक्रिया से क्या तात्पर्य है? इनमें आपस में क्या संबंध है? किस गति नियम में इनका वर्णन होता है?
उत्तर:
यदि कोई एक वस्तु किसी दूसरी वस्तु पर बल लगाए तो वह दूसरी वस्तु पर लगने वाला क्रिया बल है। बदले में दूसरी वस्तु जो बल पहली वस्तु पर लगाती है वह पहली वस्तु पर लगने वाला प्रतिक्रिया बल है।

क्रिया और प्रतिक्रिया का आपसी संबंध-क्रिया तथा प्रतिक्रिया बल आपस में बराबर, परंतु विपरीत दिशाओं में होता है। एक महत्त्वपूर्ण बात यह भी है कि क्रिया और प्रतिक्रिया के बल हमेशा भिन्न-भिन्न वस्तुओं पर क्रिया करते हैं। इनका वर्णन गति के तीसरे नियम में होता है।

प्रश्न 21.
दैनिक जीवन में न्यूटन की गति के तीसरे नियम के कुछ उदाहरण दीजिए।
उत्तर:
दैनिक जीवन में न्यूटन की गति के तीसरे नियम के कुछ उदाहरण निम्नलिखित हैं-

• बंदूक का घोड़ा दबाने पर गोली आगे की दिशा में गति करती है और प्रतिक्रिया बल के कारण बंदूक खुद पीछे की ओर हटती है।
• तैरते समय आदमी पानी को पीछे की ओर धकेलता है और पानी की उस पर लगने वाली प्रतिक्रिया के कारण वह आगे की ओर तैरता है।
• जब कोई मनुष्य किश्ती में से नदी के किनारे पर कूदता है तो प्रतिक्रिया बल के कारण किश्ती पानी में किनारे से दूर हट जाती है।
• भूमि पर चलते समय हम अपने पैरों से भूमि को पीछे की ओर धकेलते हैं और प्रतिक्रिया बल के कारण भूमि हमारे पैरों को आगे धकेलती है जिसके कारण हम आगे चलते हैं।
• नाव चलाने पर पानी को पतवारों से पीछे की ओर धकेला जाता है, जबकि नाव प्रतिक्रिया के कारण आगे की ओर बढ़ती है।
• जब कोई खिलाड़ी ऊपर की ओर छलाँग लगाता है तो पृथ्वी की सतह को नीचे की ओर धकेलता है, जिससे उसे प्रतिक्रिया मिलती है।

प्रश्न 22.
यदि कोई व्यक्ति नाव से किनारे पर कूदे तो नाव विपरीत दिशा में चली जाती है, क्यों? स्पष्ट कीजिए।
उत्तर:
कोई व्यक्ति नाव से किनारे पर कूदते समय आवश्यक गति प्राप्त करने के लिए आगे की ओर बल लगाता है। उसकी प्रतिक्रिया नाव पर होती है जो न्यूटन के गति के तीसरे नियम के आधार पर विपरीत दिशा में होती है। उसी के परिणामस्वरूप नाव विपरीत दिशा में गति करती हुई किनारे से दूर हट जाती है।

प्रश्न 23.
न्यूटन के गति के पहले नियम और दूसरे नियम में क्या संबंध है? संक्षेप में समझाइए।
उत्तर:
न्यूटन का गति का पहला नियम दूसरे नियम का ही भाग है। इसे निम्नलिखित तथ्य के आधार पर स्पष्ट किया जा सकता है। न्यूटन के गति के दूसरे नियम के अनुसार,
F = ma
यदि F = 0 हो तो
ma = 0
m = 0, a = 0
परंतु ‘m’ संहति शून्य नहीं हो सकती, क्योंकि यह एक स्थिर राशि है, इसलिए ‘a’ त्वरण शून्य हो तो वेग में परिवर्तन भी शून्य होगा, इसलिए वस्तु की अवस्था में कोई परिवर्तन नहीं होगा। यह विरामावस्था में है तो विराम में ही रहेगी और समान गति अवस्था में है तो गति में ही रहेगी जब तक उस पर कोई बल न लगाया जाए। यह न्यूटन के गति के पहले नियम की परिभाषा है। अतः न्यूटन का गति का पहला नियम दूसरे नियम का ही भाग है।

प्रश्न 24.
क्या कारण है यदि तीव्र गति से आ रही गोली खिड़की के शीशे में गोल छिद्र कर देती है जबकि पत्थर मारने पर शीशा टूट जाता है?
उत्तर:
गोली का आकार छोटा होता है, जबकि पत्थर का आकार बड़ा होता है जिससे गोली के टकराने से पूरा काँच गति ग्रहण नहीं करता, जहाँ गोली टकराती है, वही भाग गति ग्रहण करता है और वहाँ छिद्र हो जाता है, परंतु पत्थर के टकराने से छिद्र नहीं होता पूरा शीशा गति ग्रहण कर लेता है और टूट जाता है।

गणनात्मक प्रश्न

1. बल (F) = द्रव्यमान (m) x त्वरण ( a )

2. यदि प्रारंभिक वेग = u, अंतिम वेग = v, समय = t, त्वरण = a दूरी = s हो तो इनमें निम्नलिखित संबंध होता है-

• v = u + at
• s = ut + \(\frac { 1 }{ 2 }\) at²
• v² – u² = 2as

3. संवेग (p) = द्रव्यमान (m) x वेग (v)

4. बल (F) =

5. बल का SI मात्रक न्यूटन है।

प्रश्न 1.
किसी मेज पर गतिशील सिक्के का चाल – समय ग्राफ चित्र में दिया गया है। सिक्के का भार 10g है। सिक्के को रोकने के लिए मेज के द्वारा सिक्के पर कितना बल लगाना पड़ता है?
हल:
यहाँ दिया गया है-

आरंभिक वेग (u) = 24 m/s
अंतिम वेग (v) = 0 m/s
समय (t) = 8 sec.
द्रव्यमान (m) = 10 = \(\frac { 10 }{ 1000 }\) kg
हम जानते हैं कि
त्वरण (a) = \(\frac { v-u }{ t }\) = \(\frac { 0-24 }{ 8 }\)
= \(\frac { -24 }{ 8 }\) = – 3ms²
अतः बल (F) = m x a
= (\(\frac { 10 }{ 1000 }\) x – 3)N
= – 0.03 N उत्तर
(ऋणात्मक चिह्न बल द्वारा गति को कम करने का प्रतीक है।)

प्रश्न 2.
70g द्रव्यमान की क्रिकेट की कोई गेंद 0.5 m/s के वेग से गतिमान है। क्रिकेट का कोई खिलाड़ी इसे 0.5s में रोक लेता है। खिलाड़ी द्वारा बॉल को रोकने के लिए लगाए गए बल की गणना कीजिए।
हल:
गेंद का द्रव्यमान (m) = 70 g = \(\frac { 70 }{ 1000 }\) = 0.07 kg
गेंद का प्रारंभिक वेग (u) = 0.5 m/s
गेंद का अंतिम वेग (v) = 0
गेंद को रुकने में लगा समय (t) = 0.5 s
हम जानते हैं कि v = u + at
⇒ a = \(\frac { v-u }{ t }\) = \(\frac { 0-0.5 }{ 0.5 }\) = \(\frac { -0.5 }{ 0.5 }\) = – 1m/s²
अतः गेंद को रोकने के लिए खिलाड़ी द्वारा बॉल पर लगाया जाने वाला बल
(F) = m.a
= 0.07 x – 1 N
= – 0.07 N उत्तर
(ऋणात्मक चिह्न दिखाता है कि बल, संवेग के विपरीत कार्य करता है।)

प्रश्न 3.
यदि 5 kg द्रव्यमान की वस्तु पर 200 N का बल लगाया जाए तो वस्तु में उत्पन्न त्वरण कितना होगा?
हल:
यहाँ पर
द्रव्यमान (m) = 5 kg
बल (F) = 200N
त्वरण (a) = ?
हम जानते हैं कि
F = m.a
⇒ a = \(\frac { F }{ m }\) = \(\frac { 200 }{ 5 }\) = 40 m/s² उत्तर

प्रश्न 4.
एक 5 kg द्रव्यमान वाली वस्तु पर 2 s के लिए एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3 m/s से बढ़ाकर 7 m/s कर देता है। लगाए गए बल की मात्रा ज्ञात करें। अब अगर 5s के लिए बल लगाया गया, तो वस्त का अंतिम वेग क्या होगा?
हल:
यहाँ पर
वस्तु का द्रव्यमान (m) = 5 kg
वस्तु का प्रारंभिक वेग (u) = 3 m/s
वस्तु का अंतिम वेग (v) = 7 m/s
समय (t) = 2s
त्वरण (a) = ?
हम जानते हैं कि
a = \(\frac { v-u }{ t }\) = \(\frac { 7-3 }{ 2 }\)ms^-2 = \(\frac { 4 }{ 2 }\) = 2 m/s^-2
वस्तु पर लगने वाला बल (F) = m.a
= 5 x 2 = 10 N उत्तर
दूसरी अवस्था में
वस्तु का प्रारंभिक वेग (u) = 3 m/s
वस्तु का अंतिम वेग (v) = ?
समय (t) = 5s
त्वरण (a) = 2 ms^-2
हम जानते हैं कि
v = u+ at
= 3 + 2 x 5 = 13 ms^-1 उत्तर

प्रश्न 5.
1000 kg द्रव्यमान की किसी कार को तथा 10,000 kg से लदे हुए किसी ट्रक को 2 सेकंड में रोकने के लिए क्रमशः कितने बल की आवश्यकता होगी यदि दोनों 5 m/s के वेग से गतिशील हों? हल:
यहाँ पर
दोनों का प्रारंभिक वेग (u) = 5m/s
दोनों का अंतिम वेग (v) = 0
समय (t) = 2s
त्वरण (a) = ?
हम जानते हैं कि
v = u + at
⇒ a = \(\frac { v-u }{ t }\) = \(\frac { 0-5 }{ 2 }\) = \(\frac { -5 }{ 2 }\) m/s² उत्तर
कार का द्रव्यमान (m₁) = 1000 kg
ट्रक का द्रव्यमान (m₂) = 10,000 kg
कार को रोकने के लिए आवश्यक बल (F₁) = m₁ a
= 1000 x \(\frac { -5 }{ 2 }\) N
= -2500 N
अतः कार को रोकने के लिए आवश्यक बल = 2500 N उत्तर
[∵ ऋणात्मक चिह्न दिखाता है कि बल, संवेग की विपरीत दिशा में कार्य करेगा]
इसी प्रकार ट्रक को रोकने के लिए आवश्यक बल (F₂) = m₂ a
= 10000 x \(\frac { -5 }{ 2 }\) N
= – 25000 N उत्तर
अतः ट्रक को रोकने के लिए आवश्यक बल, कार को रोकने की अपेक्षा अधिक होगा।

प्रश्न 6.
किसमें अधिक बल की आवश्यकता होगी -2 kg द्रव्यमान वाली किसी वस्तु को 5 ms^-2 की दर से त्वरित करने में या 4kg द्रव्यमान वाली वस्तु को 2 ms^-2 की दर से त्वरित करने में।
हल:
यहाँ पर
m₁ = 2 kg
a₁ = 5 ms^-2
अतः बल (F₁) = m₁a₁ = 2 x 5 = 10 N
m₂ = 4 kg
a₂ = 2 ms^-2
अतः बल (F₂) = m₂a₂ = 4 x 2 = 8 N
इस प्रकार F₁ > F₂
इसलिए 2 kg द्रव्यमान वाली वस्तु को 5 ms^-2 के वेग से त्वरित करने के लिए अधिक बल की आवश्यकता होगी। उत्तर

प्रश्न 7.
2 kg के एक पिस्टल से 20g द्रव्यमान की एक गोली 150 ms^-1 के क्षैतिज वेग से छोड़ी जाती है। पिस्टल के पीछे हटने के वेग का परिकलन करें।
हल:
गोली का द्रव्यमान (m₁) = 20 g (= 0.02 kg)
पिस्टल का द्रव्यमान (m₂) = 2 kg
गोली का प्रारंभिक वेग (u₁) तथा पिस्टल का प्रारंभिक वेग (u₂) क्रमशः शून्य है।
अर्थात् u₁ = u₂ = 0
गोली का अंतिम वेग (v₁) = + 150 ms^-1
गोली की दिशा बाएँ से दाएँ परिपाटी के अनुसार धनात्मक (चित्र), ली गई है। माना कि पिस्टल का प्रतिक्षेपित वेग v है।
गोली छूटने से पहले, गोली तथा पिस्टल का कुल संवेग = (2 + 0.02) kg × 0 ms^-1
= 0 kg ms^-1
गोली छूटने के बाद कुल संवेग = 0.02 kg x (+ 150 ms^-1) + 2 kg x v ms^-1
= (3 + 2v) kg ms^-1
संवेग संरक्षण के नियम के अनुसार,
गोली छूटने के बाद का कुल संवेग = गोली छूटने से पहले का कुल संवेग
(3 + 2v) = 0
⇒ v = \(\frac { -3 }{ 2 }\)
v = – 1.5 ms^-1 उत्तर
(ऋणात्मक चिह्न यह दर्शाता है कि पिस्टल गोली के विपरीत दिशा में अर्थात् दाईं से बाईं ओर प्रतिक्षेपित होगी।)

प्रश्न 8.
24 सें०मी० प्रति सेकंड के वेग से गतिमान एक सिक्का 3 सें०मी० प्रति वर्ग सेकंड त्वरण से लुढ़कते हुए 8 सेकंड के बाद रुक जाता है। सिक्के द्वारा तय की गई दूरी ज्ञात कीजिए ।
हल:
यहाँ पर
आरंभिक वेग (u) = 24 cm/s
अंतिम वेग (v) = 0
त्वरण (a) = – 3 cm/s²
समय (t) = 8 sec
दूरी (s) = ?
हम जानते हैं कि
दूरी (s) = ut + \(\frac { 1 }{ 2 }\)at²
= 24 x 8 + \(\frac { 1 }{ 2 }\) x (-3) x (8)²
= 192 – 96 = 96 cm

प्रश्न 9.
किसी 10g के द्रव्यमान में 5m/s² का त्वरण उत्पन्न करने में अधिक बल की आवश्यकता होगी या 20 g के द्रव्यमान में 2 m/s² का त्वरण उत्पन्न करने में।
हल:
पहली स्थिति में द्रव्यमान (m) = 10 g = \(\frac { 10 }{ 1000 }\) kg
त्वरण (a) = 5²
∴ पहली अवस्था में आवश्यक बल (F) = m x a
= \(\frac { 10 }{ 1000 }\) x 5
= 0.05 न्यूटन
दूसरी स्थिति में द्रव्यमान (m) = 20 g = \(\frac { 20 }{ 1000 }\) kg
त्वरण (a) = 2 m/s²
दूसरी स्थिति में आवश्यक बल (F) = m x a = \(\frac { 20 }{ 1000 }\) x 2
= 0.04 न्यूटन
अतः 10g के द्रव्यमान में 5 m/s² का त्वरण उत्पन्न करने के लिए अधिक बल की आवश्यकता होगी। उत्तर

प्रश्न 10.
16 m/s वेग से गति करती 20g द्रव्यमान की गोली किसी रेत से भरे थैले में घुसती है तथा 0.05 s में विराम अवस्था में आ जाती है। ज्ञात कीजिए
(a) रेत में घुसने की गहराई
(b) रेत द्वारा लगाया गया औसत प्रतिरोध बल।
हल:
यहाँ पर
(a) प्रारंभिक वेग (u) = 16 m/s
अंतिम वेग (v) = 0
समय (t) = 0.05 sec
दूरी (s) = ?
औसत प्रतिरोध बल (F) = ?

(1) हम जानते हैं कि
त्वरण (a) = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}=\frac{0-16}{0.05}=\frac{-16 \times 100}{5}\)
= – 320 m/s²

(2) s = ut + \(\frac { 1 }{ 2 }\)at²
= 16 x 0.05 + \(\frac { 1 }{ 2 }\) x (-320) x (0.05)²
था s = 0.8 – 0.4 = 0.4 m उत्तर

(b) द्रव्यमान (m) = 20 g = \(\frac { 20 }{ 1000 }\) kg
औसत प्रतिरोध बल (F) = m x a
= \(\frac { 20 }{ 1000 }\) x – 320
= – 6.4 N उत्तर

प्रश्न 11.
किसी 5 किलोग्राम द्रव्यमान की वस्तु के संवेग में कितना परिवर्तन हो जाएगा? यदि उसकी चाल-
(1) 20 m/s से कम होकर 0.20 m/s हो जाए।
(2) 30 m/s से बढ़कर 40 m/s हो जाए।
हल:
यहाँ पर
वस्तु का द्रव्यमान (m) = 5 kg
(1) प्रारंभिक वेग (u) = 20 m/s
अंतिम वेग (v) = 0.20 m/s
प्रारंभिक संवेग (p₁) = m x u= 5 x 20 = 100 kg m/s
अंतिम संवेग (p₂) = m x v = 5 x 0.20
= 1.00 kg m/s
अतः संवेग में कमी = P₁ – P₂ = 100 – 1 = 99 kg m/s उत्तर

(2) प्रारंभिक वेग (u) = 30 m/s
अंतिम वेग (v) = 40 m/s
प्रारंभिक संवेग (p₁) = m x u= 5 x 30 = 150 kg m/s.
अंतिम संवेग (p₂) = m xv= 5 x 40 = 200 kg m/s
अतः संवेग में वृद्धि = 200 – 150 = 50 kg m/s उत्तर

प्रश्न 12.
एक ड्राइवर किसी कार को पहली अवस्था में 1.8 m/s से तथा दूसरी अवस्था में 1.2 m/s² के त्वरण से त्वरित करता है। दोनों अवस्थाओं में इंजन द्वारा लगाए गए बलों में अनुपात ज्ञात कीजिए।
हल:
माना कार का द्रव्यमान = m kg
पहली अवस्था में त्वरण (a₁) = 1.8 m/s²
∴ पहली अवस्था में बल (F₁) = m x a₁ = m x 1.8 m = 1.8 m न्यूटन
दूसरी अवस्था में त्वरण (a₂) = 1.2 m/s²
∴ दूसरी अवस्था में बल (F₂) = m x a₂ = m x 1.2 = 1.2 m न्यूटन
\(\frac{\mathrm{F}_1}{\mathrm{~F}_2}=\frac{1.8 \mathrm{~m}}{1.2 \mathrm{~m}}=\frac{18}{12}=\frac{3}{2}\)
अतः F₁ : F₁ = 3 : 2 उत्तर

प्रश्न 13.
किसी वस्तु पर 1.2 s समय के लिए कोई बल लगाने पर उसकी चाल 1.8 m/s से 4.2 m/s हो जाती है। बाद में उसी बल को 2 s के लिए लगाया गया। 2 सेकंड में चाल में परिवर्तन कितना होगा? हल:
पहली अवस्था में प्रारंभिक वेग (u) = 1.8 m/s
अंतिम वेग (v) = 4.2 m/s
समय (t) = 1.2 sec
सूत्रानुसार v = u + at
या u + at = v
⇒ 1.8 + a x 1.2 = 4.2
या 1.2 a = 4.2 – 1.8
या 1.2 a = 2.4
या a = \(\frac { 2.4 }{ 2 }\)= 2 मीटर सेकंड²
∴ त्वरण = 2 मीटर/सेकंड² उत्तर
दूसरी अवस्था में प्रारंभिक वेग (u) = 4.2 m/s
समय (t) = 2 sec
त्वरण (a) = 2 m/s²
अंतिम वेग (v) = u + at
= 4.2 + 2 x 2
v = 4.2 +4
v = 8.2 m/s
अतः 2 सेकंड में चाल में परिवर्तन = 8.2 – 4.2 = 4 m/s उत्तर

निबंधात्मक प्रश्न

प्रश्न 1.
गैलीलियो ने किस प्रकार सिद्ध किया कि यदि किसी वस्तु पर कोई संतुलित बल न लगाया जाए तो वह वस्तु अचर चाल से चलती रहेगी। वर्णन कीजिए।
उत्तर:
गैलीलियो ने निम्नलिखित प्रयोगों के आधार पर सर्वप्रथम यह बताया है कि यदि किसी वस्तु पर कोई बल न लगाया जाए तो वह वस्तु अचर चाल से चलती रहेगी।

सबसे पहले उसने आनत तल पर वस्तुओं की गति का अध्ययन किया। उसने पाया कि जब कोई वस्तु आनत तल पर नीचे की ओर जाती है तो उसकी चाल बढ़ जाती है, परंतु जब वस्तु आनत तल पर ऊपर की ओर जाती है तो उसकी चाल घट जाती है; जैसे कि चित्र में दिखाया गया है।

अतः उसने यह निष्कर्ष निकाला कि यदि वस्तु समतल सतह पर चले तो वस्तु की चाल न बढ़ेगी और न घटेगी बल्कि उसकी चाल अचर रहेगी। अब उसने कल्पना की कि यदि एक गेंद को खोखले अर्द्ध-गोलाकार सतह को छूते हुए नीचे जाने दिया जाए तो वह उसी ऊँचाई तक पहुँच जाएगी; जिस ऊँचाई से उसे गिराया गया था। दोलित लोलक की गति के आधार पर उसने यह निष्कर्ष निकाला, क्योंकि लोलक का गोलक सदा उसी ऊँचाई तक पहुँचता है जितनी ऊँचाई से वह चला था। अर्द्ध-गोलाकार सतह वही कार्य करती है जो लोलक में धागे का होता है।

इसके पश्चात् उसने बताया कि यदि बर्तन की आकृति चित्र की तरह लें तो इस स्थिति में भी वस्तु या गेंद उसी ऊँचाई तक पहुँच जाती है। यद्यपि ऐसा करने में उसे अधिक दूरी तय करनी पड़ेगी।

अब यदि बर्तन के दूसरी ओर ढलान जितना कम कर देते हैं तो गेंद को उसी ऊँचाई तक पहुँचने में उतनी ही अधिक दूरी तय करनी पड़ती है। इस प्रकार वह इस निष्कर्ष पर पहुँचा कि यदि बर्तन के एक तरफ ढलान कम करते जाएँगे तो वस्तु उतनी ही अधिक दूरी तय करती जाएगी। इस प्रकार यदि ढलान बिल्कुल न रहे, सतह समतल हो जाए तो वस्तु अनंत दूरी तय करेगी तथा अचर वेग से चलती रहेगी।

प्रश्न 2.
किसी वस्तु का संवेग किसे कहते हैं? एक गतिशील वस्तु के संवेग और उस पर लगे बल में संबंध स्थापित करो।
उत्तर:
संवेग-किसी वस्तु का संवेग उसकी संहति m तथा वेग v के गुणनफल के बराबर होता है।
इसे ‘p’ द्वारा दर्शाया जाता है।
संवेग = संहति x वेग
या p = mv
हम जानते हैं कि यदि किसी वस्तु पर बल लगाया जाए तो वह त्वरित हो जाती है। वस्तु में उत्पन्न त्वरण, न्यूटन के गति के दूसरे नियम के अनुसार, उस पर लगे बल पर निर्भर करता है।
यदि किसी ‘m’ संहति की वस्तु पर ‘F’ बल लगने के कारण उसमें उत्पन्न त्वरण ‘a’ हो तो गति के दूसरे नियम के अनुसार
F = ma
a = \(\frac { F }{ m }\) …. (i)
माना वस्तु का प्रारंभिक वेग = v₁ m/s तथा t समय पश्चात् अंतिम वेग = v₂ m/s
तो a = \(\frac{v_2-v_1}{t}\) …. (ii)
समीकरण (i) और (ii) से
\(\frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{t}}\)
या F = \(\frac{m\left(v_2-v_1\right)}{t}\)
या F = \(\frac{m v_2-m v_1}{t}\)
परंतु mv₁ = P₁ (प्रारंभिक संवेग)
तथा mv₂ = P₂ (अंतिम संवेग)
∴ F = \(\frac{p_2-p_1}{t}\)
∴ F = संवेग के परिवर्तन की दर
अर्थात् किसी वस्तु पर लगा बल इकाई समय में संवेग में हुए परिवर्तन के बराबर होता है।

प्रश्न 3.
संवेग के संरक्षण से तुम क्या समझते हो? संवेग-संरक्षण के नियम को गणितीय ढंग से सिद्ध करो।
उत्तर:
संवेग का संरक्षण नियम-इस नियम के अनुसार वस्तुओं के किसी समूह का कुल संवेग तब तक स्थिर रहता है, जब तक उस पर कोई बाह्य बल क्रिया नहीं करता।

क्रियाकलाप इस नियम को सिद्ध करने के लिए मान लो दो पिंड A और B जिनके पुंज m₁ और m₂ हैं, क्रमशः u₁ और u₂ वेग से चल रहे हैं। मान लो दोनों t समय तक एक-दूसरे से क्रिया करते हैं। क्रिया के बाद उनका वेग v₁ और v₂ हो जाता है। (देखो चित्र)। यदि कोई बाहरी बल क्रिया न करे तो पिंड A के संवेग में परिवर्तन की दर m₁ (\(\frac{\left(\mathrm{v}_1-\mathrm{u}_1\right)}{\mathrm{t}}\)) है।

इसी प्रकार पिंड B के संवेग में परिवर्तन की दर m₂(\(\frac{\left(\mathrm{v}_2-\mathrm{u}_2\right)}{\mathrm{t}}\)) है। यदि A के ऊपर B द्वारा लग रहा बल F, और B के ऊपर A द्वारा लग रहा बल F₂ हो तो न्यूटन के गति के दूसरे नियम द्वारा,
F₁ = m₁(\(\frac{\left(\mathrm{v}_1-\mathrm{u}_1\right)}{\mathrm{t}}\)) …. (i)
और F₂ = m₂(\(\frac{\left(\mathrm{v}_2-\mathrm{u}_2\right)}{\mathrm{t}}\)) …. (ii)
न्यूटन के गति के तीसरे नियम के अनुसार F₁ और F₂ बराबर और विपरीत दिशा में क्रिया करते हैं।
∴ F₁ = – F₂ …. (iii)
समीकरण (i), (ii) और (iii) से
\(\mathrm{m}_1 \frac{\left(\mathrm{v}_1-\mathrm{u}_1\right)}{\mathrm{t}}=-\mathrm{m}_2 \frac{\left(\mathrm{v}_2-\mathrm{u}_2\right)}{\mathrm{t}}\)
था m₁ (v₁ – u₁) = – m₂ (v₂ – u₂)
था m₁v₁ – m₁u₁ = – m₂v₂ + m₂u₂
या m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂
था m₁ u₁ + m₂ u₂ = m₁v₁ + m₂v₂ …. (iv)
अर्थात् टक्कर के पहले कुल संवेग m₁u₁ + m₂u₂ टक्कर के बाद कुल संवेग m₁v₁ + m₂v₂ के बराबर है। यह संवेग संरक्षण का नियम है।

प्रश्न 4.
घर्षण से तुम्हारा क्या अभिप्राय है? सिद्ध करो कि जहाँ यह एक तरफ वरदान है, वहीं एक शाप भी है।
उत्तर:
घर्षण-जब एक वस्तु किसी अन्य वस्तु के संपर्क में रहते हुए गति करती है तो उस गति की दिशा के विपरीत एक बल कार्य करता है, जिसे घर्षण बल या घर्षण कहते हैं।

घर्षण वरदान के रूप में घर्षण एक आवश्यक बुराई है, क्योंकि इसके बिना कोई कार्य संभव नहीं है; जैसे-

• पाँव और सड़क के बीच यदि घर्षण न हो तो हम चल-फिर नहीं सकते।
• वाहनों के टायरों तथा सड़क के बीच घर्षण न हो तो वाहन नहीं चल सकते।
• घर्षण के कारण ही दीवार तथा लकड़ी में कील आदि गाड़ी जा सकती है।
• घर्षण के कारण ही माचिस की तीली को जलाया जा सकता है।
• ब्लैकबोर्ड तथा चाक के बीच घर्षण के कारण ही ब्लैकबोर्ड पर लिखना संभव होता है।
• घर्षण के कारण ही पैन से कापी पर लिखा जा सकता है।
• घर्षण के कारण ही वाहनों को ब्रेकों द्वारा रोका जा सकता है।
• घर्षण के कारण ही मशीनों और विद्युत् मोटरों से संबद्ध पट्टे पहियों पर घूम सकते हैं।

घर्षण शाप के रूप में घर्षण एक आवश्यक बुराई होने के साथ-साथ हमें निम्नलिखित हानियाँ भी पहुंचाता है; जैसे-

• घर्षण के कारण मशीनों के पुर्जे घिसते हैं तथा टूट जाते हैं।
• घर्षण के कारण ही मशीनों की दक्षता 100% नहीं होती।
• घर्षण के कारण अधिक ऊर्जा खर्च होती है।
• घर्षण के कारण वाहनों के टायर घिस जाते हैं।
• घर्षण के कारण हमारे जूते घिस जाते हैं।

प्रश्न 5.
घर्षण कम करने की विधियों के नाम लिखें तथा इनमें से किसी एक की व्याख्या करें।
उत्तर:
घर्षण बल को निम्नलिखित ढंग से कम किया जा सकता है-

• घर्षण बल को वस्तु की सतह पर गड्ढे तथा उभारों को समतल करके कम किया जा सकता है।
• तेल या स्नेहक दो सतहों के बीच के घर्षण बल को कम करता है। इसी कारण मशीनों के पुों में तेल डालकर घर्षण कम किया जा सकता है।
• साबुन तथा पानी का मिश्रण भी दो सतहों के बीच घर्षण को कम कर सकता है।
• बॉल-बेयरिंग का प्रयोग करके भी घर्षण कम किया जा सकता है।
• कैरम बोर्ड पर थोड़ा पाऊडर छिड़कने से वह उसके उभार तथा गड्ढों को थोड़ा भर देता है, जिससे गोट आसानी से इधर-उधर जा सकती है।
• घर्षण को कम करने के लिए वाहनों को विशेष आकृति दी जाती है।
• दो तलों को पॉलिश से चमकाकर तथा सड़कों पर कोलतार डालकर घर्षण को कम किया जा सकता है।

बॉल-बेयरिंग के प्रयोग से घर्षण को कम करना घर्षण को कम करने के लिए मशीनों में प्रायः बॉल-बेयरिंगों का उपयोग किया जाता है। बॉल-बेयरिंग में छोटी-छोटी धातु की गोलियाँ होती हैं, जो मशीन की सी सतहों के बीच डाल दी जाती हैं। आपने इन्हें साइकिल के पहियों में लगा देखा होगा। ये घर्षण को कम कर देते हैं, जिससे हमें ऊर्जा व श्रम की बचत होती है।

प्रयोगात्मक कार्य

क्रियाकलाप 1.
बल के प्रभाव को दर्शाने के लिए दो क्रियाकलाप जिससे सिद्ध हो कि बल वस्तु का आकार बदल सकता है।
कार्य-विधि-
(1) एक स्प्रिंग लें तथा उसे दोनों ओर से पकड़कर बाहर की ओर खींचे तो आप देखेंगे कि स्प्रिंग का आकार बढ़ जाएगा, जो हमारे द्वारा स्प्रिंग पर लगाए गए बल को दर्शाता है। इससे सिद्ध होता है कि बल वस्तु का आकार बदल सकता है।

(2) एक गोल आकार की रबड़ की गेंद लेकर उसे अपनी दोनों हथेलियों के बीच में लेकर दबाएँ। दबाने पर आप देखेंगे कि गेंद का आकार अंडाकार हो जाएगा जिससे सिद्ध होता है कि बल वस्तु का आकार बदल देता है।

क्रियाकलाप 2.
एक क्रियाकलाप द्वारा दर्शाए कि कोई वस्तु तभी गति करना आरंभ करती है जब हमारे द्वारा लगाया गया बल घर्षण बल से अधिक हो?
कार्य-विधि-
एक बक्सा लें तथा उसे दो बच्चों को धकेलने के लिए कहें। आप देखेंगे कि यदि वे कम बल के साथ बक्से को धकलेते हैं, तो बक्सा नहीं खिसकता है, क्योंकि बक्से की नीचे की सतह तथा फर्श की खुरदरी सतह के बीच घर्षण बल, धकेलने में लगे बल को संतुलित करता है और यही कारण है कि बक्सा नहीं खिसकता है। बच्चे बक्से को जोर से धकेलते हैं, लेकिन बक्सा फिर भी नहीं खिसकता है।

ऐसा इसलिए है क्योंकि घर्षण बल अभी भी धकेलने वाले बल को संतुलित कर रहा है। अगर बच्चे बक्से को और अधिक जोर से धकेलते हैं। तब धकेलने वाला घर्षण बल से बड़ा हो जाता है। यहाँ असंतुलित बल कार्य करता है, इसलिए बक्सा खिसकने लगता है। इससे सिद्ध होता है कि यदि हमारे द्वारा लगाया गया बल घर्षण बल से अधिक हो तभी कोई वस्तु गति करती है।

क्रियाकलाप 3.
क्रिया तथा प्रतिक्रिया का प्रभाव दर्शाने के लिए एक क्रियाकलाप करें।
कार्य-विधि 1.

• एक बड़े आकार का गुब्बारा लें तथा इसमें पूरी तरह से हवा भरें।
• इसके मुख को धागे से बाँधे तथा इसकी सतह पर किसी चिपकाने वाली टेप की सहायता से एक प्लास्टिक की पतली नली लगाएँ।
• प्लास्टिक की पतली नली के बीच से एक धागे को पार कराएँ, जिसके दोनों सिरों को दीवार पर लगाएँ।
• गुब्बारे के मुँह पर बाँधे धागे को खोल दें।
• अब गुब्बारे से भरी हवा उसके मुख से बाहर की ओर निकलने लगेगी तथा नली तथा गुब्बारा विपरीत दिशा में गति करेगा जो प्रतिक्रिया दर्शाता है।

कार्य-विधि 2.

• अच्छे काँच की एक परखनली लें और उसमें थोड़ा पानी डालें।
• परखनली के मुख पर एक स्टॉप कॉर्क लगाएँ। अब परखनली को दो धागों के द्वारा स्टैंड पर क्षैतिज दिशा में लटकाएँ।
• बर्नर की सहायता से परखनली को तब तक गर्म करें, जब तक परखनली का पानी वाष्पित हो जाए तथा कॉर्क बाहर आ जाए।
• हम देखते हैं कि परखनली कॉर्क की गति की विपरीत दिशा में प्रक्षेपित होती है, जो क्रिया व प्रतिक्रिया की गति को प्रदर्शित करता है।

अध्याय का तीव्र अध्ययन

1. किसी वस्तु पर बल लगाने से-
(A) उसकी गति बदल सकती है
(B) उसका आकार बदल सकता है
(C) उसकी गति की दिशा बदल सकती है
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

2. बल का मात्रक है-
(A) जूल
(B) मीटर प्रति वर्ग सेकंड
(C) कि०ग्रा० मीटर प्रति वर्ग सेकंड
(D) मीटर प्रति सेकंड
उत्तर:
(C) कि०ग्रा० मीटर प्रति वर्ग सेकंड

3. वस्तुओं की गति को नियंत्रित करने वाले नियमों को सबसे पहले किस वैज्ञानिक ने स्थापित किया?
(A) सर आइजक न्यूटन ने
(B) सी०वी० रमन ने
(C) रदरफोर्ड ने
(D) नीलस बोर ने
उत्तर:
(A) सर आइजक न्यूटन ने

4. घर्षण बल वस्तु की गति को-
(A) कम करता है
(B) बढ़ा देता है
(C) प्रभावित नहीं करता
(D) इनमें से कोई नहीं
उत्तर:
(A) कम करता है

5. न्यूटन द्वारा दिए गए गति के मौलिक नियम हैं-
(A) 2
(B) 3
(C) 4
(D) 5
उत्तर:
(B) 3

6. न्यूटन की गति के प्रथम नियम को कहा जाता है-
(A) उत्प्लावकता का नियम
(B) संवेग संरक्षण का नियम
(C) जड़त्व का नियम
(D) गुरुत्व का नियम
उत्तर:
(C) जड़त्व का नियम

7. किसी बाह्य बल की अनुपस्थिति में किसी निकाय का कुल संवेग संरक्षित रहना कौन-सा नियम कहलाता है?
(A) गुरुत्वाकर्षण नियम
(B) न्यूटन का गति नियम
(C) संवेग संरक्षण नियम
(D) जड़त्व नियम
उत्तर:
(C) संवेग संरक्षण नियम

8. किसी वस्तु के संवेग परिवर्तन की दर उस पर आरोपित बल के समानुपाती होती है और उसी दिशा में होती है जिसमें बल लगाया जाता है। यह न्यूटन का-
(A) पहला नियम है
(B) दूसरा नियम है
(C) तीसरा नियम है
(D) चौथा नियम है
उत्तर:
(B) दूसरा नियम है

9. संवेग का SI मात्रक है-
(A) kg m/s²
(B) kg m/s
(C) kg m
(D) kg m/h
उत्तर:
(B) kg m/s

10. एक किलोग्राम संहति की वस्तु पर 1m/s² का त्वरण उत्पन्न करने के लिए आवश्यक बल कहलाता है-
(A) 1 न्यूटन
(B) 2 न्यूटन
(C) 3 न्यूटन
(D) 4 न्यूटन
उत्तर:
(A) 1 न्यूटन

11. कोई व्यक्ति 40 kg द्रव्यमान के बॉक्स को 80 न्यूटन बल लगाकर धकेलता है। बॉक्स में उत्पन्न त्वरण होगा-
(A) 3200 m/s²
(B) 3200 m/s
(C) 2 m/s
(D) 2 m/s²
उत्तर:
(D) 2 m/s²

12. वस्तुओं का वह गुण जो उसकी गति या विराम की अवस्था में परिवर्तन का विरोध करता है, वह कहलाता है-
(A) घर्षण
(B) द्रव्यमान
(C) त्वरण
(D) जड़त्व
उत्तर:
(D) जड़त्व

13. दो वस्तुओं के संपर्क में हुए बिना लगने वाला बल है-
(A) घर्षण बल
(B) चुंबकीय बल
(C) जड़त्व बल
(D) प्रतिक्रिया बल
उत्तर:
(B) चुंबकीय बल

14. रेत पर चलना कठिन होता है क्योंकि पैरों व रेत के बीच-
(A) घर्षण कम होता है
(B) घर्षण अधिक होता है
(C) घर्षण सामान्य होता है
(D) घर्षण नहीं होता
उत्तर:
(B) घर्षण अधिक होता है

15. दरी को छड़ी से पीटने पर धूल झड़ जाती है-
(A) स्थिर जड़त्व के कारण
(B) दरी की गति के कारण
(C) छड़ी की गति के कारण
(D) बल के कारण
उत्तर:
(A) स्थिर जड़त्व के कारण

16. यदि किसी 1kg द्रव्यमान की वस्तु पर 1 न्यूटन (N) बल लगाया जाए तो उसमें उत्पन्न त्वरण होगा-
(A) 1 m/s
(B) 1 m/s²
(C) 2 m/s
(D) 2 m/s²
उत्तर:
(B) 1 m/s²

17. निम्न में से कौन-सा बल किसी वस्तु को गति प्रदान करता है-
(A) गुरुत्व बल
(B) असन्तुलित बल
(C) सन्तुलित बल
(D) घर्षण बल
उत्तर:
(B) असन्तुलित बल

18. दो वस्तुओं के सम्पर्क में हुए बिना लगने वाला बल कौन-सा है?
(A) चुम्बकीय
(B) जड़त्व
(C) घर्षण
(D) उपर्युक्त सभी
उत्तर:
(A) चुम्बकीय

19. गति करने के लिए स्वतंत्र किसी वस्तु पर कोई बल लगाया गया। यदि बल का परिमाण तथा वस्तु का द्रव्यमान ज्ञात हो तो न्यूटन के गति के दूसरे नियम की सहायता से हर वस्तु-
(A) का भार ज्ञात कर सकते हैं
(B) की चाल ज्ञात कर सकते हैं
(C) का त्वरण ज्ञात कर सकते हैं
(D) की स्थिति ज्ञात कर सकते हैं
उत्तर:
(C) का त्वरण ज्ञात कर सकते हैं

20. यदि किसी वस्तु पर कोई बाह्य बल लग रहा हो तो वह बल की दिशा में त्वरित हो जाती है। इस प्रकार उत्पन्न त्वरण वस्तु-
(A) पर लगे बल के समानुपाती होता है
(B) के वेग के समानुपाती होता है
(C) के द्रव्यमान के समानुपाती होता है
(D) के जड़त्व के समानुपाती होता है
उत्तर:
(A) पर लगे बल के समानुपाती होता है

21. न्यूटन की गति के तीसरे नियम के अनुसार क्रिया तथा प्रतिक्रिया से संबद्ध बल
(A) सदैव एक ही वस्तु पर लगे होने चाहिएँ
(B) भिन्न-भिन्न वस्तुओं पर लगे होने चाहिएँ
(C) सदैव भिन्न-भिन्न वस्तुओं पर ही लगे होने चाहिएँ
(D) का परिणाम बराबर होना आवश्यक नहीं है, परंतु उनकी दिशा एकसमान होनी चाहिए
उत्तर:
(C) सदैव भिन्न-भिन्न वस्तुओं पर ही. लगे होने चाहिएँ

22. रॉकेट छोड़ने का सिद्धांत …………………… आधारित है।
(A) न्यूटन के गति के प्रथम नियम पर
(B) न्यूटन के गति के द्वितीय नियम पर
(C) न्यूटन के गति के तृतीय नियम पर
(D) उपर्युक्त सभी
उत्तर:
(C) न्यूटन के गति के तृतीय नियम पर

23. एक खिलाड़ी लंबी कूद लगाने से पहले दौड़ता है-
(A) आवेग बढ़ाने के लिए
(B) जड़त्व बढ़ाने के लिए
(C) संवेग बढ़ाने के लिए
(D) यह कोई वैज्ञानिक तथ्य नहीं है
उत्तर:
(C) संवेग बढ़ाने के लिए

24. जेट हवाई जहाज के कार्य करने का सिद्धांत आधारित है-
(A) संवेग संरक्षण पर
(B) ऊर्जा संरक्षण पर
(C) वेग संरक्षण पर
(D) द्रव्यमान संरक्षण पर
उत्तर:
(A) संवेग संरक्षण पर

25. एक किलोग्राम द्रव्यमान की वस्तु का भार होगा-
(A) 8.9 न्यूटन
(B) 9.8 न्यूटन
(C) 1 न्यूटन
(D) 9.08 न्यूटन
उत्तर:
(B) 9.8 न्यूटन

26. निम्नलिखित में से किसका जड़त्व अधिक होता है?
(A) रबड़ की गेंद का
(B) पत्थर के टुकड़े का
(C) साइकिल का
(D) रेलगाड़ी का
उत्तर:
(D) रेलगाड़ी का

27. जब कोई गतिशील बस अचानक रुकती है, तो आप आगे की ओर झुक जाते हैं और जब विराम अवस्था से गतिशील होती है तो पीछे की ओर जाते हैं-
(A) द्रव्यमान के कारण
(B) भार के कारण
(C) गतिशीलता के कारण
(D) जड़त्व के कारण
उत्तर:
(D) जड़त्व के कारण

28. मशीनों में लुब्रीकेंट का प्रयोग किसलिए किया जाता है-
(A) घर्षण बढ़ाने हेतु
(B) घर्षण कम करने हेत
(C) घर्षण शून्य करने हेतु
(D) चमकाने हेतु
उत्तर:
(B) घर्षण कम करने हेतु