HBSE 9th Class Maths Important Questions Chapter 13 Surface Areas and Volumes

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 13 Surface Areas and Volumes

Very Short Answer Type Questions

Question 1.
Three cubes each with 7 cm edge are joined end to end. Find the total surface area of the resulting cuboid.
Solution:
Since three cubes each with 7 cm edge are joined end to end.

∴ Dimensions of resulting cuboid are
l = 7 + 7 + 7 = 21 cm
b = 7 cm and h = 7 cm
Total surface area of the resulting cuboid
= 2(lb + bh + hl)
= 2(21 × 7 + 7 × 7 + 7 × 21)
= 2(147 + 49 + 147)
= 2 × 343
= 686 cm²
Hence, total surface area of resulting cuboid = 686 cm².

Question 2.
Find the length of longest pole that can be put in a room of dimensions 12 m × 9 m × 8 m.
Solution:
Dimensions of the room are
l = 12 m, b = 9 m and h = 8 m
Length of a diagonal of a room
= \(\sqrt{l^2+b^2+h^2}\)
= \(\sqrt{12^2+9^2+8^2}\)
= \(\sqrt{144+81+64}\)
= \(\sqrt{289}\) = 17 m
Hence,length of a diagonal of a room = 17 m.

Question 3.
The length and breadth of a hall are 16 m and 10 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the total surface area.
Solution:
We have,
The length and breadth of a hall are 16 m and 10 m.
Let the height of the hall be h m.
Area of floor and flat roof = 2 × l × b
= 2 × 16 × 10
= 320 m²
Area of four walls of a hall = 2(l + b) × h
= 2(16 + 10) × h = 52h
According to question,
Area of floor and flat roof = Area of four walls
⇒ 320 = 52h
⇒ h = \(\frac{320}{52}\)
⇒ h = 6.15 m (approx.)
The total surface of the hall
= 2(lb + bh + hl)
= 2(16 × 10 + 10 × 6.15 + 6.15 × 16)
= 2(160 + 61.5 + 98.4)
= 2(319.9) = 639.8 m²
Hence, total surface area of a hall = 639.8 m².

Question 4.
A well is 7.2 m deep. The cost of cementing its inner surface at 75 paise per dm² is Rs. 11880. Determine the radius of the well.
Solution:
We have,
Depth of well (h) = 7.2 m
Rate of cementing of inner surface of well 75 paise/dm² = Rs. 0.75 per dm²
Total cost of cementing the well = Rs. 11880
C.S.A. of the well = \(\frac{\text { Total cost }}{1 \mathrm{dm}^2 \cos t}\) = \(\frac{11880}{0.75}\)
= 15840 dm² = 158.4 m² …….(i)
Let the radius of the well be r m.
C.S.A. of the well = 2πrh
⇒ 158.4 = 2 × \(\frac{22}{7}\) × r × 7.2
⇒ 158.4 = \(\frac{316.8}{7}\)r
⇒ r = \(\frac{158.4 \times 7}{316.8}\)
⇒ r = 3.5 m
Hence,radius of the well = 3.5 m.

Question 5.
A rectangular sheet of paper 44 cm by 20 cm is rolled along its length and a cylinder is formed. Find the total surface area of cylinder.
Solution:
We have,
Length of rectangular sheet (l) = 44 cm
Breadth of rectangular sheet (b) = 20 cm
Since, rectangular sheet of paper is rolled along its length.
Height of the cylinder (h) = 20 cm
and base circumference of cylinder of radius r cm = 44 cm
⇒ 2πr = 44
⇒ 2 × \(\frac{22}{7}\) × r = 44
⇒ \(\frac{44}{7}\) × r = 44
⇒ r = \(\frac{44 \times 7}{44}\) = 7 cm
Total surface area of the cylinder
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 7(20 + 7)
= 44 × 27 = 1188 cm²
Hence, total surface area of the cylinder = 1188 cm².

Question 6.
The radii of the two cylinders are in the ratio 3 : 4 and their heights are in the ratio 4 : 5. Determine the ratio of their curved surface areas.
Solution:
We have,
Ratio of radii of two cylinders = 3 : 4
Let radii of two cylinders be 3x and 4x and ratio of heights of two cylinders = 4 : 5
Let heights of two cylinders be 4h and 5h.
C.S.A. of the Ist cylinder = 2 × π × 3x × 4h …(i)
C.S.A. of the IInd cylinder = 2 × π × 4x × 5h …(ii)
Dividing (i) by (ii), we get
⇒ \(\frac{\text { C.S.A. of the Ist cylinder }}{\text { C.S.A. of the IInd cylinder }}=\frac{2 \times \pi \times 3 x \times 4 h}{2 \times \pi \times 4 x \times 5 h}\)
⇒ \(\frac{\text { C.S.A. of the Ist cylinder }}{\text { C.S.A. of the IInd cylinder }}=\frac{3}{5}\)
⇒ C.S.A. of the Ist cylinder : C.S.A. of the IInd cylinder = 3 : 5
Hence, required ratio of two cylinders = 3 : 5.

Question 7.
The curved surface area of the cylinder is \(\frac{2}{3}\) of the total surface area of a cylinder whose length is 27 cm. Find the radius of the cylinder.
Solution:
We have,
Length of the cylinder (h) = 27 cm
Let radius of the cylinder be r cm.
∴ Curved surface area of the cylinder = 2лrh
= 2πr × 27 = 54πr
and total surface area of the cylinder
= 2πr(h+r) = 2πr(27 + r)
According to question,
Curved surface area of cylinder = \(\frac{2}{3}\) of total surface area of cylinder
54πr = \(\frac{2}{3}\) of 2πr(27 + r)
⇒ 54πr = \(\frac{4 \pi r}{3}\)(27 + r)
⇒ \(\frac{3 \times 54 \pi r}{4 \pi r}\) = 27 + r
⇒ 40.5 = 27+ r
⇒ r = 40.5 – 27
⇒ r = 13.5 cm
Hence, radius of the cylinder = 13.5 cm.

Question 8.
A cylindrical roller 2.5 m in length, 1.75 m in radius when rolled on a road was found to cover the area of 5500 m². How many revolutions did it make?
Solution:
We have,
Length of the roller (h) = 2.5 m
Radius of the roller (r) = 1.75 m
and total area covered by roller = 5500 m²
Area covered by roller in one revolution
= C.S.A. of the roller
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.5
= 44 × 0.25 × 2.5
= 27.5 m²
No. of revolutions = \(\frac{\text { Total area }}{\text { Area covered in one revolution }}\)
= \(\frac{5500}{27.5}\)
= 200
Hence, no. of revolutions makes by roller = 200.

Question 9.
Find the ratio of the curved surface areas of two cones, if the diameters of their bases are equal and slant heights are in the ratio 3 : 5.
Solution:
We have,
Diameters of bases of two cones are equal.
Therefore radius of their bases are also equal.
Slant height of Ist cone (l₁) : Slant height of IInd cone (l₂) = 3 : 5
Let slant height of Ist cone be 3x, second cone be 5x and same radius of their bases be r
\(\frac{\text { Curved surface area of Ist cone }}{\text { Curved surface area of IInd cone }}=\frac{\pi r l_1}{\pi r l_2}\)
\(\frac{\pi r \times 3 x}{\pi r \times 5 x}\) = 3 : 5
Hence,required ratio = 3 : 5.

Question 10.
Radii of two spheres are in the ratio 2 : 3. Find the ratio of their surface areas.
Solution:
We have, Ratio of radii of two spheres = 2 : 3
Let radii of two spheres be 2 and 3x, then
Surface area of Ist sphere = 4π(2x)²
= 4π × 4x² = 16πx²
Surface area of IInd sphere = 4π(3x)²
= 4π × 9x² = 36x²
Now, \(\frac{\text { Surface area of Ist sphere }}{\text { Surface area of IInd sphere }}\)
= \(\frac{16 \pi x^2}{36 \pi x^2}\)
⇒ \(\frac{\text { Surface area of Ist sphere }}{\text { Surface area of IInd sphere }}=\frac{4}{9}\)
⇒ Surface area of Ist sphere : Surface of IInd sphere = 4 : 9
Hence, required ratio of two spheres = 4 : 9.

Question 11.
The volume of a cuboid is 720 m³. Its length is 12 m and its breadth and height are in the ratio 5 : 3. Find the breadth and height of the cuboid.
Solution:
We have, Length of a cuboid = 12 m
Ratio of breadth and height = 5 : 3
Let the breadth of a cuboid be 5x and height be 3x
and volume of a cuboid = 720 m³
l × b × h = 720
12 × 5x × 3x = 720
180x² = 720
x² = \(\frac{720}{180}\)
x² = 4
x = \(\sqrt{4}\) = 2
∴ breadth of a cuboid = 5 × 2 = 10 m
and height of a cuboid = 3 × 2 = 6 m
Hence, breadth and height of a cuboid are 10 m and 6 m respectively.

Question 12.
The dimensions of a metallic cuboid are 54 cm × 36 cm × 24 cm. It is melted and recast into a cube. Find the surface area of the cube.
Solution:
We have,
Dimensions of the metallic cuboid = 54 cm × 36 cm × 24 cm
∴ Volume of the cuboid = 54 × 36 × 24
= 46656 cm³
Since cuboid is melted and recast into a cube.
Let the edge of new cube be a cm.
∴ Volume of a cube = Volume of cuboid
⇒ a³ = 46656
⇒ a = \(\sqrt[3]{46656}\)
⇒ a = 36 cm
Surface area of the cube = 6a²
= 6 × (36)²
= 7776 cm²
Hence,surface area of the cube = 7776 cm².

Question 13.
A cone and a cylinder have same heights and same volumes. Find the ratio of their bases radii.
Solution:
Let the radii of bases of cone and cylinder be r₁ and r₂.
Let their heights be h.
According to question,
Volume of the cone = Volume of the cylinder
⇒ \(\frac{1}{3} \pi r_1{ }^2 h=\pi r_2{ }^2 h\)
⇒ \(\frac{r_1^2}{r_2^2}=\frac{3 \pi h}{\pi h}\)
⇒ \(\frac{r_1{ }^2}{r_2{ }^2}=3\)
⇒ \(\frac{r_1}{r_2}=\frac{\sqrt{3}}{1}\)
⇒ r₁ : r₂ = \(\sqrt{3}\) : 1
Hence, required ratio of radii of bases of cone and cylinder = \(\sqrt{3}\) : 1.

Question 14.
Find the volume of the largest right circular cone that can be cut out from a cube whose edge is 21 cm.
Solution:
The base of the cone will the circle inscribed in a face of the cube and its height will be equal to the an edge of cube.
Edge of the cube = 21 cm

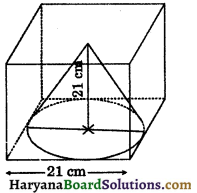
∴ Radius of base of the cone (r) = \(\frac{21}{2}\)
= 10.5 cm
Height of the cone (h) = 21 cm
Volume of the cone cut out = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × (10.5)² × 21
= 22 × 110.25
= 2425.5 cm³
Hence,volume of the cone cut out = 2425.5 cm³.

Question 15.
If h, c and V are respectively the height, the curved surface area and volume of a cone, then prove that :
3πVh³ – c²h² + 9V² = 0.
Solution:
Let r be radius and h be the height of a cone.
∴ Slant height (l) = \(\sqrt{h^2+r^2}\)
Volume of a cone (V) = \(\frac{1}{3}\)πr²h
and curved surface area (c) = πrl
⇒ c = πr(\(\sqrt{h^2+r^2}\))
⇒ c² = π²r² (h² + r²)
Now, L.H.S. = 3πVh³ – c²h² + 9V²
= 3π × \(\frac{1}{3}\)πr²h × h³ – π²r² × (h² + r²) × h² + 9 × \(\left(\frac{1}{3} \pi r^2 h\right)^2\)
= π²r²h⁴ – π²r²h⁴ – π²r⁴h² + 9 × \(\frac{1}{9}\)π²r⁴h²
= -π²r⁴h² + πr⁴h²
= 0 = R.H.S.
∴ L.H.S. = R.H.S. Hence proved.

Question 16.
The diameter of copper sphere is 6 cm. The sphere is melted and is drawn into a long wire of uniform circular section. If the length of wire is 36 cm, find its radius.
Solution:
We have,
Diameter of copper sphere = 6 cm
∴ Radius of copper sphere (R) = \(\frac{6}{2}\) = 3 cm
Length of wire (h) = 36 cm
Let radius of wire be r сm.
Since, copper sphere is melted and is drawn into a circular wire.
∴ Volume of circular wire = Volume of sphere
∴ πr²h = \(\frac{4}{3}\)πR³
⇒ π × r² × 36 = \(\frac{4}{3}\)π × (3)³
⇒ r² = \(\frac{4 \pi \times 3 \times 3 \times 3}{3 \times \pi \times 36}\)
⇒ r² = 1
⇒ r = 1 cm
Hence, radius of wire = 1 cm.

Short Answer Type Questions

Question 1.
An open box is made of wood 5 cm thick. Its external length is 1.50 m, breadth 1.30 m and height 0.90 m. Find the cost of painting the inner surface of the box at 75 paise per 100 cm².
Solution:
External dimensions of the box are
l = 1.50 m = 150 cm
b = 1.30 m = 130 cm
h = 0.90 m = 90 cm
Thickness of the wood = 5 cm. Therefore inner dimensions of the box are
l = 150 cm – 2 × 5 cm
= 140 cm
b = 130 cm – 2 × 5 cm
= 120 cm
h = 90 cm – 2 × 5 cm
= 80 cm
Inner surface area of the box = 2(lb + bh + hl)
= 2(140 × 120 + 120 × 80 + 80 × 140)
= 2(16800 + 9600 + 11200)
= 2(37600) = 75200 cm²
∵ 100 cm² painting cost of box = 75 paise
i.e., Rs. \(\frac{75}{100}\)
∴ 1 cm² painting cost of box = Rs. \(\frac{75}{100 \times 100}\)
∴ 75200 cm² painting cost of box = Rs. \(\frac{75 \times 75200}{100 \times 100}\)
= Rs. 564
Hence, painting cost of inner surface area of the box = Rs. 564.

Question 2.
A class room is 8 m long, 6 m wide and 4 m high. It has two doors 2.5 m by 1.5 m and three windows 1.5 m by 80 cm.
Find:
(i) Area of the walls excluding doors and windows.
(ii) The cost of distempering at the rate of Rs. 5.40 per m².
Solution:
Dimensions of the class room are
l = 8 m, b = 6 m and h = 4 m
(i) Surface area of walls of the class room
= 2(l + b) × h = 2(8 + 6) × 4
= 2 × 14 × 4 = 112 m²
Area of 1 door = 2.5 × 1.5 = 3.75 m²
Area of 2 doors = 2 × 3.75 = 7.5 m²
Area of 1 window = 1.5 m × 80 cm
= 1.5 m × 0·80 m
= 1.2 m²
Area of 3 windows = 3 × 1.2 = 3.6 m²
Area of 2 doors + Area of 3 windows = 7.5 + 3.6 = 11.1 m²
Area of the walls of the class room excluding doors and windows
= 112 – 11.1 = 100.9 m².

(ii) ∵ 1 m² distempering cost of walls = Rs. 5.40
∴ 100.9 m² distempering cost of walls
= Rs. 5.40 × 100.9
= Rs. 544.86
= Rs. 544.80 (approx.)
Hence, (i) Area of the walls excluding doors and windows is 100.9 m².
(ii) cost of distempering of walls of a class room = Rs. 544.80 (approx.)

Question 3.
Lateral surface area of a cuboid is 486 m². Its breadth is 12 m and length and height are in the ratio 5 : 3. Find the length and height of the cuboid.
Solution:
We have,
Lateral surface area of cuboid = 486 m²
Breadth of a cuboid = 12 m
Ratio of length : height = 5 : 3
Let the length and height of the cuboid be 5x and 3x respectively.
Lateral surface area of a cuboid = 2(l + b) × h
⇒ 486 = 2(5x + 12) × 3x
⇒ 486 = 30x² + 72x
⇒ 30x² + 72x – 486 = 0
⇒ 5x² + 12x – 81 = 0
⇒ 5x² + (27 – 15)x – 81 = 0
⇒ 5x² + 27x – 15x – 81 = 0
⇒ x(5x + 27) – 3(5x + 27) = 0
⇒ (5x + 27) (x – 3)= 0
⇒ 5x + 27 = 0 or x – 3 = 0
⇒ x = \(\frac{-27}{5}\) or x = 3
Since, length and height are not negative,
so we neglect x = \(\frac{-27}{5}\)
∴ x = 3
Length of cuboid = 5 × 3 = 15 m
height of cuboid = 3 × 3 = 9 m
Hence, length and height of the cuboid = 15 m and 9 m.

Question 4.
The dimensions of the cuboid are in the ratio 5 : 3 : 2 and the lateral surface area is 288 m². The outer surface area of the cuboid is painted with colour enamel at the rate of Rs. 6 per m². Find the total cost of painting.
Solution:
We have,
Ratio of the dimensions of the cuboid = 5 : 3 : 2
Let the dimensions of the cuboid as l = 5x m, b = 3x m and h = 2x m
Lateral surface area of the cuboid = 288 m² (given)
⇒ 2(5x + 3x) × 2x = 288
⇒ 32x² = 288
⇒ x² = \(\frac{288}{32}\)
⇒ x² =9
⇒ x = \(\sqrt{9}\) = 3 m
∴ 15 × 3 = 15 m, b = 3 × 3 = 9 m and h = 2 × 3 = 6 m
Outer surface area of the cuboid = 2(lb + bh + hl)
= 2(15 × 9 + 9 × 6 + 6 × 15)
= 2(135 + 54 + 90)
= 2 × 279 = 558 m²
∵ 1 m² colour painted cost = Rs. 6
∴ 558 m² colour painted cost= Rs. (558 × 6)
= Rs. 3348
Hence,
total cost of painting = Rs. 3348.

Question 5.
The cost of papering of four walls of a room at Rs. 1.5 per square metre is Rs. 324. The height of the room is 4.5 m. If ratio of length and breadth of a room is 5 : 3, find them.
Solution:
We have,
height of a room 4.5 m
Ratio of length and breadth of a room = 5 : 3
Let the length and breadth of a room be 5x m and 3x m.
Area of four walls of a room = 2(l + b) × h
= 2(5x + 3x) × 4.5
= 2 × 8x × 4.5 = 72x ……(1)
Rate of papering of four walls of a room = 1.5 per m²
Total cost of papering = Rs. 324
Area of four walls of a room = \(\frac{\text { Total cost }}{1 \mathrm{~m}^2 \cos t}\)
Area of four walls of a room = \(\frac{324}{1.5}\)
Area of four walls of a room = 216 m² …….(2)
From (1) and (2), we get
72x = 216
⇒ x = \(\frac{216}{72}\)
⇒ x = 3 m
Length of a room= 5 × 3 = 15 m
Breadth of a room= 3 × 3 = 9 m
Hence, length and breadth of a room= 15m, 9 m.

Question 6.
A cylindrical metallic pipe is 20 cm long. The difference between the total surface area and inner surface area is 1232 cm². Find the radius of the pipe.
Solution:
We have,
Length of metallic pipe (h) = 20 cm
Let the radius of the metallic pipe be r cm.
Then,total surface area of metallic pipe
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × r(20 + r)
and lateral surface area = 2πrh
22 × \(\frac{22}{7}\) × r × 20
According to question,
Total surface area – Lateral surface area
= 1232

Since, radius of the pipe cannot be negative, therefore, we neglect r = – 14 cm.
∴ r = 14 cm

Question 7.
The total surface area of a hollow metallic cylinder open both ends of external radius 10 cm and height 14 cm is 576π cm². Taking r to be inner radius. find the thickness of the metal in the cylinder.
Solution:
We have,
External radius of the hollow metallic cylinder (R) = 10 cm
Height of the hollow metallic cylinder (h) = 14 cm
Let inner radius of the hollow metallic cylinder be r cm.
and total surface area of the hollow metallic cylinder open both ends
= 1408 cm²
⇒ 2πRh + 2πrh + 2π(R² – r²) = 576 π
⇒ 2πh(R + r) + 2π (R + r) (R – r) = 576 π
⇒ 2π(R + r) [h + R – r] = 576 π
⇒ (10 + r) (14 + 10 – r) = \(\frac{576 \pi}{2 \pi}\)
⇒ (10 + r) (24 – r) = 288
⇒ 240 – 10r + 24r – r² = 288
⇒ 240 + 14r – r² = 288
⇒ r² – 14r + 288 – 240 = 0
⇒ r² – 14r + 48 = 0
⇒ r² – (8 + 6)r + 48 = 0
⇒ r² – 8r – 6r + 48 = 0
⇒ r(r – 8) -6 (r – 8) = 0
⇒ (r – 8)(r – 6) = 0
⇒ r – 8 = 0 or r – 6 = 0
⇒ r = 8 or r = 6
When r = 8, then thickness of the metal in the cylinder = 10 – 8 = 2 cm.
When r = 6, then thickness of the metal in the cylinder = 10 – 6 = 4 cm.
Hence, thickness of the metal in the cylinder = 2 cm or 4 cm.

Question 8.
60 two rupees coins are placed one above the other to form a right circular cylinder. If each coin has radius 1.6 cm and thickness 0.3 cm, find its total surface area.

Solution:
We have,
Radius of each circular 2 rupees coin (r) = 1.6 cm
Number of 2 rupees coins = 60
and thickness of the 2 rupees coin= 0.3 cm
Since, two rupees coins are placed one above the other.
Therefore, radius of the new formed. cylinder (R) = radius of the 2 rupees coin
= 1.6 cm
and height of the new cylinder (h) = Thickness × no. of coins
= 0·3 × 60 = 18 cm
∴ Total surface area of the new cylinder
= 2πR(h + R)
= 2 × \(\frac{22}{7}\) × 1.6(18 + 1.6)
= \(\frac{70.4 \times 19.6}{7}\)
= 197.12 cm²
Hence, total suface area of the new cylinder 197.12 cm².

Question 9.
A rectangular box 40 cm long, 30 cm wide and 25 cm deep had the same total surface area as that of a cylindrical tin of radius 18 cm. Calculate the height of the cylindrical tin correct to 2 decimal places.
Solution:
We have,
Length, breadth and height of a rectangular box are 40 cm, 30 cm and 25 cm respectively.
Total surface area of the box = 2(lb + bh + hl)
= 2(40 × 30 + 30 × 25 + 25 × 40)
= 2(2950) = 5900 cm²
Now,radius of the cylindrical tin (r) = 18 cm
Let height of the cylindrical tin be h cm.
∴ Total surface area of cylindrical tin
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 18(h + 18)
= \(\frac{792}{7}\)(h + 18)
According to question
T.S.A. of rectangular box = T.S.A. of the cylindrical tin
⇒ 5900 = \(\frac{792}{7}\)(h + 18)
⇒ \(\frac{5900 \times 7}{792}\) = h + 18
⇒ 52.15 (approx.) = h + 18.
⇒ h = 52.15 – 18
⇒ h = 34.15 cm (approx.)
Hence, height of the cylindrical tin = 34.15 cm (approx.).

Question 10.
The circumference of the base of a 14 m high conical tent is 66 metres. Calculate the length of canvas used in making the tent if width of canvas is 2.5 m. [User π = \(\frac{22}{7}\)]
Solution:
We have,
Height of the conical tent (h) = 14 m
Circumference of base of the conical tent = 66 m
⇒ 2πr = 66
⇒ 2× \(\frac{22}{7}\) × r = 66
⇒ \(\frac{44}{7}\) × r = 66
⇒ r = \(\frac{66 \times 7}{44}\)
⇒ r = 10.5 m
⇒ \(\sqrt{h^2+r^2}\)
⇒ \(\sqrt{14^2+(10.5)^2}\)
⇒ \(\sqrt{196+110.25}\)
⇒ \(\sqrt{306.25}\)
⇒ l = ± 17.5 m
⇒ l = 17.5 m
Area of canvas used in making the tent = C.S.A. of the conical tent
= πrl
= \(\frac{22}{7}\) × 10.5 × 17.5
= 577.5 m²
Width of the canvas = 2.5 m, (given)
Length of the canvas = \(\frac{\text { C.S.A. of the canvas }}{\text { Width of the canvas }}=\frac{577.5}{2.5}\)
= 231 metres
Hence, required length of the canvas = 231 metres.

Question 11.
A tent of height 8.25 m is in the form of a right circular cylinder with radius of base 15 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of canvas of the tent at the rate of Rs. 40 per m².

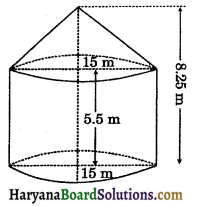
Solution:
We have, Total height of the tent = 8.25 m
Height of the cylindrical portion (h) = 5.5 m
∴ Height of the conical portion = 8.25 – 5.5
= 2.75 m
and radius of base of cylinder and base of cone (r) = 15 m
⇒ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{2.75^2+15^2}\)
⇒ l = \(\sqrt{7.5625+225}\)
⇒ l = \(\sqrt{232.5625}\)
⇒ l = 15.25 m
Required area of canvas of tent = C.S.A. of cylindrical portion + C.S.A. of conical portion
= 2πrh + πrl = πr(2h + l)
= \(\frac{22}{7}\) × 15(2 × 5.5 + 15.25)
= \(\frac{330}{7}\) × 26.25
= 1237.5 m²
∵ 1 m² canvas cost = Rs. 40
∴ 1237.5 m² canvas cost = Rs. 40 × 1237.5 = Rs. 49500
Hence,cost of canvas = Rs. 49500.

Question 12.
A cone and a hemisphere have equal bases and have equal total surface areas. Find the ratio of their heights.
Solution:
We have,
A cone and a hemisphere have equal bases
i.e., they have equal base radius.
∴ Let radius of a cone and a hemisphere be r.

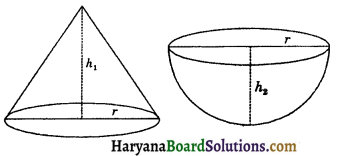
Let heights of a cone and hemisphere be h₁ and h₂ respectively, then
slant height of a cone (l₁) = \(\sqrt{h_1^2+r^2}\)
According to question,
Total surface area of a cone = Total surface area of a hemisphere
⇒ πrl + πr²= 3πr²
⇒ πr(l + r) = 3πг²

[∵ height of a hemisphere = radius of hemisphere]
⇒ h₁ : h₂ = \(\sqrt{3}\) : 1
Hence, required ratio of heights of cone and a hemisphere = \(\sqrt{3}\) : 1.

Question 13.
Curved surface area of a cone having base radius as 60 cm and height as 45 cm is same as the surface area of the sphere. Find the radius of the sphere.
Solution:
We have, Base radius of a cone (r₁) = 60 cm
Height of the cone (h) = 45 cm
Slant height of the cone (l) = \(\sqrt{h^2+r_1^2}\)
= \(\sqrt{45^2+60^2}\)
= \(\sqrt{2025+3600}\)
= \(\sqrt{5625}\) = 75 cm
Let radius of the sphere be r² cm.
According to question,
Curved surface area of a cone = Surface area of a sphere
⇒ πr₁l = 4πr₂²
⇒ π × 60 × 75 = 4 × π × r₂²
⇒ 60 × 75 = 4 × r₂²
⇒ \(\sqrt{2025+3600}\) = r₂²
⇒ 15 × 75 = r₂²
⇒ r² = \(\sqrt{15 \times 75}\)
⇒ r² = \(\sqrt{15 \times 15 \times 5}\)
⇒ r² = 15\(\sqrt{5}\) cm
Hence,radius of the sphere = 15\(\sqrt{5}\) cm.

Question 14.
A solid is the form of a right circular cylinder with hemispherical ends whose total length is 2.7 mand diameter of each hemispherical end is 0.7m. Find the total surface area of the solid.

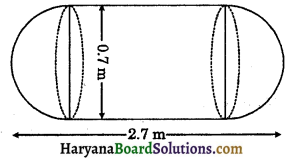
Solution:
We have,
Radius of each end of hemispherical end (r) = \(\frac{0.7}{2}\) = 0.35 m
Total length of the solid = 2.7 m
∴ Length of the cylinder (h) = 2.7 – 2 × 0.35
= 2.7 – 0.7 = 2.0 m
Total surface area of the solid = Curved surface area of the cylindrical portion + 2 × curved surface area of hemispherical end
= 2πrh + 2 × 2πr²
= 2πr(h + 2r)
= 2 × \(\frac{22}{7}\) × 0.35(2 + 2 × 0.35)
= 2.2 × 2.7 = 5.94 m²
Hence, total surface area of the solid = 5.94 m².

Question 15.
The edges of three metallic cubes are in the ratio of 3 : 4 : 5. These cubes are melted and recast into a single cube whose diagonal is 12\(\sqrt{3}\) cm. Find the edges of three cubes.
Solution:
We have,
Ratio of the edges of three metallic cubes = 3 : 4 : 5
Let the edges of three metallic cubes be 3x cm, 4x cm and 5x cm.
Sum of the volumes of three cubes = (3x)³ + (4x)³ + (5x)³ = 27x³ + 64x³ + 125x³
= (27 + 64 + 125)x³
= 216x³
Let the edge of single new cube be a cm.
Diagonal of a single new cube= 12\(\sqrt{3}\) cm (given)
a\(\sqrt{3}\) = 12\(\sqrt{3}\)
a = \(\frac{12 \sqrt{3}}{\sqrt{3}}\)
a = 12 cm
Volume of a single new case = a³
= (12)³ = 1728 cm³
Since, three cubes are melted and recast into a single cube.
∴ Sum of the volumes of three cubes = Volume of a single new cube
⇒ 216x³ = 1728
⇒ x³ = \(\frac{1728}{216}\)
⇒ x³ = 8
⇒ x = \(\sqrt{3}{8}\) = 2 cm
∴ Edges of three metallic cubes are 3 × 2 cm, 4 × 2 cm and 5 × 2 cm
= 6 cm, 8 cm and 10 cm
Hence, edges of the three metallic cubes = 6 cm, 8 cm and 10 cm.

Question 16.
A solid cube is cut into three cuboids of equal volumes. Find the ratio of the total surface area of cube to one of the cuboid.
Solution:
Let the edge of the solid cube be a units.
Since, cube is cut into three cuboids of equal volumes.
Dimensions of each of the cuboid are length = a units, breadth = a units
and height = \(\frac{a}{3}\) units
Total surface area of the cube = 6a²
and total surface area of the one cuboid.

Hence, ratio of the total surface area of cube to one of the cuboid = 9 : 5.

Question 17.
A cone of radius 8 cm is filled with water. If the water is poured into a cylinder of radius 12 cm, the height of the water rises 1.8 cm, find the height of the cone.
Solution:
We have,
Radius of a cone (r) = 8 cm
Radius of a cylinder (R) = 12 cm
Water level in the cylinder (H) = 1.8 cm
Let the height of the cone be h cm.

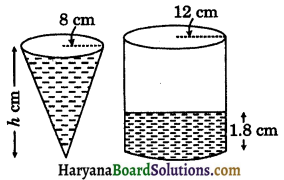
Since, water of cone poured into a cylinder.
∴ Volume of water in cone = Volume of water in cylinder upto height 1.8 cm

Hence,height of the cone = 12.15 cm.

Question 18.
Find the number of coins having 2.8 cm as diameter and 0.25 cm as thickness, to be melted to form a right circular cylinder of height 10 cm and diameter 5.6 cm.
Solution:
We have, Diameter of a coin (d) = 2.8 cm
∴ Radius of a coin (r) = \(\frac{2.8}{2}\) = 1.4 cm
Thickness of a coin (h) = 0.25 cm
Let the number of coins be x.
Volume of 1 coin = πr²h
\(\frac{22}{7}\) × 1.4 × 1.4 × 0.25
Volume of x coins = x × \(\frac{22}{7}\) × 1.4 × 1.4 × 0.25
Diameter of recast cylinder (D) = 5.6 cm, (given)
∴ Radius of recast cylinder (R) = \(\frac{5.6}{2}\)
= 2.8 cm.
And height of recast cylinder (H) = 10 cm, (given)
∴ Volume of recast cylinder = πR²H
= \(\frac{22}{7}\) × 2.8 × 2.8 × 10
Since x coins melted and recast a cylinder.
∴ Volume of x coins = Volume of recast cylinder
⇒ x × \(\frac{22}{7}\) × 1.4 × 1.4 × 0.25 = \(\frac{22}{7}\) × 2.8 × 2.8 × 10
⇒ x × 1.4 × 1.4 × 0.25 = 2.8 × 2.8 × 10
⇒ x = \(\frac{2.8 \times 2.8 \times 10}{1.4 \times 1.4 \times 0.25}\)
⇒ x = 160
Hence, number of coins = 160.

Question 19.
Water is being pumped out through a circular pipe whose internal diameter is 7 cm. If the speed of water is 72 cm per sec. how many litres of water are being pumped out in 2 hours?
Solution:
We have,
Diameter of circular pipe (d) = 7 cm
∴ Radius of circular pipe (r) = \(\frac{7}{2}\) = 3.5 cm
= 0.035 m3
Speed of water flow through a pipe = 72 cm/sec
= \(\frac{\frac{72}{100}}{\frac{1}{60 \times 60}}\) m/hr
= \(\frac{72}{100}\) × 60 × 60 m/hr
= 2592 m/hr
∴ In 2 hrs. length of water that flows through a pipe (h) = 2592 × 2 m = 5184 m
Volume of water in 2 hrs. that flows through a pipe = πr²h
\(\frac{22}{7}\) × (0.035)² × 5184
= 19.9584 m³
= 19958.4 litres
Hence, volume of water in 2 hrs. that flows through a pipe = 19958.4 litres.

Question 20.
Cost of painting the total surface area of a cylinder at the rate of Rs. 5 per m² is Rs. 1540. The height of the cylinder is 3 times its radius of the base. Find the volume of the cylinder.
Solution:
Let the radius of the base of a cylinder be x m, then
Height of the cylinder = 3x m
Rate of painting= Rs. 5 per m², (given)
Total cost of painting = Rs. 1540, (given)

So, radius of cylinder = 3.5 m and height of the cylinder = 3 × 3.5 = 10.5 m
∴ Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × (3.5)² × 10.5
= 404.25 m³
Hence,volume of the cylinder = 404.25 m³.

Long Answer Type Questions

Question 1.
Ratio of length and breadth of a room is 4 : 3. The cost of papering the walls at Rs. 1.5 per m² is Rs. 265.5 and cost of carpeting the floor of a room is at Rs. 140 per m² is Rs. 15120. If 1 door and 2 windows occupy 12 m², then find the dimensions of the room.
Solution:
We have,
Ratio of length : breadth = 4 : 3
Let length and breadth of a room be 4x m and 3x m respectively.
Rate of carpeting the floor = Rs. 140 per m²
Total cost of carpeting the floor = Rs. 15120
Floor area of the room = \(\frac{\text { Total cost }}{1 \mathrm{~m}^2 \cos t}\)
\(\frac{15120}{140}\) = 108 m² …(i)
Again,floor area of the room = 4x × 3x
⇒ Floor area of the room = 12x² …(ii)
From (i) and (ii), we get
⇒ 12x² = 108
⇒ x² = \(\frac{108}{12}\)
⇒ x² = 9
⇒ x = \(\sqrt{9}\) = ±3
So, length of room = 4 × 3 = 12 m and
breadth of the room = 3 × 3 = 9 m.
Let the height of the room be h m.
Area of four walls of a room = 2(l + b) × h
= 2(12 + 9) × h
= 2 × 21 × h = 42h m².
Area of four walls of a room excluding 1 door and 2 windows = (42h – 12) m² …(iii)
Rate of the papering the walls = Rs. 1.5 per m²
Total cost of the papering of the walls = Rs. 265.5
Area of four walls of a room excluding 1 door 2 windows
\(\frac{\text { Total cost }}{1 m^2 \cos t}=\frac{265.5}{1.5}\)
= 177 m² ……(iv)
From (iii) and (iv), we get
42h – 12 = 177
⇒ 42h = 177 + 12
⇒ 42h = 189
⇒ h = \(\frac{189}{42}\)
h = 4.5 m
Hence, dimensions of a room are 12 m × 9 m × 4.5 m.

Question 2.
A solid cylinder has total surface area of 180π. Its curved surface area is \(\frac{3}{5}\) of its total surface area. Find the radius and height of the cylinder.
Solution:
We have,
Total surface area of a cylinder = 180π
2πrh + 2πr² = 180π ……(i)
According to question,
Curved surface area of a cylinder = \(\frac{3}{5}\) of its total surface area
⇒ 2πrh = \(\frac{3}{5}\) of 180π
⇒ 2πrh = 108π ……(ii)
Subtracting (ii) from (i), we get
Total surface area – curved surface area
= 180π – 108π
⇒ 2πrh + 2πr² – 2πrh = 72π
⇒ 2πr² = 72π
⇒ r² = \(\frac{72 \pi}{2 \pi}\)
⇒ r² = 36
⇒ r = \(\sqrt{36}\)
⇒ r = ±6 cm
Since, radius of the cylinder cannot be negative.
Therefore, we neglect r = -6 cm
∴ r = 6 cm
Putting the value of r in (ii), we get
2π × 6 × h = 108π
⇒ 12πh = 108π
⇒ h = \(\frac{108 \pi}{12 \pi}\)
⇒ h = 9 cm
Hence, radius and height of a cylinder are 6 cm and 9 cm respectively.

Question 3.
A conical tent has the area of its base as 154 m and that of its curved surface area Rs 550 m². Find the height of the tent.
Solution:
We have,
Base area of a conical tent = 154 m²
⇒ πr² = 154
⇒ r² = \(\frac{154}{\pi}\)
⇒ r² = \(\frac{154 \times 7}{22}\)
⇒ r² = 7 × 7
⇒ r = \(\sqrt{7 \times 7}\) = 7 m
and curved surface area of a conical tent = 550 m²
⇒ πrl = 550
⇒ \(\frac{22}{7}\) × 7 × l = 550
⇒ 22 × l = 550
⇒ l = \(\frac{550}{22}\)
⇒ l = 25 m
Now l² = h² + r²
⇒ h² = l² – r²
⇒ h² = (25)² – (7)²
⇒ h² = (25 + 7) (25 – 7)
⇒ h² = 32 × 18
⇒ h = \(\sqrt{32 \times 18}\)
⇒ h = \(\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3}\)
⇒ h = 2 × 2 × 2 × 3
⇒ h = 24 m
Hence height of the tent = 24 metres.

Question 4.
A semicircular thin sheet of metal of diameter 28 cm is bent and an open conical cup is made. Find the height and surface area of the cup.
Solution:
We have, Diameter of the semicircular sheet (d) = 28 cm
∴ Radius of the semicircular sheet (r) = \(\frac{28}{2}\)
= 14 cm
Perimeter of the semicircular sheet = πr
= π × 14 = 14π
Let r₁ be the base radius, h be the height of conical cup.
Circumference of the circular top of the conical cup = Perimeter of the semicircular sheet
2πr₁ = 14π
r₁ = \(\frac{14 \pi}{2 \pi}\)
r₁ = 7 cm

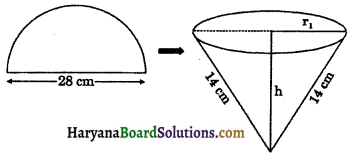
and slant height of the conical cup (l) = 14 cm
l² = h² + r₁²
⇒ h² = l² – r₁²,
⇒ h² = 14² – 7²
⇒ h² = (14 + 7)(14 – 7)
⇒ h² = 21 × 7
⇒ h = \(\sqrt{21 \times 7}\)
⇒ h = \(\sqrt{3 \times 7 \times 7}\)
⇒ h = 7\(\sqrt{3}\) cm
Curved surface area of the conical cup
= πr₁l
= \(\frac{22}{7}\) × 7 × 14
= 308 cm²
Hence, height of the conical cup is 7\(\sqrt{3}\) cm and curved surface area of the conical cup is 308 cm².

Question 5.
A right triangle whose sides are 12 cm and 16 cm is made to revolve about its hypotenuse. Find the surface area of the double cone so formed.
Solution:
Let ABC be right triangle, right angled at A whose sides AB and AC measure 12 cm and 16 cm respectively, then
Hypotenuse (BC) length = \(\sqrt{12^2+16^2}\)
= \(\sqrt{144+256}\)
= \(\sqrt{400}\) = 20 cm

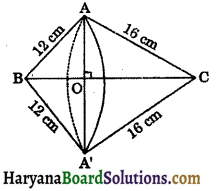
By revolving ΔABC around its hypotenuse BC, the double cone solid is generated. This solid consists of two cones (BAA’) and (CAA’).
AO or A’O is the radius of the common base of the double cone.
Let BO = x and AO = y, then
OC = 20 – x
OC and OB are the heights of the double cones (CAA’) and (BAA’) respectively.
In right ΔAOB, we have
AB² = AO² + OB²
(By Pythagoras theorem)
⇒ 12² = y² + x²
⇒ x² + y² = 144 … (1)
In right ΔAOC, we have
AC² = AO² + OC²
⇒ 16² = y² + (20 – x)²
⇒ 256 = y² + 400 + x² – 40x
⇒ 256 = 144 + 400 – 40x [using (1)]
⇒ 256 = 544 – 40x
⇒ 40x = 544 – 256
⇒ 40x = 288 ⇒ x = \(\frac{288}{40}\) = 7.2 cm
Putting the value of x in (1), we get
(7.2)² + y² = 144
⇒ 51.84 + y² = 144
⇒ y² = 144 – 51.84
⇒ y² = 92.16
⇒ y = \(\sqrt{92.16}\) = 9.6 cm
Thus radius of double cone so formed is 9.6 cm and slant heights of cone (CAA’) is 16 cm and cone (BAA’) is 12 cm.
Surface area of double cone is generated = C.S.A. of the cone (CAA’) + C.S.A. of the cone (BAA’)
= π × AO × AC + π × AO × AB
= π[9.6 × 16 + 9.6 × 12]
= π[153.6 + 115.2]
= \(\frac{22}{7}\) × 268.8 = 844.8 cm²
Hence, surface area of double cone so formed = 844.8 cm².

Question 6.
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 7 cm and heights of the cylindrical and conical portions are 12 cm and 8.4 cm respectively. Find the total surface area of the solid toy.
Solution:
We have,
Common diameter of the cylinder, a hemisphere and a cone (d) = \(\frac{7}{2}\) 7 cm
∴ Common radius of the cylinder, a hemisphere and a cone (r) = 3.5 cm
Height of the cylinder (H) = 12 cm
and height of the cone (h) = 8.4 cm

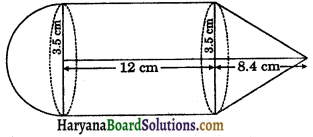
∴ Slant height of the cone (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(8.4)^2+(3.5)^2}\)
= \(\sqrt{70.56+12.25}\)
= \(\sqrt{82.81}\)
= 9.1 cm
Total surface area of the solid toy = C.S.A. of the hemispherical portion + C.S.A. of the cylindrical portion + C.S.A. of the conical portion
= 2πr² + 2πrH + πrl = πr(2r + 2H + l)
= \(\frac{22}{7}\) × 3.5(2 × 3.5 + 2 × 12 + 9.1)
= 11 × (7 + 24 + 9.1) = 11 × 40.1
= 441.1 cm²
Hence, total surface area of the solid toy = 441.1 cm².

Question 7.
Rain water which falls on a flat rectangular surface of length 6 m and breadth, 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if the rain fall is 1 cm? Give your answer to the nearest integer. (use π = 3.14)
Solution:
We have Length of rectangular surface (l) = 6 m = 600 cm
Breadth of rectangular surface (b) = 4 m = 400 cm
Height of rain fall on rectangular surface (h) = 1 cm
∴ Volume of water of rain fall = l × b × h
= 600 × 400 × 1
and internal radius of cylindrical vessel (r) = 20 cm
Let the height of water in the cylindrical vessel be h’ cm.
Volume of water in the cylindrical vessel
= πr²h’
= 3.14 × 20² × h’
According to question,
Rain water which falls on a flat rectangular surface is transferred into a cylindrical vessel.
Therefore,volume of water of rain fall = volume of water in the cylindrical vessel
⇒ 600 × 400 × 1 = 3.14 × 20² × h’
⇒ \(\frac{600 \times 400}{3 \cdot 14 \times 20^2}\) = h’
⇒ \(\frac{600 \times 400}{3.14 \times 400}\) = h’
⇒ h’ = \(\frac{600}{3.14}\)
⇒ h’ = 191.082 cm = 191 cm
Hence, height of water in the cylindrical vessel = 191 cm.

Question 8.
A cylindrical water tank of diameter 3.0 m and height 2.4 m is being fed by a pipe of diameter 4.8 cm through which water flows at the rate of 5 m/sec. Calculate the time taken by pipe to fill the tank.
Solution:
We have,
Diameter of the cylindrical tank (D) = 3 m
∴ Radius of the cylindrical tank (R) = \(\frac{3}{2}\) = 1.5 m = 150 cm
Height of the cylindrical tank (H) = 2.4 m = 240 cm
Diameter of the pipe (d) = 4.8 cm
∴ Radius of the pipe (r) = \(\frac{4.8}{2}\) = 2.4 cm

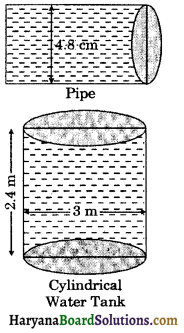
Speed of the water that flows through the pipe = 5 m/sec
Length of water that flows through the pipe in 1 sec (h) = 5 m = 500 cm
Volume of water that flows in 1 second
= πr²h = \(\frac{22}{7}\) × (2.4)² × 500
Let the time taken by pipe to fill the tank be x seconds.
Volume of water that flows in x seconds
= x × \(\frac{22}{7}\) × (2.4)² × 500
Volume of the water of cylindrical water tank = πR²H
= π × (150)² × 240
= \(\frac{22}{7}\) × 150 × 150 × 240
Since, cylindrical water tank is being fed by a pipe.
∴ Volume of water that flows in x seconds = Volume of the water of cylindrical water tank
⇒ x × \(\frac{22}{7}\) × (2.4)2 × 500
= \(\frac{22}{7}\) × 150 × 150 × 240
⇒ x × 2.4 × 2.4 × 500 = 150 × 150 × 240
⇒ x × 2880 = 5400000
⇒ x = \(\frac{5400000}{2880}\)
⇒ x = 1875 seconds
⇒ x = 31 minutes 15 seconds
Hence,time taken by the pipe = 31 min 15 sec.

Question 9.
The diameter of the cylinder is increased by 25%, then how many percent its height must be decreased so that its volume may remain same.
Solution:
Let the diameter of the cylinder be 2x and its height be h
Radius of the cyļinder = \(\frac{2 x}{2}\) = x
∴ Volume of the cylinder = πx²h
Since, diameter is increased by 25%. Then Increased diameter = 2x + 25% of 2x
= 2x + \(\frac{25}{100}\) × 2x
= 2x + \(\frac{x}{2}=\frac{5 x}{2}\)
New radius = \(\frac{5 x}{4}\)
Let new height be h’.

Hence,decrease % in height = 36%.

Question 10.
A solid metal sphere, 6 cm in diameter, is formed into a cylindrical tube 10 cm in external diameter and 4 cm in length. Find the thickness of the tube.
Solution:
We have,
Diameter of solid sphere = 6 cm
∴ Radius of solid sphere (r) = \(\frac{6}{2}\) = 3 cm
Length of cylindrical tube (h) = 4 cm
External diameter of the cylindrical tube = 10 cm
∴ External radius of the cylindrical tube (r₁) = \(\frac{10}{2}\) = 5 cm
Let the internal radius of cylindrical tube be r₂ cm.
Since, cylindrical tube formed from metal sphere.
∴ Volume of metal of cylindrical tube = Volume of metal sphere
⇒ π[r₁² – r₂²] × h = \(\frac{4}{3}\)πr³
⇒ π[5² – r₂²] × 4 = \(\frac{4}{3}\)π × (3)³
⇒ (25 – r₂²) × 4 = \(\frac{4}{3}\) × 3 × 3 × 3
⇒ 25 – r₂² = 3 × 3
⇒ r₂² = 25 – 9
⇒ r₂² = 16
⇒ r₂² = 4²
⇒ r₂ = 4 cm
∴ Thickness of the tube = r₁ – r₂
= 5 – 4 = 1 cm
Hence, thickness of the tube = 1 cm.

Question 11.
A cylindrical container is filled with ice cream whose diameter is 12 cm and height 15 cm. Whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is four times the radius of its base, find the height of the ice-cone.
Solution:
We have,
Diameter of cylindrical container = 12 cm
∴ Radius of cylindrical container (R) = \(\frac{12}{2}\) = 6 cm
Height of the cylindrical container (H) = 15 cm
∴ Volume of ice-cream in cylindrical container = πR²H
= π × 6² × 15 = 540π cm3

Let radius of base of cone ice-cream be x cm, then height of the conical portion = 4x cm
∴ Volume of 1 ice-cream cone = Volume of conical portion + Volume of hemispherical portion
= \(\frac{1}{3}\)πx² × 4x + \(\frac{2}{3}\)πx³
= \(\frac{1}{3}\)π[4x³ + 2x³]
= \(\frac{1}{3}\)π × 6x³ = 2πx³
Volume of 10 ice-cream cones = 10 × 2πx³ = 20πx³ cm³
Since, ice-cream of cylindrical container is distributed to 10 children in equal ice-cream cones.
∴ Volume of 10 ice-cream cones = Volume of ice cream in cylindrical container
⇒ 20πx³ = 540π
⇒ x³ = \(\frac{540 \pi}{20 \pi}\)
⇒ x³ = 27
⇒ x³ = 33
⇒ x = 3 cm
∴ Radius of ice-cream cone = 3 cm
and height of the conical portion = 4 × 3 = 12 cm
∴ Height of the ice-cream cone = 12 + 3 = 15 cm
Hence, height of the ice-cream cone = 15 cm.

Question 12.
The radius of a right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Solution:
Let the radius of cylinder be r and its height be h, then
Volume of cylinder (V₁) = πr²h
After increasing radius by 20%.
New radius = r + 20% of r
= r + \(\frac{20}{100}\) × r
= r + \(\frac{r}{5}=\frac{6 r}{5}\)
After decreasing height by 20%.

Hence, volume of cylinder increases by 15.2%.

Question 13.
The total surface area of a hollow metal cylinder, open both tops, is 3168 cm². Length of cylinder is 21 cm and volume of metal used in making the cylinder is 4158 cm³. Find the thickness of the metal.

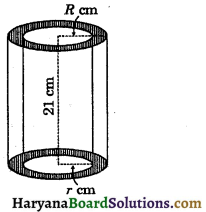
Solution:
Let the external radius of hollow cylinder be R cm and internal radius of hollow cylinder be r сm.
We have,
Length of hollow cylinder (h) = 21 cm
Volume of metal used in making the hollow cylinder = 4158 cm³
⇒ π(R² – r²) × h = 4158
⇒ π(R + r) (R – r) × 21 = 4158
⇒ π(R + r) (R – r) = \(\frac{4158}{21}\) = 198 …(1)
and total surface area = 3168 cm²
⇒ 2πRh + 2πrh + 2π(R² – r²) = 3168
⇒ 2πh(R + r) + 2π(R + r) (R – r) = 3168
⇒ 2π(R + r) [h + R – r] = 3168
⇒ π(R + r) [21 + R – r] = \(\frac{3168}{2}\) = 1584 ……(2)
Dividing (1) by (2), we get
\(\frac{\pi(R+r)(R-r)}{\pi(R+r)[21+R-r]}=\frac{198}{1584}\)
⇒ \(\frac{R-r}{21+R-r}=\frac{1}{8}\)
⇒ 8R – 8r = 21 +R – r
⇒ 7R – 7r = 21
⇒ 7(R – r) = 21
⇒ R – r = \(\frac{21}{7}\) = 3 ……(3)
Putting this value in (1), we get
⇒ π(R + r) × 3 = 198
⇒ \(\frac{22}{7}\) × 3(R + r) = 198
⇒ \(\frac{66}{7}\)(R + r) = 198
⇒ R + r = \(\frac{198 \times 7}{66}\)
⇒ R + r = 21 …….(4)
On adding (3) and (4), we get
R – r = 3
R + r = 21
2R = 24
⇒ R = \(\frac{24}{2}\) = 12 cm
Putting the value of R in (4), we get
12 + r = 21
⇒ r = 21 – 12 = 9 cm
Thickness of the metal
= R – r = 12 – 9 = 3 cm
Hence, thickness of the metal = 3 cm.

Question 14.
6 Tennis balls, diameter 70 mm each are placed in cylindrical card tube. Prove that volume of unfilled space in the tube is 33.33% of volume of the tube.

Solution:
We have,
Diameter of each tennis ball = 70 mm
∴ Radius of each tennis ball (r) = \(\frac{70}{2}\) = 35cm
Volume of 1 tennis balls = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(35)^3\)
= \(\frac{539000}{3} \mathrm{~mm}^3=\frac{539}{3} \mathrm{~cm}^3\)
Volume of 6 tennis ball = \(\frac{539}{3}\) × 6
= 1078 cm³
Radius of the cylindrical card tube (r) = 35 mm = 3.5 cm
Height of the cylindrical card tube
(h) = 6 × diameter of 1 tennis ball
= 6 × 70 = 420 mm
= 42 cm
∴ Volume of the cylindrical card tube
= πr²h = \(\frac{22}{7}\) × (3.5)² × 42
= 1617 cm³
Volume of unfilled space in the tube = Volume of the cylindrical card tube – Volume of 6 tennis balls
= 1617 – 1078
= 539 cm³
Volume of unfilled space % in the tube
= \(\frac{539}{1617}\) × 100%
= \(\frac{100}{3}\)% = 33.33%
Hence, volume of unfilled space is 33.33% of tube.
Hence proved.

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
The length, breadth and height of cuboid are 12 cm, 10 cm and 7 cm. Its total surface area is :
(a) 274 cm²
(b) 548 cm²
(c) 840 cm²
(d) 308 cm²
Answer:
(b) 548 cm²

Question 2.
The total surface area of a cube is 150 cm, then its volume is :
(a) 125 cm³
(b) 120 cm³
(c) 110 cm³
(d) 100 cm³
Answer:
(a) 125 cm³

Question 3.
If total surface area of a cube is equal to its volume. Edge of cube is :
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
Answer:
(b) 6 cm

Question 4.
Length of the longest pole that can be put in a room of demensions (10 m × 10 m × 5 m) is :
(a) 15 m
(b) 16 m
(c) 10 m
(d) 12 m
Answer:
(a) 15 m

Question 5.
The maximum length of pencil that can be placed in a rectangular box of dimensions (6 cm × 4 cm × 2\(\sqrt{3}\) cm) is :
(a) 8 cm
(b) 6\(\sqrt{3}\) cm
(c) 5\(\sqrt{3}\) cm
(d) 4\(\sqrt{3}\) cm
Answer:
(a) 8 cm

Question 6.
A 4 cm cube cut into 1 cm cubes. The total surface area of all the small cubes is :
(a) 96 cm²
(b) 64 cm²
(c) 24 cm²
(d) 384 cm²
Answer:
(d) 384 cm²

Question 7.
Two cubes each with 5 cm edge are joined end to end. The volume of resulting cuboid is :
(a) 125 cm³
(b) 150 cm³
(c) 250 cm³
(d) 300 cm³
Answer:
(c) 250 cm³

Question 8.
If three cubes of metal whose edges are 9 cm, 12 cm and 15 cm made into a single cube, then edge of the new cube so formed is :
(a) 15 cm
(b) 16 cm
(c) 18 cm
(d) 21 cm
Answer:
(c) 18 cm

Question 9.
The perimeter of one face of a cube is 32 cm. The lateral surface area of cube is :
(a) 256 cm²
(b) 384 cm²
(c) 216 cm²
(d) 300 cm²
Answer:
(a) 256 cm²

Question 10.
The length of a diagonal of a cube is 6\(\sqrt{3}\) cm. Surface area of the cube is :
(a) 648 cm²
(b) 432 cm²
(c) 216 cm²
(d) 144 cm²
Answer:
(c) 216 cm²