HBSE 9th Class Maths Important Questions Chapter 2 Polynomials

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 2 Polynomials Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 2 Polynomials

Very Short Answer Type Questions

Question 1.
Write the coefficients of x³ in each of the following :
(i) 4x³ – 3x + 9
(i) 14 – 5x³ + 7x + 2x²
(iii) \(\frac {3}{4}\)x³ + 7x – 9
(iv) 5x² + \(\sqrt{3}\)x + 1
(v) \(\sqrt{5}\)x³ + x² + 7
(vi) x – x³
Solution :
(i) The coefficient of x³ in 4x³ – 3x + 9 is 4.
(ii) The coefficient of x³ in 14 – 5x³ + 7x + 2x² is – 5.
(iii) The coefficient of x³ in \(\frac {3}{4}\)x³ + 7x – 9 is \(\frac {3}{4}\).
(iv) The coefficient of x³ in 5x² + \(\sqrt{3}\)x + 1 is 0.
(v) The coefficient of x³ in \(\sqrt{5}\)x³ + x² + 7 is
(vi) The coefficient of x3 in 1 – 13 is – 1.

Question 2.
Write a monomial of degree 30, a binomial of degree 50 and a trinomial of degree 60.
Solution:
Monomial of degree 30 = x³⁰
Binomial of degree 50 = 3x⁵⁰ + 5
Trinomial of degree 60 = 5x⁶⁰ + x + 7.

Question 3.
Classify the following as linear, quadratic, cubic and biquadratic polynomials:
(i) 3x² + 4x + 7
(ii) x² – x³
(iii) 1 + t
(iv) 5x⁴ + 2x³ + x + 5
(v) y³ + 3y² – 5
(vi) y² + 7y
(vii) t²
Solution:
(i) Degree of the given polynomial is 2. So it is the quadratic polynomial.
(ii) Degree of the given polynomial is 3. So, it is the cubic polynomial.
(iii) Degree of the given polynomial is 1. So, it is a linear polynomial.
(iv) Degree of the given polynomial is 4. So, it is a biquadratic polynomial.
(v) Degree of the given polynomial is 3. So, it is a cubic polynomial.
(vi) Degree of the given polynomial is 2. So, it is a quadratic polynomial.
(vii) Degree of the given polynomial is 2. So, it is a quadratic polynomial.

Question 4.
Find the values of the polynomial x³ – 2x² + 3x + 5 at:
(i) x = 0
(ii) x = 1
(iii) x = – 2.
Solution:
Let p(x) = x³ – 2x² + 3x + 5
(i) At x = 0, the value of the polynomial p(x) is given by
p(0) = (0)³ – 2 × (0)² + 3 × 0 + 5
= 0 – 0 + 0 + 5 = 5
Hence, p(0) = 5.

(ii) At x = 1, the value of the polynomial p(x) is given by
p(1) = (1)³ – 2 × (1)² + 3 × 1 + 5
= 1 – 2 + 3 + 5 = 7
Hence, p(1) = 7.

(iii) At x = – 2, the value of the polynomial p(x) is given by
p(-2) = (-2)³ – 2 × (-2)² + 3 × (-2) + 5
= – 8 – 8 – 6 + 5
= – 22 + 5 = – 17
Hence, p(-2) = – 17.

Question 5.
Find the remainder when x⁴ – x³ – 2x² + 4x – 10 is divided by x + 2.
Solution :
Let
p(x) = x⁴ – x³ – 2x² + 4x – 10
We know that when p(x) is divided by (x + 2), the remainder is p(-2).
(By Remainder Theorem)
So, p(-2) = (-2)⁴ – (-2)³ – 2 × (2)² + 4 × (-2) – 10
= 16 + 8 – 8 – 8 – 10
= 16 – 18 = – 2
Hence, the required remainder = – 2.

Question 6.
Find the remainder when x³ – 2x² – 11x + 15 is divided by x + 3.
Solution:
Let
p(x) = x³ – 2x² – 11x + 15
We know that when p(x) is divided by (x + 3) the remainder is p(-3).
[By Remainder Theorem]
So, p(-3) = (-3)³ – 2 × (- 3)² – 11 × (-3) + 15
= – 27 – 18 + 33 + 15
= 48 – 45 = 3.
Hence, the required remainder = 3.

Question 7.
Determine the value of k, such that (x + 3) is a factor of the polynomial f(x) = 2x³ + 11x² + kx + 6.
Solution :
We have,
f(x) = 2x³ + 11x² + kx + 6
If (x + 3) is a factor of f(x), then by factor theorem, the remainder f(-3) should be zero.
⇒ f(-3) = 0
⇒ 2x(-3)³ + 11 × (-3)² + k × (-3) + 6 = 0
⇒ – 54 + 99 – 3k + 6= 0
⇒ – 3k + 105 – 54 = 0
⇒ – 3k + 51 = 0
⇒ -3k = – 51
⇒ k = \(\frac {-51}{-3}\) = 17
Hence, k = 17.

Question 8.
Find the value of a, if x – a is a factor of x³ – ax² + 2x + a – 1. [NCEAT Exemplar Problems]
Solution :
Let p(x) = x³ – ax² + 2x + a – 1
If (x – a) is a factor of p(x), then by factor theorem, the remainder p(a) should be zero.
⇒ p(a) = 0
⇒ (a)³ – a × (a)² + 2 × a + a – 1 = 0
⇒ a³ – a³ + 2a + a – 1 = 0
⇒ 3a – 1 = 0
⇒ 3a = 1
⇒ a = \(\frac {1}{3}\)

Question 9.
If (x – 2) is a factor of the polyomial x⁵ – 3x⁴ – kx³ + 3kx² + 2kx + 4, find the value of k.
Solution :
Let p(x) = x⁵ – 3x⁴ – kx³ + 3kx² + 2kx + 4
If (x – 2) is a factor of p(x), then by factor theorem, the remainder p(2) should be zero
⇒ p(2) = 0
⇒ (2)⁵ – 3 × (2)⁴ – k × (2)³ + 3k × (2)² + 2k × 2 + 4 = 0
⇒ 32 – 48 – 8k + 12k + 4k + 4 = 0
⇒ 36 – 48 – 8k + 16k = 0
⇒ – 12 + 8k = 0
⇒ 8k = 12
⇒ k = \(\frac{12}{8}=\frac{3}{2}\)
Hence, k = \(\frac {3}{2}\)

Question 10.
Find the value of x³ + y³ – 12xy + 64, when x + y = – 4. [NCERT Exemplar Problems]
Solution :
We have,
x + y = – 4
⇒ x + y + 4 = 0
We know that, if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Here,
x + y + 4 = 0
⇒ x³ + y³ + (4)³ = 3 × x × y × 4
⇒ x³ + y³ + 64 = 12xy
⇒ x³ + y³ – 12xy + 64 = 0.
Hence, x³ + y³ – 12xy + 64 = 0.

Question 11.
Find the value of x³ – 8y³ – 36xy – 216, when x = 2y + 6. [NCERT Exemplar Problems] Solution:
We have x = 2y + 6
⇒ x – 2y – 6 = 0
We known that, it x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Here x – 2y – 6 = 0
x³ + (-2y)³ + (-6)³ = 3 × x × (-2y) × (-6)
x³ – 8y³ – 216 = 36xy
x³ – 8y³ – 36xy – 216 = 0
Hence, x³ – 8y³ – 36xy – 216 = 0.

Question 12.
If ab + bc + ca = 25 and a + b + c = 9, find a² + b² + c².
Solution :
We have, a + b + c = 9
⇒ (a + b + c)² = (9)²
⇒ a² + b² + c² + 2ab + 2bc + 2ca = 81
⇒ a² + b² + c² + 2(ab + bc + ca) = 81
⇒ a² + b² + c² + 2 × 26 = 81 [∵ ab + bc + ca = 26]
⇒ a² + b² + c² + 52 = 81
⇒ a² + b² + c² = 81 – 52
⇒ a² + b² + c² = 29.
Hence, a² + b² + c² = 29.

Question 13.
If a² + b² + c = 64 and ab + bc + ca = 18, find a + b + c.
Solution :
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
⇒ (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
⇒ (a + b + c)² = 64 + 2 × 18 [∵ a² + b² + c² = 64 and ab + bc + ca = 18]
⇒ (a + b + c)² = 64 + 36 = 100
⇒ (a + b + c)² = (10)²
⇒ a + b + c = 10
Hence, a + b + c = 10.

Question 14.
If x – y = 5 and xy = 7, find the value of x³ – y³
Solution :
We have, xy = 7
and x – y = 5
⇒ (x – y)³ = (5)³
(Cubing on both sides)
⇒ x³ – y³ – 3xy(x – y) = 125 [Using the identity,
(x – y)³ = x³ – y³ – 3xy(x – y)]
⇒ x³ – y³ – 3 × 7(5) = 125 [∵ xy = 7, x – y = 5]
⇒ x³ – y³ – 105 = 125
⇒ x³ – y³ = 125 + 105
⇒ x³ – y³ = 230.
Hence, x³ – y³ = 230.

Question 15.
Factorise the following quadratic polynomials by splitting the middle term :
(i) x² – 18x + 77
(ii) x² – 25x + 144
Solution :
(i) x² – 18x + 77 = x² – (11 + 7)x + 77
= x² – 11x – 7x + 77
= (x² – 11x) – (7x – 77)
= x(x – 11) – 7(x – 11)
= (x – 11) (x – 7).
Hence,
x² – 18x + 77 = (x – 11) (x – 7)

(ii) x² – 25x + 144 = x² – (16 + 9)x + 144
= x² – 16x – 9x + 144
= (x² – 16x) – (9x – 144)
= x(x – 16) – 9 (x – 16)
= (x – 16) (x – 9).
Hence,
x² – 25x + 144 = (x – 16) (x – 9).

Question 16.
Factorize \(\frac {1}{3}\)x² + 5x + 12
Solution :
(i) Ist method : \(\frac {1}{3}\)x² + 5x + 12 = \(\frac {1}{3}\)(x² + 15x + 36)
= \(\frac {1}{3}\)(x² + (12 + 3)x + 36]
= \(\frac {1}{3}\)(x² + 12x + 3x + 36]
= \(\frac {1}{3}\)(x² + 12x) + (3x + 36)]
= \(\frac {1}{3}\)[x(x + 12) + 3(x + 12)]
= \(\frac {1}{3}\)(x + 12) (x + 3)
= (x + 12) (\(\frac {x}{3}\) + 1)
Hence,
\(\frac {1}{3}\)x² + 5x + 12 = (x + 12) (\(\frac {x}{3}\) + 1)

Short Answer Type Questions

Question 1.
Verify, whether the following are zeroes of the polynomial indicated against them :
(i) p(x) = 4x² + 3x – 7; x = 1, – 2
(ii) p(y) = y² + y – 6; y = 2, – 3
Solution:
(i) We have,
p(x) = 4x² + 3x – 7
The value of the polynomial p(x) at x = 1, is given by
p(1) = 4 × (1)² + 3 × 1 – 7
= 4 + 3 – 7 = 0.
The value of the polynomial p(x) at x = – 2, is given by
p(-2) = 4 × (-2)² + 3 × (-2) – 7
= 16 – 6 – 7 = 3 ≠ 0.
Hence, 1 is zero of the polynomial p(x) but – 2 is not

(ii) We have, p(y) = y² + y – 6
The value of the polynomial p(y) at y = 2, is given by
p(2) = (2)² + 2 – 6
= 4 + 2 – 6 = 0.
The value of the polynomial p(y) at y = – 3, is given by
p(-3) = (-3)² – 3 – 6
= 9 – 3 – 6 = 0.
Hence, 2, – 3 are the zeroes of the polynomial p(y).

Question 2.
Find the zero of the polynomial in each of the following cases:
(i) p(x) = 2x – 3
(ii) p(y) = ay – b, a ≠ 0
(iii) q(x) = 4πx + 3
(iv) g(t) = (t + 1)² – (t – 1)².
Solution :
(i) We have,
p(x) = 2x – 3
For zero of the polynomial, p(x) = 0
⇒ 0 = 2x – 3
⇒ 2x = 3
⇒ x = \(\frac {3}{2}\)
Hence, \(\frac {3}{2}\) is the zero of the polynomial p(x).

(ii) We have, p(y) = ay – b, a ≠ 0
For zero of the polynomial, p(y) = 0
⇒ 0 = ay – b
⇒ ay = b
⇒ y = \(\frac {b}{a}\)
Hence, \(\frac {b}{a}\) is the zero of the polynomial p(y).

(iii) We have, q(x) = 4πx + 3
For zero of the polynomial, q(x) = 0
⇒ 0 = 4πx + 3
⇒ 4πx = – 3
⇒ x = \(\frac {-3}{4π}\)
Hence, \(\frac {-3}{4π}\) is the zero of the polynomial q(x).

(iv) We have, g(t) = (t + 1)² – (t – 1)²
⇒ g(t) = t² + 1 + 2t – t² – 1 + 2t
⇒ q(t) = 4t
For zero of the polynomial,
q(t) = 0
⇒ 0 = 4t
⇒ t = \(\frac {0}{4}\) = 0
Hence, 0 is the zero of the polynomial q(t).

Question 3.
Divide the polynomial 2x² + 7x³ + 4x² – 7x – 9 by x + 1.
Solution :
By Long Division, we have

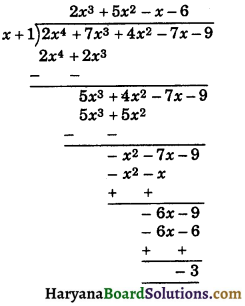
Hence, remainder = – 3.

Question 4.
Divide the polynomial x⁴ + 1 by – 1.
[NCERT Exemplar Problems]
Solution :
By long division, we have

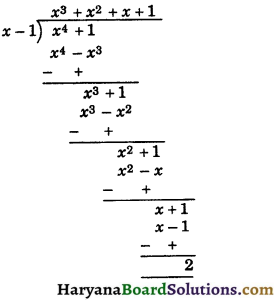
Hence, remainder = 2.

Question 5.
If p(x) = 4x³ – 12x² + 14x – 3, find the remainder when p(x) is divided by 2x – 1. Also, verify the result by actual division.
[NCERT Exemplar Problems]
Solution :
We have,
p(x) = 4x³ – 12x² + 14x – 3
We know that when p(x) is divided by (2x – 1), the remainder is p(\(\frac {1}{2}\))
[By Remainder Theorem]
So,

Remainder by actual division method is also \(\frac {3}{2}\)
Hence, the remainder in both cases is same.

Question 6.
When 4x³ + 18x² + 14x + k is divided by 2x + 5, the remainder is 0. Find the value of k.
Solution :
Let p(x) = 4x³ + 18x² + 14x + k is divided by (2x + 5), the remainder is 0.
By Remainder Theorem, remainder = p(\(\frac {-5}{2}\))

Question 7.
If the polynomials ax³ + 4z² + 3z – 4 and z³ – 4z + a leave the same remainder when divided by z – 3, find the value of a.
Solution :
Let p(x) = az³ + 4z² + 3z – 4
When p(z) is divided by (z – 3), the remainder is p(3)
∴ p(3) = a × (3)³ + 4 × (3)² + 3 × 3 – 4
= 27a + 36 + 9 – 4
= 27a + 41
Let q(z) = z³ – 4z + a
When q(z) is divided by (z – 3), the remainder is q(3).
∴ q(3) = (3)³ – 4 × 3 + a
= 27 – 12 + a
= 15 + a
According to question, the remainders in both cases are equal.
⇒ p(3) = q(3)
⇒ 27a + 41 = 15 + a
⇒ 27 – a = 15 – 41
⇒ 26a = – 26
⇒ a = – \(\frac {26}{26}\)
⇒ a = – 1
Hence a = – 1

Question 8.
If the polynomial f(x) = x³ + px² + qx – 10 is divided by (x – 3) and (x – 2) leaves the remainders 8 and – 12 respectively. Find the values of p and q.
Solution :
We have,
f(x) = x³ + px² + qx – 10
When the given polynomial f(x) is divided by (x – 3), the remainder is 8.
By Remainder Theorem, the remainder = f(3)
⇒ f(3) = 8
⇒ (3)³ + p × (3)² + q × 3 – 10 = 8
⇒ 27 + 9p + 3q – 10 = 8
⇒ 17 + 9p + 3q = 8
⇒ 9p + 3q = 8 – 17
⇒ 9p + 3q = – 9
⇒ 3p + q = – 3 …(i)
And when the given polynomial f(x) is divided by (x – 2), the remainder is – 12.
By Remainder Theorem, the remainder = f(2)
⇒ f(2) = – 12
⇒ (2)³ + p × (2)² + q × 2 – 10 = – 12
⇒ 8 + 4p + 2q – 10 = – 12
⇒ 4p + 2q – 2 = – 12
⇒ 4p + 2q = – 12 + 2
⇒ 4p + 2q = – 10
⇒ 2p + q = – 5 ……..(ii)
Subtracting the equation (ii) from (i), we get

Putting the value of p in equation (ii), we get
2 × 2 + q = – 5
⇒ 4 + 9 = – 5
⇒ q = – 5 – 4
⇒ q = – 9
Hence, P = 2 and q = – 9.

Question 9.
Let R₁ and R₂ be the remainders when the polynomials kx³ + 3x² – 14x + 5 and x³ – 5x² + kx + 12 are divided by (x + 3) and (x – 2) respectively. If R₁ – R₂ = 16, then find the value of k.
Solution :
Let p(x) = kx³ + 3x² – 14x + 5
When p(x) is divided by (x + 3), the remainder (R₁) is p(-3).
[By Remainder Theorem]
R₁ = p(-3)
R₁ = k(-3)³ + 3(-3)² – 14 × (- 3) + 5
R₁ = – 27k + 27 + 42 + 5
R₁ = – 27k + 74
And let q(x) = x³ – 5x² + kx + 12
When q(x) is divided by (x – 2), the remainder (R₂) is q(2).
(By Remainder Theorem)
⇒ R₂ = q(2)
⇒ R₂ = (2)³ – 5 × (2)² + k × 2 + 12
⇒ R₂ = 8 – 20 + 2k +12
⇒ R₂ = 20 – 20 + 2k
⇒ R₂ = 2k
According to question,
R₁ – R₂ = 16
⇒ – 27k + 74 – 2k = 16
⇒ – 29k = 16 – 74
⇒ – 29k = – 58
⇒ k = \(\frac {-58}{-29}\)
Hence, k = 2.

Question 10.
If both (x – 2) and (x – \(\frac {1}{2}\)) are factors of px² + 5x + r, then show that p = r. (NCERT Exemplar Problems)
Solution :
Let f(x) = px² + 5x + r
If (x – 2) is a factor of f(x), then by factor theorem, the remainder f(2) should be zero.
⇒ f(2) = 0
⇒ p × (2)² + 5 × 2 + r = 0
⇒ 4p + 10 + r = 0 ……(i)
If (x – \(\frac {1}{2}\)) is a factor of f(x), then by factor theorem, the remainder f(\(\frac {1}{2}\)) should be zero.
⇒ f(\(\frac {1}{2}\)) = 0
⇒ p × (\(\frac {1}{2}\))² + 5 × \(\frac {1}{2}\) + r = 0
⇒ \(\frac{p}{4}+\frac{5}{2}\) + r =0
⇒ p + 10 + 4r = 0 ……….(ii)
From equations (i) and (ii), we get
4p + 10 + r = P + 10 + 4r
⇒ 4p + r = p + 4r
⇒ 4p – p = 4r
⇒ 3p = 3r
⇒ p = \(\frac {3r}{3}\) = r
Hence, P = r. Hence Proved.

Question 11.
What must be subtracted from 3x³ – 11x² + 11x – 10 to obtain a polynomial which is exactly divisible by (x – 3).
Solution :
Let f(x) = 3x³ – 11x² + 11x – 10
Let k be subtracted from f(x), so that it may be exactly divisible by (x – 3).
∴ p(x) = 3x³ – 11x² + 11x – 10 – k
If p(x) is exactly divisible by (x – 3), then by factor theorem, the remainder p(3) should be zero.
⇒ p(3) = 0
⇒ 3 × (3)³ – 11 × (3)² + 11 × 3 – 10 – k = 0
⇒ 81 – 99 +33 – 10 – k = 0
⇒ 114 – 109 – k = 0
⇒ 5 – k = 0
⇒ k = 5
Hence, 5 must be subtracted from the given polynomial.

Question 12.
If x + \(\frac {1}{x}\) = 5, find the values of each of the following:
(i) x² + \(\frac{1}{x^2}\)
(ii) x⁴ + \(\frac{1}{x^4}\)
Solution :

Question 13.
If x² + \(\frac{1}{x^2}\) = 34, find the values of each of the following :
(i) x + \(\frac {1}{x}\)
(ii) x³ + \(\frac{1}{x^3}\)
Solution :
(i) We have,
x² + \(\frac{1}{x^2}\) = 34
⇒ x² + \(\frac{1}{x^2}\) + 2 = 34 + 2 [Adding 2 on both sides]
⇒ x² + \(\frac{1}{x^2}\) + 2 × x × \(\frac {1}{x}\) = 36
⇒ (x + \(\frac {1}{x}\))² = (6)²
[Using the identity, x² + y² + 2xy = (x+y)²]
⇒ x + \(\frac {1}{x}\) = ± 6
[Taking square root on both sides]
Hence, x + \(\frac {1}{x}\) = ± 6.

(ii) From (i), we have

Question 14.
If x + y = 7 and x² + y² = 25, find the value of x³ + y³.
Solution :
We have,
x + y = 7
⇒ (x + y)² = (7)²
[Squaring on both sides]
⇒ x² + y² + 2xy = 49
⇒ 25 + 2xy = 49, [∵ x² + y² = 25]
⇒ 2xy = 49 – 25
⇒ 2xy = 24
⇒ xy = \(\frac {24}{2}\) = 12.
Now, we have(x + y) = 7
⇒ (x + y)³ = (7)³
(Cubing on both sides)
⇒ x³ + y³ + 3xy(x + y) = 343
[Using the identity, (x + y)³ = x³ + y³ + 3xy(x + y)]
⇒ x³ + y³ + 3 × 12(7) = 343,
[∵ x + y = 7 and xy = 12]
⇒ x³ + y³ + 252 = 343
⇒ x³ + y³ = 343 – 252
⇒ x³ + y³ = 91.
Hence, x³ + y³ = 91.

Question 15.
If a² + b² + c² = 14 and a + b + c = 6, find ab + bc + ca.
Solution :
We have,
a + b + c = 6
⇒ (a + b + c)² = (6)²
(Squaring on both sides)
⇒ a² + b² + c² + 2ab + 2bc + 2ca
⇒ 14 + 2(ab + bc + ca) = 36,
[∵ a² + b² + c² = 14]
⇒ 2(ab + bc + ca) = 36 – 14
⇒ 2(ab + bc + ca) = 22
⇒ ab + bc + ca = \(\frac {22}{2}\)
⇒ ab + bc + ca = 11
Hence, ab + bc + ca = 11.

Question 16.
Evaluate each of the following by using suitable identity :
(i) \(\frac{0.94 \times 0.94 \times 0.94+0.06 \times 0.06 \times 0.06}{0.94 \times 0.94-0.94 \times 0.06+0.06 \times 0.06}\)
(ii) \(\frac{2.05 \times 2.05 \times 2.05-0.05 \times 0.05 \times 0.05}{2.05 \times 2.05+2.05 \times 0.05+0.05 \times 0.05}\)
(iii) 105³ + 95³
Solution :
We use the identity in each of the following [(i) to (iv)] :
(i) x³ + y³ = (x + y) (x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)

Question 17.
If 3x + 4y = 18 and xy = 6, then find the value of 27x³ + 64y³.
Solution :
We have,
3x + 4y = 18
⇒ (3x + 4y)³ = (18)³ (Cubing on both sides)
⇒ 27x³ + 64y³ + 3 × 3x × 4y(3x + 4y) = 5832
[Using the identity, (x + y)³ = x³ + y³ + 3xy(x + y)] +
⇒ 27x³ + 64y³ + 36xy(18) = 5832, (∵ 3x + 4y = 18)
⇒ 27x³ + 64y³ + 36 × 6 × 18 = 5832
⇒ (∵ xy = 6)
⇒ 27x³ + 64y³ + 3888 = 5832
⇒ 27x³ + 64y³ = 5832 – 3888
⇒ 27x³ + 64y³ = 1944.
Hence, 27x³ + 64y³ = 1944.

Question 18.
If a + b + c = 3, abc = – 12 and ab + bc + ca = – 4, find the value of a³ + b³ + c³.
Solution :
We have, a + b + c = 3 …(i)
⇒ (a + b + c)² = (3)²
(Squaring on both sides)
⇒ a² + b² + c² + 2ab + 2bc + 2ca = 9
⇒ a² + b² + c² + 2(ab + bc + ca) = 9
⇒ a² + b² + c² + 2 × (- 4) = 9
[∵ ab + bc + ca = – 4]
⇒ a² + b² + c² – 8 = 9
⇒ a² + b² + c² = 9 + 8 = 17 ………(ii)
We know that,
a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)
⇒ a³ + b³ + c³ – 3 × (- 12) = 3 × [17 – (ab + bc + ca)],
[∵ From (ii), a² + b² + c² = 17, abc = – 12 and a + b + c = 3 (given)]
⇒ a³ + b³ + c³ + 36 = 3 × [17 – (-4)]
⇒ [∵ ab + bc + ca = – 4]
⇒ a³ + b³ + c³ + 36 = 3 x 21
⇒ a³ + b³ + c³ + 36 = 63
⇒ a³ + b³ + c³ = 63 – 36
⇒ a³ + b³ + c³ = 27.
Hence, a³ + b³ + c³ = 27.

Question 19.
Factorise : x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
Solution :
= x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
= x² + \(\frac{1}{x^2}\) + 2 + 1 – 2x – \(\frac {2}{x}\)
= (x + \(\frac {1}{x}\))² + 1 – 2(x + \(\frac {1}{x}\))
[Using the identity, x² + y² + 2xy = (x + y)²
= a² + 1 – 2a, where a = x + \(\frac {1}{x}\)
= (a – 1)²
= (a – 1) (a – 1)
= (x + \(\frac {1}{x}\) – 1) (x + \(\frac {1}{x}\) – 1)
Hence, x² + \(\frac{1}{x^2}\) + 3 – 2x – \(\frac {2}{x}\)
= (x + \(\frac {1}{x}\) – 1) (x + \(\frac {1}{x}\) – 1)

Question 20.
If a + b + c = 3x, then prove that: (x – a)³ + (x – b)³ + (x – c)³ – 3(x – a) (x – b) (x – c) = 0.
Solution :
We have,
a + b + c = 3x
⇒ a + b + c = x + x + x
⇒ (x – a) + (x – b) + (x – c) = 0
We know that, if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Since,(x – a) + (x – b) + (x – c) = 0
Therefore, (x – a)³ + (x – b)³ + (x – c)³
= 3(x – a)(x – b)(x – c)
⇒ (x – a)³ + (x – b)³ + (x – c)³ – 3(x – a)(x – b)(x – c) = 0.
Hence proved

Question 21.
Factorise : x¹² – y¹²
Solution :
x¹² – y¹² = (x⁶)² – (y⁶)²
= (x⁶ + y⁶) (x⁶ – y⁶)
[Using the identity, x² – y² = (x + y)(x – y)]
= [(x²)³ + (y²)³] [(x³)² + (y³)²]
= (x² + y²) [(x²)² – x²y² + (y²)²] (x³ + y³) (x³ – y³)
[Using the identity,
x³ + y³ = (x + y) (x² – xy + y²)]
= (x² + y²) (x⁴ – x²y² + y⁴)(x + y) (x² – xy + y²) (x – y)(x² + xy + y²)
= (x + y) (x – y) (x² + y²) (x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴)
Hence, x¹² – y¹² = (x + y) (x – y) (x² + y²)
(x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴).

Question 22.
If x = y = 333 and z = 334, find the value of x³ + y³ + z³ – 3xyz, without actually calcuting cubes.
Solution :
We know that,
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
= \(\frac {1}{2}\) (x + y + z) [2(x² + y² + z² – xy – yz – zx)]
= \(\frac {1}{2}\) (x + y + z) (2x² + 2y² + 2z² – 2xy – 2yz – 2zx)
= \(\frac {1}{2}\) (x + y + z) (x² + y² – 2xy + y² + z² – 2yz + z² + x² – 2zx]
= \(\frac {1}{2}\) (x + y + z) [(x – y)² + (y – z)² + (z – x)²]
= \(\frac {1}{2}\) (333 + 333 + 334) [(333 – 333)² + (333 – 334)² + (334 – 333)²]
[it is given that x = 333, y = 333 and z = 334)
= \(\frac {1}{2}\) (1000) (0 + 1 + 1)
= \(\frac {1}{2}\) (1000) × 2 = 1000
Hence,
x³ + y³ + z³ – 3xyz = 1000.

Question 23.
Find the remainder when 6x³ + 12x² – 9x – 3 is divided by x + \(\frac {2}{3}\)
Solution :
Let p(x) = 6x³ + 12x² – 9x – 3
We know that when p(x) is divided by (x + \(\frac {2}{3}\)) the remainder is p(\(\frac {-2}{3}\))
[By Remainder Theorem]

Question 24.
Find p(0),p(-1) and p(-2) for each of the following polynomials :
(i) p(x) = 2x³ – 7x + 9
(ii) p(y) = 4y² + 3y – 2
Solution :
(i) We have,
p(x) = 2x³ – 7x + 9
p(0) = 2 × (0)³ – 7 × 0 + 9
= 0 – 0 + 9 = 9.
p(-1) = 2 × (-1)³ – 7 × (-1) + 9
= 2 × (-1) + 7 + 9
= – 2 + 7 + 9
= 14.
and p(-2) = 2 × (-2)³ – 7 × (-2) + 9
= – 16 + 14 + 9 = 7
Hence, p(0) = 9, p(-1)= 14 and p(-2) = 7.

(ii) We have,
p(y) = 4y² + 3y – 2
p(0) = 4 × (0)² + 3 × 0 – 2
= 0 + 0 – 2 = – 2.
p(-1) = 4 × (-1)² + 3 × (-1) – 2
= 4 – 3 – 2 = – 1.
and p(-2) = 4 × (-2)² + 3 × (-2) – 2
= 16 – 6 – 2
= 16 – 8 = 8.
Hence, p(0) = – 2, p(-1) = – 1
and p(-2) = 8.

Long Answer Type Questions

Question 1.
If the polynomial p(x) = x⁴ – 3x³ + x² + ax + b is divided by (x – 1) and (x + 1) leaves the remainders 13 and 9 respectively, find the values of a and b. Hence, find the remainder when p(x) is divided by (x – 2).
Solution :
We have,
p(x) = x⁴ – 3x³ + x² + ax + b
When the given polynomial p(x) is divided by (x – 1), the remainder is 13.
By Remainder Theorem, the remainder = p(1)
⇒ P(1) = 13
⇒ (1)⁴ – 3 × (1)³ + (1)² + a × 1 + b = 13
⇒ 1 – 3 + 1 + a + b = 13
⇒ – 1 + a + b = 13
⇒ a + b = 13 + 1
⇒ a + b = 14 …(i)
And when the given polynomial p(x) is divided by (x + 1), the remainder is 9.
By Remainder Theorem, the remainder = P(-1)
⇒ p(-1) = 9
⇒ (-1)⁴ – 3 × (-1)³ + (-1)² + a × (-1) + b = 9
⇒ 1 + 3 + 1 – a + b = 9
⇒ 5 – a + b = 9
⇒ – a + b = 9 – 5
⇒ – a + b = 4 …(ii)
Adding the equations (i) and (ii), we get
a + b = 14 …(i)
– a + b = 4 …(ii)
2b = 18
⇒ b = \(\frac {18}{2}\) = 9
Putting the value of b in equation (i), we get
a + 9 = 14
⇒ a = 14 – 9 = 5
Now, putting the values of a and b in the given polynomial p(x), we get
p(x) = x⁴ – 3x³ + x² + 5x + 9
Now, p(x) is divided by (x – 2).
By Remainder Theorem,
the remainder = p(2).
So, p(2) = (2)⁴ – 3 × (2)³ + (2)² + 5 × 2 + 9
= 16 – 24 + 4 + 10 + 9
= 39 – 24
= 15.
Hence, a = 5, b = 9 and p(2) = 15.

Question 2.
Find the values of p and q so that (x – 2) and (x + 3) are the factors of the polynomial
f(x) = 5x³ + 6x² – px + q.
Solution :
We have,
f(x) = 5x³ + 6x² – px + q
If (x – 2) is a factor of f(x), then by factor theorem, the remainder f(2) should be zero
⇒ f(2) = 0
⇒ 5 × (2)³ + 6 × (2)³ – p × 2 + q = 0
⇒ 40 + 24 – 2p + q = 0
⇒ 64 – 2p + q = 0
⇒ – 2p + q = – 64 …(i)
If (x + 3) is a factor of f(x), then by factor theorem, the remainder f(-3) should be zero.
⇒ f(-3) = 0
⇒ 5 × (-3)³ + 6 × (-3) -p × (-3) + q = 0
⇒ – 135 + 54 + 3p + q = 0
⇒ – 81 + 3p + q = 0
⇒ 3p + q = 81 …(ii)
Subtracting the equation (ii) from (i), we get

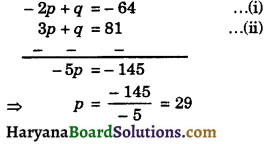
Putting the value of p in equation (ii), we get
3 × 29 + 9 = 81
⇒ 87 + q = 81
⇒ q = 81 – 87 = – 6
Hence, p = 29 and q = – 6.

Question 3.
Determine the values of h and k such that (x² – 2x – 3) is a factor of the polynomial x³ – 3x² + hx + k.
Solution :
Let p(x) = x³ – 3x² + hx + k
Now, x² – 2x – 3 = x² – (3 – 1)x – 3
⇒ x² – 2x – 3 = x² – 3x + x – 3
⇒ x² – 2x – 3 = x(x – 3) + 1(x – 3)
⇒ x² – 2x – 3 = (x – 3)(x + 1)
If (x² – 2x – 3) is a factor of p(x), then (x – 3) and (x + 1) are also the factors of p(x).
Now, (x – 3) is a factor of p(x), then by factor theorem, the remainder p(3) should be zero.
⇒ p(3) = 0
⇒ (3)³ – 3 × (3)² + h × 3 + k = 0
⇒ 27 – 27 + 3h + k = 0
⇒ 3h + k = 0 ….(i)
And if (x + 1) is a factor of p(x), then by factor theorem, the remainder p(- 1) should be zero.
⇒ p(-1) = 0
⇒ (-1)³ – 3 x (-1)² + h x (-1) + k = 0
⇒ – 1 – 3 – h + k = 0
⇒ – 4 – h + k = 0
⇒ – h + k = 4
⇒ h – k = – 4 ….(ii)
Adding equations (i) and (ii), we get

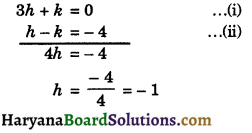
Putting the value of h in equation (ii), we get
– 1 – k = – 4
⇒ – k = – 4 + 1 = – 3
⇒ k = 3
Hence, k = 3 and h = – 1.

Question 4.
Without actual division, prove that x⁴ – 5x³ + 7x² – 5x + 6 is exactly divisible by x² – 5x + 6.
Solution :
Let p(x) = x⁴ – 5x³ + 7x² – 5x + 6
And let
g(x) = x² – 5x + 6
= x² – (3 + 2)x + 6
= x² – 3x – 2x + 6
= x(x – 3) – 2(x- 3)
= (x – 3)(x – 2)
If p(x) is exactly divisible by g(x), then p(x) is exactly divisible by (x – 3) and (x – 2) also.
Now, if p(x) is divisible by (x – 3), then by factor theorem, the remainder p(3) should be zero.
So, p(3) = (3)⁴ – 5 × (3)³ + 7 × (3)² – 5 × 3 + 6
= 81 – 135 + 63 – 15 + 6
= 150 – 150 = 0
Therefore, p(x) is divisible by (x – 3).
⇒ (x – 3) is a factor of p(x). …(i)
And if p(x) is divisible by (x – 2), then by factor theorem, the remainder p(2) should be zero.
So, p(2) = (2)⁴ – 5 × (2)³ + 7 × (2)² – 5 × 2 + 6
= 16 – 40 + 28 – 10 + 6
= 50 – 50 = 0
Therefore, p(x) is divisible by (x – 2).
⇒ (x – 2) is a factor of p(x). …(ii)
From (i) and (ii), we get
(x – 3)(x – 2) is a factor of p(x).
i.e., (x² – 5x + 6) is a factor of p(x).
Hence, p(x) is exactly divisible by (x² – 5x + 6). Proved

Question 5.
Factorise the following polynomials:
x⁴ + x³ – 7x² – x + 6
Solution :
Ist method: Let
p(x) = x⁴ + x³ – 7x² – x + 6
Factors of 6 are ±1, ±2, ±3, ±6.
Put x = 1
∴ p(1) = (1)⁴ + (1)³ – 7 × (1)² – 1 + 6
= 1 + 1 – 7 – 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Now, divide x⁴ + x³ – 7x² – x + 6 by (x – 1),
we get

So, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x³ + 2x² – 5x – 6)
Other factor of p(x) is x³ + 2x² – 5x – 6.
Factors of – 6 are ± 1, ± 2, ± 3, ± 6.
Again, put x = – 1
∴ p(-1) = (-1)³ + 2 × (-1)² – 5 × (-1) – 6
= – 1 + 2 + 5 – 6
= 7 – 7 = 0.
∴ By factor theorem, (x + 1) is a factor of x³ + 2x² – 5x – 6.
Again, divide x³ + 2x² – 5x – 6 by (x + 1), we get

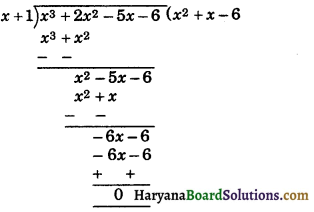
So, x³ + 2x² – 5x – 6 = (x + 1) (x² + x – 6)
And
x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1)(x² + x – 6)
= (x – 1)(x + 1) [x² + (3 – 2)x – 6]
= (x – 1)(x + 1)[x² + 3x – 2x – 6]
= (x – 1)(x + 1) [(x² + 3x) – (2x + 6)]
= (x – 1)(x + 1) (x(x + 3) – 2(x + 3)]
= (x – 1)(x + 1) (x + 3)(x – 2).
Hence, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1) (x + 3)(x – 2).

IInd method: Let
p(x) = x⁴ + x³ – 7x² – x + 6
Factors of 6 are = ± 1, ± 2, ± 3, ± 6
Put
x = 1
∴ p(1) = (1)⁴ + (1)³ – 7 × (1)² – 1 + 6
= 1 + 1 – 7 – 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Again put x = – 1
∴ p(-1) = (-1)⁴ + (-1)³ – 7 × (-1)² – (-1) + 6
= 1 – 1 – 7 + 1 + 6
= 8 – 8 = 0.
∴ By factor theorem, (x + 1) is a factor of p(x).
Again put x = 2
∴ p(2) = (2)⁴ + (2)³ – 7 × (2)² – 2 + 6
= 16 + 8 – 28 – 2 + 6
= 30 – 30 = 0.
∴ By factor theorem, (x – 2) is a factor of p(x).
And put x = – 3 .
∴ p(-3) = (-3)⁴ + (-3)³ – 7 × (-3)² – (-3) + 6
= 81 – 27 – 63 + 3 + 6
= 90 – 90 = 0.
∴ By factor theorem, (x + 3) is a factor of p(x). Now, since the given expression is of 4th degree, so it will have only four factors of first degree.
∴ x⁴ + x³ – 7x² – x + 6 = k(x – 1) (x + 1) (x – 2) (x + 3) ……….(i)
Putting x = 0 (value of other than – 1, 1, 2, + 3) on both sides of equation (i), we get
+ 6 = k(-1)(1)(-2)(+3)
⇒ + 6 = 6k
⇒ k = \(\frac {6}{6}\) = 1
Putting the value of k in equation (i), we get
x⁴ + x³ – 7x² – x + 6 = (x – 1) (x + 1) (x – 2) (x + 3)
Hence, x⁴ + x³ – 7x² – x + 6 = (x – 1)(x + 1) (x – 2)(x + 3).

Question 6.
Factorise the following polynomials:
x⁴ – 4x³ – x² + 16x – 12.
Solution :
Let
p(x) = x⁴ – 4x³ – x² + 16x – 12
Factors of – 12 are ±1, ±2, ±3, ±4, ±6, ±12.
Put x = 1
∴ p(1) = (1)⁴ – 4 × (1)³ – (1)² + 16 × 1 – 12 .
= 1 – 4 – 1 + 16 – 12
= 17 – 17 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x).
Now, divide x⁴ – 4x³ – x² + 16x – 12. by (x – 1), we get

So,
x⁴ – 4x³ – x² + 16x – 12 = (x – 1)(x³ – 3x² – 4x + 12).
Other factor of p(x) is x³ – 3x² – 4x + 12.
Factors of 12 are ±1, ±2, ±3, ±4, ±6, ±12
Again, put x = 2
∴ p(2) = (2)³ – 3 × (2)² – 4 × 2 + 12
= 8 – 12 – 8 + 12
= 20 – 20 = 0.
∴ By factor theorem, (x – 2) is a factor of x³ – 3x² – 4x + 12.
Now, divide x³ – 3x² – 4x + 12 by (x – 2), we get

So,
x³ – 3x² – 4x + 12 = (x – 2) (x² – x – 6)
And x⁴ – 4x³ – x² + 16x – 12 = (x – 1)(x – 2)(x² – x – 6)
= (x – 1) (x – 2)[x² – (3 – 2)x – 6]
= (x – 1) (x – 2)[x² – 3x + 2x – 6]
= (x – 1) (x – 2)[(x² – 3x) + (2x – 6)]
= (x – 1) (x – 2)[x(x – 3) + 2(x – 3)]
= (x – 1) (x – 2)(x – 3) (x + 2).
Hence, x⁴ – 4x³ – x² + 16x – 12
= (x – 1)(x – 2)(x – 3)(x + 2).

Question 7.
If (x + 2) be a factor of the polynomial p(x) = kx³ + x² – 12x – 4, then find the value of k and hence factorise the polynomial p(x).
Solution :
We have p(x) = kx³ + x² – 12x – 4
If (x + 2) is a factor of p(x), then by factor theorem, p(-2) should be zero.
⇒ p(-2) = 0
⇒ k(-2)³ + (-2)² – 12 × (-2) – 4 = 0
⇒ – 8k + 4 + 24 – 4 = 0
⇒ – 8k + 24 = 0
⇒ – 8k = – 24
⇒ k = \(\frac {- 24}{- 8}\) = 3
Putting the value of k in p(x), we get
p(x) = 3x³ + x² – 12x – 4
According to question, (x + 2) is a factor of p(x).
Dividing 3x³ + x² – 12x – 4 by (x + 2), we get

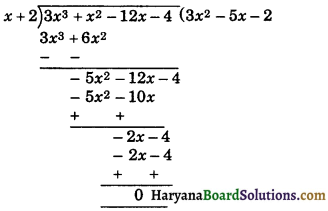
So, 3x³ + x² – 12x – 4= (x + 2) (3x² – 5x – 2)
= (x + 2) [3x² – (6 – 1)x – 2]
= (x + 2) [3x² – 6x + x – 2]
= (x + 2) [(3x² – 6x) + (x – 2)]
= (x + 2) (3x(x – 2) + 1(x – 2)]
= (x + 2)(x – 2)(3x + 1).
Hence, k = 3 and 3x³ + x² – 12x – 4 = (x + 2)(x – 2)(3x + 1).

Question 8.
If a⁴ + \(\frac{1}{a^4}\) = 322, find the value of a³ – \(\frac{1}{a^3}\).
Solution :
We have

Question 9.
If a⁴ + \(\frac{1}{a^4}\) = 47, find the value of a³ + \(\frac{1}{a^3}\)
Solution :
We have,
a⁴ + \(\frac{1}{a^4}\) = 47

Question 10.
Factorise each of the following :
(i) (a – b)³ + (b – c)³ + (c – a)³
(ii)\(\frac{\left(p^2-q^2\right)^3+\left(q^2-r^2\right)^3+\left(r^2-p^2\right)^3}{(p-q)^3+(q-r)^3+(r-p)^3}\)
Solution :
We have,
(a – b)³ + (b – c)³ + (c – a)³
We know that if x + y + z = 0, then
x³ + y³ + z³ = 3xyz
Since, a – b + b – c + c – a = 0
Therefore, (a – b)³ + (b – c)³ + (c – a)³
= 3(a – b)(b – c) (c – a).

(ii) We have, \(\frac{\left(p^2-q^2\right)^3+\left(q^2-r^2\right)^3+\left(r^2-p^2\right)^3}{(p-q)^3+(q-r)^3+(r-p)^3}\)
We know that, if x + y + z = 0, then x³ + y³ + z³ = 3xyz
Since, p² – q² + q² – r² + r² – p² = 0
Therefore, (p² – q²)³ + (q² – r²)³ + (r² – p²)³
= 3(p² – q²) (q² – r²) (r² – p²) and p – q + q – r + r – p = 0

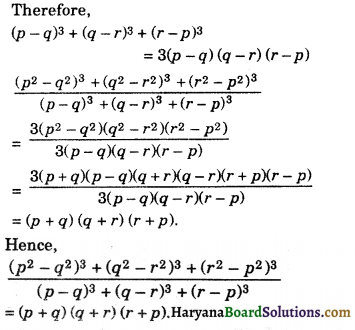
Question 11.
If \(\frac{x}{(b-c)(b+c-2 a)}=\frac{y}{(c-a)(c+a-2 b)}\) = \(\frac{z}{(a-b)(a+b-2 c)}\) then find the value of x + y + z.
Solution :
Let
\(\frac{x}{(b-c)(b+c-2 a)}=\frac{y}{(c-a)(c+a-2 b)}\) = \(\frac{z}{(a-b)(a+b-2 c)}\) = k
∴ x = k(b – c)(b + c – 2a),
y = k(c – a) (c + a – 26)
And z = k(a – b)(a + b – 2c)
Now, x + y + z = (b – c)(b + c – 2a) + k(c – a) (c + a – 2b) + k(a – b)(a + b – 2c)
= k[(b – c)(b + c – 2a) + (c – a)(c + a – 2b) + (a – b)(a + b – 2c)]
= k[b² + bc – 2ab – bc – c² + 2ac + c² + ac – 2bc – ac – a² + 2ab + a² + ab – 2ac – ab – b² + 2bc]
= k[b² – c² + c² – a² + a² – b² + bc – bc – 2ab + 2ab + 2ac – 2ac + ac – ac – 2bc + 2bc + ab – ab]
= k(0) = 0
Hence, x + y + z = 0.

Question 12.
Prove that : (a + b)³ + (b + c)³ + (c + a)³ – 3(a + b)(b + c) (c + a) = 2(a³ + b³ + c³ – 3abc).
Solution :
We have,
L.H.S. = (a + b)³ + (b + c)³ + (c + a)³ – 3(a + b)(b + c)(c + a)
Let, a + b = x, b + c = y, c + a = z, we get
L.H.S. = x³ + y³ + z³ – 3xyz
= (x + y + z)(x² + y² + z² – xy – yz – zx)
= (a + b + b + c + c + a) [(a + b)² + (b + c)² + (c + a)² – (a + b)(b + c) – (b + c)(c + a) – (c + a)(a + b)]
= 2(a + b + c) (a² + b² + 2ab + b² + c² + 2bc + c² + a² + 2ac – ab – ac – b² – bc – bc – ab – c² – ac – ac – bc – a² – ab)
= 2(a + b + c) (2a² + 2b² + 2c² – a² – b² – c² + 2ab + 2bc + 2ca – 3ab – 3bc – 3ca]
= 2(a + b + c)(a² + b² + c² – ab – bc – ca)
= 2(a³ + b³ + c³ – 3abc)
= R.H.S.
Hence, L.H.S. = R.H.S. Proved

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
Which of the following is a polynomial in variable x?
(a) x + \(\frac {1}{x}\)
(b) \(\sqrt{x^2}+\frac{1}{\sqrt{x^2}}\)
(c) x2 + \(\frac{x^{3 / 2}}{\sqrt{x}}\)
(d) x3/2 + \(\frac{1}{\sqrt{x^2}}\)
Solution :
(c) x2 + \(\frac{x^{3 / 2}}{\sqrt{x}}\)

Question 2.
\(\sqrt{2}\) is a polynomial of degree: [NCERT Exemplar Problems]
(a) 2
(b) 0
(c) 1
(d) \(\frac {1}{2}\)
Solution :
(b) 0

Question 3.
Which of the following is binomial in y:
(a) y2 + 5
(b) y2 + 5y + 6
(c) y2 + \(\frac{1}{y^2}\) + 2
(d) y\(\sqrt{y}\) + 7
Solution :
(a) y2 + 5

Question 4.
Which of the following is trinomial in x:
(a) x3 + 1
(b) x3 + 3x
(c) x\(\sqrt{x^2}\) + \(\sqrt{x^2}\) + 7
(d) x3 + x2
Solution :
(c) x\(\sqrt{x^2}\) + \(\sqrt{x^2}\) + 7

Question 5.
Degree of a zero polynomial is [NCERT Exemplar Problems]
(a) 2
(b) 0
(c) 1
(d) not defined
Solution :
(d) not defined

Question 6.
Which of the following polynomial’s degree is zero?
(a) x2
(b) x + \(\frac {1}{x}\)
(c) 7
(d) x.
Solution :
(c) 7

Question 7.
Degree of the polynomial 27 + y2 – 3y3 + 5y5 is :
(a) 5
(b) 3
(c) 2
(d) o
Solution :
(a) 5

Question 8.
Zero of the polynomial p(x) = 2x + 5 is : [NCERT Exemplar Problems]
(a) –\(\frac {2}{5}\)
(b) – \(\frac {5}{2}\)
(c) \(\frac {2}{5}\)
(d) \(\frac {5}{2}\)
Solution :
(b) – \(\frac {5}{2}\)

Question 9.
If (x – 2) is a factor of x3 – 6×2 + 12x – k, then value of k is :
(a) 4
(b) 8
(c) 6
(d) 10
Solution :
(b) 8

Question 10.
If x120 + 4×143 + k is divisible by x + 1, then value of k is :
(a) 2
(b) – 2
(c) 3
(d) – 3
Solution :
(c) 3

Question 11.
(x + 1) is a factor of xn + 1, only if :
(a) n is a positive integer
(b) n is a negative integer
(c) n is an odd integer
(d) n is an even integer
Solution :
(c) n is an odd integer

Question 12.
If x51 + 51 is divided by x + 1, the remainder is: [NCERT Exemplar Problems]
(a) o
(b) 1
(c) 49
(d) 50
Solution :
(d) 50