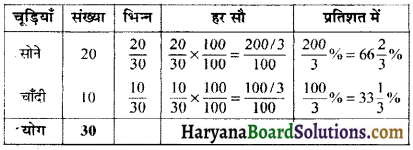
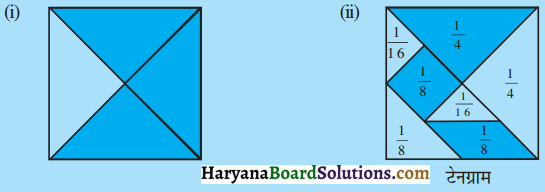
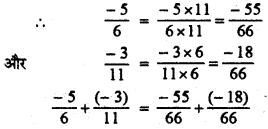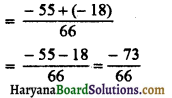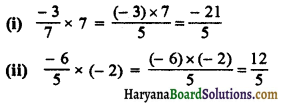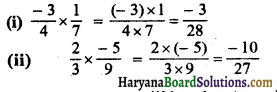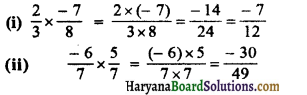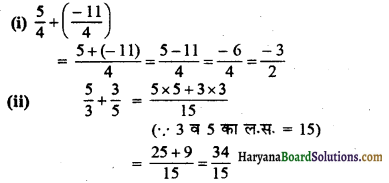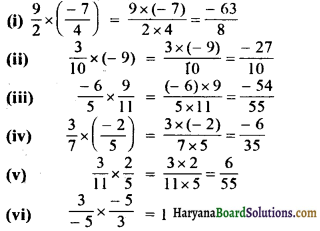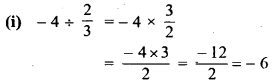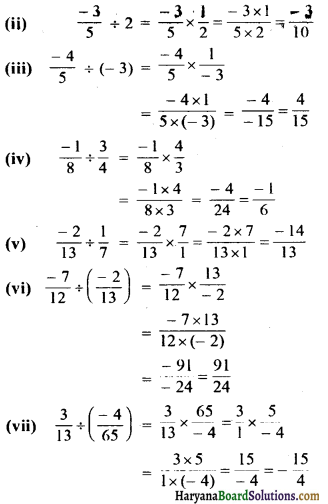HBSE 7th Class Science Solutions Chapter 10 जीवों में श्वसन
Haryana State Board HBSE 7th Class Science Solutions Chapter 10 जीवों में श्वसन Textbook Exercise Questions and Answers.
Haryana Board 7th Class Science Solutions Chapter 10 जीवों में श्वसन
HBSE 7th Class Science जीवों में श्वसन InText Questions and Answers
बूझो/पहेली
प्रश्न 1.
बूझो ने नोट किया कि जब कुछ देर तक साँस रोके रखने के बाद उसने साँस छोड़ी, तो उसे तेज साँस लेनी पड़ी। क्या आप उसे बता सकते हैं कि ऐसा क्यों हुआ?
उत्तर:
क्योंकि उसके फेफड़ों में ऑक्सीजन की आपूर्ति काफी देर तक नहीं हो पाई जिससे फेफड़ों में कार्बन डाइऑक्साइड की मात्रा बढ़ गई थी।
प्रश्न 2.
पहेली जानना चाहती है कि जब हमें नींद आती है या झपकी आती है, तो हम जम्हाई क्यों लेते हैं ?
उत्तर:
जब हमें नींद आती है तो श्वसन दर कम हो जाती है। श्वसन दर में कमी होने से शरीर में ऑक्सीजन की आपूर्ति कम हो जाती है। जम्हाई लेने से हम अतिरिक्त ऑक्सीजन लेकर कमी को पूरा कर लेते हैं।
प्रश्न 3.
बूझो जानना चाहता है कि कोई व्यक्ति अपने फेफड़ों में कितनी वायु भर सकता है?
उत्तर:
लगभग आधा लीटर (500 mL)।
![]()
प्रश्न 4.
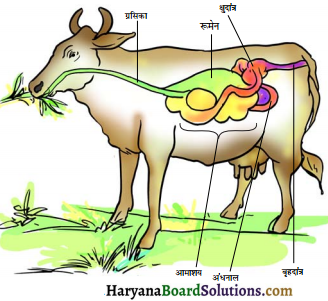
बूझो जानना चाहता है कि क्या कॉकरोच (तिलचट्टा), घोंघे, मछली, केंचुए, चींटी और मच्छर में भी फेफड़े होते हैं।
उत्तर:
नहीं, इन जन्तुओं में फेफड़े नहीं होते हैं। इनमें श्वसन के लिए विशेष प्रकार के श्वसन अंग पाये जाते हैं।
प्रश्न 5.
बूझो ने दूरदर्शन कार्यक्रमों में देखा था कि व्हेल और डॉल्फिन अक्सर पानी की सतह पर ऊपर आ जाती हैं। कभी-कभी ऊपर की ओर आते समय वे पानी की फुहार भी छोड़ती हैं ? वे ऐसा क्यों करती हैं ?
उत्तर:
व्हेल और डॉल्फिन अन्तःश्वसन के दौरान अन्तःश्वसित वायु को सतह पर आकर उच्छ्वसित करती हैं। इसी दौरान जल वाष्प फुहार के रूप में दिखाई देती है।
प्रश्न 6.
पहेली जानना चाहती है कि क्या भूमिगत होते हुए भी पादपों की जड़ें ऑक्सीजन ग्रहण करती हैं ? यदि ऐसा है, तो वे ऐसा किस प्रकार करती हैं?
उत्तर:
हाँ, जड़ें मृदा कणों के बीच खाली स्थानों में उपस्थित वायु से ऑक्सीजन लेती हैं।
HBSE 7th Class Science जीवों में श्वसन Textbook Questions and Answers
प्रश्न 1.
कोई धावक दौड़ समाप्त होने पर सामान्य से अधिक तेजी से गहरी साँसें क्यों लेता है ?
उत्तर:
दौड़ने के समय बहुत अधिक ऊर्जा खर्च होती है, इस ऊर्जा की पूर्ति शरीर में ग्लूकोस के विखण्डन से होती है। ग्लूकोस का विखण्डन ऑक्सीजन द्वारा होता है। तेजी से साँस लेने से ऑक्सीजन की अधिक आपूर्ति होती है तथा अधिक से अधिक कार्बन डाइऑक्साइड बाहर निकल जाती है।
प्रश्न 2.
वायवीय और अवायवीय श्वसन के बीच समानताएं और अन्तर बताइए।
उत्तर:
समानताएँ-
- दोनों ही प्रकार के श्वसन में ऊर्जा उत्पन्न होती है।
- दोनों ही प्रकार के श्वसन में कार्बन डाइऑक्साइड बनती है।
- दोनों में ही भोज्य पदार्थ समान होते हैं।
अन्तर-
- वायवीय श्वसन में ऑक्सीजन की उपस्थिति अनिवार्य होती है, जबकि अवायवीय श्वसन में नहीं।
- वायवीय श्वसन में ग्लूकोस का पूर्ण विखण्डन होता है, जबकि अवायवीय श्वसन में ग्लूकोस का अपूर्ण विखण्डन होता है।
- वायवीय श्वसन में अधिक ऊर्जा निर्मुक्त होती है जबकि अवायवीय श्वसन में कम ऊर्जा निर्मुक्त होती है।
![]()
प्रश्न 3.
जब हम अत्यधिक धूल भरी वायु में साँस लेते हैं, तो हमें छींक क्यों आ जाती है?
उत्तर:
हमारे आस-पास की वायु में बहुत सारे अवांछनीय कण, जैसे- धूल, धुंआ आदि उपस्थित होते हैं। श्वसन के दौरान ये कण हमारे नथुनों में उपस्थित बालों एवं श्लेष्म में फंस जाते हैं। यदि ये कण बालों को पार करके आगे निकल जाते हैं तो नथुनों में खुजलाहट होती है तथा छींक आती है। छींक के रूप में तीन वायु प्रवाह से ये कण बाहर निकल जाते हैं तथा स्वच्छ वायु अन्दर प्रवेश होती है।
प्रश्न 4.
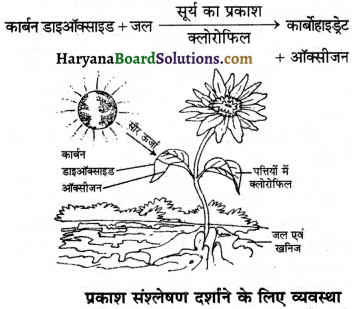
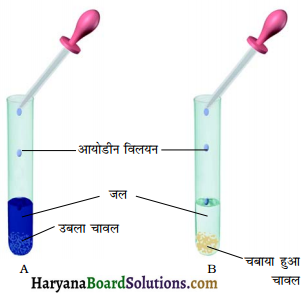
तीन परखनलियाँ लीजिए। प्रत्येक को 3/4 भाग तक जल से भरिये। इनें A, B तथा C द्वारा चिन्हित कीजिए। परखनली A में एक घोंघा रखिए। परखनली B में कोई जलीय पादप रखिए और C में एक घोंघा और पादप दोनों को रखिए। किस परखनली में कार्बन डाईऑक्साइड की सान्द्रता सबसे अधिक होगी।
उत्तर:
परखनली A में कार्बन डाइऑक्साइड की सान्द्रता अधिक होगी। क्योंकि परखनली में केवल घोंधा है जो श्वसन क्रिया में कार्बन डाइऑक्साइड निर्मुक्त करता है। परखनली B में पादप है जो प्रकाश संश्लेषण करके कार्बन डाइऑक्साइड को सोख लेता है। परखनली C में पादप तथा घोंघा हैं। इसमें घोंघा द्वारा छोड़ी गई कार्बन डाइऑक्साइड को पौध ग्रहण कर लेता है।
प्रश्न 5.
सही उत्तर पर (✓) का निशान लगाइए
(क) तिलचट्टों के शरीर में वायु प्रवेश करती है, उनके
(i) फेफड़ों द्वारा
(ii) क्लोमों द्वारा
(iii) श्वास रन्ध्रों द्वारा
(iv) त्वचा द्वारा।
उत्तर:
(ख) अत्यधिक व्यायाम करते समय हमारी टाँगों में जिस पदार्थ के संचयन के कारण ऐंठन होती है, वह है
(i) कार्बन डाइऑक्साइड
(ii) लैक्टिक अम्ल
(iii) ऐल्कोहॉल
(iv) जल
उत्तर:
(iii) ऐल्कोहॉल
(ग) किसी सामान्य वयस्क व्यक्ति की विश्राम अवस्था में औसत श्वसन दर होती है
(i) 9-12 प्रति मिनट
(ii) 15-18 प्रति मिनट
(iii) 21-24 प्रति मिनट
(iv) 30-33 प्रति मिनट
उत्तर:
(ii) 15-18 प्रति मिनट
![]()
(घ) उच्छ्व सन के समय पसलियों
(i) बाहर की ओर गति करती हैं
(ii) नीचे की ओर गति करती हैं
(iii) ऊपर की ओर गति करती हैं
(iv) बिल्कुल गति नहीं करती हैं।
उत्तर:
(ii) नीचे की ओर गति करती हैं
प्रश्न 6.
कॉलम A में दिये गये शब्दों का कॉलम B के साथ मिलान कीजिए-
| कॉलम A | कॉलम B |
| (क) यीस्ट | (i) केंचुआ |
| (ख) डायाफ्राम (मध्यपट) | (ii) क्लोम |
| (ग) त्वचा | (iii) एल्कोहॉल |
| (घ) पत्तियाँ | (iv) वक्ष-गुहा |
| (च) मछली | (v) रन्ध्र |
| (छ) मेंढक | (vi) फेफड़े और त्वचा |
| (vii) श्वासप्रणाल (वातक) |
उत्तर:
| कॉलम A | कॉलम B |
| (क) यीस्ट | (iii) एल्कोहॉल |
| (ख) डायाफ्राम (मध्यपट) | (iv) वक्ष-गुहा |
| (ग) त्वचा | (i) केंचुआ |
| (घ) पत्तियाँ | (v) रन्ध्र |
| (च) मछली | (ii) क्लोम |
| (छ) मेंढक | (vi) फेफड़े और त्वचा |
![]()
प्रश्न 7.
बताइए कि निम्नलिखित वक्तव्य ‘सत्य’ हैं अथवा ‘असत्य’
(क) अत्यधिक व्यायाम करते समय व्यक्ति की श्वसन दर धीमी हो जाती है।
(ख) पादपों में प्रकाश संश्लेषण केवल दिन में, जबकि श्वसन केवल रात्रि में होता है।
(ग) मेंढक अपनी त्वचा के अतिरिक्त अपने फेफड़ों से भी श्वसन करते हैं।
(घ) मछलियों में श्वसन के लिए फेफड़े होते हैं।
(च) अंतःश्वसन के समय वक्ष-गुहा का आयतन बढ़ जाता है।
उत्तर:
(क) असत्य
(ख) असत्य
(ग) सत्य
(घ) असत्य
(च) सत्य।
प्रश्न 8.
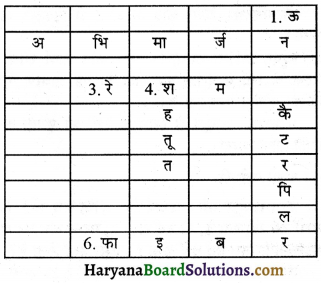
दी गई पहेली के प्रत्येक वर्ग में जीवों के श्वसन से सम्बन्धित हिन्दी वर्णाक्षर अथवा संयुक्ताक्षर दिये गये हैं। इनको मिलाकर जीवों तथा उनके श्वसन अंगों से सम्बन्धित शब्द बनाये जा सकते हैं। शब्द वर्गों के जाल में किसी भी दिशा में, ऊपर, नीचे अथवा विकर्ण में पाये जा सकते हैं। श्वसन तंत्र तथा जीवों के नाम खोजिए।
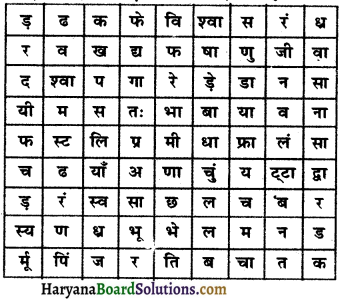
(1) कीर्टो की वायु नलियाँ।
(2) वक्ष-गुहा को घेरे हुए हड्डियों की संरचना।
(3) वक्ष-गुहा का पेशीय तल।
(4) पत्ती की सतह पर सूक्ष्म छिद्र।
(5) कीट के शरीर के पार्श्व भागों के छोटे छिद्र।
(6) मनुष्यों के श्वसन अंग।
(7) वे छिद्र जिनसे हम साँस भीतर लेते (अंतःश्वसन) करते हैं।
(8) एक अवायवीय जीव।
(9) श्वासप्रणाल तंत्र वाला एक जीव।
उत्तर:
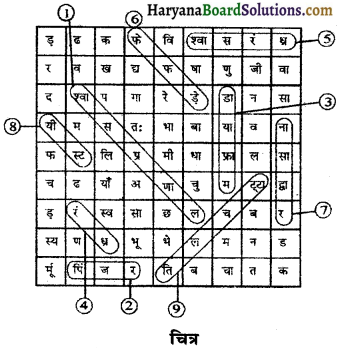
प्रश्न 9.
पर्वतारोही अपने साथ ऑक्सीजन सिलिंडर ले जाते हैं, क्योंकि
(क) 5km से अधिक ऊँचाई पर वायु नहीं होती है।
(ख) वहाँ उपलब्ध वायु की मात्रा भू-तल पर उपलब्ध मात्रा से कम होती है।
(ग) वहाँ वायु का ताप भू-तल के ताप से अधिक होता है।
(घ) पर्वत पर वायुदाब भू-तल की अपेक्षा अधिक होता है।
उत्तर:
(ख) वहाँ उपलब्ध वायु की मात्रा भू-तल पर उपलब्ध मात्रा से कम होती है।
HBSE 7th Class Science जीवों में श्वसन Important Questions and Answers
वस्तुनिष्ठ प्रश्न
I. बहुविकल्पीय प्रश्न
निम्नलिखित प्रश्नों में से सही विकल्प का चयन कीजिए
1. वायवीय श्वसन में ग्लूकोज का विखण्डन होता है
(क) ऑक्सीजन द्वारा
(ख) कार्बन डाइऑक्साइड द्वारा
(ग) ऊर्जा द्वारा
(घ) जल द्वारा
उत्तर:
(क) ऑक्सीजन द्वारा
2. अवायवीय जीव कहलाते हैं, जो
(क) ऑक्सीजन द्वारा ऊर्जा प्राप्त करते हैं
(ख) अवायवीय श्वसन द्वारा ऊर्जा प्राप्त करते हैं
(ग) वायु द्वारा ऊर्जा प्राप्त करते हैं।
(घ) ऊर्जा खर्च नहीं करते हैं।
उत्तर:
(ख) अवायवीय श्वसन द्वारा ऊर्जा प्राप्त करते हैं
3. अत्यधिक व्यायाम करने पर पेशियों में ऐंठन उत्पन्न होने का कारण है
(क) ऑक्सीजन एकत्र होना
(ख) ग्लूकोज एकत्र होना
(ग) लैक्टिक अम्ल एकत्र होना
(घ) एल्कोहॉल एकत्र होना।
उत्तर:
(ग) लैक्टिक अम्ल एकत्र होना
4. मनुष्य की श्वसन दर होती है लगभग
(क) 8-10/मिनट
(ख) 16-18/मिनट
(ग) 25-30/मिनट
(घ) 30-40/मिनट
उत्तर:
(ख) 16-18/मिनट
![]()
5. हमारे फेफड़े स्थित होते हैं
(क) वक्ष गुहा में
(ख) उदर गुहा में
(ग) हृदयावरणी गुहा में
(घ) मस्तिष्क गुहा में
उत्तर:
(क) वक्ष गुहा में
II. रिक्त स्थान
निम्नलिखित वाक्यों में रिक्त स्थान भरिए
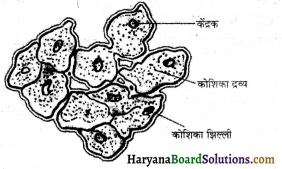
1. ………… जीव की सबसे छोटी संरचनात्मक एवं क्रियात्मक इकाई होती है।
2. भोजन के विखण्डन से ………… निर्मुक्त होती है।
3. ग्लूकोज का विखण्डन जब ऑक्सीजन की उपस्थिति में होता है तो ………… और ……. बनते है और ऊर्जा मुक्त होती है।
4. ………… जल में घुली ऑक्सीजन का उपयोग करने में मछली की सहायता करते हैं।
उत्तर:
1. कोशिका
2. ऊर्जा
3. कार्बन डाइऑक्साइड, जल
4. क्लोम।
III. सुमेलन
कॉलम A तथा कॉलम B के शब्दों का मिलान कीजिए-
| कॉलम A | कॉलम B |
| 1. मनुष्य | (a) रन्ध्र |
| 2. केंचुआ | (b) श्वास रन्ध्र |
| 3. कॉकरोच | (c) नम त्वचा |
| 4. पौधा | (d) फेफड़े |
उत्तर:
| कॉलम A | कॉलम B |
| 1. मनुष्य | (d) फेफड़े |
| 2. केंचुआ | (c) नम त्वचा |
| 3. कॉकरोच | (b) श्वास रन्ध्र |
| 4. पौधा | (a) रन्ध्र |
IV. सत्य/असत्य
निम्नलिखित वाक्यों में से सत्य एवं असत्य कथन छाँटिए
1. उच्छवसन की प्रक्रिया में पसलियाँ नीचे की ओर एवं डायफ्राम ऊपर की ओर गति करता है।
2. श्वसन के दौरान वक्ष गुहा के आयतन में कोई परिवर्तन नहीं होता है।
3. कीटों में गैस विनिमय के लिए वायु नलियों का जाल बिछा होता है।
4. पादपों में भी जन्तुओं की भाँति कोशिकीय श्वसन पाया जाता है।
उत्तर:
1. सत्य
2. असत्य
3. सत्य
4. सत्य।
![]()
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
कोशिकीय श्वसन किसे कहते हैं ?
उत्तर:
भोजन के विखण्डन से ऊर्जा निर्मुक्त होने की प्रक्रिया कोशिका में होती है, इसे कोशिकीय श्वसन कहते हैं।
प्रश्न 2.
अन्तःश्वसन तथा उच्छ्वसन किसे कहते हैं ?
उत्तर:
ऑक्सीजन से समृद्ध वायु को अन्दर लेना अन्तःश्वसन तथा कार्बन डाइऑक्साइड युक्त वायु को शरीर से बाहर करना उच्छ्व सन कहलाता है।।
प्रश्न 3.
कुछ समय तक नथुने और मुंह दोनों बन्द रखने पर क्या महसूस होता है? (क्रियाकलाप)
उत्तर:
श्वासावरोध महसूस होता है।
प्रश्न 4.
एक मिनट में हम कितनी बार साँस लेते हैं एवं छोड़ते हैं? (क्रियाकलाप)
उत्तर:
लगभग 15-16 बार प्रति मिनट।
प्रश्न 5.
तेज चलने के बाद श्वसन दर बताइए। (क्रियाकलाप)
उत्तर:
20-25 बार प्रति मिनट।
![]()
प्रश्न 6.
शरीर की क्रियाओं के संचालन के लिए ऊर्जा कहाँ से आती है?
उत्तर:
भोजन के विखण्डन से।
प्रश्न 7.
क्या आप बता सकते हैं कि आपके माता-पिता आपसे नियमित रूप से भोजन करने के लिए आग्रह क्यों करते हैं?
उत्तर:
भोजन से हमें ऊर्जा प्राप्त होती है। शरीर के निर्माणकारी तत्व भोजन से ही प्राप्त होते हैं।
प्रश्न 8.
क्या हम जल में जीवित रह सकते हैं ?
उत्तर:
नहीं, क्योंकि हम जल में श्वसन नहीं कर सकते।
प्रश्न 9.
सर्पो एवं छिपकलियों में श्वसन अंग क्या होते हैं ?
उत्तर:
फेंफड़े।
प्रश्न 10.
मनुष्य में कितने फेंफड़े होते हैं?
उत्तर:
एक जोड़ी।
प्रश्न 11.
क्या अन्तःश्वसन तथा उच्छ्वसन में पसलियाँ भी सहायक होती हैं ?
उत्तर:
हाँ।
प्रश्न 12.
साँस खींचने तथा बाहर निकालने में प्रमुख भूमिका किसकी होती है ?
उत्तर:
डायाफ्राम की।
प्रश्न 13.
क्या पौधों में भी श्वसन होता है ?
उत्तर:
हाँ, पौधे भी श्वसन क्रिया करते हैं।
![]()
लयु उत्तरीय प्रश्न
प्रश्न 1.
जब हम चूने के पानी में एक पतली नली द्वारा फूंक मारते हैं तो क्या होता है? हमारी फूंक में हम कौन-सी गैस उच्छवसित करते हैं? (क्रियाकलाप)
उत्तर:
जब हम चूने के पानी में फूंक मारते हैं तो चूने का पानी दूधिया होने लगता है। चूंकि चूने के पानी में कार्बन डाइऑक्साइड प्रवाहित करने पर यह दूधिया हो जाता है। इससे स्पष्ट है कि हमारी फूंक में कार्बन डाइऑक्साइड गैस उपस्थित है।
प्रश्न 2.
मछलियाँ जल में श्वसन किस प्रकार करती
उत्तर:
मछलियों के पार्श्व भाग में क्लोम छिद्र होते हैं। इनके क्लोमों में महीन रुधिर वाहिनियों का जाल फैला रहता है। जब ऑक्सीजन समृद्ध जल क्लोमों में प्रवेश करता है तो रुधिर वाहिनियों का रुधिर जल से ऑक्सीजन अवशोषित कर लेता है। जहाँ से सम्पूर्ण शरीर में ऑक्सीजन पहुँचा दी जाती है।

प्रश्न 3.
पौधों की जड़ें किस प्रकार श्वसन करती हैं ?
उत्तर:
पौधों की जड़ें मृदा कों के बीच उपस्थित वायु को ग्रहण करती हैं। मृदा कणों के बीच उपस्थित वायु मूलों में विसरण करके प्रवेश करती हैं जहाँ से ऑक्सीजन सभी मूल कोशिकाओं को पहुँचा दी जाती है।
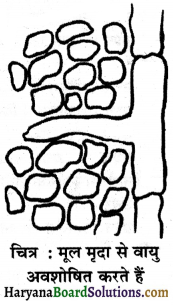
प्रश्न 4.
क्या आप अनुमान लगा सकते हैं कि यदि किसी गमले के पौधे में बहुत अधिक पानी डाल दिया जाये तो क्या होगा?
उत्तर:
यदि गमले में अत्यधिक पानी डाल दिया जायेगा तो पानी मृदा कणों के बीच के खाली स्थानों में भर जायेगा तथा वहाँ की वायु बाहर निकल जायेगी। ऐसी स्थिति में पौधे की जड़ों के लिए ऑक्सीजन उपलब्ध नहीं हो पायेगी और ऊर्जा की उत्पत्ति नहीं होगी फलस्वरूप जड़ें मरने लगेंगी और अन्य क्रियाएँ प्रभावित हो जाएँगी। अन्ततः पौधा सूख जायेगा।
![]()
प्रश्न 5.
श्वासप्रणाल तंत्र क्या होता है ?
उत्तर:
कॉकरोच के शरीर के पार्श्व भाग में छोटे-छोटे छिद्र होते हैं। अन्य कीटों के शरीर में भी इस प्रकार के छिद्र होते हैं। ये छिद्र श्वास रन्ध्र कहलाते हैं। कीटों में गैस के विनिमय के लिए वायु नलियों का जाल बिछा रहता है जो श्वासप्रणाल या वातक कहलाते हैं। ऑक्सीजन समृद्ध वायु श्वास रन्धों से होकर श्वास प्रणाली में जाती है जहाँ से यह सम्पूर्ण शरीर में विसरित होती है।
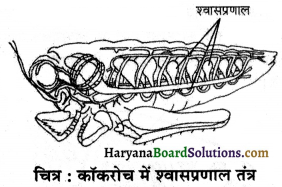
प्रश्न 6.
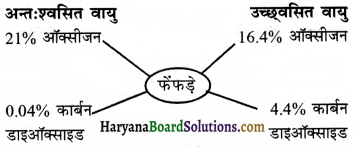
अन्तःश्वसित और उच्छ्वसित वायु में ऑक्सीजन और कार्बन डाइऑक्साइड का प्रतिशत बताइए।
उत्तर:
अन्तःश्वसित और उच्छ्वसित वायु में ऑक्सीजन और कार्बन डाइऑक्साइड का प्रतिशत
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
श्वसन क्या है ? यह कितने प्रकार का होता है ? ग्लूकोस के विखण्डन समीकरण देकर समझाइए।
उत्तर:
श्वसन:
भोज्य पदार्थों के जारण से ऊर्जा उत्पन्न होने की प्रक्रिया श्वसन कहलाती है। इस प्रक्रिया में ऑक्सीजन ग्रहण की जाती है तथा कार्बन डाइऑक्साइड मुक्त की जाती है। श्वसन दो प्रकार का होता है
(1) वायवीय श्वसन-जब ग्लूकोस का विखण्डन ऑक्सीजन के उपयोग द्वारा होता है तब इसे वायवीय श्वसन कहते हैं। इस प्रक्रिया में ग्लूकोस का विखण्डन होकर कार्बन डाइऑक्साइड तथा जल बनता है साथ ही अधिक ऊर्जा उत्पन्न होती है।

(2) अवायवीय श्वसन – जब ग्लूकोस का विखण्डन ऑक्सीजन के उपयोग के बिना होता है तो इसे अवायवीय श्वसन कहते हैं। इसमें ग्लूकोस के विखण्डन से एल्कोहॉल तथा कार्बन डाइऑक्साइड उत्पन्न होती है तथा कम मात्रा में ऊर्जा निकलती है।

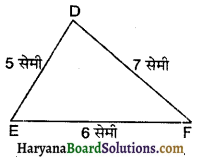
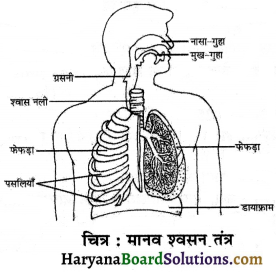
प्रश्न 2.
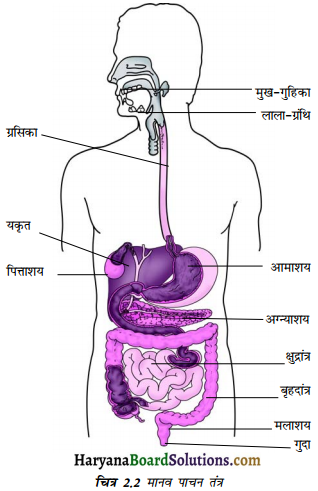
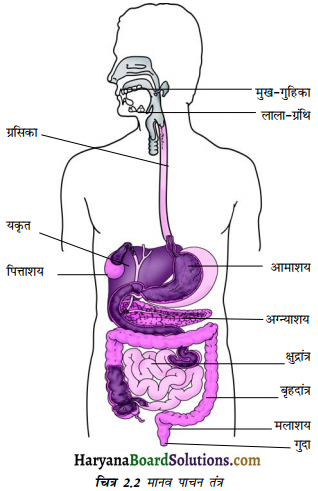
मनुष्य के श्वसन अंगों का नामांकित चित्र बनाइए।
उत्तर:
![]()
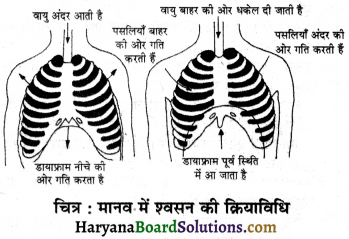
प्रश्न 3.
मानव में श्वसन की क्रियाविधि का सचित्र वर्णन कीजिए।
उत्तर:
श्वसन की क्रियाविधि सामान्यतः हम अपने नथुनों (नासा-द्वार) से वायु अन्दर लेते हैं। जब हम वायु को अन्तःश्वसन द्वारा अन्दर लेते हैं तो यह हमारे नथुनों से नासा-गुहा में चली जाती है। नासा-गुहा से वायु, श्वास नली से होकर हमारे फेफड़ों (फुफ्फुस) में जाती है। फेफड़े वक्ष गुहा में स्थित होते हैं। वक्ष गुहा पार्श्व में पसलियों से घिरी होती है। एक बड़ी पेशीय परत जो डायाफ्राम (मध्य पट) कहलाती है, वक्ष गुहा को आधार प्रदान करती है। श्वसन में डायाफ्राम और पसलियों से बने पिंजर की गति सम्मिलित है। अंतःश्वसन के समय पसलियाँ ऊपर और बाहर की ओर गति करती हैं और डायाफ्राम नीचे की ओर गति करता है। यह गति हमारी वक्षगुहा के आयतन को बढ़ा देती है और वायु फेफड़ों में आ जाती है। फेंफड़े वायु से भर जाते हैं। उच्छ्व सन के समय पसलियाँ नीचे और अन्दर की ओर आ जाती हैं, जबकि डायाफ्राम ऊपर की ओर अपनी पूर्व स्थिति में आ जाता है। इससे वक्ष गुहा का आयतन कम हो जाता है। इस कारण वायु फेंफड़ों से बाहर धकेल दी जाती है।
जीवों में श्वसन Class 7 HBSE Notes in Hindi
→ श्वसन क्रिया सभी जीवों के जीवित रहने के लिए अनिवार्य है। यह जीव द्वारा ग्रहण किये गये भोजन से ऊर्जा को निर्मुक्त करती है।
→ हम अन्तःश्वसन द्वारा, जो वायु शरीर के अन्दर लेते हैं, उसमें उपस्थित ऑक्सीजन का उपयोग ग्लूकोस को कार्बन डाइऑक्साइड और जल में विखण्डन के लिए किया जाता है। इस प्रक्रिया में ऊर्जा मुक्त होती है।
→ ग्लकोस का विखण्डन जीव की कोशिकाओं में होता है, जिसे कोशिकीय श्वसन कहते हैं।
→ यदि भोजन (ग्लूकोस), ऑक्सीजन के उपयोग द्वारा विखण्डित होता है, तो यह वायवीय श्वसन कहलाता है। यदि विखण्डन ऑक्सीजन की अनुपस्थिति में होता है तो यह श्वसन अवायवीय श्वसन कहलाता है।
→ अत्यधिक व्यायाम करते समय जब हमारी पेशी- कोशिकाओं में ऑक्सीजन की आपूर्ति अपर्याप्त होती है तब भोजन का विखण्डन अवायवीय श्वसन द्वारा होता है।
→ साँस लेना श्वसन प्रक्रम का एक चरण है, जिसमें जीव ऑक्सीजन समृद्ध वायु को शरीर के अन्दर लेता है और कार्बन डाइऑक्साइड समृद्ध वायु को बाहर निकालता है। गैसों के विनिमय के लिए विभिन्न जीवों में श्वसन अंग अलग-अलग प्रकार के होते हैं।
→ साँस को अन्दर खींचना अन्तःश्वसन तथा साँस बाहर निकालना उच्छ्वसन कहलाता है। इस प्रक्रम को श्वासोच्छवास भी कहते हैं।
→ शारीरिक सक्रियता के बढ़ने पर श्वसन दर बढ़ जाती है।
→ एक जोड़ी फेंफड़े हमारे मुख्य श्वसन अंग होते हैं, इसके अतिरिक्त नासिका, नासागुहा, श्वासनली आदि सहायक श्वसन अंग हैं।
→ गाय, भैंस, कुत्ते और बिल्ली जैसे जीवों में श्वसन अंग और श्वसन प्रक्रम मानव के समान ही होते हैं।
→ कॉकरोच एवं अन्य कीटों में श्वसन क्रिया श्वास रन्ध्रों द्वारा होती है।
→ केंचुए में गैसों का विनिमय उसकी आई त्वचा के माध्यम से होता है। मछलियों में यह क्लोम से और कीटों में श्वास प्रणाली से होता है।
→ मछलियों में श्वसन के अंग क्लोम होते हैं।
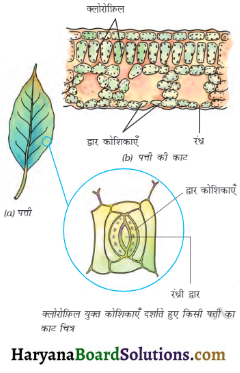
→ पादपों में मूल, मृदा में उपस्थित वायु को ग्रहण करती हैं। पत्तियों में सूक्ष्म छिद्र होते हैं, जिन्हें रन्ध्र कहते हैं, जिनमें गैसों का विनिमय होता है। पादप कोशिकाओं में ग्लूकोस का विखण्डन अन्य जीवों की ही भाँति होता है।
→ श्वसन – भोज्य पदार्थों के विखण्डन द्वारा ऊर्जा उत्पादन की प्रक्रिया।
→ कोशिकीय श्वसन – ग्लूकोस का विखण्डन, विकरों की सहायता से कोशिका के अन्दर होता है, इसे कोशिकीय श्वसन कहते हैं।
→ वायवीय श्वसन – यदि भोजन (ग्लूकोस) ऑक्सीजन के उपयोग द्वारा विखण्डित होता है तो यह प्रक्रम वायवीय श्वसन कहलाता है।
→ अवायवीय श्वसन – यदि भोजन ऑक्सीजन के अभाव में विखण्डित होता है तो इसे अवायवीय श्वसन कहते हैं।
→ अन्तःश्वसन – ऑक्सीजन युक्त वायु को फेफड़ों के अन्दर भरना।
→ उच्छ्वसन – कार्बन डाइऑक्साइड युक्त वायु को फेफड़ों से बाहर निकालना। .
→ श्वसन दर – एक व्यक्ति एक मिनट में जितनी बार साँस लेता है, उसे श्वसन दर कहते हैं।
→ फेफड़ा – मनुष्य के मुख्य श्वसन अंग।
→ श्वासनली – नासा गुहा से फेफड़ों को साँस ले जाने वाली नली।
→ डायाफ्राम – वक्ष गुहा को आधार प्रदान करने वाली एक बड़ी पेशीय परत डायाफ्राम कहलाती है।
→ श्वास रंध्र – कुछ कीटों में वायु के आदान-प्रदान के लिए शरीर पर सूक्ष्म छिद्र पाये जाते हैं, इन्हें श्वास रन्ध्र कहते
→ श्वास प्रणाल – कीटों में गैस विनिमय के लिए वायु नलिकाओं का जाल बिछा रहता है। जो श्वासप्रणाल या वातक कहलाता है।
→ क्लोम–मछलियों में ऑक्सीजन युक्त जल को अन्दर खींचने के लिए छिद्र जो श्वसन में सहायक होते हैं।
→ रन्ध – पौधों के हरे भार्गों में पाए जाने वाले विशेष छिद्र जिनसे गैसीय आदान-प्रदान होता है।
HBSE 7th Class Science Solutions Chapter 10 जीवों में श्वसन Read More »