HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.5

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.5

प्रश्न 1.
PQR एक त्रिभुज है जिसका P एक समकोण है। यदि PQ = 10 सेमी तथा PR = 24 सेमी हो, तब QR ज्ञात कीजिए।
हल :

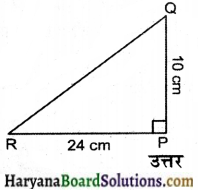
समकोण ΔPQR में पाइथागोरस प्रमेय से,
QR² = PQ² + PR²
= 24² + 10²
= 576 + 100 = 676
QR = \(\sqrt{676}\)
QR = \(\sqrt{26 \times 26}\)
OR = 26 सेमी। उत्तर

प्रश्न 2.
ABC एक त्रिभुज है जिसका एक समकोण है। यदि AB = 25 सेमी तथा AC = 7 सेमी हो, तब BC ज्ञात कीजिए।
हल :

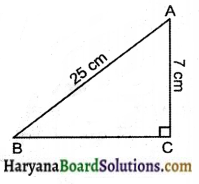
समकोण ΔABC में पाइथागोरस प्रमेय से,
AB² = AC² + BC²
BC² = AB² – AC²
= 25² – 7²
= 625 – 49 = 576
∴ BC = \(\sqrt{576}\)
BC = \(\sqrt{24 \times 24}\)
BC = 24 सेमी। उत्तर

प्रश्न 3.
दीवार के सहारे उसके पैर कुछ दूरी पर टिका कर 15 मीटर लम्बी एक सीढ़ी भूमि से 12 मीटर ऊँचाई पर स्थित खिड़की तक पहुँच जाती है। दीवार से सीढ़ी के पैर की दूरी ज्ञात कीजिए।
हल :

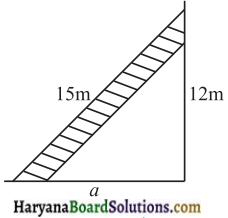
माना AB एक सीढ़ी है और B खिड़की है।
AB = 15 मीटर
BC = 12 मीटर
∵ ΔABC एक समकोण Δ है जिसमें ∠C समकोण है।
∴ AC² = AB² – BC² = 15² – 12²
= 225 – 144 = 81
AC² = 81
AC = \(\sqrt{9 \times 9}\) = 9 मीटर ।
अतः दीवार से सीढ़ी के पैर की दूरी 9 मीटर है। उत्तर

प्रश्न 4.
निम्नलिखित में भुजाओं के कौन-से समूह एक समकोण त्रिभुज बना सकते हैं ?
(i) 2.5 सेमी, 6.5 सेमी, 6 सेमी
(ii) 2 सेमी, 2 सेमी, 5 सेमी
(iii) 1.5 सेमी, 2 सेमी, 2.5 सेमी
समकोण त्रिभुज होने की स्थिति में उसके समकोण को भी पहचानिए।
हल :
(i) मांना a = 2.5 सेमी, b = 6.5 सेमी और c = 6 सेमी, तो
a² + c² = (2.5)² + 6²
= 6.25 + 36 = 42.25
b² = 42.25
b² = (6.5)²
b = 6.5
अतः a² + c² = b²
इसलिए दी गई भुजाएँ समकोण Δ बनाती हैं। और ∠B = 90°

(ii) माना a = 2 सेमी, b = 2 सेमी और c = 5 सेमी
a² + b² = (2)² + (2)² = 4 + 4 = 8
(c)² = (5)² = 25
a² + b² ≠ c²
अतः दी गई भुजाएँ समकोण Δ नहीं बनाती हैं।

(iii) माना a = 1.5 सेमी, b = 2 सेमी और c = 2.5 सेमी
a² + b² = (1.5)² + (2)²
= 2.25 + 4 = 6.25
(c)² = (2.5)² = 6.25
⇒ a² + b² = c²
अतः दी गई भुजाएँ समकोण त्रिभुज बनाती हैं। और ∠C = 90°

प्रश्न 5.
एक पेड़ भूमि से 5 मीटर की ऊंचाई पर टूट जाता है और उसके ऊपरी भाग को उसके आधार से 12 मीटर की दूरी पर छूता है। पेड़ की पूरी ऊँचाई ज्ञात कीजिए।
हल :

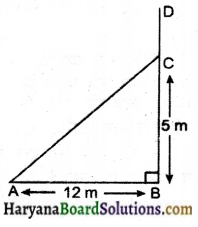
माना BCD एक पेड़ है, जो बिन्दु C से टूटता है और इसका ऊपरी सिरा D जमीन पर बिन्दु A को छूता है।
CD = AC
BC = 5 मीटर
AB = 12 मीटर
समकोण ΔABC में,
AC² = AB² + BC²
= 12² + 5²
= 144 + 25 = 169
AC² = 169
(AC)² = (13)²
AC = 13 सेमी
∴ CD = AC = 13 मीटर
पेड़ की ऊँचाई BD = BC + CD
= 5 + 13
= 18 मीटर। उत्तर

प्रश्न 6.
त्रिभुज PQR में ∠Q = 25° तथा कोण R = 65° है। निम्नलिखित में कौन-सा कथन सत्य है ?
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²

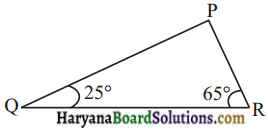
हल :
कोण योग गुण से,
∠P + ∠Q + ∠R = 180°
⇒ ∠P + 25° + 65° = 180°
⇒ ∠P + 90° = 180°
⇒ ∠P = 180° – 90° = 90°
∴ ΔPQR समकोण त्रिभुज है, जिसमें ∠P = 90° है।
∴ पाइथागोरस प्रमेय से,
PR² + PQ² = QR²
∴ (ii) सत्य हैं। उत्तर

प्रश्न 7.
एक आयत की लम्बाई 40 सेमी है तथा उसका एक विकर्ण 41 सेमी है। इसका परिमाप ज्ञात कीजिए।
हल :

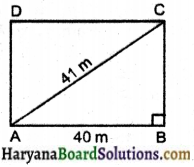
माना ABCD एक आयत है। जिसमें AB = 40 मीटर और AC = 41 मीटर।
समकोण ΔABC में कोण B समकोण है।
पाइथागोरस प्रमेय से,
BC² = AC² – AB²
= 41² – 40²
= (41 + 40) (41 – 40)
= 81 × 1
BC² = 81
(BC)² = (9)²
BC = 9 मीटर
अब आयत का परिमाप = 2(AB + BC)
= 2(40 + 9) मीटर
= 2 × 49
= 98 मीटर। उत्तर

प्रश्न 8.
एक समचतुर्भुज के विकर्ण 16 सेमी तथा 30 सेमी हैं। इसका परिमाप ज्ञात कीजिए।
हल :

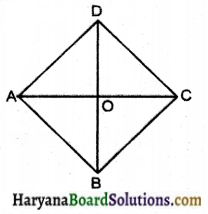
माना ABCD एक समचतुर्भुज है, जिसमें
विकर्ण AC = 16 सेमी और विकर्ण BD = 30 सेमी
हम जानते हैं कि समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं।
∴ ΔAOB में,
AO = \(\frac {1}{2}\)AC
= \(\frac {1}{2}\) × 16 = 8 सेमी
OB = \(\frac {1}{2}\)BD = \(\frac {1}{2}\) × 30 = 15 सेमी
समकोण ΔAOB में,
AB² = OA² + OB² = 8² + 15² = 64 +225 = 289.
AB = \(\sqrt{289}\)
AB = \(\sqrt{17 \times 17}\) = 17 सेमी
अतः समचतुर्भुज का परिमाप = 4 × 17 = 68 सेमी। उत्तर