Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.4 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.4
प्रश्न 1.
बराबर लम्बाई के रेखाखण्डों से बनाए गए अंकों के पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलैक्ट्रॉनिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।
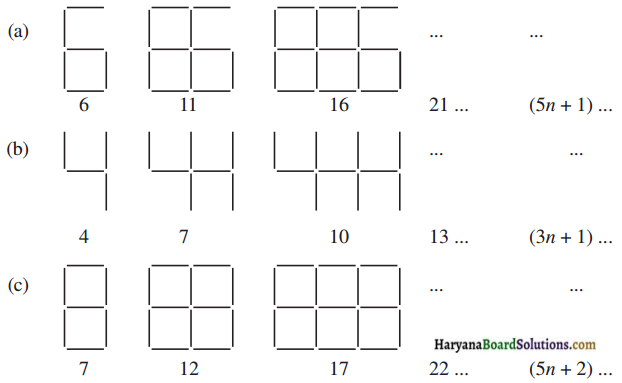
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की (n) संख्या दर्शाने वाला बीजीय व्यंजक प्रत्येक पैटर्न के दाईं ओर लिखा गया है। 6,4,8 के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
हल :
(a) हम जानते हैं कि 6 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (5n + 1)
अतः 5, 10, 100 अंकों को बनाने में लगे रेखाखण्डों की संख्या क्रमशः (5 × 5 + 1) = 25 + 1 = 26; (5 × 10 + 1) = 50 + 1 = 51 और (5 × 100 + 1)= 500 + 1 = 501.
(b) हम जानते हैं कि 4 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (3n + 1).
अतः 5, 10, 100 अंकों को बनाने में लगे रेखाखण्डों की संख्या क्रमशः (3 × 5 + 1)= 15 + 1 = 16; (3 × 10 + 1) = 30 + 1 = 31 और (3 × 100 + 1)= 300 + 1 = 301.
(c) हम जानते हैं कि 8 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (5n + 2).
अतः 5, 10, 100 अंकों को बनाने में लगे रेखाखण्डों की संख्या क्रमशः (5 × 5 + 2) = 25 + 2 = 27; (5 × 10 + 2) = 50 + 2 = 52 और (5 × 100 + 2) = 500 + 2 = 502.
![]()
प्रश्न 2.
संख्या पैटों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए।
हल :
दिए हुए पैटर्न से तालिका को पूरा करने पर,
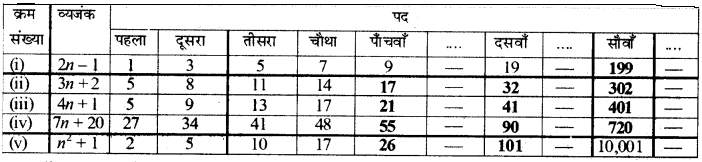
क्योंकि (i) 100वाँ पद = 2 × 100 – 1
= 200 – 1 = 199
(ii) 5वाँ पद = 3 × 5 + 2
= 15 + 2 = 17
10वाँ पद = 3 × 10 + 2
= 30 + 2 = 32
और 100वाँ पद = 3 × 100 + 2
= 300 + 2 = 302
(iii) 5वाँ पद = 4 × 5 + 1
= 20 + 1 = 21
10वाँ पद = 4 × 10 + 1
= 40 + 1 = 41
और 100वाँ पद = 4 × 100 + 1
= 400 + 1 = 401
(iv) 5वाँ पद = 7 × 5 + 20
= 35 + 20 = 55
10वाँ पद = 7 × 10 + 20
= 70 + 20 = 90
और, 100वाँ पद = 7 × 100 + 20
= 700 + 20 = 720
(v) 5वाँ पद = 52 + 1
= 25 + 1 = 26
10वाँ पद = 102 + 1
= 100 + 1
= 101