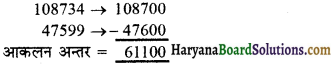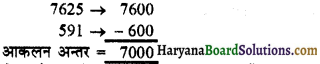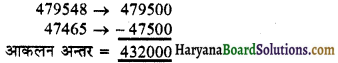Haryana State Board HBSE 6th Class Maths Solutions Chapter 1 अपनी संख्याओं की जानकारी InText Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 1 अपनी संख्याओं की जानकारी InText Questions
पृष्ठ सं. 2 से (प्रयास कीजिए)
प्रश्न 1.
क्या आप तुरन्त ज्ञात कर सकते हैं कि प्रत्येक पंक्ति में कौन-सी संख्या सबसे बड़ी है और कौन-सी संख्या सबसे छोटी है ?
(i) 382, 4972, 18, 59785, 750
(ii) 1473, 89423, 100, 5000, 310
(iii) 1834, 75284, 111, 2333, 450
(iv) 2853, 7691, 9999, 12002, 124
क्या यह सरल था? यह सरल क्यों था?
हल :
(i) 59785 सबसे बड़ी है और 18 सबसे छोटी है।
(ii) 89423 सबसे बड़ी है और 100 सबसे छोटी है।
(iii) 75284 सबसे बड़ी है और 111 सबसे छोटी है।
(iv) 12002 सबसे बड़ी है और 124 सबसे छोटी है।
यह सरल था क्योंकि.
(i) एक संख्या जिसमें अंकों की संख्या अधिक हो, दूसरी संख्या से बड़ी होती है।
(ii) जब दो संख्याओं में अंकों की संख्या समान हो, तो जिस संख्या में सबसे बाई ओर का अंक बड़ा होगा वह संख्या बड़ी होगी।
(iii) यदि सबसे बाईं ओर का अंक बराबर हो, तो उसके दाईं ओर के अंक से तुलना करते हैं।

पृष्ठ सं. 3 से
प्रश्न 1.
प्रत्येक समूह में सबसे बड़ी और सबसे छोटी संख्याएँ ज्ञात कीजिए:
(a) 4536, 4892, 4370, 4452
(b) 15623, 15073,15189,15800
(c) 25286,25245,25270, 25210
(d) 6895, 23787, 24569,24659.
हल :
(a) सभी संख्याओं 4536, 4892, 4370 तथा 4452 में बायीं ओर के अंकों की संख्या समान है अर्थात् सभी में हजार के स्थान पर अंक समान हैं। अतः सौ के स्थान पर लिखे अंकों को अवरोही क्रम में लिखते हैं :
8 > 5 > 4 > 3
∴ 4892 सबसे बड़ी संख्या है तथा 4370 सबसे छोटी संख्या है।
(b) सभी संख्याओं 15623, 15073, 15189 तथा 15800 में अंकों की संख्या समान है। आगे सभी में दस हजार तथा हजार के स्थान पर समान अंक हैं। अतः सौ के स्थान पर लिखे अंकों को अवरोही क्रम में लिखते हैं :
8 > 6 > 1 > 0
∴ 15800 सबसे बड़ी संख्या है तथा 15073 सबसे छोटी संख्या है।
(c) सभी संख्याओं 25286,25245,25270 तथा 25210 में अंकों की संख्या समान है। आगे सभी में दस हजार के स्थान पर, हजार के स्थान पर तथा सौ के स्थान पर सभी अंक समान हैं। अत: दहाई के स्थान पर अंकों को अवरोही क्रम में लिखते हैं :
8 > 7 > 4 > 1
∴ 25286 सबसे बड़ी संख्या है और 25210 सबसे छोटी संख्या है।
(d) ∵ दी गई संख्याओं में 6895 में अंकों की संख्या सबसे कम है। अत: 6895 सबसे छोटी संख्या है। पुनः शेष बची संख्याओं 23787,24569 तथा 24659 सभी में अंकों की संख्या समान है। आगे दस हजार के स्थान पर तथा हजार के स्थान पर सभी अंक समान हैं। (23787 को छोड़कर, क्याकि हम सबसे बड़ा सख्या दख रह है।)
सौवें स्थान पर अंकों की तुलना करने पर हम पाते हैं कि
5 < 6
∴ 24659 सबसे बड़ी संख्या है।
पृष्ठ सं. 3 से
प्रश्न 1.
बिना पुनरावृत्ति किए, दिए हुए अंकों का प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(a) 2, 8, 7, 4
(b) 9, 7, 4, 1
(c) 4, 7, 5, 0
(d) 1, 7, 6, 2
(e) 5, 4, 0, 3.
हल :
(a) दिए हुए अंक : 2, 8, 7, 4
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
8, 7, 4, 2
∴ 8742 चार अंकों की सबसे बड़ी संख्या है तथा 2478 चार अंकों की सबसे छोटी संख्या है।
(b) दिए हुए अंक : 9, 7, 4, 1
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
9, 7, 4, 1
∴ 9741 चार अंकों की सबसे बड़ी संख्या है तथा 1479 चार अंकों की सबसे छोटी संख्या है।
(c) दिए हुए अंक : 4, 7, 5, 0
दिए हुए अंर्को को अवरोही क्रम में लिखने पर,
7, 5, 4, 0
∴ 7540 चार अंकों की सबसे बड़ी संख्या है तथा चार अंकों की सबसे छेटी संख्या 4057 है।
(d) दिए हुए अंक : 1, 7, 6, 2
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
7, 6, 2, 1
∴ 7621 चार अंकों की सबसे बड़ी संख्या है तथा चार अंकों की सबसे छोटी संख्या 1267 है।
(e) दिए हुए अंक : 5, 4, 0, 3
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
5, 4, 3, 0
∴ 5430 चार अंकों की सबसे बड़ी संख्या है तथा चार अंकों की सबसे छोटी संख्या 3045 है।

प्रश्न 2.
किसी एक अंक का दो बार प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(a) 3, 8, 7
(b) 9, 0, 5
(c) 0, 4, 9
(d) 8, 5, 1.
हल :
(a) दिए हुए अंक : 3, 8, 7
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
8, 7, 3
∵ एक अंक का दो बार प्रयोग करने पर चार अंकों की सबसे बड़ी संख्या 8873 है तथा चार अंकों की सबसे छोटी संख्या 3378 है।
(b) दिए हुए अंक : 9, 0, 5
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
9, 5, 0
∵ एक अंक का दो बार प्रयोग करने पर चार अंकों की सबसे बड़ी संख्या 9950 है तथा 5009 चार अंकों की सबसे छोटी संख्या है।
(c) दिए गए अंक : 0, 4, 9
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
9, 4, 0
∵ एक अंक का दो बार प्रयोग करने पर चार अंकों की सबसे बड़ी संख्या 9940 है तथा चार अंकों की सबसे छोटी संख्या 4009 है।
(d) दिए गए अंक : 8, 5, 1
दिए हुए अंकों को अवरोही क्रम में लिखने पर,
8, 5, 1
∵ एक अंक का दो बार प्रयोग करने पर चार अंकों की सबसे बड़ी संख्या 8851 है तथा चार अंकों की सबसे छोटी संख्या 1158 है।
प्रश्न 3.
दिए हुए प्रतिबन्धों के साथ किन्हीं चार अंकों का प्रयोग करके 4 अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(ध्यान दीजिए, अंक 0 से संख्या प्रारम्भ नहीं हो सकती। क्यों?)
हल :
अंकों को अवरोही क्रम में लिखने पर,
9, 8, 7, 6, 5, 4, 3, 2, 1, 0
(a) अंक 7 सदैव इकाई के स्थान पर रहे :
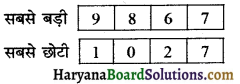
(b) अंक 4 सदैव दहाई के स्थान पर रहे :
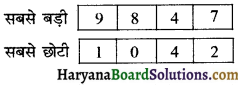
(c) अंक 9 सदैव सौ के स्थान पर रहे:
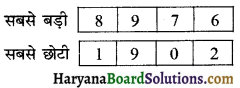
(d) अंक 1 सदैव हजार के स्थान पर रहे :
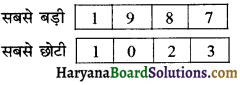
अंक 0 से संख्या प्रारम्भ नहीं हो सकती क्योंकि 0 के संख्या के प्रारम्भ में आने पर, संख्या तीन अंकों की रह जायेगी।
प्रश्न 4.
मान लीजिए, आप दो अंक 2 और 3 लेते हैं। इन अंकोंको समानबार दोहरातेहुए चार अंकों की संख्याएँ बनाइए। कौन-सी संख्या सबसे बड़ी है ? कौन-सी संख्या सबसे छोटी है? आप ऐसी कुल कितनी संख्याएँ बना सकते हैं?
हल :
दो अंक 2 और 3 दिए गए हैं। इन अंकों को समान बार दोहराते हुए चार अंकों की संख्या लिखने पर,
2233, 3322, 2332, 2323 और 3232
इनमें सबसे बड़ी संख्या 3322 है तथा 2233 सबसे छोटी संख्या है। इससे हम 6 विभिन्न संख्याएँ बना सकते हैं।

पृष्ठ सं. 4 से
उचित क्रम में खड़े होना-
प्रश्न 1. इनमें कौन सबसे लम्बा है?
प्रश्न 2. इनमें कौन सबसे छोटा है ?
(a) क्या आप इन्हें इनकी लम्बाइयों के बढ़ते हुए क्रम में खड़ा कर सकते हैं?
(b) क्या आप इन्हें इनकी लम्बाइयों के घटते हुए क्रम में खड़ा कर सकते हैं?

हल :
1. ∵ 160 > 159 > 158 > 154
∴ रामहरि सबसे लम्बा है।
2. ∵ 154 < 158 < 159 < 160
∴ डोली सबसे छोटी है।
(a) हाँ, इनको इनकी लम्बाइयों के बढ़ते हुए क्रम में इस प्रकार खड़ा किया जा सकता है:
1. डोली,
2. मोहन,
3. शशि,
4. रामहरि।
(b) हाँ, इनको इनकी लम्बाइयों के घटते हुए क्रम में इस प्रकार खड़ा किया जा सकता है:
1. रामहरि,
2. शशि,
3. मोहन,
4. डोली।
पृष्ठ सं. 4 से (क्या खरीदें)
प्रश्न 1.
सोहन और रीता एक अलमारी खरीदने गए। वहाँ कई अलमारियाँ उपलब्ध थीं जिन पर उनके मूल्यों की पर्चियाँ लगी हुई थीं।
(a) क्या आप इनके मूल्यों को बढ़ते हुए क्रम में . व्यवस्थित कर सकते हैं?
(b) क्या आप इनके मूल्यों को घटते हुए क्रम में व्यवस्थित कर सकते हैं ?
हल :
(a) हाँ, अलमारियों के मूल्यों को बढ़ते हुए क्रम में व्यवस्थित कर सकते हैं :
₹ 1,788, ₹ 1,897, ₹ 2,635,₹ 2,854, ₹ 3,975
(b) हाँ, अलमारियों के मूल्यों को घटते हुए क्रम में व्यवस्थित कर सकते हैं :
₹ 3,975, ₹ 2,854, ₹ 2,635, ₹ 1,897, ₹ 1,788

पृष्ठ सं. 5 से
प्रश्न 1.
निम्नलिखित संख्याओं को आरोही क्रम में व्यवस्थित कीजिए:
(a) 847, 9754, 8320, 571
(b) 9801, 25751, 36501, 38802.
हल :
(a) दिए हुए अंकों को आरोही क्रम में लिखने पर,
571, 847, 8320, 9754.
(b) दिए हुए अंकों को आरोही क्रम में लिखने पर,
9801, 25751, 36501, 38802.
प्रश्न 2.
निम्नलिखित संख्याओं को अवरोही क्रम में व्यवस्थित कीजिए :
(a) 5000, 7500, 85400, 7861
(b) 1971, 45321, 88715, 92547.
हल :
(a) दिए हुए अंकों को अवरोही क्रम में लिखने पर,
85400, 7861, 7500, 5000.
(b) दिए हुए अंकों को अवरोही क्रम में लिखने पर,
92547, 88715, 45321, 1971.
पृष्ठ सं. 7 से
प्रश्न 1.
संख्याओं को पढ़िए और जहाँ-जहाँ रिक्त स्थान है, उनके नाम लिखिए और प्रसारित रूप में लिखिए।
हल:
| संख्या | संख्या का नाम | प्रसारित रूप |
| 50000 | पचास हजार | 5 × 10000 |
| 41000 | इक्तालीस हजार | 4 × 10000 + 1 × 1000 |
| 47300 | सैंतालीस हजार तीन सौ | 4 × 10000 + 7 × 1000 + 3 × 100 |
| 57630 | सत्तावन हजार छ: सौ तीस | 5 × 10000 + 7 × 1000 + 6 × 100 + 3 × 10 |
| 29485 | उन्तीस हजार चार सौ पिच्चासी | 2 × 10000 + 9 × 1000 + 4 × 100 + 8 × 10 + 5 × 1 |
| 29085 | उन्तीस हजार पिच्चासी | 2 × 10000 + 9 × 1000 + 8 × 10 + 5 × 1 |
| 20085 | बीस हजार पिच्चासी | 2 × 10000 + 8 × 10 + 5 × 1 |
| 20005 | बीस हजार पाँच | 2 × 10000 + 5 × 1 |
पृष्ठ सं. 8 से
प्रश्न 1.
संख्याओं को पढ़कर उन्हें रिक्त स्थानों में प्रसारित रूप में और उनके नाम लिखिए।
हल:
| संख्या | संख्या का नाम | प्रसारित रूप |
| 4,57,928 | चार लाख सत्तावन हजार नौ सौ अट्ठाईस | 4 × 100000 + 5 × 10000 + 7 × 1000 + 9 × 100 + 2 × 10 + 8 × 1 |
| 4,07,928 | चार लाख सात हजार नौ सौ अट्ठाईस | 4 × 100000 + 7 × 1000 + 9 × 100 + 2 × 10 + 8 × 1 |
| 4,00,829 | चार लाख आठ सौ उन्तीस | 4 × 100000 + 8 × 100 + 2 × 10 + 9 × 1 |
| 4,00,029 | चार लाख उन्तीस | 4 × 100000 + 2 × 10 + 9 × 1 |

पृष्ठ सं. 8 से
प्रश्न 1.
1. 10 – 1 क्या है?
2. 100 – 1 क्या है?
3. 10,000 – 1 क्या है?
4. 1,00,000 – 1 क्या है?
5. 1,00,00,000 – 1 क्या है?
हल :
1. 10 – 1 = 9
दो अंकों की सबसे छोटी संख्या – 1
एक अंक की सबसे बड़ी संख्या
2. 100 – 1 = 99
तीन अंकों की सबसे छोटी संख्या – 1
= दो अंकों की सबसे बड़ी संख्या
3. 10,000 – 1 = 9,999
पाँच अंकों की सबसे छोटी संख्या – 1
= चार अंकों की सबसे बड़ी संख्या
4. 1,00,000 – 1 = 99,999
छ: अंकों की सबसे छोटी संख्या – 1
= पाँच अंकों की सबसे बड़ी संख्या
5. 1,00,00,000 – 1 = 99,99,999
आठ अंकों की सबसे छोटी संख्या – 1
= सात अंकों की सबसे बड़ी संख्या।
पृष्ठ सं. 9 से
प्रश्न 1.
ऐसे पाँच उदाहरण दीजिए, जहाँ गिनी जाने वाली वस्तुओं की संख्या 6 अंकों की संख्या से अधिक होगी।
हल :
5 उदाहरण जहाँ पर गिनी जाने वाली वस्तुओं की संख्या 6 अंकों की संख्या से अधिक होगी :
(i) एक जिले में वाहनों की संख्या।
(ii) एक बड़े शहर में व्यक्तियों की संख्या।
(iii) दिल्ली के सभी विद्यालयों में विद्यार्थियों की संख्या।
(iv) एक बड़े खेत में उगे हुए मक्के के पौधों की संख्या।
(v) एक भरी हुई बोरी में गेहूँ के दानों की संख्या।
प्रश्न 2.
6 अंकों की सबसे बड़ी संख्या से प्रारम्भ करते हुए, अवरोही क्रम में पिछली 5 संख्याएँ लिखिए।
हल :
छः अंकों की सबसे बड़ी संख्या 9,99,999 है। अवरोही क्रम में पिछली 5 संख्याएँ इस प्रकार हैं :
9,99,998, 9,99,997, 9,99,996, 9,99,995, 9,99,994.
प्रश्न 3.
8 अंकों की सबसे छोटी संख्या से प्रारम्भ करते हुए, आरोही क्रम में अगली 5 संख्याएँ लिखिए और उन्हें पढ़िए।
हल :
8 अंकों की सबसे छोटी संख्या 1,00,00,000 (एक करोड़) है।
आरोही क्रम में अगली 5 संख्याएँ इस प्रकार हैं : 1,00,00.001, 1,00,00,002, 1,00,00,003, 1,00,00,004 तथा 1,00,00,005
ये संख्याएँ क्रमशः इस प्रकार पढ़ी जायेंगी : एक करोड़ एक, एक करोड़ दो, एक करोड़ तीन, एक करोड़ चार तथा एक करोड़ पाँच।

पृष्ठ सं. 11 से
प्रश्न 1.
इन संख्याओं को बॉक्सों का प्रयोग करते हुए लिखिए और फिर प्रसारित रूप में लिखिए :
(i) 475320
(ii) 9847215
(iii) 97645310
(iv) 30458094
(a) इनमें कौन-सी संख्या सबसे छोटी है ?
(b) इनमें कौन-सी संख्या सबसे बड़ी है?
(c) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
हल :
दी गई संख्याओं को बॉक्सों का प्रयोग कर, प्रसारित रूप में निम्न प्रकार लिखते हैं :
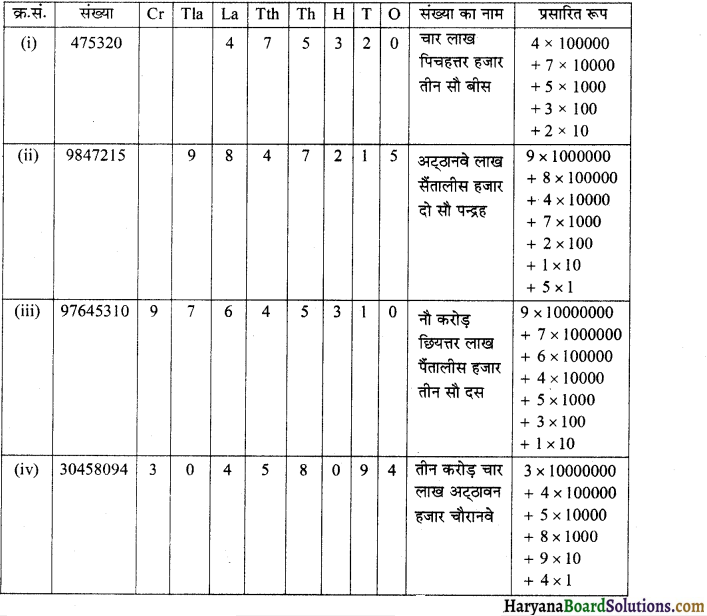
(a) सबसे छोटी संख्या = 475320
(b) सबसे बड़ी संख्या = 97645310
(c) इन संख्याओं को आरोही क्रम में रखने पर, 475320, 9847215, 30458094, 97645310
तथा इन संख्याओं को अवरोही क्रम में रखने पर, 97645310, 30458094, 9847215,475320.
प्रश्न 2.
निम्नलिखित संख्याओं को देखिए :
(i) 527864
(ii) 95432
(iii) 18950049
(iv) 70002509
(a) इन संख्याओं को बॉक्सों का प्रयोग करते हुए लिखिए।
(b) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
हल :
(a) दी गई संख्याओं को बॉक्सों का प्रयोग कर, अल्पविराम का प्रयोग कर अग्र प्रकार से लिखते हैं :
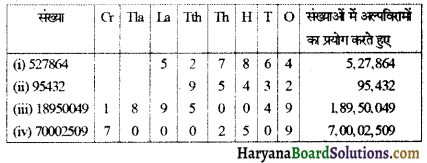
(b) इन संख्याओं को आरोही क्रम में लिखने पर, 95,432, 5,27,864, 1,89,50,049, 7,00,02,509
तथा इन संख्याओं को अवरोही क्रम में लिखने पर, 7,00,02,509, 1,89,50,049, 5,27,864, 95,432.
प्रश्न 3.
ऐसी ही तीन और बड़ी संख्याएँ लेकर इस प्रक्रिया को दोहराइए।
हल :
इस प्रश्न को छात्र/छात्राएँ प्रश्न 1 तथा प्रश्न 2 के अनुसार विभिन्न अंकों की संख्याएँ लेकर स्वयं हल करने का प्रयास करें।

पृष्ठ सं. 12 से
प्रश्न 1.
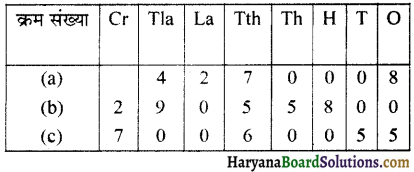
क्या आप संख्यांक लिखने में मेरी सहायता कर सकते हैं
(a) बयालीस लाख सत्तर हजार आठ।
(b) दो करोड़ नब्बे लाख पचपन हजार आठ सौ।
(c) सात करोड़ साठ हजार पचपन।
हल :
पृष्ठ सं. 12 से
प्रश्न 1.
आपके पास 4, 5, 6, 0, 7 और 8 के अंक हैं। इनका प्रयोग करते हुए 6 अंकों की पाँच संख्याएँ बनाइए:
(a) पढ़ने में सरलता के लिए अल्पविराम लगाइए।
(b) इन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
हल :
अंक 4, 5, 6, 0, 7 और 8 का प्रयोग करते हुए 6 अंकों की पाँच संख्याएँ :
456078, 870654, 540687, 786045 तथा 607845.
(a) इन संख्याओं को अल्पविरामों का प्रयोग कर दोबारा लिखने पर,
456,078, 8,70,654, 5,40,68787, 86,045 तथा 6,07,845
(b) इन्हें आरोही क्रम में व्यवस्थित करने पर,
456078, 540687, 607845, 786045, 870654
तथा अवरोही क्रम में व्यवस्थित करने पर,
870654, 786045, 607845, 540687, 456078.
प्रश्न 2.
अंकों 4, 5, 6, 7, 8 और 9 का प्रयोग कर 8 अंकों की कोई तीन संख्याएँ बनाइए। पढ़ने में सरलता के लिए अल्पविरामों का प्रयोग कीजिए।
हल :
अंकों 4,5,6,7,8 और 9 का प्रयोग करते हुए 8 अंकों की तीन संख्याएँ :
45678945, 54987654 तथा 67458945.
इन संख्याओं में अल्पविरामों का प्रयोग करते हुए पुनः लिखने पर,
4,56,78,945, 5,49,87,654 तथा 6,74,58,945.

प्रश्न 3.
अंकों 3, 0 और 4 का प्रयोग कर 6 अंकों की पाँच संख्याएँ बनाइए। अल्पविरामों का भी प्रयोग कीजिए।
हल :
अंक 3,0 और 4 का प्रयोग करते हुए 6 अंकों की 5 संख्याएँ:
330044, 440033, 340043, 430034 तथा 403043 इन संख्याओं में अल्पविरामों का प्रयोग कर पुनः लिखने पर,
3,30,044, 4,40,033, 3,40,043, 4,30,034 तथा 4.03,043.
पृष्ठ सं. 13 से
प्रश्न 1.
कितने सेण्टीमीटरों से एक किलोमीटर बनता है?
हल :
1 किमी = 1000 मीटर
= 1000 × 100 सेमी
[1 मीटर = 100 सेमी]
= 100000 सेमी
अतः 100000 सेण्टीमीटरों से एक किलोमीटर बनता है। उत्तर
प्रश्न 2.
भारत के पाँच बड़े शहरों के नाम लिखिए। उनकी जनसंख्या पता कीजिए। इन शहरों में से प्रत्येक युग्म शहरों के बीच की दूरी भी किलोमीटरों में पता कीजिए।
हल :
भारत के पाँच बड़े शहरों के नाम :
- दिल्ली, चेन्नई, बंगलुरू, कोलकाता और हैदराबाद।
- इन शहरों की जनसंख्या तथा दूरी की जानकारी सामान्य ज्ञान पुस्तक से पता की जा सकती है।
पृष्ठ सं. 13 से
प्रश्न 1.
कितने मिलीग्राम से एक किलोग्राम बनता है?
हल :
1 किलोग्राम = 1000 ग्राम
= 1000 × 1000 मिलीग्राम
[1 ग्राम = 1000 मिलीग्राम]
= 1000000 मिलीग्राम
अतः 100000 मिलीग्राम से एक किलोग्राम बनता है। उत्तर

प्रश्न 2.
दवाई की गोलियों के एक बक्से में 2,00,000 गोलियाँ हैं, जिनमें प्रत्येक का भार 20 मिग्रा है। इस बक्से में रखी सभी गोलियों का कुल भार ग्रामों में कितना है और किलोग्रामों में कितना है?
हल :
एक गोली का भार = 20 मिलीग्नाम
गोलियों के बक्से का भार
= 2,00,000 गोलियों का भार
= 2,00,000 × 20 मिलीग्नाम
= \(\frac{200000 \times 20}{1000}\) ग्राम = 4000 ग्राम
= \(\frac {4000}{1000}\) किलोग्राम = 4 किलोग्राम
अतः बक्से में रखी सभी गोलियों का कुल भार ग्रामों में 4000 ग्राम है और किलोग्राम में 4 किलोग्राम है। उत्तर
पृष्ठ सं. 14 से
प्रश्न 1.
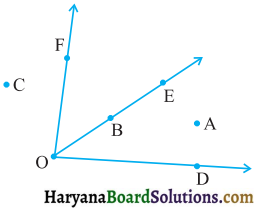
एक बस ने अपनी यात्रा आरम्भ की और 60 किमी/घण्टा की चाल से विभिन्न स्थानों पर पहुंची। इस यात्रा को नीचे दर्शाया गया है:
(i) A से D तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(ii) D से G तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iii) बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iv) क्या आप C से D तक और D से E तक की दूरियों का अन्तर ज्ञात कर सकते हैं?
(v) बस द्वारा निम्नलिखित यात्रा में लिया समय ज्ञात कीजिए:
(a) A से B तक
(b) C से D तक
(c) E से G तक
(d) कुल यात्रा।
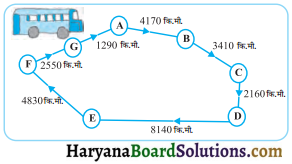
हल :
आकृति से स्पष्ट है :
(i) बस द्वारा A से D तक जाने में तय की गई कुल दूरी
= (4170 + 3410 + 2160) किमी
= 9740 किमी।
(ii) बस द्वारा D से G तक जाने में तय की गई कुल दूरी
= 8140 किमी + 4830 किमी + 2550 किमी
= (8140 + 4830 + 2550) किमी
= 15520 किमी।
(iii) बस द्वारा तय की गई कल दूरी = (4170 + 3410 + 2160 + 8140 + 4830 + 2550 + 1290) किमी
= 26550 किमी।
(iv) C से D तक की दूरी = 2160 किमी
D से E तक की दूरी = 8140 किमी
∴ C से D तक और D से E तक की दूरियों का अन्तर
= (8140 – 2160) किमी = 5980 किमी
(v) (a) बस द्वारा A से B तक लिया गया समय
समय = दूरी / चाल
यहाँ दूरी = 4170
चाल = 60 किमी / घण्टा
समय = \(\frac {4170}{60}\) घण्टे = 69 \(\frac {30}{60}\) घण्टे
= 69 घण्टे \(\frac {30}{60}\) × 60 मिनट
= 69 घण्टे 30 मिनट।
(b) C से D तक लिया गया समय
समय = दूरी / चाल = \(\frac {2160}{60}\) घण्टे = 36 घण्टे।
(c) E से G तक लिया गया समय
समय = दूरी / चाल = \(\frac{4830+2550}{60}\) घण्टे
= \(\frac {7380}{60}\) घण्टे = 123 घण्टे।
(d) कुल यात्रा में लगा समय
समय = कुल दूरी / चाल = \(\frac {26550}{60}\) घण्टे
= 442\(\frac {3}{6}\) घण्टे
= 442 घण्टे \(\frac {3}{6}\) × 60 मिनट
= 442 घण्टे 30 मिनट।

प्रश्न 2.
रमन की दुकान
| वस्तुएँ | दर |
| सेब | ₹ 40 प्रति किग्रा |
| संतरा | ₹ 30 प्रति किग्रा |
| कंघा | ₹ 3 प्रति नग |
| दाँतों का ब्रुश | ₹ 10 प्रति नग |
| पेंसिल | ₹ 1 प्रति नग |
| अभ्यास-पुस्तिका | ₹ 6 प्रति नग |
| साबुन की टिकिया | ₹ 8 प्रति नग |
पिछले वर्ष की बिक्री
| सेब | 2457 किग्रा |
| संतरा | 3004 किग्रा |
| कधा | 22760 नग |
| दाँतों का बुश | 25367 नग |
| पेंसिल | 38530 नग |
| अभ्यास-पुस्तिका | 40002 नग |
| साबुन की टिकिया | 20005 नग |
(a) क्या आप रमन द्वारा पिछले वर्ष बेचे गए सेब और संतरों का कुल भार ज्ञात कर सकते हैं ?
सेबों का भार = ………………. किग्रा
संतरों का भार = ………………. किग्रा
अतः कुल भार = ………. किग्रा + ………. किग्रा ………… किग्रा
(b) क्या आप रमन द्वारा सेबों को बेचने से प्राप्त कल धनराशि ज्ञात कर सकते हैं ?
(e) क्या आप रमन द्वारा सेबों और संतरों को बेचने से प्राप्त कुल धनराशि ज्ञात कर सकते हैं ?
(d) रमन द्वारा प्रत्येक वस्तु के बेचने से प्राप्त धनराशियों को दर्शाने वाली एक सारणी बनाइए। धनराशियों की इन प्रविष्टियों को अवरोही क्रम में व्यवस्थित कीजिए। वह कौन-सी वस्तु है जिससे रमन को सबसे अधिक धनराशि प्राप्त हुई ? यह धनराशि क्या है ?
हल :
(a) सेबों का वजन = 2457 किग्रा
संतरों का वजन = 3004 किग्रा
कुल वजन = (2457 + 3004) किग्रा
= 5461 किग्रा
अत: पिछले वर्ष बेचे गए सेबों और संतरों का कुल
वजन = 5461 किग्ना।
(b) बेचे गए सेबों का वजन = 2457 किग्रा
सेबों का विक्रय मूल्य = ₹ 40 प्रति किग्रा
∴ सेबों को बेचने से प्राप्त राशि = ₹(2457 × 40)
= ₹ 98,280
(c) बेचे गए संतरों का वजन = 3004 किग्रा
संतरों का विक्रय मूल्य = ₹30 प्रति किग्रा
= ₹(3004 × 30)
= ₹ 90,120
∴ कुल सेबों और संतरों को बेचने से प्राप्त कुल राशि
= ₹(98,280 + 90,120)
= ₹ 1,88,400
(d) रमन द्वारा प्रत्येक वस्तु के बेचने से प्राप्त धन राशियों को दर्शाने वाली एक सारणी :
| वस्तु | दर | कुल | धनराशि (रुपयों में) |
| सेब | 40 रु. प्रति किग्रा | 2457 | 98,280 |
| संतर | 30 रु. प्रति किग्रा | 3004 | 90,120 |
| कंघा | 3 रु. प्रति किग्रा | 22760 | 68,280 |
| दाँतों का बुश | 10 रु. प्रति किग्रा | 25367 | 2,53,670 |
| पेसिल | 1 रु. प्रति किग्रा | 38530 | 38,530 |
| अभ्यास-पुस्तिका | 6 रु. प्रति किग्रा | 40002 | 2,40,012 |
| साबुन की टिकिया | 8 रु. प्रति किग्रा | 20005 | 1,60,040 |
धनराशियों की इन प्रविष्टियों को अवरोही क्रम में व्यवस्थित करने पर,
2,53,670, 2,40,012, 1,60,040,98,280,90,120, 68,280, 38,530
रमन को सबसे अधिक धनराशि दाँतों के ब्रुश से प्राप्त हुई। यह धनराशि = ₹ 2,53,670 है।

पृष्ठ सं. 20 से
प्रश्न 1.
इन संख्याओं को निकटतम दहाई तक सन्निकटित कीजिए:
28 32 52 41 39 48
64 59 99 215 1453 2936
हल :
संख्या 5 तथा 5 से अधिक को 10 के सन्निकटित कर हल करते हैं।
28 → 30
64 → 60
32 → 30
59 → 60
52 → 50
99 → 100
41 → 40
215 → 220
39 → 40
1453 → 1450
48 → 50
2936 → 2940
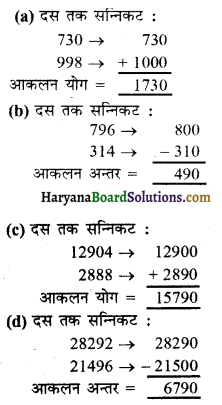
प्रश्न 2.
निम्नलिखित सन्निकटों की जाँच कीजिए और उन्हें सही कीजिए जो गलत हैं।
(i) 2573 → 3000
(ii) 53552 → 53000
(iii) 6404 → 6000
(iv) 65537 → 65000
(v) 7805 → 7000
(vi) 3499 → 4000
हल:
(i) 2573 → 3000 (सही)
(ii) 53552 → 53000 (गलत) → 54000 (सही)
(iii) 6404 → 6000 (सही)
(iv) 65537 → 65000 (गलत) → 66000 (सही)
(v) 7805 → 7000 (गलत) → 8000 (सही)
(vi) 3499 → 4000 (गलत) → 3000 (सही)
पृष्ठ सं. 21 से
प्रश्न 1.
दी हुई संख्या को निकटतम दहाई, सौ, हजार और दस हजार तक सन्निकटित कीजिए :
| दी हुई संख्या | निम्न के निकटतम | सन्निकटित रूप |
| 75847 | दहाई | ___________________ |
| 75847 | सौ | ___________________ |
| 75847 | हजार | ___________________ |
| 75847 | दस हजार | ___________________ |
हल:
| दी हुई संख्या | निम्न के निकटतम | सन्निकटित रूप |
| 75847 | दहाई | 75850 |
| 75847 | सौ | 75800 |
| 75847 | हजार | 76000 |
| 75847 | दस हजार | 80000 |
पृष्ठ सं. 23 से
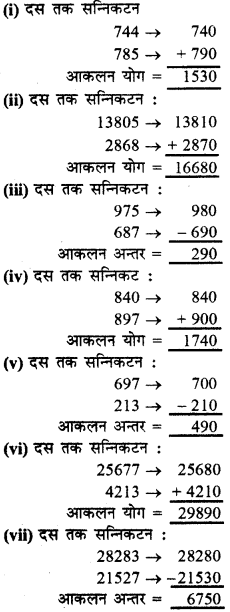
निम्नलिखित गुणनफलों का आकलन कीजिए :
(a) 87 × 313
(b) 9 × 795
(c) 898 × 785
(d) 958 × 387
हल :
(a) 87 → 90 (दस के सन्निकटित) और
313 → 300 (सौ के सन्निकटित)
∴ गुणनफलों का आकलन = 90 × 300 = 27000
(b) 9 → 10 (दस के सन्निकटित)
795 → 800 (सौ के सन्निकटित)
∴ गुणनफल का आकलन = 10 × 800 = 8000
(c) 898 → 900 (सी के सन्निकटित)
785 → 800 (सौ के सन्निकटित)
∴ गुणनफल का आकलन = 900 × 800 = 720000
(d) 958 → 1000 (सौ के सन्निकरित) और
387 → 400 (सौ के सन्निकटित)
∴ गुणनफल का अवकलन = 1000 × 400 = 400000

पृष्ठ सं. 25 से
प्रश्न 1.
कोष्ठकों का प्रयोग करते हुए, निम्नलिखित में से प्रत्येक के लिए व्यंजक लिखिए :
(a) नौ और दो के योग का चार से गुणा।
(b) अठारह और छ: के अंतर को चार से भाग।
(c) पैंतालीस को तीन और दो के योग के तिगुने से भाग देना।
हल :
(a) 4 × (9 + 2)
(b) (18 – 6) ÷ 4
(c) 45 ÷ 3 × (3 + 2).
प्रश्न 2.
(5 + 8) × 6 के लिए तीन विभिन्न स्थितियाँ लिखिए।
हलं :
स्थिति नं. 1 : राम और मोती ने 6 दिन कार्य किया। राम 5 घण्टे प्रतिदिन कार्य करता है और मोती 8 घण्टे प्रतिदिन कार्य करता है। दोनों ने एक सप्ताह में कुल कितने घण्टे कार्य किया ?
स्थिति नं. 2 : रीता तथा सीता ने एक मन्दिर का भ्रमण 6 साल तक किया। रीता साल में 5 बार जाती थी। सीता 8 बार जाती थी। 6 सालों में दोनों ने मिलकर कितनी बार मन्दिर का भ्रमण किया ?
स्थिति नं. 3 : सूरज तथा सोनू 6 दिन के लिए खेलने गए। सूरज एक दिन में 5 घण्टे तथा सोनू एक दिन में 8 घण्टे खेले। 6 दिन में दोनों कितने घण्टे खेले ?
प्रश्न 3.
निम्नलिखित के लिए पाँच स्थितियां लिखिए, जहाँ कोष्ठकों का प्रयोग आवश्यक हो :
(a) 7(8 – 3)
(b) (7 + 2) (10 – 3)
हल :
(a) स्थिति नं. 1 : 5 और 2 के योग को 7 से गुणा अर्थात् (5 + 2) × 7
स्थिति नं. 2 : 15 और 8 के अन्तर को 5 से गुणा अर्थात् (15 – 8) × 5
स्थिति नं. 3 : 3 और 4 के योग को 5 से गुणा अर्थात् (3 + 4) × 5
स्थिति नं. 4 : 5 और 7 का योग कर 1 से भाग अर्थात् (5 + 7) ÷ 1
स्थिति नं. 5 : 9 और 4 के अन्तर को 7 से गुणा अर्थात् (9 – 4) × 7
(b) स्थिति नं. 1 : 2 और 5 के योग से 12 और 3 के अन्तर का गुणा अर्थात् (2 + 5) × (12 – 3)
2 : 1 और 8 के योग में 11 और 4 के अन्तर का गुणा अर्थात् (1 + 8) × (11 – 4)
स्थिति नं. 3 : 9 और 2 के अन्तर से 5 और 4 के योग का गुणा अर्थात् (9 – 2) × (5 + 4)
स्थिति नं. 4 : 11 और 2 के अन्तर से 3 और 4 के योग का गुणा अर्थात् (11 – 2) × (3 + 4)
स्थिति नं. 5 : 2 और 7 के योग से 8 और 1 के अन्तर का गुणा अर्थात् (2 + 7) × (8 – 1)

पृष्ठ सं. 27 से
प्रश्न 1.
रोमन पद्धति में लिखिए :
(i) 73
(ii) 92
हल :
(i) 73 = 70 + 3 = 50 + 20 + 3
= L + XX + III
= LXXIII.
(ii) 92 = 90 + 2 = (100 – 10) + 2
= XC + II = XCII.
![]()
![]()
![]()