Class 6

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Exercise 4.5

प्रश्न 1.
चतुर्भुज PQRS का एक रफ चित्र खींचिए। इसके विकर्ण खींचिए। इनके नाम लिखिए। क्या विकर्णों का प्रतिच्छेद बिन्दु चतुर्भुज के अभ्यन्तर में स्थित है या बहिर्भाग में स्थित है ?
हल :

चतुर्भुज PORS जिसके दो विकर्ण PR और QS हैं जो बिन्दु O पर प्रतिच्छेद करते हैं बिन्दु O चतुर्भुज के अभ्यंतर में स्थित हैं।

प्रश्न 2.
चतुर्भुज KLMN का एक रफ चित्र खींचिए। बताइए:
(a) सम्मुख भुजाओं के दो युग्म
(b) सम्मुख कोणों के दो युग्म
(c) आसन्न भुजाओं के दो युग्म
(d) आसन्न कोणों के दो युग्म।
हल :

चतुर्भुज KLMN का रफ चित्र बनाते हैं, जिसमें :
(a) KL, MN और LM, NK इसकी दो सम्मुख भुजाओं के युग्म
(b) ∠K, ∠M और ∠L, ∠N इसके दो सम्मुख कोणों के युग्म हैं।
(c) KL, LM और LM, MN इसकी दो आसन्न भुजाओं के युग्म हैं।
(d) ∠K, ∠L और ∠L, ∠M इसके दो आसन्न कोणों के युग्म हैं।

प्रश्न 3.
खोज कीजिए : पट्टियाँ और उन्हें बाँधने की वस्तुएँ लेकर एक त्रिभुज और एक चतुर्भुज बनाइए। त्रिभुज के किसी एक शीर्ष पर पट्टियों को अन्दर की ओर दबाने का प्रयत्न कीजिए। यही कार्य चतुर्भुज के लिए भी कीजिए। क्या त्रिभुज में कोई परिवर्तन आया ? ‘क्या चतुर्भुज में कोई परिवर्तन हुआ ? क्या निभुज एक दृढ़ (rigid) आकृति है ? क्या कारण है कि विद्युत टावरों (Electric Towers) जैसी संरचनाओं में त्रिभुजीय आकारों का प्रयोग किया जाता है, चतुर्भुजीय आकारों का नहीं?
हल :
त्रिभुज के किसी भी एक शीर्ष पर पट्टियों को अन्दर की और दबाने से त्रिभुज में कोई परिवर्तन नहीं आया, जबकि चतुर्भुज में ऐसा करने पर परिवर्तन आता है। त्रिभुज एक दृढ़ आकृति है। इसलिए हम विद्युत टावरों जैसी संरचनाओं में त्रिभुजीय आकारों का प्रयोग करते हैं चतुर्भुजीय आकारों का नहीं, क्योंकि त्रिभुज का आकार दृढ़ होता है।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Exercise 4.2

प्रश्न 1.
नीचे दी हुई वक्रों को (i) खुली या (ii) बन्द वक्रों के रूप में वर्गीकृत कीजिए :

हल :
(a) और (c) खली वक्र हैं।
(b), (d) और (e) बन्द वक्र हैं।

प्रश्न 2.
निम्न को स्पष्ट करने के लिए रफ आकृतियाँ बनाइए:
(a) खुला वक्र
(b) बन्द वक्र।
हल :

प्रश्न 3.
कोई भी बहुभुज खींचिए और उसके अभ्यन्तर को छायांकित (shade) कीजिए।
हल :
हम जानते हैं कि बन्द वक़ का अभ्यन्तर वक्र के अन्दर होता है।
यहाँ छायांकित भाग बहुभुज के अभ्यंतर को दर्शाता है।

प्रश्न 4.
संलग्न आकृति को देखकर निम्न प्रश्नों के उत्तर दीजिए :
(a) क्या यह एक वक्र है?
(b) क्या यह बन्द है ?

हल :
(a) हाँ, दी हुई आकृति वक्र है।
(b) हाँ, यह वक्र बन्द है।

प्रश्न 5.
रफ आकृतियाँ बनाकर, यदि संभव हो तो निम्न को स्पष्ट कीजिए:
(a) एक बन्द वक्र जो बहुभुज नहीं है।
(b) केवल रेखाखण्डों से बनी हुई खुली वक़्।
(c) दो भुजाओं वाला एक बहुभुज।
हल :
(a) हाँ इस प्रकार हो सकता है।

(b) हाँ, यह इस प्रकार हो सकता है :

(c) असम्भव, क्योंकि दो भुजाओं वाला बहुभुज नहीं बनाया जा सकता।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.9 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.9

प्रश्न 1.
निम्न का समेलन कीजिए :

इन आकारों में से प्रत्येक के दो और उदाहरण दीजिए।
हल :
सुमेलन निम्न प्रकार हैं :
(a) → (ii)
(b) → (iv)
(c) → (v)
(d) → (iii)
(e) → (i)
दो और उदाहरण
(a) शंकु – आइसक्रीम का कोन, शंक्वाकार टैन्ट
(b) गोला – ऊन का गोला, टेनिस बॉल।
(c) बेलन – ड्राम, गैस सिलिण्डर।
(d) घनाभ – माचिस की डिब्बी, ईंट।
(e) पिरामिड – मिस्र के पिरामिड, प्रिज्म।

प्रश्न 2.
निम्न किस आकार के हैं ?
(a) आपका ज्यामितीय बक्स
(b) एक ईंट
(c) एक माचिस की डिब्बी
(d) सड़क बनाने वाला रोलर (roller)
(e) एक लड्डू।
हल :
(a) घनाभ,
(b) घनाभ,
(c) घनाभ,
(d) बेलन,
(e) गोला।

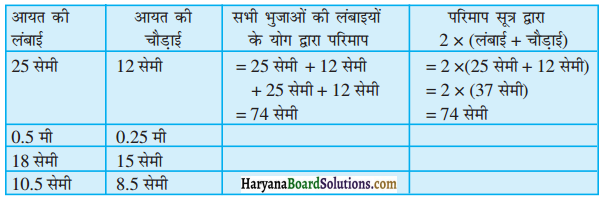
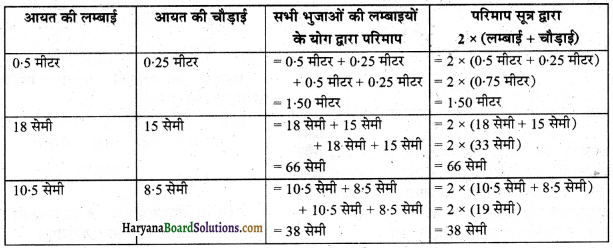
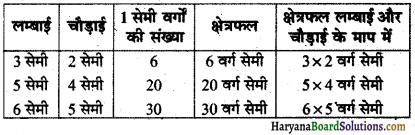
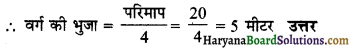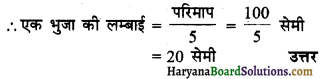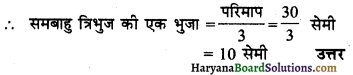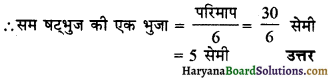Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 क्षेत्रमिति Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 क्षेत्रमिति Exercise 10.1

प्रश्न 1.
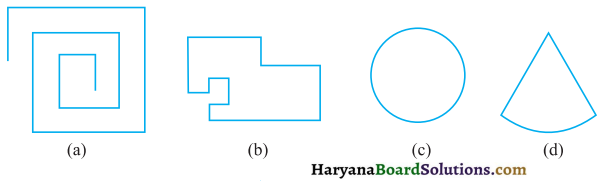
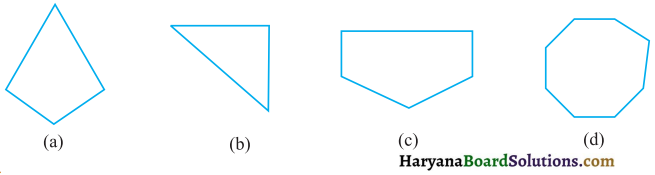
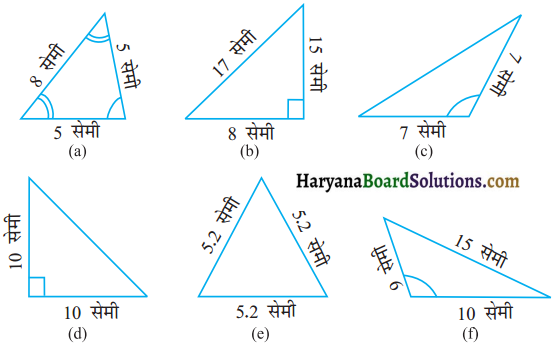
नीचे दी हुई आकृतियों का परिमाप ज्ञात कीजिए :

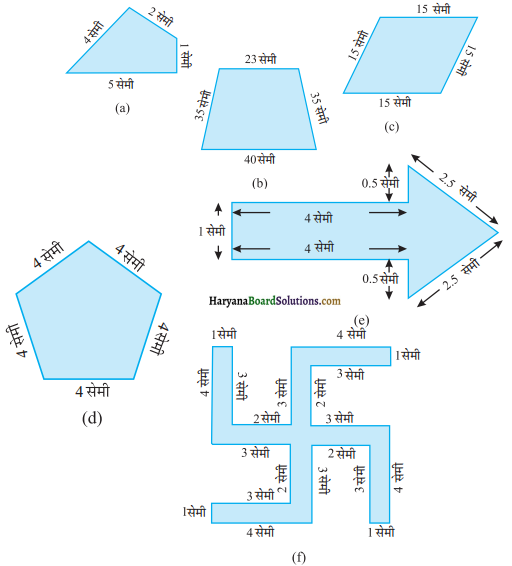
हल :
(a) परिमाप = भुजाओं की लम्बाइयों का योग
= 5 सेमी + 1 सेमी + 2 सेमी + 4 सेमी
= 12 सेमी उत्तर

(b) परिमाप = भुजाओं की लम्बाइयों का योग
= 40 सेमी + 35 सेमी + 23 सेमी + 35 सेमी
= 133 सेमी उत्तर

(c) परिमाप = 4 × एक भुजा की लम्बाई
= 4 × 15 सेमी = 60 सेमी उत्तर

(d) परिमाप = 5 × एक भुजा की लम्बाई
= 5 × 4 सेमी = 20 सेमी उत्तर

(e) परिमाप = भुजाओं की लम्बाइयों का योग
= 4 सेमी + 0.5 सेमी + 2.5 सेमी + 2.5 सेमी + 0.5 सेमी + 4 सेमी + 1 सेमी
= 15 सेमी उत्तर

(f) परिमाप = भुजाओं की लम्बाइयों का योग
= 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी + 4 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 1 सेमी
= 52 सेमी उत्तर

प्रश्न 2.
40 सेमी लम्बाई और 10 सेमी चौड़ाई वाले एक आयताकार बॉक्स के ढक्कन को चारों ओर से पूरी तरह एक टेप द्वारा बन्द कर दिया जाता है। आवश्यक टेप की लम्बाई ज्ञात कीजिए।
हल :
आयताकार बॉक्स के ढक्कन में लगे टेप की कुल लम्बाई = आयत का परिमाप = 2 × (ल. + चौ.)
= 2 × (40 सेमी + 10 सेमी)
= 2 × 50 सेमी = 100 सेमी
अतः आवश्यक टेप की लम्बाई 100 सेमी है। उत्तर

प्रश्न 3.
एक मेज की ऊपरी सतह की विमाएँ 2 मीटर 25 सेमी और 1 मीटर 50 सेमी हैं। मेज की ऊपरी सतह का परिमाप ज्ञात कीजिए।
हल :
मेज की ऊपरी सतह का परिमाप
= 2 × (ल. + चौ.)
= 2 × (2 मीटर 25 सेमी + 1 मीटर 50 सेमी)
= 2 × (3 मीटर 75 सेमी)
= 2 × 3.75 मीटर
= 7.50 मीटर उत्तर
अत: मेज की ऊपरी सतह का परिमाप 7.50 मीटर है। उत्तर

प्रश्न 4.
32 सेमी लम्बाई और 21 सेमी चौड़ाई वाले एक फोटो को लकड़ी की पट्टी से प्रेम करना है। आवश्यक लकड़ी की पट्टी की लम्बाई ज्ञात कीजिए।
हल :
फोटो का फ्रेम आयताकार होता है।
∴ फ्रेम में आवश्यक लकड़ी का परिमाप
= 2 × (ल. + चौ.)
= 2 × (32 सेमी + 21 सेमी)
= 2 × (53 सेमी) = 106 सेमी
अतः आवश्यक लकड़ी की पट्टी की लम्बाई = 106 सेमी उत्तर

प्रश्न 5.
एक आयताकार भूखण्ड की लम्बाई और चौड़ाई क्रमशः 0.7 किमी और 0.5 किमी है। इसके चारों ओर एक तार से 4 पंक्तियों में बाड़ लगाई जानी है। आवश्यक तार की लम्बाई ज्ञात कीजिए।
हल :
आयताकार भूखण्ड का परिमाप
= 2 × (ल. + चौ.)
= 2 × (0.7 किमी + 0.5 किमी)
= 2 × 1.2 किमी = 2.4 किमी
आवश्यक तार की लम्बाई भूखण्ड के परिमाप की 4 गुना होगी।
∴ तार की लम्बाई = 4 × परिमाप
= 4 × (2.4 किमी)
= 9.6 किमी
अतः आवश्यक तार की लम्बाई 9.6 किमी है। उत्तर

प्रश्न 6.
निम्न आकृतियों में प्रत्येक का परिमाप ज्ञात
कीजिए:
(a) एक त्रिभुज जिसकी भुजाएँ 3 सेमी, 4 सेमी तथा 5 सेमी हैं।
(b) एक समबाहुत्रिभुज जिसकी एक भुजा की लम्बाई 9 सेमी है।
(c) एक समद्विबाहु त्रिभुज जिसकी प्रत्येक समान भुजा 8 सेमी की हो तथा तीसरी भुजा 6 सेमी हो।
हल :
(a) त्रिभुज का परिमाप = तीनों भुजाओं का योग
= 3 सेमी + 4 सेमी + 5 सेमी
= 12 सेमी उत्तर

(b) समबाहु त्रिभुज का परिमाप = 3 × एक भुजा की लम्बाई
= 3 × 9 सेमी
= 27 सेमी उत्तर

(c) समद्विबाहु त्रिभुज का परिमाप = तीनों भुजाओं का योग
= 8 सेमी + 8 सेमी + 6 सेमी
= 22 सेमी उत्तर

प्रश्न 7.
एक त्रिभुज का परिमाप ज्ञात कीजिए जिसकी भुजाएँ 10 सेमी, 14 सेमी तथा 15 सेमी हैं।
हल :
त्रिभुज का परिमाप = तीनों भुजाओं की लम्बाइयों का योग
= 10 सेमी + 14 सेमी + 15 सेमी
= 39 सेमी

प्रश्न 8.
एक सम षट्भुज का परिमाप ज्ञात कीजिए, जिसकी प्रत्येक भुजा की माप 8 मीटर है।
हल :
एक सम षट्भुज में 6 समान भुजाएँ होती हैं।
∴ इसका परिमाप = 6 × एक भुजा की लम्बाई
= 6 × (8 मीटर)
= 48 मीटर

प्रश्न 9.
एक वर्ग की भुजा ज्ञात कीजिए, जिसका परिमाप 20 मीटर है।
हल :
वर्ग का परिमाप = 20 मीटर
∴ वर्ग में 4 समान भुजाएँ होती हैं।

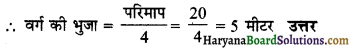
प्रश्न 10.
एक सम पंचभुज का परिमाप 100 सेमी है। प्रत्येक भुजा की लम्बाई ज्ञात कीजिए।
हल :
सम पंचभुज का परिमाप = 100 सेमी
∵ सम पंचभुज में 5 समान भुजाएँ होती हैं।

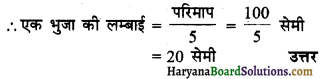
प्रश्न 11.
एक धागे का टुकड़ा 30 सेमी लम्बाई का है। प्रत्येक भुजा की लम्बाई क्या होगी, यदि धागे से बनाया जाता है:
(a) एक वर्ग ?
(b) एक समबाहु त्रिभुज ?
(c) एक सम षट्भुज ?
हल :
(a) धागे की लम्बाई = परिमाप = 30 सेमी
∵ एक वर्ग में 4 समान भुजाएँ होती हैं।

(b) धागे की लम्बाई = परिमाप
= 30 सेमी
∴ एक समबाहु त्रिभुज में तीन समान भुजाएँ होती हैं।

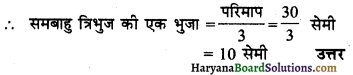
(c) धागे की लम्बाई = परिमाप = 30 सेमी
∵ एक सम षट्भुज में 6 समान भुजाएं होती हैं।

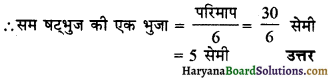
प्रश्न 12.
एक त्रिभुज की दो भुजाएँ 12 सेमी तथा 14 सेमी हैं। इस त्रिभुज का परिमाप 36 सेमी है। इसकी तीसरी भुजा की लम्बाई क्या होगी?
हल :
माना दिया गया त्रिभुज ABC है, जिसमें AB = 12 सेमी, BC = 14 सेमी और इसका परिमाप = 36 सेमी।
अर्थात् AB+ BC + CA = 36 सेमी
⇒ 12 सेमी + 14 सेमी + CA = 36 सेमी
⇒ 26 सेमी + CA = 36 सेमी
⇒ CA = 36 सेमी – 26 सेमी
= 10 सेमी
∴ तीसरी भुजा की लम्बाई 10 सेमी है। उत्तर

प्रश्न 13.
250 मीटर भुजा वाले वर्गाकार बगीचे के चारों ओर बाड़ लगाने का व्यय 20 रु. प्रति मीटर की दर से ज्ञात कीजिए।
हल :
वर्गाकार पार्क की भुजा = 250 मीटर
∴ वर्गाकार पार्क का परिमाप = 4 × भुजा
= 4 × 250 मीटर
= 1000 मीटर
∴ बाड़ लगाने का कुल व्यय = 1000 × 20 रु.
= 20,000 रु. उत्तर

प्रश्न 14.
एक आयताकार बगीचा जिसकी लम्बाई 175 मीटर तथा चौड़ाई 125 मीटर है, के चारों ओर 12 रु. प्रति मीटर की दर से बाड़ लगाने का व्यय ज्ञात कीजिए।
हल :
आयताकार बगीचे की लम्बाई = 175 मीटर
और आयताकार बगीचे की चौड़ाई = 125 मीटर
∴ आयताकार बगीचे का परिमाप = 2 × (ल. + चौ.)
32 × (175 + 125) मीटर
= 2 × 300 मीटर
= 600 मीटर
∴ बाड़ लगाने का व्यय = 600 × 12 रु.
= 7,200 रुपये उत्तर

प्रश्न 15.
स्वीटी 75 मीटर भुजा वाले वर्ग के चारों ओर दौड़ती है और बुलबुल 60 मीटर लम्बाई और 45 मीटर चौड़ाई वाले आयत के चारों ओर दौड़ती है। कौन कम दूरी तय करती है ?
हल :
प्रत्येक लड़की द्वारा एक चक्कर में तय की गई दूरी उस मैदान के परिमाप के बराबर है। इसलिए एक चक्कर में स्वीटी द्वारा तय की गई दूरी = वर्ग का परिमाप
= 4 × भुजा
= 4 × (75 मीटर) = 300 मीटर
बुलबुल द्वारा एक चक्कर में तय की गई दूरी = आयत का परिमाप
= 2 × (लम्बाई + चौड़ाई)
= 2 × (60 मीटर + 45 मीटर)
= 2 × 105 मीटर = 210 मीटर
यह दर्शाता है कि बुलबुल, स्वीटी से कम दूरी तय करती है। उत्तर

प्रश्न 16.
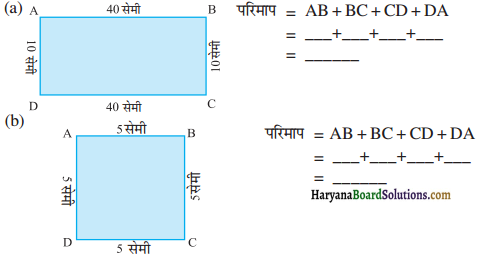
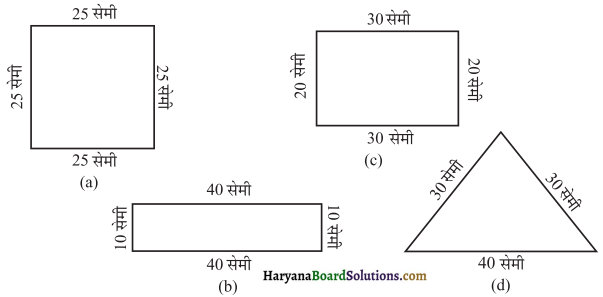
निम्न प्रत्येक आकृति का परिमाप ज्ञात कीजिए। आप उत्तर से क्या निष्कर्ष निकालते हैं ?

हल :
(a) वर्ग का परिमाप = 4 × भुजा
= 4 × (25 सेमी) = 100 सेमी उत्तर

(b) आयत का परिमाप = 2 × (ल. + चौ.)
= 2 × (40 सेमी + 10 सेमी)
= 2 × (50 सेमी.) = 100 सेमी उत्तर

(c) आयत का परिमाप = 2 × (ल. + चौ.)
= 2 × (30 सेमी + 20 सेमी)
= 2 × (50 सेमी) = 100 सेमी उत्तर

(d) त्रिभुज का परिमाप = 30 सेमी + 30 सेमी + 40 सेमी
= 100 सेमी उत्तर
हम देखते हैं कि प्रत्येक आकृति का परिमाप 100 सेमी है। अतः इन सभी आकृतियों का परिमाप समान हैं। उत्तर

प्रश्न 17.
अवनीत 9 वर्गाकार टाइल खरीदता है, जिसकी प्रत्येक भुजा \(\frac{1}{2}\) मीटर है और वह इन टाइलों को एक वर्ग के रूप में रखता है।

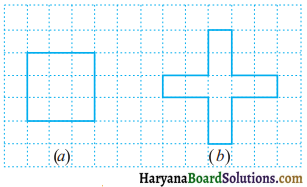
(a) नए वर्ग का परिमाप क्या है [आकृति (a)] ?
(b) शैरी को उसके द्वारा टाइलों को रखने की व्यवस्था पसन्द नहीं आती है। वह इन टाइलों को एक क्रॉस के रूप में रखवाती है। इस व्यवस्था का परिमाप कितना होगा [आकृति (b)] ?
(c) किसका परिमाप अधिक है ?
(d) अवनीत सोचता है, क्या कोई ऐसा भी तरीका है जिससे इनसे भी बड़ा परिमाप प्राप्त किया जा सकता हो? क्या आप ऐसा करने का कोई सुझाव दे सकते हैं? (टाइलें किनारों से आपस में मिली हुई हों और वे दूटी न हों।)
हल :
(a) अवनीत की व्यवस्था की स्थिति में नये वर्ग का

परिमाप = 4 × भुजा
= 4 × \(\frac{3}{2}\) मीटर
नये वर्ग की भुजा = \(\left(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}\right)\) मीटर = \(\frac{3}{2}\) मीटर
= \(\frac{12}{2}\) मीटर
= 6 मीटर उत्तर

(b) शैरी की व्यवस्था की स्थिति में :

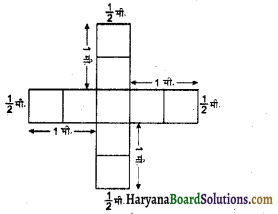
परिमाप = \(\frac{1}{2}\) मीटर + 1 मीटर + 1 मीटर + \(\frac{1}{2}\) मीटर + 1 मीटर + 1 मीटर + \(\frac{1}{2}\) मीटर + 1 मीटर + 1 मीटर + \(\frac{1}{2}\) मीटर + 1 मीटर + 1 मीटर = 10 मीटर उत्तर

(c) शैरी की स्थिति में परिमाप बड़ा है। उत्तर
(d) नोट : विद्यार्थी इस प्रश्न को स्वयं हल करने का प्रयास करें। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.8 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.8

प्रश्न 1.
जाँच कीजिए कि निम्न में से कौन-सी आकृतियाँ बहुभुज हैं। यदि इनमें से कोई बहुभुज नहीं है, तो कारण बताइए।

हल :
(a) नहीं, क्योंकि यह एक खुली आकृति है।
(b) हाँ, क्योंकि यह रेखाखण्डों से बनी बन्द आकृति
(c) नहीं, क्योंकि यह बन्द आकृति रेखाखण्डों से बनी नहीं है।
(d) नहीं, क्योंकि यह बन्द आकृति रेखाखण्डों से बनी नहीं है।

प्रश्न 2.
प्रत्येक बहुभुज का नाम लिखिए :

इनमें से प्रत्येक के दो और उदाहरण बनाइए।
हल :
(a) चतुर्भुज,
(b) त्रिभुज,
(c) पंचभुज,
(d) अष्टभुज।
नोट : विद्यार्थी स्वयं उदाहरण बनाने का प्रयास करें।

प्रश्न 3.
एक सम षट्भुज (regular hexagon) का एक रफ चित्र खींचिए। उसके किन्हीं तीन शीर्षों को जोड़कर एक त्रिभुज बनाइए। पहचानिए कि आपने किस। प्रकार का त्रिभुज खींच लिया है।

हल :
ABCDEF एक सम षट्भुज का रफ चित्र बनाया, जिसमें AC और AD को मिलाया। इस प्रकार एक त्रिभुज ACD प्राप्त होता है जिसमें AC ≠ CD ≠ AD अत: ΔACD विषमबाहु त्रिभुज है।

प्रश्न 4.
एक सम अष्टभुज (regular octagon) का रफ चित्र खींचिए। यदि आप चाहें, तो वाकित कागज (squared paper) का प्रयोग कर सकते हैं। इस अष्टभुज के ठीक चार शीर्षों को जोड़कर एक आयत खींचिए।
हल :

दिया गया रफ चित्र ABCDEFGH एक सम अष्टभुज जिसमें AC, CE, EG और GA को मिलाने पर आयत ACEG प्राप्त होता है।

प्रश्न 5.
किसी बहुभुज का विकर्ण उसके किन्हीं दो शीर्षों (आसन्न शीर्षों को छोड़कर) को जोड़ने से प्राप्त होता है (यह इसकी भुजाएँ नहीं होती है)। एक पंचभुज का एक रफ चित्र खींचिए और उसके विकर्ण खींचिए।
हल :

ABCDE एक पंचभुज का रफ चित्र बनाया। इसके विकर्ण AC, AD, BD, BE और CE को मिलाया। अत: AC, AD, BD, BE और CE इसके विकर्ण हैं।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Exercise 4.1

प्रश्न 1.
संलग्न आकृति का प्रयोग करके निम्न के नाम लिखिए :
(a) पाँच बिन्दु
(b) एक रेखा
(c) चार किरणें
(d) पाँच रेखाखण्ड

हल :
दी गई आकृति से स्पष्ट है कि
(a) O, C, B, E और D पाँच बिन्दु हैं।
(b) एक रेखा \(\stackrel{\leftrightarrow}{B D}\) है।
(c) चार किरणें \(\overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O D}\) और \(\overrightarrow{E D}\) हैं।
(d) \(\overline{O E}, \overline{O D}, \overline{D E}, \overline{O B}\) और \(\overline{B D}\) पाँच रेखाखण्ड है।

प्रश्न 2.
संलग्न आकृति में दी हुई रेखा के सभी संभव प्रकारों के नाम लिखिए। आप इन चार बिन्दुओं में से किसी भी बिन्दु का प्रयोग कर सकते हैं।

हल :
दी हुई रेखा के सभी सम्भव प्रकारों के नाम, जिसमें चार बिन्दुओं में से केवल कोई दो अक्षरों का प्रयोग किया गया है :
\(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}, \overrightarrow{B C}, \overrightarrow{B D}, \overrightarrow{C D}, \overrightarrow{D C}, \overrightarrow{D B}\), \(\overrightarrow{C B}, \overrightarrow{D A}, \overrightarrow{C A}\) और \(\overrightarrow{B A}\)

प्रश्न 3.
संलग्न आकृति को देखकर नाम लिखिए :

(a) रेखाएँ जिसमें बिन्दु E सम्मिलित है
(b) A से होकर जाने वाली रेखा
(c) वह रेखा जिस पर बिन्दु O स्थित है
(d) प्रतिच्छेदी रेखाओं के दो युग्म।
हल :
आकृति से स्पष्ट है कि
(a) \(\overleftrightarrow{A E}, \overleftrightarrow{F E}\) वह रेखा है जिसमें बिन्दु E सम्मिलित
(b) \(\overleftrightarrow{A E}\) वह रेखा है जो A से होकर जाती है।
(c) \(\overleftrightarrow{C O}\) या \(\overleftrightarrow{O C}\) वह रेखा है जिस पर बिन्दु O स्थित है।
(d) \(\overleftrightarrow{C O}, \overleftrightarrow{A E}\) तथा \(\overleftrightarrow{A E}, \overleftrightarrow{E F}\) प्रतिच्छेदी रेखाओं के दो युग्म हैं।

प्रश्न 4.
निम्नलिखित से होकर कितनी रेखाएँ खींची जा सकती हैं?
(a) एक बिन्दु
(b) दो बिन्दु ।
हल :
(a) एक बिन्दु से होकर असंख्य रेखाएँ खींची जा सकती है।
(b) दो बिन्दुओं से केवल एक ही रेखा खींची जा सकती है।

प्रश्न 5.
निम्नलिखित स्थितियों में से प्रत्येक के लिए एक रफ (Rough) आकृति बनाइए और उचित रूप से उसे नामांकित कीजिए :
(a) बिन्दु P रेखाखण्ड \(\overline{A B}\) पर स्थित है।
(b) रेखाएँ XY और PQ बिन्दुज M पर प्रतिच्छेद करती हैं।
(c) रेखा l पर E और F स्थित हैं, परन्तु D स्थित नहीं है।
(d) \(\overleftrightarrow{O P}\) और \(\overleftrightarrow{O Q}\) बिन्दु O पर मिलती हैं।
हल :
दी गई स्थितियों के लिए रफ आकृतियाँ निम्न प्रकार हैं:
(a) बिन्दु P रेखाखण्ड \(\overline{A B}\) पर स्थित है।

(b) रेखाएँ XY और PQ बिन्दु M पर प्रतिच्छेद करती हैं।

(c) रेखा l पर E और F स्थित हैं, परन्तु D स्थित नहीं है।

(d) \(\overleftrightarrow{O P}\) और \(\overleftrightarrow{O Q}\) बिन्दु O पर मिलती हैं।

प्रश्न 6.
रेखा \(\overline{M N}\) की संलग्न आकृति को देखिए। इस आकृति के संदर्भ में बताइए कि निम्नलिखित कथन सत्य हैं या असत्य:

(a) Q, M, O, N और P रेखा \(\overleftrightarrow{M N}\) पर स्थित बिन्दु हैं।
(b) M, O और N रेखाखण्ड \(\overleftrightarrow{M N}\) पर स्थित बिन्दु हैं।
(c) M और N रेखाखण्ड \(\overleftrightarrow{M N}\) के अन्त बिन्दु हैं।
(d) O और N रेखाखण्ड \(\overrightarrow{O P}\) के अन्त बिन्दु हैं।
(e) M रेखाखण्ड \(\overline{Q O}\) के दोनों अन्त बिन्दुओं में से एक बिन्दु है।
(f) M किरण \(\overrightarrow{O P}\) पर एक बिन्दु है।
(g) किरण \(\overrightarrow{O P}\) किरण \(\overrightarrow{Q P}\) से भिन्न है।
(h) किरण \(\overrightarrow{O P}\) वही है जो किरण \(\overrightarrow{O M}\) है।
(i) किरण \(\overrightarrow{O M}\) किरण \(\overrightarrow{O P}\) के विपरीत (Opposite) नहीं है।
(j) O किरण \(\overrightarrow{O P}\) का प्रारम्भिक बिन्दु नहीं है।
(k) N किरण \(\overrightarrow{N P}\) और \(\overrightarrow{N M}\) का प्रारम्भिक बिन्दु है। हल :
दी हुई आकृति के सन्दर्भ में उपर्युक्त कथन इस प्रकार हैं:
(a) सत्य,
(b) सत्य,
(c) सत्य,
(d) असत्य,
(e) असत्य,
(f) असत्य,
(g) सत्य,
(h) असत्य,
(i) असत्य,
(j) असत्य,
(k) सत्य।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.7 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.7

प्रश्न 1.
सत्य (T) या असत्य (F) कहिए:
(a) आयत का प्रत्येक कोण समकोण होता है।
(b) आयत की सम्मुख भुजाओं की लम्बाई बराबर होती है।
(c) वर्ग के विकर्ण एक-दूसरे पर लम्ब होते हैं।
(d) समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(e) समान्तर चतुर्भुज की सभी भुजाएँ बराबर लम्बाई की होती हैं।
(f) समलम्ब की सम्मुख भुजाएँ समान्तर होती हैं।
हल :
(a) सत्य,
(b) सत्य,
(c) सत्य,
(d) सत्य,
(e) असत्य,
(f) असत्य।

प्रश्न 2.
निम्नलिखित के लिए कारण दीजिए :
(a) वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
(b) आयत को एक विशेष प्रकार का समांतर चतुर्भुज समझा जा सकता है।
(c) वर्ग को एक विशेष प्रकार का समचतुर्भुज समझा जा सकता है।
(d) वर्ग, आयत, समचतुर्भुज और समान्तर चतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
(e) वर्ग एक समान्तर चतुर्भुज भी है।
हल :
(a) आयत के सभी गुण वर्ग में होते हैं, इसलिए वर्ग को एक विशेष प्रकार का आयत समझा जाता है।
(b) आयत में समान्तर चतुर्भुज के सभी गुण होते हैं, इसलिए आयत को एक विशेष प्रकार का समान्तर चतुर्भुज समझा जा सकता है।
(c) समचतुर्भुज के सभी गुण वर्ग में होते हैं, इसलिए वर्ग को एक विशेष प्रकार का समचतुर्भुज समझा जा सकता है।
(d) चार रेखाओं से घिरी आकृति को चतुर्भुज कहते हैं। अतः वर्ग, आयन, समचतुर्भज और समान्तर चतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
(e) वर्ग की सम्मुख भुजाएँ समान्तर होती हैं, इसलिए यह समान्तर चतुर्भुज हैं।

प्रश्न 3.
एक बहुभुज सम (regular) होता है, यदि उसकी सभी भुजाएँ बराबर हों और सभी कोण बराबर हों। क्या आप समचतुर्भुज (regular quadrilateral) की पहचान कर सकते हैं ?
हल :
वर्ग एक सम चतुर्भुज है।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात InText Questions

प्रयास कीजिए (पृष्ठ सं. 265 से)

प्रश्न 1.
एक कक्षा में 20 लड़के और 40 लड़कियाँ हैं। लड़कों की संख्या का, लड़कियों की संख्या से क्या अनुपात होगा?
हल :
कक्षा में लड़कों की संख्या = 20
और कक्षा में लड़कियों की संख्या = 40
∴ लड़कों की संख्या का, लड़कियों की संख्या से
अनुपात = 20 : 40.
= \(\frac{20}{40}=\frac{1}{2}\)
= 1 : 2 उत्तर

प्रश्न 2.
रवि एक घण्टे में 6 किमी चलता है जबकि रोशन एक घण्टे में 4 किमी चलता है। रवि द्वारा तय की गई दूरी से रोशन द्वारा तय की गई दूरी का अनुपात ज्ञात कीजिए।
हल :
1 घण्टे में रवि द्वारा तय की गई दूरी= 6 किमी
1 घण्टे में रोशन द्वारा तय की गई दूरी = 4 किमी
∴ रवि द्वारा तय की गई दूरी से रोशन द्वारा तय की गई दूरी का अनुपात = 6 किमी : 4 किमी
= 6 : 4
= \(\frac{6}{4}=\frac{3}{2}\)
= 3 : 2 उत्तर

पृष्ठ सं. 267 से

प्रश्न 1.
सौरभ घर से स्कूल पहुँचने में 15 मिनट लेता है और सचिन एक घण्टा लेता है। सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात ज्ञात कीजिए।
हल :
सौरभ द्वारा घर से स्कूल पहुँचने में लिया समय
= 15 मिनट
सचिन द्वारा घर से स्कूल पहुँचने में लिया समय
= 1 घण्टा
= 1 × 60 मिनट = 60 मिनट
∴ सौरभ और सचिन द्वारा लिए गए समय का अनुपात
= 15 मिनट : 60 मिनट = 15 : 60
= \(\frac{15}{60}=\frac{1}{4}\)
= 1 : 4 उत्तर

प्रश्न 2.
एकटॉफी का मूल्य 50 पैसे और एक चॉकलेट का मूल्य 10 रुपये है। टॉफी के मूल्य का चॉकलेट के मूल्य से अनुपात ज्ञात कीजिए।
हल :
टॉफी का मूल्य = 50 पैसे
चॉकलेट का मूल्य = ₹ 10
= 10 × 100 पैसे = 1000 पैसे
∴ टॉफी और चॉकलेट के मूल्य का अनुपात
= 50 पैसे : 1000 पैसे
= 50 : 1000 = 1 : 20 उत्तर

प्रश्न 3.
एक स्कूल में एक वर्ष में 73 छुट्टियाँ बनती हैं। छुट्टियों का वर्ष के कुल दिनों के साथ अनुपात ज्ञात कीजिए।
हल :
1 वर्ष में छुट्टियों के दिन = 73
1 वर्ष में कुल दिन = 365
∴ छुट्टियों की संख्या और 1 वर्ष के कुल दिनों का अनुपात = 73 : 365
= \(\frac{73}{365}=\frac{73 \div 73}{365 \div 73}\)
= \(\frac{1}{5}\)
= 1 : 5 उत्तर

पृष्ठसं. 268 से

प्रश्न 1.
अपने बैग में रखी कॉपियों की संख्या का पुस्तकों की संख्या से अनुपात ज्ञात कीजिए।
हल :
माना बैग में 12 काँपियाँ और 6 पुस्तकें हैं।
कॉपियों की संख्या = 12
पुस्तकों की संख्या = 6
कॉपियों की संख्या और पुस्तकों की संख्या का अनुपात = 12 : 6 = 2 : 1 उत्तर

प्रश्न 2.
अपनी कक्षा की कुल डैस्कों की संख्या का कुल कुर्सियों की संख्या से अनुपात ज्ञात कीजिए।
हल :
माना कि कक्षा में 15 डैस्क और 45 कुर्सियाँ हैं।
∴ डैस्कों की संख्या = 15
कुर्सियों की संख्या = 45
∴ डैस्कों और कुर्सियों की संख्या का अनुपात = 15 : 45 = 1 : 3 उत्तर

प्रश्न 3.
अपनी कक्षा में उन छात्रों की संख्या ज्ञात कीजिए जिनकी आयु 12 वर्ष से ऊपर है। अब 12 वर्ष से ऊपर आयु वाले छात्रों की संख्या का कक्षा के बाकी छात्रों की संख्या के साथ अनुपात ज्ञात कीजिए।
हल :
माना कक्षा में कुल छात्रों की संख्या = 45 जिसमें से 15 ऐसे छात्र हैं जिनकी आयु 12 वर्ष से ऊपर है।
∴ कक्षा में छात्रों की संख्या = 45
12 वर्ष से ऊपर आयु के छात्रों की संख्या = 15
12 वर्ष से कम आयु के छात्रों की संख्या = (45 – 15) 30
∴ 12 वर्ष से ऊपर आयु वाले छात्रों का कक्षा के बाकी छात्रों से अनुपात = 15 : 30 = 1 : 2 उत्तर

प्रश्न 4.
अपनी कक्षा के दरवाजों की संख्या का खिड़कियों की संख्या से अनुपात निकालिए।
हल :
माना एक कक्षा में 3 दरवाजे और 6 खिड़कियाँ हैं।
∴ दरवाजों की संख्या = 3
खिड़कियों की संख्या = 6
∴ दरवाजों की संख्या का खिड़कियों की संख्या से अनुपात = 3 : 6
= 1 : 2

प्रश्न 5.
एक आयत बनाइए। उसकी लम्बाई का चौड़ाई से अनुपात ज्ञात कीजिए।
हल :
माना एक आयत ABCD है और इसकी विमाएँ आकृति में दिखाई गई हैं।

∴ आयत की लम्बाई = 32 सेमी
और आयतन की चौड़ाई = 8 सेमी
∴ इसकी लम्बाई और चौड़ाई का अनुपात = 32 सेमी : 8 सेमी = 32 : 8 = 4:1 उत्तर

पृष्ठ सं. 275 से

प्रश्न 1.
जाँच कीजिए कि दिए गए अनुपात समान हैं अर्थात् वे समानुपात में हैं। यदि हाँ, तो उन्हें सही ढंग से लिखिए :
1. 1 : 5 और 3 : 15
2. 2 : 9 और 18 : 81
3. 15 : 45 और 5 : 25
4. 4 : 12 और 9 : 27
5. ₹ 10 का ₹ 15 और 4 का 6 से।
हल :
(1) 1 : 5 और 3 : 15
चरम पदों का गुणनफल = 1 × 15 = 15
मध्य पदों का गुणनफल = 3 × 5 = 15
अत: चरम पदों का गुणनफल = मध्य पदों का गुणनफल
सही ढंग = 1 : 5 :: 3 : 15 समानुपात में हैं। उत्तर

(2) 2 : 9 और 18 : 81
चरम पदों का गुणनफल = 2 × 81 = 162
मध्य पदों का गुणनफल = 9 × 18 = 162
अतः चरम पदों का गुणनफल = मध्य पदों का गुणनफल
सही ढंग = 2 : 9 :: 18 : 81 उत्तर

(3) 15 : 45 और 5 : 25
चरम पदों का गुणनफल = 15 × 25 = 375
मध्य पदों का गुणनफल = 45 × 5 = 225
अतः चरम पदों का गुणनफल ≠ मध्य पदों का गुणनफल
सही ढंग = 15 : 45 :: 5 : 25 उत्तर

(4) 4 : 12 और 9 : 27
चरम पदों का गुणनफल = 4 × 27 = 108
मध्य पदों का गुणनफल = 12 × 9 = 108
अतः चरम पदों का गुणनफल = मध्य पदों का गुणनफल
सही ढंग = 2 : 9 :: 18 : 81 उत्तर

(5) ₹ 10 का ₹ 15 और 4 का 6 से
चरम पदों का गुणनफल = 10 × 6 = ₹ 60
मध्य पदों का गुणनफल = 15 × 4 = ₹ 60
अतः चरम पदों का गुणनफल = मध्य पदों का गुणनफल
सही ढंग = ₹ 10 : ₹ 15 :: 4 : 6 उत्तर

पृष्ठ सं. 277 से

नोट : प्रश्न 1 छात्र स्वयं करें।

प्रश्न 2.
निम्न सारणी को पढ़कर पूरा करें।

हल :
सम्पूर्ण सारणी इस प्रकार है-

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 आँकड़ों का प्रबंधन Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 आँकड़ों का प्रबंधन Exercise 9.1

प्रश्न 1.
गणित के एक टेस्ट में 40 विद्यार्थियों द्वारा निम्नलिखित अंक प्राप्त किए गए। इन अंकों को मिलान चिह्नों का प्रयोग करके, एक सारणी के रूप में व्यवस्थित कीजिए :
8 1 3 7 6 5 5 4 4 2
4 9 5 3 7 1 6 5 2 7
7 3 8 4 2 8 9 5 8 6
7 4 5 6 9 6 4 4 6 6
(a) ज्ञात कीजिए कि कितने विद्यार्थियों ने 7 या उससे अधिक अंक प्राप्त किए।
(b) कितने विद्यार्थियों ने 4 से कम अंक प्राप्त किए ?
हल :
अभीष्ट सारणी :

(a) सारणी से स्पष्ट है कि 7 या उससे अधिक अंक प्राप्त किए गए विद्यार्थियों की संख्या
= 5 + 4 + 3 = 12
(b) सारणी से स्पष्ट है कि 4 से कम अंक प्राप्त किए गए विद्यार्थियों की संख्या = 2 + 3 + 3
= 8. उत्तर

प्रश्न 2.
कक्षा VI के 30 विद्यार्थियों की मिठाइयों की पसंद निम्नलिखित है :
लड्डू, बरफी, लड्डू, जलेबी, लड्डू, रसगुल्ला
जलेबी, लड्डू, बरफी, रसगुल्ला, लड्डू, जलेबी, लड्डू
जलेबी, रसगुल्ला, लड्डू, रसगुल्ला, जलेबी, लड्डू
रसगुल्ला, लड्डू, लड्डू बरफी, रसगुल्ला, रसगुल्ला
जलेबी, रसगुल्ला, लड्डू, रसगुल्ला, जलेबी, लड्डू।
(a) मिठाइयों के इन नामों को मिलान चिह्नों का प्रयोग करते हुए एक सारणी में व्यवस्थित कीजिए।
(b) कौन-सी मिठाई विद्यार्थियों द्वारा अधिक पसन्द की गई?
हल :
(a) अभीष्ट सारणी :

(b) लड्डू सबसे ज्यादा विद्यार्थियों द्वारा पसन्द किया गया। उत्तर

प्रश्न 3.
केथरिन ने एक पासा (dice) लिया और उसको 40 बार उछालने पर प्राप्त संख्या को लिख लिया। उसने इस कार्य को 40 बार किया और प्रत्येक बार प्राप्त संख्याओं को निम्न प्रकार लिखा :

1 3 5 6 6 3 5 4 1 6
2 5 3 4 6 1 5 5 6 1
1 2 2 3 5 2 4 5 5 6
5 1 6 2 3 5 2 4 1 5
एक सारणी बनाइए और आँकड़ों को मिलान चिह्नों का प्रयोग करके लिखिए। अब ज्ञात कीजिए:
(a) न्यूनतम बार आने वाली संख्या।
(b) अधिकतम बार आने वाली संख्या।
(c) समान बार आने वाली संख्याएँ।

हल :
अभीष्ट सारणी :

(a) सारणी से स्पष्ट है कि 4 न्यूनतम बार आया है।
(b) सारणी से स्पष्ट है कि 5 अधिकतम बार आया है।
(c) सारणी से स्पष्ट है कि 1 और 6 समान बार आये हैं।

प्रश्न 4.
निम्नलिखित चित्रालेख पाँच गाँवों में ट्रैक्टरों की संख्या दर्शाता है:

चित्रालेख को देखिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) किस गाँव में ट्रैक्टरों की संख्या न्यूनतम है ?
(ii) किस गाँव में ट्रैक्टरों की संख्या अधिकतम है ?
(iii) गाँव C में गाँव B से कितने ट्रैक्टर अधिक हैं ?
(iv) पाँचों गाँवों में कुल मिलाकर कितने ट्रैक्टर हैं ?
हल :
दिए गए चित्रालेख को देखने पर,
(i) गाँव D में सबसे कम ट्रैक्टर हैं।
(ii) गाँव C में सबसे ज्यादा ट्रैक्टर हैं।
(iii) गाँव C में गाँव B से 3 ट्रैक्टर ज्यादा हैं।
(iv) पाँचों गाँवों में ट्रैक्टरों की कुल संख्या
= 6 +5+ 8 + 3 + 6
= 28. उत्तर

प्रश्न 5.
एक सह-शिक्षा माध्यमिक विद्यालय की प्रत्येक कक्षा में लड़कियों की संख्या अग्र चित्रालेख द्वारा प्रदर्शित है :

इस चित्रालेख को देखिए और निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) किस कक्षा में लड़कियों की संख्या न्यूनतम है ?
(b) क्या कक्षा VI में लड़कियों की संख्या कक्षा V की लड़कियों की संख्या से कम है ?
(c) कक्षा VII में कितनी लड़कियाँ हैं ?
हल :
चित्रालेख को देखने पर स्पष्ट है :
(a) कक्षा VIII में लड़कियों की संख्या सबसे कम है।
(b) नहीं।
(c) कक्षा VII में लड़कियों की संख्या 3 × 4 = 12 है।

प्रश्न 6.
किसी सप्ताह के विभिन्न दिनों में बिजली के बल्बों की बिक्री नीचे दर्शाई गई है :

चित्रालेख को देखिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) शुक्रवार को कितने बल्ब बेचे गए ?
(b) किस दिन बेचे गए बल्बों की संख्या अधिकतम थी?
(c) किन दिनों में बेचे गए बल्बों की संख्या समान थी?
(d) किस दिन बेचे गए बल्बों की संख्या न्यूनतम थी?
(e) यदि एक बड़े डिब्बे में 9 बल्ब आ सकते हैं, तो इस सप्ताह कितने डिब्बों की आवश्यकता पड़ी?
हल :
चित्रालेख को देखने पर, स्पष्ट रूप से :
(a) शुक्रवार को बेचे गए बल्बों की संख्या = 7 × 2 = 14.
(b) रविवार को बेचे गए बल्बों की संख्या अधिकतम थी।
(c) बुधवार और शनिवार को बेचे एग बल्बों की संख्या समान थी।
(d) बुधवार और शनिवार को बेचे गए बल्बों की संख्या न्यूनतम थी।
(e) पूरे सप्ताह में बेचे गए बल्बों की कुल संख्या
= (6 + 8 + 4 + 5 + 7 + 4 + 9) × 2
= 43 × 2
= 86
चूँकि एक डिब्बे में बल्ब आ सकते है = 9
तब डिब्बे चाहिए = 86 ÷ 9 = 9.55
अर्थात् इस सप्ताह 10 डिब्बो की आवश्यकता पड़ी। उत्तर

प्रश्न 7.
एक विशेष मौसम में, एक गाँव में 6 फल विक्रेताओं द्वारा बेची गई फलों की टोकरियों की संख्या निम्न चित्रालेख द्वारा प्रदर्शित है।

इस चित्रालेख को देखिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) किस फल विक्रेता ने अधिकतम फलों की टोकरियाँ बेचीं ?
(b) अनवर ने फलों की कितनी टोकरियाँ बेचीं ?
(c) वे विक्रेता जिन्होंने 600 या उससे अधिक टोकरियाँ बेचीं, अगले मौसम में गोदाम खरीदने की योजना बना रहे हैं। क्या आप इनके नाम बता सकते हैं?
हल :
चित्रालेख को देखने पर स्पष्ट है :
(a) मार्टिन फल विक्रेता ने अधिकतम फलों की टोकरियाँ बेचीं।
(b) अनवर ने 7 × 100 = 700 फलों की टोकरियाँ बेचीं।
(c) अनवर, मार्टिन, रंजीत सिंह ने 600 या उससे अधिक टोकरियाँ बेची और ये तीनों अगले मौसम में गोदाम खरीदने की योजना बना रहे हैं।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.6 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.6

प्रश्न 1.
निम्नलिखित त्रिभुजों के प्रकार लिखिए :
(a) त्रिभुज जिसकी भुजाएँ 7 सेमी, 8 सेमी और 9 सेमी है।
(b) ΔABC जिसमें AB = 8.7 सेमी, AC = 7 सेमी और BC = 6 सेमी है।
(c) ΔPQR जिसमें PQ = OR = RP = 5 सेमी है।
(d) ΔDEF जिसमें m∠D = 90° है।
(e) ΔXYZ जिसमें m∠Y= 90° और XY = YZ है।
(f) ΔLMN जिसमें m∠L = 30°, m∠M = 70° और m∠N= 80° है।
हल :
(a) दिये गये त्रिभुज की भुजाओं की लम्बाइयाँ अलग-अलग हैं।
∴ यह विषमबाहु त्रिभुज है।

(b) ΔABC में,
AB = 8.7 सेमी, AC = 7 सेमी,
BC = 6 सेमी
∴ AB ≠ BC ≠ AC
अत: ΔABC विषमबाहु त्रिभुज है।

(c) ΔPQR में, PQ = QR = RP = 5 सेमी
∴ ΔPQR समबाहु त्रिभुज है।

(d) ΔDEF में, m∠D = 90°
∴ ΔDEF समकोण त्रिभुज है।

(e) ΔXYZ में, m∠Y = 90° और XY = YZ
∴ ΔXYZ समद्विबाहु समकोण त्रिभुज है।

(f) ΔLMN में,
m∠L = 30°, m∠M = 70° और m∠N = 80° प्रत्येक कोण 90° से कम है।
∴ ΔLMN न्यूनकोण त्रिभुज है।

प्रश्न 2.
निम्न का सुमेलन कीजिए :

हल :

प्रश्न 3.
निम्नलिखित त्रिभुजों में से प्रत्येक का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।):

हल :
(a) न्यूनकोण त्रिभुज, समद्विबाहु त्रिभुज
(b) विषमबाहु त्रिभुज, समकोण त्रिभुज
(c) समद्विबाहु त्रिभुज, अधिककोण त्रिभुज
(d) समद्विबाहु त्रिभुज, समकोण त्रिभुज
(e) समबाहु त्रिभुज, न्यूनकोण रिभुज
(f) विषमबाहु त्रिभुज, अधिककोण त्रिभुज।

प्रश्न 4.
माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति में दिखाए गए हैं। क्या आप निम्न से त्रिभुज बना सकते हैं ?

(a) माचिस की 3 तीलियाँ
(b) माचिस की 4 तीलियाँ
(c) माचिस की 5 तीलियाँ
(d) माचिस की 6 तीलियाँ
(ध्यान रखिए कि आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है। प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
हल :
(a) हाँ, एक समबाहु त्रिभुज बना सकते हैं।
(b) नहीं, (क्योंकि त्रिभुज की दो भुजाओं का योग तीसरी भुजा की लम्बाई से अधिक होता है।)
(c) हाँ, एक समद्विबाहु त्रिभुज बना सकते हैं।
(d) हाँ, एक समबाहु त्रिभुज बना सकते हैं।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 क्षेत्रमिति InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 क्षेत्रमिति InText Questions

प्रयास कीजिए (पृष्ठ सं. 222 से)

प्रश्न 1.
अपनी अध्ययन टेबल के ऊपरी चारों सिरों की लंबाइयों को मापिए तथा उन्हें लिखिए।

AB = ………….. सेमी
BC = ……….. सेमी
CD = …………… सेमी
DA = ………… सेमी
अब चारों भुजाओं की लंबाइयों का योगफल
= AB + BC + CD + AD
= …….. सेमी + …. सेमी + …. सेमी + ……. सेमी
= …………….. सेमी
क्या आप बता सकते हैं कि परिमाप कितना है?
हल :
अध्ययन टेबल के ऊपरी चारों सिरों की लम्बाइयाँ मापने पर,
AB = 90 सेमी
BC = 60 सेमी
CD = 90 सेमी
DA = 60 सेमी
अब चारों भुजाओं की लम्बाइयों का योगफल
= AB + BC + CD + DA
= 90 सेमी + 60 सेमी + 90 सेमी + 60 सेमी
= 300 सेमी
परिमाप 300 सेमी है। उत्तर

प्रश्न 2.
अपनी नोटबुक के एक पृष्ठ की चारों भुजाओं की लंबाइयों को मापिए और उन्हें लिखिए। चरों भुजाओं की लंबाइयों का योगफल
= AB + BC + CD + DA
= ….. सेमी + ….. सेमी + ….. सेमी + ….. सेमी
= …… सेमी पृष्ठ का परिमाप कितना है?
हल :
नोटबुक के एक पृष्ठ की चारों भुजाओं की लंबाइयाँ मापने पर, AB = 30 सेमी, BC = 20 सेमी, CD = 30 सेमी, DA = 20 सेमी
चारों भुजाओं की लम्बाइयों का योगफल
= AB + BC + CD + DA
= 30 सेमी + 20 सेमी + 30 सेमी + 20 सेमी
= 100 सेमी
पृष्ठ का परिमाप 100 सेमी है।

प्रश्न 3.
मीरा 150 मीटर लम्बाई तथा 80 मीटर चौड़ाई वाले एक पार्क में जाती है। वह इस पार्क का पूरा एक चक्कर लगाती है। उसके द्वारा तय की गई दूरी ज्ञात कीजिए।
हल :
पार्क का पूरा चक्कर लगाने पर मीरा द्वारा तय की गई दूरी = पार्क की चारों भुजाओं को लम्बाइयों का योग
= 150 मीटर + 80 मीटर + 150 मीटर + 80 मीटर
= 460 मीटर, जो कि परिमाप है। उत्तर

प्रश्न 4.
निम्न आकृतियों के परिमार ज्ञात कीजिए :


हल :
(a) परिमाप = AB + BC + CD + DA
= 40 सेमी + 10 सेमी + 40 सेमी + 10 सेमी
= 100 सेमी उत्तर

(b) परिमाप = AB + BC + CD + DA
= 5 सेमी + 5 सेमी + 5 सेमी + 5 सेमी
= 20 सेमी उत्तर

(c) परिमाप = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
= (1 + 3 + 3 + 1 + 3 + 3 + 1 + 3 + 3 + 1 + 3 + 3) सेमी
= 28 सेमी उत्तर

(d) परिमाप = AB + BC + CD + DE + EF + FA
= 100 मी + 120 मी + 90 मी + 45 मी + 60 मी + 80 मी
= 495 मी उत्तर

पृष्ठ सं. 224 से

प्रश्न 1.
निम्नलिखित आयतों के परिमाप ज्ञात कीजिए।

हल :

पृष्ठ सं. 234 से

प्रश्न 1.
ग्राफ पेपर पर कोई एक वृत्त खींचिए। इस वृत्त में उपस्थित वर्गों की संख्या को गिनकर वृत्ताकार क्षेत्र का अनुमानित क्षेत्रफल ज्ञात कीजिए।
हल :
ग्राफ पेपर पर कोई एक वृत्त खींचा जिसका प्रत्येक वर्ग 1 सेमी × 1 सेमी माप का है।

पूर्ण वर्ग जो वृत्त में है = 1
आधे से ज्यादा भरे वर्ग = 1
आधे से कम भरे वर्ग = 4
पूरे वर्गों द्वारा घेरा गया क्षेत्रमा = (1 × 1) वर्ग सेमी
= 1 वर्ग सेमी
आधे से ज्यादा भरे वर्गों द्वा: करा गया क्षेत्रफल
= (4 × \(\frac{1}{2}\)) वर्ग सेमी
= 2 वर्ग सेमी
आधे से कम भरे वर्गों द्वारा घेरा गया क्षेत्रफल
= 4 × 0 वर्ग सेमी
= 0 सेमी
∴ कुल क्षेत्रफल = 1 + 4 + 0 वर्ग सेमी
= 5 वर्ग सेमी उत्तर

प्रश्न 2.
ग्राफ पेपर पर पत्तियों, फूल की पंखुड़ियों तथा ऐसी ही अन्य वस्तु को छायांकित कीजिए और उनका क्षेत्रफल ज्ञात कीजिए।
नोट :
छात्र स्वयं करें।

आयत का क्षेत्रफल

(पृष्ठ सं. 235 से)

प्रश्न 1.
कुछ आयतों की भुजाओं की मापें दी गई हैं। इन्हें ग्राफ पेपर पर रखकर तथा वर्गों की संख्या को गिनकर, इनका क्षेत्रफल ज्ञात कीजिए।

इससे हर क्या निष्कर्ष निकालते हैं ?
हल:

इस तालिका से स्पष्ट है कि
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
इससे हम इस निष्कर्ष पर पहुँचते हैं कि बिना आलेख कागज का प्रयोग किए भी आयत का क्षेत्रफल ज्ञात कर सकते हैं।

वर्ग का क्षेत्रफल

(पृष्ठ सं. 236 से)

प्रश्न 1.
कुछ वर्गों की एक भुजा की लम्बाई दी गई है। ग्राफ पेपर की सहायता से उनके क्षेत्रफलों को ज्ञात कीजिए।

इससे हम क्या निष्कर्ष निकालते हैं ?
हल:

इस तालिका से स्पष्ट है कि
वर्ग का क्षेत्रफल = भुजा × भुजा
इससे हम इस निष्कर्ष पर पहुँचते हैं कि ग्राफ पेपर का प्रयोग किए बिना भी वर्ग का क्षेत्रफल ज्ञात कर सकते हैं।

एक चुनौती

(पृष्ठ सं. 239 से)

प्रश्न 1.
एक सेण्टीमीटर वर्गांकित पेपर पर आप जितने भी आयत बना सकते हैं बनाइए, जिससे कि आयत का क्षेत्रफल 16 वर्ग सेमी हो जाए (केवल पूर्ण संख्या की लम्बाई पर ही विचार करना है):
(a) किस आयत का परिमाप सबसे अधिक है ?
(b) किस आयत का परिमाप सबसे कम है ?
यदि आप एक ऐसा आयत लें जिसका क्षेत्रफल 24 वर्ग सेमी हो, तो आपके उत्तर क्या होंगे?
दिए हुए क्षेत्रफल के लिए, क्या अधिकतम परिमाप के आयत के आकार को बताना सम्भव है? क्या सबसे कम परिमाप के आयत के बारे में बता सकते हैं? उदाहरण दीजिए और कारण बताइए।
हल :

एक सेण्टीमीटर वर्गांकित पेपर लेते हैं, जिस पर 16 वर्ग सेमी वाले सम्भव आयत निम्नलिखित भुजाओं वाले बनाए जा सकते हैं :
(i) 16 सेमी × 1 सेमी
(ii) 8 सेमी × 2 सेमी
(iii) 4 सेमी × 4 सेमी
इन्हें ABCD, EFGH और IJKL आयतों द्वारा दर्शाया गया है :
आयत ABCD में,
परिमाप = 2 × (AB + BC)
= 2 × (1 + 16) सेमी
= 2 × 17 सेमी = 34 सेमी
[∵ क्षेत्रफल = 1 × 16 वर्ग सेमी = 16 वर्ग सेमी]
आयत EFGH में,
परिमाप = 2 × (EF + FG)
= 2 × (2 + 8) सेमी
=2 × 10 सेमी = 20 सेमी
[∵ क्षेत्रफल = 2 × 8 वर्ग सेमी = 16 वर्ग सेमी]
आयत IJKL में,
परिमाप = 2 × (IJ + JK)
= 2 × (4 + 4) सेमी
= 2 × 8 सेमी = 16 सेमी
[∵ क्षेत्रफल = 4 × 4 वर्ग सेमी = 16 वर्ग सेमी]
इस प्रकार, यहाँ 3 आयत बनेंगे, जिनमें प्रत्येक का क्षेत्रफल 16 वर्ग सेमी समान है।
(a) आयत ABCD का परिमाप सबसे अधिक है।
(b) आयत IJKL का परिमाप सबसे कम है।
स्थिति : जब आयत का क्षेत्रफल 24 वर्ग सेमी हो:
सम्भव आयत 4 होंगे:
(i) 24 सेमी × 1 सेमी
(ii) 12 सेमी × 2 सेमी
(iii) 8 सेमी × 3 सेमी
(iv) 6 सेमी × 4 सेमी
इनका परिमाप क्रमशः 50 सेमी, 28 सेमी, 22 सेमी और 20 सेमी होगा।
इस प्रकार, (a) आयत (i) का परिमाप सबसे बड़ा है, जिसकी भुजाएँ 24 सेमी × 1 सेमी हैं।
(b) आयत (iv) का परिमाप सबसे कम है जिसकी भुजाएँ 6 सेमी × 4 सेमी हैं।
हाँ, दिए हुए क्षेत्रफल से सबसे बड़े परिमाप वाले और सबसे छोटे परिमाप वाले आयत के आकार को बता सकते हैं। दिए गए क्षेत्रफल के अनुसार बनाए गए आयतों में जिस आयत की लम्बाई अधिकतम तथा चोड़ाई न्यूनतम होगी उसी आयत का परिमाप सबसे ज्यादा होगा।