Class 6

Haryana State Board HBSE 6th Class Maths Solutions Chapter 8 दशमलव Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 8 दशमलव Exercise 8.1

प्रश्न 1.
निम्न के लिए दी गई सारणी में संख्याएँ लिखिए :

हल :
दी गई तालिका को भरने पर :

प्रश्न 2.
निम्न दशमलव संख्याओं को स्थानीय मान सारणी में लिखिए :
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
हल :
दी गई दशमलव संख्याओं के स्थानीय मान सारणी में लिखने पर :

प्रश्न 3.
निम्न में से प्रत्येक को दशमलव रूप में लिखिए :
(a) 7 दशांश
(b) 2 दहाई, 9 दशांश
(c) चौदह दशमलव छः
(d) एक सौ और 2 इकाई
(e) छः सौ दशमलव आठ
हल :
(a) 7 दशांश = \(\frac{7}{10}\) = 0.7 उत्तर
(b) 2 दहाई, 9 दशांश = 20 + \(\frac{9}{10}\)
= 20 + 0.9 = 20.9 उत्तर
(c) चौदह दशमलव छः = 14.6 उत्तर
(d) एक सौ और 2 इकाई = 1 × 100 + 0 × 10 + 2 × 1 + 0 × \(\frac{1}{10}\)
= 100 + 0 + 2 + 0.0 = 102.0 उत्तर
(e) छः सौ दशमलव आठ = 600.8

प्रश्न 4.
निम्न को दशमलव रूप में व्यक्त कीजिए :
(a) \(\frac{5}{10}\)
(b) 3 + \(\frac{7}{10}\)
(c) 200 + 60 + 5 + \(\frac{1}{10}\)
(d) 70 + \(\frac{8}{10}\)
(e) \(\frac{88}{10}\)
(f) 4\(\frac{2}{10}\)
(g) \(\frac{3}{2}\)
(h) \(\frac{2}{5}\)
(i) \(\frac{12}{5}\)
(j) 3\(\frac{3}{5}\)
(k) 4\(\frac{1}{2}\)
हल :
(a) \(\frac{5}{10}\) = 0.5 उत्तर
(b) 3 + \(\frac{7}{10}\) = 3 + 0.7 = 3.7 उत्तर
(c) 200 + 60 + 5 + \(\frac{1}{10}\) = 200 + 60 + 5 + 0.1
= 265.1 उत्तर
(d) 70 + \(\frac{8}{10}\) = 70 + 0.8 = 70.8 उत्तर
(e) \(\frac{88}{10}\) = 8.8 उत्तर

प्रश्न 5.
निम्न दशमलव संख्याओं को भिन्न के रूप में लिखकर न्यूनतम (सरलतम) रूप में बदलिए:
(a) 0.6
(b) 2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6.4
हल :

प्रश्न 6.
सेमी का प्रयोग कर निम्न को दशमलव रूप में बदलिए:
(a) 2 मिमी
(b) 30 मिमी
(c) 116 मिमी
(d) 4 सेमी 2 मिमी
(e) 11 सेमी 52 मिमी
(f) 83 मिमी
हल :
(a) 2 मिमी = \(\frac{2}{10}\) सेमी = 0.2 सेमी (∵ 10 मिमी = 1 सेमी)
(b) 30 सेमी = \(\frac{30}{10}\) = 3.0 सेमी (∵10 मिमी = 1 सेमी)

(c) 116 मिमी = \(\frac{116}{10}\)सेमी = \(\left(\frac{110+6}{10}\right)\) सेमी
(∵ 10 मिमी = 1 सेमी)
= \(\left(\frac{110}{10}+\frac{6}{10}\right)\) सेमी
= (11 + 0.6) सेमी = 11.6 सेमी उत्तर

(d) 4 सेमी 2 मिमी = 4 सेमी + 2 मिमी
= 4 सेमी + \(\frac{2}{10}\) सेमी
(∵ 10 मिमी = 1 सेमी)
= \(\left(4+\frac{2}{10}\right)\) सेमी
= (4 + 0.2) सेमी = 4.2 सेमी। उत्तर

(e) 11 सेमी 52 मिमी = 11 सेमी + 52 मिमी
= 11 सेमी + \(\frac{52}{10}\) सेमी,
[∵ 10 मिमी = 1 सेमी]
= \(\left(11+\frac{52}{10}\right)\) सेमी
= (11 + 5.2) सेमी = 16.2 सेमी उत्तर

(f) 83 मिमी = \(\frac{83}{10}\) सेमी
(∵ 10 मिमी = 1 सेमी)
= \(\left(\frac{80+3}{10}\right)\) सेमी = \(\left(\frac{80}{10}+\frac{3}{10}\right)\) सेमी
= (8 + 0.3) सेमी = 8.3 सेमी उत्तर

प्रश्न 7.
संख्या रेखा पर किन दो पूर्ण संख्याओं के बीच निम्न संख्याएँ स्थित हैं? इनमें से कौन-सी पूर्ण संख्या दी हुई दशमलव संख्या के अधिक निकट है?
(a) 0.8
(b) 5.1
(c) 2.6
(d) 6.4
(e) 9.0
(f) 4.9

हल:

प्रश्न 8.
निम्न को संख्या रेखा पर दर्शाओ :
(a) 0.2
(b) 1.9
(c) 1.1
(d) 2.5
हल :
(a) ∵ 0.2, 0 से बड़ी और 1 से छोटी है। यह संख्या दो दशांश है। 0 और 1 के बीच इकाई की लम्बाई को 10 बराबर भागों में विभाजित करते हैं। इसके दूसरे भाग पर A बिन्दु अंकित किया, जैसा कि आकृति में दर्शाया गया है :

अतः बिन्दु A, संख्या रेखा पर 0.2 को व्यक्त करता है। उत्तर

(b) ∵ 1.9, 1 से बड़ी और 2 से छोटी है। इसलिए 1 और 2 के बीच लम्बाई को 10 बराबर भागों में बाँटते हैं। इसके 9वें भाग पर बिन्दु A अंकित किया, जैसा कि आकृति में दर्शाया गया है।

अतः बिन्दु A, संख्या रेखा पर 1.9 को दर्शाता है। उत्तर

(c) ∵ 1.1, 1 से बड़ी और 2 से छोटी है। इसलिए संख्या रेखा पर 1 और 2 के बीच की लम्बाई को 10 बराबर भागों में बाँटते हैं। इसके पहले भाग पर बिन्दु A अंकित किया, जैसा कि आकृति में दर्शाया गया है :

अतः बिन्दु A, संख्या रेखा पर 1.1 को व्यक्त करता है। उत्तर

(d) ∵ 2.5, 2 से बड़ी और 3 से छोटी है। इसलिए संख्या रेखा पर 2 और 3 के बीच की लम्बाई को 10 बराबर भागों में बाँटते हैं। इसके पाँचवें भाग पर बिन्दु A अंकित किया, जैसा कि आकृति में दर्शाया गया है :

अतः बिन्दु A, संख्या रेखा पर 2.5 को दर्शाता है। उत्तर

प्रश्न 9.
दी हुई संख्या रेखा पर स्थित A, B, C, D बिन्दुओं के लिए दशमलव संख्या लिखिए :

हल :
बिन्दु A की स्थिति :
चूँकि बिन्दु A संख्या रेखा पर 0 और 1 के बीच में है, और 0 और 1 के बीच में इकाई की लम्बाई को 10 बराबर भागों में विभाजित किया तथा बिन्दु A आठवें भाग पर अंकित किया।
इसलिए बिन्दु A, 0.8 को दर्शाता है। उत्तर

बिन्दु B की स्थिति :
चूँकि बिन्दु B, 1 और 2 के बीच में स्थित है, तथा 1 और 2 के बीच इकाई लंबाई को 10 बराबर भागों में बाँटा गया है। B बिन्दु 1 से 3 भाग आगे है। इसलिए बिन्दु B, 1.3 को दर्शाता है। उत्तर

बिन्दु C और बिन्दु D की स्थिति :
चूँकि बिन्दु C और D, 2 और 3 के बीच में स्थित हैं, और 2 और 3 के बीच में इकाई की लम्बाई को 10 बराबर भागों में बाँटा गया है तथा बिन्दु C और D क्रमशः 2 भाग और 9 भाग आगे हैं।
इसलिए C, 2.2 को तथा D, 2.9 को दर्शाता है। उत्तर

प्रश्न 10.
(a) रमेश की कॉपी की लम्बाई 9 सेमी 5 मिमी है। सेमी में इसकी लम्बाई क्या होगी?
(b) चने के एक छोटे पौधे की लम्बाई 65 मिमी है। इसकी लम्बाई सेमी में व्यक्त कीजिए।
हल :
(a) रमेश की कॉपी की लम्बाई = 9 सेमी 5 मिमी
= 9 सेमी + 5 मिमी = 9 सेमी + \(\frac{5}{10}\) सेमी।
(∵ 10 मिमी = 1 सेमी)
= 9 सेमी + 0.5 सेमी
= (9 + 0.5) सेमी = 9.5 सेमी उत्तर

(b) चने के छोटे पौधे की लम्बाई = 65 मिमी
= \(\frac{65}{10}\) सेमी = 6\(\frac{5}{10}\) सेमी (∵ 10 मिमी = 1 सेमी)
(6 + \(\frac{5}{10}\)) सेमी = (6 + 0.5) सेमी
= 6.5 सेमी उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 भिन्न Ex 7.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 7 भिन्न Exercise 7.5

प्रश्न 1.
निम्न भिन्नों को योग या घटाने के उचित रूप में लिखिए :

हल :
(a) \(\frac{1}{5}+\frac{2}{5}=\frac{3}{5}\)
(b) \(\frac{5}{5}-\frac{3}{5}=\frac{2}{5}\)
(c) \(\frac{2}{6}+\frac{3}{6}=\frac{5}{6}\)

प्रश्न 2.
हल कीजिए :

हल :

प्रश्न 3.
शुभम ने अपने कमरे की दीवार के \(\frac {2}{3}\) भाग पर पेंट किया। उसकी बहिन माधवी ने उसकी सहायता की और उस दीवार के \(\frac {1}{3}\) भाग पर पेंट किया। उन दोनों ने मिलकर कुल कितना पेंट किया?
हल :
शुभम द्वारा पेंट की गई दीवार = \(\frac {2}{3}\) भाग
माधवी द्वारा पेंट की गई दीवार = \(\frac {1}{3}\) भाग
दोनों द्वारा मिलकर पेंट की गई दीवार = \(\frac{2}{3}+\frac{1}{3}=\frac{3}{3}\) = 1
अतः दोनों ने मिलकर पूरी दीवार पर पेंट कर दिया।

प्रश्न 4.
रिक्त स्थानों को भरिए :

हल :

प्रश्न 5.
जावेद को संतरों की एक टोकरी का \(\frac {5}{7}\) भाग मिला। टोकरी में संतरों का कितना भाग शेष रहा ?
हल :
जावेद को सन्तरों की एक टोकरी का \(\frac {5}{7}\) भाग मिला।
∴ टोकरी में शेष सन्तरे = 1 – \(\frac{5}{7}=\frac{7}{7}-\frac{5}{7}\)
= \(\frac{7-5}{7}=\frac{2}{7}\) भाग। उत्तर

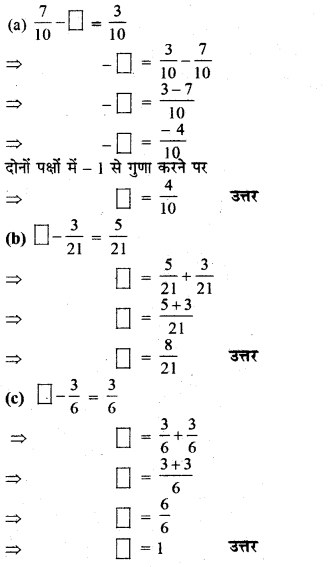
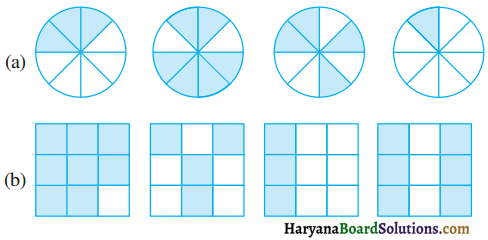
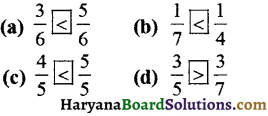
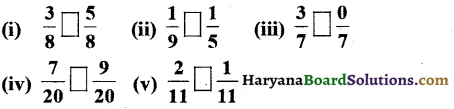
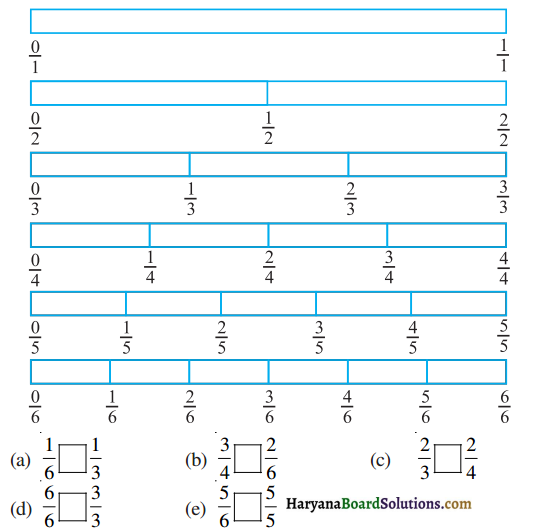
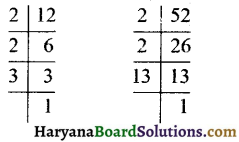
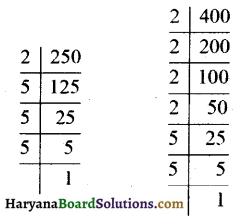
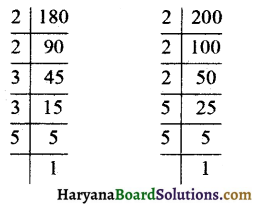
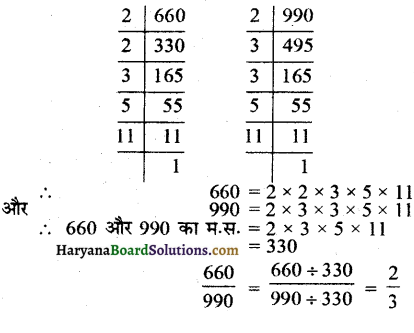
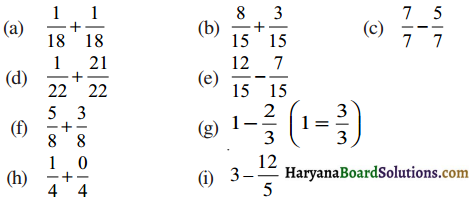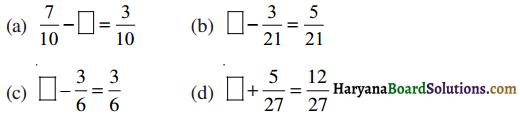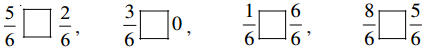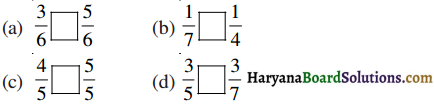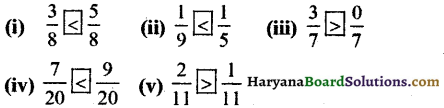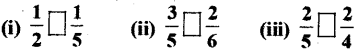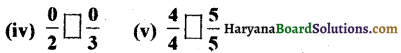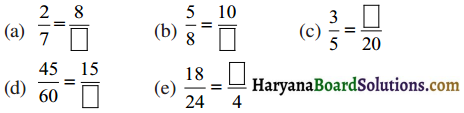Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभि क आकारों को समझना InText Questions

पृष्ठ सं. 97 से (प्रयास कीजिए)

प्रश्न 1.
एक पोस्टकार्ड लीजिए। उपयुक्त तकनीक का प्रयोग करके, इसकी दो आसन्न भुजाओं को मापिए।
हल :
एक पोस्टकार्ड की आसन्न भुजाओं को मापने पर , पोस्टकार्ड की लम्बाई 14 सेमी तथा चौड़ाई 9 सेमी है।

प्रश्न 2.
कोई तीन वस्तुएँ चुनिए जिनमें ऊपरी सिरे सपाट हों। डिवाइडर और रूलर का प्रयोग करते हुए, इन ऊपरी सिरों की सभी भुजाओं को मापिए।
हल :
कोई तीन वस्तुएँ पेन्सिल बॉक्स, कापी तथा मोबाइल लिए इनके ऊपरी सिरे सपाट है। डिवाइडर और रूलर का प्रयोग करते हुए इनके ऊपरी सिरों की सभी भुजाओं को मापने पर पेन्सिल बॉक्स की लम्बाई 17.5 सेमी तथा चौड़ाई 10.5 सेमी है। कापी की लम्बाई 22 सेमी तथा चौड़ाई 14 सेमी है। मोबाइल की लम्बाई 12 सेमी तथा चौड़ाई 7 सेमीप्रयास कीजिए |

पृष्ठ सं. 99 से

प्रश्न 1.
आधे घूर्णन के लिए कोण का नाम क्या है?
हल :
आधे घूर्णन के लिए कोण का नाम ऋजु कोण (180°) अथवा दो समकोण है।

प्रश्न 2.
एक-चौथाई घूर्णन के लिए कोण का नाम क्या है?
हल :
एक-चौथाई घूर्णन के लिए कोण का नाम एक समकोण (90°) है।

प्रश्न 3.
एक घड़ी पर आधे घूर्णन, एक-चौथाई घूर्णन और तीन-चौथाई घूर्णन के लिए पाँच अन्य स्थितियाँ दीजिए।
हल :
घूर्णन के लिए घड़ी में पाँच स्थितियों निम्न प्रकार हैं:
एक-चौथाई घूर्णन के लिए :

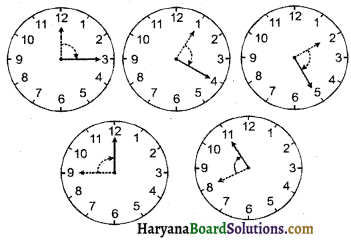
आधे घूर्णन के लिए

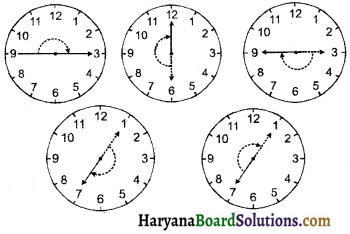
तीन-चौथाई घूर्णन के लिए:

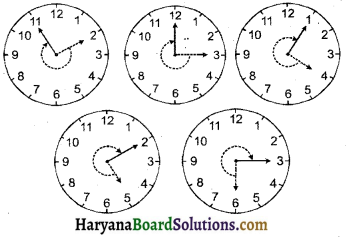
पृष्ठ सं. 102 से

प्रश्न 1.
घड़ी की घण्टे वाली सुई 12 से 5 तक चलती है। क्या इसका घूर्णन 1 समकोण से अधिक है ?

हल :
हाँ, घड़ी की घण्टे की सुई का घूर्णन एक समकोण (90°) से र अधिक है।

प्रश्न 2.
घड़ी पर यह कोण कैसा दिखता है ? घड़ी की घण्टे वाली सुई 5 से 7 तक चलती है। क्या इस सुई द्वारा घूमा गया कोण 1 समकोण से अधिक है?

हल :
नहीं, घड़ी पर यह कोण न्यूनकोण जैसा दिखता है। घड़ी की घण्टे वाली सुई 5 से 7 तक चलते पर इस सुई द्वारा घूमा कोण 1 समकोण से अधिक नहीं है। अर्थात् 1 समकोण में कम है।

प्रश्न 3.
घड़ी पर सुइयों की स्थिति निम्न प्रकार बनाकर कोणों की जाँच RA टेस्टर द्वारा कीजिए :
(a) 12 से 2 तक जाना
(b) 6 से 7 तक जाना
(c) 4 से 8 तक जाना
(d) 2 से 5 तक जाना।
हल :
(a) घड़ी की घण्टे वाली सुई द्वारा 12 से 2 तक चलने में बनाए गए कोण की जाँच RA टेस्टर द्वारा करने पर ज्ञात होता है कि यह एक समकोण से कम है।

(b) घड़ी की घण्टे वाली सुई द्वारा 6 से 7 तक चलने में बनाए गए कोण की जाँच RA टेस्टर द्वारा करने पर ज्ञात होता है कि यह एक समकोण से कम है।

(c) घड़ी की घण्टे वाली सुई द्वारा 4 से 8 तक चलने में बनाये गए कोण की जाँच RA टेस्टर द्वारा करने पर पता चलता है कि यह एक समकोण से अधिक है।

(d) घड़ी की घण्टे वाली सुई ला सुइ 412 द्वारा 2 से 5 तक चलने में बनाए गए। कोण की जाँच RA टेस्टर द्वारा करने पर पता चलता है कि यह एक समकोण है।

पृष्ठ सं. 104 से

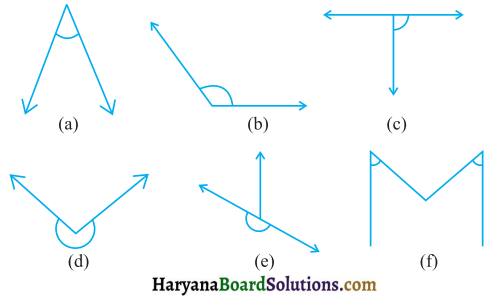
प्रश्न 1:
आप अपने आस-पास देखिए और कोनों पर मिलने वाले किनारों को पहचानिए, जो कोण बना रहे हों। ऐसी दस स्थितियाँ लिखिए।
हल :
ऐसी दस स्थितियाँ निम्न हो सकती है

1. छत का ऊपरी सिरा,
2. सी-सा,
3. पुस्तक खोलना,
4. दरवाजा खोलता,
5. मेज की आसन्न भुजाओं द्वारा बना कोण,
6. पुस्तक पढ़ने की डेस्क,
7. झूला,
8. बक्सा खोलना,
9. चिमटा,
10. सेट-स्क्वेयर।

प्रश्न 2.
ऐसी दस स्थितियाँ लिखिए, जहाँ न्यूनकोण बन रहे हों।
हल :
ऐसी स्थितियाँ निम्न हो सकती है

1. डिवाइडर,
2. सेट-स्क्वेयर,
3. कैंची,
4. पुस्तक खोलना,
5. दरवाजा खोलना,
6. चिमटा,
7. बॉक्स खोलना,
8. प्लास,
9. झूला,
10. घड़ी की सूइयों द्वारा बना कोण।

प्रश्न 3.
ऐसी दस स्थितियाँ लिखिए, जहाँ समकोण बन रहे हों।
हल :
ऐसी दस स्थितियाँ निम्न दो सकती है

1. सेट-स्क्वे यर,
2. मेज की आसन्न भुजाओं द्वारा बना कोण,
3. कमरे की आसन्न भुजाएँ.
4. फोटो फ्रेम,
5. टी. वी,
6. मोबाइल,
7. पेन्सिल बॉक्स,
8. कापी,
9. पुस्तक,
10. गुनिया।

प्रश्न 4.
ऐसी पाँच स्थितियाँ लिखिए, जहाँ अधिक कोण बन रहे हों।
हल :
ऐसी पाँच स्थितियाँ निम्न हो सकती है।

1. छत का ऊपरी सिरा,
2. पुस्तक खोलना,
3. डिवाइडर खोलना,
4. परकार खोलना,
5. कैची खोलना।

प्रश्न 5.
ऐसी पाँच स्थितियाँ लिखिए, जहाँ प्रतिवर्ती कोण बन रहे हों।
हल :
ऐसी पाँच स्थितियाँ निम्न हो सकती है

1. घड़ी की सुइयों द्वारा बना कोण,
2. परकार खोलना,
3. डिवाइडर खोलना,
4. पुस्तक खोलना,
5. बॉक्स का ढक्कन खोलना।

पृष्ठ सं. 105 से (सोचिए, चर्चा कीजिए और लिखिए)

प्रश्न 1.
\(\frac {1}{2}\) घूर्णन में कितनी डिग्री हैं ? 1 समकोण में कितनी डिग्री हैं?
1 ऋजुकोण में कितनी डिग्री (अंश) हैं ? कितने समकोणों से 180° बनते हैं ? कितने समकोणों से 360° बनते हैं?
हल :
∵ 1 घूर्णन में 360° का कोण बनता है।
∴ \(\frac {1}{2}\) घूर्णन में 360° × \(\frac {1}{2}\) = 180° का कोण बनेगा और 1 समकोण ( \(\frac {1}{4}\) घूर्णन) में बना कोण
= 360° × \(\frac {1}{4}\) = 90°
1 ऋजु कोण या सरल कोण (\(\frac {1}{2}\) घूर्णन) में बना कोण
= 360° × \(\frac {1}{2}\) = 180°
180° = \(\frac {180°}{90°}\) = 2 समकोण
अत: 2 समकोणों से 180° बनते है।
360° = \(\frac {180°}{90°}\) = 4 समकोण।
अत: 4 समकोणों से 360° बनते हैं।

पृष्ठ सं. 109 से (सोचिए, चर्चा कीजिए और लिखिए)

प्रश्न 1.
यदि AB ⊥ CD, तो हमें क्या यह भी कहना चाहिए कि CD ⊥ AB है?
हल :

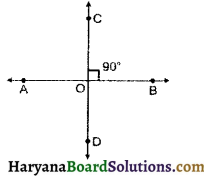
यदि CD ⊥ AB हो, तो
∠COB = 90°,
जो कि सत्य है
क्योंकि AB ⊥ CD है।
अत: AB ⊥ CD ⇒ CD ⊥ AB.
अर्थात् यदि AB ⊥ CD, तो हम यह भी कह सकते है कि CD ⊥ AB.

प्रश्न 2.
क्या कोई अन्य अक्षर (T के अलावा) है, जो लम्बवत् दर्शाता है ?
हल :
अंग्रेजी अक्षर L अन्य अक्षर है, जो लम्ब को दर्शाता है।

क्या पोस्टकार्ड के किनारे लम्ब होते हैं ?
हल :
हाँ, पोस्टकार्ड के किनारे एक-दूसरे पर लम्बवत् होते हैं।

पृष्ठ सं. 111, 112 से (इन्हें कीजिए)

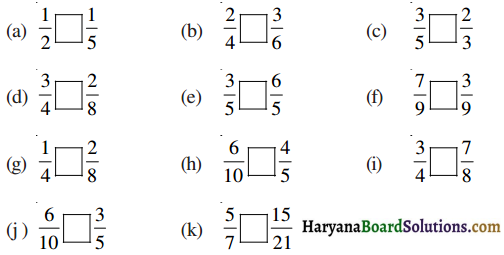
प्रश्न 1.
आइए, नीचे दिए हुए त्रिभुजों के कोणों और भुजाओं को क्रमश: चाँद और रूलर से मा। दी हुई सारणी में इनकी मापों को भरिए :

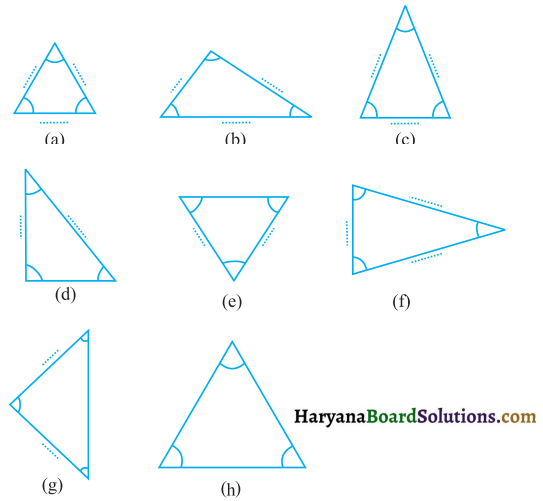
उपर्युक्त कोण, त्रिभुज और उनकी भुजाओं की मापों को ध्यानपूर्वक देखिए। क्या इनके बारे में कोई बात कही जा सकती है?
हल :
चाँद की सहायता से त्रिभुज के कोणों को मापने पर

पृष्ठ सं. 112 से (आप क्या प्राप्त करते है?)

रिक्त स्थान भरिए
1. त्रिभुज जिनके सभी कोण बराबर है।
यदि किसी त्रिभुज के सभी कोण बराबर है, तो इसकी भुजाएँ भी…………..हैं।
2. त्रिभुज जिनमें सभी भुजाएँ बराबर हैं। यदि एक त्रिभुज की सभी भुजाएँ बराबर हैं, तो उसके कोण भी…………..हैं। .
3. त्रिभुज जिनमें दो कोण बराबर हैं और दो भुजाएँ बराबर हैं। यदि किसी त्रिभुज की दो भुजाएँ बराबर हैं, तो उसके………….कोण बराबर होते हैं।
4. त्रिभुज जिनमें कोई भी दो भुजाएँ बराबर नहीं हैं। यदि किसी त्रिभुज के कोई भी दो कोण बराबर नहीं है, तो उसकी कोई भी दो भुजाएँ बराबर नहीं होती हैं। यदि किसी त्रिभुज की तीनों भुजाएँ बराबर नहीं है। भी………….नहीं हैं।
हल :
1. बराबर,
2. बराबर,
3. दो,
4. बराबर ।

पृष्ठ सं. 113 से (इन्हें कीजिए)

प्रश्न 1.
निम्न के रफ चित्र खींचने का प्रयत्न कीजिए :
(a) एक विषमबाहु न्यूनकोण त्रिभुज
(b) एक अधिक कोण समद्विबाहु त्रिभुज
(c) एक समकोण समद्विबाहु त्रिभुज
(d) एक विषमबाहु समकोण त्रिभुज
हल :
(a) विषमबाहु न्यूनकोण त्रिभुज की रफ आकृति :

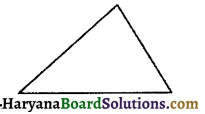
(b) अधिक कोण समद्विबाहु त्रिभुज की रफ आकृति :

(c) समकोण समद्विबाहु त्रिभुज की रफ आकृति :

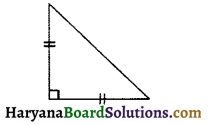
(d) विषमबाहु समकोण त्रिभुज की रफ आकृति :

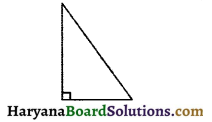
क्या आप सोचते हैं कि निम्न आकृति खींचना संभव है :
(e) एक अधिक कोण समबाहु त्रिभुज ?
(f) एक समकोण समबाहु त्रिभुज?
(g) एक त्रिभुज जिसमें दो समकोण हों ?
सोचिए, चर्चा कीजिए और फिर अपने निष्कर्षों को लिखिए।
हल :
(e) एक अधिक कोण समबाहु त्रिभुज सम्भव नहीं है, क्योंकि समबाहु त्रिभुज का प्रत्येक कोण 60° का होता है। अतः अधिक कोण नहीं बनेगा।
(f) समबाहु त्रिभुज में समकोण नहीं हो सकता, क्योंकि इसका प्रत्येक कोण 60° का होता है।
(g) एक त्रिभुज में दो समकोण सम्भव नहीं है, क्योंकि त्रिभुज में केवल एक ही समकोण हो सकता है।

पृष्ठ सं. 115 से (इन्हें कीजिए)

प्रश्न 1.
दो डंडी लीजिए और उन्हें इस प्रकार रखिए कि उनका एक-एक सिरा एक सिरे पर मिले। अब डंडियों के एक अन्य युग्म को इस प्रकार रखिए कि उनके सिरे इंडियों के पहले युग्म के स्वतन्त्र सिरों से जुड़ जाएँ। इस प्रकार हमें क्या आकृति प्राप्त होती है ?
हल :
प्रश्नानुसार, डंडियों को रखने पर हमें चतुर्भुज की आकृति प्राप्त होती है जिसकी भुजाएँ \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D A}\) हैं।
और इसके चार कोण ∠BAD, ∠ADC, ∠DCB और ∠ABC हैं।
यह एक चतुर्भुज है, जो आप सामने देख रहे हैं। इस चतुर्भुज की भुजाएँ \(\overline{A B}, \overline{B C}\), ………… है।
इस चतुर्भुज के चार कोण हैं। ये ∠BAD, ∠ADC, ∠DCB और ……… है।

\(\overline{A C}\) एक विकर्ण है।
अन्य विकर्ण कौन-सा है ?
सभी भुजाओं और विकर्णों की लंबाइयाँ मापिए। सभी कोणों को भी मापिए।
अन्य विकर्ण \(\overline{B D}\) है।
भुजाओं और विकर्णों को मापने पर,

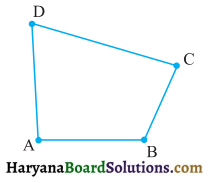
AB = 2.7 सेमी
BC = 2.1 सेमी
CD = 3.6 सेमी
DA = 3.9 सेमी
AC = 3.7 सेमी
और BD = 3.8 सेमी

सभी कोणों को मापने पर,
∠BAD = 90°
∠ABC = 65°
∠DCB = 100°
और ∠ADC = 105° है।

प्रश्न 2.
जैसा आपने ऊपर क्रियाकलाप किया है, चार इंडियाँ लेकर देखिए कि क्या आप इनसे ऐसा चतुर्भुज बना सकते हैं, जिसमें:
(a) चारों कोण न्यून कोण हैं।
(b) एक कोण अधिक कोण है।
(c) एक कोण समकोण है।
(d) दो कोण अधिककोण है।
(e) दो कोण समकोण हैं।
(f) विकर्ण परस्पर समकोण पर हैं।
हल :
(a) नहीं,
(b) हाँ,
(c) हाँ,
(d) हाँ,
(e) हाँ,

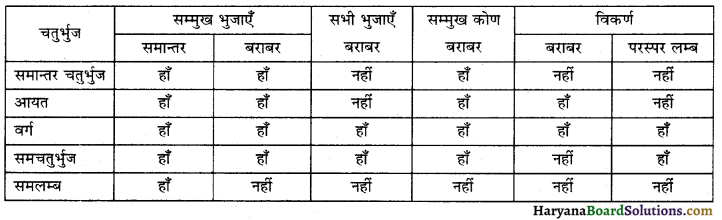
पृष्ठ सं. 115, 116, 117 से

प्रश्न 1.
आप और आपका मित्र मिलकर इस क्रिया को कर सकते हैं:

(a) आप दोनों के पास N21
जा एक-एक 30° – 60°- 90° सेट स्क्वे यर हैं। इनको आकृति में दर्शाए अनुसार : रखिए। क्या आप इस प्रकार बने चतुर्भुज का नाम बता सकते हैं ? आप इसके कौन से गुण ज्ञात कर सकते हैं? इसके प्रत्येक कोण का माप क्या है?
हल :

यह चतुर्भुज एक आयत है, जिसमें
(i) सम्मुख भुजाएँ समान होती हैं।
(ii) विकर्ण बराबर होते हैं तथा परस्पर समद्विभाजित करते हैं।
(iii) प्रत्येक कोण 90° का होता है।

(b) यदि अन्य सेट स्क्वे यर 45° – 45° – 90° के युग्म का प्रयोग करें, तो आपको किस प्रकार का चतुर्भुज प्राप्त होगा? इसके गुण ज्ञात करने का प्रयत्न कीजिए ।
हल :

यह चतुर्भुज एक वर्ग है, जिसमें
(i) सभी भुजाएँ समान होती हैं।
(ii) प्रत्येक कोण 90° का होता है।
(iii) विकर्ण समान होते हैं।
(iv) विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।

(c) यदि आप 30° – 60° – 90° सेट स्क्वेयरोंको आकृति में दर्शाए अनुसार रखें, तो आपको किस प्रकार का चतुर्भुज प्राप्त होगा? क्या इसकी सम्मुख भुजाएँसमान्तर हैं? क्या इसके विकर्ण बराबर हैं?
हल :

हमें एक समान्तर चतुर्भुज प्राप्त होता है, जिसमें :
(i) सम्मुख भुजाएँ समान्तर होती हैं।
(ii) सम्मुख भुजाएँ समान होती हैं।
(iii) सम्मुख कोण समान होते हैं।
(iv) आसन्न कोणों का योग 180° होता है।
(v) इसके विकर्ण एक-दूसरे को समद्विभाजित करते हैं, लेकिन समान नहीं होते।

(d) यदि आप 30° – 60° – 90° सेट स्क्वे यरों का आकृतिनुसार प्रयोग करें, तो आपको किस प्रकार का चतुर्भुज प्राप्त होगा?

हल :
एक समचतुर्भुज (Rhombus) प्राप्त होगा।

(e) यदि आप आकृति में दर्शाए अनुसार कई सेट स्क्वेयरों का प्रयोग करें, तो आपको किस प्रकार का चतुर्भुज प्राप्त होगा?

हल :
एक समलम्ब चतुर्भुज प्राप्त होगा जिसकी दो भुजाएँ समान्तर होंगी।

प्रश्न 2.
यहाँ आपकी खोजों के सारांश की एक रूपरेखा दी जा रही है। इसे पूरा कीजिए।
हल:

पृष्ट सं. 119 से (त्रिविमीय आकार)

प्रश्न 1.
किन्हीं पाँच वस्तुओं के नाम बताइए जो एक गोले से मिलती-जुलती हों।
हल :
पाँच वस्तुएँ जो गोले से मिलती-जुलती है। निम्न दो सकती हैं

1. गेंद,
2. फुटबॉल,
3. ग्लोब,
4. अमरूद,
5. सन्तरा।

प्रश्न 2.
किन्हीं ऐसी पाँच वस्तुओं के नाम बताइए, जो एक शंकु से मिलती-जुलती है।
हल :
पाँच वस्तुएँ जो शंकु से मिलती-जुलती है निम्न हो सकती है

1. सोफ्टी,
2. जोकर की टोपी,
3. भुट्टा,
4. गुलाब की कली,
5. बच्चों का खिलौना लटू।

पृष्ठ सं. 121 से

1. एक घनाभ एक आयताकार बक्स जैसा है। इसके 6 फलक है। प्रत्येक फलक के चार किनारे हैं। प्रत्येक फलक के चार कोने हैं (जो इसके शीर्ष कहलाते हैं)।

2. एक घन ऐसा घनाभ होता है, जिसके सभी किनारे बराबर लम्बाई के होते हैं।
इसके 6 फलक हैं।
प्रत्येक फलक के किनारे हैं।
प्रत्येक फलक के 4 शीर्ष हैं।

3. एक त्रिभुजाकार पिरामिड का
आधार एक त्रिभुज होता है। यह चतुष्फलक (tetrahedron) भी कहलाता है।
फलक : 4
किनारे : 6
कोने : 4

4. एक वर्ग पिरामिड का आधार एक
वर्ग होता है।
फलक : 6
किनारे : 12
कोने : 8

5. एक त्रिभुजाकार प्रिज्म प्रायः एक केलाइडोस्कोप (Kaleidoscope) के आकार का होता है। इसका आधार और ऊपरी सिरा त्रिभुज के । आकार के होते हैं।
फलक : 5
किनारे : 9
कोने : 6

Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 भिन्न Ex 7.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 7 भिन्न Exercise 7.4

प्रश्न 1.
प्रत्येक चित्र के लिए भिन्नों को लिखिए। भिन्नों के बीच में सही चिह्न ‘<‘, ‘=’, ‘>’ का प्रयोग करते हुए, इन्हें आरोही और अवरोही क्रम में व्यवस्थित कीजिए :

(c) \(\frac{2}{6}, \frac{4}{6}, \frac{8}{6}\) और \(\frac {6}{6}\) को संख्या रेखा पर दर्शाइए। दी हुई भिन्न के बीच में उचित चिह्न ‘<‘ या ‘>’ भरिए :

हल :
(a) दिए गए चित्रों के लिए भिन्नें हैं :
\(\frac{3}{8}, \frac{6}{8}, \frac{4}{8}\) और \(\frac {1}{8}\)
आरोही क्रम में रखने पर, \(\frac {1}{8}\) < \(\frac {3}{8}\) < \(\frac {4}{8}\) < \(\frac {6}{8}\)
अवरोही क्रम में रखने पर, \(\frac {6}{8}\) < \(\frac {4}{8}\) < \(\frac {3}{8}\) < \(\frac {1}{8}\) उत्तर

(b) चित्रों द्वारा दर्शाई गई भिन्नें हैं : \(\frac{8}{9}, \frac{4}{9}, \frac{3}{9}\) और \(\frac {6}{9}\)
आरोही क्रम में रखने पर, \(\frac {3}{9}\) < \(\frac {4}{9}\) < \(\frac {6}{9}\) < \(\frac {8}{9}\)
अवरोही क्रम में रखने पर, \(\frac {8}{9}\) < \(\frac {6}{9}\) < \(\frac {4}{9}\) < \(\frac {3}{9}\) उत्तर

(c) \(\frac{2}{6}, \frac{4}{6}, \frac{8}{6}\) और \(\frac {6}{6}\) को संख्या रेखा पर व्यक्त करना :
∴ \(\frac {2}{6}\) और \(\frac {4}{6}\) < 1, \(\frac {8}{6}\) = 1\(\frac {2}{6}\) > 1 और \(\frac {6}{6}\) = 1 है।
एक रेखा खींची जिस पर 0, 1 और 2 पर क्रमश: बिन्दु O, A और B अंकित करते हैं।
प्रत्येक इकाई को 6 बराबर भागों में बाँटते हैं। तब बिन्दु M, N, A और P क्रमशः \(\frac{2}{6}, \frac{4}{6}, \frac{6}{6}\) और \(\frac {8}{6}\) को दर्शाते हैं।

प्रश्न 2.
भिन्नों की तुलना कीजिए और उचित चिह्न लगाइए –

हल :

प्रश्न 3.
ऐसे ही पाँच और युग्म लीजिए और उचित चिह्न लगाइए।
हल :
ऐसे ही पाँच युग्म :

उचित चि
लगाने पर,

प्रश्न 4.
निम्न आकृतियों को देखिए और भिन्नों के बीच में उचित चिह्न ‘>’, ‘=’ या ‘<‘ लिखिए :

ऐसे ही पाँच और प्रश्न बनाइए और अपने मित्रों के साथ उन्हें हल कीजिए।
हल :

ऐसे ही पाँच और प्रश्न :


हल :

प्रश्न 5.
देखें कितनी जल्दी आप करते हैं? उचित चिह्न भरिए (<, =, >):

हल :

प्रश्न 6.
निम्नलिखित भिन्न तीन अलग-अलग संख्याएँ निरूपित करती हैं, इन्हें सरलतम रूप में बदलकर उन तीन तुल्य भिन्नों के समूहों में लिखिए :

हल :
दी गई भिन्नों को सरलतम रूप में बदलने पर,

इन्हें तीन बराबर भिन्नों वाले तीन समूह में बाँटने पर,

प्रश्न 7.
निम्नलिखित के उत्तर दीजिए। लिखिए और दर्शाइए कि आपने इन्हें कैसे हल किया है ?
(a) क्या \(\frac{5}{9}, \frac{4}{5}\) के बराबर है?
(b) क्या \(\frac{9}{16}, \frac{5}{9}\) के बराबर है?
(c) क्या \(\frac{4}{5}, \frac{16}{20}\) के बराबर है?
(d) क्या \(\frac{1}{15}, \frac{4}{30}\) के बराबर है?
हल :

प्रश्न 8.
इला 100 पृष्ठों वाली एक पुस्तक के 25 पृष्ठ पढ़ती है। ललिता इसी पुस्तक का \(\frac {1}{2}\) भाग पढ़ती है। किसने कम पढ़ा?
हल :
इला द्वारा पढ़ा गया किताब का भाग = \(\frac {25}{100}\)
और ललिता द्वारा पढ़ा गया किताब का भाग = \(\frac{\frac{1}{2} \times 100}{100}\)
= \(\frac {50}{100}\)
अत: \(\frac {25}{100}\) < \(\frac {50}{100}\) इला द्वारा कम पढ़ा गया। उत्तर प्रश्न 9. रफीक ने एक घण्टे के \(\frac {3}{6}\) भाग तक व्यायाम किया, जबकि रोहित ने एक घण्टे के \(\frac {3}{4}\) भाग तक व्यायाम किया। किसने लम्बे समय तक व्यायाम किया ? हल : रफीक ने व्यायाम किया = \(\frac {3}{6}\) घण्टे और रोहित ने व्यायाम किया = \(\frac {3}{4}\) घण्टे \(\frac {3}{4}\) > \(\frac {3}{6}\)
क्योंकि दोनों भिन्नों में अंश बराबर है। अतः जिसका हर छोटा होगा, वह भिन्न बड़ी माप की होगी। अत: रोहित ने ज्यादा लम्बे समय तक व्यायाम किया। उत्तर

प्रश्न 10.
25 विद्यार्थियों की एक कक्षा में 20 विद्यार्थी 60% या अधिक अंक लेकर पास हुए और 30 विद्यार्थियों की एक कक्षा B में 24 विद्यार्थी 60% या अधिक अंक लेकर पास हुए। किस कक्षा में विद्यार्थियों का अधिक भाग 60% या अधिक अंक लेकर पास हुआ?
हल :
कक्षा A के 60% या अधिक अंक लेकर पास विद्यार्थियों की संख्या = \(\frac {20}{25}\) भाग = \(\frac{20 \div 5}{25 \div 5}=\frac{4}{5}\) भाग
कक्षा B के 60% या अधिक अंक लेकर पास विद्यार्थियों की संख्या = \(\frac {24}{30}\) भाग = \(\frac{24 \div 6}{30 \div 6}=\frac{4}{5}\) भाग
अतः दोनों कक्षाओं में 60% या अधिक अंक लेकर पास विद्यार्थियों का भाग समान है। उत्तर

Haryana State Board HBSE 6th Class Social Science Solutions Geography Chapter 1 ग्लोब: अक्षांश एवं देशांतर Textbook Exercise Questions and Answers.

Haryana Board 6th Class Social Science Solutions Geography Chapter 2 ग्लोब: अक्षांश एवं देशांतर

HBSE 6th Class Geography ग्लोब: अक्षांश एवं देशांतर Textbook Questions and Answers

ग्लोब : अक्षांश एवं देशांतर प्रश्न उत्तर HBSE 6th Class Social Science प्रश्न 1.
निम्नलिखित प्रश्नों के उत्तर संक्षेप में दीजिए:
(i) पृथ्वी का सही आकार क्या है?
What is the true shape of the earth?
उत्तर:
पृथ्वी की वास्तविक आकृति भूगणितीय अल्पांतरी गोल है।

(ii) ग्लोब क्या है?
What is a globe?
उत्तर:
ग्लोब मानव द्वारा निर्मित पृथ्वी का त्रि-आयामी प्रतिरूप है।

(iii) कर्क रेखा का अक्षांशीय मान क्या है?
What is the latitude value of Tropic of Cancer?
उत्तर:
231/2° उत्तरी अक्षांश।

(iv) पृथ्वी के तीन ताप कटिबंध कौन-से हैं?
What are the three heat zones of the earth?
उत्तर:
पृथ्वी के तीन ताप क्षेत्र हैं:

• ऊष्ण कटिबंध
• शीतोष्ण कटिबंध
• शीत कटिबंध।

(v) अक्षांश एवं देशांतर रेखाएँ क्या हैं?
What are the parallels of latitude and meridians of longitude ?
उत्तर:

• देशांतर रेखाएँ (Longitudes): वे काल्पनिक रेखायें जो ध्रुवों को मिलाती हैं और उत्तर से दक्षिण को खिंची हुई हैं।
• अक्षांश (Latitude) : वे काल्पनिक रेखायें जो भूमध्य रेखा के उत्तर तथा दक्षिण में ध्रुवों के समांतर खिंची मानी गई हैं।

(vi) ऊष्मा की सबसे अधिक मात्रा उष्ण कटिबंध क्यों प्राप्त करते हैं?
Torrid zone receives maximum amount of heat. Why?
उत्तर:
ऊष्ण कटिबंध वर्ष भर अधिकतम ताप प्राप्त करता है क्योंकि सूर्य की किरणें इस क्षेत्र में सीधी पड़ती हैं। यह क्षेत्र कर्क वृत्त से लेकर मकर वृत्त तक विस्तृत है।

(vii) जब भारत में शाम के 5:30 बजते हैं तो लंदन में दोपहर के 12 क्यों बजते हैं?
It is 5.30 p.m. in India, when it is 12 ‘0 clock in London.,Why?
उत्तर:
भारत ग्रीनविच से 82°.30’.पूर्व में स्थित है। इसलिये भारत का समय ग्रीनविच के समय से 5.30 घंटे आगे रहता है। यही कारण है कि जब लंदन जो ग्रीनविच के समीप 0° देशांतर पर है, में दोपहर के 12 बजेंगे तो भारत में सायं 5.30 का समय होगा।

ग्लोब अक्षांश एवं देशांतर HBSE 6th Class Social Science प्रश्न 2.
सही उत्तर चिह्नित (√) कीजिए:
Tick the correct option:
(i) प्रमुख याम्योत्तर का मान है :
(क) 900
(ख) 0°
(ग) 60°
उत्तर:
(ख) 0°.

(ii) शीत कटिबंध किसके नजदीक पाया जाता है?
(क) ध्रुवों
(ख) विषुवत् वृत्त
(ग) कर्क रेखा
उत्तर:
(क) ध्रुवों के।

(iii) देशांतरों की कुल संख्या है :
(क) 360
(ख) 180
(ग) 90
उत्तर:
(क) 360

(iv) उत्तरी ध्रुव वृत्त स्थित है:
(क) उत्तरी गोलार्ध में
(ख) दक्षिणी गोलार्ध में
(ग) पूर्वी गोलार्ध में
उत्तर:
(क) उत्तरी गोलार्ध में।

(ङ) ग्रिड किसका जाल है:
(क) अक्षांशों (समानांतर) रेखाओं एवं देशांतरीय याम्योत्तरों का
(ख) कर्क रेखा एवं मकर रेखा का
(ग) उत्तरी ध्रुव एवं दक्षिणी ध्रुव का
उत्तर:
(क) अक्षांश तथा देशांतर रेखाओं का।

HBSE 6th Class Social Science ग्लोब अक्षांश एवं देशांतर प्रश्न 3.
खाली स्थान भरें:
Fill in the blanks:
(i) मकर रेखा ……………………. पर स्थित है।
उत्तर:
231° दक्षिणी अक्षांश।

(ii) भारत का मानक याम्योत्तर ………………….. है।
उत्तर:
821° पूर्व देशांतर।

(iii) 0° याम्योत्तर को ————— के नाम से जाना जाता है।
उत्तर:
प्रधान मध्याह्न रेखा।

(iv) देशांतरों के बीच की दूरी ………………….. की तरफ घटती जाती है।
उत्तर:
ध्रुवों की।

(iv) दक्षिणी ध्रुव वृत्त ————- गोलार्ध में स्थित है।
उत्तर:
दक्षिणी।

आओ कुछ करें:
पृथ्वी के अक्ष, विष्वत् वृत्त. कर्क रेखा एवं मकर रेखा, उत्तरी ध्रुव वृत्त तथा दक्षिणी ध्रुव वृत्त को दर्शाते हुए एक चित्र बनाएँ। • छात्र चार्ट बनाएँ।

HBSE 6th Class Geography ग्लोब: अक्षांश एवं देशांतर Important Questions and Answers

अति लघु उत्तरात्मक प्रश्न

प्रश्न 1.
कर्क वृत्त क्या है?
What is Tropic of Cancer?
उत्तर:
231/2° उत्तरी अक्षांश को कर्क वृत्त कहते हैं।

प्रश्न 2.
मकर वृत्त क्या है?
What is Tropic of Capricorn?
उत्तर:
231/2° दक्षिणी अक्षांश को मकर वृत्त कहते हैं।

प्रश्न 3.
पृथ्वी की सही आकृति का ज्ञान किससे मिलता हैं?
Which we get true knowledge of earth form?
उत्तर:
ग्लोब से।

प्रश्न 4.
ग्लोब पर कौन-कौन सी आकृतियाँ सही दिखाई देती हैं?
Which shapes are shown true on globe?
उत्तर:
ग्लोब पर दोनों ध्रुव, अक्षांश तथा देशांतर रेखायें, महासागर और महाद्वीप दिखाये जाते हैं।

प्रश्न 5.
पृथ्वी अपनी घूर्णन गति किस पर करती है?
On which the earth rotates?
उत्तर:
पृथ्वी अपनी घूर्णन गति अपने अक्ष पर करती है।

प्रश्न 6.
पृथ्वी के दो बिंदु क्या हैं?
What are the two points of earth?
उत्तर:
पृथ्वी के दो बिंदु उत्तरी ध्रुव तथा दक्षिणी ध्रुव हैं।

प्रश्न 7.
भूमध्य रेखा किसे कहते हैं?
Define equator.
उत्तर:
वह काल्पनिक रेखा जो पृथ्वी के मध्य पूर्व-पश्चिम खींची गई है। यह पृथ्वी को दो भागों में विभाजित करती है।

प्रश्न 8.
भारत की मानक समय रेखा क्या है?
What is the Standard Meridian of India?
उत्तर:
भारत की मानक समय रेखा 829° पूर्व देशांतर है।

प्रश्न 9.
स्थानीय समय किसे कहते हैं?
What is local time?
उत्तर:
किसी स्थान पर जब सूर्य ठीक सिर के ऊपर होता है तो इस समय को उस स्थान का स्थानीय समय कहते हैं।

लघु उत्तरात्मक प्रश्न

प्रश्न 1.
ग्लोब के कोई दो लाभ बताओ।
Mention two advantages of globe.
उत्तर:
ग्लोब के लाभ :

• ग्लोब पर महाद्वीप, महासागर आदि एक दृष्टि में देखे जा सकते हैं।
• ग्लोब को उसी प्रकार घुमाया जा सकता है जिस प्रकार पृथ्वी घूमती है।

प्रश्न 2.
ग्लोब की क्या कमियाँ हैं?
What are the disadvantages of globe?
उत्तर:

• ग्लोब का उपयोग अधिक विवरण दिखाने के लिये नहीं किया जा सकता।
• ग्लोब का प्रयोग पृथ्वी के किसी भाग विशेष अथवा क्षेत्र या देश, जिला आदि के लिये नहीं किया जा सकता है।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर संक्षेप में दीजिए:
Answer the following questions in brief:
(i) पृथ्वी के धरातल पर कौन से दो आधारभूत संदर्भ बिंदु हैं? उनके नाम लिखिए।
Which are the two basic points of reference on the earth’s surface ? Name them.
उत्तर:
दो आधार बिंदु उत्तरी ध्रुव तथा दक्षिणी ध्रुव हैं।

(ii) हम पृथ्वी पर सबसे बड़ा वृत्त कैसे बना सकते हैं?
How can we draw the greatest circle on the earth?
उत्तर:
यदि हम ग्लोब पर मध्य में पश्चिम से पूर्व को रेखा खींचे तो वह सबसे बड़ा वृत्त बनाएगी। यह भूमध्य रेखा कहलाएगी।

प्रश्न 4.
स्थानीय समय तथा मानक समय में क्या अंतर हैं?
What is the difference between the local time and the standard time?
उत्तर:
स्थानीय समय (Local Time): किसी स्थान पर जब सूर्य आकाश में सबसे अधिक ऊँचाई पर अर्थात् ठीक सिर के ऊपर होता है उस समय दिन के 12 बजे का समय होता है। इसी समय को उस स्थान का स्थानीय समय कहा जाता है। इस देशांतर पर स्थित सभी स्थानों का समय दोपहर के 12 बजे ही होगा।

मानक समय (Standard Time) : विभिन्न देशांतर रेखाओं पर स्थानीय समय भिन्न-भिन्न होता है। इससे यातायात तथा संचार साधनों के परिचालन समय में कठिनाई आ जाती है। इस समस्या को दूर करने के लिये रूस तथा भारत जैसे देशों ने अपना एक स्थानीय समय माना है जो देश की मानक मध्याह्न रेखा से माना जाता है। जैसे भारत की मानक मध्याह्न रेखा 827° पू. देशांतर रेखा है। इस रेखा के समय को सारे भारत का मानक समय माना जाता है।

प्रश्न 5.
तीन ताप कटिबंधों के नाम उनकी सीमाओं के साथ बताइये।
Name the three heat zones along with their exact boundaries.
उत्तर:
तीन ताप कटिबंध निम्न प्रकार हैं:
1. ऊष्ण कटिबंध (Torrid Zones) : यह क्षेत्र अधिकतम ऊष्मा ग्रहण करता है इसलिये इसे ऊष्ण कटिबंध कहते हैं। यह कर्क वृत्त (231/2°) उत्तर तथा मकर वृत्त (231/2°) दक्षिण के मध्य स्थित है।

2. शीतोष्ण कटिबंध (Temperate Zones) : यह क्षेत्र कर्क वृत्त (231/2°) उत्तरी तथा आर्कटिक वृत्त (661/2°) उत्तरी के मध्य उत्तरी गोलार्द्ध में तथा दक्षिणी गोलार्द्ध में मकर वृत्त (231/2°) तथा अंटार्कटिक वृत्त (661/2°) दक्षिणी के मध्य स्थित है। यहाँ मध्यम स्तर पर तापमान होता है। इसलिये इसे शीतोष्ण कटिबंध कहा जाता है। इस क्षेत्र में सूर्य की किरणें लंबवत् नहीं चमकतीं।

3. शीत कटिबंध (Frigid Zones) : वे क्षेत्र जो उत्तरी गोलार्द्ध में आर्कटिक वृत्त से उत्तरी ध्रुव के मध्य तथा दक्षिणी गोलार्द्ध में अंटार्कटिक वृत्त से दक्षिणी ध्रुव के मध्य में फैले हैं। यहाँ बहुत अधिक ठंड होती है। यहाँ सूर्य की किरणें तिरछी ही पड़ती हैं। बहुत अधिक शीत होने के कारण ही इन क्षेत्रों को शीत कटिबंध कहते हैं।

प्रश्न 6.
ग्लोब पर अक्षांश तथा देशांतर रेखायें क्यों खींची जाती हैं?
Why are the longitudes and latitudes drawn on the globe?
उत्तर:
पृथ्वी के गोलाकार होने के कारण किसी स्थान की स्थिति का ठीक ज्ञान नहीं कर सकते। किसी स्थान की स्थिति का ठीक ज्ञान करने के लिये अक्षांश तथा देशांतर रेखाओं को बनाया जाता है। उस स्थान की सही स्थिति वही हो सकती है, जहाँ अक्षांश तथा देशांतर रेखायें मिलती हैं तथा एक दूसरे को काटती हैं। उदाहरण के लिये काहिरा की स्थिति 30° उत्तरी अक्षांश तथा 30° पूर्वी देशांतर के मिलन बिंदु पर है।

ग्लोब: अक्षांश एवं देशांतर Class 6 HBSE Notes in Hindi

• ग्लोब (Globe): मानव-निर्मित पृथ्वी का प्रतिरूप।
• अक्ष (Axis) : पृथ्वी के मध्य खिंची काल्पनिक रेखा को अक्ष कहते हैं। यह दोनों ध्रुवों को मिलाती है।
• भूमध्य रेखा (Equator): पृथ्वी को दो बराबर भागों में बाँटने वाली काल्पनिक रेखा को भूमध्य रेखा कहते हैं। यह 0° अक्षांश रेखा भी कहलाती है।
• देशांतर रेखायें (Longitudes) : पृथ्वी पर उत्तर से दक्षिण खींची हुई काल्पनिक रेखायें जो ध्रुवों को मिलाती हैं. देशांतर रेखायें
• अक्षांश रेखायें (Latitudes) : भूमध्य रेखा के उत्तर तथा दक्षिण खींची हुई काल्पनिक रेखायें जो कोणीय दूरी पर खींची हुई मानी गई हैं, अक्षांश रेखायें हैं।
• मानक समय (Standard Time) : मानक मध्याह्न रेखा के समय को मानक समय कहते हैं।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Ex 4.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 4 आधारभूत ज्यामितीय अवधारणाएँ Exercise 4.4

प्रश्न 1.
त्रिभुज ABC का एक रफ चित्र खींचिए। इस त्रिभुज के अभ्यन्तर में एक बिन्दु P अंकित कीजिए और उसके बहिर्भाग में एक बिन्दु Q अंकित कीजिए। बिन्दु A इसके अभ्यन्तर में स्थित है या बहिर्भाग में स्थित है ?
हल :

त्रिभुज ΔABC का एक रफ चित्र बनाते हैं, जिसमें बिन्दु P और Q, ΔABC के अभ्यन्तर और बहिर्भाग पर स्थित हैं तथा बिन्दु A, त्रिभुज ΔABC के शीर्ष पर स्थित हैं।

प्रश्न 2.
(a) संलग्न आकृति में तीन त्रिभुजों की पहचान कीजिए।
(b) सात कोणों के नाम लिखिए।
(c) इसी आकृति में छः रेखाखण्डों के नाम लिखिए।
(d) किन दो त्रिभुजों में ∠B उभयनिष्ठ है ?

हल :
(a) दी गई आकृति में तीन त्रिभुज ΔABC, ΔABD और ΔMCD हैं।
(b) ∠BAD, ∠BAC, ∠CAD, ∠ABD, ∠ACD, ∠ADC और ∠ADB सात कोण हैं।
(c) AB, BD, DC, CA, BC और AD छ: रेखाखण्डों के नाम हैं।
(d) AABC और ΔABD में ∠B उभयनिष्ठ है।

Haryana State Board HBSE 6th Class English Solutions A Pact with the Sun Chapter 5 Tansen Textbook Exercise Questions and Answers.

Haryana Board 6th Class English Solutions A Pact with the Sun Chapter 5 Tansen

HBSE 6th Class English Tansen Textbook Questions and Answers

Class 6 English Chapter 5 Tansen Question Answer Question 1.
Why did Swami Haridas say Tansen was ‘talented’?
Answer:
Swami Haridas said Tansen was talented because Tansen could produce the exact calls of birds and animals.

HBSE 6th Class Tansen Chapter 5 Question Answer Question 2.
Why did Akbar ask Tansen to join his court?
Answer:
Akbar asked Tansen to join his court because he found Tansen very talented.

Chapter 5 Question Answer HBSE 6th Class Tansen Question 3.
How do we know that Akbar was fond of Tansen? Give two reasons.
Answer:
(i) Akbar could call upon Tansen to sing at any times during the day and night
(ii) Akbar would just walk into Tansen’s house to hear him practising.

Question 4.
What did the other courtiers feel about Tansen?
Answer:
The other courtiers felt jealous about Tansen.

Question 5.
(i) What happens if Raga Deepak is sung properly?
(ii) Why did Tansen’s enemies want him to sing the Raga?
Answer:
(i) The singer is burnt to ashes if Raga Deepak is sung properly.
(ii) Tansen’s enemies knew that if Raga Deepak is sung properly, the singer is burnt to ashes. Since Tansen was a great singer he could sing Raga Deepak properly. Thus Tansen’s enemies would get rid of him.

Question 6.
Why did Tansen agree to sing Raga Deepak?
Answer:
Tansen agreed to sing Raga Deepak because he could not disobey Emperor Akbar.

Question 7.
(i) What steps did he take to save himself?
(ii) Did his plan work? How?
Answer:
(i) He prepared his daughter Saraswati and her friend Rupvati to sing Raga Megh when the lamps lighted up.
(ii) Yes, his plan worked as when the lamps lighted up due to time heat, the rainfall helped cool the temperature.

Question 8.
Are you interested in music? Do you like classical music? Name a few distinguished Indian musicians.
Answer:
Do it yourself.

HBSE 6th Class English Tansen Important Questions and Answers

Question 1.
Who were the parents of Tansen?
Answer:
A singer called Mukundan Misra and his wife were the parents of Tansen.

Question 2.
How did Tansen try to frighten Swami Haridas and his disciples?
Answer:
Tansen hid behind a tree and roared like a tiger to frighten Swami Haridas and his disciples.

Question 3.
Who was Mohammad Ghaus? Why did Tansen go to him?
Answer:
Mohammad Ghaus was a holy man. Tansen went to him because his father, Mukundan Misra’s dying wish was that Tansen should visit Mohammad Ghaus.

Question 4.
“Let us make him sing Raga Deepak”.
(i) Who said this?
(ii) Who is ‘him’ refered to here?
Answer:
(i) One of Akbar’s courtier, Shaukat Mian said this.
(ii) Tansen is ‘him’ referred to here.

Question 5.
What happens when Raga Megh is sung perfectly?
Answer:
If Raga Megh is sung perfectly, it brings rain.

Tansen Word Meanings

musician (म्यूजिसिअन) = संगीतकार, produced ( प्रोडयूसड) = पैदा किया, naughty (नॉॅी) = नटख्, imitate (इमिटेट) = नकल करना, perfectly (परफेक्टली) = पूर्ण रूप से, travelling (ट्रेवलिंग)= यात्रा करते हुए, disciples (डिसाइपल्स) = चेले, grove (ग्रोव)=पेड़ों का झुंड, strangers (स्ट्रेन्जअस = अजनबी, frighten (फ्रायटन)= डराना, scattered (स्केटड = तितर-बितर हो गया, hiding ( हाइडिंग) = छिपते हुए, naughty (नॉटी) = नटखट, punish (पनिश) = सजा, talented (टैलेन्टेड) = प्रतिभावान, singer ( सिंगर )= गायक, devoted (डिवोटेड) = सेवानिष्ठ, children (चिल्ड्रेन)= बच्चे, musical (म्यूजीकिल)= संगीतमय, impressed (इम्प्रेस्ड) = प्रभावित किया, insisted (इनसिस्टे )= जोर दिया, court (कोट )= दरबार, favourite (फेवरिट )= प्रिय, Emperor (एम्परयर )= सम्राट, practise (प्रैक्टिस) = अभ्यास करना, Presents (प्रेजेन्टस) = भेंट, jealous (जिलीअस) = ईष्ष्यालु, ruined (रूइन्ड) =बर्बाद करना, bright (ब्राइट) = चमकीला, Properly (प्रोपअरली) = उचित रूप sung (संग) = गाना, burnt ( ब्रन्ट) = जलाना, ashes (आशेज) = राख, \operator name{rid} (रिड) = छुटकारा, afraid (अफ्रेड)= भयभीत था, disobey (डिसओबे) = आज्ञा नहीं मानना, downcast (डाऊनकास्ट) = उदास, बेचैन, alight (एलाअट) = जला देना, legend (लिजेन्ड) = कहानी, appointed (अपॉयन्टेड) = चुना हुआ (दिवस), assembled (असेम्बलेड) = इकट्ठे हुए। bathed (बाथेड) = नहा लिये, perspiration (परस्पाइरेशन)= पसीना, terror (टेरर)= भय, sky (स्काई)= आकाश, clouded (क्लाउडेड) = बादल से ढके हुए, Suffering (सफरिंग) = पीड़ा, rejoiced (रिजॉइस्ड) = खुशी मनाई। composed (कम्पोज्ड) = रचना की, pilgrimage (पिलग्रिमेज) = तीर्थयात्रा, musicians (म्यूजिसिन्स)= संगीतकार।

Tansen Summary in English

Tansen who was the only son of his parents was very naughty but talented. He could imitate the calls of birds and animals quite perfectly. Once he tried to frighten Swami Haridas’s group of travellers by roaring like a tiger. But for Swami Haridas, everybody was frightened. Swami Haridas chose him as his disciple. He got musical training for eleven years. Then he stayed with Mohammad Ghous, a holy man. Later he married Hussaini who was one of the ladies in the court of Rani Mrignaini. Later he joined Akbar’s court and became very famous. His opponents grew very jealous, and made him sing Raga Deepak. But he trained his daughter and her friend to sing Raga Megh after Raga Deepak to mitigate the effect of Raga Deepak. Thus he could escape the effect of Raga Deepak.

Tansen Summary in Hindi

तानसेन, जो कि अपने माँ-बाप की इकलौती संतान था, बहुत ही शरारती और प्रतिभावान था। वह पक्षियों और जानवरों की आवाजों का पूर्णरूप से नकल कर सकता था। एक बार उसने स्वामी हरिदास के यात्री समूह को चीते की तरह दहाड़कर डराने की कोशिश की। स्वामी हरिदास के अलावा सभी डर गये। स्वामी हरिदास ने उसका शिष्य के रूप में चुनाव कर लिया। उसने ग्यारह वर्षों तक संगीत का प्रशिक्षण दिया। तब वह मोहम्मद घोष, एक पवित्र आदमी के साथ रहा। बाद में उसने हुसैनी जो कि रानी मृगनयनी के दरबार में एक महिला थी, से शादी कर ली। बाद में वह अकबर के दरबार में शामिल हो गया। अकबर के दरबार में वह बहुत प्रसिद्ध हो गया। उसके विरोधी उससे बहुत ईर्ष्यालु हो गये और उससे राग दीपक गवाया। लेकिन उसने अपनी पुत्री और उसकी सहेली को राग दीपक का प्रभाव कम करने के लिए राग मेघ गाना सिखा दिया था। इस प्रकार वह राग दीपक के दुष्प्रभावों से बच पाया।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 7 भिन्न Ex 7.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 7 भिन्न Exercise 7.3

प्रश्न 1.
प्रत्येक चित्र में छायांकित भागों के लिए भिन्न लिखिए। क्या ये सभी भिन्न तुल्य है?

हल :

प्रश्न 2.
छायांकित भागों के लिए भिन्नों को लिखिए और प्रत्येक पंक्ति में से तुल्य भिन्नों को चुनिए :

हूल :
दिये गए चित्रों में छायांकित भागों के लिए भिन्न निम्न हैं:


पंक्ति I और पंक्ति II में तुल्य भिन्नों के जोड़े : (a) → (ii), (b) → (iv), (c) → (i), (d) → (v) और (e) → (iii).

प्रश्न 3.

हूल :

प्रश्न 4.
के तुल्य वह भिन्न ज्ञात कीजिए, जिसका :
(a) हर 20 है,
(b) अंश 9 है,
(e) हर 30 है
(d) अंश 27 है।
हल :
(a) ∵ 20 ÷ 5 =4
∴ हर को 20 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 4 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 4}{5 \times 4}=\frac{12}{20}\) उत्तर

(b) ∵ 9 ÷ 3 = 3
∴ अंश को 9 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 3 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\) उत्तर

(c) ∵ 30 ÷ 5 = 6
हर को 30 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश व हर में 6 से गुणा करने पर, \(\frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}\) उत्तर

(d) ∵ 27 ÷ 3 = 9
अंश को 27 बनाने के लिए भिन्न \(\frac {3}{5}\) के अंश और हर में 9 से गुणा करने पर,
\(\frac{3}{5}=\frac{3 \times 9}{5 \times 9}=\frac{27}{45}\) उत्तर

प्रश्न 5.
\(\frac {36}{48}\) के तुल्य वह भिन्न ज्ञात कीजिए, जिसका :
(a) अंश 9 है
(b) हर 4 है।
हल :
(a) ∵ 36 ÷ 9 = 4
∴ अंश को 9 बनाने के लिए भिन्न \(\frac {36}{48}\) के अंश और हर में 4 से भाग करते हैं :
\(\frac{36}{48}=\frac{36 \div 4}{48 \div 4}=\frac{9}{12}\) उत्तर

(b) ∵ 48 ÷ 4 = 12
∴ हर को 4 बनाने के लिए भिन्न \(\frac {36}{48}\) के अंश और हर में 12 से भाग करते हैं:
\(\frac{36}{48}=\frac{36 \div 12}{48 \div 12}=\frac{3}{4}\) उत्तर

प्रश्न 6.
जाँच कीजिए कि निम्न भिन्न तुल्य हैं या नहीं :
(a) \(\frac {5}{9}\), \(\frac {30}{54}\)
(b) \(\frac {3}{10}\), \(\frac {12}{50}\)
(c) \(\frac {7}{13}\), \(\frac {5}{11}\)
हल :
(a)

तिर्यक गुणा करने पर
5 × 54 = 270 और 9 × 30 = 270
∵ 270 = 270
∴ दोनों भिन्न तुल्य हैं। उत्तर

(b)

तिर्यक गुणा करने पर
3 × 50 = 150 और 12 × 10 = 120
150 ≠ 120
अतः \(\frac {3}{10}\) और \(\frac {12}{50}\) तुल्य भिन्न नहीं हैं। उत्तर

(c)

तिर्यक गुणा करने पर
7 × 11 = 77 और 13 × 5 = 65
⇒ 77 ≠ 65
\(\frac {7}{13}\) और \(\frac {5}{11}\) तुल्य भिन्न नहीं हैं। उत्तर

प्रश्न 7.
निम्नलिखित भिन्नों को उनके सरलतम रूप में बदलिए:
(a) \(\frac {48}{60}\)
(b) \(\frac {150}{60}\)
(c) \(\frac {84}{98}\)
(d) \(\frac {12}{52}\)
(e) \(\frac {7}{28}\)
हल :
(a) \(\frac {48}{60}\) को सरलतम रूप में लिखने के लिए पहले इम 48 और 60 का म.स. निकालते हैं:

∴ 48 = 2 × 2 × 2 × 2 × 3, 60 = 2 × 2 × 3 × 5
∴ 48 और 60 का म.स. = 2 × 2 × 3 = 12
48 48+12 4 अतः 60-60+12
अतः \(\frac{48}{60}=\frac{48 \div 12}{60 \div 12}=\frac{4}{5}\) उत्तर

(b) \(\frac {150}{60}\) को सरलतम रूप में लिखने के लिए पहले हम 150 और 60 का म.स. निकालते हैं :

∴ 150 = 2 × 3 × 5 × 5
और 60 = 2 × 2 × 3 × 5
∴ 150 और 60 का म.स. = 2 × 3 × 5 = 30
\(\frac{150}{60}=\frac{150+30}{60 \div 30}=\frac{5}{2}\) उत्तर

(c) \(\frac {84}{98}\) को सरलतम रूप में लिखने के लिए पहले हम 84 और 98 का म.स. निकालते हैं:

∴ 84 = 2 × 2 × 3 × 7 और 98 = 2 × 7 × 7
∴ 84 और 98 का म.स. = 2 × 7 = 14
अतः \(\frac{84}{98}=\frac{84 \div 14}{98 \div 14}=\frac{6}{7}\) उत्तर

(d) \(\frac {12}{52}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 12 और 52 का म.स. निकालते हैं :

∴ 12 = 2 × 2 × 3 और 52 = 2 × 2 × 13
∴ 12 और 52 का म.स. = 2 × 2 = 4
अत: \(\frac{12}{52}=\frac{12 \div 4}{52 \div 4}=\frac{3}{13}\) उत्तर

(e) \(\frac {7}{28}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 7 और 28 का म.स. निकालते हैं:

7 = 1 × 7 और 28 = 2 × 2 × 7
∴ 7 और 28 का स.स. = 7
अतः \(\frac{7}{28}=\frac{7 \div 7}{28 \div 7}=\frac{1}{4}\) उत्तर

प्रश्न 8.
रमेश के पास 20 पेंसिल थीं। शीलू के पास 50 पेंसिल और जमाल के पास 80 पेंसिल थीं। 4 महीने के बाद रमेश ने 10 पेंसिल प्रयोग कर ली,शीलू ने 25 पेंसिल प्रयोग कर ली और जमाल ने 40 पेंसिल प्रयोग कर लीं। प्रत्येक ने अपनी पेंसिलों की कौन-सी भिन्न प्रयोग कर ली? जाँच कीजिए कि प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग की है।
हल :
रमेश, शीलू और जमाल द्वारा प्रयोग की जाने वाली पेंसिलों के भाग क्रमशः
\(\frac {10}{20}\), \(\frac {25}{50}\) और \(\frac {40}{80}\) हैं।
यहाँ \(\frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\)
\(\frac{25}{50}=\frac{25 \div 25}{50 \div 25}=\frac{1}{2}\)
\(\frac{40}{80}=\frac{40 \div 40}{80 \div 40}=\frac{1}{2}\)
ये सभी भिन्न बराबर हैं, अतः प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग में है। उत्तर

प्रश्न 9.
तुल्य भिन्नों का मिलान कीजिए और प्रत्येक के लिए दो भिन्न और लिखिए :

हल :
(i) \(\frac {250}{400}\) को सरलतम रूप में लिखने के लिए पहले हम 250 और 400 का म.स. निकालते हैं :

∴ 250 = 2 × 5 × 5 × 5
और 400 = 2 × 2 × 2 × 2 × 5 × 5
∴ म.स. = 2 × 5 × 5 = 50
\(\frac{250}{400}=\frac{250 \div 50}{400 \div 50}=\frac{5}{8}\)
∴ (i) का मिलान (d) से होगा। उत्तर

दो अन्य तुल्य भिन्न
\(\frac{5 \times 2}{8 \times 2}=\frac{10}{16}\) और \(\frac{5 \times 3}{8 \times 3}=\frac{15}{24}\) उत्तर

(ii) \(\frac {180}{200}\) को सरलतम रूप में व्यक्त करने के लिए पहले हम 180 और 200 का म.स. निकालते हैं :

∴ 180 = 2 × 2 × 3 × 3 × 5
और 200 = 2 × 2 × 2 × 5 × 5
∴ 180 और 200 का म.स. = 2 × 2 × 5 = 20
\(\frac{180}{200}=\frac{180 \div 20}{200 \div 20}=\frac{9}{10}\)
अत: (ii) का मिलान (e) से होगा। उत्तर

दो अन्य तुल्य भिन्न:
\(\frac{9 \times 2}{10 \times 2}=\frac{18}{20}\) और \(\frac{9 \times 3}{10 \times 3}=\frac{27}{30}\) उत्तर

(iii) \(\frac {660}{990}\) को सरलतम रूप में लिखने के लिए पहले हम 660 और 990 का म.स. निकालते हैं

अत: (iii) का मिलान (a) से होगा।
दो अन्य तुल्य भिन्न : \(\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\) और \(\frac{2 \times 3}{3 \times 3}=\frac{6}{9}\) उत्तर

(iv) \(\frac {180}{360}\) को सरलतम रूप में लिखने के लिए पहले हम 180 और 360 का म.स. निकालते हैं :

∴ 180 = 2 × 2 × 3 × 3 × 5
360 = 2 × 2 × 2 × 3 × 3 × 5
∴ अभीष्ट म.स. = 2 × 2 × 3 × 3 × 5 = 180
\(\frac{180}{360}=\frac{180 \div 180}{360 \div 180}=\frac{1}{2}\)
अत: (iv) का मिलान (c) से होगा। उत्तर

दो अन्य तुल्य भिन्न :
\(\frac{1 \times 2}{2 \times 2}=\frac{2}{4}\) और \(\frac{1 \times 3}{2 \times 3}=\frac{3}{6}\) उत्तर

(v) \(\frac {220}{550}\) को सरलतम रूप में लिखने के लिए पहले हम 220 और 550 का म.स. निकालते हैं :

अतः (v) का मिलान (b) से होगा। उत्तर
दो अन्य तुल्य भिन्न:
\(\frac{2 \times 2}{5 \times 2}=\frac{4}{10}\) और \(\frac{2 \times 3}{5 \times 3}=\frac{6}{15}\) उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 11 बीजगणित Ex 11.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 11 बीजगणित Exercise 11.5

प्रश्न 1.
बताइए कि निम्नलिखित में से कौन-से कथन समीकरण (चर-संख्याओं के) हैं? सकारण उत्तर दीजिए। समीकरणों में समबद्ध चर भी लिखिए :
(a) 17 = x + 7
(b) (t – 7) > 5
(c) \(\frac{4}{2}\) = 2
(d) 7 × 3 – 13 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = 11 × 5 – 12 × 4
(j) 7 = 11 × 2 + p
(k) 20 = 5y
(l) \(\frac{3 q}{2}\) < 5
(m) z + 12 > 24
(n) 20 – (10 – 5)= 3 × 5
(o) 7 – x = 5
हल :
(a) समीकरण है, x चर वाली समीकरण।
(b) समीकरण नहीं है, क्योंकि = का चिह्न नहीं है।
(c) समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(d) समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(e) समीकरण है, x चर वाली समीकरण।
(f) समीकरण है, x चर वाली. समीकरण।
(g) समीकरण नहीं है, क्योंकि = का चिहन नहीं है।
(h) समीकरण है, n चर वाली समीकरण।
(i) समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(j) समीकरण है, p चर वाली समीकरण।
(k) समीकरण है, y चर वाली समीकरण।
(l) समीकरण नहीं है, क्योंकि = का चिह्न नहीं है।
(m) समीकरण नहीं है, क्योंकि = का चिह्न नहीं है।
(n) समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(o) समीकरण है, x चर वाली समीकरण ।

प्रश्न 2.
सारणी के तीसरे स्तंभ में प्रविष्टियों को पूरा लिखिए :

हल :
प्रविष्टियों की पूर्ति करने पर :

प्रश्न 3.
प्रत्येक समीकरण के सम्मुख कोष्ठकों में दिए मानों में से समीकरण का हल चुनिए। दर्शाइए कि अन्य मान समीकरण को संतुष्ट नहीं करते हैं।
(a) 5m = 60, (10, 5, 12, 15)
(b) n + 12 = 20, (12, 8, 20,0)
(c) p – 5 = 5, (0, 10, 5, -5)
(d) \(\frac{q}{2}\) = 7, (7, 2, 10, 14)
(e) r – 4 = 0 (4,- 4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
हल :
(a) दी गई समीकरण है : 5m = 60
m = 10 के लिए : 5m = 5 × 10 = 50 ≠ 60
अत: m = 10 समीकरण को सन्तुष्ट नहीं करता है।
m = 5 के लिए : 5m = 5 × 5 = 25 ≠ 60
अतः m = 5 समीकरण को सन्तुष्ट नहीं करता है।
m = 12 के लिए : 5m = 5 × 12 = 60
अतः m = 12 समीकरण को सन्तुष्ट करता है।
∴ m = 12 समीकरण का हल है।
m = 15 के लिए : 5m = 5 × 15 = 75 ≠ 60
अतः m = 15 समीकरण को सन्तुष्ट नहीं करता है।

(b) दी गई समीकरण है : n + 12 = 20
n = 12 के लिए : n + 12 = 12 + 12 = 24 ≠ 20
अत: n = 12 समीकरण को सन्तुष्ट नहीं करता है।
n = 8 के लिए : n + 12 = 8 + 12 = 20
अतः n = 8 समीकरण को सन्तुष्ट करता है।
∴ n = 8 समीकरण का हल है।
n = 20 के लिए : n + 12 = 20 + 12 = 32 ≠ 20
अतः n = 20 समीकरण को सन्तुष्ट नहीं करता है।
n = 0 के लिए : n+ 12 = 0 + 12 = 12 ≠ 20
अतः n = 0 समीकरण को सन्तुष्ट नहीं करता है।

(c) दी गई समीकरण है : p – 5 = 5
p = 0 के लिए : p – 5 = 0 – 5 = – 5 ≠ 5
अतः p = 0 समीकरण को सन्तुष्ट नहीं करता है।
p = 10 के लिए : p – 5 = 10 – 5 = 5
अतः p = 10 समीकरण को सन्तुष्ट करता है।
∴ p = 10 समीकरण का हल है।
p = 5 के लिए : p – 5 = 5 – 5 = 0 ≠ 5
अतः p = 5 समीकरण को सन्तुष्ट नहीं करता है।
p = -5 के लिए : p – 5 = – 5 – 5 = – 10 ≠ 5
अतः p = – 5 समीकरण को सन्तुष्ट नहीं करता है।

(d) दी गई समीकरण है : \(\frac{q}{2}\)
q = 7 के लिए : \(\frac{q}{2}=\frac{7}{2} \neq 7\)
अतः q = 7 समीकरण को सन्तुष्ट नहीं करता है।
q = 2 के लिए : \(\frac{q}{2}=\frac{2}{2}=1 \neq 7\)
अतः q = 2 समीकरण को सन्तुष्ट नहीं करता है।
q = 10 के लिए : \(\frac{q}{2}=\frac{10}{2}=5 \neq 7\)
अतः q = 10 समीकरण को सन्तुष्ट नहीं करता है।
q = 14 के लिए : \(\frac{q}{2}=\frac{14}{2}=7\)
अतः q = 14 समीकरण को सन्तुष्ट करता है।
∴ q = 14 समीकरण का हल है।

(e) दी गई समीकरण है : r – 4 = 0
r = 4 के लिए : r – 4 = 4 – 4 = 0
अत: r = 4 समीकरण को सन्तुष्ट करता है।
∴ r= 4 समीकरण का हल है।
r = -4 के लिए : r – 4 = – 4 – 4 = – 8 ≠ 0
अतः r = – 4 समीकरण को सन्तुष्ट नहीं करता है।
r = 8 के लिए : r – 4 = 8 – 4 = 4 + 0
अतः r = 8 समीकरण को सन्तुष्ट नहीं करता है।
r = 0 के लिए : r – 4 = 0 – 4 = – 4 ≠ 0
अतः r = 0 समीकरण को सन्तुष्ट नहीं करता है।

(f) दी गई समीकरण है : x + 4 = 2
x = -2 के लिए : x + 4 = – 2 + 4 = 2
अतः x = – 2 समीकरण को सन्तुष्ट करता है।
∴ x = – 2 समीकरण का हल है।
x = 0 के लिए : x + 4 = 0 + 4 = 4 ≠ 2
अतः x = 0 समीकरण को सन्तुष्ट नहीं करता है।
x = 2 के लिए : x + 4 = 2 + 4 = 6 ≠ 2
अतः x = 2 समीकरण को सन्तुष्ट नहीं करता है।
x = 4 के लिए: x + 4 = 4 + 4 = 8 ≠ 2
अतः x = 4 समीकरण को सन्तुष्ट नहीं करता है।

प्रश्न 4.
(a) नीचे दी हुई सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण m + 10 = 16 का हल ज्ञात कीजिए।

हल :
(a) दी गई सारणी को पूरा करने पर,

उपर्युक्त सारणी को देखने पर स्पष्ट है कि m = 6 समीकरण m + 10 = 16 को सन्तुष्ट करता है।
∴ m = 6 समीकरण का हल है। उत्तर

(b) आगे दी हुई सारणी को पूरा कीजिए और इससारणी को देखकर ही समीकरण 5t = 35 का हल ज्ञात कीजिए।

हल :
दी गई सारणी को पूरा करने पर,

उपर्युक्त सारणी को देखने पर स्पष्ट है कि t = 7, समीकरण 5t = 35 को सन्तुष्ट करता है।
अतः t = 7 समीकरण का हल है। उत्तर

(c) सारणी को पूरा कीजिए और समीकरण \(\frac{z}{3}\) = 4 का हल ज्ञात कीजिए।

हल :
दी गई सारणी को पूरा करने पर,

उपर्युक्त सारणी को देखने पर स्पष्ट है कि z = 12
समीकरण \(\frac{z}{3}\) = 4 को सन्तुष्ट करता है।
अतः z = 12 समीकरण का हल है। उत्तर

(d) सारणी को पूरा कीजिए और समीकरण m – 7 = 3 का हल ज्ञात कीजिए।

हल :
दी गई सारणी को पूरा करने पर,

उपर्युक्त सारणी को देखने पर स्पष्ट है कि m = 10
समीकरण m – 7 = 3 को सन्तुष्ट करता है।
अतः m = 10 समीकरण का हल है। उत्तर

प्रश्न 5.
निम्नलिखित पहेलियों को हल कीजिए। आप ऐसी पहेलियाँ स्वयं भी बना सकते हैं :
मैं कौन हैं?
(i) एक वर्ग के अनुदिश जाइए।
प्रत्येक कोने को तीन बार
गिनकर और उससे अधिक नहीं,
मुझमें जोड़िए और
ठीक चौंतीस प्राप्त कीजिए।

(ii) सप्ताह के प्रत्येक दिन के लिए,
मेरे से ऊपर गिनिए।
यदि आपने कोई गलती नहीं की है,
तो आप तेइस प्राप्त करेंगे।
(iii) मैं एक विशिष्ट संख्या हूँ।
मुझमें से एक छः निकालिए,
और क्रिकेट की एक टीम बनाइए।

(iv) बताइए मैं कौन हूँ।
मैं एक सुन्दर संकेत दे रही हूँ।
आप मुझे वापस पाएँगे,
यदि मुझे बाइस में से निकालेंगे।
हल :
(i) माना ‘मैं’ x हूँ। वर्ग के चार कोने हैं। तीन बार प्रत्येक कोने को गिनने पर = 3 × 4 = 12 प्राप्त होता है।
प्रश्नानुसार, x + 12 = 34
⇒ x = 34 – 12
⇒ x = 22
अतः मैं 22 हैं। उत्तर

(ii) प्रश्नानुसार, x + 7 = 23
(x – 6) + 6 = 11 +6
⇒ x = 23 – 7
⇒ x = 16 उत्तर

(iii) माना विशिष्ट संख्या x है।
प्रश्नानुसार, x – 6 = 11
(∵ क्रिकेट की टीम में 11 सदस्य होते हैं)
⇒ x = 11 +6
⇒ x = 17
अतः विशिष्ट संख्या 17 है। उत्तर

(iv) माना मैं x हूँ।
प्रश्नानुसार, 22 – x = x
⇒ 22 = x + x
⇒ 2x = 22
⇒ \(\frac{2 x}{2}=\frac{22}{2}\)
⇒ x = 11
अतः मैं 11 हैं। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.3

प्रश्न 1.
निम्न को सुमेलित (match) कीजिए :

हल :

प्रश्न 2.
निम्न में से प्रत्येक कोण को समकोण, ऋजुकोण, न्यूनकोण, अधिक कोण या प्रतिवर्ती कोण के रूप में वर्गीकृत कीजिए :

हल :
दी गई आकृतियों से स्पष्ट है :
(a) न्यूनकोण
(b) अधिककोण
(c) समकोण
(d) प्रतिवर्ती कोण
(e) ऋजु कोण
(f) न्यूनकोण।

Haryana State Board HBSE 6th Class Maths Solutions Chapter 9 आँकड़ों का प्रबंधन Ex 9.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 9 आँकड़ों का प्रबंधन Exercise 9.4

प्रश्न 1.
एक स्कूल के 120 विद्यार्थियों का इस आशय से सर्वेक्षण किया गया कि वे अपने खाली समय में किस क्रियाकलाप को पसन्द करते हैं। निम्न आँकड़े प्राप्त हुए :

1इकाई लम्बाई = 5 विद्यार्थी का पैमाना लेकर, एक दण्ड आलेख बनाइए। खेलने के अतिरिक्त कौन-सा क्रियाकलाप अधिकांश विद्यार्थियों द्वारा पसन्द किया जाता है ?
हल :
यहाँ आँकड़ों के 5 मान दिए गये हैं, अतः क्षैतिज रेखा पर बराबर दूरी के 5 बिन्दु अंकित करते हैं तथा समान चौड़ाई और आनुपातिक ऊँचाई के आयत बनाते हैं।

दण्ड आलेख से, खेलने के अतिरिक्त कहानी की पुस्तके पढ़ना क्रियाकलाप अधिकांश विद्यार्थियों द्वारा पसन्द किया जाता है।

प्रश्न 2.
छः क्रमागत दिनों में दुकानदार द्वारा बेची गई गणित की पुस्तकों की संख्या नीचे दी गई है :

अपनी पसन्द का पैमाना चुनते हुए उपर्युक्त सूचना के लिए एक दण्ड आलेख खींचिए।
हल :
दिए गए आँकड़ों से आलेख दर्शाने के लिए क्षैतिज रेखा पर बराबर दूरी के 6 बिन्दु अंकित करते हैं और समान चौड़ाई के आयत इन बिन्दुओं पर बनाते हैं तथा आयत की ऊँचाई निम्न प्रकार निकालते हैं :

प्रश्न 3.
वर्ष 1998 से 2002 के बीच एक फैक्ट्री द्वारा निर्मित साइकिलों की संख्या निम्नलिखित सारणी द्वारा दर्शाई गई है:

इन आँकड़ों को एक दण्ड आलेख द्वारा प्रदर्शित कीजिए। अपनी पसन्द का पैमाना चुनिए।
(a) किस वर्ष में अधिकतम संख्या में साइकिलें निर्मित की गईं ?
(b) किस वर्ष में न्यूनतम संख्या में साइकिलें निर्मित की गई ?
हल :
दिए गए आँकड़ों में 5 मान दिए गए हैं। क्षैतिज रेखा पर बराबर दूरी पर 5 बिन्दु अंकित करते हैं और समान चौड़ाई तथा आनुपातिक ऊँचाई के आयत खींचते हैं।
(a) वर्ष 2002 में सबसे अधिक संख्या में साइकिलें निर्मित की गईं।

(b) वर्ष 1999 में न्यूनतम संख्या में साइकिलें निर्मित की गईं।

प्रश्न 4.
किसी शहर के व्यक्तियों की संख्या विभिन्न आयु समूहों के अनुसार नीचे सारणी में दी हुई है :

इन आँकड़ों को एक दण्ड आलेख द्वारा निरूपित कीजिए। (1 इकाई लम्बाई = 20 हजार लीजिए)
निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) किन दो आयु समूहों में जनसंख्या बराबर है ?
(b) 60 वर्ष और उससे अधिक आयु के सभी व्यक्ति वरिष्ठ नागरिक कहलाते हैं। इस शहर में कितने वरिष्ठ नागरिक हैं ?
हल :
आँकड़ों के 6 मान दिए गए हैं। इसलिए क्षैतिज रेखा पर बराबर दूरी के 6 बिन्दु अंकित करते हैं तथा समान चौड़ाई और आनुपातिक ऊँचाई के आयत बनाते हैं।

(a) आयु समूह 30-44 तथा 45-59 में समान जनसंख्या है।
(b) वरिष्ठ नागरिकों की संख्या = 80000 + 40000
= 120000 = एक लाख 20 हजार