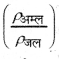
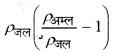HBSE 10th Class Science Solutions Chapter 2 Acids, Bases and Salts
Haryana State Board HBSE 10th Class Science Solutions Chapter 2 Acids, Bases and Salts Textbook Exercise Questions and Answers.
Haryana Board 10th Class Science Solutions Chapter 2 Acids, Bases and Salts
HBSE 10th Class Science Acids, Bases and Salts Textbook Questions and Answers
Question 1.
A solution turns red litmus blue, its pH is likely to be ……………
(a) 1
(b) 4
(c) 5
(d) 10
Answer:
(d) 10
![]()
Question 2.
A solution reacts with crushed egg-shells to give a gas that turns lime-water milky. The solution contains ………….
(a) NaCI
(b) HCI
(c) LiCI
(d) KCI
Answer:
(b) HCI
Question 3.
10 mL of a solution of NaOH is found to be completely neutralized by 8 mL of a given solution of HCI. If we take 20 mL of the same solution of NaOH, the amount HCI solution (the same solution as before) required to neutralize it will be ………………..
(a) 4 mL
(b) 8 mL
(c) 12 mL
(d) 16 mL
Answer:
(d) 16 mL
Here, 10 mL NaOH neutralizes 8 mL HCI
∴ 20 mL NaOH is neutralized by = \(\frac{20 \mathrm{~mL} \times 8 \mathrm{~mL}}{10 \mathrm{~mL}}=16 \mathrm{~mL}\)
Question 4.
Which one of the following types of medicines is used for treating indigestion?
(a) Antibiotic
(b) Analgesic
(c) Antacid
(d) Antiseptic
Answer:
(c) Antacid
Question 5.
Write word equations and then balanced equations for the reaction taking place when –
(a) dilute sulphuric acid reacts with zinc granules.
(b) dilute hydrochloric acid reacts with magnesium ribbon.
(c) dilute sulphuric acid reacts with aluminium powder.
(d) dilute hydrochloric acid reacts with iron filings.
Answer:
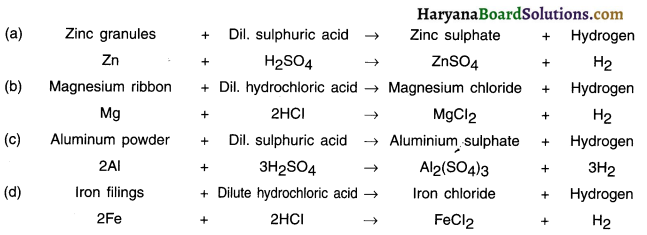
![]()
Question 6.
Compounds such as alcohols and glucose also contain hydrogen but are not categorized as acids. Describe an activity to prove it.
Answers:
1. Take a cork and fix two nails on it.
2. Keep the cork inside a beaker.
3. Connect the nails to the battery, bulb and key.
4. Take some solution of alcohol say ethanol and solution of glucose.
5. First put ethanol in the beaker and see f the bulb glows.
6. Remove ethanol and put glucose in the beaker and observe.
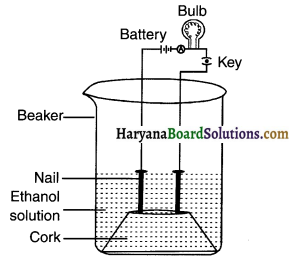
Observation:
You will observe that the bulb does not glow with any of Ethar these solutions. This means that these solutions do not release H+ ions. H+ ions conduct electricity and are produced by ions. Hence, none of these solutions is acidic.
Question 7.
Why does distilled water not conduct electricity, whereas rain water does?
Answer:
1. Distilled water is pure and so it does not form ions. Hence, it does not conduct electricity.
2. Rain water contains impurities such as acidic components. So, rain water release ions and hence conducts electricity.
Question 8.
Why do acids not show acidic behaviour In the absence of water?
Answer:
1. Acids cannot release H+ ions in absence of water.
2. Only when acids are dissolved in water, they release H ions which then enable conduction of electricity.
![]()
Question 9.
Five solutions A,B,C,D and E when tested with universal Indicator showed pH as 4,1,11,7 and 9, respectively.
(i) Which solution is
(a) neutral?
(b) strongly alkaline?
(c) strongly acidic?
(d) weakly acidic?
(e) weakly alkaline?
(ii) Arrange the pH in increasing order of hydrogen-ion concentration.
Answer:
(i)
- Solution ‘D’ with pH = 7 is neutral
- Solution ‘C’ with pH = 11 is strongly alkaline
- Solution ‘B’ with pH = 1 is strongly acidic
- Solution ‘A’ with pH = 4 is weakly acidic
- Solution ‘E’ with pH = 9 is weakly alkaline
(ii) Arrangement of these solutions in increasing order of hydrogen ion concentration:
C = 11 < E = 9< D = 7< A = 4< B = 1
Question 10.
Equal lengths of magnesium ribbons are taken in test tubes A and B. Hydrochloric acid (HCI) is added to test tube A, while acetic acid (CH3COOH) is added to test-tube B. Amount and concentration taken for both the acids are same. In which test tube will the fizzing occur more vigorously and why?
Answer:
Hydrochloric acid (HCI) is a strong acid as compared to acetic acid (CH3COOH). Hence, the fizzing will occur more vigorously in test-tube A which contains HCI.
Question 11.
Fresh milk has a pH of 6. How do you think the pH will change as it turns into curd? Explain your answer.
Answer:
Formation of curd from milk means milk becoming acidic. Hence, pH of milk will decrease when it turns to curd due to the formation of lactic acid. Formation of acid will make curd sour.
Question 12.
A milkman adds a very small amount of baking soda to fresh milk.
(a) Why does he shift the pH of the fresh milk from 6 to slightly alkaline?
(b) Why does this milk take a long time to set as curd?
Answer:
(a) By shifting the pH of milk a bit towards alkaline the milkman is preventing the milk from becoming sour.
(b) Baking soda was added to the milk. Baking soda is a base substance and so it neutralizes the formation of lactic acid. Hence, the milk takes more time to set as curd because it will now take more time to become acidic.
Question 13.
Plaster of Paris should be stored in a moisture-proof container. Explain why?
Answer:
If plaster of Paris is kept in a moist environment it will absorb moisture and get converted to hard gypsum.
![]()
Question 14.
What is a neutralization reaction? Give two examples.
Answer:
The reaction between an acid and a base to give salt and water is called neutralization reaction.
Example:
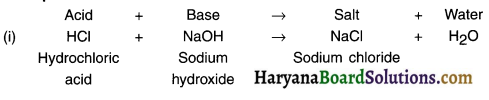

Question 15.
Give two Important uses of washing soda and baking soda.
Answer:
Uses of baking soda:
- In a bakery for making bread, cakes, etc.
- In fire extinguisher
Uses of washing soda:
- For manufacturing soap and detergent
- For removing the permanent hardness of water.
HBSE 10th Class Science Acids, Bases and Salts InText Activity Questions and Answers
Text Book Page no – 18.
Question 1.
You have been provided with three test tubes. One of them contains distilled water and the other two contain an acidic solution and a basic solution, respectively. If you are given only red litmus paper, how will you identify the contents of each test tube?
Answer:
1. Cut the litmus paper into three parts. Dip each part in a test tube and observe the change in colour.
2. The test-tube in which red litmus paper turns blue contains a basic solution. Now dip this blue litmus paper in remaining two test-tubes.
3. The solution that turns the blue litmus paper again red is an acidic solution.
4. The tube in which there occurs no change in the colour of blue litmus contains water.
![]()
Text Book Page no – 22.
Question 1.
Why should curd and sour substances not be kept in brass anal copper vessels?
Answer:
1. Both curd and sour substances such as lemon juice are acids whereas brass and copper are highly reactive metals.
2. When acids come in contact with metals they react and form salts and release hydrogen gas. Consuming such substances causes harm to the body.
3. Hence, food items acidic in nature should not be kept in copper and brass vessels.
Question 2.
Which gas is usually liberated when an acid reacts with a metal? Illustrate with an example. How will you test for the presence of this gas?
Answer:
Hydrogen (H2) gas is liberated when an acid reacts with a metal.
Example: Take some zinc granules in a test-tube. Add 5 mL dilute hydrochloric (HCI) acid in it. Following reaction will occur.
Zn + 2HCI → ZnCI2 + H2
Testing evolution of gas:
Hydrogen (H2) gas is insoluble in water. If you pass the gas in soap solution, it will form bubbles. The bubbles will burn with a popping sound when match stick is brought near the solution. This proves presence of gas.
![]()
Question 3.
Metal compound A reacts with dilute hydrochloric acid to produce effervescence. The gas evolved extinguishes a burning candle. Write a balanced chemical equation for the reaction if one of the compounds formed is calcium chloride.
Answer:
1. The gas extinguishes the burning candle, so it must be carbon dioxide gas. Moreover, since the end product is calcium chloride, the metal compound A must be calcium carbonate.
2. The reaction between calcium carbonate and hydrochloric acid which produces calcium chloride and carbon dioxide gas is:

Text Book Page no – 25.
Question 1.
Why do HCI, HNO3, etc., show acidic characters in aqueous solutions while solutions of compounds like alcohol and glucose do not show acidic character?
Answer:
1. If on adding a substance to an aqueous solution, H+ ions get/eleased it means the substance added is acid.
2. On adding HCI and HNO3, H+ ions are released in the aqueous solution and so they show acidic characteristic whereas C2H5OH and glucose do not release H+ ions. Hence they do not show acidic character.
Question 2.
Why does an aqueous solution of an acid conduct electricity?
Answer:
When an acid is added to an aqueous solution, it releases H+ ions. H+ ions are responsible for conducting electricity. Hence, aqueous solution of an acid conducts electricity.
![]()
Question 3.
Why does dry HCI gas not change the colour of the dry litmus paper?
Answer:
Dry hydrochloric (HCI) gas does not release H+ ions. So it does not possess acidic character Hence, it does not change the colour of dry litmus paper.
Question 4.
While diluting an acid, why is it recommended that the acid should be added to water and not water to the acid?
Answer:
1. The process of dissolving an acid or a base is highly exothermic.
2. If one adds acid to water suddenly and in large amount or if one adds water to acid, the reaction will emit a lot of heat. This can even break the glass container.
3. The hot contents may come out of the container with an explosion and burn our eyes and body.
4. Hence, while making dilute solution of acid, acid must only be added to water that too slowly and by stirring continuously.
Question 5.
How is the concentration of hydronium ions (H3O+) affected when a solution of an acid is diluted?
Answer:
1. There exists a fix number of hydronium ions per unit volume of the acidic solution.
2. On dilution, the number of hydronium ions decreases and the solution becomes less acidic.
Question 6.
How is the concentration of hydroxide ions (OH–) affected when excess base is dissolved in a solution of sodium hydroxide?
Answer:
When the excess base is dissolved in the solution of sodium hydroxide, the amount of hydroxide (H–) ions per unit volume increases. Hence, the concentration of hydroxide ions increases. This happens only when base added dissolves in water.
Text Book Page no – 28.
Question 1.
You have two solutions, A and B. The pH of solution A is 6 and pH of solution B is 8. Which solution has more hydrogen ion concentration? Which of this is acidic and which one is basic?
Answer:
The pH of solution A is 6 which means it is an acidic solution and has higher concentration of hydrogen ions. On the other hand, pH of solution B is 8 which means it is basic and so has lower concentration of hydrogen ions.
![]()
Question 2.
What effect does the concentration of H+(aq) ions have on the nature of the solution?
Answer:
As the concentration of H+(aq) ions increase, the solution goes on becoming more and more acidic.
Question 3.
Do basic solutions also have H+(aq) ions? If yes, then why are these basic?
Answer:
Yes, basic solutions have H+(aq) ions, but their number is quite less as compared to OH– ions. This make a solution basic. Hence, solutions that have much higher number of OH– compared to H+ are basic.
Question 4.
Under what soil condition do you think a farmer would treat the soil of his fields with quick lime (calcium oxide) or slaked lime (calcium hydroxide) or chalk (calcium carbonate)?
Answer:
1. Good soil for farming should have pH range of 6 to 8.
2. When the soil becomes acidic i.e. when the pH of soil becomes lesser than 7, the farmers would add quick lime (calcium oxide) or slaked lime (calcium hydroxide) or such base substances to maintain the pH level.
Text Book Page no – 33.
Question 1.
What is the common name of the compound CaOCl2?
Answer:
The common name of CaOCl2 is bleaching powder.
Question 2.
Name the substance which on treatment with chlorine yields bleaching powder.
Answer:
Calcium hydroxide (Dry slaked lime)
Question 3.
Name the sodium compound which is used for softening hard water.
Answer:
Sodium carbonate (Na2CO3)
![]()
Question 4.
What will happen if a solution of sodium hydrocarbonate is heated? Give the equation of the reaction involved.
Answer:
When sodium hydrocarbonate is heated, sodium carbonate, water and carbon dioxide gas are obtained.
![]()
Question 5.
Write an equation to show the reaction between plaster of Paris and water.
Answer:
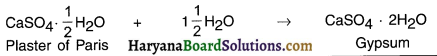
Activities
Activity 1.
Aim:
To test certain acids and bases in the laboratory.
Answer:
1. Collect the following solutions from the science laboratory — hydrochloric acid (HCI), sulphuric acid (H2SO4), nitric acid (HNO3). acetic acid (CH3COOH), sodium hydroxide (NaOH). calcium hydroxide [Ca(OH)2], potassium hydroxide (KOH), magnesium hydroxide [Mg(OH)2] and ammonium hydroxide (NH4OH).
2. Put a drop of each of the above solutions on a watch-glass one by one and test with a drop of the indicators shown in table.
3. What change in colour did you observe with red litmus, blue litmus, phenolphthalein and methyl orange solutions for each of the solutions taken?
4. Tabulate your observations in Table
The observations noted during various tests are tabulated in the table below:
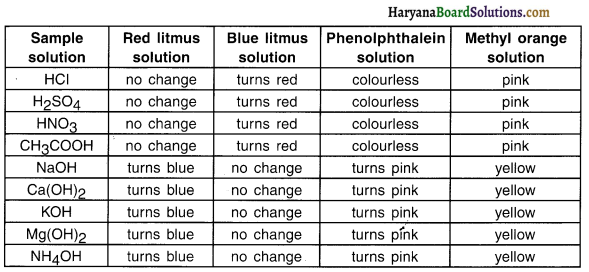
![]()
Activity 2.
Aim:
To test acids and bases using olfactory indicators.
Question 1.
Take some finely chopped onions in a plastic bag along with some strips of clean cloth. Tie up the bag tightly and leave overnight in the fridge. The cloth strips can now be used to test for acids and bases. Take two of these cloth strips and check their odour.
Answer:
When cloth strips are kept in a bag with finely chopped onions for overnight the strips emit smell of onion.
Question 2.
Keep them on a clean surface and put a few drops of dilute HCI solution on one strip and a few drops of dilute NaOH solution on the other. Rinse both cloth strips with water and again check their odour. Note your observations.
Answer:
1. Cloth strip + dilute HCI solution = Smell of onion ÷ colour of strip changes to pale red.
2. Cloth strip + dilute NaOH solution = Red coloured cloth strip changes to green.
Question 3.
Now take some dilute vanilla essence and clove oil and check their odour. Take some dilute HCI solution in one test tube and dilute NaOH solution in another. Add a few drops of dilute vanilla essence to both test tubes and shake well. Check the odour once again and record changes in odour, if any.
Answer:
On adding vanilla essence —
1. In dilute NaOH: No smell,
2. In dilute HCI: Smell of vanilla is still present
Question 4.
Similarly, test the change in the odour of clove oil with dilute HCI and dilute NaOH solutions and record your observations.
Answer:
On adding clove oil:
1. In dilute HCI: Smell of clove is present.
2. In dilute NaOH: Smell of clove is absent
Activity 3.
Perform an activity to study how metal (zinc) reacts with acid (sulphuric acid) and products formed.
Answer:
Set the apparatus as shown in
1. Set the apparatus as shown in figure.
2. Take about 5 mL of dilute sulphuric acid in a test tube and add a few pieces of zinc granules to it.
![]()
Observation:
1. We can observe that bubbles form on the surface of zinc granules. The bubbles indicate formation of gas.
2. When we pass this gas through the soap solution, the gas gets trapped in soap molecules and bubbles are formed.
3. When a burning candle is brought near the gas tilled bubbles, the gas bubbles break up with a pop
sound. This indicates that the gas formed is hydrogen (H2) gas.
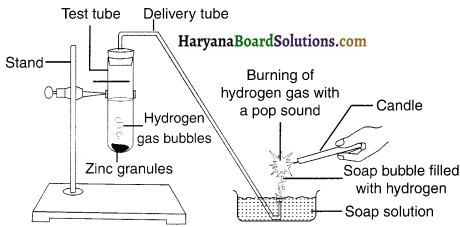
Reaction: 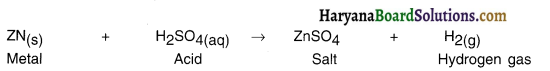
We can record similar observations even when we repeat this activity with some more acids like HCI, HNO3 and CH2COOH.
Conclusion:
When a metal reacts with acid, it gives salt and hydrogen gas.
Activity 4.
Perform an activity to study how metal (zinc) reacts with base (sodium hydroxide) and products formed.
Answer:
1. Place a few pieces of granulated zinc metal in a test tube.
2. Add 2 mL of sodium hydroxide (NaOH) solution and warm the contents of the test tube.
Observation:
- We can observe that bubbles form on the surface of zinc granules. The bubbles indicate formation of gas.
- When we pass this gas through the soap solution, the gas gets trapped In soap molecules and bubbles are formed.
- When a burning candle is brought near a gas filled bubble, the gas bubbles break up with a pop sound. This indicates that the gas formed is hydrogen (H2) gas.
Reaction:

Conclusion: When a metal reacts with a base, it gives salt and hydrogen gas.
Activity 5.
Perform an activity to study how acid reacts with metal carbonates and metal hydrogen
Answer:
1. Take two test tubes and label them as A and B.
2. Take about 0.5 g of sodium carbonate (Na2CO3) in test tube A and about 05 g of sodium hydrogencarbonate (NaHCO3) in test tube B.
3. Add about 2 mL of dilute HCI in both the test tubes.
![]()
Observation:
When acids react with metal carbonates and metal hydrogencarbonates, they produce salt, water and carbon dioxide gas. This happens in both the test tubes.
Reaction

4. On passing carbon dioxide produced through lime water (calcium hydroxide solution), a milky precipitate of calcium carbonate is formed.

5. On passing excess carbon dioxide through above solution, precipitate of calcium carbonate dissolves due to formation of soluble calcium bicarbonate.
![]()
Activity 6.
Perform an activity to study how acids and bases react with each other?
Answer:
1. Take about 2 mL of dilute NaOH solution in a test tube and add two drops of phenolphthalein solution.
2. The solution will become pink.
3. Add dilute HCI solution to the above solution drop by drop and record your observation.
Observation:
- On adding dilute HCI to the solution of phenolphthalein and sodium hydroxide, the pink colour of the solution slowly disappears. This suggests that NaOH (base) gets neutralized by acid.
- If we add a few drops of NaOH to the above mixture we will see that the solution again becomes pink. This suggests that the solution becomes alkaline again due to excess of NaOH over HCI. Hence, the pink colour reappears.
Conclusion:
When acid and base react with each other, the solution becomes neutral. The reaction that takes place is called neutralization reaction.
Activity 7.
Perform an activity to study reaction of metallic oxides with acids.
Answer:
1. Take a small amount of copper oxide in a beaker. it is black in colour.
2. Add dilute hydrochloric acid slowly while stirring.
Observation:
Copper oxide reacts with dilute hydrochloric acid. This gives a blue coloured solution of copper chloride salt.

Conclusion:
When acid reacts with metallic oxides, salt and water are produced.
![]()
Activity 8.
Perform an activity to study conduction of electricity by acids and bases.
Answer:
1. Take solutions of glucose, alcohol, hydrochloric acid, sulphuric acid, sodium hydroxide, etc.
2. Fix two nails on a cork, and place the cork in a 100 mL beaker.
3. Connect the nails to the two terminals of a 6 volt battery through a bulb and a switch, as shown in fig.
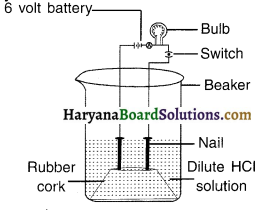
4. Now pour some dilute HCI in the beaker and switch on the current. Note down what happens.
5. Repeat the steps with dilute sulphuric acid (H2SO4), glucose and alcohol.
Observation:
- We can observe that the bulb glows when it is passed through acids and bases. This happens because the ions present in the acid and base enable flow of electric current.
- Glucose and alcohol solutions do not have ions. So, electricity is not conducted and the bulb does not glow.
Conclusion:
Acids have H+ ions and bases have OH– ions. As a result. they are able to conduct electricity.
Activity 9.
Perform an activity to show that HCI solution is acidic but its dry form is not.
Answer:
1. Take about 1 g solid NaCI in a clean and dry test tube and set up the apparatus as shown in figure.
2. Add some concentrated sulphuric acid to the test tube.
Observation:
- On adding concentratec sulphuric acid reaction takes place and hydrochloric acid gas is produced.
- NaCI(s) + H2SO4 → Na2SO4(aq) + 2HCI(g)
The gas produced has no effect on dry litmus paper. However, the gas changes the colour of wet litmus paper into red.
Conclusion:
The experiment suggests that hydrochloric acid produces hydrogen ions in the presence of water. But, dry hydrochloric acid does not release hydrogen ions. Thus, only HCI solution is acidic whereas dry HCI is not.
Note for teachers: If the climate is humid, you will have to pass the gas produced through a guard tube (drying tube) containing calcium chloride to dry the gas.
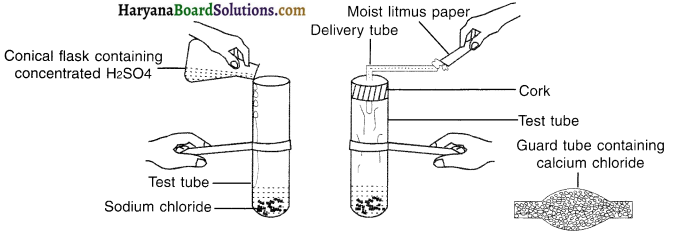
Activity 10.
Perform an activity to demonstrate that reaction between acid (or base) and water is an exothermic reaction.
Answer:
1. Take 10 mL water in a beaker.
2. Add a few drops of concentrated H2SO4 (or sodium hydroxide) to it and swirl the beaker slowly.
3. Touch the base of the beaker.
![]()
Observation:
On touching the beaker it can be felt that the temperature of the solution has increased. This means the reaction is exothermic.
Dissolution of acid (or base) in water releases heat and so this is an exothermic process.
Activity 11.
1. Test the pH values of solutions given in table 2.
2. Record your observations.
Q. What is the nature of each substance on the basis of your observations?
Answer:
Observations and answers are recorded in the table below.
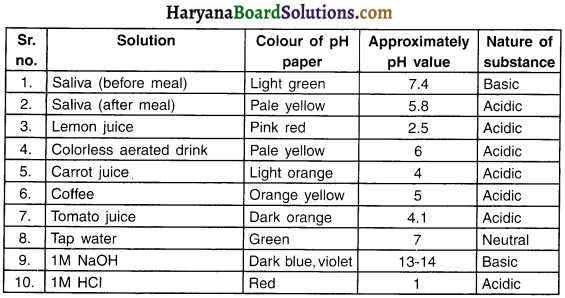
Activity 12.
Aim:
To find out pH of the soil.
Answer:
1. Put about 2 gm soil in a test tube and add 5 mL water to it.
2. Shake the contents of the test tube.
3. Filter the contents and collect the filtrate in a test tube.
4. Check the pH of this filtrate with the help of universal indicator paper.
Q. What can you conclude about the ideal soil pH for the growth of plants in your region?
Answer: If the pH of soil is near 7, plants will grow well. If the pH <6.5, the soil will be acidic and hinder plant growth.
Activity 13.
Question 1.
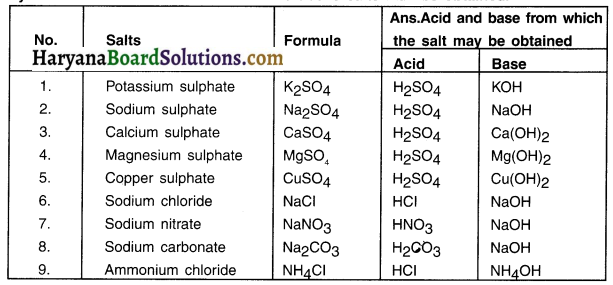
Write the formula of the salts given below:
Potassium sulphate, sodium sulphate, calcium sulphate, magnesium sulphate, copper sulphate sodium chloride, sodium nitrate, sodium carbonate and ammonium chloride.
Identify the acids and bases from which the above salts may be obtained.
Answer:
Question 2.
Salts having the same positive or negative radicals are said to belong to a family. For example, NaCI and Na2SO4 belong to the family of sodium salts. Similarly, NaCI and KCI belong to the family of chloride salts. How many families can you identify among the salts given in this activity?
Answer:
The following families can be identified:
Family of sulphate salts: K2SO4, Na2SO4, Ca2SO4, MgSO4, CuSO4
Family of chloride salts: NaCI NH4CI
Family of sodium salts: NaCI, Na2SO4, NaNO3, Na2CO3
![]()
Activity 14.
Aim: To find the pH and test the solubility of soil in water.
Answer:
1. Collect the following salt samples – sodium chloride, potassium nitrate, aluminium chloride, zinc sulphate, copper sulphate, sodium acetate, sodium carbonate and sodium hydrogen carbonate (some other salts available can also be taken).
2. Check their solubility in water (use distilled water only).
3. Check the action of these solutions on litmus and find the pH using a pH paper.
- Which of the salts are acidic, basic or neutral?
- Identify the acid or base used to form the salt.
- Report your observations in table below.
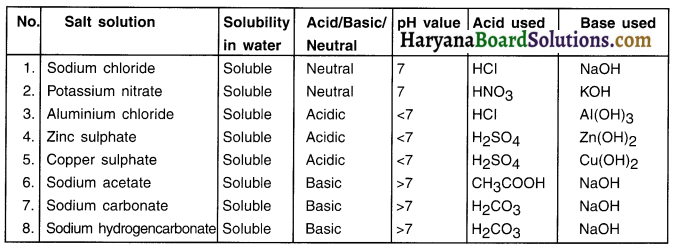
Give an idea about the pH of the salt formed with acid and base pH ot salt:

Activity 15.
Perform an activity to demonstrate that crystals of salt are not dry.
Answer:
1. Heat a few crystals of copper sulphate in a dry boiling tube. The colour of copper sulphate will be blue.
2. Heat the tube and observe the colour. Then add 2-3 drops of water and again check the colour.
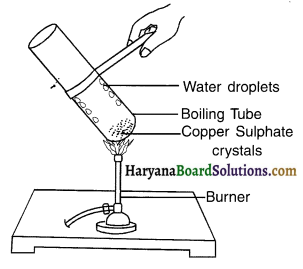
Observation:
- On heating the tube you will observe that the colour of the copper sulphate changes to white.
- Water droplets can be seen in the boiling tube due to condensation of water of crystallization of copper sulphate.
- On adding 2-3 drops of water on the sample of copper sulphate obtained after heating the blue colour of copper sulphate is restored.
![]()
Conclusion:
This experiment suggests that there are a fixed number of water of crystallization in the molecule of copper sulphate salt. When we heat this salt, the water gets removed and so it becomes colourless.
HBSE 10th Class Science Solutions Chapter 2 Acids, Bases and Salts Read More »