Author name: Bhagya

Haryana State Board HBSE 9th Class Maths Notes Chapter 3 निर्देशांक ज्यामिति Notes.

Haryana Board 9th Class Maths Notes Chapter 3 निर्देशांक ज्यामिति

→ एक तल में किसी वस्तु या बिंदु का स्थान निर्धारण करने के लिए हमें दो लांबिक रेखाओं की आवश्यकता होती है, जिनमें से एक क्षैतिज तथा दूसरी ऊर्ध्वाधर होती है ।

→ तल को कार्तीय या निर्देशांक तल कहा जाता है और रेखाओं को निर्देशांक अक्ष कहा जाता है।

→ एक तल पर एक बिंदु की स्थिति का निर्धारण करने में प्रयुक्त पद्धति को दकार्ते के सम्मान में कार्तीय पद्धति कहा जाता है ।

→ क्षैतिज रेखा x अक्ष तथा ऊर्ध्वाधर रेखा y-अक्ष कहलाती है।

→ x-अक्ष व y-अक्ष के प्रतिच्छेद बिंदु को मूलबिंदु (origin) कहा जाता है।

→ y-अक्ष से किसी बिंदु की दूरी को उसका x-निर्देशांक या भुज कहते हैं ।

→ x-अक्ष से किसी बिंदु की दूरी को उसका y-निर्देशांक या कोटि कहते हैं।

→ निर्देशांक तल में एक बिंदु के निर्देशांक लिखते समय पहले x-निर्देशांक लिखते हैं और उसके बाद y-निर्देशांक लिखते हैं। हम निर्देशांकों को कोष्ठक के अंदर लिखते हैं।

→ मूलबिंदु के निर्देशांक (0, 0), x-अक्ष पर किसी बिंदु के निर्देशांक (x, 0) व y-अक्ष पर किसी बिंदु के निर्देशांक (0, y) होते हैं।

→ ध्यान रहे-

(i) यदि बिंदु पहले चतुर्थांश में है, तो बिंदु (+, +) के रूप का होगा, क्योंकि पहला चतुर्थांश धनात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(ii) यदि बिंदु दूसरे चतुर्थाश में है, तो बिंदु (-, +) के रूप का होगा, क्योंकि दूसरा चतुर्थांश ऋणात्मक x-अक्ष और धनात्मक y-अक्ष से परिबद्ध है।
(iii) यदि बिंदु तीसरे चतुर्थांश में है, तो बिंदु (-, -) के रूप में होगा, क्योंकि तीसरा चतुर्थांश ऋणात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है।
(iv) यदि बिंदु चौथे चतुर्थांश में है तो बिंदु (+, -) के रूप में होगा, क्योंकि चौथा चतुर्थांश धनात्मक x-अक्ष और ऋणात्मक y-अक्ष से परिबद्ध है।

Haryana State Board HBSE 9th Class Maths Notes Chapter 2 बहुपद Notes.

Haryana Board 9th Class Maths Notes Chapter 2 बहुपद

→ बहुपद – बहुपद एक ऐसा व्यंजक होता है, जिसमें एक या एक से अधिक पद होते हैं। सामान्यतः चर x में एक बहुपद को निम्नलिखित प्रकार से लिखा जा सकता है-
p(x) = a₀xⁿ + a₁x^n-1 + ……. + a_n-1x + a_n
जिसमें a₀, a₁, a₂, …………., a_n आदि सभी गुणांक वास्तविक संख्याएँ हैं तथा a_n ≠ 0 और n एक ऋणोतर पूर्णांक है।

→ बहुपद की घात- बहुपद की अधिकतम घात वाले पद के घातांक को उस बहुपद की घात कहते हैं; जैसे x⁴ + x³ – x में बहुपद की घात 4 है।

→ एक घात वाले बहुपद को रैखिक बहुपद कहा जाता है।

→ दो घात वाले बहुपद को द्विघाती या द्विघात बहुपद कहा जाता है।

→ तीन घात वाले बहुपद को त्रिघाती बहुपद कहा जाता है।

→ एक शून्येतर अचर बहुपद की घात शून्य होती है अर्थात अचर बहुपद 0 को शून्य बहुपद कहा जाता है।

→ केवल एक पद वाले बहुपद को एकपदी (monomial), दो पदों वाले बहुपद को द्विपद (binomial) तथा तीन पदों वाले बहुपद को त्रिपद (trinomial) कहा जाता है।

→ भाग के किसी प्रश्न के लिए-
भाज्य = (भाजक × भागफल) + शेषफल

→ p(x) = 3x² + x – 1 को (x + 1) से भाग देने पर जो शेषफल प्राप्त होता है, यह वही होता है जोकि बहुपद (x + 1) के शून्यक अर्थात -1 पर बहुपद p(x) का मान होता है।

→ शेषफल प्रमेय- मान लीजिए p(x) एक से अधिक या एक के बराबर घात वाला एक बहुपद है और मान लीजिए a कोई वास्तविक संख्या है। यदि p(x) को रैखिक बहुपद (x – a) से भाग दिया जाए तो शेषफल p(a) होता है।

→ गुणनखंड प्रमेय- यदि p(x) घात n ≥ 1 वाला एक बहुपद हो और कोई वास्तविक संख्या हो तो-
(i) x – a, p(x) का एक गुणनखंड होता है, यदि p(a) = 0 हो और (ii) p(a) = 0 होता है, यदि (x – a), p(x) का एक गुणनखंड हो ।

→ बीजीय सर्वसमिकाएँ-
(i) (x + y)² = x² + 2xy + y²
(ii) (x – y)² = x² – 2xy + y²
(iii) x² – y² = (x + y)(x – y)
(iv) (x + a)(x + b) = x² + (a + b)x + ab
(v) (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
(vi) (x + y)³ = x³ + y³ + 3xy(x + y)
(vii) (x – y)³ = x³ – y³ – 3xy(x – y)
(viii) x + y + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)

Haryana State Board HBSE 9th Class Maths Notes Chapter 1 संख्या पद्धति Notes.

Haryana Board 9th Class Maths Notes Chapter 1 संख्या पद्धति

→ प्राकृत संख्याएँ (N) = 1, 2, 3, 4, 5, …………..

→ सबसे छोटी प्राकृत संख्या 1 है।

→ पूर्ण संख्याएँ = 0, 1, 2, 3, 4, ………….

→ सबसे छोटी पूर्ण संख्या 0 (शून्य) है।

→ पूर्णांक (Z) = …………, -3, -2, -1, 0, 1, 2, 3, …………….

→ परिमेय संख्या – संख्या r को परिमेय संख्या कहा जाता है, यदि इसेद \(\frac{p}{q}\) के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है।

→ किन्हीं दो दी हुई परिमेय संख्याओं के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं।

→ अपरिमेय संख्या – संख्या ‘s’ को अपरिमेय संख्या कहा जाता है यदि इसे \(\frac{p}{q}\) के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है; जैसे \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{15}\), π आदि ।

→ वास्तविक संख्याएँ – परिमेय संख्याओं और अपरिमेय संख्याओं के संग्रह को वास्तविक संख्याएँ कहा जाता है।

→ सांत दशमलव संख्या – यदि किसी संख्या के अंश को हर से भाग करने पर शेष शून्य हो जाता है तो ऐसी संख्या के दशमलव प्रसार को सांत दशमलव कहते हैं।

→ असांत दशमलव या अनवसानी आवर्ती संख्या – यदि किसी संख्या के अंश को हर से भाग करने पर शेष कभी भी शून्य नहीं होता तो ऐसी संख्या के दशमलव प्रसार को असांत दशमलव या अनवसानी आवर्ती संख्या कहते हैं।

→ एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार सांत या अनवसानी आवर्तीीं है, परिमेय होती है।

→ एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती है, अपरिमेय होती है।

→ एक परिमेय संख्या और एक अपरिमेय संख्या का जोड़ या घटाना, अपरिमेय होता है।

→ एक अपरिमेय संख्या के साथ एक शून्येतर (non-zero) परिमेय संख्या का गुणनफल या भागफल अपरिमेय होता है।

→ यदि हम दो अपरिमेय संख्याओं को जोड़े, घटाएँ, गुणा करें या एक अपरिमेय संख्या को दूसरी अपरिमेय संख्या से भाग दें, तो परिणाम परिमेय या अपरिमेय कुछ भी हो सकता है।

→ यदि a और b धनात्मक वास्तविक संख्याएँ हों तो-
(i) \(\sqrt{a b}=\sqrt{a} \cdot \sqrt{b}\)
(ii) \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)
(iii) \((\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b\)
(iv) \((a+\sqrt{b})(a-\sqrt{b})=a^2-b\)
(v) \((\sqrt{a}+b)(\sqrt{a}-b)=a-b^2\)
(vi) \((\sqrt{a}+\sqrt{b})^2=a+2 \sqrt{a b}+b\)

→ घातांक के नियम परिमेय संख्याओं पर भी लागू होते हैं अर्थात यदि a > 0, एक वास्तविक संख्या हो और p तथा q परिमेय संख्याएँ हों तो-
(i) a^p · a^q = a^p+q
(ii) \(\left(a^p\right)^q=a^{p q}\)
(iii) \(\frac{a^p}{a^q}=a^{p-q}\)
(iv) a^p · b^p = (ab)^p

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 12 हीरोन सूत्र Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 12 हीरोन सूत्र

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
उस त्रिभुज का क्षेत्रफल ज्ञात करें जिसकी भुजाएँ 40 m, 24 m व 32 m हों।
हल :
यहाँ पर
a = 40 m, b = 24 m, c= 32 m
∴ s = \(\frac{a+b+c}{2}=\frac{40+24+32}{2}=\frac{96}{2}\) = 48 m.
हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{48(48-40)(48-24)(48-32)}\) m²
= \(\sqrt{48 \times 8 \times 24 \times 16}\) m²
= \(\sqrt{6 \times 8 \times 8 \times 6 \times 4 \times 4 \times 2 \times 2}\) m²
= 6 × 8 × 4 × 2 = 384 m²

प्रश्न 2.
10 cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल ज्ञात करें।
हल :
यहाँ पर
a = 10 cm, b = 10 cm, c = 10 cm
∴ s = \(\frac{a+b+c}{2}=\frac{10+10+10}{2}=\frac{30}{2}\) = 15 cm
हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-10)(15-10)(15-10)}\) cm²
= \(\sqrt{15 \times 5 \times 5 \times 5}\) cm²
= \(\sqrt{3 \times 5 \times 5 \times 5 \times 5}\) cm²
= 5 × 5 × √3 cm² = 25√3 cm²

प्रश्न 3.
एक त्रिभुजाकार पार्क ABC की भुजाएँ 120 m, 80 m और 50 m हैं (देखिए आकृति)। एक मालिन धनिया को इसके चारों ओर एक बाड़ लगानी है और इसके अंदर घास उगानी है। उसे कितने क्षेत्रफल में घास उगानी है ? एक ओर 3m चौड़े एक फाटक के लिए स्थान छोड़ते हुए इसके चारों ओर ₹ 20 प्रति मीटर की दर से काँटेदार बाड़ लगाने का व्यय भी ज्ञात कीजिए।
हल :
यहाँ पर
a = 120m, b = 80 m, c = 50 m

s = \(\frac{a+b+c}{2}=\frac{120+80+50}{2} \mathrm{~m}=\frac{250}{2} \mathrm{~m}\)
= 125 m
घास उगाने के लिए उपलब्ध क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{125(125-120)(125-80)(125-50)}\) m²
= \(\sqrt{125 \times 5 \times 45 \times 75}\) m²
= \(\sqrt{5 \times 5 \times 5 \times 5 \times 3 \times 3 \times 5 \times 3 \times 5 \times 5}\) m²
= 5 × 5 × 5 × 3 \(\sqrt{3 \times 5}\) m²
= 375√15 m²
पार्क का परिमाप = a + b + c = 120 + 80 + 50 = 250 m
बाड़ लगाने के लिए आवश्यक तार की लंबाई = परिमाप – फाटक की लंबाई
= 250 m – 3 m
= 247 m
अतः बाड़ लगाने के लिए कुल व्यय = 20 × 247 = ₹ 4940.

प्रश्न 4.
किसी त्रिभुज की भुजाओं का अनुपात 3 : 5 : 7 है। उसका परिमाप 300 cm है। त्रिभुज का क्षेत्रफल ज्ञात करें।
हल :
यहाँ पर त्रिभुज की भुजाओं का अनुपातa : b : c= 3 : 5 : 7
अनुपाती योग = 3 + 5 + 7 = 15
a = \(\frac{3}{15}\) × 300 = 60 cm
b = \(\frac{5}{15}\) × 300 = 100 cm
c = \(\frac{7}{15}\) × 300 = 140 cm
s = \(\frac{a+b+c}{2}=\frac{300}{2}\) = 150 cm
अतः हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{150(150-60)(150-100)(150-140)}\) cm²
= \(\sqrt{150 \times 90 \times 50 \times 10}\) cm²
= \(\sqrt{2 \times 3 \times 5 \times 5 \times 2 \times 3 \times 3 \times 5 \times 2 \times 5 \times 5 \times 2 \times 5}\) cm²
= 2 × 2 × 3 × 5 × 5 × 5 × √3 = 1500√3 cm²

प्रश्न 5.
कमला के पास 240 m, 200 m और 360 m भुजाओं वाला एक त्रिभुजाकार खेत है, जहाँ वह गेहूँ उगाना चाहती है। इसी खेत से संलग्न 240 m,320 m और 400 m भुजाओं वाला एक अन्य खेत है, जहाँ वह आलू और प्याज उगाना चाहती है (देखिए आकृति)। उसने इस खेत की सबसे लंबी भुजा के मध्य-बिंदु को सम्मुख शीर्ष से जोड़कर उसे दो भागों में विभाजित कर दिया। इनमें से एक भाग में उसने आलू उगाए और दूसरे भाग में प्याज उगाए। गेहूँ, आलू और प्याज के लिए कितने-कितने क्षेत्रफलों (हेक्टेयर में) का प्रयोग किया गया है ? (1 हेक्टेयर = 10000 m² है)
हल :

माना ABC वह खेत है, जहाँ गेहूँ उगाया गया है।
साथ ही, ACD वह खेत है जिसकी भुजा AD के मध्य-बिंदु E को C से जोड़कर इस खेत को दो भागों में विभाजित करती है।
∆ABC के लिए
a = 200 m, b = 240 m, c = 360 m
अतः s = \(\frac{a+b+c}{2}=\frac{200+240+360}{2} \mathrm{~m}\) = 400 m
इसलिए गेहूँ उगाने के लिए क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{400(400-200)(400-240)(400-360)}\) m²
= \(\sqrt{400 \times 200 \times 160 \times 40}\) m²
= 16000 √2 m²
= 1.6 × √2
= 1.6 × 1.41 हेक्टेयर
= 2.26 हेक्टेयर (लगभग)

अब, ∆ACD के लिए =
a = 240 m, b = 320m, c = 400 m
s = \(\frac{a+b+c}{2}=\frac{240+320+400}{2} \mathrm{~m}\) = 480 m

अतः ∆ACD का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{480(480-240)(480-320)(480-400)}\) m²
= \(\sqrt{480 \times 240 \times 160 \times 80}\) m²
= 38400 m² = 3.84 हेक्टेयर
अतः आलू उगाने के लिए क्षेत्रफल = प्याज उगाने के लिए क्षेत्रफल
= \(\frac{3.84}{2}\) = 1.92 हेक्टेयर

प्रश्न 6.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात करें जिसमें विकर्ण AC की लंबाई 10 cm तथा Ba D से AC पर खींचे गए लंबों की लंबाइयाँ क्रमशः 7 cm तथा 5 cm हैं।
हल :

आकृति अनुसार,
AC = 10 cm
BE = 7 cm
DF = 5 cm
चतुर्भुज ABCD का क्षेत्रफल = (∆ABC + ∆ACD) का क्षेत्रफल
= \(\frac{1}{2}\) × AC × BE + \(\frac{1}{2}\) × AC × DF
= [\(\frac{1}{2}\) × 10 × 7 + \(\frac{1}{2}\) × 10 × 5] cm²
= (35 + 25) cm² = 60 cm²

प्रश्न 7.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात करें जिसकी भुजाओं की लंबाई क्रमशः 6 cm, 8 cm, 7 cm व 9 cm हो। पहली दो भुजाओं के बीच का कोण समकोण है।
हल :
माना चतुर्भुज ABCD में

AB = 6 cm, BC = 8 cm, CD = 7 cm व DA = 9 cm
∠B = 90°
समकोण ∆ABC में
AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC} \mathrm{C}^2}\)
= \(\sqrt{(6)^2+(8)^2}=\sqrt{36+64}=\sqrt{100}\) = 10 cm

समकोण ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) × AB × BC
= \(\frac{1}{2}\) × 6 × 8 cm² = 24 cm²
∆ADC के लिए a = 7 cm, b = 9 cm, c = 10 cm
s = \(\frac{a+b+c}{2}=\frac{7+9+10}{2} \mathrm{~cm}=\frac{26}{2}\) = 13 cm

हीरोन सूत्र से
∆ADC का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{13(13-7)(13-9)(13-10)}\) cm²
= \(\sqrt{13 \times 6 \times 4 \times 3}\) cm²
= \(\sqrt{13 \times 2 \times 3 \times 2 \times 2 \times 3}\) cm²
= 2 × 3 × 26 cm²
= 6√26 cm²

चतुर्भुज ABCD का क्षेत्रफल = (∆ABC + ∆ADC) का क्षेत्रफल
= (24 + 6√26) cm²

प्रश्न 8.
एक समचतुर्भुज का परिमाप 24 cm है। इसके एक विकर्ण का माप 8 cm है। समचतुर्भुज का क्षेत्रफल ज्ञात करें।
हल :
माना ABCD एक समचतुर्भुज है जिसमें विकर्ण
AC = 8 cm
समचतुर्भुज की प्रत्येक भुजा = \(\frac{24}{4}\) = 6 cm

∆ABC के लिए
a = 6 cm, b = 6 cm, c = 8 cm
s = \(\frac{a+b+c}{2}=\frac{6+6+8}{2}=\frac{20}{2}\) = 10 cm
हीरोन सूत्र से
∆ABC का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{10(10-6)(10-6)(10-8)}\)
= \(\sqrt{10 \times 4 \times 4 \times 2}\) = 8√5 cm²
चतुर्भुज ABCD का क्षेत्रफल = 2 × ∆ABC का क्षेत्रफल
= 2 × 8√5 cm²
= 16√5 cm²

Multiple Choice Questions with Answers:

प्रश्न 1.
एक त्रिभुज जिसका आधार 12 cm तथा ऊँचाई 5 cm हो, तो उसका क्षेत्रफल होगा-
(A) 60 cm²
(B) 30 cm²
(C) 30 m²
(D) 60 m²
उत्तर-
(B) 30 cm²

प्रश्न 2.
10 cm भुजा वाली समबाहु त्रिभुज का क्षेत्रफल होगा-
(A) 25√2 cm²
(B) 25√5 cm²
(C) 50√3 cm²
(D) 50√2 cm²
उत्तर-
(B) 25√3 cm²

प्रश्न 3.
असमान भुजा 8 cm और बराबर भुजाएँ 5 cm वाले समद्विबाहु त्रिभुज का क्षेत्रफल क्या होगा ?
(A) 12 cm²
(B) 12 m²
(C) 12 cm
(D) 12 m
उत्तर-
(A) 12 cm²

प्रश्न 4.
एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ‘a’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल होगा
(A) \(\frac{\sqrt{3}}{4}\) a
(B) \(\frac{\sqrt{3}}{4}\) a²
(C) \(\frac{\sqrt{3}}{2}\) a
(D) \(\frac{\sqrt{3}}{2}\) a²
उत्तर-
(B) \(\frac{\sqrt{3}}{4}\) a²

प्रश्न 5.
ABCD एक चतुर्भुज है तथा BD इसके विकर्णों में से एक है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल होगा-

(A) 20 cm²
(B) 15 cm²
(C) 10 cm²
(D) 40 cm²
उत्तर-
(A) 20 cm²

प्रश्न 6.
उस त्रिभुज का क्षेत्रफल क्या होगा जिसकी दो भुजाएँ 18 m और 10 m हैं तथा परिमाप 42 m है ?
(A) 21√11 cm
(B) 21√11 cm²
(C) 21√11 cm³
(D) 21√11 m²
उत्तर-
(D) 21√11 m²

प्रश्न 7.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इसकी सबसे बड़ी भुजा की लंबाई होगी-
(A) 120 cm
(B) 170 cm
(C) 250 cm
(D) 540 cm
उत्तर-
(C) 250 cm

प्रश्न 8.
एक समबाहु त्रिभुज जिसका परिमाप 180 cm है, इसका क्षेत्रफल होगा-
(A) 900√3 cm
(B) 900√3 cm²
(C) 90√3 m
(D) 90√3 m²
उत्तर-
(B) 900√3 cm²

प्रश्न 9.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल होगा-
(A) 9000 cm²
(B) 9000 m²
(C) 9000 cm³
(D) 9000 m³
उत्तर-
(A) 9000 cm²

प्रश्न 10.
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल होगा-
(A) 9√15 cm³
(B) 9√15 m³
(C) 9√15 cm²
(D) 9√15 m²
उत्तर-
(C) 9√15 cm²

प्रश्न 11.
समांतर चतुर्भुज ABCD में, AB = 12 cm है। भुजाओं AB तथा AD के संगत शीर्षलंब क्रमशः 6 cm और 8 cm हैं जैसा कि संलग्न आकृति में दर्शाया गया है। AD का मान होगा-

(A) 4.5 cm
(B) 9 cm
(C) 13.5cm
(D) 18 cm
उत्तर-
(B) 9 cm

प्रश्न 12.
आकृति में ∠ACO = 90°, AC = BC, OA = 12 cm तथा OC = 6.5 cm है। ∆AOB का क्षेत्रफल होगा जबकि AC =10 cm हो-

(A) 30 cm
(B) 60 cm²
(C) 65 cm²
(D) 70 cm²
उत्तर-
(C) 65 cm²

प्रश्न 13.
सानिया के पास एक खेत है, जो एक समचतुर्भुज के आकार का है। वह अपनी एक पुत्री और एक पुत्र से यह चाहती थी कि वे इस खेत पर काम करके अलग-अलग फसलों (या उपजों) का उत्पादन करें। उसने इस खेत को दो बराबर भागों में विभाजित कर दिया। यदि इस खेत का परिमाप 400 m है और एक विकर्ण 160 m है, तो प्रत्येक को खेती के लिए कितना क्षेत्रफल प्राप्त होगा ?
(A) 4800 m²
(B) 9600 m²
(C) 4800 m
(D) 9600 m
उत्तर-
(A) 4800 m²

प्रश्न 14.
एक पार्क चतुर्भुज PQRS के आकार का है, जिसमें ZR = 90%, PQ= 9 m, QR = 12 m, RS = 5 m और PS = 8 m है। इस पार्क का क्षेत्रफल होगा-
(A) 65.5 m²
(B) 65.5 cm²
(C) 65.5 m
(D) 65.5 cm
उत्तर-
(A) 65.5 m²

प्रश्न 15.
एक चतुर्भुज ABCD का क्षेत्रफल क्या होगा, जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm और AC = 5 cm है ?
(A) 15.2 m²
(B) 15.2 cm²
(C) 15.2 m
(D) 15.2 cm
उत्तर-
(B) 15.2 cm²

प्रश्न 16.
एक त्रिभुज और एक समांतर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समांतर चतुर्भुज 28 cm के आधार पर स्थित है, तो उसकी संगत ऊँचाई होगी-
(A) 12 cm
(B) 12 cm²
(C) 12 m
(D) 12 m²
उत्तर-
(A) 12 cm

प्रश्न 17.
किसी समलंब का क्षेत्रफल ज्ञात करने का सूत्र होता है-
(A) समांतर भुजाओं का योग × उनके बीच की दूरी
(B) असमांतर भुजाओं का योग × उनके बीच की दूरी
(C) \(\frac{1}{2}\) × समांतर भुजाओं का योग × उनके बीच
(D) असमांतर भुजाओं का योग × उनके बीच की दूरी की दूरी
उत्तर-
(C) \(\frac{1}{2}\) × समांतर भुजाओं का योग × उनके बीच की दूरी

प्रश्न 18.
6 cm, 8 cm तथा 10 cm भुजाओं वाली त्रिभुज का क्षेत्रफल होगा-
(A) 18 cm²
(B) 22 cm²
(C) 24 cm²
(D) 12 cm²
उत्तर-
(C) 24 cm²

प्रश्न 19.
एक समकोण त्रिभुज जिसमें समकोण बनाने वाली भुजाओं की लंबाई 5 cm तथा 12 cm है। इसका क्षेत्रफल होगा-
(A) 30 cm²
(B) 60 cm²
(C) 90 cm²
(D) 75 cm²
उत्तर-
(A) 30 cm²

प्रश्न 20.
समांतर चतुर्भुज के क्षेत्रफल का सूत्र होता है-
(A) \(\frac{1}{2}\) × आधार × ऊँचाई
(B) आधार × ऊँचाई
(C) 2 × आधार × ऊँचाई
(D) 3 × आधार × ऊँचाई
उत्तर-
(B) आधार × ऊँचाई

प्रश्न 21.
एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस’ समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा ?
(A) 48 m²
(B) 48 m
(C) 48 cm²
(D) 48 cm
उत्तर-
(A) 48 m²

प्रश्न 22.
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है जैसाकि आकृति में दिखाया गया है। प्रत्येक टुकड़े के माप 20 cm, 50 cm और 50 cm हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है ?

(A) 200√6 cm²
(B) 2000√6 cm²
(C) 1000√6 cm²
(D) 400√6 cm²
उत्तर-
(C) 1000√6 cm²

प्रश्न 23.
एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए शेड III में कितना कागज प्रयुक्त हुआ ?

(A) 256 cm
(B) 256 cm²
(C) 17.92 cm
(D) 17.92 cm²
उत्तर-
(D)17.92 cm²

प्रश्न 24.
एक समद्विबाहु त्रिभुज का आधार 10 cm है तथा समान भुजाओं में से एक भुजा 13 cm है। हीरोन के सूत्र द्वारा इसका क्षेत्रफल होगा-
(A) 60 cm²
(B) 30 cm²
(C) 90 cm²
(D) 45 cm²
उत्तर-
(A) 60 cm²

प्रश्न 25.
एक समचतुर्भुज का परिमाप 24 cm है, उसके एक विकर्ण का माप 8 cm है। इसका क्षेत्रफल होगा-
(A) 8√5 cm²
(B) 12√5 cm²
(C) 16√5 cm²
(D) 24√5 cm²
उत्तर-
(C) 16√5 cm²

प्रश्न 26.
उस समद्विबाहु त्रिभुज की ऊँचाई क्या होगी जिसका आधार 30 cm और क्षेत्रफल 120 cm- हो ?
(A) 4 cm
(B) 8 cm
(C) 4 cm²
(D) 8 cm²
उत्तर-
(B) 8 cm

प्रश्न 27.
किसी समांतर चतुर्भुज की दो आसन्न भुजाओं की माप 5 cm और 3.5 cm हैं। उसके एक विकर्ण की माप 6.5 cm हो, तो समांतर चतुर्भुज का क्षेत्रफल होगा-
(A) 10√3 cm
(B) 10√3 m
(C) 10√3 cm²
(D) 10√3 m²
उत्तर-
(C) 10√3 cm²

प्रश्न 28.
यदि किसी त्रिभुज की भुजाओं को दुगुना कर दिया जाए तो उसका क्षेत्रफल कितने प्रतिशत बढ़ जाएगा ?
(A) 100%
(B) 200%
(C) 300%
(D) 400%
उत्तर-
(B) 200%

प्रश्न 29.
एक त्रिभुजाकार खेत की भुजाएँ 60 m, 80 m और 100 m हैं। ₹ 2.50 प्रति वर्ग मीटर की दर से इस खेत को जोतने पर कितना खर्च आएगा ?
(A) ₹ 60
(B) ₹ 600
(C) ₹ 5000
(D) ₹ 6000
उत्तर-
(D) ₹ 6000

प्रश्न 30.
किसी त्रिभुज का अर्ध-परिमाप क्या होगा यदि उसकी भुजाएँ 40 m, 24 m और 32 m हो?
(A) 3072 m
(B) 96 m
(C) 48 m²
(D) 48 m
उत्तर-
(D) 48 m

प्रश्न 31.
उस समांतर चतुर्भुज का क्षेत्रफल क्या होगा जिसकी दो आसन्न भुजाओं की लंबाई 5 cm तथा 6 cm है और एक विकर्ण की लंबाई 7 cm है ?
(A) 6√6 cm²
(B) 12√6 cm²
(C) 24√6 cm²
(D) 18√6 cm²
उत्तर-
(B) 12√6 cm²

प्रश्न 32.
एक खेत समलंब के आकार का है, जिसकी समांतर भुजाएँ 25 m और 10 m हैं। इसकी असमांतर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल होगा-
(A) 196 m²
(B) 196 m³
(C) 196 m
(D) 196 cm²
उत्तर-
(A) 196 m²

प्रश्न 33.
किसी समांतर चतुर्भुज की दो आसन्न भुजाओं की लंबाइयाँ क्रमशः 51 cm और 37 cm हैं। इसका एक विकर्ण 20 cm हो, तो समांतर चतुर्भुज का क्षेत्रफल होगा-
(A) 306 cm²
(B) 612 cm²
(C) 612 m²
(D) 306 m²
उत्तर-
(B) 612 cm²

प्रश्न 34.
एक त्रिभुजाकार प्लेट की भुजाएँ 8 cm, 15 cm और 17 cm हैं। यदि इसका भार 96 ग्राम हो, तो प्लेट का प्रति वर्ग सें०मी० भार क्या होगा ?
(A) 16 gm
(B) 8 gm
(C) 1.6 gm
(D) 0.8 gm
उत्तर-
(C) 1.6 gm

प्रश्न 35.
एक त्रिभुज का परिमाप 270 m है तथा इसकी भुजाओं में अनुपात 12 : 17 : 25 है, तो इसकी सबसे छोटी भुजा होगी-
(A) 60 m
(B) 85 m
(C) 125 m
(D) 270 m
उत्तर-
(A) 60 m

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 11 रचनाएँ Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 11 रचनाएँ

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
60° के कोण की रचना कीजिए।
हल :

रचना के चरण :
(1) एक किरण AB खींचिए।
(2) A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
(3) परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
(4) E से जाने वाली किरण AC खींचिए।
(5) ∠CAB अभीष्ट कोण है जो 60° का है।

प्रश्न 2.
एक दिए हुए ∠ABC के समद्विभाजक की रचना कीजिए।
हल :
रचना के चरण :
(1) B को केंद्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण BA और BC को क्रमशः E और D पर प्रतिच्छेद करे।
(2) अब D और E को केंद्र मानकर तथा \(\frac{1}{2}\) DE से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को F पर प्रतिच्छेद करे।
(3) किरण BF खींचिए।
(4) यही किरण BF, कोण ABC का अभीष्ट समद्विभाजक है।

प्रश्न 3.
4.5 cm भुजा वाली एक समबाहु त्रिभुज की रचना कीजिए।
हल :
रचना के चरण :
(1) एक रेखाखंड BC = 4.5 cm खींचिए।
(2) B और C को केंद्र मानकर BC = 4.5 cm त्रिज्या की परकार खोलकर दो चापें जो परस्पर A पर प्रतिच्छेद करें।
(3) A को B व C से मिलाओ।
(4) इस प्रकार ∆ABC अभीष्ट समबाहु त्रिभुज है।

प्रश्न 4.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 5 cm, ∠B = 60° तथा AB + AC = 7.8 cm हो।
हल :
रचना के चरण :
(1) एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 5 cm लीजिए।

(2) अब बिंदु B पर ∠YBX = 60° बनाओ।
(3) BY से BD = 7.8 cm काटो।
(4) D को C से मिलाओ।
(5) CD का लंब समद्विभाजक खींचिए जो BD को A पर प्रतिच्छेद करे।
(6)A और C को मिलाइए।
(7) इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 5.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 7 cm; ∠B = 45° और AB – AC = 2 cm हो।
हल :
रचना के चरण :

(1) एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 7cm लीजिए।
(2) अब बिंदु B पर ∠YBC = 45° बनाओ।
(3) BY से BD = 2 cm काटो।
(4) D को C मिलाओ।
(5) CD का लंब समद्विभाजक RS खींचो जो BY को A पर प्रतिच्छेद करता है।
(6) A और C को मिलाइए।
(7) इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 6.
एक त्रिभुज ABC की रचना कीजिए, जिसमें ∠B = 90° तथा ∠C = 60° और AB + BC + CA = 11.5 cm हो।
हल :
रचना के चरण :
(1) एक रेखाखंड PQ = 11.5 cm खींचिए।
(2) P पर एक किरण PL खींचिए जिससे कि ∠LPQ = \(\frac{1}{2}\) × 90° = 45° हो।
(3) Q पर एक किरण QM खींचिए जिससे कि ∠MQP = \(\frac{1}{2}\) × 60° = 30° हो जो PL को A पर काटे।
(4) PA का लंब समद्विभाजक XY खींचिए जो PQ को B पर प्रतिच्छेद करे।
(5) AQ का लंब समद्विभाजक RS खींचिए जो PQ को C पर प्रतिच्छेद करे।

(6) AB और AC को मिलाइए।
(7) इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 7.
एक त्रिभुज की रचना करें जिसमें AB = 4 cm, BC = 5 cm तथा BC पर माध्यिका AD = 2.5 cm हो।
हल :
रचना के चरण :
(1) एक रेखाखंड BC = 5 cm खींचिए।
(2) BC का लंब समद्विभाजक खींचे जो BC को D पर काटे।
(3) अब B को केंद्र मानकर 4 cm त्रिज्या की परकार से एक चाप लगाओ।
(4) D को केंद्र मानकर 2.5 cm त्रिज्या की परकार से एक चाप लगाओ। जो चरण (3) की चाप को A पर काटे।
(5) AB और AC को मिलाओ।
(6) ABC अभीष्ट त्रिभुज है।

Multiple Choice Questions with Answers:

प्रश्न 1.
निम्नलिखित कोण का माप होगा-

(A) 90°
(B) 60°
(C) 450
(D) 180°
उत्तर-
(A) 90°

प्रश्न 2.
आकृति में ∠ABC का मान 60° है इसके समद्विभाजक का मान होगा-

(A) 60°
(B) 30°
(C) 90°
(D) 120°
उत्तर-
(B) 30°

प्रश्न 3.
एक त्रिभुज ABC का परिमाप 11 cm है, इसमें AB = 3 cm तथा BC = 4 cm हैं, तो CA का मान होगा-
(A) 3 cm
(B) 4 cm
(C) 2.5 cm
(D) 5 cm
उत्तर-
(B) 4 cm

प्रश्न 4.
105° के कोण के समद्विभाजक का मान होगा-
(A) 50\(\frac{1}{2}\)°
(B) 51\(\frac{1}{2}\)°
(C) 52\(\frac{1}{2}\)°
(D) 53\(\frac{1}{2}\)°
उत्तर-
(C) 52\(\frac{1}{2}\)°

प्रश्न 5.
किसी त्रिभुज में शीर्ष को सामने वाली भुजा के मध्य-बिंदु से मिलाने वाली रेखा को कहा जाता है-
(A) माध्यिका
(B) लंब समद्विभाजक
(C) कोण समद्विभाजक
(D) कर्ण
उत्तर-
(A) माध्यिका

प्रश्न 6.
एक त्रिभुज के आधार की लंबाई 5 cm, दो शेष भुजाओं की लंबाई का योग 7.8 cm है तथा इसका आधार कोण 60° है, तो परिमाप होगा-
(A) 2.8 cm
(B) 17.8 cm
(C) 12.8 cm
(D) 15.6 cm
उत्तर-
(C) 12.8 cm

प्रश्न 7.
75° के कोण के समद्विभाजक का मान होगा-
(A) 75°
(B) 150°
(C) 37\(\frac{1}{2}\)°
(D) 45°
उत्तर-
(C) 37\(\frac{1}{2}\)°

प्रश्न 8.
निम्नलिखित में से कौन-सा कोण परकार की सहायता से नहीं बनाया जा सकता है ?
(A) 30°
(B) 22\(\frac{1}{2}\)°
(C) 15°
(D) 20°
उत्तर-
(D) 20°

प्रश्न 9.
निम्नलिखित में से कौन-सा कोण परकार की सहायता से बनाया जा सकता है ?
(A) 37\(\frac{1}{2}\)°
(B) 20\(\frac{1}{2}\)°
(C) 10\(\frac{1}{2}\)°
(D) 65\(\frac{1}{2}\)°
उत्तर-
(A) 37\(\frac{1}{2}\)°

प्रश्न 10.
किस कोण के समद्विभाजक द्वारा 22\(\frac{1}{2}\)° का कोण प्राप्त होता है ?
(A) 60°
(B) 45°
(C) 30°
(D) 90°
उत्तर-
(B) 45°

प्रश्न 11.
जिस त्रिभुज का प्रत्येक कोण 60° हो, उसे कहा जाता है-
(A) समकोण त्रिभुज
(B) अधिक कोण त्रिभुज
(C) समबाहु त्रिभुज
(D) समद्विबाहु त्रिभुज
उत्तर-
(C) समबाहु त्रिभुज

प्रश्न 12.
75° का कोण प्राप्त होता है-
(A) 60° व 90° के समद्विभाजक द्वारा
(B) 60° व 120° के समद्विभाजक द्वारा
(C) 90° व 45° के समद्विभाजक द्वारा
(D) 0° व 90° के समद्विभाजक द्वारा
उत्तर-
(A) 60° व 90° के समद्विभाजक द्वारा

प्रश्न 13.
105° का कोण प्राप्त होता है-
(A) 60° व 90° के समद्विभाजक द्वारा
(B) 60° व 120° के समद्विभाजक द्वारा
(C) 90° व 120° के समद्विभाजक द्वारा
(D) 120° व 0° के समद्विभाजक द्वारा
उत्तर-
(C) 90° व 120° के समद्विभाजक द्वारा

प्रश्न 14.
135° का कोण प्राप्त होता है-
(A) 90° व 180° के समद्विभाजक द्वारा
(B) 90° व 150° के समद्विभाजक द्वारा
(C) 90° व 120° के समद्विभाजक द्वारा
(D) 150° व 180° के समद्विभाजक द्वारा
उत्तर-
(A) 90° व 180° के समद्विभाजक द्वारा

प्रश्न 15.
22\(\frac{1}{2}\)° का कोण प्राप्त किया जा सकता है-
(A) 0° व 30° के समद्विभाजक द्वारा
(B) 0° व 45° के समद्विभाजक द्वारा
(C) 0° व 60° के समद्विभाजक द्वारा
(D) 0° व 90° के समद्विभाजक द्वारा
उत्तर-
(B) 0° व 45° के समद्विभाजक द्वारा

प्रश्न 16.
निम्नलिखित में से कौन-सा कोण सेट-स्क्वायर द्वारा नहीं बनाया जा सकता ?
(A) 30°
(B) 45°
(C) 90°
(D) 75°
उत्तर-
(D) 75°

प्रश्न 17.
किस कोण को समकोण कहा जाता है ?
(A) 0°
(B) 30°
(C) 90°
(D) 180°
उत्तर-
(C) 90°

प्रश्न 18.
निम्नलिखित में से कौन-सा न्यून कोण है ?
(A) 22\(\frac{1}{2}\)°
(B) 90°
(C) 122\(\frac{1}{2}\)°
(D) 182\(\frac{1}{2}\)°
उत्तर-
(A) 22\(\frac{1}{2}\)°

प्रश्न 19.
निम्नलिखित में से कौन-सा अधिक कोण है ?
(A) 22\(\frac{1}{2}\)°
(B) 90°
(C) 122\(\frac{1}{2}\)°
(D) 62\(\frac{1}{2}\)°
उत्तर-
(C) 122\(\frac{1}{2}\)°

प्रश्न 20.
निम्नलिखित में से कौन-सा शून्य कोण है ?
(A) 90°
(B) 45°
(C) 22\(\frac{1}{2}\)°
(D) 0°
उत्तर-
(D) 0°

प्रश्न 21.
60° व 120° के कोणों के बीच के समद्विभाजक से प्राप्त होने वाला कोण होता है-
(A) 90°
(B) 105°
(C) 75°
(D) 67\(\frac{1}{2}\)°
उत्तर-
(A) 90°

प्रश्न 22.
समबाहु त्रिभुज का प्रत्येक कोण होता है-
(A) 30° का
(B) 45° का
(C) 60° का
(D) 90° का
उत्तर-
(C) 60° का

प्रश्न 23.
त्रिभुज के तीनों कोणों का योग होता है-
(A) एक समकोण
(B) दो समकोण
(C) तीन समकोण
(D) चार समकोण
उत्तर-
(B) दो समकोण

प्रश्न 24.
एक त्रिभुज ABC में ∠B = 60° तथा ∠C = 45° है तो ∠A का मान होगा-
(A) 60°
(B) 45°
(C) 75°
(D) 30°
उत्तर-
(C) 75°

प्रश्न 25.
समकोण त्रिभुज में समकोण के सामने की भुजा कहलाती है-
(A) आधार
(B) लम्ब
(C) विकर्ण
(D) कर्ण
उत्तर-
(D) कर्ण

प्रश्न 26.
जिस त्रिभुज में दो भुजाएँ समान हों उसे कहा जाता है-
(A) समद्विबाहु त्रिभुज
(B) विषमबाहु त्रिभुज
(C) समबाहु त्रिभुज
(D) समकोण त्रिभुज
उत्तर-
(A) समद्विबाहु त्रिभुज

प्रश्न 27.
जिस त्रिभुज में तीन भुजाओं की लम्बाइयाँ अलग-अलग हों उसे कहा जाता है-
(A) समद्विबाहु त्रिभुज
(B) विषमबाहु त्रिभुज
(C) समबाहु त्रिभुज
(D) उपरोक्त में से कोई नहीं
उत्तर-
(B) विषमबाहु

प्रश्न 28.
त्रिभुज निम्नलिखित में से कौन-सा त्रिभुज बनाना सम्भव नहीं है ?
(A) दो न्यून कोणों वाला
(B) एक समकोण वाला
(C) दो अधिक कोणों वाला
(D) एक समकोण व दो न्यून कोणों वाला
उत्तर-
(C) दो अधिक कोणों वाला

प्रश्न 29.
एक समकोण त्रिभुज का आधार 12 cm तथा लम्ब 5 cm है। इसका परिमाप होगा-
(A) 30 cm
(B) 25 cm
(C) 17 cm
(D) 18 cm
उत्तर-
(A) 30 cm

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 10 वृत्त

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
सिद्ध करें कि वृत्त की बराबर जीवाएं केंद्र पर बराबर कोण बनाती हैं।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 है तथा दो जीवाएं AB व CD बराबर हैं।
सिद्ध करना है : ∠AOB = ∠COD.

प्रमाण : ∆AOB तथा ∆COD में,
OA = OC [एक वृत्त की त्रिज्याएं]
OB = OD [एक वृत्त की त्रिज्याएं]
AB = CD [दिया है]
अतः ∆AOB ≅ ∆COD [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠AOB = ∠COD [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम]

प्रश्न 2.
सिद्ध करो कि तीन असरेख बिंदुओं से होकर एक और केवल एक वृत्त जाता है।
हल :

दिया है : तीन अंसरेख बिंदु A, B और C हैं।
सिद्ध करना है : बिंदुओं A, B और C से होकर जाने वाला एक और केवल एक ही वृत्त है।
रचना : रेखाखंड AB और BC खींचिए। AB और BC के लंब समद्विभाजक क्रमशः PL और QM खींचिए। क्योंकि AB, BC के समांतर नहीं है, इसलिए PL भी QM के समांतर नहीं होगा। इसलिए वे किसी बिंदु 0 पर प्रतिच्छेद करेंगे। OA, OB और OC को मिलाइए।
प्रमाण : O, AB के लंब समद्विभाजक PL पर स्थित है।
∴ OA = OB ………………(i)
इसी प्रकार, OB = OC ………………(ii)
इसलिए (i) और (ii) से,
OA= OB = OC = r, माना।
त्रिज्या r लेकर और 0 केंद्र मानकर एक वृत्त खींचिए। वह बिंदुओं A, B और C से होकर जाएगा।

इससे यह सिद्ध होता है कि A, B और C से होकर एक वृत्त जाता है। अब हम यह सिद्ध करेंगे कि A, B और C से होकर जाने वाला केवल यही एक वृत्त है। यदि संभव हो, तो मान लीजिए कि A, B और C से जाने वाला दूसरा वृत्त भी है, जिसका केंद्र 0′ और त्रिज्या s है।

तब O’, PL और QM के लंब समद्विभाजक पर अवश्य स्थित होगा। क्योंकि दो रेखाएं एक से अधिक बिंदुओं पर प्रतिच्छेद नहीं कर सकती हैं, अतः O’ और O संपाती होंगे। इसलिए, OA = O’A = r (= s) है। अर्थात A, B और C से जाने वाला एक और केवल एक ही (अद्वितीय) वृत्त है।

प्रश्न 3.
यदि एक वृत्त की दो प्रतिच्छेदी जीवाएं प्रतिच्छेद बिंदु से जाने वाले व्यास से समान कोण बनाएं, तो सिद्ध कीजिए कि वे जीवाएं बराबर हैं।
हल :

दिया है : एक वृत्त, जिसका केंद्र 0 है, की दो जीवाएं AB और CD बिंदु । E पर प्रतिच्छेद करती हैं। E से होकर जाने वाला PQ एक ऐसा व्यास है कि ∠AEQ = ∠DEQ है।
सिद्ध करना है : AB = CD.
रचना : जीवाओं AB और CD पर क्रमशः OL तथा OM लंब खींचिए।
प्रमाण : ∠LOE = 180° – 90° – ∠LEO = 90° – ∠LEO [त्रिभुज के कोणों के योग के कारण]
= 90° – ∠AEQ
= 90° – ∠DEQ [∵ ∠AEQ = ∠DEQ]
= 90° – ∠MEO = ∠MOE
त्रिभुजों OLE तथा ONE में,
∠LEO = ∠MEO [दिया है]
∠LOE = ∠MOE [प्रमाणित]
EO = EO [उभयनिष्ठ]
अतः, ∆OLE ≅ ∆OME [कोण-कोण-भुजा सर्वांगसमता]
इससे प्राप्त होता है- OL = OM [सर्वांगसम त्रिभुजों के संगत भाग]
इसलिए AB = CD [क्योंकि केंद्र से समान दूरी पर स्थित जीवाएं समान होती हैं।]
[इति सिद्धम]

प्रश्न 4.
सिद्ध करो कि एक ही वृत्तखंड के कोण समान होते हैं।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 है तथा ∠ACB और ∠ADB वृत्त के एक ही वृत्तखंड में बने दो कोण हैं।
सिद्ध करना है : ∠ACB = ∠ADB.
रचना : OA और OB को मिलाइए।

प्रमाण : ∠AOB = 2 ∠ACB …………….. (i)
किसी चाप द्वारा वृत्त के केंद्र पर बना कोण शेष भाग पर बने कोण का दुगुना होता है]
और ∠AOB = 2 ∠ADB …………………..(ii)
समीकरण (i) व (ii) से,
∴ 2 ∠ACB = 2 ∠ADB
या ∠ACB = ∠ADB [इति सिद्धम]

प्रश्न 5.
सिद्ध करो कि चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग 180° होता है।
हल :

दिया है : एक चक्रीय चतुर्भुज ABCD है।
सिद्ध करना है : ∠BAD + ∠BCD = 180° तथा
∠ADC + ∠CBA = 180°
रचना : माना कि शीर्षों A, B, C और D से जाने वाले वृत्त का केंद्र 0 है। OB और OD को मिलाइए।
प्रमाण : ∠BAD = \(\frac{1}{2}\) ∠BOD
= \(\frac{1}{2}\) x ………………..(i)
[∵ वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है]
और ∠BCD = \(\frac{1}{2}\)∠BOD = \(\frac{1}{2}\) y ……………. (ii)
[वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है]
समीकरण (i) और (ii) को जोड़ने पर,
∠BAD + ∠BCD = \(\frac{1}{2}\)x + \(\frac{1}{2}\)y
= \(\frac{1}{2}\) (x + y)
= \(\frac{1}{2}\) × 360° = 180° [क्योंकि x + y = 360°]
क्योंकि चतुर्भुज के कोणों का योग 360° होता है।
∠ADC + ∠CBA = 360° – ( ∠BAD + ∠BCD )
= 360° – 180° = 180°
अतः ∠BAD + ∠BCD = 180°
तथा ∠ADC + ∠CBA = 180° [इति सिद्धम]

प्रश्न 6.
आकृति में, ABCD एक चक्रीय चतुर्भुज है, जिसमें AC और BD विकर्ण हैं। यदि ∠DBC = 55° तथा ∠BAC = 45° हो, तो ∠BCD ज्ञात कीजिए।

हल :
अतः,
∠CAD = ∠DBC = 55° (एक वृत्तखंड के कोण)
∠DAB = ∠CAD + ∠BAC
= 55° + 45° = 100°
परन्तु, ∠DAB + ∠BCD = 180° (चक्रीय चतुर्भुज के सम्मुख कोण)
इसलिए, ∠BCD = 180° – 100° = 80°

Multiple choice Questions with Answers:

प्रश्न 1.
किसी तल के उन सभी बिन्दुओं के समूह को क्या कहा जाता है जो तल के एक स्थिर बिन्दु से समान दूरी पर हो-
(A) आयत
(B) वृत्त
(C) वर्ग
(D) समचतुर्भुज
उत्तर-
(B) वृत्त

प्रश्न 2.
वृत्त का केन्द्र वृत्त के ___________ में स्थित होता है।
(A) बहिर्भाग
(B) परिधि
(C) अभ्यन्तर
(D) परिमाप
उत्तर-
(C) अभ्यन्तर

प्रश्न 3.
एक बिन्दु जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो वृत्त के ___________ में स्थित होता है। (A) बहिर्भाग
(B) परिमाप
(C) अभ्यन्तर
(D) वृत्तखण्ड
उत्तर-
(A) बहिर्भाग

प्रश्न 4.
वृत्त की सबसे बड़ी जीवा वृत्त का ___________ होता है।
(A) परिमाप
(B) अर्धव्यास
(C) केन्द्र
(D) व्यास
उत्तर-
(D) व्यास

प्रश्न 5.
एक चाप ___________ होता है, जब इसके सिरे एक व्यास के सिरे हों।
(A) अर्धव्यास
(B) अर्धवृत्त
(C) लघु वृत्तखण्ड
(D) दीर्घ वृत्तखण्ड
उत्तर-
(B) अर्धवृत्त

प्रश्न 6.
वृत्तखण्ड एक चाप तथा ___________ के बीच का भाग होता है।
(A) परिधि
(B) त्रिज्या
(C) जीवा
(D) केन्द्र
उत्तर-
(C) जीवा

प्रश्न 7.
निम्नलिखित में से कौन-सा कथन सत्य है?
(A) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं ।
(B) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है
(C) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है
(D) त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
उत्तर-
(C) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है

प्रश्न 8.
दो वृत्त सर्वांगसम होते हैं, यदि उनकी ___________ बराबर हों।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) चाप
(D) लम्ब रेखाएँ
उत्तर-
(A) त्रिज्याएँ

प्रश्न 9.
सर्वांगसम वृत्तों की बराबर ___________ उनके केन्द्रों पर बराबर कोण अन्तरित करती हैं।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) अर्धव्यास
(D) लम्ब रेखाएँ
उत्तर-
(B) जीवाएँ

प्रश्न 10.
सम्पूर्ण वृत्त की लम्बाई को उसकी ___________ कहा जाता है-
(A) क्षेत्रफल
(B) व्यास
(C) परिधि
(D) आयतन
उत्तर-
(C) परिधि

प्रश्न 11.
एक वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को ___________ करता है।
(A) समत्रिभाजित
(B) समचतुर्भाजित
(C) असमद्विभाजित
(D समद्विभाजित
उत्तर-
(D) समद्विभाजित

प्रश्न 12.
एक वृत्त के केन्द्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर ___________ का कोण बनाती है।
(A) 90°
(B) 120°
(C) 60°
(D) 180°
उत्तर-
(A) 90°

प्रश्न 13.
दो बिन्दुओं से होती हुई कितनी रेखाएँ खींची जा सकती हैं ?
(A) केवल दो
(B) केवल एक
(C) तीन
(D) चार
उत्तर-
(B) केवल एक

प्रश्न 14.
एक बिन्दु से होते हुए कितने वृत्त खींचे जा सकते हैं ?
(A) एक
(B) दो
(C) चार
(D) अनगिनत
उत्तर-
(D) अनगिनत

प्रश्न 15.
तीन असरेखी बिन्दुओं से होता हुआ खींचा जा सकता है-
(A) एक वृत्त
(B) दो वृत्त
(C) कोई वृत्त नहीं
(D) तीन वृत्त
उत्तर-
(A) एक वृत्त

प्रश्न 16.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) एक वृत्त की बराबर जीवाएँ केन्द्र से समान दूरी पर होती हैं
(B) एक वृत्त के केन्द्र से समदूरस्थ जीवाएँ लम्बाई में समान होती हैं
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों

प्रश्न 17.
5 सें०मी० तथा 3 सें०मी० त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सें०मी० है। उभयनिष्ठ जीवा की लम्बाई होगी-

(A) 6 cm
(B) 5 cm
(C) 7 cm
(D) 8 cm
उत्तर-
(A) 6 cm

प्रश्न 18.
संलग्न आकृति में यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र 0 है, A, B, C और D पर प्रतिच्छेद करे तो निम्नलिखित में से कौन-सा कथन सत्य होगा ?

(A) AB = BC
(B) AB = BD
(C) AB = CD
(D) AC = CD
उत्तर-
(C) AB = CD

प्रश्न 19.
एक चाप द्वारा केन्द्र पर अन्तरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का ___________ होता है।
(A) आधा
(B) एक-तिहाई
(C) तीन-गुना
(D) दुगुना
उत्तर-
(D) दुगुना

प्रश्न 20.
आकृति में, वृत्त के छायांकित भाग को कहते हैं-

(A) दीर्घ त्रिज्याखंड
(B) दीर्घ वृत्तखंड
(C) लघु त्रिज्याखंड
(D) लघु वृत्तखंड
उत्तर-
(D) लधु वृत्तखंड

प्रश्न 21.
संलग्न आकृति में ∠x का मान होगा-

(A) 70°
(B) 140°
(C) 35°
(D) 105°
उत्तर-
(C) 35°

प्रश्न 22.
संलग्न आकृति में, तीन बिन्दु A, B और C किसी वृत्त पर इस प्रकार स्थित हैं कि जीवाएं AB और AC केन्द्र 0 पर क्रमशः 90° और 110° के कोण अंतरित करती हैं। ∠BAC का मान होगा-

(A) 90°
(B) 110°
(C) 160°
(D) 80°
उत्तर-
(D) 80°

प्रश्न 23.
संलग्न आकृति में, O वृत्त का केन्द्र हो तो ∠x का मान होगा-

(A) 90°
(B) 45°
(C) 22\(\frac{1}{2}\)°
(D) 135°
उत्तर-
(A) 90°

प्रश्न 24.
संलग्न आकृति में, 0 वृत्त का केन्द्र हो तो ∠x का मान होगा-

(A) 70°
(B) 35°
(C) 171
(D) 105°
उत्तर-
(B) 35°

प्रश्न 25.
चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग ……………… होता है।
(A) 90°
(B) 135°
(C) 180°
(D) 360°
उत्तर-
(C) 180°

प्रश्न 26.
संलग्न आकृति में, O वृत्त का केन्द्र है तो ∠x और ∠y का मान होगा-

(A) ∠x = ∠y = 120°
(B) ∠x = ∠y = 240°
(C) ∠x = ∠y = 480°
(D) ∠x = 120°, ∠y = 240°
उत्तर-
(A) ∠x = ∠y = 120°

प्रश्न 27.
दी गई आकृति में, ABCD एक चक्रीय चतुर्भुज है, जिसमें AC और BD विकर्ण हैं। यदि ∠DBC = 55° तथा ∠BAC = 45° हो, तो ∠BCD का मान होगा-

(A) 100°
(B) 50°
(C) 40°
(D) 80°
उत्तर-
(D) 80°

प्रश्न 28.
संलग्न आकृति में, ∠PQR = 100° है जहाँ P, Q और R केन्द्र 0 वाले एक वृत्त पर स्थित बिन्दु हैं ∠OPR का मान होगा-

(A) 160°
(B) 10°
(C) 20°
(D) 200°
उत्तर-
(B) 10°

प्रश्न 29.
आकृति में, ∠ABC = 69° और ∠ACB = 31° हों, तो ∠BDC का मान होगा-

(A) 100°
(B) 90°
(C) 80°
(D) 110°
उत्तर-
(C) 80°

प्रश्न 30.
संलग्न आकृति में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC का मान होगा-

(A) 45°
(B) 30°
(C) 15°
(D) 50°
उत्तर-
(A) 45°

प्रश्न 31.
संलग्न आकृति में, एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC का मान होगा-

(A) 150°
(B) 110°
(C) 70°
(D) 105°
उत्तर-
(B) 110°

प्रश्न 32.
संलग्न आकृति में, ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD का मान होगा-

(A) 50°
(B) 140°
(C) 100°
(D) 80°
उत्तर-
(D) 80°

प्रश्न 33.
अर्धवृत्त में बना प्रत्येक कोण होता है-
(A) एक समकोण
(B) दो समकोण
(C) अर्ध समकोण
(D) न्यून कोण
उत्तर-
(A) एक समकोण

प्रश्न 34.
वृत्त के दीर्घ वृत्तखण्ड में किसी जीवा द्वारा बना कोण ___________ कोण होता है।
(A) सम
(B) अधिक
(C) न्यून
(D) दो सम
उत्तर-
(C) न्यून

प्रश्न 35.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) एक ही वृत्तखण्ड के कोण बराबर होते हैं
(B) अर्धवृत्त में बना कोण समकोण होता है
(C) चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
एक ही आधार और एक ही समांतर रेखाओं के बीच . स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते है।

हल :
दिया है : दो समांतर चतुर्भुज ABCD और ABEF एक ही आधार AB तथा एक ही समांतर रेखाओं AB तथा FC के मध्य स्थित हैं।
सिद्ध करना है : ar (|| चतुर्भुज ABCD) = ar (|| चतुर्भुज ABEF)
प्रमाण : त्रिभुजो ADF तथा BCE में,
∠AFD = ∠BEC [संगत कोण]
∠ADF = ∠BCF [संगत कोण]
AF = BE [|| चतुर्भुज की सम्मुख भुजा]
∴ ∆ADF ≅ ∆BCE (कोण-कोण-भुजा सर्वांगसमता)
∴ ar (∆ADF) = ar (∆BCE)
दोनों ओर ABED का क्षेत्रफल जोड़ने पर,
ar (∆ADF) + ar (चतुर्भुज ABED) = ar (∆BCE) + ar (चतुर्भुज ABED)
⇒ ar (|| चतुर्भुज ABEF) = ar (|| चतुर्भुज ABCD) [इति सिद्धम]

प्रश्न 2.
एक ही आधार तथा एक ही समांतर रेखाओं के मध्य वाले त्रिभुजों के क्षेत्रफल समान होते हैं।

हल :
दिया है : ABC तथा PBC दो त्रिभुज हैं जो कि एक ही आधार BC तथा समांतर रेखाओं BC तथा AP के मध्य स्थित हैं।
सिद्ध करना है : क्षेत्रफल (∆ABC) = क्षेत्रफल (∆PBC)
रचना : B से, BD || CA खींचे, जोकि D तक बढ़ाई हुई रेखा PA, को प्रतिच्छेद करे तथा C से, CQ || BP खींचे, जो रेखा AP को Q पर प्रतिच्छेद करें।
प्रमाण : यहां पर, BD || CA (रचना से)
तथा BC || DA (दिया है)
∴ BCAD एक समांतर चतुर्भुज है।
इसी प्रकार, BCQP एक समांतर चतुर्भुज है।
अब, समांतर चतुर्भुज BCQP तथा समांतर चतुर्भुज BCAD एक ही आधार BC पर तथा एक ही समांतर रेखाओं के मध्य स्थित हैं।
∴ क्षेत्रफल (समांतर चतुर्भुज BCQP) = क्षेत्रफल (समांतर चतुर्भुज BCAD) ……………(i)
जैसे कि, हम जानते हैं कि समांतर चतुर्भुज के विकर्ण इसको समान क्षेत्रफल वाले दो त्रिभुजों में बांटते हैं।
तथा
क्षेत्रफल (∆PBC) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCQP) ……………(ii)
क्षेत्रफल (∆ABC) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCAD) ……………(iii)
अब,
क्षेत्रफल (समांतर चतुर्भुज BCQP) = क्षेत्रफल (समांतर चतुर्भुज BCAD) [∵ (i) से]
⇒ \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCAD) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCQP)
समीकरण (ii) तथा (iii) से,
⇒ क्षेत्रफल (∆ABC) = क्षेत्रफल (∆PBC) [इति सिद्धम]

प्रश्न 3.
समान क्षेत्रफल तथा समान आधार वाले त्रिभुजों के संगत शीर्षलंब भी समान होते हैं।

हल :
दिया है : दो त्रिभुज ABC तथा DEF इस प्रकार हैं कि
(i) क्षेत्रफल (∆ABC) = क्षेत्रफल (∆DEF)
(ii) AB = DE
दो त्रिभुजों के CL तथा FM क्रमागत AB तथा DE पर संगत शीर्षलंब हैं।
सिद्ध करना है : CL = FM
प्रमाण : ∆ABC में, CL भुजा AB पर संगत शीर्षलंब है।
∴ क्षेत्रफल (∆ABC) = \(\frac{1}{2}\) (AB × CL) इसी प्रकार, …………..(i)
क्षेत्रफल (∆DEF) = \(\frac{1}{2}\) (DE × FM) ……………..(ii)
क्षेत्रफल (∆ABC) = क्षेत्रफल (∆DEF) (दिया है)
⇒ \(\frac{1}{2}\) (AB × CL) = \(\frac{1}{2}\) (DE × FM) [(i) तथा (ii) से]
⇒ AB × CL = DE × FM
⇒ DE × CL = DE × FM [∵ AB = DE (दिया है)]
⇒ CL = FM [इति सिद्धम]

प्रश्न 4.
दर्शाइए कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों मे विभाजित करती है।

हल :
दिया है : ∆ABC में AD उसकी माध्यिका है।
सिद्ध करना है : ar (∆ABD) = ar (∆ACD)
रचना : शीर्ष A से AN ⊥ BC खींचो।
प्रमाण:
ar (ABD) = \(\frac{1}{2}\) × आधार × शीर्षलंब
= \(\frac{1}{2}\) BD × AN
= \(\frac{1}{2}\) × CD × AN (∵ BD = CD)
= \(\frac{1}{2}\) × आधार × शीर्षलंब (∆ACD का)
= ar (∆ACD) [इति सिद्धम]

प्रश्न 5.
दर्शाइए कि समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लंबाइयों के गुणनफल का आधा होता है।
हल :

दिया है : समचतुर्भुज ABCD जिसके विकर्ण AC तथा BD, O पर प्रतिच्छेद करते हैं।
सिद्ध करना है : क्षेत्रफल (समचतुर्भुज ABCD) = =(AC × BD)
प्रमाण : क्योंकि समचतुर्भुज के विकर्ण 90° के कोण पर प्रतिच्छेद करते हैं
अतः OB ⊥ AC व OD ⊥ AC
अब ar (समचतुर्भुज ABCD) = ar (∆ABC) + ar (∆ADC)
= \(\frac{1}{2}\) × (AC × BO) + \(\frac{1}{2}\) (AC × DO)
= \(\frac{1}{2}\) × AC × (BO + DO)
= \(\frac{1}{2}\) × (AC × BD) [इति सिद्धम]

Multiple choice Questions with Answers:

प्रश्न 1.
एक आकृति का _______________ उस आकृति द्वारा घेरे गए तल के भाग से सम्बन्ध (किसी मात्रक में) एक संख्या होती है।
(A) परिमाप
(B) क्षेत्रफल
(C) आयतन
(D) घेरा
उत्तर-
(B) क्षेत्रफल

प्रश्न 2.
समान्तर चतुर्भुज का क्षेत्रफल ज्ञात करने का सूत्र है-
(A) आधार × संगत शीर्षलम्ब .
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब
(C) 2 × आधार × संगत शीर्षलम्ब
(D) \(\frac{1}{3}\) × आधार संगत शीर्षलम्ब
उत्तर-
(A) आधार × संगत शीर्षलम्ब

प्रश्न 3.
निम्नांकित में से किस आकृति में दोनों आकृतियाँ एक ही समान्तर रेखाओं के बीच स्थित नहीं हैं-

उत्तर-
(B)

प्रश्न 4.
एक ही आधार वाले और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज _____________ में बराबर होते हैं।
(A) परिमाप
(B) आयतन
(C) लम्बाई
(D) क्षेत्रफल
उत्तर-
(D) क्षेत्रफल

प्रश्न 5.
एक ही आधार वाले और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुज _____________ में बराबर होते हैं।
(A) परिमाप
(B) आयतन
(C) चौड़ाई
(D) क्षेत्रफल
उत्तर-
(D) क्षेत्रफल

प्रश्न 6.
किसी त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र है-
(A) आधार × संगत शीर्षलम्ब
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब
(C) 2 × आधार × संगत शीर्षलम्ब
(D) \(\frac{1}{3}\) × आधार × संगत शीर्षलम्ब
उत्तर-
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब

प्रश्न 7.
त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले _____________ त्रिभुजों में विभाजित करती है।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(B) दो

प्रश्न 8.
किसी समान्तर चतुर्भुज का आधार और शीर्षलम्ब क्रमशः 16 cm और 8 cm हैं, इसका क्षेत्रफल होगा-
(A) 128 cm²
(B) 128 cm
(C) 64 cm²
(D) 64 cm
उत्तर-
(A) 128 cm²

प्रश्न 9.
आधार 20 cm और शीर्षलम्ब 5 cm वाले समान्तर चतुर्भुज का क्षेत्रफल होगा-
(A) 100 cm
(B) 100 cm²
(C) 50 cm
(D) 50 cm²
उत्तर-
(B) 100 cm²

प्रश्न 10.
उस समान्तर चतुर्भुज का क्षेत्रफल क्या होगा जिसका आधार 28.5 cm और संगत शीर्षलम्ब 10 cm है-
(A) 142.5 cm
(B) 142.5 cm²
(C) 285 cm²
(D) 285 cm³
उत्तर-
(C) 285 cm²

प्रश्न 11.
आधार 124 cm और शीर्षलम्ब 10 dm वाले समान्तर चतुर्भुज का क्षेत्रफल होगा-
(A) 1.24 cm²
(B) 1.24 dm²
(C) 1.24 mm²
(D) 1.24 m²
उत्तर-
(D) 1.24 m²

प्रश्न 12.
उस समान्तर चतुर्भुज का शीर्षलम्ब क्या होगा जिसकी एक भुजा 6.5 cm और क्षेत्रफल 26 cm है ?
(A) 4 cm
(B) 4 cm²
(C) 8 cm
(D) 8 cm²
उत्तर-
(A) 4 cm

प्रश्न 13.
क्षेत्रफल 390 cm² और ऊँचाई 26 cm वाले समान्तर चतुर्भुज का आधार होगा-
(A) 15 cm²
(B) 15 cm
(C) 30 cm²
(D) 30 cm
उत्तर-
(B) 15 cm

प्रश्न 14.
क्षेत्रफल 400 cm² और ऊँचाई 8 cm वाले समान्तर चतुर्भुज का आधार होगा-
(A) 100 cm
(B) 100 cm²
(C) 50 cm
(D) 50 cm²
उत्तर-
(C) 50 cm

प्रश्न 15.
संलग्न आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सें०मी०, AE = 8 सें०मी० और CF = 10 सें०मी० है, तो AD का मान होगा-

(A) 0.64 cm
(B) 6.4 cm
(C) 1.28 cm
(D) 12.8 cm
उत्तर-
(D) 12.8 cm

प्रश्न 16.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हों तो ar (EFGH) = _________ × ar (ABCD)
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) 2
(D) 3
उत्तर-
(A) \(\frac{1}{2}\)

प्रश्न 17.
संलग्न आकृति में-Pऔर Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं तो निम्न में से कौन-सा कथन सत्य होगा ?

(A) ar (APB) = ar (APD)
(B) ar (APB) = ar (BQC)
(C) ar (APB) = ar (BPC)
(D) ar (BQC) = ar (ABQ)
उत्तर-
(B) ar (APB) = ar (BQC)

प्रश्न 18.
समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का ______________.
(A) दो-गुना
(B) तीन-गुना
(C) आधा
(D) एक-तिहाई
उत्तर-
(C) आधा

प्रश्न 19.
समांतर चतुर्भुज ABCD में, AB = 12 सें०मी० हैं। भुजाओं AB तथा AD के संगत शीर्षलंब क्रमशः 6 सें०मी० तथा 8 सें०मी० हैं जैसे कि आकृति में दिखाया गया है। AD का मान होगा-

(A) 6 cm
(B) 8 cm
(C) 12 cm
(D) 9 cm
उत्तर-
(D) 9 cm

प्रश्न 20.
∆ABC में, E माध्यिका AD का मध्य-बिन्दु है तो निम्नलिखित में से कौन-सा कथन सत्य होगा?

(A) ar (BED) = \(\frac{1}{2}\) ar (ABC)
(B) ar (BED) = \(\frac{1}{3}\) ar (ABC)
(C) a (BED) = \(\frac{1}{4}\) ar (ABC)
(D) ar (BED) = \(\frac{1}{5}\) ar (ABC)
उत्तर-
(C) ar (BED) = \(\frac{1}{4}\) ar (ABC)

प्रश्न 21.
समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले ____________ त्रिभुजों में बाँटते हैं।
(A) चार
(B) तीन
(C) दो
(D) आठ
उत्तर-
(A) चार

प्रश्न 22.
संलग्न आकृति में D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। निम्नलिखित में से कौन-सा कथन सत्य है ?

(A) BDEF एक समांतर चतुर्भुज है
(B) ar (DEF) = \(\frac{1}{4}\) ar (ABC)
(C) ar (BDEF) = \(\frac{1}{2}\) ar (ABC)
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 23.
संलग्न आकृति में बिन्दु D और E क्रमशः AABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। निम्नलिखित में से कौन-सा कथन सत्य होगा ?

(A) DE ⊥ BC
(B) DE || BC
(C) DE = BC
(D) DE ⊥ AB
उत्तर-
(B) DE || BC

प्रश्न 24.
किसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, इसका क्षेत्रफल होगा-
(A) 24 cm
(B) 12 cm
(C) 12 cm²
(D) 24 cm²
उत्तर-
(C) 12 cm²

प्रश्न 25.
त्रिभुज की ऊँचाई ज्ञात करने का सूत्र है-

उत्तर-
(B)

प्रश्न 26.
आधार 60 cm और क्षेत्रफल 600 cm² वाले त्रिभुज की ऊँचाई होगी-
(A) 20 cm
(B) 10 cm
(C) 5 cm
(D) 40 cm
उत्तर-
(A) 20 cm

प्रश्न 27.
आधार 80 cm और क्षेत्रफल 0.08 m² वाले त्रिभुज की ऊँचाई होगी-
(A) 10 cm
(B) 20 cm
(C) 10 m
(D) 20 m
उत्तर-
(B) 20 cm

प्रश्न 28.
विकर्णों 80 cm और 60 cm वाले एक समचतुर्भुज का क्षेत्रफल होगा-
(A) 3600 cm²
(B) 9600 cm²
(C) 4800 cm²
(D) 2400 cm²
उत्तर-
(D) 2400 cm²

प्रश्न 29.
त्रिभुज का आधार ज्ञात करने का सूत्र हैक्षेत्रफल

उत्तर-
(B)

प्रश्न 30.
शीर्षलम्ब 10 cm और क्षेत्रफल 0.5 m² वाले त्रिभुज का आधार होगा-
(A) 10 m
(B) 20 m
(C) 10 cm
(D) 20 cm
उत्तर-
(A) 10 m

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 8 चतुर्भुज Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 8 चतुर्भुज

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
सिद्ध कीजिए कि चतुर्भुज के कोणों का योग 360° होता है।

हल :
दिया है : ABCD एक चतुर्भुज है।
सिद्ध करना है : ∠A + ∠B + ∠C + ∠D = 360°
रचना : विकर्ण AC को मिलाओ।
प्रमाण : ∆ABC में,
∠1 + ∠B + ∠3 = 180° [त्रिभुज के कोणों का योग] …………… (i)
∆ACD में,
∠2 + ∠4 + ∠D = 180° [त्रिभुज के कोणों का योग] …………… (ii)
समीकरण (i) व (ii) को जोड़ने पर,
∠1 + ∠2 + ∠B + ∠3 + ∠4 + ∠D = 180° + 180°
[∵ ∠1 + ∠2 = ∠A
तथा ∠3 + ∠4 = ∠D ]
∠A + ∠B + ∠C + ∠D = 360°
अतः चतुर्भुज के कोणों का योग 360° होता है। [इति सिद्धम]

प्रश्न 2.
सिद्ध कीजिए कि किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है।
हल :

दिया है : ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।
सिद्ध करना है : ∆ABC = ∆ADC
प्रमाण : जैसा कि हम जानते हैं कि समांतर चतुर्भुज की सम्मुख भुजाएं समांतर होती हैं।
∆ABC व ∆ADC में,
AC = AC [उभयनिष्ठ]
∠1 = ∠2 [एकांतर कोण]
∠3 = ∠4 [एकांतर कोण]
∴ ∆ABC = ∆ADC [कोण-भुजा-कोण सर्वांगसमता] [इति सिद्धम]

प्रश्न 3.
सिद्ध कीजिए कि किसी समांतर चतुर्भुज की सम्मुख भुजाएं समान होती हैं।
हल :

दिया है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
सिद्ध करना है : AB = DC तथा AD = BC
रचना : A तथा C को मिलाएं।
प्रमाण : ∆ADC तथा ∆CBA में,
∵ ∠DAC = ∠BCA [एकांतर कोण] B
AC = AC [उभयनिष्ठ भुजा]
∠DCA = ∠BAC [एकांतर कोण]
∴ ∆ADC = ∆CBA [कोण-भुजा-कोण सर्वांगसमता]
इस प्रकार,
AB = DC व AD = BC [सर्वांगसम त्रिभुजों के संगत भाग]
अतः समांतर चतुर्भुज की सम्मुख भुजाएं समान होती हैं। [इति सिद्धम]

प्रश्न 4.
सिद्ध कीजिए कि समांतर चतुर्भुज के सम्मुख कोण समान होते हैं।

हल :
दिया है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
सिद्ध करना है : ∠A = ∠C तथा ∠B = ∠D.
प्रमाण : ∵ AB || DC तथा AD इनको प्रतिच्छेद करती है।
∴ ∠A + ∠D = 180° [प्रतिच्छेदी रेखा के एक ही तरफ के आंतरिक कोण] ……………. (i)
अब
∵ AD || BC तथा DC इनको प्रतिच्छेद करती है।
∴ ∠A + ∠C = 180° [प्रतिच्छेदी रेखा के एक ही तरफ के आंतरिक कोण] ……………. (ii)
समीकरण (i) व (ii) से,
∠A + ∠D = ∠D + ∠C
∠A = ∠C
इसी प्रकार, यह सिद्ध किया जा सकता है कि
∠B = ∠D [इति सिद्धम]

प्रश्न 5.
सिद्ध कीजिए कि चतुर्भुज में यदि सम्मुख कोण समान हों वह समांतर चतुर्भुज होता है।

हल :
दिया है : चतुर्भुज ABCD, जिसमें
∠A = ∠C तथा
∠B = ∠D
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
प्रमाण : चतुर्भुज ABCD में,
∠A = ∠C (दिया है)…(i) तथा
∠B = ∠D (दिया है)…(ii) समीकरण (i) व (ii) से, हमें प्राप्त होता है।
∴ ∠A + ∠B = ∠C + ∠D
∵ चतुर्भुज के चारों कोणों का योग 360° होता है।
∵ ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B = ∠C + ∠D = 180°
अब, रेखा AB, AD तथा BC को A तथा B पर प्रतिच्छेद करती है।
तथा ∠A + ∠B = 180° [आसन्न आंतरिक कोण]
∴ AD || BC …………….(iii)
इसी प्रकार, (i) व (ii) से, हमें प्राप्त होता है।
∠A + ∠D = ∠B + ∠C = 180°
रेखा AD, AB तथा CD को A तथा D पर प्रतिच्छेद करती है,
∠A + ∠D = 180° [आसन्न आंतरिक कोण]
∴ AB || DC ……………(iv)
समीकरण (iii) व (iv) से, हमें प्राप्त होता है, चतुर्भुज ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 6.
यदि चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हों, तो वह समांतर चतुर्भुज होता है।

हल :
दिया है : चतुर्भुज ABCD जिसमें विकर्ण AC तथा BD, O पर इस प्रकार प्रतिच्छेद करते हैं कि OA = OC तथा OB = OD
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
प्रमाण : ∆AOD तथा ∆COB में,
OA = OC [दिया है]
∠AOD = ∠COB [शीर्षाभिमुख कोण]
OD = OB [दिया है]
∴ ∆AOD ≅ ∆COB [भुजा-कोण-भुजा सर्वांगसमता]
∴ ∠1 = ∠2 तथा ∠3 = ∠4
[सर्वांगसम त्रिभुजों के संगत भाग]
क्योंकि, यह प्रतिच्छेदी रेखा AC, द्वारा बनाए गए एकांतर कोण हैं, जो कि AD तथा BC को प्रतिच्छेद करती है।
∴ AD || BC ………………(i)
इसी प्रकार, हम सिद्ध कर सकते हैं कि,
AB || DC ………….. (ii)
समीकरण (i) व (ii) से, हमें प्राप्त होता है, चतुर्भुज ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 7.
एक चतुर्भुज समांतर चतुर्भुज होता है यदि उसकी सम्मुख भुजाओं का एक युग्म परस्पर समान तथा समांतर हो।

हल :
दिया है : एक चतुर्भुज ABCD जिसमें, AB || DC तथा AB = DC है।
सिद्ध करना है : ABCD एक समांतर चतुर्भुज है। रचना : A तथा C को मिलाएं।
प्रमाण : AB || DC और तिर्यक रेखा AC उनको प्रतिच्छेद करती है।
∴ ∠BAC = ∠DCA (एकांतर कोण)…(i)
अब, ∆ABC तथा ∆CDA में,
AB = DC (दिया है)
AC = AC (उभयनिष्ठ)
∠BAC = ∠DCA [(i) से]
∴ ∆ABC ≅ ∆CDA [भुजा-कोण-भुजा सर्वांगसमता]
अब, AD तथा BC दो रेखाएं हैं तथा तिर्यक रेखा AC इनको प्रतिच्छेद करती है इसलिए एकांतर कोण ACB तथा कोण CAD समान है।
इस प्रकार,
AD || BC
अब, AB || DC
तथा AD || BC
इसलिए, ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 8.
एक चतुर्भुज के कोण 1 : 2 : 3 : 4 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल :
माना चतुर्भुज के कोण = (1x), (2x), (3x), (4x)
हम जानते हैं कि
चतुर्भुज के कोणों का योग = 360°
x + 2x + 3x + 4x = 360°
10x = 360°
x = \(\frac{360^{\circ}}{10}\) = 36°
अतः चतुर्भुज के कोण = (1 × 36)°, (2 × 36)°, (3 × 36)°, (4 × 36)°
= 36°, 72°, 108°, 144°.

प्रश्न 9.
सिद्ध कीजिए कि एक चतुर्भुज में यदि सम्मुख भुजाएं समान हों तो वह समांतर चतुर्भुज होता है।

हल :
दिया है : चतुर्भुज ABCD जिसमें AB = DC तथा AD = BC हैं।
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
रचना : A तथा C को मिलाएं।
प्रमाण : ∆ABC तथा ∆CDA में,
AB = DC [दिया है]
AD = BC[दिया है]
AC = AC [उभयनिष्ठ]
∆ABC ≅ ∆DAC [भुजा-भुजा-भुजा सर्वांगसमता]
∴ ∠1 = ∠3
तथा ∠2 = ∠4 [सर्वांगसम त्रिभुजों को संगत भाग] …………(i)
अब, रेखा AC, AB तथा CD को A तथा C पर प्रतिच्छेद करती है इसलिए एकांतर आंतरिक कोण
∠2 = ∠4 [जैसे कि समीकरण (i) में सिद्ध किया है]
∴ AB || CD …………..(ii)
इसी प्रकार, रेखा AC, CB तथा AD को C तथा A पर प्रतिच्छेद करती है इसलिए एकांतर आंतरिक कोण
∠1 = ∠3 [जैसे कि समीकरण (i) में सिद्ध किया है]
∴ BC || AD ……………(iii)
समीकरण (ii) व (iii) से, हमें प्राप्त होता है।
ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 10.
सिद्ध कीजिए कि यदि तीन या अधिक रेखाएं दी हों और उनके द्वारा एक तिर्यक रेखा पर बनाए गए अंतः खंड समान हों तो किसी P अन्य तिर्यक रेखा पर संगत अंतः खंड भी समान होते हैं।

हल :
दिया है : l, m, n, तीन समांतर रेखाएं हैं तथा दो तिर्यक रेखाएं AB तथा CD इन्हें क्रमशः P, Q, R तथा S, T, U बिंदुओं पर प्रतिच्छेद करती हैं तथा साथ ही PQ = QR
सिद्ध करना है : ST = TU
रचना : T से AB के समांतर VTW खींचे।
प्रमाण :
PQ || VT (रचना से)
PV || QT (दिया है)
∴ PVTQ एक समांतर चतुर्भुज है।
⇒ PQ = VT …………….(i)
इसी प्रकार, QTWR एक समांतर चतुर्भुज है।
⇒ QR = TW ………….(ii)
क्योंकि, PQ = QR [दिया है]
∴ VT = TW [(1) तथा (ii) से] …………..(iii)
पुनः l, n के समांतर है तथा तिर्यक रेखा CD इनको प्रतिच्छेद करती है।
∴ ∠VST = ∠TUW [∵ एकांतर कोण] ……………(iv)
∆VST तथा ∆WUT में,
VT = TW [(iii) से]
∠VST = ∠TUW [(iv) से]
तथा, ∠VTS = ∠WTU [शीर्षाभिमुख कोण]
∴ ∆VST = ∆WUT [कोण-भुजा-कोण सर्वांगसमता]
इस प्रकार,
ST = UT [सर्वांगसम त्रिभुजों के संगत भाग][इति सिद्धम]

Multiple Chpice Questions with Answers:

प्रश्न 1.
चार रेखाखण्डों से बनी बन्द आकृति को कहा जाता है-
(A) त्रिभुज
(B) चतुर्भुज
(C) पंचभुज
(D) षड्भुज
उत्तर-
(B) चतुर्भुज

प्रश्न 2.
चतुर्भुज के चारों कोणों का योग होता है-
(A) 180°
(B) 270°
(C) 360°
(D) 540°
उत्तर-
(C) 360°

प्रश्न 3.
जिस चतुर्भुज में सम्मुख भुजाओं का केवल एक युग्म समान्तर हो उसे कहा जाता है-
(A) समलम्ब
(B) समान्तर चतुर्भुज
(C) आयत
(D) समचतुर्भुज
उत्तर-
(A) समलम्ब

प्रश्न 4.
किसी समान्तर चतुर्भुज का एक विकर्ण उसे ___________ सर्वांगसम त्रिभुजों में विभाजित करता है।
(A) 4
(B) 3
(C) 1
(D) 2
उत्तर-
(D) 2

प्रश्न 5.
प्रत्येक कोण समकोण नहीं होता है-
(A) आयत का
(B) वर्ग का
(C) त्रिभुज का
(D) घन का
उत्तर-
(C) त्रिभुज का

प्रश्न 6.
एक समान्तर चतुर्भुज में ____________ बराबर होते/होती हैं।
(A) सम्मुख भुजाएँ
(B) संलग्न कोण
(C) संलग्न भुजाएँ
(D) विकर्ण
उत्तर-
(A) सम्मुख भुजाएँ

प्रश्न 7.
किसी समान्तर चतुर्भुज का गुण है-
(A) सम्मुख भुजाएँ बराबर
(B) सम्मुख कोण बराबर
(C) विकर्ण परस्पर समद्विभाजित करने वाले
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 8.
आयत का प्रत्येक कोण ___________ का होता है।
(A) 45°
(B) 90°
(C) 1350
(D) 180°
उत्तर-
(B) 90°

प्रश्न 9.
एक समचतुर्भुज के विकर्ण परस्पर ___________ होते हैं।
(A) लम्ब
(B) समान्तर
(C) बराबर
(D) समान्तर व बराबर
उत्तर-
(A) लम्ब

प्रश्न 10.
एक समान्तर चतुर्भुज के कोणों के समद्विभाजक एक __________ बनाते हैं।
(A) वर्ग
(B) समचतुर्भुज
(C) आयत
(D) त्रिभुज
उत्तर-
(C) आयत

प्रश्न 11.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इसका सबसे छोटा कोण होगा-
(A) 156°
(B) 108°
(C) 60°
(D) 36°
उत्तर-
(D) 36°

प्रश्न 12.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इसका सबसे बड़ा कोण होगा-
(A) 156°
(B) 108°
(C) 60°
(D) 36°
उत्तर-
(A) 156°

प्रश्न 13.
वर्ग का गुण है-
(A) विकर्ण बराबर होते हैं ।
(B) विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों

प्रश्न 14.
आयत का गुण है-
(A) प्रत्येक कोण 90° का होता है
(B) विकर्ण बराबर होते हैं
(C) विकर्ण परस्पर समद्विभाजित करते हैं
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 15.
एक समान्तर चतुर्भुज का एक कोण 60° है इसका आसन्न कोण होगा-
(A) 60°
(B) 120
(C) 90°
(D) 30°
उत्तर-
(B) 120°

प्रश्न 16.
एक समान्तर चतुर्भुज का एक कोण 75° है। इसका सम्मुख कोण होगा-
(A) 75°
(B) 15°
(C) 105°
(D) 285°
उत्तर-
(A)75°

प्रश्न 17.
एक समान्तर चतुर्भुज के दो आसन्न कोण क्रमशः 70° व 110° हैं। अन्य दो कोण होंगे-
(A) 100°, 80°
(B) 105°, 75°
(C) 110°, 70°
(D) 120°, 60°
उत्तर-
(C) 110°, 70°

प्रश्न 18.
एक चतुर्भुज के तीन कोण 70%, 100°, 110° हैं इसका चौथा कोण होगा-
(A) 110°
(B) 100°
(C) 70°
(D) 80°
उत्तर-
(D) 80°

प्रश्न 19.
किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर और उसका __________ होता है।
(A) आधा
(B) एक-चौथाई
(C) एक-तिहाई
(D) दुगुना
उत्तर-
(A) आधा

प्रश्न 20.
किसी त्रिभुज की एक भुजा के मध्य-विन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को __________ करती है।
(A) समत्रिभाजित
(B) समद्विभाजित
(C) समचतुर्भाजित
(D) समद्विभाजित नहीं
उत्तर-
(B) समद्विभाजित

प्रश्न 21.
∆ABC में D, E और Fक्रमशः भुजाओं AB, BC और CA के मध्य-बिन्दु हैं। बताइए बिन्दुओं D, E और F को मिलाने पर ∆ABC _________ सर्वांगसम त्रिभुजों में विभाजित हो जाता है।
(A) दो
(B) तीन
(C) चार
(D) पाँच
उत्तर-
(C) चार

प्रश्न 22.
किसी चतुर्भुज की भुजाओं के मध्य-बिन्दुओं को एक क्रम से मिलाने वाले रेखाखण्डों द्वारा बना चतुर्भुज एक ___________ होता है।
(A) समचतुर्भुज
(B) आयत
(C) वर्ग
(D) समान्तर चतुर्भुज
उत्तर-
(D) समान्तर चतुर्भुज

Haryana State Board HBSE 10th Class Maths Notes Chapter 6 Triangles Notes.

Haryana Board 10th Class Maths Notes Chapter 6 Triangles

Introduction
In earlier classes, we have studied the triangles and their properties. We have also studied, the congruence of two geometric figures, and some basic theorems and results on the congruence of triangles. Recall that two figures are said to be congruent, if they have the same shape and same size.

It this chapter, we shall study about those figures which have same shape but not necessarily the same size. Two figures having the same shape but not necessarily of same size are known as similar figures.

Two congruent figures are always similar, but two similar figures may not be congruent.
All regular polygon of same number of sides such as squares, equilateral triangles, rectangles, etc. are similar. All circles are similar but a square and a triangle cannot be similar. In case of two triangles which may appear to be similar but actually, they may not be similar. So, we apply some criteria to determine the similarity of two polygons. In this chapter, we shall study the similarity of triangles.

• A simple closed curve made up of only line segments is called a polygon.
• A polygon of three sides is called a triangle.
• A median of a triangle is a line joining a vertex to the midpoint of the opposite side.
• If corresponding angles of two triangles are equal, then they are known as equiangular triangles.
• The same ratio of the corresponding sides of two polygons is known as the scale factor or the representative fraction for the polygons.
• The angle bisector of a triangle is a line segment that bisects one of the vertex angle of a triangle.
• The altitude of a triangle is a line that extends from one vertex of a triangle and perpendicular to the opposite side.
• The angle of elevation of the Sun is the angle between the direction of the geometric centre of the sun’s apparent disc and the horizontal level.
• A triangle having any three sides of different lengths is called scalene triangle.
• A triangle having any two sides of same lengths is called isosceles triangle.
• A triangle having all three sides of same lengths is called equilateral triangle.
• A triangle having all three angles acute (less than 90°) is called acute angled triangle.
• A triangle having an angle obtuse (greater than 90°) is called obtuse angled triangle.
• A triangle having an angle of measure 90° is called a right angled triangle or right triangle. The perimeter of a triangle is the sum of all its sides.

Similar Figures
Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
For example : Quadrilateral ABCD and PQRS given below are similar.

We observe that ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R and ∠D = ∠S

Hence, quadrilateral ABCD and PQRS are similar.

Similarity of Triangles
Two triangles are similar, if their
(i) Corresponding angles are equal, and
(ii) Corresponding sides are in the same ratio (or proportion)

For Example: Two triangles ABC and PQR are similar, if
(i) ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R and
(ii) \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}\)
If two trianges ABC and PQR are similar we write ΔABC ~ ΔPQR.
A famous Greek mathematician Thales gave an important truth relating to two equiangular triangles which is as follows:
The ratio of any two corresponding sides in two equiangular trianglen is always the same.

Theorem 6.1:
(Basic Proportionality Theorem OR Thales theorem)
If a line is drawn parallel to one side of a triangle to interveet the other two sides in distinct points, the other two sides are divided in the same ratio.
Given: A triangle ABC in which DE || BC and DE intersects AB and AC at D and E respectively.
To Prove: \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
Construction : Join BE and CD. Draw EN ⊥ AB and DM ⊥ AC.
Proof : Since EN ⊥ AB. Therefore EN is the height of triangles ADE and DBE.
Now area (ΔADE) = \(\frac{1}{2}\) base × height
= \(\frac{1}{2}\) AD × EN
and area (ΔDBE) = \(\frac{1}{2}\) base × height
= \(\frac{1}{2}\) BD × EN


But ΔDBE and ΔDEC are on the same base DE and between the same parallels BC and DE
So, Area (ΔDBE) = Area (ΔDEC) …….(3)
Therefore from (1), (2) and (3), we have
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) Proved.

Theorem 6.2:
[Converse of Thales Theorem]
If a line divides any two sides of a triangle in the same ratio then the line is parallel to the third side.
Or

Or
In the given figure ABC is atriangle. If \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) then prove that DE || BC.

Given: A ΔABC and a line l intersecting AB at D and AC at E, such that
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
To Prove: DE || BC
Proof: If possible, Let DE is not parallel te BC, then there must be another line through D which is parallel to BC. Let DF || BC.
∵ DF || BC. Therefore by Basic proportionality theorem, we have,3

This is possible only when E and F coinside.
Hence, DE || BC. Proved

Some Important Results Related to Basic Proportionality Theorem
(a) The internal bisector of an angle of a triangle divides the opposite wide internally in the ratio of the sides containing the angle.
Given: A triangle ABC in which AD is the internal bisector of ∠A
To Prove: \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
Construction: Draw CP || DA meets BA produced.
Proof: Since CP || DA and AC is a transversal
∠2 = ∠3 …….. (1)
[alternate Interior angles]

CP || DA and BP is a transversal
∠1 = ∠4 …….(2)
[corresponding angles]
But ∠1 = ∠2 …… (3)
[AD bisects the ∠A]
From (1), (2) and (3) we get,
∠3 = ∠4
⇒ AP = AC ……(4)
[sides opposite to equal angles are equal]
Now in ΔBCP, DA || CP
⇒ \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AP}}\)
[By Basic Proportionality Theorem]
⇒ \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) [Using (4)]
Hence \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) Proved.

(b) The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
Given : A ΔABC such that CE is the bisector of exterior ∠C and intersects AB produced at E.
To Prove: \(\frac{\mathrm{AE}}{\mathrm{BE}}=\frac{\mathrm{CA}}{\mathrm{CB}}\)
Construction : Draw BD || EC Intersecting AC at D.
Proof: Since BD || EC and CB is a transversal
[alternate interior angles]
BD || EC and AC is transversal
∠1 = ∠4 ……(2)
[corresponding angles]
But ∠1 = ∵2 …….(3)
[∵ CE is the bisector of exterior ∠C]
From (1), (2) and (3), we get
∠3 = ∠4 …….(4)
⇒ DC = BC …….(4)
[sides opposite to equal angles are equal]

In ΔAEC, BD || EC
\(\frac{\mathrm{AB}}{\mathrm{BE}}=\frac{\mathrm{AD}}{\mathrm{DC}}\)
[By Basic Proportionality Theorem]

Criteria for Similarity of Triangles
We know two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding aides are in the same ratio (or proportion)
e.g., In ΔABC and ΔPQR
(i) ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
(ii) \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CA}}{\mathrm{RP}}\)
Then two triangles are similar.

Now, we shall discuss some important results which show that if three property choosen out of the six conditions are satisfied, then the other three conditions satisfy automatically, and the two triangles are similar.

Theorem 6.3 (AAA Similarity Criterion)
If in two triangles, the corresponding angles are equal, then their corresponding sides are in the same proportional and hence the two triangles are similar.
Given: Two triangles ABC and DEF such that
∠A = ∠D, ∠B = ∠E And ∠C = ∠F

To prove : ΔABC ~ ΔDEF
Construction: Cut DP = AB and DQ = AC. Join PQ
Proof: In ΔABC And ΔDPQ, we have
AB = DP (By construction)
AC = DQ (By construction)
∠A = ∠D (given)
ΔABC ≅ ΔDPQ (by SAS congruence)
⇒ ∠B = ∠P (By CPCT)
⇒ ∠E = ∠B [∵ ∠B = ∠E (given)]
But ∠E and ∠P are corresponding angles.
Therefore, PQ || EP

and ∠A = ∠D, ∠B = ∠E, ∠C = ∠F (given)
Hence ΔABC ~ ΔDEF Hence Proved
Remark: It follows from the above theorem that two triangles are similar ⇔ They are equiangular.

Corollary [AA (angle-angle) similarity criterion]
If two angles of one triangle are respectively equal to two angles of another triangle then the two triangles are similar.
Proof: In triangle ABC and triangle DEF
Let ∠A = ∠D and ∠B = ∠E
We know that sums of 2s of ∠s of triangle is 180°
∴ ∠A + ∠B + ∠C = 180°
and ∠D + ∠E + ∠F = 180°
⇒ ∠A + ∠B + ∠C = ∠D + ∠E + ∠F
⇒ ∠A + ∠B + ∠C = ∠A + ∠B + ∠F
⇒ ∠C = ∠F

Thus, the two triangles are equiangular and hence they are similar.
Remark : AA similarity is the same as AAA similarity.

Theorem 6.4:
[SSS (side-side-side) similarity criterion]
If the corresponding sides of one triangle are proportional to (i.e. in the same ratio) the sides of other triangle, then their corresponding angles are equal and hence the two triangles are similar.
Given: Two triangles ΔABC and ΔDEF such that
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)

To Prove: ΔABC ~ ΔDEF
Construction: Let is take ΔABC and ΔDEF such that
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) (<1)
cut DP = AB and DQ = AC. Join PQ
Proof: \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
\(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}\)
[∵ AB = DP and AC = DQ]
PQ || EF [By converse of BPT]
∠P = ∠E [corresponding angles] …….(1)
and ∠Q = ∠F [corresponding angles] …….(2)
⇒ \(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{PQ}}{\mathrm{EF}}\)
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{PQ}}{\mathrm{EF}}\) ……(3) [∵ DP = AB]
But
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}\) ……(4) (given)
From (3) and (4), we get
\(\frac{\mathrm{PQ}}{\mathrm{EF}}=\frac{\mathrm{BC}}{\mathrm{EF}}\) BC ⇒ BC = PQ
AB = DP and AC = DQ (by construction)
Thus, AB = DP, AC = DQ, BC = PQ
∴ ΔABC ≅ ΔDPQ [By SSS Congruence]
∴ ∠A = ∠D, ∠B = ∠P, ∠C = ∠Q. [By CPCT]
But ∠P = ∠E
and ∠Q = ∠F [From (1) And (2)]
∠A = ∠D, ∠B = ∠E , ∠C = ∠F
Thus, ΔABC ~ ΔDEF
[by AAA Similarity criterion]
Hence Proved

Theorem 6.5:
[SAS (side angle side similarity)]
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
Given: Two triangles ΔABC and ΔDEF such that ∠A = ∠D and \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
To Prove: ΔABC ~ ΔDEF
Construction: Cut DP = AB and DQ = AC. Join PQ.
Proof: In ΔABC and ΔDPQ, we have

AB = DP [by construction]
∠A = ∠D (given)
and AC = DQ [by construction]
∴ ΔABC ≅ ΔDPQ [By SAS congruence]
∠A = ∠D, ∠B = ∠P and ∠C = ∠Q [By CPCT] ……. (1)
Now \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) (given)
\(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}\)
[∵ AB = DP and AC = DQ]
PQ || EF [By converse of BPT]
∠P = ∠E [Corresponding ∠s] …(2)
and ∠Q = ∠F
From (1) and (2), we get
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
Thus ΔABC ~ ΔDEF.
[by AAA Similarity criterion]
Hence Proved
Remark: If two triangles ΔABC and ΔDEF are similar, then
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{AB}+\mathrm{BC}+\mathrm{AC}}{\mathrm{DE}+\mathrm{EF}+\mathrm{DF}}\)
[By ratio and proportion]
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\text { Perimeter of } \triangle \mathrm{ABC}}{\text { Perimeter of } \triangle \mathrm{DEF}}\)

Area of Similar Triangles
In this section, we shall discuss the relationship between the ratio of the areas of two similar triangles and the ratio of their corresponding sides. This is stated as follows.

Theorem 6.6:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: Two triangles ABC and DEF such that ΔABC ~ ΔDEF
To Prove :

Construction : Draw AL ⊥ BC and DM ⊥ EF.

Proof : Since ΔABC ~ ΔDEF, it follows that they are equiangular and their corresponding sides are proportional.
∠A = ∠D, ∠B = ∠E, ∠C = ∠F.
and \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) …..(1)
Thus in ΔALC and ΔDMF.
∠ALC = ∠DMY (each = 90°)
∠C = ∠F (given)
∴ ΔALC ~ ΔDMF (By AA similarity criterion)
⇒ \(\frac{A L}{D M}=\frac{A C}{D F}\)
[Corresponding sides of two similar Δs proportional] …..(2)
From (1) and (2), we get

Therefore, from (4) and (5), we get

Hence Proved

Remark: According to theorem 6.6. we shall prove that areas of two similar triangles are in the ratio of the squares of the corresponding
(i) Altitudes (ii) Medians (iii) Angle bisectors.
(i) Given : ΔABC ~ ΔDEF
AM ⊥ BC and DN ⊥ EF.


Proof: In ΔAMC and ΔDNP
∠AMC = ∠DNF [each = 90°]
∠C = ∠F [∵ ΔABC ~ ΔDEF]
ΔAMC ~ ΔDNF [By AA similarity criterion]
\(\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{AM}}{\mathrm{DN}}\)
[Corresponding sides of similar Δs are proportional] …..(1)

Hence Proved

(ii) Given: AX and DY are the median a to side BC and EF respectively.
To Prove :

Proof : ΔABC ~ ΔDEF (given)
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
(corresponding sides of similar Δs are proportional)

(iii) Given ΔABC ~ ΔDEF and AM is the bisector of ∠A and DN is the bisector of ∠D

To Prove:

Proof: ∵ ΔABC ~ ΔDEF
∴ ∠A = ∠D
[Corresponding ∠s of similar Δs are equal]
⇒ \(\frac{1}{2}\)∠A = \(\frac{1}{2}\)∠D
⇒ ∠CAM = ∠FDN
[∵ AM is the bisector of ∠A and DN is the bisector of ∠D]
Now, in ΔAMC and ΔDNF
∠C = ∠F [∵ ΔABC ~ ΔDEF]
and ∠CAM = ∠FDN [Proved above]
∴ ΔAMC ~ ΔDNF
[By AA similarity criterion]
\(\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{AM}}{\mathrm{DN}}\) …..(1)

Hence Proved

Pythagoras Theorem
We have study about Pythagoras theorem in previous classes. We shall prove this theorem using the concept of similarity of triangles. We shall use an important result related to similarity of two triangles formed by the perpendicular to the hypotenuse drawn from the opposite vertex to the hypotenuse of a right triangle. This is stated as follows:

Theorem 6.7:
If perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenune then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
Given: Aright ΔABC right angled at ∠B and BD ⊥ AC.
To Prove: (i) ΔADB ~ ΔABC (ii) ΔBDC ~ ΔABC (III) ΔADB ~ ΔBDC
Proof: (i) In ΔADB and ΔABC,
∠ADB = ∠ABC (∵ ∠B = 90° and BD ⊥ AC)
∠A = ∠A (common)
ΔADB ~ ΔABC
[By AA similarity criterian] … (1)
Hence Proved

(ii) In ΔBDC and ΔABC
∠BDC = ∠ABC (each is 90°)
∠C = ∠C (common)
ΔBDC ~ ΔABC ……(2) [By AA similarity criterion]
Hence Proved

(iii) From (1) and (2), we get
ΔADB ~ ΔBDC. Hence Proved
A very important property of a right triangle was given by a Greek mathematician Phythagoras more than 2000 years ago, which is called the Pythagoras theorem. Thus is stated as follows:

Theorem 6.8:
In a right triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: A right triangle ΔABC right angled at B.
To Prove (Hypotenuse)² = (Base)² + (Perpendicular)²
i.e., AC² = AB² + BC²
Construction : Draw BD ⊥ AC.
Proof: ΔADB ~ ΔABC [By theorem 6.7]
⇒ \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
[Corresponding sides of similar Δs are proportional]
⇒ AD × AC = AB² …….(1)
and ΔBDC ~ ΔABC [By theorem 6.7]

⇒ \(\frac{C D}{B C}=\frac{B C}{A C}\)
Corresponding sides of similar Δs are proportional]
⇒ CD × AC = BC² …..(2)
Adding equations (1) and (2), we get
AD × AC + CD × AC = AB² + BC²
⇒ AC(AD + CD) = AB² + BC²
⇒ AC × AC = AB² + BC²
⇒ AC² = AB² + BC²
Hence Proved
This theorem was given by an ancient Indian mathematician Baudhayan about (800 BC) in the following form:
The diagonal of a rectangle produces by itself the same area as produced by its both sides (i.e., length and breadth)
For this reason this theorem is sometimes also referred to as Baudhayan theorem.

Theorem 6.9:
[Converse of Pythagoras theorem]
In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Given: A ΔABC such that AC² + AB² + BC²
To Prove: ∠B = 90°
Construction : Construct a ΔDEF such that DE = AB, EF = BC and ∠E = 90°
Proof: In ΔDEP, ∠E = 90°

So, by the Pythagoras theorem, we have
DF² = DE² + EF²
DF² = AB² + BC² ……(1)
[By construction, DE = AB, EF = BC]
But, AC² = AB² + BC² ……(2) (given)
From (1) and (2) we get
DF² = AC²
⇒ DF = AC ……(3)
Thus, in ΔABC and ΔDEF
AB = DE [By construction]
BC = EF [By construction]
AC = DF [From (3)]
ΔABC ≅ ΔDEF
[By SSS congruente criterian]
⇒ ∠B = ∠E [By CPCT]
⇒ ∠B = ∠E = 90° [∵ ∠E = 90°]
Hence Proved

Some Results related to Pythagoras Theorem
(1) If ΔABC is an abtuse Δ, obtuse angled at B and AD ⊥ CB (Produced), Prove that AC² = AB² + BC² + 2BC × BD.
Given: An obtuse ΔABC in which ∠ABC > 90° and AD ⊥ CB (Produced)
To Prove: AC² = AB² + EC² + 2BC × BD
Proof : In ΔADB, ∠ADB = 90°
∴ AB² = AD² + BD² …….(i)
[By Pythagoras theorem]

Again In ΔADC, ∠ADC = 90°
∴ AC² = AD² + CD²
[By Pythagoras theorem]
⇒ AC² = AD² + (BC + BD)²
⇒ AC² = AD² + BC² + BD² + 2BC ×BD
⇒ AC² = (AD² + BD²) + BC² + 2BC × BD
⇒ AC² = AB² + BC² + 2BC × BD [Using (i)]
Hence Proved

(2) In a ΔABC, ∠B is an acute angle and AD ⊥ BC, Prove that
AC² = AB² + BC² – 2BC × BD.
Given: A ΔABC in which ∠B < 90° and AD ⊥ BC
To Prove: AC² = AB² + BC² – 2BC × BD
Proof: In ΔADB, ∠ADB = 90
∴ AB² = AD² + BD²
[By Pythagoras theorem]
In ΔADC, ∠ADC = 90° …..(i)

∴ AC² = AD² + CD² …..(ii)
[By Pythagoras theorem]
⇒ AC² = AD² + [BC – BD]²
⇒ AC² = AD² + BC² + BD² – 2BC × BD
⇒ AC² = (AD² + BD²) + BC² – 2BC× BD
⇒ AC² = AB² + BC² – 2BC × BD [Using (1)]
Hence Proved

(3) Prove that in any triangle them of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side.
Glven: A triangle ABC in which AD is median
To Prove : AB² + AC² = 2AD² + 2(\(\frac{1}{2}\)BC)²

Or AB² + AC² = 2AD² + 2BD²
⇒ AB² + AC² = 2(AD² + BD²)
Construction : Draw AM ⊥ BC
Proof: In ΔAMD, ∠AMD – 90°
∴ ∠ADM < 90°
∴ ∠ADB > 90° and AM ⊥ BD produced
∴ AB² = AD² + BD² + 2BD × DM ……(i) [By Result (1)]
In ΔADC, ∠ADC < 90° and AM ⊥ CD
∴ AC² = AD² + CD² – 2CD × DM [By Result (2)]
AC² = AD² + BD² – 2BD × DM ……(ii) [CD = BD]
Addding (i) and (ii), we get
AB² + AC² = AD² + BD² + 2BD × DM + AD² + BD² – 2BD × DM.
⇒ AB² + AC² = 2AD² + 2BD²,
OR, AB² + AC² = 2AD² + 2(\(\frac{1}{2}\)BC)²
[∵ BD = \(\frac{1}{2}\)BC]
Hence Proved

(4) Prove that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
Given: A triangle ABC in which AD, BE and CF are three medi
To Prove: 3(AB²+ BC² + CA²) = 4(AD² + BE² + CF²)

Proof: In ΔABC, AD is the median
AB² + AC² = 2(AD² + BD²) [By Result (3)]
⇒ AB² + AC² = 2AD² + \(\frac{1}{2}\)BC²
⇒ AB² + AC² = 2AD² + \(\frac{1}{2}\)BC
⇒ 2AB² + 2AC² = 4AD² + BC² ….(i)
Similarly in ΔABC, BE and CF are the mediana, we get
2AB² + 2BC² = 4BE² + AC² ……(ii)
and 2AC² + 2BC² = 4CF² + AB² ……(iii)
Adding (i), (ii) and (iii), we get
4AB² + 4BC² + 4AC² = 4AD² + 4BE² + 4CF² + BC² + AC² + AB²
3AB² + 3BC² + 3AC² = 4AD² + 4CF²
3(AB² + BC² + AC²) = 4(AD² + BE² + CF²)
Hence Proved.

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 7 त्रिभुज Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 7 त्रिभुज

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
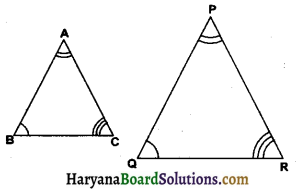
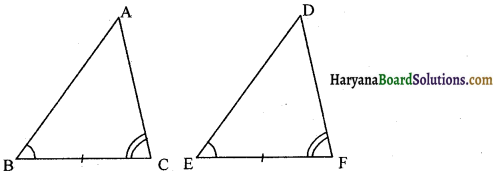
सिद्ध करें कि दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हो।
हल :
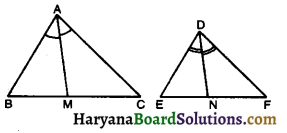
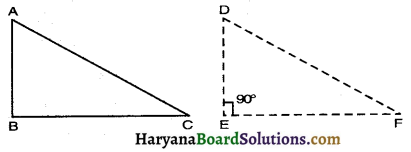
दिया है : दो त्रिभुज ABC और DEF में ∠B = ∠E, ∠C = ∠F तथा BC = EF.
सिद्ध करना है : ∆ABC ≅ ∆DEE.
प्रमाण : स्थिति (1) : जब AB = DE हो तो ∆ABC और ∆DEF में
AB = DE [माना]
∠B = ∠E [दिया है]
BC = EF [दिया है]
अतः ∆ABC ≅ ∆DEF [SAS नियम द्वारा]

स्थिति (ii) : जब AB > DE हो तो AB पर एक बिंदु P ऐसा ले कि PB = DE हो।

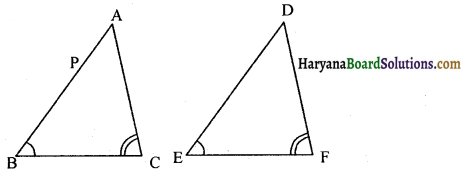
अब ∆PBC और ∆DEF में,
PB = DE [रचना से]
∠B = ∠E [दिया है]
BC = EF [दिया है]
अतः
∆PBC = ∆DEF [SAS सर्वांगसमता अभिगृहीत द्वारा]
चूँकि दोनों त्रिभुज सर्वांगसम हैं, इसलिए इनके संगत भाग बराबर होने चाहिएँ। अतः
अतः ∠PCB = ∠DFE
परंतु हमें दिया है कि
∠ACB = ∠DFE
अतः ∠ACB = ∠PCB
परंतु यह तभी संभव है, जब P बिंदु A के साथ संपाती हो।
BA = ED
अतः ∆ABC = ∆DEF [SAS अभिगृहीत द्वारा]

स्थिति (iii) :
जब AB < DE हो तो DE पर एक बिंदु M इस प्रकार ले सकते हैं कि ME = AB हो अब स्थिति (ii) को दोहराते हुए हम सिद्ध कर सकते हैं। AB = DE
∴ ∆ABC ≅ ∆DEF [इति सिद्धम]

प्रश्न 2.
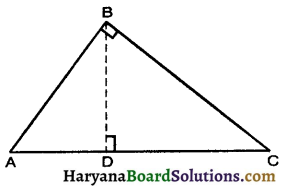
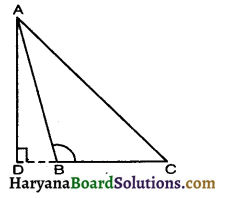
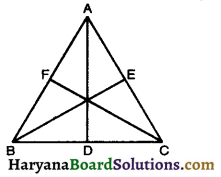
∆ABC में, ∠A का समद्विभाजक AD, भुजा BC पर लंब है, दर्शाइए कि AB = AC है और ∆ARC एक समद्विबाहु त्रिभुज है।
हल:

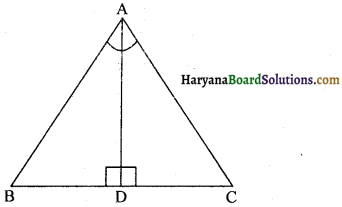
दिया है : ∆ABC में ∠A का समद्विभाजक AD, भुजा BC पर लंब है
अर्थात् AD ⊥ BC.
सिद्ध करना है : ∆ABC एक समद्विबाहु त्रिभुज है।
प्रमाण : ∆ABD और ∆ACD में
∠BAD = ∠CAD [दिया है]
AD = AD [उभयनिष्ठ]
∠ADB = ∠ADC [प्रत्येक 90°]
∴ ∆ABD = ∆ACD [ASA नियम से]
AB = AC [सर्वांगसम त्रिभुजों के संगत भाग]
अतः ∆ABC एक समद्विबाहु त्रिभुज है। [इति सिद्धम]

प्रश्न 3.
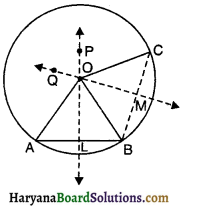
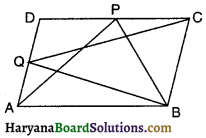
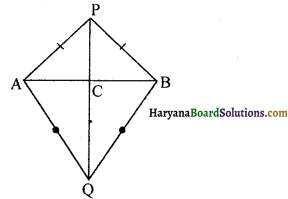
AB एक रेखाखंड है तथा बिंदु Pऔर Q इस रेखाखंड AB के विपरीत ओर इस प्रकार स्थित है कि इनमें से प्रत्येक A और B से समदूरस्थ है (आकृति अनुसार)। दर्शाइए कि रेखा PQ रेखाखंड AB का लंब समद्विभाजक है।

हल :
दिया है : AB एक रेखाखंड है तथा बिंदु P और Q रेखाखंड AB के विपरीत ओर इस प्रकार हैं कि PA = PB तथा QA = QB.
सिद्ध करना है : PQ ⊥ AB तथा PQ रेखाखंड AB को समद्विभाजित करती है।
रचना : माना रेखा PQ रेखाखंड AB को C पर प्रतिच्छेद करती है।
प्रमाण : ∆PAQ और ∆PBQ में,
AP = BP [दिया है]
AQ = BQ [दिया है]
PQ = PQ [उभयनिष्ठ]
अतः ∆PAQ = ∆PBQ [SSS नियम से]
इसलिए ∠APQ = ∠BPQ [सर्वांगसम त्रिभुजों के संगत भाग]
अतः ∆PAC और ∆PBC में, AP = BP [दिया है]
अतः ∠APC = ∠BPC [∠APQ = ∠BPQ प्रमाणित]
PC = PC [उभयनिष्का]
अतः ∆PAC ≅ ∆PBC [SAS नियम से]
इसलिए AC = BC [सर्वांगसम त्रिभुजों के संगत भाग] ……………..(1)
और ∠ACP = ∠BCP (सर्वांगसम त्रिभुजों के संगत भाग)
परंतु ∠ACP + ∠BCP = 180° (रैखिक युग्म]
इसलिए 2 ∠ACP = 180° ∠ACP = 90° ……………..(2)
समीकरण (1) व (2) से रेखा PQ रेखाखंड AB का लंब समद्विभाजक है।

प्रश्न 4.
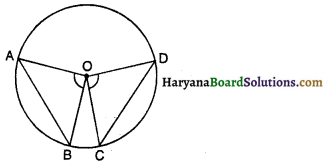
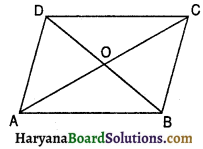
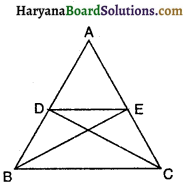
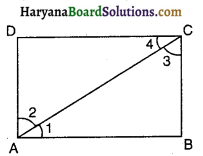
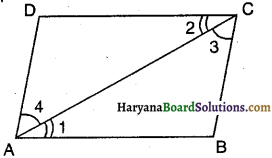
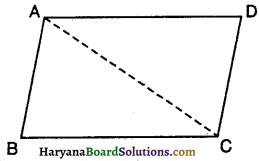
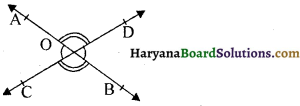
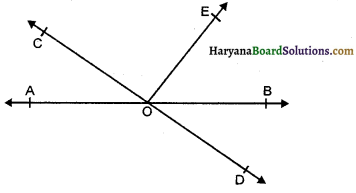
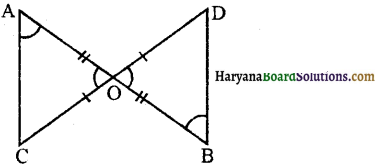
आकृति में, AB तथा CD का मध्य बिंदू 0 है सिद्ध करें कि AC = BD तथा AC || BD.

हल :
∆OAC तथा ∆OBD में, OA = OB [दिया है]
∠AOC = ∠BOD [शीर्षाभिमुख कोण]
OC = OD [दिया है]
∴ ∆OAC ≅ ∆OBD [भुजा-कोण-भुजा सर्वांगसमता से]
⇒ AC = BD तथा ∠OAC = ∠OBD [सर्वांगसम त्रिभुजों के संगत भाग]
परंतु ∠OAC और ∠OBD एकांतर कोण हैं।
∴ AC || BD
अतः AC = BD तथा AC || BD [इति सिद्धम|

प्रश्न 5.
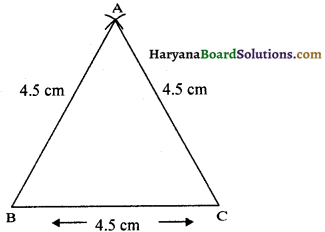
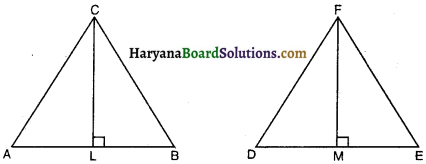
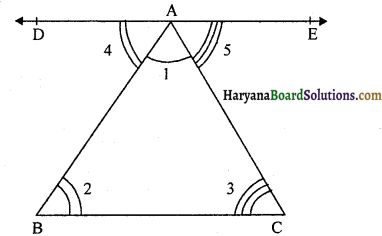
सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
हल :
दिया है : एक समद्विबाहु त्रिभुज ABC है जिसमें AB = AC है।

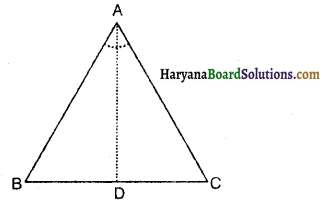
सिद्ध करना है : ∠B = ∠C
रचना : ∠A का समद्विभाजक खींचे, जो BC से D पर मिलता है।
प्रमाण : ∆BAD और ∆CAD में, AB = AC (दिया है)
∠BAD = ∠CAD (रचना से) AD = AD (उभयनिष्ठ)
अतः ∆BAD = ∆CAD (भुजा-कोण-भुजा सर्वांगसमता नियम)
इसलिए ∠ABD = ∠ACD (CPCT)
अर्थात् ∠B = ∠C (इति सिद्धम)

प्रश्न 6.
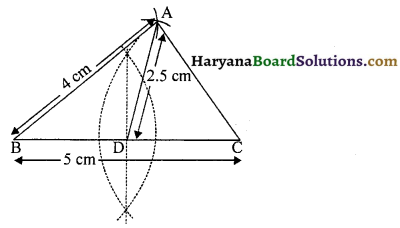
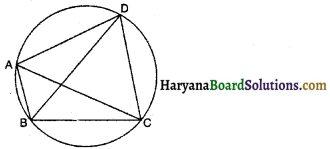
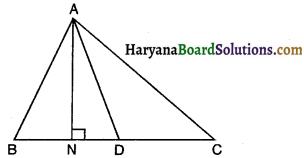
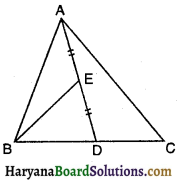
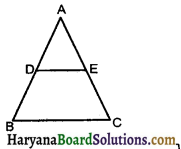
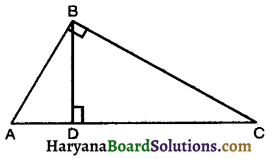
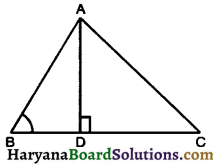
∆ABC की भुजा BC पर D एक ऐसा बिंदु है कि AD = AC है (देखिए आकृति)। दर्शाइए कि AB >AD है।

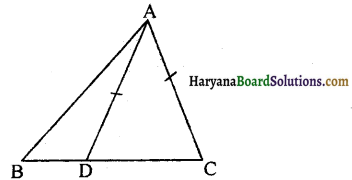
हल :
∆DAC में,
AD = AC [दिया है]
इसलिए ∠ADC = ∠ACD ……………(1)
[बराबर भुजाओं के सम्मुख कोण]
क्योंकि, ∠ADC त्रिभुज ABD का एक बहिष्कोण है।
इसलिए
∠ADC > ∠ABD
या ∠ACD > ∠ABD [समीकरण (1) से]
या ∠ACB > ∠ABC
AB > AC [∆ABC में बड़े कोण की सम्मुख भुजा]
या AB > AD [AD = AC]

प्रश्न 7.
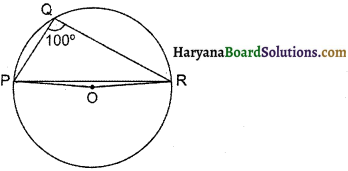
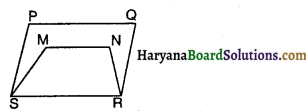
PQR एक समद्विबाहु त्रिभुज है जिसमें PQ = PR तथा भुजा QP को बिंदु S तक इस प्रकार बढ़ाया गया है कि PQ = PS (आकृति अनुसार)। सिद्ध करें कि ∠QRS एक समकोण है।

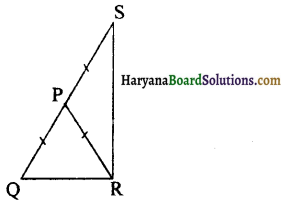
हल :
यहाँ पर
PQ = PR [दिया है]
∴ ∠PRQ = ∠PQR …………..(1)
[समान भुजाओं के सम्मुख कोण]
इसी प्रकार
PQ = PS [दिया है]
∴ PR = PS [∵ PQ = PR]
अतः ∠PRS = ∠PSR …………….(2)
[समान भुजाओं के सम्मुख कोण]
समीकरण (1) व (2) से
∠PRQ + ∠PRS = ∠PQR + ∠PSR
∠QRS = ∠PQR + ∠PSR …………..(3)
परंतु ∠QRS + ∠PQR + ∠PSR = 180° [त्रिभुज के कोणों का योग]
∠QRS + ∠QRS = 180° [समीकरण (3) से]
2 ∠QRS = 180°
∠QRS = \(\frac{180^{\circ}}{2}\) = 90°
अतः ∠QRS एक समकोण है।

Multiple Choice Questions with Answers:

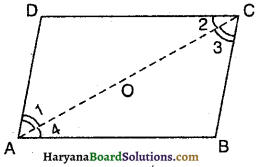
प्रश्न 1.
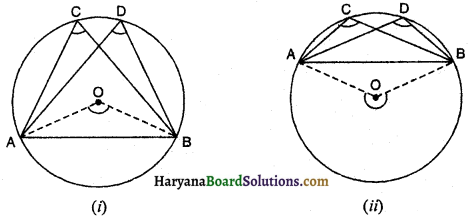
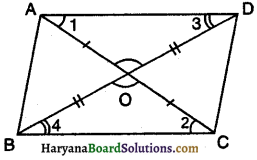
आकृति में, OA = OB और OD = OC है, तो ∆AOD ≅ ∆BOC किस नियम पर आधारित है ? \

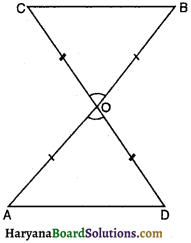
(A) भुजा-कोण-भुजा सर्वांगसमता
(B) कोण-भुजा-कोण सर्वांगसमता
(C) भुजा-भुजा-भुजा सर्वांगसमता
(D) समकोण-कर्ण-भुजा सर्वांगसमता
उत्तर-
(A) भुजा-कोण-भुजा सर्वांगसमता

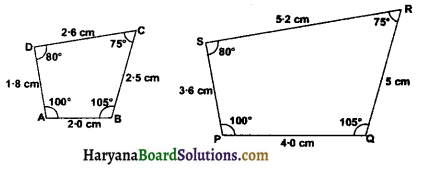
प्रश्न 2.
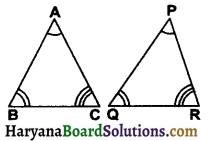
क्या आकृति में, ∆ABC और ∆PQR सर्वांगसम है ?

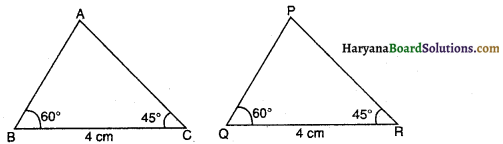
(A) नहीं
(B) हाँ, कोण-भुजा-कोण सर्वांगसमता से
(C) हाँ, भुजा-कोण-भुजा सर्वांगसमता
(D) हाँ, भुजा-भुजा-भुजा सर्वांगसमता से
उत्तर-
(B) हाँ, कोण-भुजा-कोण सर्वांगसमता से

प्रश्न 3.
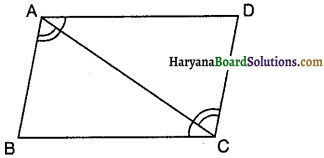
चतुर्भुज ∆CBD में, AC = AD है और AB कोण A को समद्विभाजित करता है, तो ∆ABC = ∆ABD क्योंकि

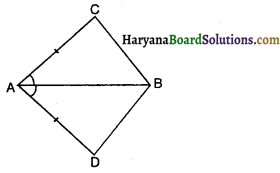
(A) AC = AD है
(B) AB = AB है
(C) ∠BAC = ∠BAD है
(D) उपरोक्त सभी हैं
उत्तर-
(D) उपरोक्त सभी हैं

प्रश्न 4.
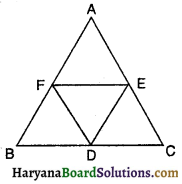
एक समकोण त्रिभुज की भुजाओं के मध्य-बिंदुओं को मिलाने से निर्मित त्रिभुज _____________ होता है।
(A) समकोण त्रिभुज
(B) समबाहु त्रिभुज
(C) अधिक कोण त्रिभुज
(D) समद्विबाहु त्रिभुज
उत्तर-
(A) समकोण त्रिभुज

प्रश्न 5.
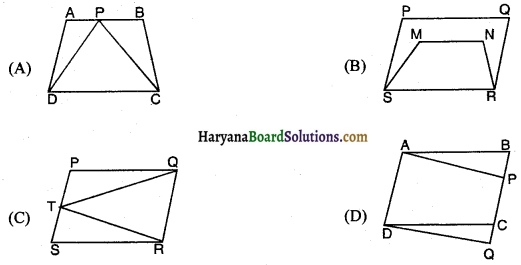
एक चतुर्भुज की क्रमागत भुजाओं के मध्य-बिंदु को मिलाकर बनाई गई आकृति ___________ होती है।
(A) समचतुर्भुज
(B) वर्ग
(C) समांतर चतुर्भुज
(D) आयत
उत्तर-
(C) समांतर चतुर्भुज

प्रश्न 6.
त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के ___________ तथा उसका ___________ होता है।
(A) असमांतर, दुगुना
(B) समांतर, आधा
(C) समांतर, दुगुना
(D) असमांतर, आधा
उत्तर-
(B) समांतर, आधा

प्रश्न 7.
समकोण त्रिभुज में अन्य दो कोणों में से प्रत्येक होता है-
(A) अधिक कोण
(B) न्यून कोण
(C) समकोण
(D) शून्य कोण
उत्तर-
(B) न्यून कोण

प्रश्न 8.
यदि किसी त्रिभुज की दो भुजाएँ समान ना हों, तो बड़ी भुजा का सम्मुख कोण ____________ होता है।
(A) बराबर
(B) छोटा
(C) बड़ा
(D) (A) और (B) दोनों
उत्तर-
(C) बड़ा

प्रश्न 9.
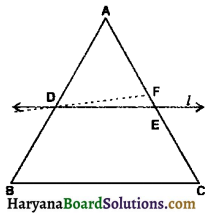
रेखा l कोण A को समद्विभाजित करती है और B रेखा । पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं, तो निम्नलिखित में से कौन-सा कथन असत्य है ?

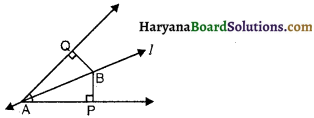
(A) BP = BQ
(B) ∆APB = ∆AQB
(C) AB = AP
(D) ∠AQB = ∠APB
उत्तर-
(C) AB = AP

प्रश्न 10.
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है, तो BC = DE है क्योंकि-

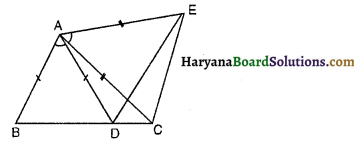
(A) ∆BAC = ∆DAE
(B) ∆ABD = ∆AEC
(C) ∆BAC = ∆ABD
(D) ∆DAE = ∆AEC
उत्तर-
(A) ∆BAC = ∆DAE

प्रश्न 11.
किसी APQR में निम्नलिखित में से कौन-सा कथन सत्य होगा ?
(A) PQ + QR < RP
(B) QR + RP < PQ (C) RP + PQ > QR
(D) RP + PQ < QR उत्तर- (C) RP + PQ > QR

प्रश्न 12.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) त्रिभुज के तीन कोणों का योग 180° होता है
(B) चतुर्भुज के चार कोणों का योग तीन समकोण होता है
(C) त्रिभुज में दो समकोण बन सकते हैं
(D) त्रिभुज में दो अधिक कोण हो सकते हैं
उत्तर-
(A) त्रिभुज के तीन कोणों का योग 180° होता है

प्रश्न 13.
जिस त्रिभुज की दो भुजाएँ समान हों, उसे कहा जाता है-
(A) समबाहु त्रिभुज
(B) समद्विबाहु त्रिभुज
(C) विषमबाहु त्रिभुज
(D) समकोण त्रिभुज
उत्तर-
(B) समद्विबाहु त्रिभुज

प्रश्न 14.
जिस त्रिभुज का एक कोण 90° हो, उसे कहा जाता है-
(A) समकोण त्रिभुज
(B) समबाहु त्रिभुज
(C) समद्विबाहु त्रिभुज
(D) विषमबाहु त्रिभुज
उत्तर-
(A) समकोण त्रिभुज

प्रश्न 15.
निम्नलिखित में से कौन-से कोणों वाली त्रिभुज संभव नहीं है ?
(A) तीनों न्यून कोण हों
(B) एक समकोण व दो न्यून कोण हों
(C) तीनों अधिक कोण हों।
(D) तीनों समान कोण 60° के हों
उत्तर-
(C) तीनों अधिक कोण हों

प्रश्न 16.
त्रिभुज ABC में, AB = AC = 5cm है तथा ∠C = 50° हो, तो ∠A का मान होगा-

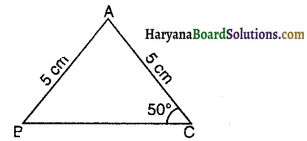
(A) 50°
(B) 80°
(C) 40°
(D) 90°
उत्तर-
(B) 80°

प्रश्न 17.
∆PQR में, यदि ∠QPR = ∠PRQ = 50° हो, तो निम्नलिखित में से कौन-सा कथन सत्य है ?

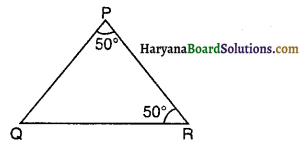
(A) PQ = QR
(B) QR = RP
(C) PQ = RP
(D) इनमें से कोई नहीं
उत्तर-
(A) PQ = QR

प्रश्न 18.
∆ABC एक समकोण त्रिभुज है जिसमें ∠A = 90° है और AB = AC है, तो ∠B = ∠C होगा-
(A) 30°
(B) 45°
(C) 60°
(D) 90°
उत्तर-
(B) 45°

प्रश्न 19.
किसी समबाहु त्रिभुज का प्रत्येक कोण होता है-
(A) 60° का
(B) 45° का
(C) 30° का
(D) 90° का
उत्तर-
(A) 60° का

प्रश्न 20.
निम्नलिखित में से कौन-से कोणों वाली त्रिभुज संभव है ?
(A) 120°, 30°, 50°
(B) 120°, 30°, 30°
(C) 90°, 45°, 60°
(D) 60°, 65°, 70°
उत्तर-
(B) 120°, 30°, 30°

प्रश्न 21.
आकृति में, ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है, तो ∠BCD का मान होगा-

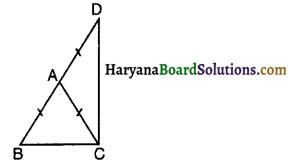
(A) 45°
(B) 90°
(C) 135°
(D) 180°
उत्तर-
(B) 90°

प्रश्न 22.
आकृति में, ∆ABC और ∆PQR किस सर्वांगसमता के अंतर्गत सर्वांगसम है ?

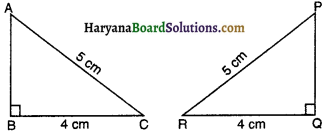
(A) भुजा-भुजा-भुजा सर्वांगसमता
(B) भुजा-कोण-भुजा सर्वांगसमता
(C) कोण-भुजा-कोण सर्वांगसमता
(D) समकोण-कर्ण-भुजा सर्वांगसमता
उत्तर-
(D) समकोण-कर्ण-भुजा सर्वांगसमता

प्रश्न 23.
∆ABC = ∆PQR है यदि ∆ABC में AB = 4 cm, ∠B = 60°, BC = 5 cm हो और ∆PQR में, PQ = 4 cm, ∠Q = 60° हो, तो QR का मान होगा-
(A) 4 cm
(B) 5 cm
(C) 1 cm
(D) 9 cm
उत्तर-
(B) 5 cm

प्रश्न 24.
यदि ∆ABC ≅ ∆PQR हो, तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) AB = PQ
(B) BC = QR
(C) CA = RP
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 25.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलंब है, जिसमें AB = AC है। निम्नलिखित में से कौन-सा कथन असत्य है ?
(A) AD रेखाखंड BC को समद्विभाजित करता है
(B) AD कोण A को समद्विभाजित करता है
(C) (A) व (B) दोनों सत्य हैं
(D) (A) व (B) दोनों असत्य हैं
उत्तर-
(D) (A) व (B) दोनों असत्य हैं

प्रश्न 26.
एक त्रिभुज ABC सर्वांगसम है ∆PQR के। यदि AABC में ∠A = 90°, कर्ण BC = 5 cm तथा भुजा AC = 4 cm तथा ∆ PQR में ∠P = 90° तथा भुजा PR = 4 cm हो, तो कर्ण QR का मान होगा-
(A) 4 cm
(B) 5 cm
(C) 3 cm
(D) 6 cm
उत्तर-
(B) 5 cm

प्रश्न 27.
आकृति में ∆ABC में, ∠ABC = 120° तथा ∠BCA = 30° है, तो निम्नलिखित में से कौन-सा कथन सत्य है ?

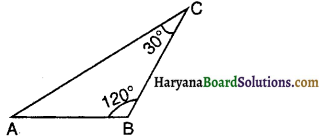
(A) AC > AB
(B) AC < AB (C) AC = AB (D) AC > AB + BC
उत्तर-
(A) AC > AB

प्रश्न 28.
यदि ∆ABC में, AB = 8 cm, BC = 5 cm है, तो निम्नलिखित में से कौन-सा कथन सत्य होगा ?

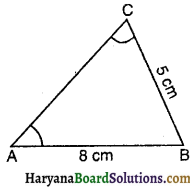
(A) ∠C > ∠A
(B) ∠C < ∠A (C)∠C = ∠A (D) उपरोक्त में से कोई भी नहीं उत्तर- (A) ∠C > ∠A

प्रश्न 29.
किसी त्रिभुज ABC के लिए निम्नलिखित में से कौन-सा कथन असत्य है ?
(A) AB + BC > AC
(B) BC + AC > AB
(C) AC + AB > BC
(D) AC + AB < BC
उत्तर-
(D) AC + AB < BC

प्रश्न 30.
समकोण त्रिभुज में सबसे बड़ी भुजा होती है-
(A) लंब
(B) आधार
(C) कर्ण
(D) उपरोक्त में से कोई भी नहीं
उत्तर-
(C) कर्ण

प्रश्न 31.
किसी समकोण त्रिभुज के लिए निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) (कण)² = (आधार)² – (लंब)²
(B) (कण)² = (आधार)² + (लंब)²
(C) (कर्ण)² + (आधार)² = (लंब)²
(D) (कण)² + (लंब)² = (आधार)²
उत्तर-
(B) (कण²) = (आधार)² + (लंब²)

प्रश्न 32.
आकृति में, PR > PQ है और PS कोण QPR को समद्विभाजित करता है, तो निम्नलिखित में से कौन-सा कथन सत्य है ?

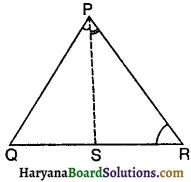
(A) ∠PSR < ∠PSQ
(B) ∠PSR = ∠PSQ
(C) ∠PSR > ∠PSO
(D) उपरोक्त में से कोई भी नहीं
उत्तर-
(C) ∠PSR > ∠PSQ

प्रश्न 33.
“दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।” यह निम्नलिखित में से सर्वांगसमता का कौन-सा नियम है ?
(A) AAS
(B) ASA
(C) SAS
(D) SSS
उत्तर-
(C) SAS

प्रश्न 34.
किसी वर्ग का विशेष गुण होता है-
(A) प्रत्येक भुजा समान
(B) प्रत्येक कोण समान 90° का
(C) प्रत्येक विकर्ण समान
(D) उपरोक्त सभी
उत्तर-
(C) प्रत्येक विकर्ण समान

प्रश्न 35.
यदि एक त्रिभुज के कोण 2 : 3 : 4 के अनुपात में हों, तो सबसे बड़े कोण का मान होगा-
(A) 40°
(B) 60°
(C) 80°
(D) 100°
उत्तर-
(C) 80°

प्रश्न 36.
एक चतुर्भुज के तीन कोण 110°, 40° एवं 50° हैं। चौथा कोण होगा-
(A) 160°
(B) 80°
(C) 260°
(D) 200°
उत्तर-
(A) 160°

प्रश्न 37.
एक षट्भुज के कोणों का योगफल होता है-
(A) 180°
(B) 360°
(C) 540°
(D) 720°
उत्तर-
(D) 720°

प्रश्न 38.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) त्रिभुज का एक बहिष्कोण अपने किसी एक अंतः अभिमुख कोण से छोटा होता है
(B) त्रिभुज के दो समकोण हो सकते हैं
(C) त्रिभुज का एक बहिष्कोण दो अंतः अभिमुख कोणों के योगफल के बराबर होता है
(D) त्रिभुज के दो अधिक कोण हो सकते हैं
उत्तर-
(C) त्रिभुज का एक बहिष्कोण दो अंतः अभिमुख कोणों के योगफल के बराबर होता है

प्रश्न 39.
“दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हो। निम्नलिखित में से यह सर्वांगसमता के किस नियम की पालना करता है?
(A) ASA
(B) SAS
(C) AAS
(D) RHS
उत्तर-
(A) ASA

प्रश्न 40.
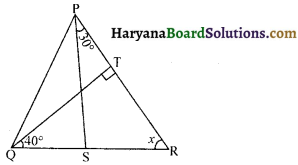
आकृति में, ∆PQR की भुजा QR को S तक बढ़ाया गया है। यदि ∠P : ∠Q : ∠R = 3 : 2 : 1 और RT ⊥ PR तो ∠TRS का मान होगा-

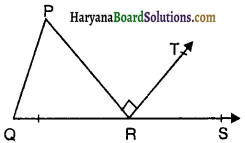
(A) 60°
(B) 30°
(C) 90°
(D) 120°
उत्तर-
(A) 60°

प्रश्न 41.
एक त्रिभुज का बहिष्कोण 115° का है और एक अंतः अभिमुख कोण 35° का है। अन्य दो कोण होंगे-
(A) 80°, 35°
(B) 80°, 65°
(C) 35°, 65°
(D) 80°, 100°
उत्तर-
(B) 80°, 65°

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 6 रेखाएँ और कोण Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 6 रेखाएँ और कोण

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
सिद्ध करें कि यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं।
हल :
दिया है :
दो रेखाएँ AB और CD परस्पर बिंदु 0 पर प्रतिच्छेद करती हैं। जैसा कि आकृति में दर्शाया गया है। इससे शीर्षाभिमुख कोणों के दो युग्म
(i) ∠AOC और ∠BOD व
(ii) ∠AOD और ∠BOC प्राप्त होते हैं
सिद्ध करना है :
(i) ∠AOC = ∠BOD
(ii) ∠AOD = ∠BOC

प्रमाण : आकृति अनुसार किरण OA, रेखा CD पर खड़ी है।
∴ ∠AOC + ∠AOD = 180° [रैखिक युग्म अभिगृहीत] …(1)
इसी प्रकार किरण OD, रेखा AB पर खड़ी है।
∴ ∠AOD + ∠BOD = 180° [रैखिक युग्म अभिगृहीत] …(2)
समीकरण (1) व (2) की तुलना करने पर
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
इसी प्रकार सिद्ध किया जा सकता है ∠AOD = ∠BOC.

प्रश्न 2.
आकृति में, OP, OQ, OR और OS चार किरणें हैं। सिद्ध कीजिए कि ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° है।

हल :

किरण OQ को एक बिंदु T तक पीछे बढ़ा दें ताकि TOQ एक रेखा हो (आकृति अनुसार) अब किरण OP रेखा TOQ पर खड़ी है।
अतः ∠TOP + ∠POQ = 180° ………….(1)
रैखिक युग्म अभिगृहीत]
इसी प्रकार, किरण OS रेखा TOQ पर खड़ी है।
अतः ∠TOS + ∠SOQ = 180° …………..(2)
∠SOQ = ∠SOR + ∠QOR है।
अतः समीकरण (2) निम्न हो जाती है :
∠TOS + ∠SOR + ∠QOR = 180° …………..(3)
समीकरण (1) और (3) को जोड़ने पर,
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360°
∠TOP + ∠TOS = ∠POS ………………(5)
समीकरण (4) व (5) से –
∠POQ + ∠QOR + ∠SOR + ∠POS = 360° [इति सिद्धम]

प्रश्न 3.
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समांतर हों, तो सिद्ध कीजिए कि दोनों रेखाएँ भी परस्पर समांतर होती हैं।
हल :
दिया है : एक तिर्यक रेखा AD दो रेखाओं PQ और RS को क्रमशः बिंदुओं B और C पर प्रतिच्छेद करती है। किरण BE, ∠ABQ की समद्विभाजक है और किरण CG ∠BCS की समद्विभाजक है तथा BE || CG है।

सिद्ध करना है : PQ || RS
प्रमाण : क्योंकि किरण BE, ∠ABQ की समद्विभाजक है।
∠ABE = \(\frac{1}{2}\) ∠ABQ
इसी प्रकार किरण CG ∠BCS की समद्विभाजक है।
∠BCG = \(\frac{1}{2}\) ∠BCS ……………..(2)
परंतु, BE || CG है और AD एक तिर्यक रेखा है।
अतः ∠ABE = ∠BCG …………….(3)
[संगत कोण अभिगृहीत] समीकरण (1), (2) व (3) से
\(\frac{1}{2}\)∠ABQ = \(\frac{1}{2}\) ∠BCS अर्थात्
∠ABQ = ∠BCS
परंतु, ये तिर्यक रेखा AD द्वारा रेखाओं PQ और RS के साथ बनाए गए संगत कोण हैं और ये बराबर हैं।
अतः PQ || RS [इति सिद्धम]

प्रश्न 4.
सिद्ध करें कि त्रिभुज के तीनों कोणों का योग 180° होता है।
हल :
दिया है : एक त्रिभुज ABC जिसके तीन कोण ∠1, ∠2 व ∠3 हैं।
सिद्ध करना है : ∠1 + ∠2 + ∠3 = 180°
रचना : बिंदु A से BC के समांतर रेखा DE खींचे जिससे दर्शाए अनुसार दो कोण ∠4 व ∠5 बन जाएँ।
प्रमाण : क्योंकि DE || BC तथा AB तिर्यक रेखा है।
∴ ∠2 = ∠4 (एकांतर कोण) ………………..(1)
इसी प्रकार DE || BC तथा AC तिर्यक रेखा है।
∠3 = ∠5 (एकांतर कोण) ………………..(2)

समीकरण (1) व (2) से
∠2 + ∠3 = ∠4 + ∠5
परंतु
दोनों ओर ∠1 जोड़ने पर
∠1 + ∠2 + ∠3 = ∠1 + ∠4 + ∠5
∠1 + ∠4 + ∠5 = 180° [रैखिक युग्म अभिगृहीत]
∴ ∠1 + ∠2 + ∠3 = 180° [इति सिद्धम]

प्रश्न 5.
आकृति में, यदि PQ || RS, ∠MXQ = 135° और ∠MYR= 40° है, तो ∠XMY का मान ज्ञात कीजिए।

हल :
यहाँ m से होकर, रेखा PQ के समांतर एक रेखा AB खींचिए जैसा कि आकृति में दिखाया गया है। अब, AB || PQ और PQ || RS है।
अतः AB || RS है।

अब ∠QXM + ∠XMB = 180°
(AB || PQ, तिर्यक रेखा XM के एक ही ओर के अंतः कोण)
परन्तु ∠QXM = 135° है।
इसलिए, 135° + ∠XMB = 180°
अतः ∠XMB = 45° …………..(1)
अब ∠BMY = ∠MYR (AB || RS, एकांतर कोण)
अतः ∠BMY = 40°
(1) और (2) को जोड़ने पर, आपको प्राप्त होगा
∠XMB + ∠BMY = 45° + 40°
अर्थात् ∠XMY = 85°.

प्रश्न 6.
आकृति में, AB || CD और CD || Er है। साथ ही EA ⊥ AB है। यदि ZBEF = 55° है, तो x, y और z के मान ज्ञात कीजिए।

हल :
क्योंकि AB || CD व CD || EF
∴ AB || EF
परन्तु EA ⊥ AB
EA ⊥ EF
∠BEF + ∠BCA = 90°
55° + z = 90°
z = 90° – 55° = 35°
अब क्योंकि CD || EF (दिया है)
y + 55° = 180° (तिर्यक रेखा के एक ओर के अन्तः कोण)
y = 180° – 55° = 125°
इसी प्रकार
AB || CD (दिया है)। (एकान्तर कोण युग्म)
∠x = ∠y
x = 125°
x = 125°, y = 125°, z = 35°.

Multiple Choice Questions with Answers:

प्रश्न 1.
यदि रैखिक युग्म का एक कोण न्यून कोण हो तो दूसरा __________ कोण होगा।
(A) सम
(B) न्यून
(C) अधिक
(D) समान
उत्तर-
(C) अधिक

प्रश्न 2.
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेदित करती हों, तो शीर्षाभिमुख कोण __________ होते हैं।
(A) समान
(B) असमान
(C) समकोण
(D) अधिक कोण
उत्तर-
(A) समान

प्रश्न 3.
निम्नलिखित में से कौन-सा कथन असत्य है ?
(A) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं
(B) यदि दो आसन्न कोण समान हों, तो प्रत्येक कोण 90° का होता है
(C) यदि रैखिक युग्म बनाने वाले कोण बराबर हों, तो इनमें से प्रत्येक कोण 90° का है
(D) यदि दो रेखाएँ आपस में काटती हों तथा शीर्षाभिमुख कोणों का एक युग्म न्यून कोणों से बना हो, तो दूसरा युग्म अधिक कोणों द्वारा बनेगा
उत्तर-
(B) यदि दो आसन्न कोण समान हों, तो प्रत्येक कोण 90° का होता है

प्रश्न 4.
आकृति में, रेखाएँ PQ और RS परस्पर बिंदु 0 पर प्रतिच्छेद करती हैं। यदि ∠POR : ∠ROQ = 5 : 7 है, तो ∠SOQ का मान होगा-

(A) 105°
(B) 75°
(C) 100°
(D) 80°
उत्तर-
(B) 75°

प्रश्न 5.
आकृति में, OP, OQ, OR और OS चार किरणें हैं तो ∠POQ + ∠QOR + ∠SOR + ∠POS का मान होगा-

(A) 180°
(B) 90°
(C) 270°
(D) 360°
उत्तर-
(D) 360°

प्रश्न 6.
आकृति में, रेखाएँ AB और CD बिंदु 0 पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° हो और ∠BOD = 40° हो, तो ∠BOE का मान होगा-

(A) 30°
(B) 70°
(C) 40°
(D) 90°
उत्तर-
(A) 30°

प्रश्न 7.
आकृति में, ∠PRQ = 70° है तो ∠PRT का मान होगा-

(A) 70°
(B) 20°
(C) 100°
(D) 110°
उत्तर-
(D) 110°

प्रश्न 8.
आकृति के अनुसार, यदि x + y = w + z हो, तो निम्नलिखित में से कौन-सा कथन सत्य है ?

(A) AOB एक रेखा है
(B) AOC एक रेखा है
(C) COD एक रेखा है
(D) BOD एक रेखा है
उत्तर-
(A) AOB एक रेखा है

प्रश्न 9.
आकृति में, AB || CD और CD || EF है। साथ ही, EA ⊥ AB है। यदि ∠BEF = 55° है, तो x और y के मान क्रमशः होंगे-

(A) 125° व 35°
(B) 55° व 35°
(C) 35° व 55°
(D) 125° व 55°
उत्तर-
(A) 125° व 35°

प्रश्न 10.
आकृति में, यदि ∠BOC = 50° हो, तो ∠x और ∠y का मान क्रमशः होगा-

(A) 50° व 130°
(B) 130° व 50°
(C) 50° व 40°
(D) 40° व 50°
उत्तर-
(A) 50° व 130°

प्रश्न 11.
आकृति में, यदि AB || CD, CD || EF और y : 2 = 3 : 7 है, तो x का मान होगा

(A) 54०
(B) 126°
(C) 180°
(D) 90°
उत्तर-
(B) 126°

प्रश्न 12.
आकृति में, यदि AB || CD, EF ⊥ CD और ∠GED = 126° है, तो ∠FGE का मान होगा-

(A) 126°
(B) 36°
(C) 54°
(D) 90°
उत्तर-
(C) 54°

प्रश्न 13.
आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS का मान होगा-

(A) 20°
(B) 40°
(C) 60°
(D) 130°
उत्तर-
(C) 60°

प्रश्न 14.
आकृति में, ∆ABC की भुजाओं BA और CB को क्रमशः बिंदुओं D और E तक बढ़ाया गया है। यदि ∠DAC = 135° और ∠ABE = 110° हो, तो ∠ACB का मान होगा-

(A) 110°
(B) 135°
(C) 65°
(D) 115°
उत्तर-
(C) 65°

प्रश्न 15.
आकृति में, यदि ∠X = 62° और ∠XYZ = 54° है। यदि YO और 70 क्रमशः ∆XYZ के ∠XYZ और ∠XZY के समद्विभाजक है, तो ∠OZY का मान होगा-

(A) 110°
(B) 121°
(C) 122°
(D) 64°
उत्तर-
(A) 32°

प्रश्न 16.
आकृति में, ∆ABC की भुजा BC को D तक बढ़ाया गया है तथा ∠BAC = 60° व ∠ACD = 110° है तो ∠x का मान होगा-

(A) 110°
(B) 60°
(C) 50°
(D) 70°
उत्तर-
(C) 50°

प्रश्न 17.
किसी त्रिभुज में __________ से अधिक समकोण नहीं हो सकते।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(A) एक

प्रश्न 18.
किसी चतुर्भुज में __________ से अधिक समकोण नहीं हो सकते।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(B) दो

प्रश्न 19.
चतुर्भुज के चार कोणों का योग __________ होता है।
(A) एक समकोण
(B) दो समकोण
(C) तीन समकोण
(D) चार समकोण
उत्तर-
(D) चार समकोण

प्रश्न 20.
त्रिभुज के तीनों कोणों का योग होता है-
(A) 90°
(B) 180°
(C) 270°
(D) 360°
उत्तर-
(B) 180°

प्रश्न 21.
आकृति में, x का मान होगा-

(A) 50°
(B) 70°
(C) 120°
(D) 20°
उत्तर-
(C) 120°

प्रश्न 22.
आकृति में QT ⊥ PR, ∠TQR = 40° और ∠SPR = 30° है, तो x का मान होगा-

(A) 30°
(B) 40°
(C) 50°
(D) 90°
उत्तर-
(C) 50°

प्रश्न 23.
आकृति में, POQ एक रेखा है, ∠POR = 4x और ∠QOR = 2x है, तो x का मान होगा-

(A) 15°
(B) 30°
(C) 120°
(D) 60°
उत्तर-
(B) 30°

प्रश्न 24.
आकृति में,∠POR और ∠QOR एक रैखिक युग्म बनाते हैं, यदि a – b = 80° हो, तो ∠a का मान होगा-

(A) 50°
(B) 80°
(C) 70°
(D) 90°
उत्तर-
(C) 130°

प्रश्न 25.
आकृति में, यदि ∠AOC + ∠BOD = 70° हो, तो ∠COD का मान होगा-

(A) 20°
(B) 150°
(C) 70°
(D) 110°
उत्तर-
(D) 110°

प्रश्न 26.
आकृति में, ∠NOP का मान होगा-

(A) 68°
(B) 61°
(C) 51°
(D) 41°
उत्तर-
(B) 61°

प्रश्न 27.
आकृति में, ∠BOD का मान होगा-

(A) 180
(B) 36°
(C) 54°
(D) 90°
उत्तर-
(B) 36°

प्रश्न 28.
आकृति में, x के किस मान के लिए AOB एक रेखा बनेगी यदि ∠AOC = 4x और ∠BOC = 6x + 30° हो ?

(A) 15°
(B) 60°
(C) 120°
(D) 180°
उत्तर-
(A) 15°

प्रश्न 29.
आकृति में, AB, CD और PQ तीन रेखाएँ हैं जोकि 0 पर संगामी हैं यदि ∠AOP = 5y, ∠QOD = 2y और ∠BOC = 5y हो, तो y का मान होगा-

(A) 15°
(B) 30°
(C) 75°
(D) 150°
उत्तर-
(A) 15°

प्रश्न 30.
निम्नलिखित कथनों में से कौन-सा कथन सत्य है
(A) यदि दो आसन्न कोण समान हों तो प्रत्येक कोण 90° का होता है
(B) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं
(C) रैखिक युग्म बनाने वाले दोनों कोण न्यून कोण हो सकते हैं
(D) किसी समतल में दो भिन्न रेखाओं के दो उभयनिष्ठ बिंदु हो सकते हैं
उत्तर-
(B) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं

प्रश्न 31.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) यदि दो रेखाएँ एक तिर्यक रेखा के द्वारा प्रतिच्छेदित होती हैं तब संगत कोण बराबर होते हैं
(B) दो रेखाएँ जोकि एक ही रेखा पर लंब हैं, परस्पर लंब होती हैं।
(C) यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो रेखा के एक ओर के आंतरिक कोण समान होते हैं
(D) दो रेखाएँ जोकि एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं
उत्तर-
(D) दो रेखाएँ जोकि एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं

प्रश्न 32.
यदि रैखिक युग्म का एक कोण समकोण हो, तो दूसरा होगा-
(A) न्यून कोण
(B) समकोण
(C) अधिक कोण
(D) ऋजु कोण
उत्तर-
(B) समकोण

प्रश्न 33.
यदि एक किरण एक रेखा पर स्थित हो, तो इस प्रकार निर्मित दो आसन्न कोणों का योग होता है-
(A) 90°
(B) 150°
(C) 180°
(D) 360°
उत्तर-
(C) 180°

प्रश्न 34.
70° के कोण का संपूरक कोण युग्म होगा-
(A) 70°
(B) 20°
(C) 110°
उत्तर-
(C) 110°

प्रश्न 35.
35° के कोण का पूरक कोण युग्म होगा-
(A) 35°
(B) 55°
(C) 145°
उत्तर-
(B) 55°

प्रश्न 36.
निम्नलिखित में से कौन-सा पूरक कोण युग्म है ?
(A) 110°, 70°
(B) 50°, 30°
(C) 150°, 30°
(D) 50°, 40°
उत्तर-
(D) 50°, 40°

प्रश्न 37.
निम्नलिखित में से कौन-सा संपूरक कोण युग्म है ?
(A) 110°, 70°
(B) 50°, 40°
(C) 100°, 70°
(D) 70°, 20°
उत्तर-
(A) 110°, 70°

प्रश्न 38.
दो कोणों का योग 180° हो, तो ऐसे कोण कहलाते हैं-
(A) न्यून कोण
(B) पूरक कोण
(C) संपूरक कोण
(D) प्रतिवर्ती कोण
उत्तर-
(C) संपूरक कोण