Haryana State Board HBSE 9th Class Maths Important Questions Chapter 8 चतुर्भुज Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 8 चतुर्भुज
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:
प्रश्न 1.
सिद्ध कीजिए कि चतुर्भुज के कोणों का योग 360° होता है।
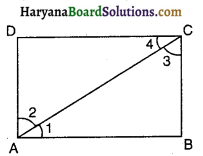
हल :
दिया है : ABCD एक चतुर्भुज है।
सिद्ध करना है : ∠A + ∠B + ∠C + ∠D = 360°
रचना : विकर्ण AC को मिलाओ।
प्रमाण : ∆ABC में,
∠1 + ∠B + ∠3 = 180° [त्रिभुज के कोणों का योग] …………… (i)
∆ACD में,
∠2 + ∠4 + ∠D = 180° [त्रिभुज के कोणों का योग] …………… (ii)
समीकरण (i) व (ii) को जोड़ने पर,
∠1 + ∠2 + ∠B + ∠3 + ∠4 + ∠D = 180° + 180°
[∵ ∠1 + ∠2 = ∠A
तथा ∠3 + ∠4 = ∠D ]
∠A + ∠B + ∠C + ∠D = 360°
अतः चतुर्भुज के कोणों का योग 360° होता है। [इति सिद्धम]
![]()
प्रश्न 2.
सिद्ध कीजिए कि किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है।
हल :
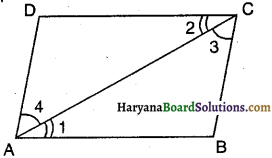
दिया है : ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है।
सिद्ध करना है : ∆ABC = ∆ADC
प्रमाण : जैसा कि हम जानते हैं कि समांतर चतुर्भुज की सम्मुख भुजाएं समांतर होती हैं।
∆ABC व ∆ADC में,
AC = AC [उभयनिष्ठ]
∠1 = ∠2 [एकांतर कोण]
∠3 = ∠4 [एकांतर कोण]
∴ ∆ABC = ∆ADC [कोण-भुजा-कोण सर्वांगसमता] [इति सिद्धम]
प्रश्न 3.
सिद्ध कीजिए कि किसी समांतर चतुर्भुज की सम्मुख भुजाएं समान होती हैं।
हल :
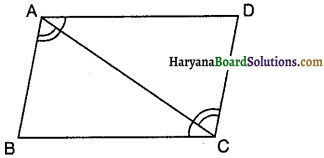
दिया है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
सिद्ध करना है : AB = DC तथा AD = BC
रचना : A तथा C को मिलाएं।
प्रमाण : ∆ADC तथा ∆CBA में,
∵ ∠DAC = ∠BCA [एकांतर कोण] B
AC = AC [उभयनिष्ठ भुजा]
∠DCA = ∠BAC [एकांतर कोण]
∴ ∆ADC = ∆CBA [कोण-भुजा-कोण सर्वांगसमता]
इस प्रकार,
AB = DC व AD = BC [सर्वांगसम त्रिभुजों के संगत भाग]
अतः समांतर चतुर्भुज की सम्मुख भुजाएं समान होती हैं। [इति सिद्धम]
![]()
प्रश्न 4.
सिद्ध कीजिए कि समांतर चतुर्भुज के सम्मुख कोण समान होते हैं।

हल :
दिया है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
सिद्ध करना है : ∠A = ∠C तथा ∠B = ∠D.
प्रमाण : ∵ AB || DC तथा AD इनको प्रतिच्छेद करती है।
∴ ∠A + ∠D = 180° [प्रतिच्छेदी रेखा के एक ही तरफ के आंतरिक कोण] ……………. (i)
अब
∵ AD || BC तथा DC इनको प्रतिच्छेद करती है।
∴ ∠A + ∠C = 180° [प्रतिच्छेदी रेखा के एक ही तरफ के आंतरिक कोण] ……………. (ii)
समीकरण (i) व (ii) से,
∠A + ∠D = ∠D + ∠C
∠A = ∠C
इसी प्रकार, यह सिद्ध किया जा सकता है कि
∠B = ∠D [इति सिद्धम]
प्रश्न 5.
सिद्ध कीजिए कि चतुर्भुज में यदि सम्मुख कोण समान हों वह समांतर चतुर्भुज होता है।
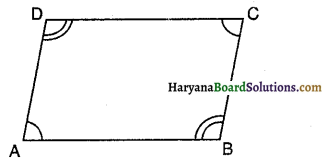
हल :
दिया है : चतुर्भुज ABCD, जिसमें
∠A = ∠C तथा
∠B = ∠D
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
प्रमाण : चतुर्भुज ABCD में,
∠A = ∠C (दिया है)…(i) तथा
∠B = ∠D (दिया है)…(ii) समीकरण (i) व (ii) से, हमें प्राप्त होता है।
∴ ∠A + ∠B = ∠C + ∠D
∵ चतुर्भुज के चारों कोणों का योग 360° होता है।
∵ ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B = ∠C + ∠D = 180°
अब, रेखा AB, AD तथा BC को A तथा B पर प्रतिच्छेद करती है।
तथा ∠A + ∠B = 180° [आसन्न आंतरिक कोण]
∴ AD || BC …………….(iii)
इसी प्रकार, (i) व (ii) से, हमें प्राप्त होता है।
∠A + ∠D = ∠B + ∠C = 180°
रेखा AD, AB तथा CD को A तथा D पर प्रतिच्छेद करती है,
∠A + ∠D = 180° [आसन्न आंतरिक कोण]
∴ AB || DC ……………(iv)
समीकरण (iii) व (iv) से, हमें प्राप्त होता है, चतुर्भुज ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]
![]()
प्रश्न 6.
यदि चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हों, तो वह समांतर चतुर्भुज होता है।
हल :
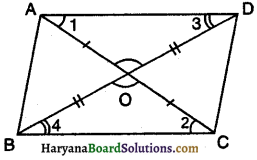
दिया है : चतुर्भुज ABCD जिसमें विकर्ण AC तथा BD, O पर इस प्रकार प्रतिच्छेद करते हैं कि OA = OC तथा OB = OD
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
प्रमाण : ∆AOD तथा ∆COB में,
OA = OC [दिया है]
∠AOD = ∠COB [शीर्षाभिमुख कोण]
OD = OB [दिया है]
∴ ∆AOD ≅ ∆COB [भुजा-कोण-भुजा सर्वांगसमता]
∴ ∠1 = ∠2 तथा ∠3 = ∠4
[सर्वांगसम त्रिभुजों के संगत भाग]
क्योंकि, यह प्रतिच्छेदी रेखा AC, द्वारा बनाए गए एकांतर कोण हैं, जो कि AD तथा BC को प्रतिच्छेद करती है।
∴ AD || BC ………………(i)
इसी प्रकार, हम सिद्ध कर सकते हैं कि,
AB || DC ………….. (ii)
समीकरण (i) व (ii) से, हमें प्राप्त होता है, चतुर्भुज ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]
प्रश्न 7.
एक चतुर्भुज समांतर चतुर्भुज होता है यदि उसकी सम्मुख भुजाओं का एक युग्म परस्पर समान तथा समांतर हो।
हल :
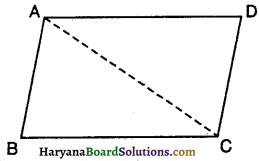
दिया है : एक चतुर्भुज ABCD जिसमें, AB || DC तथा AB = DC है।
सिद्ध करना है : ABCD एक समांतर चतुर्भुज है। रचना : A तथा C को मिलाएं।
प्रमाण : AB || DC और तिर्यक रेखा AC उनको प्रतिच्छेद करती है।
∴ ∠BAC = ∠DCA (एकांतर कोण)…(i)
अब, ∆ABC तथा ∆CDA में,
AB = DC (दिया है)
AC = AC (उभयनिष्ठ)
∠BAC = ∠DCA [(i) से]
∴ ∆ABC ≅ ∆CDA [भुजा-कोण-भुजा सर्वांगसमता]
अब, AD तथा BC दो रेखाएं हैं तथा तिर्यक रेखा AC इनको प्रतिच्छेद करती है इसलिए एकांतर कोण ACB तथा कोण CAD समान है।
इस प्रकार,
AD || BC
अब, AB || DC
तथा AD || BC
इसलिए, ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]
![]()
प्रश्न 8.
एक चतुर्भुज के कोण 1 : 2 : 3 : 4 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल :
माना चतुर्भुज के कोण = (1x), (2x), (3x), (4x)
हम जानते हैं कि
चतुर्भुज के कोणों का योग = 360°
x + 2x + 3x + 4x = 360°
10x = 360°
x = \(\frac{360^{\circ}}{10}\) = 36°
अतः चतुर्भुज के कोण = (1 × 36)°, (2 × 36)°, (3 × 36)°, (4 × 36)°
= 36°, 72°, 108°, 144°.
प्रश्न 9.
सिद्ध कीजिए कि एक चतुर्भुज में यदि सम्मुख भुजाएं समान हों तो वह समांतर चतुर्भुज होता है।
हल :
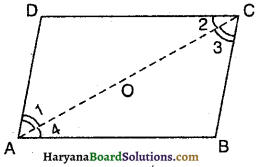
दिया है : चतुर्भुज ABCD जिसमें AB = DC तथा AD = BC हैं।
सिद्ध करना है : चतुर्भुज ABCD एक समांतर चतुर्भुज है।
रचना : A तथा C को मिलाएं।
प्रमाण : ∆ABC तथा ∆CDA में,
AB = DC [दिया है]
AD = BC[दिया है]
AC = AC [उभयनिष्ठ]
∆ABC ≅ ∆DAC [भुजा-भुजा-भुजा सर्वांगसमता]
∴ ∠1 = ∠3
तथा ∠2 = ∠4 [सर्वांगसम त्रिभुजों को संगत भाग] …………(i)
अब, रेखा AC, AB तथा CD को A तथा C पर प्रतिच्छेद करती है इसलिए एकांतर आंतरिक कोण
∠2 = ∠4 [जैसे कि समीकरण (i) में सिद्ध किया है]
∴ AB || CD …………..(ii)
इसी प्रकार, रेखा AC, CB तथा AD को C तथा A पर प्रतिच्छेद करती है इसलिए एकांतर आंतरिक कोण
∠1 = ∠3 [जैसे कि समीकरण (i) में सिद्ध किया है]
∴ BC || AD ……………(iii)
समीकरण (ii) व (iii) से, हमें प्राप्त होता है।
ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]
![]()
प्रश्न 10.
सिद्ध कीजिए कि यदि तीन या अधिक रेखाएं दी हों और उनके द्वारा एक तिर्यक रेखा पर बनाए गए अंतः खंड समान हों तो किसी P अन्य तिर्यक रेखा पर संगत अंतः खंड भी समान होते हैं।
हल :
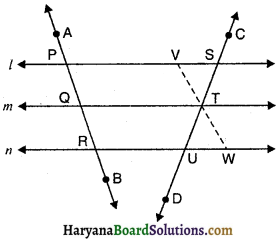
दिया है : l, m, n, तीन समांतर रेखाएं हैं तथा दो तिर्यक रेखाएं AB तथा CD इन्हें क्रमशः P, Q, R तथा S, T, U बिंदुओं पर प्रतिच्छेद करती हैं तथा साथ ही PQ = QR
सिद्ध करना है : ST = TU
रचना : T से AB के समांतर VTW खींचे।
प्रमाण :
PQ || VT (रचना से)
PV || QT (दिया है)
∴ PVTQ एक समांतर चतुर्भुज है।
⇒ PQ = VT …………….(i)
इसी प्रकार, QTWR एक समांतर चतुर्भुज है।
⇒ QR = TW ………….(ii)
क्योंकि, PQ = QR [दिया है]
∴ VT = TW [(1) तथा (ii) से] …………..(iii)
पुनः l, n के समांतर है तथा तिर्यक रेखा CD इनको प्रतिच्छेद करती है।
∴ ∠VST = ∠TUW [∵ एकांतर कोण] ……………(iv)
∆VST तथा ∆WUT में,
VT = TW [(iii) से]
∠VST = ∠TUW [(iv) से]
तथा, ∠VTS = ∠WTU [शीर्षाभिमुख कोण]
∴ ∆VST = ∆WUT [कोण-भुजा-कोण सर्वांगसमता]
इस प्रकार,
ST = UT [सर्वांगसम त्रिभुजों के संगत भाग][इति सिद्धम]
![]()
Multiple Chpice Questions with Answers:
प्रश्न 1.
चार रेखाखण्डों से बनी बन्द आकृति को कहा जाता है-
(A) त्रिभुज
(B) चतुर्भुज
(C) पंचभुज
(D) षड्भुज
उत्तर-
(B) चतुर्भुज
प्रश्न 2.
चतुर्भुज के चारों कोणों का योग होता है-
(A) 180°
(B) 270°
(C) 360°
(D) 540°
उत्तर-
(C) 360°
प्रश्न 3.
जिस चतुर्भुज में सम्मुख भुजाओं का केवल एक युग्म समान्तर हो उसे कहा जाता है-
(A) समलम्ब
(B) समान्तर चतुर्भुज
(C) आयत
(D) समचतुर्भुज
उत्तर-
(A) समलम्ब
![]()
प्रश्न 4.
किसी समान्तर चतुर्भुज का एक विकर्ण उसे ___________ सर्वांगसम त्रिभुजों में विभाजित करता है।
(A) 4
(B) 3
(C) 1
(D) 2
उत्तर-
(D) 2
प्रश्न 5.
प्रत्येक कोण समकोण नहीं होता है-
(A) आयत का
(B) वर्ग का
(C) त्रिभुज का
(D) घन का
उत्तर-
(C) त्रिभुज का
प्रश्न 6.
एक समान्तर चतुर्भुज में ____________ बराबर होते/होती हैं।
(A) सम्मुख भुजाएँ
(B) संलग्न कोण
(C) संलग्न भुजाएँ
(D) विकर्ण
उत्तर-
(A) सम्मुख भुजाएँ
प्रश्न 7.
किसी समान्तर चतुर्भुज का गुण है-
(A) सम्मुख भुजाएँ बराबर
(B) सम्मुख कोण बराबर
(C) विकर्ण परस्पर समद्विभाजित करने वाले
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी
![]()
प्रश्न 8.
आयत का प्रत्येक कोण ___________ का होता है।
(A) 45°
(B) 90°
(C) 1350
(D) 180°
उत्तर-
(B) 90°
प्रश्न 9.
एक समचतुर्भुज के विकर्ण परस्पर ___________ होते हैं।
(A) लम्ब
(B) समान्तर
(C) बराबर
(D) समान्तर व बराबर
उत्तर-
(A) लम्ब
प्रश्न 10.
एक समान्तर चतुर्भुज के कोणों के समद्विभाजक एक __________ बनाते हैं।
(A) वर्ग
(B) समचतुर्भुज
(C) आयत
(D) त्रिभुज
उत्तर-
(C) आयत
प्रश्न 11.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इसका सबसे छोटा कोण होगा-
(A) 156°
(B) 108°
(C) 60°
(D) 36°
उत्तर-
(D) 36°
![]()
प्रश्न 12.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इसका सबसे बड़ा कोण होगा-
(A) 156°
(B) 108°
(C) 60°
(D) 36°
उत्तर-
(A) 156°
प्रश्न 13.
वर्ग का गुण है-
(A) विकर्ण बराबर होते हैं ।
(B) विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों
प्रश्न 14.
आयत का गुण है-
(A) प्रत्येक कोण 90° का होता है
(B) विकर्ण बराबर होते हैं
(C) विकर्ण परस्पर समद्विभाजित करते हैं
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी
![]()
प्रश्न 15.
एक समान्तर चतुर्भुज का एक कोण 60° है इसका आसन्न कोण होगा-
(A) 60°
(B) 120
(C) 90°
(D) 30°
उत्तर-
(B) 120°
प्रश्न 16.
एक समान्तर चतुर्भुज का एक कोण 75° है। इसका सम्मुख कोण होगा-
(A) 75°
(B) 15°
(C) 105°
(D) 285°
उत्तर-
(A)75°
प्रश्न 17.
एक समान्तर चतुर्भुज के दो आसन्न कोण क्रमशः 70° व 110° हैं। अन्य दो कोण होंगे-
(A) 100°, 80°
(B) 105°, 75°
(C) 110°, 70°
(D) 120°, 60°
उत्तर-
(C) 110°, 70°
प्रश्न 18.
एक चतुर्भुज के तीन कोण 70%, 100°, 110° हैं इसका चौथा कोण होगा-
(A) 110°
(B) 100°
(C) 70°
(D) 80°
उत्तर-
(D) 80°
![]()
प्रश्न 19.
किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर और उसका __________ होता है।
(A) आधा
(B) एक-चौथाई
(C) एक-तिहाई
(D) दुगुना
उत्तर-
(A) आधा
प्रश्न 20.
किसी त्रिभुज की एक भुजा के मध्य-विन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को __________ करती है।
(A) समत्रिभाजित
(B) समद्विभाजित
(C) समचतुर्भाजित
(D) समद्विभाजित नहीं
उत्तर-
(B) समद्विभाजित
प्रश्न 21.
∆ABC में D, E और Fक्रमशः भुजाओं AB, BC और CA के मध्य-बिन्दु हैं। बताइए बिन्दुओं D, E और F को मिलाने पर ∆ABC _________ सर्वांगसम त्रिभुजों में विभाजित हो जाता है।
(A) दो
(B) तीन
(C) चार
(D) पाँच
उत्तर-
(C) चार
![]()
प्रश्न 22.
किसी चतुर्भुज की भुजाओं के मध्य-बिन्दुओं को एक क्रम से मिलाने वाले रेखाखण्डों द्वारा बना चतुर्भुज एक ___________ होता है।
(A) समचतुर्भुज
(B) आयत
(C) वर्ग
(D) समान्तर चतुर्भुज
उत्तर-
(D) समान्तर चतुर्भुज