Haryana State Board HBSE 9th Class Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 10 वृत्त
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:
प्रश्न 1.
सिद्ध करें कि वृत्त की बराबर जीवाएं केंद्र पर बराबर कोण बनाती हैं।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 है तथा दो जीवाएं AB व CD बराबर हैं।
सिद्ध करना है : ∠AOB = ∠COD.
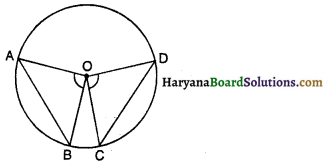
प्रमाण : ∆AOB तथा ∆COD में,
OA = OC [एक वृत्त की त्रिज्याएं]
OB = OD [एक वृत्त की त्रिज्याएं]
AB = CD [दिया है]
अतः ∆AOB ≅ ∆COD [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠AOB = ∠COD [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम]
प्रश्न 2.
सिद्ध करो कि तीन असरेख बिंदुओं से होकर एक और केवल एक वृत्त जाता है।
हल :
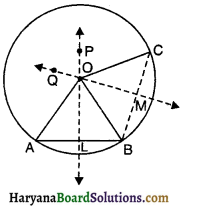
दिया है : तीन अंसरेख बिंदु A, B और C हैं।
सिद्ध करना है : बिंदुओं A, B और C से होकर जाने वाला एक और केवल एक ही वृत्त है।
रचना : रेखाखंड AB और BC खींचिए। AB और BC के लंब समद्विभाजक क्रमशः PL और QM खींचिए। क्योंकि AB, BC के समांतर नहीं है, इसलिए PL भी QM के समांतर नहीं होगा। इसलिए वे किसी बिंदु 0 पर प्रतिच्छेद करेंगे। OA, OB और OC को मिलाइए।
प्रमाण : O, AB के लंब समद्विभाजक PL पर स्थित है।
∴ OA = OB ………………(i)
इसी प्रकार, OB = OC ………………(ii)
इसलिए (i) और (ii) से,
OA= OB = OC = r, माना।
त्रिज्या r लेकर और 0 केंद्र मानकर एक वृत्त खींचिए। वह बिंदुओं A, B और C से होकर जाएगा।
इससे यह सिद्ध होता है कि A, B और C से होकर एक वृत्त जाता है। अब हम यह सिद्ध करेंगे कि A, B और C से होकर जाने वाला केवल यही एक वृत्त है। यदि संभव हो, तो मान लीजिए कि A, B और C से जाने वाला दूसरा वृत्त भी है, जिसका केंद्र 0′ और त्रिज्या s है।
तब O’, PL और QM के लंब समद्विभाजक पर अवश्य स्थित होगा। क्योंकि दो रेखाएं एक से अधिक बिंदुओं पर प्रतिच्छेद नहीं कर सकती हैं, अतः O’ और O संपाती होंगे। इसलिए, OA = O’A = r (= s) है। अर्थात A, B और C से जाने वाला एक और केवल एक ही (अद्वितीय) वृत्त है।
![]()
प्रश्न 3.
यदि एक वृत्त की दो प्रतिच्छेदी जीवाएं प्रतिच्छेद बिंदु से जाने वाले व्यास से समान कोण बनाएं, तो सिद्ध कीजिए कि वे जीवाएं बराबर हैं।
हल :
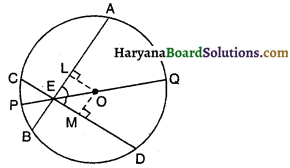
दिया है : एक वृत्त, जिसका केंद्र 0 है, की दो जीवाएं AB और CD बिंदु । E पर प्रतिच्छेद करती हैं। E से होकर जाने वाला PQ एक ऐसा व्यास है कि ∠AEQ = ∠DEQ है।
सिद्ध करना है : AB = CD.
रचना : जीवाओं AB और CD पर क्रमशः OL तथा OM लंब खींचिए।
प्रमाण : ∠LOE = 180° – 90° – ∠LEO = 90° – ∠LEO [त्रिभुज के कोणों के योग के कारण]
= 90° – ∠AEQ
= 90° – ∠DEQ [∵ ∠AEQ = ∠DEQ]
= 90° – ∠MEO = ∠MOE
त्रिभुजों OLE तथा ONE में,
∠LEO = ∠MEO [दिया है]
∠LOE = ∠MOE [प्रमाणित]
EO = EO [उभयनिष्ठ]
अतः, ∆OLE ≅ ∆OME [कोण-कोण-भुजा सर्वांगसमता]
इससे प्राप्त होता है- OL = OM [सर्वांगसम त्रिभुजों के संगत भाग]
इसलिए AB = CD [क्योंकि केंद्र से समान दूरी पर स्थित जीवाएं समान होती हैं।]
[इति सिद्धम]
प्रश्न 4.
सिद्ध करो कि एक ही वृत्तखंड के कोण समान होते हैं।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 है तथा ∠ACB और ∠ADB वृत्त के एक ही वृत्तखंड में बने दो कोण हैं।
सिद्ध करना है : ∠ACB = ∠ADB.
रचना : OA और OB को मिलाइए।
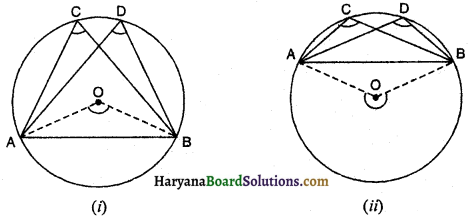
प्रमाण : ∠AOB = 2 ∠ACB …………….. (i)
किसी चाप द्वारा वृत्त के केंद्र पर बना कोण शेष भाग पर बने कोण का दुगुना होता है]
और ∠AOB = 2 ∠ADB …………………..(ii)
समीकरण (i) व (ii) से,
∴ 2 ∠ACB = 2 ∠ADB
या ∠ACB = ∠ADB [इति सिद्धम]
![]()
प्रश्न 5.
सिद्ध करो कि चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग 180° होता है।
हल :
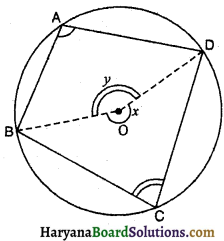
दिया है : एक चक्रीय चतुर्भुज ABCD है।
सिद्ध करना है : ∠BAD + ∠BCD = 180° तथा
∠ADC + ∠CBA = 180°
रचना : माना कि शीर्षों A, B, C और D से जाने वाले वृत्त का केंद्र 0 है। OB और OD को मिलाइए।
प्रमाण : ∠BAD = \(\frac{1}{2}\) ∠BOD
= \(\frac{1}{2}\) x ………………..(i)
[∵ वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है]
और ∠BCD = \(\frac{1}{2}\)∠BOD = \(\frac{1}{2}\) y ……………. (ii)
[वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है]
समीकरण (i) और (ii) को जोड़ने पर,
∠BAD + ∠BCD = \(\frac{1}{2}\)x + \(\frac{1}{2}\)y
= \(\frac{1}{2}\) (x + y)
= \(\frac{1}{2}\) × 360° = 180° [क्योंकि x + y = 360°]
क्योंकि चतुर्भुज के कोणों का योग 360° होता है।
∠ADC + ∠CBA = 360° – ( ∠BAD + ∠BCD )
= 360° – 180° = 180°
अतः ∠BAD + ∠BCD = 180°
तथा ∠ADC + ∠CBA = 180° [इति सिद्धम]
प्रश्न 6.
आकृति में, ABCD एक चक्रीय चतुर्भुज है, जिसमें AC और BD विकर्ण हैं। यदि ∠DBC = 55° तथा ∠BAC = 45° हो, तो ∠BCD ज्ञात कीजिए।
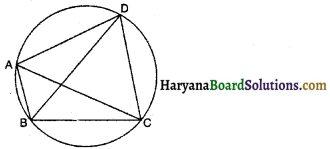
हल :
अतः,
∠CAD = ∠DBC = 55° (एक वृत्तखंड के कोण)
∠DAB = ∠CAD + ∠BAC
= 55° + 45° = 100°
परन्तु, ∠DAB + ∠BCD = 180° (चक्रीय चतुर्भुज के सम्मुख कोण)
इसलिए, ∠BCD = 180° – 100° = 80°
![]()
Multiple choice Questions with Answers:
प्रश्न 1.
किसी तल के उन सभी बिन्दुओं के समूह को क्या कहा जाता है जो तल के एक स्थिर बिन्दु से समान दूरी पर हो-
(A) आयत
(B) वृत्त
(C) वर्ग
(D) समचतुर्भुज
उत्तर-
(B) वृत्त
प्रश्न 2.
वृत्त का केन्द्र वृत्त के ___________ में स्थित होता है।
(A) बहिर्भाग
(B) परिधि
(C) अभ्यन्तर
(D) परिमाप
उत्तर-
(C) अभ्यन्तर
प्रश्न 3.
एक बिन्दु जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो वृत्त के ___________ में स्थित होता है। (A) बहिर्भाग
(B) परिमाप
(C) अभ्यन्तर
(D) वृत्तखण्ड
उत्तर-
(A) बहिर्भाग
![]()
प्रश्न 4.
वृत्त की सबसे बड़ी जीवा वृत्त का ___________ होता है।
(A) परिमाप
(B) अर्धव्यास
(C) केन्द्र
(D) व्यास
उत्तर-
(D) व्यास
प्रश्न 5.
एक चाप ___________ होता है, जब इसके सिरे एक व्यास के सिरे हों।
(A) अर्धव्यास
(B) अर्धवृत्त
(C) लघु वृत्तखण्ड
(D) दीर्घ वृत्तखण्ड
उत्तर-
(B) अर्धवृत्त
प्रश्न 6.
वृत्तखण्ड एक चाप तथा ___________ के बीच का भाग होता है।
(A) परिधि
(B) त्रिज्या
(C) जीवा
(D) केन्द्र
उत्तर-
(C) जीवा
![]()
प्रश्न 7.
निम्नलिखित में से कौन-सा कथन सत्य है?
(A) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं ।
(B) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है
(C) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है
(D) त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
उत्तर-
(C) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है
प्रश्न 8.
दो वृत्त सर्वांगसम होते हैं, यदि उनकी ___________ बराबर हों।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) चाप
(D) लम्ब रेखाएँ
उत्तर-
(A) त्रिज्याएँ
प्रश्न 9.
सर्वांगसम वृत्तों की बराबर ___________ उनके केन्द्रों पर बराबर कोण अन्तरित करती हैं।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) अर्धव्यास
(D) लम्ब रेखाएँ
उत्तर-
(B) जीवाएँ
![]()
प्रश्न 10.
सम्पूर्ण वृत्त की लम्बाई को उसकी ___________ कहा जाता है-
(A) क्षेत्रफल
(B) व्यास
(C) परिधि
(D) आयतन
उत्तर-
(C) परिधि
प्रश्न 11.
एक वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को ___________ करता है।
(A) समत्रिभाजित
(B) समचतुर्भाजित
(C) असमद्विभाजित
(D समद्विभाजित
उत्तर-
(D) समद्विभाजित
प्रश्न 12.
एक वृत्त के केन्द्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर ___________ का कोण बनाती है।
(A) 90°
(B) 120°
(C) 60°
(D) 180°
उत्तर-
(A) 90°
![]()
प्रश्न 13.
दो बिन्दुओं से होती हुई कितनी रेखाएँ खींची जा सकती हैं ?
(A) केवल दो
(B) केवल एक
(C) तीन
(D) चार
उत्तर-
(B) केवल एक
प्रश्न 14.
एक बिन्दु से होते हुए कितने वृत्त खींचे जा सकते हैं ?
(A) एक
(B) दो
(C) चार
(D) अनगिनत
उत्तर-
(D) अनगिनत
प्रश्न 15.
तीन असरेखी बिन्दुओं से होता हुआ खींचा जा सकता है-
(A) एक वृत्त
(B) दो वृत्त
(C) कोई वृत्त नहीं
(D) तीन वृत्त
उत्तर-
(A) एक वृत्त
![]()
प्रश्न 16.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) एक वृत्त की बराबर जीवाएँ केन्द्र से समान दूरी पर होती हैं
(B) एक वृत्त के केन्द्र से समदूरस्थ जीवाएँ लम्बाई में समान होती हैं
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों
प्रश्न 17.
5 सें०मी० तथा 3 सें०मी० त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सें०मी० है। उभयनिष्ठ जीवा की लम्बाई होगी-
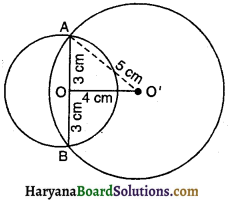
(A) 6 cm
(B) 5 cm
(C) 7 cm
(D) 8 cm
उत्तर-
(A) 6 cm
प्रश्न 18.
संलग्न आकृति में यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र 0 है, A, B, C और D पर प्रतिच्छेद करे तो निम्नलिखित में से कौन-सा कथन सत्य होगा ?
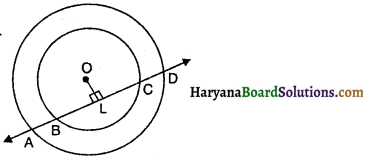
(A) AB = BC
(B) AB = BD
(C) AB = CD
(D) AC = CD
उत्तर-
(C) AB = CD
![]()
प्रश्न 19.
एक चाप द्वारा केन्द्र पर अन्तरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का ___________ होता है।
(A) आधा
(B) एक-तिहाई
(C) तीन-गुना
(D) दुगुना
उत्तर-
(D) दुगुना
प्रश्न 20.
आकृति में, वृत्त के छायांकित भाग को कहते हैं-
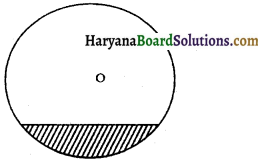
(A) दीर्घ त्रिज्याखंड
(B) दीर्घ वृत्तखंड
(C) लघु त्रिज्याखंड
(D) लघु वृत्तखंड
उत्तर-
(D) लधु वृत्तखंड
प्रश्न 21.
संलग्न आकृति में ∠x का मान होगा-
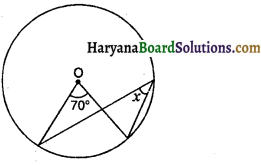
(A) 70°
(B) 140°
(C) 35°
(D) 105°
उत्तर-
(C) 35°
![]()
प्रश्न 22.
संलग्न आकृति में, तीन बिन्दु A, B और C किसी वृत्त पर इस प्रकार स्थित हैं कि जीवाएं AB और AC केन्द्र 0 पर क्रमशः 90° और 110° के कोण अंतरित करती हैं। ∠BAC का मान होगा-
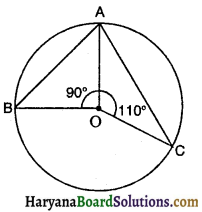
(A) 90°
(B) 110°
(C) 160°
(D) 80°
उत्तर-
(D) 80°
प्रश्न 23.
संलग्न आकृति में, O वृत्त का केन्द्र हो तो ∠x का मान होगा-
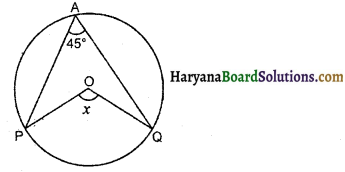
(A) 90°
(B) 45°
(C) 22\(\frac{1}{2}\)°
(D) 135°
उत्तर-
(A) 90°
प्रश्न 24.
संलग्न आकृति में, 0 वृत्त का केन्द्र हो तो ∠x का मान होगा-
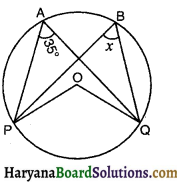
(A) 70°
(B) 35°
(C) 171
(D) 105°
उत्तर-
(B) 35°
![]()
प्रश्न 25.
चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग ……………… होता है।
(A) 90°
(B) 135°
(C) 180°
(D) 360°
उत्तर-
(C) 180°
प्रश्न 26.
संलग्न आकृति में, O वृत्त का केन्द्र है तो ∠x और ∠y का मान होगा-
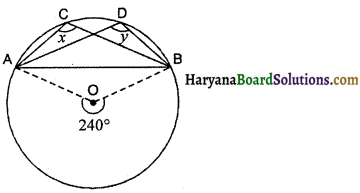
(A) ∠x = ∠y = 120°
(B) ∠x = ∠y = 240°
(C) ∠x = ∠y = 480°
(D) ∠x = 120°, ∠y = 240°
उत्तर-
(A) ∠x = ∠y = 120°
प्रश्न 27.
दी गई आकृति में, ABCD एक चक्रीय चतुर्भुज है, जिसमें AC और BD विकर्ण हैं। यदि ∠DBC = 55° तथा ∠BAC = 45° हो, तो ∠BCD का मान होगा-
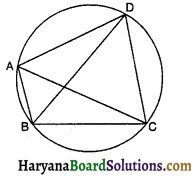
(A) 100°
(B) 50°
(C) 40°
(D) 80°
उत्तर-
(D) 80°
![]()
प्रश्न 28.
संलग्न आकृति में, ∠PQR = 100° है जहाँ P, Q और R केन्द्र 0 वाले एक वृत्त पर स्थित बिन्दु हैं ∠OPR का मान होगा-
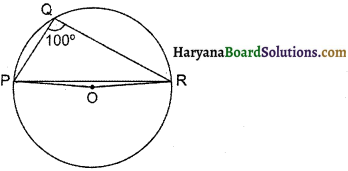
(A) 160°
(B) 10°
(C) 20°
(D) 200°
उत्तर-
(B) 10°
प्रश्न 29.
आकृति में, ∠ABC = 69° और ∠ACB = 31° हों, तो ∠BDC का मान होगा-
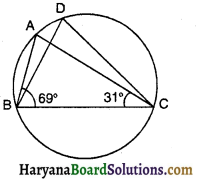
(A) 100°
(B) 90°
(C) 80°
(D) 110°
उत्तर-
(C) 80°
प्रश्न 30.
संलग्न आकृति में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC का मान होगा-
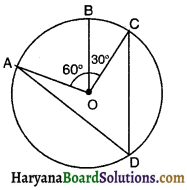
(A) 45°
(B) 30°
(C) 15°
(D) 50°
उत्तर-
(A) 45°
![]()
प्रश्न 31.
संलग्न आकृति में, एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC का मान होगा-
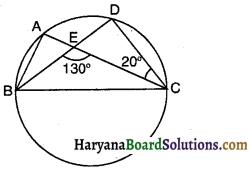
(A) 150°
(B) 110°
(C) 70°
(D) 105°
उत्तर-
(B) 110°
प्रश्न 32.
संलग्न आकृति में, ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD का मान होगा-
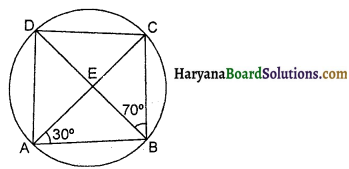
(A) 50°
(B) 140°
(C) 100°
(D) 80°
उत्तर-
(D) 80°
प्रश्न 33.
अर्धवृत्त में बना प्रत्येक कोण होता है-
(A) एक समकोण
(B) दो समकोण
(C) अर्ध समकोण
(D) न्यून कोण
उत्तर-
(A) एक समकोण
![]()
प्रश्न 34.
वृत्त के दीर्घ वृत्तखण्ड में किसी जीवा द्वारा बना कोण ___________ कोण होता है।
(A) सम
(B) अधिक
(C) न्यून
(D) दो सम
उत्तर-
(C) न्यून
प्रश्न 35.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) एक ही वृत्तखण्ड के कोण बराबर होते हैं
(B) अर्धवृत्त में बना कोण समकोण होता है
(C) चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी