Haryana State Board HBSE 9th Class Maths Important Questions Chapter 6 रेखाएँ और कोण Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 6 रेखाएँ और कोण
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:
प्रश्न 1.
सिद्ध करें कि यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं।
हल :
दिया है :
दो रेखाएँ AB और CD परस्पर बिंदु 0 पर प्रतिच्छेद करती हैं। जैसा कि आकृति में दर्शाया गया है। इससे शीर्षाभिमुख कोणों के दो युग्म
(i) ∠AOC और ∠BOD व
(ii) ∠AOD और ∠BOC प्राप्त होते हैं
सिद्ध करना है :
(i) ∠AOC = ∠BOD
(ii) ∠AOD = ∠BOC
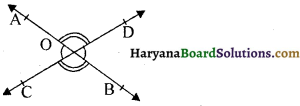
प्रमाण : आकृति अनुसार किरण OA, रेखा CD पर खड़ी है।
∴ ∠AOC + ∠AOD = 180° [रैखिक युग्म अभिगृहीत] …(1)
इसी प्रकार किरण OD, रेखा AB पर खड़ी है।
∴ ∠AOD + ∠BOD = 180° [रैखिक युग्म अभिगृहीत] …(2)
समीकरण (1) व (2) की तुलना करने पर
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
इसी प्रकार सिद्ध किया जा सकता है ∠AOD = ∠BOC.
![]()
प्रश्न 2.
आकृति में, OP, OQ, OR और OS चार किरणें हैं। सिद्ध कीजिए कि ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° है।
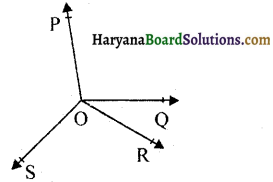
हल :
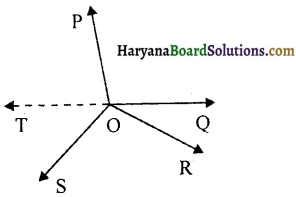
किरण OQ को एक बिंदु T तक पीछे बढ़ा दें ताकि TOQ एक रेखा हो (आकृति अनुसार) अब किरण OP रेखा TOQ पर खड़ी है।
अतः ∠TOP + ∠POQ = 180° ………….(1)
रैखिक युग्म अभिगृहीत]
इसी प्रकार, किरण OS रेखा TOQ पर खड़ी है।
अतः ∠TOS + ∠SOQ = 180° …………..(2)
∠SOQ = ∠SOR + ∠QOR है।
अतः समीकरण (2) निम्न हो जाती है :
∠TOS + ∠SOR + ∠QOR = 180° …………..(3)
समीकरण (1) और (3) को जोड़ने पर,
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360°
∠TOP + ∠TOS = ∠POS ………………(5)
समीकरण (4) व (5) से –
∠POQ + ∠QOR + ∠SOR + ∠POS = 360° [इति सिद्धम]
प्रश्न 3.
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समांतर हों, तो सिद्ध कीजिए कि दोनों रेखाएँ भी परस्पर समांतर होती हैं।
हल :
दिया है : एक तिर्यक रेखा AD दो रेखाओं PQ और RS को क्रमशः बिंदुओं B और C पर प्रतिच्छेद करती है। किरण BE, ∠ABQ की समद्विभाजक है और किरण CG ∠BCS की समद्विभाजक है तथा BE || CG है।
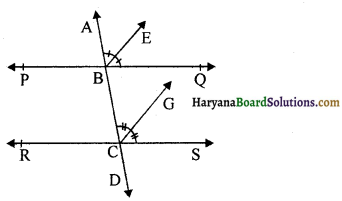
सिद्ध करना है : PQ || RS
प्रमाण : क्योंकि किरण BE, ∠ABQ की समद्विभाजक है।
∠ABE = \(\frac{1}{2}\) ∠ABQ
इसी प्रकार किरण CG ∠BCS की समद्विभाजक है।
∠BCG = \(\frac{1}{2}\) ∠BCS ……………..(2)
परंतु, BE || CG है और AD एक तिर्यक रेखा है।
अतः ∠ABE = ∠BCG …………….(3)
[संगत कोण अभिगृहीत] समीकरण (1), (2) व (3) से
\(\frac{1}{2}\)∠ABQ = \(\frac{1}{2}\) ∠BCS अर्थात्
∠ABQ = ∠BCS
परंतु, ये तिर्यक रेखा AD द्वारा रेखाओं PQ और RS के साथ बनाए गए संगत कोण हैं और ये बराबर हैं।
अतः PQ || RS [इति सिद्धम]
![]()
प्रश्न 4.
सिद्ध करें कि त्रिभुज के तीनों कोणों का योग 180° होता है।
हल :
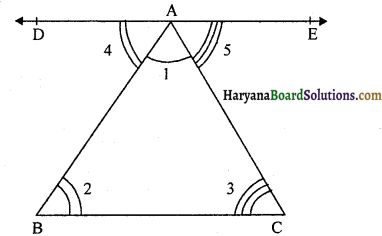
दिया है : एक त्रिभुज ABC जिसके तीन कोण ∠1, ∠2 व ∠3 हैं।
सिद्ध करना है : ∠1 + ∠2 + ∠3 = 180°
रचना : बिंदु A से BC के समांतर रेखा DE खींचे जिससे दर्शाए अनुसार दो कोण ∠4 व ∠5 बन जाएँ।
प्रमाण : क्योंकि DE || BC तथा AB तिर्यक रेखा है।
∴ ∠2 = ∠4 (एकांतर कोण) ………………..(1)
इसी प्रकार DE || BC तथा AC तिर्यक रेखा है।
∠3 = ∠5 (एकांतर कोण) ………………..(2)
समीकरण (1) व (2) से
∠2 + ∠3 = ∠4 + ∠5
परंतु
दोनों ओर ∠1 जोड़ने पर
∠1 + ∠2 + ∠3 = ∠1 + ∠4 + ∠5
∠1 + ∠4 + ∠5 = 180° [रैखिक युग्म अभिगृहीत]
∴ ∠1 + ∠2 + ∠3 = 180° [इति सिद्धम]
प्रश्न 5.
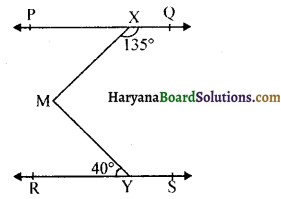
आकृति में, यदि PQ || RS, ∠MXQ = 135° और ∠MYR= 40° है, तो ∠XMY का मान ज्ञात कीजिए।
हल :
यहाँ m से होकर, रेखा PQ के समांतर एक रेखा AB खींचिए जैसा कि आकृति में दिखाया गया है। अब, AB || PQ और PQ || RS है।
अतः AB || RS है।
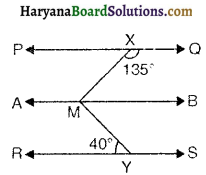
अब ∠QXM + ∠XMB = 180°
(AB || PQ, तिर्यक रेखा XM के एक ही ओर के अंतः कोण)
परन्तु ∠QXM = 135° है।
इसलिए, 135° + ∠XMB = 180°
अतः ∠XMB = 45° …………..(1)
अब ∠BMY = ∠MYR (AB || RS, एकांतर कोण)
अतः ∠BMY = 40°
(1) और (2) को जोड़ने पर, आपको प्राप्त होगा
∠XMB + ∠BMY = 45° + 40°
अर्थात् ∠XMY = 85°.
![]()
प्रश्न 6.
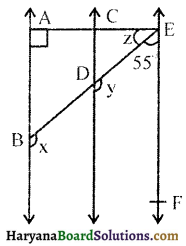
आकृति में, AB || CD और CD || Er है। साथ ही EA ⊥ AB है। यदि ZBEF = 55° है, तो x, y और z के मान ज्ञात कीजिए।
हल :
क्योंकि AB || CD व CD || EF
∴ AB || EF
परन्तु EA ⊥ AB
EA ⊥ EF
∠BEF + ∠BCA = 90°
55° + z = 90°
z = 90° – 55° = 35°
अब क्योंकि CD || EF (दिया है)
y + 55° = 180° (तिर्यक रेखा के एक ओर के अन्तः कोण)
y = 180° – 55° = 125°
इसी प्रकार
AB || CD (दिया है)। (एकान्तर कोण युग्म)
∠x = ∠y
x = 125°
x = 125°, y = 125°, z = 35°.
Multiple Choice Questions with Answers:
प्रश्न 1.
यदि रैखिक युग्म का एक कोण न्यून कोण हो तो दूसरा __________ कोण होगा।
(A) सम
(B) न्यून
(C) अधिक
(D) समान
उत्तर-
(C) अधिक
प्रश्न 2.
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेदित करती हों, तो शीर्षाभिमुख कोण __________ होते हैं।
(A) समान
(B) असमान
(C) समकोण
(D) अधिक कोण
उत्तर-
(A) समान
![]()
प्रश्न 3.
निम्नलिखित में से कौन-सा कथन असत्य है ?
(A) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं
(B) यदि दो आसन्न कोण समान हों, तो प्रत्येक कोण 90° का होता है
(C) यदि रैखिक युग्म बनाने वाले कोण बराबर हों, तो इनमें से प्रत्येक कोण 90° का है
(D) यदि दो रेखाएँ आपस में काटती हों तथा शीर्षाभिमुख कोणों का एक युग्म न्यून कोणों से बना हो, तो दूसरा युग्म अधिक कोणों द्वारा बनेगा
उत्तर-
(B) यदि दो आसन्न कोण समान हों, तो प्रत्येक कोण 90° का होता है
प्रश्न 4.
आकृति में, रेखाएँ PQ और RS परस्पर बिंदु 0 पर प्रतिच्छेद करती हैं। यदि ∠POR : ∠ROQ = 5 : 7 है, तो ∠SOQ का मान होगा-
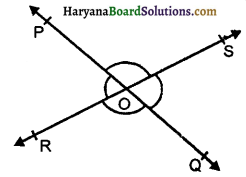
(A) 105°
(B) 75°
(C) 100°
(D) 80°
उत्तर-
(B) 75°
प्रश्न 5.
आकृति में, OP, OQ, OR और OS चार किरणें हैं तो ∠POQ + ∠QOR + ∠SOR + ∠POS का मान होगा-
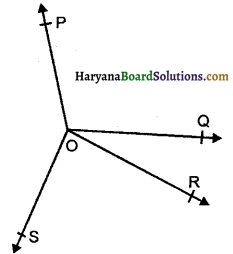
(A) 180°
(B) 90°
(C) 270°
(D) 360°
उत्तर-
(D) 360°
![]()
प्रश्न 6.
आकृति में, रेखाएँ AB और CD बिंदु 0 पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° हो और ∠BOD = 40° हो, तो ∠BOE का मान होगा-
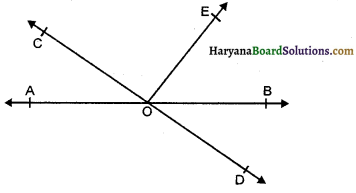
(A) 30°
(B) 70°
(C) 40°
(D) 90°
उत्तर-
(A) 30°
प्रश्न 7.
आकृति में, ∠PRQ = 70° है तो ∠PRT का मान होगा-
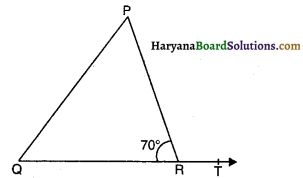
(A) 70°
(B) 20°
(C) 100°
(D) 110°
उत्तर-
(D) 110°
प्रश्न 8.
आकृति के अनुसार, यदि x + y = w + z हो, तो निम्नलिखित में से कौन-सा कथन सत्य है ?
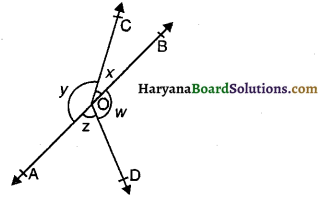
(A) AOB एक रेखा है
(B) AOC एक रेखा है
(C) COD एक रेखा है
(D) BOD एक रेखा है
उत्तर-
(A) AOB एक रेखा है
![]()
प्रश्न 9.
आकृति में, AB || CD और CD || EF है। साथ ही, EA ⊥ AB है। यदि ∠BEF = 55° है, तो x और y के मान क्रमशः होंगे-
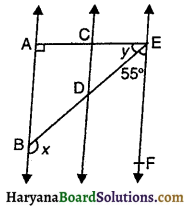
(A) 125° व 35°
(B) 55° व 35°
(C) 35° व 55°
(D) 125° व 55°
उत्तर-
(A) 125° व 35°
प्रश्न 10.
आकृति में, यदि ∠BOC = 50° हो, तो ∠x और ∠y का मान क्रमशः होगा-
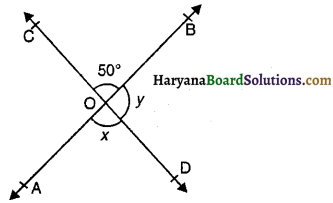
(A) 50° व 130°
(B) 130° व 50°
(C) 50° व 40°
(D) 40° व 50°
उत्तर-
(A) 50° व 130°
प्रश्न 11.
आकृति में, यदि AB || CD, CD || EF और y : 2 = 3 : 7 है, तो x का मान होगा

(A) 54०
(B) 126°
(C) 180°
(D) 90°
उत्तर-
(B) 126°
![]()
प्रश्न 12.
आकृति में, यदि AB || CD, EF ⊥ CD और ∠GED = 126° है, तो ∠FGE का मान होगा-
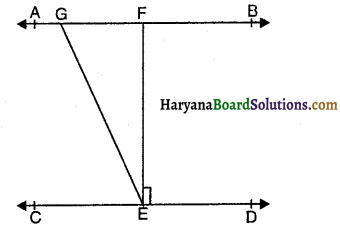
(A) 126°
(B) 36°
(C) 54°
(D) 90°
उत्तर-
(C) 54°
प्रश्न 13.
आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS का मान होगा-
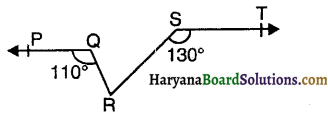
(A) 20°
(B) 40°
(C) 60°
(D) 130°
उत्तर-
(C) 60°
प्रश्न 14.
आकृति में, ∆ABC की भुजाओं BA और CB को क्रमशः बिंदुओं D और E तक बढ़ाया गया है। यदि ∠DAC = 135° और ∠ABE = 110° हो, तो ∠ACB का मान होगा-
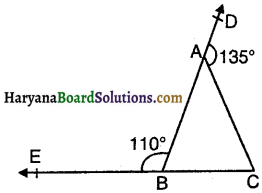
(A) 110°
(B) 135°
(C) 65°
(D) 115°
उत्तर-
(C) 65°
![]()
प्रश्न 15.
आकृति में, यदि ∠X = 62° और ∠XYZ = 54° है। यदि YO और 70 क्रमशः ∆XYZ के ∠XYZ और ∠XZY के समद्विभाजक है, तो ∠OZY का मान होगा-
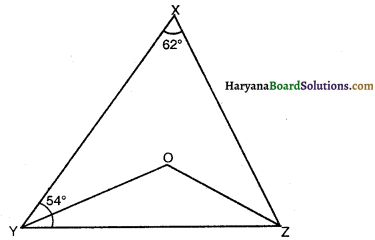
(A) 110°
(B) 121°
(C) 122°
(D) 64°
उत्तर-
(A) 32°
प्रश्न 16.
आकृति में, ∆ABC की भुजा BC को D तक बढ़ाया गया है तथा ∠BAC = 60° व ∠ACD = 110° है तो ∠x का मान होगा-
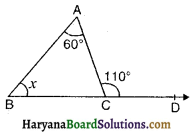
(A) 110°
(B) 60°
(C) 50°
(D) 70°
उत्तर-
(C) 50°
प्रश्न 17.
किसी त्रिभुज में __________ से अधिक समकोण नहीं हो सकते।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(A) एक
प्रश्न 18.
किसी चतुर्भुज में __________ से अधिक समकोण नहीं हो सकते।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(B) दो
![]()
प्रश्न 19.
चतुर्भुज के चार कोणों का योग __________ होता है।
(A) एक समकोण
(B) दो समकोण
(C) तीन समकोण
(D) चार समकोण
उत्तर-
(D) चार समकोण
प्रश्न 20.
त्रिभुज के तीनों कोणों का योग होता है-
(A) 90°
(B) 180°
(C) 270°
(D) 360°
उत्तर-
(B) 180°
प्रश्न 21.
आकृति में, x का मान होगा-
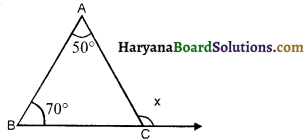
(A) 50°
(B) 70°
(C) 120°
(D) 20°
उत्तर-
(C) 120°
![]()
प्रश्न 22.
आकृति में QT ⊥ PR, ∠TQR = 40° और ∠SPR = 30° है, तो x का मान होगा-
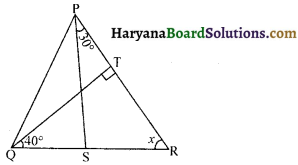
(A) 30°
(B) 40°
(C) 50°
(D) 90°
उत्तर-
(C) 50°
प्रश्न 23.
आकृति में, POQ एक रेखा है, ∠POR = 4x और ∠QOR = 2x है, तो x का मान होगा-
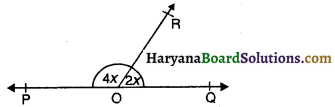
(A) 15°
(B) 30°
(C) 120°
(D) 60°
उत्तर-
(B) 30°
प्रश्न 24.
आकृति में,∠POR और ∠QOR एक रैखिक युग्म बनाते हैं, यदि a – b = 80° हो, तो ∠a का मान होगा-
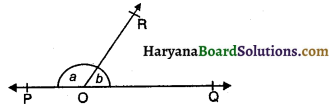
(A) 50°
(B) 80°
(C) 70°
(D) 90°
उत्तर-
(C) 130°
![]()
प्रश्न 25.
आकृति में, यदि ∠AOC + ∠BOD = 70° हो, तो ∠COD का मान होगा-
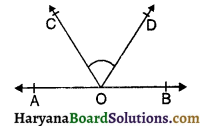
(A) 20°
(B) 150°
(C) 70°
(D) 110°
उत्तर-
(D) 110°
प्रश्न 26.
आकृति में, ∠NOP का मान होगा-
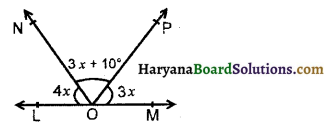
(A) 68°
(B) 61°
(C) 51°
(D) 41°
उत्तर-
(B) 61°
प्रश्न 27.
आकृति में, ∠BOD का मान होगा-
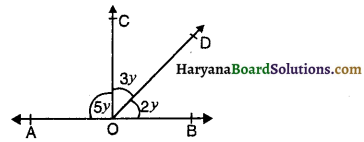
(A) 180
(B) 36°
(C) 54°
(D) 90°
उत्तर-
(B) 36°
![]()
प्रश्न 28.
आकृति में, x के किस मान के लिए AOB एक रेखा बनेगी यदि ∠AOC = 4x और ∠BOC = 6x + 30° हो ?
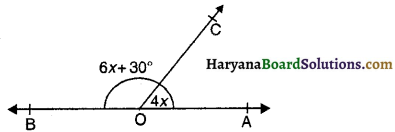
(A) 15°
(B) 60°
(C) 120°
(D) 180°
उत्तर-
(A) 15°
प्रश्न 29.
आकृति में, AB, CD और PQ तीन रेखाएँ हैं जोकि 0 पर संगामी हैं यदि ∠AOP = 5y, ∠QOD = 2y और ∠BOC = 5y हो, तो y का मान होगा-
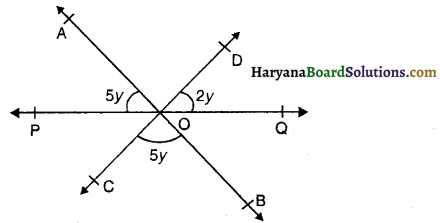
(A) 15°
(B) 30°
(C) 75°
(D) 150°
उत्तर-
(A) 15°
प्रश्न 30.
निम्नलिखित कथनों में से कौन-सा कथन सत्य है
(A) यदि दो आसन्न कोण समान हों तो प्रत्येक कोण 90° का होता है
(B) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं
(C) रैखिक युग्म बनाने वाले दोनों कोण न्यून कोण हो सकते हैं
(D) किसी समतल में दो भिन्न रेखाओं के दो उभयनिष्ठ बिंदु हो सकते हैं
उत्तर-
(B) रैखिक युग्म बनाने वाले कोण संपूरक होते हैं
![]()
प्रश्न 31.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) यदि दो रेखाएँ एक तिर्यक रेखा के द्वारा प्रतिच्छेदित होती हैं तब संगत कोण बराबर होते हैं
(B) दो रेखाएँ जोकि एक ही रेखा पर लंब हैं, परस्पर लंब होती हैं।
(C) यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो रेखा के एक ओर के आंतरिक कोण समान होते हैं
(D) दो रेखाएँ जोकि एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं
उत्तर-
(D) दो रेखाएँ जोकि एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं
प्रश्न 32.
यदि रैखिक युग्म का एक कोण समकोण हो, तो दूसरा होगा-
(A) न्यून कोण
(B) समकोण
(C) अधिक कोण
(D) ऋजु कोण
उत्तर-
(B) समकोण
प्रश्न 33.
यदि एक किरण एक रेखा पर स्थित हो, तो इस प्रकार निर्मित दो आसन्न कोणों का योग होता है-
(A) 90°
(B) 150°
(C) 180°
(D) 360°
उत्तर-
(C) 180°
प्रश्न 34.
70° के कोण का संपूरक कोण युग्म होगा-
(A) 70°
(B) 20°
(C) 110°
उत्तर-
(C) 110°
![]()
प्रश्न 35.
35° के कोण का पूरक कोण युग्म होगा-
(A) 35°
(B) 55°
(C) 145°
उत्तर-
(B) 55°
प्रश्न 36.
निम्नलिखित में से कौन-सा पूरक कोण युग्म है ?
(A) 110°, 70°
(B) 50°, 30°
(C) 150°, 30°
(D) 50°, 40°
उत्तर-
(D) 50°, 40°
![]()
प्रश्न 37.
निम्नलिखित में से कौन-सा संपूरक कोण युग्म है ?
(A) 110°, 70°
(B) 50°, 40°
(C) 100°, 70°
(D) 70°, 20°
उत्तर-
(A) 110°, 70°
प्रश्न 38.
दो कोणों का योग 180° हो, तो ऐसे कोण कहलाते हैं-
(A) न्यून कोण
(B) पूरक कोण
(C) संपूरक कोण
(D) प्रतिवर्ती कोण
उत्तर-
(C) संपूरक कोण