HBSE 9th Class Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
एक ही आधार और एक ही समांतर रेखाओं के बीच . स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते है।

हल :
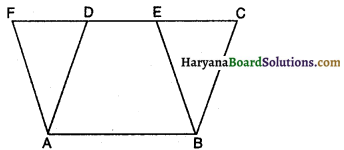
दिया है : दो समांतर चतुर्भुज ABCD और ABEF एक ही आधार AB तथा एक ही समांतर रेखाओं AB तथा FC के मध्य स्थित हैं।
सिद्ध करना है : ar (|| चतुर्भुज ABCD) = ar (|| चतुर्भुज ABEF)
प्रमाण : त्रिभुजो ADF तथा BCE में,
∠AFD = ∠BEC [संगत कोण]
∠ADF = ∠BCF [संगत कोण]
AF = BE [|| चतुर्भुज की सम्मुख भुजा]
∴ ∆ADF ≅ ∆BCE (कोण-कोण-भुजा सर्वांगसमता)
∴ ar (∆ADF) = ar (∆BCE)
दोनों ओर ABED का क्षेत्रफल जोड़ने पर,
ar (∆ADF) + ar (चतुर्भुज ABED) = ar (∆BCE) + ar (चतुर्भुज ABED)
⇒ ar (|| चतुर्भुज ABEF) = ar (|| चतुर्भुज ABCD) [इति सिद्धम]

प्रश्न 2.
एक ही आधार तथा एक ही समांतर रेखाओं के मध्य वाले त्रिभुजों के क्षेत्रफल समान होते हैं।

हल :
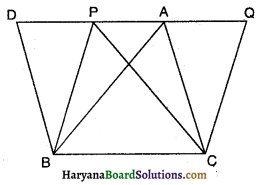
दिया है : ABC तथा PBC दो त्रिभुज हैं जो कि एक ही आधार BC तथा समांतर रेखाओं BC तथा AP के मध्य स्थित हैं।
सिद्ध करना है : क्षेत्रफल (∆ABC) = क्षेत्रफल (∆PBC)
रचना : B से, BD || CA खींचे, जोकि D तक बढ़ाई हुई रेखा PA, को प्रतिच्छेद करे तथा C से, CQ || BP खींचे, जो रेखा AP को Q पर प्रतिच्छेद करें।
प्रमाण : यहां पर, BD || CA (रचना से)
तथा BC || DA (दिया है)
∴ BCAD एक समांतर चतुर्भुज है।
इसी प्रकार, BCQP एक समांतर चतुर्भुज है।
अब, समांतर चतुर्भुज BCQP तथा समांतर चतुर्भुज BCAD एक ही आधार BC पर तथा एक ही समांतर रेखाओं के मध्य स्थित हैं।
∴ क्षेत्रफल (समांतर चतुर्भुज BCQP) = क्षेत्रफल (समांतर चतुर्भुज BCAD) ……………(i)
जैसे कि, हम जानते हैं कि समांतर चतुर्भुज के विकर्ण इसको समान क्षेत्रफल वाले दो त्रिभुजों में बांटते हैं।
तथा
क्षेत्रफल (∆PBC) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCQP) ……………(ii)
क्षेत्रफल (∆ABC) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCAD) ……………(iii)
अब,
क्षेत्रफल (समांतर चतुर्भुज BCQP) = क्षेत्रफल (समांतर चतुर्भुज BCAD) [∵ (i) से]
⇒ \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCAD) = \(\frac{1}{2}\) क्षेत्रफल (समांतर चतुर्भुज BCQP)
समीकरण (ii) तथा (iii) से,
⇒ क्षेत्रफल (∆ABC) = क्षेत्रफल (∆PBC) [इति सिद्धम]

प्रश्न 3.
समान क्षेत्रफल तथा समान आधार वाले त्रिभुजों के संगत शीर्षलंब भी समान होते हैं।

हल :
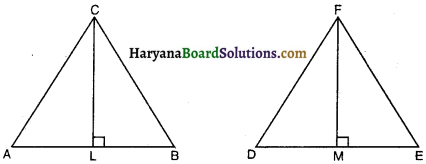
दिया है : दो त्रिभुज ABC तथा DEF इस प्रकार हैं कि
(i) क्षेत्रफल (∆ABC) = क्षेत्रफल (∆DEF)
(ii) AB = DE
दो त्रिभुजों के CL तथा FM क्रमागत AB तथा DE पर संगत शीर्षलंब हैं।
सिद्ध करना है : CL = FM
प्रमाण : ∆ABC में, CL भुजा AB पर संगत शीर्षलंब है।
∴ क्षेत्रफल (∆ABC) = \(\frac{1}{2}\) (AB × CL) इसी प्रकार, …………..(i)
क्षेत्रफल (∆DEF) = \(\frac{1}{2}\) (DE × FM) ……………..(ii)
क्षेत्रफल (∆ABC) = क्षेत्रफल (∆DEF) (दिया है)
⇒ \(\frac{1}{2}\) (AB × CL) = \(\frac{1}{2}\) (DE × FM) [(i) तथा (ii) से]
⇒ AB × CL = DE × FM
⇒ DE × CL = DE × FM [∵ AB = DE (दिया है)]
⇒ CL = FM [इति सिद्धम]

प्रश्न 4.
दर्शाइए कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों मे विभाजित करती है।

हल :
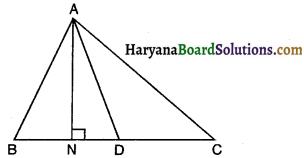
दिया है : ∆ABC में AD उसकी माध्यिका है।
सिद्ध करना है : ar (∆ABD) = ar (∆ACD)
रचना : शीर्ष A से AN ⊥ BC खींचो।
प्रमाण:
ar (ABD) = \(\frac{1}{2}\) × आधार × शीर्षलंब
= \(\frac{1}{2}\) BD × AN
= \(\frac{1}{2}\) × CD × AN (∵ BD = CD)
= \(\frac{1}{2}\) × आधार × शीर्षलंब (∆ACD का)
= ar (∆ACD) [इति सिद्धम]

प्रश्न 5.
दर्शाइए कि समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लंबाइयों के गुणनफल का आधा होता है।
हल :

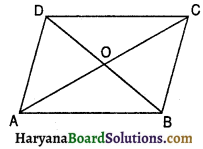
दिया है : समचतुर्भुज ABCD जिसके विकर्ण AC तथा BD, O पर प्रतिच्छेद करते हैं।
सिद्ध करना है : क्षेत्रफल (समचतुर्भुज ABCD) = =(AC × BD)
प्रमाण : क्योंकि समचतुर्भुज के विकर्ण 90° के कोण पर प्रतिच्छेद करते हैं
अतः OB ⊥ AC व OD ⊥ AC
अब ar (समचतुर्भुज ABCD) = ar (∆ABC) + ar (∆ADC)
= \(\frac{1}{2}\) × (AC × BO) + \(\frac{1}{2}\) (AC × DO)
= \(\frac{1}{2}\) × AC × (BO + DO)
= \(\frac{1}{2}\) × (AC × BD) [इति सिद्धम]

Multiple choice Questions with Answers:

प्रश्न 1.
एक आकृति का _______________ उस आकृति द्वारा घेरे गए तल के भाग से सम्बन्ध (किसी मात्रक में) एक संख्या होती है।
(A) परिमाप
(B) क्षेत्रफल
(C) आयतन
(D) घेरा
उत्तर-
(B) क्षेत्रफल

प्रश्न 2.
समान्तर चतुर्भुज का क्षेत्रफल ज्ञात करने का सूत्र है-
(A) आधार × संगत शीर्षलम्ब .
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब
(C) 2 × आधार × संगत शीर्षलम्ब
(D) \(\frac{1}{3}\) × आधार संगत शीर्षलम्ब
उत्तर-
(A) आधार × संगत शीर्षलम्ब

प्रश्न 3.
निम्नांकित में से किस आकृति में दोनों आकृतियाँ एक ही समान्तर रेखाओं के बीच स्थित नहीं हैं-

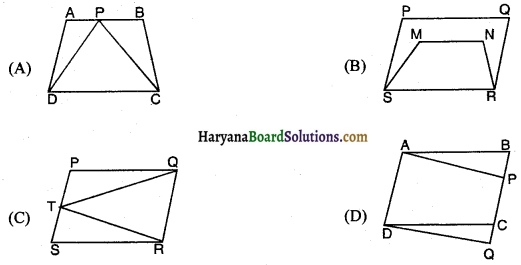
उत्तर-
(B)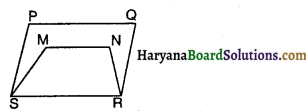

प्रश्न 4.
एक ही आधार वाले और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज _____________ में बराबर होते हैं।
(A) परिमाप
(B) आयतन
(C) लम्बाई
(D) क्षेत्रफल
उत्तर-
(D) क्षेत्रफल

प्रश्न 5.
एक ही आधार वाले और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुज _____________ में बराबर होते हैं।
(A) परिमाप
(B) आयतन
(C) चौड़ाई
(D) क्षेत्रफल
उत्तर-
(D) क्षेत्रफल

प्रश्न 6.
किसी त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र है-
(A) आधार × संगत शीर्षलम्ब
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब
(C) 2 × आधार × संगत शीर्षलम्ब
(D) \(\frac{1}{3}\) × आधार × संगत शीर्षलम्ब
उत्तर-
(B) \(\frac{1}{2}\) × आधार × संगत शीर्षलम्ब

प्रश्न 7.
त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले _____________ त्रिभुजों में विभाजित करती है।
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर-
(B) दो

प्रश्न 8.
किसी समान्तर चतुर्भुज का आधार और शीर्षलम्ब क्रमशः 16 cm और 8 cm हैं, इसका क्षेत्रफल होगा-
(A) 128 cm²
(B) 128 cm
(C) 64 cm²
(D) 64 cm
उत्तर-
(A) 128 cm²

प्रश्न 9.
आधार 20 cm और शीर्षलम्ब 5 cm वाले समान्तर चतुर्भुज का क्षेत्रफल होगा-
(A) 100 cm
(B) 100 cm²
(C) 50 cm
(D) 50 cm²
उत्तर-
(B) 100 cm²

प्रश्न 10.
उस समान्तर चतुर्भुज का क्षेत्रफल क्या होगा जिसका आधार 28.5 cm और संगत शीर्षलम्ब 10 cm है-
(A) 142.5 cm
(B) 142.5 cm²
(C) 285 cm²
(D) 285 cm³
उत्तर-
(C) 285 cm²

प्रश्न 11.
आधार 124 cm और शीर्षलम्ब 10 dm वाले समान्तर चतुर्भुज का क्षेत्रफल होगा-
(A) 1.24 cm²
(B) 1.24 dm²
(C) 1.24 mm²
(D) 1.24 m²
उत्तर-
(D) 1.24 m²

प्रश्न 12.
उस समान्तर चतुर्भुज का शीर्षलम्ब क्या होगा जिसकी एक भुजा 6.5 cm और क्षेत्रफल 26 cm है ?
(A) 4 cm
(B) 4 cm²
(C) 8 cm
(D) 8 cm²
उत्तर-
(A) 4 cm

प्रश्न 13.
क्षेत्रफल 390 cm² और ऊँचाई 26 cm वाले समान्तर चतुर्भुज का आधार होगा-
(A) 15 cm²
(B) 15 cm
(C) 30 cm²
(D) 30 cm
उत्तर-
(B) 15 cm

प्रश्न 14.
क्षेत्रफल 400 cm² और ऊँचाई 8 cm वाले समान्तर चतुर्भुज का आधार होगा-
(A) 100 cm
(B) 100 cm²
(C) 50 cm
(D) 50 cm²
उत्तर-
(C) 50 cm

प्रश्न 15.
संलग्न आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सें०मी०, AE = 8 सें०मी० और CF = 10 सें०मी० है, तो AD का मान होगा-

(A) 0.64 cm
(B) 6.4 cm
(C) 1.28 cm
(D) 12.8 cm
उत्तर-
(D) 12.8 cm

प्रश्न 16.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हों तो ar (EFGH) = _________ × ar (ABCD)
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) 2
(D) 3
उत्तर-
(A) \(\frac{1}{2}\)

प्रश्न 17.
संलग्न आकृति में-Pऔर Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं तो निम्न में से कौन-सा कथन सत्य होगा ?

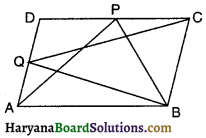
(A) ar (APB) = ar (APD)
(B) ar (APB) = ar (BQC)
(C) ar (APB) = ar (BPC)
(D) ar (BQC) = ar (ABQ)
उत्तर-
(B) ar (APB) = ar (BQC)

प्रश्न 18.
समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का ______________.
(A) दो-गुना
(B) तीन-गुना
(C) आधा
(D) एक-तिहाई
उत्तर-
(C) आधा

प्रश्न 19.
समांतर चतुर्भुज ABCD में, AB = 12 सें०मी० हैं। भुजाओं AB तथा AD के संगत शीर्षलंब क्रमशः 6 सें०मी० तथा 8 सें०मी० हैं जैसे कि आकृति में दिखाया गया है। AD का मान होगा-

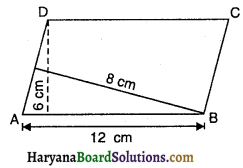
(A) 6 cm
(B) 8 cm
(C) 12 cm
(D) 9 cm
उत्तर-
(D) 9 cm

प्रश्न 20.
∆ABC में, E माध्यिका AD का मध्य-बिन्दु है तो निम्नलिखित में से कौन-सा कथन सत्य होगा?

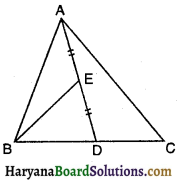
(A) ar (BED) = \(\frac{1}{2}\) ar (ABC)
(B) ar (BED) = \(\frac{1}{3}\) ar (ABC)
(C) a (BED) = \(\frac{1}{4}\) ar (ABC)
(D) ar (BED) = \(\frac{1}{5}\) ar (ABC)
उत्तर-
(C) ar (BED) = \(\frac{1}{4}\) ar (ABC)

प्रश्न 21.
समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले ____________ त्रिभुजों में बाँटते हैं।
(A) चार
(B) तीन
(C) दो
(D) आठ
उत्तर-
(A) चार

प्रश्न 22.
संलग्न आकृति में D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। निम्नलिखित में से कौन-सा कथन सत्य है ?

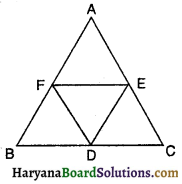
(A) BDEF एक समांतर चतुर्भुज है
(B) ar (DEF) = \(\frac{1}{4}\) ar (ABC)
(C) ar (BDEF) = \(\frac{1}{2}\) ar (ABC)
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 23.
संलग्न आकृति में बिन्दु D और E क्रमशः AABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। निम्नलिखित में से कौन-सा कथन सत्य होगा ?

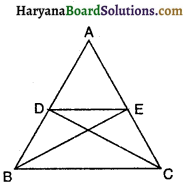
(A) DE ⊥ BC
(B) DE || BC
(C) DE = BC
(D) DE ⊥ AB
उत्तर-
(B) DE || BC

प्रश्न 24.
किसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, इसका क्षेत्रफल होगा-
(A) 24 cm
(B) 12 cm
(C) 12 cm²
(D) 24 cm²
उत्तर-
(C) 12 cm²

प्रश्न 25.
त्रिभुज की ऊँचाई ज्ञात करने का सूत्र है-

उत्तर-
(B)

प्रश्न 26.
आधार 60 cm और क्षेत्रफल 600 cm² वाले त्रिभुज की ऊँचाई होगी-
(A) 20 cm
(B) 10 cm
(C) 5 cm
(D) 40 cm
उत्तर-
(A) 20 cm

प्रश्न 27.
आधार 80 cm और क्षेत्रफल 0.08 m² वाले त्रिभुज की ऊँचाई होगी-
(A) 10 cm
(B) 20 cm
(C) 10 m
(D) 20 m
उत्तर-
(B) 20 cm

प्रश्न 28.
विकर्णों 80 cm और 60 cm वाले एक समचतुर्भुज का क्षेत्रफल होगा-
(A) 3600 cm²
(B) 9600 cm²
(C) 4800 cm²
(D) 2400 cm²
उत्तर-
(D) 2400 cm²

प्रश्न 29.
त्रिभुज का आधार ज्ञात करने का सूत्र हैक्षेत्रफल

उत्तर-
(B)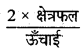

प्रश्न 30.
शीर्षलम्ब 10 cm और क्षेत्रफल 0.5 m² वाले त्रिभुज का आधार होगा-
(A) 10 m
(B) 20 m
(C) 10 cm
(D) 20 cm
उत्तर-
(A) 10 m