Author name: Bhagya

Haryana State Board HBSE 6th Class Science Solutions Chapter 10 Motion and Measurement of Distances Textbook Exercise Questions and Answers.

Haryana Board 6th Class Science Solutions Chapter 10 Motion and Measurement of Distances

HBSE 6th Class Science Motion and Measurement of Distances Textbook Questions and Answers

Exercises

Question 1.
Give two examples each of modes of transport used on land, water and air.
Answer:
Modes of transport used are:
(i) Land: Buses, railways, cars etc.
(ii) Water: Boats, ships.
(iii) Air: Air planes, gas balloons, etc.

Question 2.
Fill in the blanks:
(i) One metre is ………….. cm.
(ii) Five kilometres is ………….. m.
(iii) Motion of a child on a swing is ……………. .
(iv) Motion of a needle of a swing machine is ………….. .
(v) Motion of a wheel of a bicycle is …………… .
Answer:
(i) 100
(ii) 5000
(iii) oscillatory motion
(iv) oscillatory motion
(v) circular motion.

Question 3.
Why can a pace or a foot step not be used as a standard unit of length?
Answer:
The pace or foot step has different lengths for different persons. So they cannot be used as a standard unit of length.

Question 4.
Arrange the following lengths in their increasing magnitude:
1 metre, 1 centimetre, 1 kilometre, 1 millimetre.
Answer:
1 millimetre > 1 centimetre > 1 metre > kilometre.

Question 5.
The height of a person is 1.65 m. Express it into cm and mm.
Answer:
(i) 165 centimetre
(ii) 1650 millimetre.

Question 6.
The distance between Radha’s home and her school is 3250 m. Express this distance into kilometre.
Answer:
3.250 kilometre.

Question 7.
While measuring the length of a knitting needle, the reading of the scale at one end is 3.0 cm and at the other end is 33.1 cm. What is the length of needle?
Answer:
Length of needle = 33.1 cm
(-) 03.0 cm
= 30.1 m

Question 8.
Write the similarity and dissimilarity between the motion of a bicycle and a ceiling fan that has been switched on.
Answer:
The motion of a bicycle and a ceiling fan are in circular motion. Thus both show similar motion. But the ceiling fan moves without changing its position while the bicycle moves with changing its position with time. This shows dissimilarities between two motions.

Question 9.
Why could you not use an elastic measuring tape to measure distance? What would be some of the problems you would meet in telling someone about a distance you measured with an elastic tape?
Answer:
We should not use elastic measuring tape to measure distance because the length of the measuring tape will increase when we pull or stretch the tape for measuring the length. The length may increase or decrease due to its elasticity. So we cannot measure the correct length by elastic measuring tape. The length measured by this tape either will be more or less depending on the elasticity of tape.

Question 10.
Give two examples of periodic motion.
Answer:
Examples of periodic motion:
(i) Motion of a pendulum.
(ii) Motion of a branch of a tree.
(iii) Motion of a child on a swing.

HBSE 6th Class Science Motion and Measurement of Distances Important Questions and Answers

Very Short Answer Type Questions

Question 1.
Give one example where your estimate about the length of an object may be wrong.
Answer:
To measure the length of a table with stretched palm.

Question 2.
Give two examples of measurements that you make in your daily life.
Answer:
(i) To measure the length of cloth before sewing.
(ii) To measure the weight of vegetables before buying.

Question 3.
Name the S.I. unit of length.
Answer:
Metre (m).

Question 4.
Name the unit of length which should be used to express the thickness of a coin?
Answer:
Millimetre (mm).

Question 5.
What is measurement?
Answer:
The comparison of an unknown quantity with a standard known quantity is known as measurement.

Question 6.
Define unit.
Answer:
A quantity adopted as a standard of measurements of a physical quantity is called a unit.

Question 7.
What is a year?
Answer:
Time taken by the earth to revolve around the sun is called a year.

Question 8.
Name two devices used to measure length.
Answer:
(i) Metre scale
(ii) Screw gauge.

Question 9.
If you are sitting in a moving bus, you are at rest or in motion?
Answer:
We are in motion.

Question 10.
Is your class room at rest or in motion?
Answer:
The class room is at rest.

Question 11.
Is the hour is hand of a wall- clock at rest or in motion?
Answer:
Hour’s hand of the wall-dock is in motion.

Question 12.
What type of motion do the vehicles on a straight road perform?
Answer:
The vehicle motion is linear.

Question 13.
What type of motion do the wheels of a bicycle perform?
Answer:
Circular motion.

Question 14.
Give two examples of periodic motion.
Answer:
(i) Rotation of the earth on its axis.
(ii) Moon moves around the sun.

Question 15.
Give one example of an object changing their speed while in motion.
Answer:
Wind changes the speed of man while running with open umbrella.

Question 16.
Name two types of motion.
Answer:
(i) Circular motion
(ii) Oscillatory motion.

Question 17.
Give two examples of rectilinear motion.
Answer:
(i) A bullet fired from a rifle.
(ii) A boy sliding down a slope.

Question 18.
Give two examples of rotational motion.
Answer:
(i) The motion of blades of a ceiling fan.
(ii) Seconds hand in a clock.

Question 19.
What is motion?
Answer:
A body is said to be in motion when it changes its position with time.

Question 20.
Give two examples of linear motion.
Answer:
(i) Motion of bus in a straight line.
(ii) Motion of bullet.

Question 21.
Give an example of objects which move in a line.
Answer:
Falling of a ball freely.

Question 22.
Give an example of objects which move in a circle.
Answer:
Spinning wheel, blades of fan.

Question 23.
Give an example 9f objects which move to and fro.
Answer:
Pendulum of a wall clock.

Question 24.
Define translatory motion.
Answer:
Wheel of a car.

Question 25.
Give one example of rotatory motion.
Answer:
Spinning of a top, spinning wheel’s.

Short Answer Type Questions

Question 1.
State two precautions which you should take while using a metre-scale to measure the length of an object.
Answer:
(i) The scale should be placed along the length to measure. It should be very close to the objects to be measured.
(ii) Eye must be kept vertical above the end point of the object or point where the measurement is taken.

Question 2.
How do you measure the circumference of a one-rupee coin?
Answer:
To measure the circumference of coin wrap the thread around the coin. The length of the thread can be measured with the help of a metre scale.

Question 3.
Describe a method you would use to measure the thickness of a thin wire with the help of a metre scale.
Answer:
Wrap say 25 turns of thin wire around a pencil and see that the wrap should be very close to one another. The wire would form a coil. With the help of meter scale, measure the length of wire and divide it by total number of turns. It will be the thick-ness of a thin wire.

Question 4.
Write three rules which should be observed while writing symbols for S.I. units.
Answer:
Rules to be observed while writing S.I. units and their symbols:
(i) Symbols for units of quantities are to be written with a small letter. For example: symbol of Metre-m.
(ii) Symbol of unit named after a scientist is to be written in capital letters. Examples: Symbol for Kelvin-K.
(iii) Symbols for units are not to be followed by full stop. For example: Symbol for metre is m (and not m.)

Question 5.
Define circular motion.
Answer:
When the object moves along a circular track around a fixed axis. It is said to be in circular motion. Examples: Spinning top and spinning wheel.

Question 6.
Define oscillatory motion.
Answer:
A to and fro motion about its mean position is known as oscillatory motion.

Question 7.
Give some examples of oscillatory motion.
Answer:
Motion of a pendulum, motion of swing etc.

Question 8.
Give an example of objects for each of the following:
1. Object which moves in a line.
2. Object which moves in a circle.
3. Object which has a periodic motion.
Answer:
1. Light comes from the sun.
2. Movement of marry go around.
3. Motion of earth around the sun in one year.

Long Answer Type Questions

Question 1.
What is meant by a standard unit of measurement? Why is it necessary to have standard units of measurement? Name the SI unit of length. Write its symbol.
Answer:
Standard unit of measurement: A unit of measurement which has a fixed value which does not change from person to person or place to place, is called a standard unit of measurement.

It is necessary to have standard units of measurements for the sake of uniformity in measurements.
S.I. unit of length is metre. Its symbol of metre is m.

Question 2.
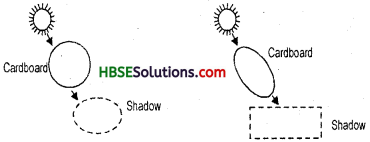
State the precautions which should be taken while using a metre scale to measure the length of an object (like a post card).
Answer:
Precautions to be taken while using a scale:
1. The scale should be placed parallel to the side of the object being measured. It should also be in a touch with the object being measured.
In Fig. 10.18(a) the scale is placed parallel to the side AB of the card which is to be measured. So, this is the correct placement of scale. This will give the correct reading for the length of card. From Fig. 10.18(a) we can see that the correct value of the length of card is 4.2 cm.

In Fig. 10.18(6), however, the scale is not exactly parallel to the side AB of the card being measured. So, it is a wrong placement of the scale. In this case the scale will give a wrong reading for the length of card (which will be greater than the actual length). For example, in Fig. 10.18(6), the scale shows a reading of 4.3 cm for the length of card, which is wrong.

2. While reading the scale, the eye must be placed vertically above the scale mark being read. If the eye is not vertically above the scale mark being read, then the reading becomes wrong.

In Fig. 10.19, the correct position of eye for reading the scale mark on the right side end of the card is at ‘A’ which is vertically above the scale mark being read. So, in Fig. 10.19, the correct reading of length of card from position A is 4.2 cm.

If we read the scale by keeping our eye somewhat towards left side at position B, then the scale reading appears to be 4.3 cm. And if the eye is kept at position C on the right side, then the scale reading appears to be 4.1 cm. The scale readings of 4.3 cm and 4.1 cm taken by keeping eye at positions B and C are wrong.

3. If the scale has a damaged zero mark or broken left end, measure the length of ah object starting from 1 cm mark of scale and then subtract 1 cm from the reading taken at the right end to get the actual length of object.

Question 3.
What is meant by: (a) circular motion and (b) rotational motion? Give two examples of circular motion and two examples of rotational motion.
Answer:
(a) Circular motion:
When an object moves along a circular path, it is called circular motion.
Examples:
(i) The movement of moon around the earth.
(ii) The move of earth around the sun:

(b) Rotational motion:
When an object turns (or spins) about a fixed axis, it is called rotational motion.
Examples:
(i) The motion of a spinning top.
(ii) The spinning of earth on its axis.

Question 4.
When an object is said to be in motion? Explain with the help of an example. State any four types of motion.
Answer:
An object is said to be in motion when its position changes with time. For example, when the position of a car changes with time, we say that car is moving or that the car is in motion. In Fig. 10.20, we see a car at position A in front of a house and tree at a particular urne. After 5 seconds we see the saine car at position B this quit far away from the house. This means that the position of this car is changing with time. So, we say that this car is in motion.
Four types of motion are:
(i) Rectilinear motion
(ii) Circular motion
(iii) Rotational motion and
(iv) Periodic motion.
(i) Rectilinear motion: Motion in a straight line is called rectilinear motion.
(ii) Circular motion: When an object moves along a circular path is called circular motion.
(iii) Rotational motion: When an object turns (or spins) about a fixed axis, it is called rotational motion.
(iv) Periodic motion: The motion which repeats itself after regular intetvals of time, is called periodic motion.

Question 5.
Give a method to measure the length of a pencil.
Answer:
To measure the length of a pencil, we choose a metre scale which should be placed along its length. In Fig. 10.21, zero mark on the scale coincides with the one end of the pencil and the reading coinciding with the other end of the pencil is taken. Since the ruler has some thickness, we may make an error if the eye is not correctly placed. The eye is to be placed exactly above the point where the measurement is to be taken as shown in Fig. 10.21 from the position A. The other end of the pencil coincides with 8.5 cm mark. The length of the pencil is 8.5 cm.

Motion and Measurement of Distances Class 6  HBSE Notes

• Different modes of transport are used to go from one place to another.
• In ancient times, people used length of a foot, the width of a finger and the distance of a step etc. as units of measurements. This caused confusion and a need to develop a uniform system of measurement arose.
• Now we use international system of unit (S.I. unit). This is accepted all over the world. 7.
• Metre is the unit of length in S.I, unit.
• Motion is the change in the position of an object. Motion may be rectilineal’, circular, rotational or
• periodic. gs
• Need of standard units: In ancient times, people used foot, arm, stretched palm as units of lengths. These methods were not satisfactory, because length of arm, foot and stretched palm vary from person to person. However if there are different units of length in the different parts of the world, it is very inconvenient for the exchange of scientific informations. Thus the need of standard units were felt. The unit which people agree to use as a basic unit for measurements, becomes a standard unit for that group of people for the sake of uniformity. Scientists all over the world have accepted following the standard unit for measuring length.
• The standard unit of length is metre. Its sub units are:
  10 mm = 1 cm, 100 cm = 1 metre,
  1000 m = 1 km, 3 x 10⁸ m = 1 light year.
• Measurements of length: In the S.I. system, the length is measured in unit metre (m). It is defined as the distance at 0°C between two lines drawn on a platinum irridium rod kept in the international bureau of weights and measure at screws near Paris. The following table shows the units of length and their relations to metre:

• Rules for measuring length correctly:
  → Fig. 10.1 shows the correct position of the scale:
  
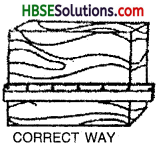
  → To measure the length of the block. It is necessary to place the scale along the length you want to measure more than the actual length.
  → The eye must be placed directly above the points you are reading otherwise there will be an error due to parallex. The magnitude of the error is minimum when the scale is next to the point. The error increases as the distance of scale from the object increases.
  → While measuring the length of an object, if one end of that lies somewhere between few mm marks of the scale. If it is more than 1/2 mm, count it 1 mm or if less than 1/2, neglect it.
  → If the zero mark of the scale is damaged or edge of scale is not smooth, then start measuring from another mark. The difference between two marks gives its correct length.
  → To minimise the error due to wrong marking on the measuring scale, measure the length several times, using different parts of the measuring scale and take average to get nearest correct length.
• Measuring the length of a curved line: To measure the length of a curved line, we can use a thread or a divider from the geometry box.
  → Use a thread to measure the length of curved line AB (Fig. 11.4). Put a knot on the thread near one of its end and place this knot on point A. Now with the help of thumb and finger place a small portion of thread along the line. Now move the thumb which is towards the point A little further so that it takes the position of other thumb next portion of the line. Repeat this process till last end point B is reached.
  → Now, stretched the thread along a metre scale and measure the length between the knot and the mark on the thread. This gives the length of the curved line.
• Motion is a state in which an object is steady or is at rest and the other object is moving. Motion may be rectilinear, circular, rotational or periodic.
• Periodic motion: Motion of a pendulum or motion of a branch of tree are examples of periodic motion. In such type of motion an object repeats its motion after a fixed interval of time.

Haryana State Board HBSE 6th Class Science Solutions Chapter 11 Light Shadows and Reflection Textbook Exercise Questions and Answers.

Haryana Board 6th Class Science Solutions Chapter 11 Light Shadows and Reflection

HBSE 6th Class Science Light Shadows and Reflection Textbook Questions and Answers

Exercises

Question 1.
Rearrange the boxes given below to make a sentence that helps us understand opaque objects.

Answer:

Question 2.
Classify the objects or materials given below as opaque, transparent or translucent and luminous or non-luminous:
Air, water, a piece of rock, a sheet of aluminium, a mirror, a wooden board, a sheet of polythene, a CD, smoke, a sheet of plane glass, fog, a piece of red hot iron, an umbrella, a lighted fluorescent tube, a wall, a sheet of carbon paper, a flame of a gas burner, a sheet of card board, a lighted torch, a sheet of cellophone, a mix mesh, kerosene stone, sun, firefly, moon.
Answer:
(i) Opaque things: A piece of rock, a sheet of aluminum, a mirror, a wooden board, a wall, a sheet xrd board.
(ii) Transparent things: Air, water, a sheet of plane glass.
(iii) Translucent things: A sheet of polythene, a CD, smoke, fog, a sheet of carbon paper, a sheet of cellphone.
(iv) Luminous things: A piece of red hot iron, a lighted fluorescent tube, the flame of a gas burner, a lighted torch, sun, fixfly, moon.
(v) Non-luminous things: An umbrella, a wire mesh, kerosene stove.

Question 3.
Can you think of creating a shape that would give a circular shadow if held in one way and a rectangular shadow if held in another way?
Answer:
Yes, we can think of creating a shape that would give a circular shadow if held in one way and a rectmigular shadow if held in another way. If we held a round card board in front of source of light, it will create a round shadow on the ground and if we turn it at some other position, then it creats a rectangular shadow.

Question 4.
In a completely dark room, if you hold up a mirror in front of you, will you see a right-left inverted image of yourself in the mirror?
Answer:
In a completely dark room, we cannot see our right-left inverted image in the mirror, because there is no mrce of light and we only can see our image in the mirror, when light is reflected from the mirror.

HBSE 6th Class Science Light Shadows and Reflection Important Questions and Answers

Very Short Answer Type Questions

Question 1.
Does the flame of a gas stove emit light?
Answer:
Yes, a gas stove flame emits light.

Question 2.
Give one example of a living thing which emits light.
Answer:
Firefly (Jugnu) is a living source of light.

Question 3.
Give the names of four different sources of light.
Answer:
Sources of light are: Sun, stars, firefly, electric bulb etc.

Question 4.
How does light travel from one point to the other?
Answer:
Light travels from one point to other in straight line.

Question 5.
What is the shape of the shadow?
Answer:
It is similar to the object which forms shadow.

Question 6.
How are shadows formed?
Answer:
Light coming from the source of light falling on the objects obstructed by the objects and does not go ahead. So a shadow is formed.

Question 7.
Are the edges of shadow sharp and distinct?
Answer:
Yes, the edges of the shadow are sharp and distinct.

Question 8.
Does the direction of shadow change during the day?
Answer:
Yes, the direction of shadow changes because the position of the sun changes during the day.

Question 9.
Does, the length of shadow change from season to season?
Answer:
Yes. The length of shadow changes from season to season.

Question 10.
What is a shadow?
Answer:
A dark patch formed behind an opaque object when it is placed in the path of light is called a shadow.

Question 11.
What is umbra?
Answer:
A region of total darkness is called umbra. No ray of light enters this region.

Question 12.
Define penumbra.
Answer:
A region of partial darkness which surrounds the umbra is called penumbra, some light rays reach this region.

Question 13.
What do we call a body that shines of its own?
Answer:
Luminous body.

Question 14.
Name one transparent and one opaque body.
Answer:
Trasparent air, glass, stone, wood (opaque).

Question 15.
What do we call a substance through which light can pass?
Answer:
Transparent substances.

Question 16.
Define opaque substance?
Answer:
The substance through which no light can pass.

Question 17.
Name two translucent substances.
Answer:
Glazed paper, oil paper.

Question 18.
Name two opaque substances.
Answer:
Ordinary paper, rubber sheet.

Question 19.
Name two cold sources of light.
Answer:
Firefly, tube light.

Question 20.
Define reflection of light.
Answer:
When a beam of light is incident on a smooth surface, apart of it os scattered back into the same medium, it is called reflection.

Short Answer Type Questions

Question 1.
Name any four artificial sources to scattering of fight. The air around the objects of light. allows this scattered fight to pass through it and
Answer:
1. Candle,
2. the oil jaino
3. tube
4. toren
5.electric bulb.

Question 2.
Why do objects in a room become transparent, translucent and opaque objects: visible even if sunlight does not enter it?
Answer:
The objects in a room become visible even if the sunlight dose not enter the room, due to scattering of light. The air around the objects allows this scattered light to pass through it and we can see the objects.

Question 3.
Classify the following into transparent, translucent and opaque objects: Wax, spectacle, a heap of salt, stone, dense smoke, wood, skin, balloon, rubber, membrane of tabla, blood, milk.
Answer:
Answer:
Transparent objects: Membrane of tabla, spectacles. Translucent objects: Dense smoke, blood, wax, balloon. Opaque objects: Stone, wood, rubber, milk

Question 4.
How will you convert a transparent glass sheet into a translucent sheet. Suggest any two ways.
Answer:
(i) By covering one side by butter paper.
(ii) By covering one side by thin sheet of plastics.

Question 5.
State the difference between umbra and penumbra.
Answer:

Question 6.
Define regular reflection.
Answer:
When a beam of light falls on a smooth and polished surface, then regular reflection takes place. The smooth surface gives a clear image due to regular reflection. Example: Reflection from a plane mirror.

Question 7.
State laws of reflection.
Answer:
Laws of reflection:
(i) The angle of incidents is equal to the angle of reflection.
(ii) The incident ray, reflected ray and the normal are in the same plane.

Question 8.
Name the features of the image formed by a plane mirror.
Answer:
(i) The image formed by a plane mirror is as far behind the mirror as the object is in front of it.
(ii) It is exactly the same size and shape.
(iii) Image is virtual.
(iv) It is erect but laterally inverted.

Question 9.
Give two effects of light on plants.
Answer:
(i) Plants use light energy to prepare their own food.
(ii) The tips or short apex of a photogenic plant moves towards it. Light acts as a stimulus to plants.

Question 10.
State two differences between transparent and translucent objects.
Answer:

Question 11.
Distinguish between regular and irregular reflection.
Answer:

Question 12.
What is lateral inversion?
Answer:
When we look in a plane mirror, we see the image of the objects placed in front of it. The left of the qbject becomes right of the image and the right of the objects becomes left of the image. This is called lateral inversion.

Question 13.
Why is firefly considered to be a cold source of light?
Answer:
The energy of some chemical reactions within the firefly is released not as heat but as light hence it is called a cold source of light.

Question 14.
Does the length of a shadow change during the day?
Answer:
Yes, the length of a shadow changes during a day. It is longer in the morning. After that it begins to decrease and it is shortest at 12.00 noon. Then begins to increase in length again.

Question 15.
Under what special circumstances, light does not travel in straight line?
Answer:
If the size of the object in the path of light is very small (0.0001 cm/less) light bends at the edge of the object. Thus in such case, light does not travel in straight line.

Question 16.
What would be the shape of an object so that it will cast no shadows on the ground in the light of sun?
Answer:
An object casts no shadow (or very little shadow) on the ground in sunlight when it is either transparent or it is at such a height from the earth that the umbra does not reach the surface of the earth. .

Question 17.
Why is your shadow longest at sunrise and shortest at noon?
Answer:
In the morning at the time of sunrise and in the evening at the time of sunset light rays falling on the earth are not straight. They are inclined. This is why our shadow at this time both (morning and evening) is the longest. At noon the sun is just over above our head and sun-rays fall vertically on the earth. Due to the vertical sun-rays, our shadow formed at noon is the shortest.

Question 18.
What does an object do when light falls on it?
Answer:
It may allow to pass the light through or it may completely cut the light from passing through by absorbing the light or it may scatter the light incident on it.

Question 19.
Why is silvered glass used as a mirror?
Answer:
The silvered glass has a smooth surface and the smoothness helps in forming clear image. Silvering makes it shiny and the shiny surface helps in reducing the absorption.

Long Answer Type Questions

Question 1.
Define the structure and working of a pin-hole camera.
Answer:
Pin-hole camera: It is a simple application of the rectilinear propagation of light.
Construction:
It consists of a rectangular card board box, such that its one side is made of ground glass screen, the side opposite to ground glass has a hole in the middle, whose size is equal to the pin-head of a common pin. The box is blackened from inside, so as to absorb any light falling on its walls.

Working:
(1) Consider a lighted candle AB, in front of pin-hole camera. The rays starting from points of candles, travel in all directions.
(2) A ray of light starting from point ‘A’ along with AH after passing through the pin-hole falls on ground glass screen at point ‘A’.
Similarly another ray starting from point ‘B’ along with BH after passing through the pin-hole will fall on ground glass screen at point ‘Bj
(3) A1B1 is the image of AB. The image formed here is turned upside down, because light travels in straight line.

Light Shadows and Reflection Class 6  HBSE Notes

• Light is an invisible energy which causes in us a sensation of vision. Though it cannot be seen, it unables us to see things.
• An object which emits light is called a source of light. Sources of light are natural as well as artificial. Sun is the main and brightest source of light. Stars, and jugnu (glow worm) and some fish also emit light.
• Artificial sources of light are man-made sources such as candles, lantern, gas lamps and electric bulbs. Bodies are visible only by ’ the light they send to our eyes. They may be luminous and non-luminous sources.
• Light travels in a straight line, which is called rectilinear propagation of light. It explains the formation of the image of an object in a pin-hole camera.
• When light falls on an object, three things can happen:
  → It is almost completely transmitted through the object.
  → Only one part of it may be transmitted and the rest is absorbed or spread out.
  → It may not be allow’ed to pass through at all. On this basis, we can classify the materials into three categories.
• Transparent materials, which allow light to pass through them and through which we can see clearly are known as transparent materials. Examples: Air, water, glass etc.
• Translucent materials: Substances through which light can pass partially and through which we cannot see clearly are called translucent materials. Examples: Wax paper, butter paper, greased paper etc.
• Opaque materials: Substances which do not allow light to pass through them are called opaque substances. We cannot see through them wood, stone etc.
• In the presence of light, opaque objects act as obstacles to propagate light and form in shadows behind them in the form of umbra and penumbra. The region of space where light from the source does not reach and hence the darkest region is called umbra.
• The region where the light does not reach from all parts of the source is called penumbra.
• When light falls on a smooth surface, they change their direction in a well defined manner, called regular reflection.
• There are two laws of reflection:
  → Angle ofincidence is equal to angle of reflection.
  → Incident ray, reflected ray and the normal all lie in the same plane.
• In a plane mirror, the reflected rays appears to come from some objects kept behind the mirror. This is called a virtual image. A real image can be obtained on a screen.
• Luminous objects. Objects which emit light their own are called luminous objects. Sun, stars, firefly, burning candle, electric bulb and gas lamps are examples of luminous objects. One lumin is the luminous flux of that source whose illuminating power is 1/4rc candela. The brightness is the property measured in units called foot candles. The modern unit now is lux. 1 Foot candle = 10.76 lux.
• Light travels in straight lines:
  → Take three pieces of a card board. Use supports to make them stand vertically on the table.
  → Make holes A, B, C in each of them such that the holes are in one straight line.
  → Now place a candle near hole A at the same height as the hole in the card board.
  → Now see from C. You will notice that the flame of the candle is visible. Now displace one of the card boards from its position so that the holes are no longer in a straight line. The flame is not visible.
  This activity shows that light from the candle travels in a straight line from the candle to the eyes.
• Formation of shadows: Shadows are formed when light is obstructed by objects. An opaque object casts a dark shadow, translucent casts a weak shadow and transparent objects cast no shadows.
  A shadow of the object is formed in the direction opposite to the side of the source of light. Take a wooden stick about half a metre long. Fix one end of it in open ground where there are no trees and buildings near it. Look its shadow in the morning and mark its points of shadow. Note the direction of sun with respect to the stick. It is formed opposite to the direction of sun.
  Again look at the shadow at about 11 a.m. and then about 2 p.m. At 11 a.m. the shadow formed is on the same side and about 2 p.m. shadow is formed in a direction opposite to that seen in the morning.
• Conclusion:
  → A shadow of an object is formed in the direction opposite to the side of the source of light.
  → Shadow moves according to the movement of sources of light or objects.
  → The length of shadow changes with time.
• Reflection of light: When a beam of light strikes on a plane surface a part of it is turned back into the same direction, it is called reflection.
• On a polished surface, regular reflection takes place and on rough surface irregular reflection takes place.
• Lateral inversion: When we look in a plane mirror, we see the image of the objects placed in front of it. The left of the objects become right and right of the objects become left of the image. Left hand side appears right handside in the image. This is called lateral inversion.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Intext Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Intext Questions

(पाठगत प्रश्न – पृष्ठ 210-211)

प्रश्न 1.
मोहन स्वयं अपने और अपनी बहन के लिए चाय बनाता है। वह 300 mL पानी, 2 चम्मच चीनी, 1 चम्मच चाय-पत्ती और 50 mL दूध का उपयोग करता है। यदि वह पाँच व्यक्तियों के लिए चाय बनाए, तो उसे प्रत्येक वस्तु की कितनी मात्रा की आवश्यकता होगी?
हल:
दो व्यक्तियों के लिए आवश्यक पानी की मात्रा = 300 mL
∴ पाँच व्यक्तियों के लिए आवश्यक पानी की मात्रा = \(\frac{300}{2}\) × 5mL
∴ पानी की मात्रा = 750 mL

दो व्यक्तियों के लिए आवश्यक चीनी की मात्रा = 2 चम्मच

∴ पाँच व्यक्तियों के लिए आवश्यक चीनी की मात्रा = \(\frac{2}{2}\) × 5
∴ चीनी की मात्रा = 5 चम्मच

दो व्यक्तियों के लिए आवश्यक चाय-पत्ती की मात्रा = 1 चम्मच

∴ पाँच व्यक्तियों के लिए आवश्यक चाय-पत्ती की मात्रा y
= \(\frac{1}{2}\) × 5

∴ चाय पत्ती की मात्रा = \(2 \frac{1}{2}\) चम्मच
दो व्यक्तियों के लिए आवश्यक दूध की मात्रा = 50 mL
∴ पाँच व्यक्तियों के लिए आवश्यक दूध की मात्रा
= \(\frac{50}{2}\) × 5mL
∴ = 125 mL
अतः, पाँच व्यक्तियों के लिए चाय बनाने के लिए मोहन को 750 mL पानी, 5 चम्मच चीनी, \(2 \frac{1}{2}\) चम्मच चाय-पत्ती और 125 mL दूध की आवश्यकता होगी।

(प्रयास कीजिए – पृष्ठ 212)

प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि क्या x और y अनुक्रमानुपाती हैं?

हल:
(i) प्रश्नानुसार
\(\frac{20}{40}\) = \(\frac{17}{34}\) = \(\frac{14}{28}\) = \(\frac{11}{22}\) = \(\frac{8}{16}\) = \(\frac{5}{10}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\), इस प्रकार, x और y की अनुरूप कीमत का औसत स्थिर है और \(\frac{1}{2}\) के बराबर है। अतः x और y स्थिर विचरण \(\frac{1}{2}\) के साथ अनुक्रमानुपाती हैं।

(ii) प्रश्नानुसार,
\(\frac{6}{4}\) ≠ \(\frac{10}{8}\) ≠ \(\frac{14}{12}\) ≠ \(\frac{18}{16}\) ≠ \(\frac{22}{20}\) ≠ \(\frac{26}{24}\) ≠ \(\frac{30}{28}\), इस प्रकार, x और y के अनुरूप कीमतों का औसत स्थिर नहीं है। अतः, x और y अनुक्रमानुपाती नहीं हैं

(iii) प्रश्नानुसार,
\(\frac{5}{15}\) = \(\frac{8}{24}\) = \(\frac{12}{36}\) ≠ \(\frac{15}{60}\) = \(\frac{18}{72}\) ≠ \(\frac{20}{100}\) इत्यादि इस प्रकार, x और y की अनुरूप कीमतें स्थिर नहीं हैं । अतः Jx और y अनुक्रमानुपाती नहीं हैं।

प्रश्न 2.
मूलधन = ₹ 1000, ब्याज दर = 8% वार्षिक। निम्नलिखित सारणी को भरिए तथा ज्ञात कीजिए कि, किस प्रकार का ब्याज (साधारण या चक्रवृद्धि) समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता या परिवर्तित होता है।

हल:
दिया है-P = ₹ 1000, R = 8% वार्षिक
साधारण ब्याज के लिए
1 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×1}{100}\))
= ₹ 80

2 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×2}{100}\))
= ₹ 160

3 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×3}{100}\))
= ₹ 240

चक्रवृद्धि ब्याज के लिए
1 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{1}\)
= ₹ 1000 × \(\frac{108}{100}\)
= ₹ 1080

∴ 1 वर्ष का चक्रवृद्धि ब्याज = ₹ (1080 – 1000)
= ₹ 80

2 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{2}\)
= ₹ 1000 × \(\frac{108}{100}\) × \(\frac{108}{100}\)
= ₹ 1166.40

∴ 2 वर्ष का चक्रवृद्धि ब्याज = ₹ (1166.40 – 1000)
= ₹ 166.40

3 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{3}\)
= ₹ 1000 × \(\frac{108}{100}\) × \(\frac{108}{100}\) × \(\frac{108}{100}\)
= ₹ 1259.712

∴ 3 वर्ष का चक्रवृद्धि ब्याज = ₹ (1259.712 – 1000)
= ₹ 259.712

∴ सारणी अग्रांकित होगी

साधारण ब्याज समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता है।

(इन्हें कीजिए – पृष्ठ 216-217)

प्रश्न 1.
एक वर्गांकित कागज़ पर भिन्न-भिन्न भुजाओं के पाँच वर्ग खींचिए। निम्नलिखित सूचना को एकसारणी के रूप में लिखिए:

ज्ञात कीजिए कि क्या भुजा की लंबाई
(a) वर्ग के परिमाप के अनुक्रमानुपाती है।
(b) वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।
हल :
• वर्ग-1
माना वर्ग के एक भुजा की लम्बाई (L) = 3 cm

वर्ग का परिमाप (P) = (3 + 3 + 3 + 3) cm = 12 cm
\(\frac{L}{P}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)

वर्ग का क्षेत्रफल (A) = 3 cm × 3 cm = 9 cm

वर्ग – 2
माना वर्ग की एक भुजा की लम्बाई (L) = 4 cm

वर्ग का परिमाप (P) = (4 + 4 + 4 + 4) cm = 16 cm
\(\frac{L}{A}\) = \(\frac{4}{16}\) = \(\frac{1}{4}\)
वर्ग का क्षेत्रफल (A) =4 cm × 4 cm = 16 cm
\(\frac{L}{A}\) = \(\frac{4}{16}\) = \(\frac{1}{4}\)

• वर्ग – 3
माना वर्ग की एक भुजा की लम्बाई (L) = 5 cm

वर्ग की परिमाप (P) = (5 + 5 + 5 + 5) cm = 20 cm
\(\frac{L}{A}\) = \(\frac{5}{20}\) = \(\frac{1}{5}\)
वर्ग का क्षेत्रफल (A) =5 cm × 5 cm = 20 cm
\(\frac{L}{P}\) = \(\frac{5}{20}\) = \(\frac{1}{5}\)

• वर्ग – 4
माना वर्ग की एक भुजा की लम्बाई (L) = 6 cm

वर्ग की परिमाप (P) = (6 + 6 + 6 + 6) cm = 24 cm
\(\frac{L}{P}\) = \(\frac{6}{24}\) = \(\frac{1}{6}\)
वर्ग का क्षेत्रफल (A) =6 cm × 6 cm = 20 cm
\(\frac{L}{A}\) = \(\frac{6}{24}\) = \(\frac{1}{6}\)

• वर्ग – 5
माना वर्ग की एक भुजा की लम्बाई (L) = 7 cm

वर्ग की परिमाप (P) = (7 + 7 + 7 + 7) cm = 24 cm
\(\frac{L}{P}\) = \(\frac{7}{28}\) = \(\frac{1}{4}\)
वर्ग का क्षेत्रफल (A) =7 cm × 7 cm = 49 cm
\(\frac{L}{A}\) = \(\frac{7}{49}\) = \(\frac{1}{7}\)

(a) भुजा की लम्बाई वर्ग के परिमाप के अनुक्रमानुपाती होती है।
(b) भुजा की लम्बाई वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 217)

प्रश्न 1.
सीधा समानुपात (विचरण)’ की अब तक हल की गई समस्याओं में से कुछ को लीजिए। क्या आप सोचते हैं कि इन समस्याओं को इकाई की विधि या ऐकिक विधि (unitary method) से हल किया जा सकता है?
हल:
हम प्रश्नावली 13.1 से कुछ प्रश्न लेकर उन्हें ऐकिक विधि से निम्नानुसार हल करते हैं
प्रश्न 3:
∵ 75 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = 1 भाग
∴ 1 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = \(\frac{1}{75}\) भाग
∴ 1800 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = \(\frac{1}{75}\) × 1800 भाग
= 24 भाग

प्रश्न 4:
∵ 6 घंटे में भरने वाली बोतलों की संख्या = 840
∴ 1 घंटे में बोतलें भरेंगी = \(\frac{840}{6}\)

∴ 5 घंटे में बोतलें भरेंगी = \(\frac{840}{6}\) × 5
= 700

प्रश्न 10:
25 मिनट अर्थात् \(\frac{25}{60}\) घंटे में, तय दूरी = 14 km
∴ 1 घंटे में तय दूरी = 14 ÷ \(\frac{25}{60}\)
= (14 × \(\frac{60}{25}\)) km
∴ 5 घंटे में तय दूरी = (14 × \(\frac{60}{25}\) × 5) km
= 168 km

(प्रयास कीजिए – पृष्ठ 219)

प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि कौन से चरों ( यहाँx और ) के युग्म परस्पर प्रतिलोम समानुपात में हैं

हल:
(i) प्रश्नानुसार,
x × y = 50 × 5 ≠ 40 × 6 ≠ 30 × 7 ≠ 20 × 8
इस प्रकार, x और y परस्पर व्युत्क्रमानुपाती नहीं हैं।

(ii) प्रश्नानुसार,
x × y = 100 × 60 = 200 × 30
= 300 × 20 = 400 × 15
= 6000 = स्थिर
इस प्रकार, x और y परस्पर व्युत्क्रमानुपाती हैं।

(iii) प्रश्नानुसार
x × y = 90 × 10 = 60 × 15 = 45 × 20
≠ 30 × 25 ≠ 20 × 30 ≠ 5 × 35
इस प्रकार, x और y व्युत्क्रमानुपात में नहीं हैं।

Haryana State Board HBSE 8th Class Maths Solutions Chapter 12 घातांक और घात Intext Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 12 घातांक और घात Intext Questions

(पाठगत प्रश्न – पृष्ठ 201)

प्रश्न 1.
10^-10 किसके बराबर है?
हल:
ऐसी संख्या जो शून्य न हो तथा a का एक पूर्णांक n हो तो a^-n को an का व्युत्क्रम कहते हैं।
अर्थात् a^-n = \(\frac{1}{a^{n}}\)
∴ 10^-10 = \(\frac{1}{10^{10}}\)

(प्रयास कीजिए – पृष्ठ 202)

प्रश्न 1.
गुणात्मक प्रतिलोम लिखिए
(i) 2^-4
(ii) 10^-5
(iii) 7^-2
(iv) 5^-3
(v) 10^-100
हल:
हम जानते हैं कि a का गुणात्मक प्रतिलोम \(\frac{1}{a}\) है।
अतः
(i) 2^-4 का गुणात्मक प्रतिलोम है \(\frac{1}{2^{4}}\) = 2⁴
(ii) 10^-5 का गुणात्मक प्रतिलोम है \(\frac{1}{10^{5}}\) = 10⁵
(iii) 7^-2 का गुणात्मक प्रतिलोम है \(\frac{1}{7^{2}}\) = 10⁵
(iv) 5^-3 का गुणात्मक प्रतिलोम है \(\frac{1}{5^{3}}\) = 5³
(v) 10^-100 का गुणात्मक प्रतिलोम है \(\frac{1}{10^{100}}\) = 10¹⁰⁰

(प्रयास कीजिए – पृष्ठ 202)

प्रश्न 1.
घातांकों का उपयोग करते हुए निम्न को विस्तारित रूप में लिखिए
(i) 1025.63
(ii) 1256.249
हल:
(i) 1025.63 = 1 × 1000 + 2 × 10 + 5 × 1 + \(\frac{6}{10}\) + \(\frac{3}{100}\)
= 1 × 10³ + 0 × 10² + 2 × 10¹ + 5 + 6 × 10^-1 + 3 × 10^-2.

(ii) 1256.249 = 1 × 1000 + 2 × 100 + 5 × 10 + 6 × 1 + \(\frac{2}{10}\) + \(\frac{4}{100}\) + \(\frac{9}{1000}\)
= 1 × 10³ + 2 × 10² + 5 × 10¹ + 6 × 10⁰ + 2 × 10^-1 + 4 × 10^-2 + 9 × 10^-3.

(प्रयास कीजिए – पृष्ठ 203)

प्रश्न 1.
घातांक रूप को सरल कीजिए और लिखिए
(i) (-2)^-3 × (-2)^-4
(ii) p³ × p^-10
(iii) 3² × 3^-5 × 3⁶.
हल:
हम जानते हैं कि a (जो शून्य नहीं है) पूर्णांक है
और m, n पूर्णांक हैं तो a^m × aⁿ = a^m+n

(i) (-2)^-3 × (-2)^-4 = (-2)^{(-3) + (-4)} = (-2)^-7

(ii) p³ × p^-10 = p^{3 – 10} = p^-7 = \(\frac{1}{p^{7}}\)

(iii) 3² × 3^-5 × 3⁶ = (3)^2+(-5)+6 = 3³.

(प्रयास कीजिए – पृष्ठ 206)

निम्न तथ्यों का अवलोकन कीजिए

1. पृथ्वी से सूर्य की दूरी 149,600,000,000 m है।
2. प्रकाश का वेग 300,000,000 m/s है।
3. कक्षा VII की गणित की पुस्तक की मोटाई 20 mm है।
4. लाल रक्त कोशिकाओं का औसत व्यास 0.000007 mm है।
5. मनुष्य के बाल की मोटाई की परास 0.005 cm से 0.01 cm होती है।
6. पृथ्वी से चंद्रमा की दूरी लगभग 384,467,000 m होती है।
7. पौधों की कोशिकाओं का आकार 0.00001275 m है।
8. सूर्य की औसत त्रिज्या 695000 km है।
9. अंतरिक्ष शटल में ठोस राकेट बूस्टर को प्रेरित करने के लिए शटल का द्रव्यमान 503600 kg है।
10. एक कागज की मोटाई 0.0016 cm है।
11. कम्प्यूटर चिप के एक तार का व्यास 0.000003 m है।
12. माउंट एवरेस्ट की ऊँचाई 8848 m है।
उपरोक्त तथ्यों के आधार पर बहुत बड़ी तथा बहुत छोटी संख्याओं की पहचान कीजिए और संगत सारणी में लिखिए-

हल:
बहुत बड़ी तथा बहुत छोटी संख्याओं की पहचान

(प्रयास कीजिए। – पृष्ठ 207)

प्रश्न 1.
निम्न संख्याओं को मानक रूप में लिखिए
(i) 0.000000564
(ii) 0.0000021
(iii) 21600000
(iv) 15240000
हल:
(i) 0.000000564
= \(\frac{564}{1000000000}\) = \(\frac{564}{10^{9}}\)
= \(\frac{5.64 \times 100}{10^{9}}\)
= 5.64 × 10² × 10^-9
= 5.64 × 10^-7.

(ii) 0.0000021 = \(\frac{21}{10000000}\) = \(\frac{21}{10^{7}}\)
= \(\frac{2.1 \times 10}{10^{7}}\)
= 2.1 × 10¹ × 10^-7
= 2.1 × 10^-6

(iii) 21600000 = 216 × 10⁵ = 2.16 × 100 × 10⁵
= 2.16 × 10² × 10⁵ = 2.16 × 10⁷

(iv) 15240000 = 1524 × 10⁴
= 1.524 × 1000 × 10⁴
= 1.524 × 10³ × 10⁴
= 1.524 × 10⁷.

प्रश्न 2.
दिए गए तथ्यों (पाठ्यपुस्तक का पृष्ठ 206) को मानक रूप में लिखिए।
हल:
सभी तथ्य मानक रूप में निम्नानुसार हैं
1. पृथ्वी से सूर्य की दूरी = 149,600,000,000 m
= 1.496 × 10¹¹ m

2. प्रकाश का वेग = 300,000,000 m/sec
= 3 × 10⁸ m/sec

3. कक्षा VII की गणित की पुस्तक की मोटाई
= 20 mm = 2 × 10¹ mm

4. लाल रक्त कोशिकाओं का औसत व्यास
= 0.000007 mm
= 7 × 10^-6mm

5. मनुष्य के बाल की मोटाई की परास
= 0.005 cm से 0.01 cm
= 5 × 10^-3 cm से 1 × 10^-2 cm

6. पृथ्वी से चन्द्रमा की दूरी = 384,467,000 m (लगभग)
= 3.84467 × 10⁸ m

7. पौधों की कोशिकाओं का आकार = 0.00001275 m
= 1.275 × 10-5 m

8. सूर्य की औसत त्रिज्या = 695000 km
= 6.95 × 10^-5 km

9. अंतरिक्ष शटल में ठोस रॉकेट बूस्टर को प्रेरित करने के लिए रॉकेट का द्रव्यमान 503600 kg = 5.036 × 10⁵ kg

10. एक कागज की मोटाई = 0.0016 cm
= 1.6 × 10^-3 cm

11. कम्प्यूटर चिप के एक तार का व्यास = 0.000003 m
= 3 × 10^-6 m

12. माउंट एवरेस्ट की ऊँचाई = 8848 m
= 8.848 × 10³ m

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4

प्रश्न 1.
आपको एक बेलनाकार टैंक दिया हुआ है, निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयतन:

(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा र सकता है।
(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।
(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।
हल:
(a) आयतन ज्ञात करेंगे।
(b) पृष्ठीय क्षेत्रफल ज्ञात करेंगे।
(c) आयतन ज्ञात करेंगे।

प्रश्न 2.
बेलन A का व्यास 7 cm और ऊँचाई 14 cm है। बेलन B का व्यास 14 cm और ऊँचाई 7 cm है। परिकलन किए बिना क्या आप बता सकते हैं कि इन दोनों में किसका आयतन अधिक है। दोनों बेलनों का आयतन ज्ञात करते हुए इसका सत्यापन कीजिए। जाँच कीजिए कि क्या अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

हल:
(i) बेलन A के लिए-
पहले बेलन (A) के लिए आयतन = πr²h
दूसरे बेलन (B) के लिए आयतन = π(2r)² × \(\frac{h}{2}\)
= \(\frac{4πr²h}{2}\)
= 2πr²h

अतः दूसरे बेलन (B) का आयतन पहले बेलन (A) के आयतन का दूना होगा।
अंत: दूसरे बेलन (B) का आयतन अधिक है।
त्रिज्या = \(\frac{7}{2}\) = 3.5 cm
ऊँचाई (h) = 14 cm
बेलन का आयतन = πr²h
= \(\frac{22}{7}\) × (3.5)² × 14 cm³
= \(\frac{22}{7}\) × \(\frac{35}{10}\) × \(\frac{35}{10}\) × 14 cm³
आयतन = \(\frac{44 \times 35 \times 35}{100}\) cm³
= 539 cm³
अत: बेलन A का आयतन = 539 cm³
बेलन A का पृष्ठीय क्षेत्रफल = 2πr(r+h)
= 2 × \(\frac{22}{7}\) × 3.5 (3.5 + 14)
= 2 × 22 × 0.5 × 17.5
= 22 × 17.5
= 385 cm²

(ii) बेलन B के लिए –
त्रिज्या r = \(\frac{14}{2}\) =7 cm
ऊँचाई h = 7cm बेलन का आयतन = πr²h
= \(\frac{22}{7}\) × (7)² × 7
= \(\frac{22}{7}\) × 49 × 7
= 49 × 22 cm³
अत: आयतन = 1078 cm³ = 2 × 539
= 2 × पहले बेलन A का आयतन

बेलन B का पृष्ठीय क्षेत्रफल = 2πr(r+h)
= 2 × \(\frac{22}{7}\) × 7 (7+7)
= 44 × 14 = 616 cm²
अतः बेलन B का आयतन, बेलन A के आयतन से अधिक होगा । अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

प्रश्न 3.
एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए, जिसके आधार का क्षेत्रफल 180 cm और जिसका आयतन 900 cm है।
हल :
माना, घनाभ की ऊँचाई = h
अत: घनाभ का आयतन = घनाभ के आधार का क्षेत्रफल × h
900 = 180 × h
h = \(\frac{900}{180}\) = 5
अत: घनाभ की ऊँचाई = 5 cm.

प्रश्न 4.
एक घनाभ की विमाएँ 60 cm × 54 cm × 30 cm हैं । इस घनाभ के अन्दर 6 cm भुजा वाले कितने छोटे घन रखे जा सकते हैं ?
हल:
लम्बाई (l) = 60 cm
चौड़ाई (b) = 54 cm
ऊँचाई (h) = 30 cm
घनाभ का आयतन = 60 × 54 × 30 (V = lbh)
= 97200 cm³

घन की भुजा = 6 cm
घन का आयतन = (6)³ [V = a³]
= 216 cm³

घनों की संख्या = \(\frac{97200}{216}\) = 450
अतः घनों की संख्या = 450

प्रश्न 5.
एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए, जिसका आयतन 1.54 m’ और जिसके आधार का व्यास 140 cm है?
हल:
बेलन का व्यास = 140 cm
त्रिज्या (r) = \(\frac{140}{2}\) = 70 cm
त्रिज्या (r) = 0.7 m
बेलन की ऊँचाई h = ?
बेलन का आयतन = πr²h =1.54
h = \(\frac{1.54}{\pi r^{2}}\)
h = \(\frac{1.54×7}{22 ×0.7×0.7}\)
h = 1
अतः, बेलन की ऊँचाई = 1 m

प्रश्न 6.
एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या 1.5 mऔर । लम्बाई 7 m है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञातं कीजिए।

हल:
बेलनाकार टैंक की त्रिज्या (r) = 1.5m
टैंक की लम्बाई (h) = 7m
टैंक का आयतन = πr²h
= \(\frac{22}{7}\) × (1.5)² × 7
= \(\frac{22}{7}\) × 1.5 × 1.5 × 7
= 2.25 × 22 m³

आयतन = 49.5 m²
अत: टैंक का आयतन = 49.5 m²
.. 1 m² = 1000 लीटर
49.5 m² = 49.5 x 1000 लीटर
= 49500 लीटर
टैंक में दूध की मात्रा = 49500 लीटर

प्रश्न 7.
यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो
(i) इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
(ii) इसके आयतन में कितने गुना वृद्धि होगी?
हल:
(i) माना, घन का किनारा = x
पृष्ठीय क्षेत्रफल = 6x²
अब, घन का किनारा दुगुना किया जाता है।
नया किनारा = 2x
अब, नया पृष्ठीय के. = 6(2x)²
= 6 × 4x²
नया पृष्ठीय से. = 24x²
= 4(6x²)
घन के पृष्ठीय क्षे. में 4 गुना वृद्धि होगी।

(ii) घन का आयतन = x³
भुजा (किनारा) दुगुना करने पर, आयतन = (2x)²
नया आयतन = (8x)²
अतः आयतन में 8 गुना वृद्धि होगी।

प्रश्न 8.
एक कुंड के अन्दर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108zi है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

हल:
दिया है, कुंड का आयतन = 108 m³
पानी का आयतन = 108 × 1000 लीटर = 108000 लीटर
60 लीटर पानी कुंड में गिरता है = 1 मिनट में
108000 लीटर पानी कुंड में गिरेगा है
= \(\frac{1}{60}\) × 108000 मिनट में
= 1800 मिनट
= \(\frac{1800}{60}\) घंटे
= 30 घंटे
अतः कुल समय = 30 घंटे

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Intext Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Intext Questions

(पाठगत प्रश्न – पृष्ठ 177-178)

प्रश्न 1.
यह एक आयताकार बगीचे की आकृति है 3 जिसकी लम्बाई 30 मीटर और चौड़ाई 20 मीटर है (आकृति देखिए।
(i) इस बगीचे को चारों ओर से घेरने वाली बाड़ की लम्बाई क्या है?
(ii) कितनी भूमि बगीचे द्वारा व्याप्त है।
(iii) बगीचे के परिमाप के साथ-साथ अन्दर की तरफ एक मीटर चौड़ा रास्ता है जिस पर सीमेंट लगवाना है। यदि 4 वर्गमीटर (m2) क्षेत्रफल पर सीमेंट लगवाने के लिए एक बोरी सीमेंट चाहिए तो इस पूरे रास्ते पर सीमेंट लगवाने के लिए कितनी सीमेंट की बोरियों की आवश्यकता है?

(iv) जैसा कि आरेख (आकृति देखिए) में दर्शाया गया है। इस बगीचे में फूलों की दो आयताकार क्यारियाँ हैं, जिनमें से प्रत्येक का आकार 1.5 m × 2 m है और शेष बगीचे के ऊपर घास है। घास द्वारा घिरा हुआ क्षेत्रफल ज्ञात कीजिए।
हल:
(i) बगीचे को चारों ओर से घेरने वाली बाड़ की लम्बाई
= बगीचे का परिमाप
= 2(लम्बाई + चौड़ाई)
= 2 (30+ 20) मीटर
= 2 × 50 मीटर
= 100 मीटर

(ii) बगीचे द्वारा व्याप्त भूमि = बगीचे का क्षेत्रफल
= लम्बाई × चौड़ाई
= (30 × 20) मी²
= 600 मी²

(iii) यहाँ, AB की लम्बाई = 30 मीटर,
चौड़ाई = QR = 20 मी
ABCD का क्षेत्रफल = (30 × 20) मी² = 600 मी²
लम्बाई PQ = (30 मी – 2 मी)= 28 मी
चौड़ाई QR = (20 मी – 2 मी)= 18 मी
∴ PQRS का क्षेत्रफल = (28 × 18) मी² = 504 मी²

अब, सीमेंट लगवाने वाले रास्ते का क्षेत्रफल
= ABCD का क्षेत्रफल – PQRS का क्षेत्रफल = (600 – 504) मी²
= 96 मी²

सीमेंट की बोरियों की संख्या की गणना-

= \(\frac{96}{4}\)
= 24 : अतः 24 बोरी सीमेंट की आवश्यकता होगी।

(iv) 1.5 मी × 2 मी आकार वाले 2 आयताकार फूल लगी क्यारियों का क्षेत्रफल
= (2 × 1.5 × 2) मी²
= 2 × 3 मी² = 6 मी²

घास द्वारा घिरा हुआ क्षेत्रफल = ABCD का क्षेत्रफल – 2 फूल लगी क्यारियों का क्षेत्रफल
= (504 – 6) मी²
= 498 मी²
∴ घास लगे भाग का क्षेत्रफले = 498 मी²

(पृष्ठ 178)

प्रश्न 1.
निम्नलिखित का मिलान कीजिए-
हल:

उपर्युक्त दी गई आकृतियों में से प्रत्येक के परिमाप के लिए व्यंजक (सूत्र) निम्नलिखित हैं-
आयत : 2(a+b)
वर्ग : 4a
त्रिभुज : तीनों भुजाओं का योग
समान्तर चतुर्भुज : 2 × आसन्न भुजाओं का योग
वृत्त . : 2πb

(प्रयास कीजिए – पृष्ठ 179)

प्रश्न 1.
(a) निम्नलिखित आकृतियों का उनके क्षेत्रफलों से मिलान कीजिए
(b) प्रत्येक आकार का परिमाप लिखिए।
हल:
(a) आकृतियों का उनके क्षेत्रफलों से मिलान निम्न प्रकार है

(b) संगत आकार का परिमाप
(i) 2(14 + a) सेमी, जहाँ a सेमी आसन्न भुजा की लम्बाई है।
(ii) (\(\frac{22}{7}\) × 4 + 14) सेमी = 36 सेमी
(iii) (14 + 11 + 9) सेमी = 34 सेमी
(iv) 2 (14 + 7) सेमी = 42 सेमी
(v) (4 × 7) सेमी = 28 सेमी

(प्रयास कीजिए – पृष्ठ 180)

प्रश्न 1.
नजमा की बहन के पास भी एक समलम्ब के आकार का प्लॉट है जैसा कि आकृति में दर्शाया गया है। इसे तीन भागों में बाँटिए। दर्शाइए कि समलम्ब =WXYZ का क्षेत्रफल = h
(\(\frac{a+b}{2}\)

हल:
माना कि बिन्दु Z तथा बिन्दु Y से WX पर डाले गए लम्ब के पाद क्रमशः L तथा M हैं।
तब, WXYZ समलम्ब का क्षेत्रफल = समकोण AWLZ का क्षेत्रफल + आयत LMYZ का क्षेत्रफल + समकोण ΔMXY का क्षेत्रफल
=
\(\frac{1}{2}\)(WL × ZL) + LM × MY × \(\frac{1}{2}\) (MX × YM)
= \(\frac{1}{2}\)(WL × h) + LM × h + \(\frac{1}{2}\)(MX × h) [∵ ZL = MY = h]
= \(\frac{1}{2}\) h × (WL + 2LM + MX)
= \(\frac{1}{2}\)h × (WL + LM + MX + LM)
= \(\frac{1}{2}\)h × (WX + ZY)
[∵ WL + LM + MX = WX और LM = ZY]
= \(\frac{1}{2}\)h × (a + b) = h\(\frac{a+b}{2}\)

प्रश्न 2.
यदि h = 10 cm, c = 6 cm, b = 12 cm, d =4 cm, तो इसके प्रत्येक भाग का मान अलग-अलग ज्ञात कीजिए और WXYZ का क्षेत्रफल ज्ञात करने के लिए इनका योग कीजिए। h, a तथा b का मान व्यंजक \(\frac{a+b}{2}\) में रखते हुए इसका सत्यापन कीजिए।
हल:
स्पष्टतः, h = 10 cm, c = 6 cm, b = 12 cm तथा d =4cm लेने पर a = c + b + d = (6 + 12 + 4) cm = 22 cm
समलम्ब WXYZ का क्षेत्रफल = ΔWLZ का क्षेत्रफल + आयत LMYZ का क्षेत्रफल + ΔMXY का क्षेत्रफल
= \(\frac{1}{2}\) × c × h + b × h + \(\frac{1}{2}\) × d × h
= (\(\frac{1}{2}\) × 6 × 10 + 12 × 10 + \(\frac{1}{2}\) × 4 × 10) cm²
= (30 + 120 + 20) cm²
= 170 cm²
और सूत्र के अनुसार-

समलम्ब WXYZ का क्षेत्रफल = \(\frac{h \times (a+b)}{2}\)
= \(\frac{10 \times (22+12)}{2}\) cm²
= 5 × 34 cm²
= 170 cm²
अतः, क्षेत्रफल सत्यापित होता है।

(पृष्ठ 181)

प्रश्न 1.
निम्नलिखित समलम्बों का क्षेत्रफल ज्ञात कीजिए-

हल:
(i) क्षेत्रफल = \(\frac{1}{2}\)(9 + 7) × 3 cm²
= \(\frac{1}{2}\) × 16 × 3cm²
= 8 × 3 cm²
= 24 cm²

(ii) क्षेत्रफल = \(\frac{1}{2}\)(10 + 5) × 6 cm²
= \(\frac{1}{2}\) × 15 × 6 cm²
= 15 × 3 cm²
= 45 cm²

(पृष्ठ 182)

प्रश्न 1
हम जानते हैं कि 2 0समान्तर चतुर्भुज भी एक चतुर्भुज है। आइए, इसे भी हम दो त्रिभुजों में है विभक्त करते हैं और इन दोनों त्रिभुजों का क्षेत्रफल ज्ञात करते हैं। इस प्रकार समान्तर चतुर्भुज का क्षेत्रफल भी ज्ञात करते हैं। क्या यह सूत्र आपको पूर्व में ज्ञात सूत्र से मेल खाता है? (आकृति देखिए)

हल:
समान्तर चतुर्भुज PORS का क्षेत्रफल = ΔPQS का क्षेत्रफल + ΔQRS का क्षेत्रफल
= \(\frac{1}{2}\) × b × h + \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = bh
हम समलम्ब के क्षेत्रफल का सूत्र जानते हैं। आइए इसका प्रयोग करते हैं।

समान्तर चतुर्भुज PQRS का क्षेत्रफल = \(\frac{1}{2}\) × (समान्तर भुजाओं का योग) × इन भुजाओं के बीच की दूरी
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = bh
हाँ, यह सूत्र हमें पूर्व में ज्ञात सूत्र से मेल खाता है।

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 183)

प्रश्न 1.
समान्तर चतुर्भुज का विकर्ण खींचकर इसे दो सर्वांगसम त्रिभुजों में बाँटा जाता है। क्या समलम्ब को भी दो सर्वांगसम त्रिभुजों में बाँटा जा सकता है?
हल:
एक समलम्ब को दो सर्वांगसम त्रिभुजों में नहीं बाँटा जा सकता है।

(प्रयास कीजिए – पृष्ठ 183)

प्रश्न 1.
निम्नलिखित चतुर्भुजों का क्षेत्रफल ज्ञात कीजिए (आकृति देखिए)

हल:
(i) चतुर्भुज ABCD का क्षेत्रफल = क्षेत्रफल (ΔABC) + क्षेत्रफल (ΔACD)
= (\(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5) cm²
= (3 × 3 + 3 × 5) cm²
= (9 + 15) cm² = 24 cm²

(ii) चतुर्भुज EFGH का क्षेत्रफल = समचतुर्भुज EFGH का क्षेत्रफल
= \(\frac{1}{2}\) × EG × FH
= (\(\frac{1}{2}\) × 7 × 6) cm²
= 21 cm²

(iii) चतुर्भुज PQRS का क्षेत्रफल = समान्तर चतुर्भुज PQRS का क्षेत्रफल
= 2 × ΔPSR का क्षेत्रफल
= 2 × \(\frac{1}{2}\) × PR × SN
= (8 × 2) cm²
= 16 cm²

(पृष्ठ 184)

प्रश्न 1.
(i) निम्नलिखित बहुभुजों (आकृति देखिए) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलम्बों) में विभाजित कीजिए।

हल:
बहुभुज EFGHI को जैसा कि आकृति में दिखाया गया है, अलग-अलग भागों में बाँटा जाता है।

बहुभुज EFGHI का क्षेत्रफल = क्षेत्रफल (ΔEFI) + क्षेत्रफल (ΔFLG) + क्षेत्रफल (समलम्ब LKHG) + क्षेत्रफलं (ΔHKI)
= \(\frac{1}{2}\) × FI × EM + latex]\frac{1}{2}[/latex] × FL × GL + \(\frac{1}{2}\)(KH + LG) × LK + \(\frac{1}{2}\) × KI × KH
बहुभुज MNOPQR को जैसा कि आकृति में दिखाया गया है, अलग-अलग भागों में N B बाँटा जाता है।

बहुभुज MNOPQR का क्षेत्रफल = क्षेत्रफल (MBN) + क्षेत्रफल (समलम्ब MBDR) + क्षेत्रफल (ΔRDQ) + क्षेत्रफल (ΔFCQ) + क्षेत्रफल (समलम्ब CPOA) + क्षेत्रफल (ΔOAN)
= \(\frac{1}{2}\) × BN × MB + \(\frac{1}{2}\) ×(DR+MB) × BD + \(\frac{1}{2}\) × QD × RD +
\(\frac{1}{2}\) × CQ × PC + \(\frac{1}{2}\) × (CP + AO) × AC + \(\frac{1}{2}\) × NA × OA

(ii) बहुभुज ABCDE को विभिन्न भागों में बाँटा गया है जैसा कि आकृति में दर्शाया गया है। यदि AD = AE = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm और BF = 2 cm, CH = 3cm, EG = 2.5 cm तो इसका क्षेत्रफल ज्ञात कीजिए।

हल:
बहुभुज ABCDE का क्षेत्रफल = ΔAFB का क्षेत्रफल + समलम्ब FBCH का क्षेत्रफल + ΔCHD का क्षेत्रफल + ADE का क्षेत्रफल
= \(\frac{1}{2}\) × AF × BF + \(\frac{1}{2}\) × (BF + CH) × FH + \(\frac{1}{2}\) × HD × CH +
\(\frac{1}{2}\) × AD × GE
= \(\frac{1}{2}\) × 3 × 2 cm² + \(\frac{1}{2}\) × (2 + 3) × 3 cm² + \(\frac{1}{2}\) × 2 × 3 cm² + \(\frac{1}{2}\) × 8 × 2.5 cm²
[∵ FH = AH – AF= (6 – 3) cm = 3 cm और HD = AD – AH= (8 – 6) cm = 2 cm]
= (3 + \(\frac{1}{2}\) + 3 + 10) cm²
= (\(\frac{6+15+6+20}{2}\)) cm²
= \(\frac{47}{2}\) cm²
= \(23 \frac{1}{2}\) cm²

(iii) यदि MP = 9cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm तो बहुभुज MNOPQR (आकृति देखिए) का क्षेत्रफल ज्ञात कीजिए। NA, OC, QD एवं RB विकर्ण MP पर खींचे गए लम्ब हैं।

हल:
बहुभुज MNOPQR का क्षेत्रफल = ΔMAN का क्षेत्रफल + समलम्ब ΔNOC का क्षेत्रफल + ΔOCP का क्षेत्रफल + ΔMBR का क्षेत्रफल + समलम्ब RBDQ का क्षेत्रफल + ΔQDP का क्षेत्रफल
= \(\frac{1}{2}\) × MA × AN + \(\frac{1}{2}\) × (AN + CO) × AC + \(\frac{1}{2}\) × CP × CO + \(\frac{1}{2}\) × MB × RB + \(\frac{1}{2}\) × (RB+QD) + \(\frac{1}{2}\) × BD + \(\frac{1}{2}\) × DP × QD
= \(\frac{1}{2}\) × 2 × 2.5 cm² + \(\frac{1}{2}\) × (2.5 + 3) × 4 cm² +1 × 3 × 3 cm² + \(\frac{1}{2}\) × 4 × 2.5 cm² + \(\frac{1}{2}\) × (2.5 + 2) × 3 cm² + \(\frac{1}{2}\) × 2 × 2 cm²
[∵ AC = MC – MA = (6 – 2) =4 cm, CP = MP- MC = (9 – 6) cm = 3 cm, BD = MD – MB = (7 – 4)= 3 cm और DP = MP – MD = (9 – 7) cm = 2 cm]
= (2.5 + 11 + 4.5 + 5 + 6.75 + 2) cm²
= 31.75 cm²

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 188)

प्रश्न 1.
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?

हल:
क्योंकि बेलन की वृत्ताकार सर्वांगसम फलकें होती हैं जो एकदूसरे के समान्तर होती हैं । इसलिए दिए गए ठोस को बेलन कहना गलत है।

(प्रयास कीजिए – पृष्ठ 189)

प्रश्न 1.
निम्नलिखित घनाभों (आकृति देखिए) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए

हल:
(i) दिया गया हैलम्बाई (l) = 6cm, चौड़ाई (b) =4cm तथा ऊँचाई (h) =2 cm
∴ घनाभ का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6)
= 2 (24 + 8 + 12)
= 2 × 44
= 88 cm²

(ii) दिया गया हैलम्बाई (l) = 4 cm, चौड़ाई (b) = 4 cm तथा ऊँचाई (h) = 10 cm
∴ घनाभ का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 2(56 + 40)
= 192 cm²

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 190)

प्रश्न 1.
क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल?
हल:
अतः घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल।

प्रश्न 2.
यदि हम किसी घनाभ [आकृति (i)) की ऊँचाई और आधार की लम्बाई को परस्पर बदलकर एक दूसरा घनाभ [आकृति (ii)] प्राप्त कर लें तो क्या पार्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?

हल:
घनाभ (i) का पार्श्व क्षेत्रफल = 2(l + b) h
और घनाभ (ii) का पार्श्व पृष्ठीय क्षेत्रफल = 2(h + b) × l
स्पष्ट रूप से, ये परिणाम भिन्न हैं।
अतः, घनाभ की स्थिति को बदलने से इसका पार्श्व पृष्ठीय क्षेत्रफल बदल जाता है।

(प्रयास कीजिए – पृष्ठ 191)

प्रश्न 1.
घन A का पृष्ठीय क्षेत्रफल और घन B का पाव पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल:
घन (A) का पृष्ठीय क्षेत्रफल = 6l²
= 6(10)² cm²
= 600 cm²

घन (B) का पार्श्व पृष्ठीय क्षेत्रफल = 4(side)²
= 4(8)²
= 4 × 64
= 256 cm²

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 191)

प्रश्न 1.
(i) b भुजा वाले दो घनों को मिलाकर एक घनाभ बनाया गया है (आकृति)। इस घनाभ का पृष्ठीय क्षेत्रफल क्या है? क्या यह 12b² है? क्या ऐसे तीन घनों को मिलाकर बनाए गए घनाभ का पृष्ठीय क्षेत्रफल 18b² है? क्यों?
(ii) न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?

(iii) किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है? कितने घनों के 2 फलक पेंट हुए हैं? कितने घनों के तीन फलक पेंट हुए हैं?

हल:
(i) दो घनों को मिलाने से हमें एक घनाभ प्राप्त
जिसकी लम्बाई, L = b + b = 2b इकाई
चौड़ाई, B = b इकाई
ऊँचाई, H = b इकाई
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 (LB + BH + LH)
= 2(2b × b + b × b + 2b × b) वर्ग इकाई
= 2(2b² + b² + 2b²) वर्ग इकाई = 10b² वर्ग इकाई
इसलिए, यह 12b² नहीं है।

तीन घन को क्रमनुसर मिलाया जाये, तब इस प्रकार प्राप्त घनाभ की विमाएँ निम्न होंगी :
L = लम्बाई = 3b, B = चौड़ाई = b और H = ऊँचाई = b
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2(LB + BH + LH)
= 2(3b × b + b × b + 3b × b) वर्ग इकाई
= 2(3b² + b² + 3b²) वर्ग इकाई
= 14b² वर्ग इकाई
इसलिए, यह = 18b² नहीं है।

(ii) बराबर भुजाओं के 12 घनों को मिलाने से निम्न घनाभ प्राप्त होता होता है :
(b)
इस स्थिति में : l = 12b, b = b तथा h = b
∴ इसका पृष्ठीय क्षेत्रफल = 2(12b × b + b × b + 12b × b)
= 2(12b² + b² + 12b²)
= 2 × 25b²
= 50b²

इस स्थिति में : l = 6b, b = b तथा h = 2b
∴ इसका पृष्ठीय क्षेत्रफल = 2(6b × b + b × 2b + 6b × 2b)
= 2(6b² + 2b² + 12b²)
= 2 × 20b²
= 40b²

(c)
इस स्थिति में : l = 4b, b = b तथा h = 3b
∴ इसका पृष्ठीय क्षेत्रफल = 2(4b × b + b × 3b + 4b × 3b)
= 2(4b² + 3b² + 12b²)
= 2 × 19b²
= 38b²
अतः, सबसे कम पृष्ठीय क्षेत्रफल के लिए घनों को, चित्र के व्यवस्थित किया जा सकता है।

(iii) घनों की संख्या, जिनकी एक भी फलक पेंट नहीं किया गया है = 16
घनों की संख्या, जिनकी एक फलक पेंट किया गया है = 24
घनों की संख्या, जिनकी दो फलक पेंट किए गए हैं = 16
घनों की संख्या, जिनकी तीन फलकें पेंट किए गए हैं = 8

(प्रयास कीजिए – पृष्ठ 193)

प्रश्न 1.
निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए

हल:
(i) प्रशनुसार , r = 14 cm और h = 8 cm
∴ कुल पृष्ठीय क्षेत्रफल = 2πrh + 2πr²
= (2 × \(\frac{22}{7}\) × 14 × 8 + 2 × \(\frac{22}{7}\) × 14 × 14) cm²
= (704 + 1232) cm²
= 1936 cm²

(ii) चित्रानुसार, r = 7, m = 1 m तथा h = 2 m
कुल पृष्ठीय क्षेत्रफल = 2πrh + 2πr²
= (2 × \(\frac{22}{7}\) × 1 × 2 + 2 × \(\frac{22}{7}\) × 1 × 1) m²
= (\(\frac{88}{7}\) +\(\frac{44}{7}\)) m²
= \(\frac{132}{7}\) m²
= \(18 \frac{6}{7}\) m²

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 193)

प्रश्न 1.
नोट कीजिए कि किसी बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय)क्षेत्रफल, आधार की परिधि- बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप x घनाभ की ऊँचाई के रूप में लिख सकते हैं?
हल:

हम जानते हैं कि घनाभ का पार्श्व पृष्ठीय क्षेत्रफल = 2(l + b) × h
= आधार का परिमाप × ऊँचाई इस प्रकार, हम एक घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप × घनाभ की ऊँचाई के रूप में लिख सकते हैं।

(पृष्ठ 196)

प्रश्न 1.
समान आकार (प्रत्येक घन की लम्बाई समान) वाले 36 घन लीजिए, एक घनाभ बनाने के लिए उन्हें व्यवस्थित कीजिए। आप इन्हें अनेक रूपों में व्यवस्थित कर सकते हैं। निम्नलिखित सारणी पर विचार कीजिए

हल:

हम देखते हैं कि इन घनाभों को बनाने के लिए हमने 36 घनों का प्रयोग किया है। इसलिए प्रत्येक स्थिति में इसका आयतन 36 घन इकाई है। स्पष्ट रूप से, यह लम्बाई × चौड़ाई × ऊँचाई के बराबर है।

(प्रयास कीजिए – पृष्ठ 197)

प्रश्न 1.
निम्नलिखित घनाभों (आकृति) का आयतन ज्ञात कीजिए

हल:
(i) घनाभ का आयतन = (8 × 3 × 2) cm³
= 48 cm³
(ii) घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई
= (24 × \(\frac{3}{100}\)) m
= 0.72 m³

(प्रयास कीजिए – पृष्ठ 197)

प्रश्न 1.
निम्नलिखित घनों का आयतन ज्ञात कीजिए-
(a) 4 cm भुजा वाला
(b) 1.5 m भुजा वाला
हल:
(a) घन का आयतन = (भुजा)³
= (4)³ cm³
= 64 cm³

(b) घन का आयतन = (भुजा)³
= (1.5)³ m³
= 3.375 m³

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 197-198)

प्रश्न 1.
एक कम्पनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा A → 3 cm × 8 cm × 20 cm, डिब्बा B → 4 cm × 12 cm × 10 cm. डिब्बे का कौन-सा आकार कम्पनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परन्तु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो?
हल:
डिब्बा A :
आयतन = (3 × 8 × 20) cm³
= 480 cm³

पृष्ठीय क्षेत्रफल = 2(3 × 8 + 8 × 20 + 20 × 3) cm²
= 2(24 + 160 + 60) cm²
= 2 × 244 cm³
= 488 cm²

डिब्बा B:
आयतन = (4 × 12 × 10) cm²
= 480 cm²

पृष्ठीय क्षेत्रफल
= 2(4 × 12+ 12 × 10 + 10 × 4) cm²
= 2(48 + 120+ 40) cm²
= 2 × 208 cm = 416 cm²

स्पष्ट है कि B प्रकार के डिब्बे का आयतन = A प्रकार के डिब्बे का आयतन

परन्तु, B प्रकार के डिब्बे का पृष्ठीय क्षेत्रफल A प्रकार के डिब्बे के पृष्ठीय क्षेत्रफल से कम है।
∴ डिब्बा B में कम सामग्री लगेगी।
इसलिए डिब्बा B आर्थिक रूप से अधिक लाभदायक है। एक अन्य प्रकार का डिब्बा जिसका आकार 8 cm × 6 cm × 10 cm है अर्थात् आयतन 480 cm³ है।
इसका पृष्ठीय क्षेत्रफल = 2(48 + 60 + 80) cm²
= 2 (188) cm²
= 376 cm²
स्पष्ट है कि इस डिब्बे का पृष्ठीय क्षेत्रफल डिब्बा B से भी कम है। इसलिए यह दिए गए दोनों प्रकार के डिब्बों से आर्थिक रूप से अधिक लाभदायक है।

(प्रयास कीजिए – पृष्ठ 198)

प्रश्न 1.
नीचे दिए बेलनों का आयतन ज्ञात कीजिए

हल:
(i) बेलन का आयतन = πr²h
जहाँ r = 7 cm, h = 10 cm
= (\(\frac{22}{7}\) × 7 × 7 × 10) cm³
= (2 × 70) cm³
= 1540 cm³

(ii) बेलन का आयतन = (आधार का क्षेत्रफल) x ऊँचाई
= (250 × 2) m³
= 500 m³

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.3

प्रश्न 1.
दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है । किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?

हल :
घनाभाकार डिब्बे
(a) का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (60 × 40 + 40 × 50 + 50 × 60) cm²
= 2(2400 + 2000 + 3000) cm²
= 2 × 7400 cm²
= 14800 cm²

घनाकार डिब्बे (b) का कुल पृष्ठीय क्षेत्रफल = 6 × (50)²
= 6 × 50 × 50
= 15000 cm²
डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल, डिब्बे (b) के कुल पृष्ठीय क्षेत्रफल से कम है, अतः डिब्बे (a) को बनाने मैं कम सामग्री की आवश्यकता होगी।

प्रश्न 2.
80 cm × 48 cm × 24 cm माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। ऐसे 100 सूटकेसों को रुकने के लिए 96 cm चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता होगी?
हल :
सूटकेस की ल. = 80 cm
चौ. = 48 cm
ऊँ. = 24 cm
सूटकेस की कुल सतह का क्षेत्रफल = 2(lb + bh + hl)
=2 (80 × 48 + 48 × 24 + 24 × 80)
= 2(3840 + 1152 + 1920)
= 2 × 6912
= 13824 cm²
अब, तिरपाल की चौ. = 96 cm
माना तिरपाल की ल. = x cm
∴ तिरपाल का क्षेत्रफल = l × b
= 96x cm²
∴ 96x = 13824
∴ ल., x = \(\frac{13824}{96}\) = 144 cm

अब,
100 सूटकेसों को तिरपाल से ढकने के लिए ल. = 144 × 100 cm
= \(\frac{144 \times 100}{100}\)m

∴ तिरपाल की कुल लम्बाई = 144 m

प्रश्न 3.
एक ऐसे घन की भुजा ज्ञात कीजिए, जिसका पृष्ठीय क्षेत्रफल 600 cm है।
हल :
माना घन की भुजा = x
घन का पृष्ठीय क्षेत्रफल = 6x²
दिया है पृष्ठीय क्षेत्रफल = 600
∴ 6x² = 600
x² = 100
अत: घन की भुजा x = 10 cm

प्रश्न 4.
रूखसार ने 1 m x 2 m x 1.5 m माप वाली एक पेटी को बाहर से पेंट किया । यदि उसने पेटी – के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया ?

हल:
पेटी की, ल. (l) = 1 m
चौ. (b) = 2 m
ऊँ. (h) = 1.5 m
पेटी का कुल पृष्ठीय क्षेत्रफल =2 (lb + bh + hl)
= 2 (1 × 2 + 2 × 1.5 + 1 × 1.5)
= 2(2 + 3 + 1.5)
= 2 (6.5)
= 13 m²

पेटी के तल का क्षे. (जिस पर पेंट नहीं होना है) = l × b = 2 ×1
= 2 m²
अत: वह पेटी के = (13 – 2) m²
= 11 m² क्षेत्रफल को पेंट करती है

प्रश्न 5.
डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है, जिसकी ल., चौ. और ऊँ. क्रमश: 15 m, 10 m, एवं 7 m है । पेंट की प्रत्येक कैन की सहायता से 100 m² क्षेत्रफल को पैंट किया जा सकता है तो उस कमरे के लिए उसे पैंट की कितनी कैनों की आवश्यकता होगी?
हल:
कमरे की माप : लम्बाई (l) = 15 m
चौड़ाई (b) = 10 m
ऊँचाई (h) = 7 m
कमरे का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh +hl)
= 2(15 × 10 + 10 × 7 + 7 × 15)
= 2(150 + 70 + 105)
= 2 × 325
= 650 m²

परन्तु वह फर्श पर पेंट नहीं कर रहा है।
तब, फर्श का क्षे. = l × b.
= 15 × 10
= 150 m²

∴ पेंट किया गया क्षेत्र = 650 – 150
= 500 m²

∵ 100 m² में आवश्यक कैन = 1
∴ 500 m² में आवश्यक कैन = \(\frac{500}{100}\) = 5
∴ कैनों की संख्या = 5

प्रश्न 6.
वर्णन कीजिए कि निम्न आकृतियाँ किस प्रकार एकसमान हैं और किस प्रकार एक-दूसरे से भिन्न हैं? किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है ?

हल :
(i) समानता – दोनों की समान ऊँचाई है।
(ii) असमानता – एक बेलन तथा दूसरा घन है।
वेलन की त्रिज्या = \(\frac{7}{2}\) = 3.5 cm,
ऊँ (h) = 7 cm

∴ बेलन का पार्श्व पृष्ठीय क्षे. = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 7
= 44 x 3.5
∴ पार्श्व पृष्ठीय क्षे. = 154 cm²
घन की भुजा (1) =7 cm
घन के पार्श्व का पृष्ठीय क्षे. = 6l²
= 6 × (7)²
=6 × 49
∴ पार्श्व पृष्ठीय क्षे. = 294 cm²
अत: घन का पार्श्व पृष्ठीय क्षे. अधिक है।

प्रश्न 7.
7 m त्रिज्या और 3 m ऊंचाई वाला एक बन्द बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
हल :
टैंक की त्रिज्या = 7 m
तथा, ऊँचाई = 3 m

बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr(h+r) = 2 × \(\frac{22}{7}\) × 7 (3+7) m²
= 44 × (10) m²
= 440 m²
अतः आवश्यक चादर = 440 m²

प्रश्न 8.
एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल 4224 cm है । इसे इसकी ऊंचाई के अनुदिश काटकर 33 cm चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए ।
हल :
माना, आयताकार चादर की लम्बाई = l cm
तथा दिया है – चादर की चौड़ाई = 33 cm
∴ बेलन का पार्श्व पृष्ठीय क्षेत्रफल = आयताकार चादर का क्षेत्रफल
4224 = l × 33
∴ लम्बाई = 4224
∴ लम्बाई (l) = 128 cm
आयताकार चादर का परिमाप = 2 (लम्बाई + डाई)
= 2(128 + 33)
= 2 × 161
अत: चादर का परिमाप =322 cm

प्रश्न 9.
किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं । यदि सड़क रोलर का व्यास 84 cm और लम्बाई 1 m हैं तो सड़क का क्षेत्रफल ज्ञात कीजिए।

हल :
रोलर का व्यास = 84 cm
∴ अर्द्धव्यास r = 42 cm
अतः r = 10.42 m
(∵ 1 m = 100 cm)

रोलर की ल. (h) = 1 m
रोलर की आकृति बेलनाकार है, तब
∵ रोलर द्वारा 1 चक्कर में तय किया क्षेत्रफल = रोलर का पृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × (0.42) × 1
= \(\frac{44 \times 42 \times 1}{7 \times 100}\)
= 2.64 m²

∵ रोलर के 1 चक्कर में चला आवश्यक क्षेत्र = 2.64 m²
∴ 750 चक्कर में आवश्यक क्षेत्र = 2.64 × 750
= 1980 m²
अतः रोलर को चक्कर चलने के लिए सड़क का क्षेत्र
= 1980 m²

प्रश्न 10.
एक कम्पनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है, जिनका व्यास 14 cm और ऊँचाई 20 cm हैं । कम्पनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है, तो लेवल का क्षेत्रफल क्या है ?

हल :
बेलन का व्यास = 14cm
∴ बेलन की त्रिज्या (r) = 7 cm
कर्तन की कुल ऊँचाई (h) = 20 cm
∴ लेवल की ऊँचाई (h) = 20 – (2 + 2)
= 20 – 4
h = 16 cm

अत: चिपकाने वाले लेबल की आकृति भी बेलनाकार ही होगी, जिसकी त्रिज्य, r = 7 cm
तथा ऊँचाई (h) = 16 cm
अतः लेबल का क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 16
= 44 × 16 = 704 cm²
अतः लेबल का क्षेत्रफल = 704 cm²

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 1.
एक मेज के ऊपरी पृष्ठ ( सतह) का आकार समलम्ब जैसा है। यदि इसकी समान्तर भुजाएँ 1 m और 1.2 m हैं तथा इन समान्तर भुजाओं के बीच की दूरी 0.8 m है, तो इसका क्षेत्रफल ज्ञात कीजिए।

हल:
हल :
मेज के ऊपरी पृष्ठ (समलम्ब) का क्षेत्रफल = \(\frac{1}{2}\) × (समान्तर भुजाओं का योग) × ऊँचाई
= \(\frac{1}{2}\) (1+ 1.2) × 0.8
= \(\frac{1}{2}\) × 2.2 × 0.8
= 1.1 × 0.8
= 0.88 m²

प्रश्न 2.
एक समलम्ब का क्षेत्रफल 34 cm और ऊंचाई 4cm है। यदि समान्तर भुजाओं में से एक की 10 cm लम्बाई है। दूसरी समान्तर भुजा की लम्बाई ज्ञात कीजिए।

हल:
माना दुसरी समान्तर भुजा = x cm.
हम जानते हैं कि समलम्ब का क्षे. = \(\frac{1}{2}\) ×(समान्तर भुजाओं का योग) × ऊँचाई
34 = \(\frac{1}{2}\) (10+ x) × 4
2 × 34 = (10+x) × 4 (2 का पक्षान्तरण करने पर)
\(\frac{2 \times 34}{4}\) = 10 + x (4 का पक्षान्तरण करने पर)
= 10 + x = 17
∴ x = 17 – 10 = 7 (10 का पक्षान्तरण करने पर)
∴ अतः, दूसरी समान्तर भुजा = 7 cm

प्रश्न 3.
एक समलम्ब के आकार के खेत ABCD की बाड़ की लम्बाई 120 m है। यदि BC = 48 m, CD = 17 m और AD = 40 m है, तो A इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा AB समान्तर भुजाओं AD तथा BC पर लम्ब है।

हल:
समलम्ब की भुजाएँ :
BC = 48 m
AD = 40 m
∠ABC = 90°.
D= 17 m
समलम्ब ABCD का परिमाप = 120 m
= AB + BC + CD + DA = 120
= AB+48+ 17+ 40 = 120
= AB+ 105 = 120
AB = 120 – 105 = 15
AB = 15m
अब, समलम्ब ABCD का क्षेत्रफल = \(\frac{1}{2}\) (समान्तर भुजाओं का योग) × ऊँचाई
= \(\frac{1}{2}\)(48 + 40) × 15
खेत का क्षेत्रफल = 660 m².

प्रश्न 4.
एक चतुर्भुज के आकार के खेत का विकर्ण 24 m है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गये लम्ब 8 m तथा 13 m हैं । खेत का क्षेत्रफल ज्ञात कीजिए।

हल:
चतुर्भुज ABCD को विकर्ण AC द्वारा 13m दो त्रिभुजों में बाँटा गया है।

(i) ∆ABC का क्षे. = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 24 × 8
= 24 × 4
= 96 m²

(ii) ∆ACD का क्षे. = \(\frac{1}{2}\) × AC × DE
= \(\frac{1}{2}\) × 24 × 3
= 12 × 13
= 156 m²

चतुर्भुज ABCD का क्षे= ∆ABC का क्षे. + ∆ACD का क्षे.
= 96 + 156 = 252 m²

प्रश्न 5.
किसी समचतुर्भुज के विकर्ण 7.5cm एवं 12 cm हैं । इसका क्षेत्रफल ज्ञात कीजिए।
हल:
हम जानते हैं –

किसमचतुर्भुज का क्षेत्रफल = \(\frac{दोनों विकर्णों का गुणनफल}{2}\)
= \(\frac{12 \times 7.5}{2}\)
= 6 × 7.5
= 45.0 cm²
अत: क्षेत्रफल = 45 cm²

प्रश्न 6.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा 6 cm और शीर्षलम्ब 4 cm हैं । यदि एक विकर्ण की लम्बाई 8 cin है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल :
विकर्ण AC, समचतुर्भुज ABCD को दो ΔABC तथा ΔACD में बाँटता है।

अतः समचतुर्भुज का क्षे. = ΔACD का छे + ΔABC का क्षे.
अत: \(\frac{1}{2}\)(AB+ CD) × ऊँचाई (शीर्षलम्ब)
= \(\frac{1}{2}\) × AC × OD + \(\frac{1}{2}\) × AC × OB
= \(\frac{1}{2}\)(6+6) × 4
= \(\frac{1}{2}\) × 8 × OD + \(\frac{1}{2}\) × 8 × OD
= 12 × 2 = 4 DO + 4 DO (∵ OB = OD)
24 = 8 DO (∵ OD = \(\frac{24}{3}\) = 3)
∴ विकर्ण, BD = DO + BO
= 3 + 3 = 6cm
अत: समचतुर्भुज का क्षे० = 24 cm²
तथा, विकर्ण = 6 cm

प्रश्न 7.
किसी भवन के फर्श में चतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण 45 cm तथा 30 cm लम्बाई के हैं । 14 प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।
हल :
हम जानते हैं कि,


= \(\frac{45 \times 30}{2}\)
= 45 × 15.
= 675 cm²
= \(\frac{675}{100 \times 100}\) m²
= 0.0675 mm²
अत: समचतुर्भुजाकार टाइल का क्षेत्रफल = 0.0675 m²

अब, 3000 टाइलों का क्षे. = 0.0675 × 3000 m²
= 202.5 m²
3000 टाइलों का क्षेत्रफल = 202.5 m²
अब, खर्च = 202.5 × 4 = 810.0
पॉलिश कराने का खर्च = ₹810

प्रश्न 8.
मोहन एक समलम्ब के आकार का खेत खरीदना चाहता है । इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समान्तर हैं और लम्बाई में दुगुनी है । यदि इस खेत का क्षेत्रफल 10500 m है² और दो समान्तर भुजाओं के बीच की लम्बवत् दूरी 100 m है, तो नदी के साथ वाली भुजा की लम्बाई ज्ञात कीजिए।
हल :
समलम्ब का क्षे.= 10500 m²
प्रश्नानुसार, DC = 2AB
तथा, DC||AB

समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) (AB+ CD) × 100
10500 = \(\frac{1}{2}\) (AB+ 2AB) × 100
10500 = \(\frac{3}{2}\) AB × 100
\(\frac{10500 \times 2}{10o \times 3}\) = AB = 70
∴ AB = 70 m

अत: भुजा AB = 70 m
तथा CD = 70 × 2 = 140 m

प्रश्न 9.
एक ऊपर उठे हुए। चबूतरे का ऊपरी पृष्ठ 44m अष्टभुज के आकार का है। GHb जैसा कि आकृति में दर्शाया । गया है । अष्टभुजी पृष्ठ का । क्षेत्रफल ज्ञात कीजिए।

हल :
चबूतरे का ऊपरी पृष्ठ एक आयत GHCD
तथा दो समलम्ब चतुर्भुजों DEFG तथा ARCH में बँटा है।

अत: ऊपरी पृष्ठ का क्षेत्रफल = आयत CDGH का क्षे. + 2 समलम्बों का क्षे.
⇒ 11 × 5 + 2 [\(\frac{1}{2}\)(5 + 4) × 4]
⇒ 55 + (5 + 4) × 4
⇒ 55 + 16 × 4
⇒ 55 + 64 = 119
अतः क्षेत्रफल = 119 m²

प्रश्न 10.
एक पंचभुज आकार का बगीचा है, जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया । दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए । क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?

हल :
(i) ज्योति के आरेख के अनुसार-
DF भुजा के द्वारा पंचभुज को दो भागों में बाँटा गया है।

इस प्रकार, 2 समान समलम्ब चतुर्भुजों में बैंट जायेगा ।
अतः बगीचे का क्षेत्रफल = AFDE का क्षे. + FBCD का क्षे.
या 2 × समलम्ब AFDE का क्षेत्र = 2 × [\(\frac{1}{2}\)(FD + AE) × AF]
= [(30 + 15) × \(\frac{15}{2}\)]
= 45 × \(\frac{15}{2}\)
= \(\frac{675}{2}\)
= 337.5 m²

∴ बगीचे का क्षेत्रफल = 337.5 m²

(ii) कविता के आरेख के अनुसार,
पंचभुज ABCDE को दो भागों में बाँटा गया है।

∵ दो बगीचे का क्षेत्रफल ज्ञात करने की अन्य विधि भी है।
बगीचे AEDCBA का क्षेत्रफल = वर्ग ABCE का क्षेत्रफल + AEDC का क्षेत्रफल
= 15 × 15 + \(\frac{1}{2}\) × 15 ×15
= 225 + \(\frac{1}{2}\) × 225
= 225 + 112.5 = 337.5 m²

प्रश्न 11.
संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अन्त:विमाएँ क्रमश: 24 cm × 28 cm एवं 16 cm × 20 cm हैं । यदि फ्रेम के प्रत्येक खण्ड की चौड़ाई समान है, तो प्रत्येक खण्ड का क्षेत्रफल ज्ञात कीजिए ।

हल :
प्रत्येक खण्ड की चौड़ाई समान है।
= 28 – 20 = 8cm

प्रत्येक खण्ड की चौड़ाई (x) = \(\frac{8}{2}\) = 4 cm
अत: x = 4cm

समलम्ब ABFE का क्षेत्रफल = समलम्ब DHGC का क्षे.
∴ समलम्ब ABFE का क्षे = \(\frac{1}{2}\)(24 + 16) × 4
= \(\frac{1}{2}\) × 40 × 4
= 80 cm²
तथा समलम्ब DHGC का क्षे.= 80 cm²
अब, समलम्ब, ADHE का क्षेत्रफल = समलम्ब BCGF का क्षेत्रफल
= \(\frac{1}{2}\)(28 + 20) × 4
= \(\frac{1}{2}\) × 48 × 4

∴ समलम्ब ADHE का क्षे. = 96 cm²
इसी प्रकार समलम्ब BCGF का क्षे. = 96 cm²
फ्रेम के खण्डों के क्षेत्रफल क्रमश 80 cm², 96 cm², 80 cm², 96 cm² होंगे।

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1

प्रश्न 1.
जैसा कि नीचे दी गई आकृति में दर्शाया गया है, एक आयताकार और एक वर्गाकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान हैं, तो किस खेत का क्षेत्रफल अधिक होगा?

हल:
वर्ग का परिमाप = 4 × भुजा
= 4 × 60
= 240 मीटर

दिया है –
वर्ग का परिमाप = आयत का परिमाप
240 = 2(लम्बाई + चौड़ाई)
240 = 2(80 + चौड़ाई)
\(\frac{240}{2}\) = 80 + चौड़ाई
120 – 80 = चौड़ाई
∴ चौड़ाई = 40 मीटर

अब, आयत का क्षेत्रफल = ल. × चौ.
= 80 × 40
= 3200 मी.
तथा वर्ग का क्षे = (भुजा)²
= 60 × 60 = 3600 मी²
अत: वर्ग का क्षेत्रफल अधिक होगा।

प्रश्न 2.
श्रीमती कौशिक के पास चित्र में दर्शाई गई मापों वाला एक वर्गाकार प्लॉट है । वह प्लॉट के बीच में एक घर बनाना चाहता है । घर के चारों ओर एक बगीचा विकसित किया गया है।₹55 प्रति वर्गमीटर की दर से इस बगीचे के विकसित करने का व्यय ज्ञात कीजिए।

हल :
वर्गाकार प्लाट की भुजा = 25m
प्लाट का क्षे. = (25)²
= 625 m²
घर की ल. = 20 m
तथा की चौ. = 15 m
घर का क्षे. = ल. × चौ.
= 20 x 15
= 300 m²

अब, बगीचे का क्षेत्रफल = प्लाट का क्षे. – घर का क्षे.
= 625 – 300
बगीचे का क्षे. = 325 m ²
अत: बगीचे को विकसित करने का खर्च = ₹325 × 55
अतः खर्च = ₹ 17875

प्रश्न 3.
जैसा कि आरेख में दर्शाया गया है एक बगीचे का आकार मध्य में आयताकार है और किनारों पर अर्द्धवृत्त के रूप में है। इस बगीचे का परिमाप और क्षेत्रफल ज्ञात कीजिए। [आयत की लम्बाई 20 – (3.5 + 3.5) मीटर है]

हल:
आयत की लम्बाई = 20 – (3.5 + 3.5)
= 20 – 7 = 13 m

आयताकार भाग का क्षेत्रफल = ल. × चौ…
= 13 × 7
= 91 m²

अब, किनारों पर बने दो अर्द्धवृत्त मिलकर एक पूरा वृत्त
बन जायेगा, जिसकी त्रिज्या r = 3.5 m होगी ।
अत: दो अर्द्धवृत्तों (एक वृत्त) का क्षे. = πr²
= \(\frac{22}{7}\) × (3.5)²
= \(\frac{22}{7}\) × \(\frac{35}{10}\) × \(\frac{35}{10}\)
= \(\frac{11 \times 35}{10}\) = \(\frac{385}{10}\)
= 38.5 m²

अतः बगीचे का कुल क्षेत्रफल = आयत का क्षे. + वृत्त का. क्षे.
= 91 + 38.5
= 129.5 m

(ii) बगीचे का परिमाप = 2 × आयत की लम्बाई + वृत्त का परिमाप (2πr)
=2 × 13 + 2 × \(\frac{22}{7}\) × 3.5
= 26 + 22
= 48 m

प्रश्न 4.
फर्श बनाने के लिए उपयोग की जाने वाली एक टाइल का आकार समान्तर चतुर्भुज का है, जिसका आधार 24cm तथा संगत ऊँचाई 10 cm है। 1080 वर्ग मीटर क्षेत्रफल के एक फर्श को ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता है ? (फर्श के कोनों को भरने के लिए आप टाइल को किसी भी रूप में तोड़ सकते हैं।)
हल:
टाइल की ल. (l) = 24 cm
तथा चौ. (b) = 10 cm
प्रत्येक टाइल का क्षे. = l × b = 24 × 10 cm²
= 240 cm²
= \(\frac{240}{100 \times 100}\) m² (∵ 1 m = 100 cm)

∴ क्षे. = 0.024 m² (∵ 1 m² = 100 × 100 cm²)

\(\frac{1080}{0.024}\) = \(\frac{1080 \times 1000}{24}\)
= \(\frac{1080000}{24}\)
अत: संख्या = 45000 टाइल

प्रश्न 5.
एक चींटी किसी फर्श पर बिखरे हुए विभिन्न आकारों के भोज्य पदार्थों के टुकड़ों के चारों ओर घूम रही है। भोज्य पदार्थ के किस टुकड़े के लिए चींटी को लम्बा चक्कर लगाना पड़ेगा।

हल :

(a) प्रथम टुकड़े का चक्कर लगाने में दूरी = (अर्द्धवृत्त की परिधि + 2.8 cm)
= πr + 2.8
= \(\frac{22}{7}\) × 1.4 + 2.8
= 22 × 0.2 + 2.8
= 4.4 + 2.8
= 7.2 cm
अत: कुल दूरी = 7.2 cm ………(i)

(b) चीटी बिन्दु A से चलकर B,C, D से होकर A पर आवेगी ।

अत: चीटी द्वारा तय की गई दूरी = आयताकार तीन भुजाओं का योग + अर्द्धवृत्त की परिधि
= (1.5+2.8+ 1.5) + πr
= 5.8 + \(\frac{22}{7}\) × 1.4
= 5.8 + 22 × 0.2
= 5.8 + 4.4
∴ कुल दूरी = 10.2 cm …………. (ii)

(c) चीटी द्वारा चली गई दूरी = 2 + 2 + अर्द्धवत्त की परिधि चींटी द्वारा चली गई दूरी

= 4 + πr
= 4+ \(\frac{22}{7}\) × 1.4
= 4 + 22 × 0.2
= 4 + 4.4 = 8.4 cm …………. (iii)
अत: समीकरण (i), (i) तथा (iii) की तुलना करने पर-
समी. (ii) के चित्र (b) (भोज्य पदार्थ के टुकड़े) के चक्कर लगने में सबसे अधिक दूरी तय करनी पड़ेगी और वह दूरी = 10.2 cm है।

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.3

प्रश्न 1.
निम्नलिखित युग्मों में प्रत्येक के व्यंजकों का गुणन कीजिए
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a² – 9, 4a
(v) pq + qr + rp, 0.
हल:
(i) 4p, q + r
गुणनफल = 4p × (q+ r)
= 4p × q + 4p × r
= 4pq + 4pr

(ii) ab, a – b
गुणनफल = ab × (a – b)
= (ab × a) – (ab × b)
= a²b – ab².

(iii) a + b, 7a²b²
गुणनफल = (a + b) × (7a²b²)
= 7a²b² + 7a²b³.

(iv) a² – 9, 4a
गुणनफल = 4a × (az – 9)
= (4a × a²) – (4a × 9)
= 4a³ – 36a.

(v) pq + qr + rp, 0.
गुणनफल = 0 × (pq – qr + rp)
= 0

प्रश्न 2.
सारणी पूर्ण कीजिए-

हल:

प्रश्न 3.
गुणनफल ज्ञात कीजिए
(i) (a²) × (2a²²) × (4a²⁶)
(ii) (\(\frac{2}{3}\)xy) × (\(-\frac{9}{10}\)x²y²
(iii) (\(\frac{-10}{3}\)pq³) × (\(\frac{6}{5}\)p³q)
(iv) x × x² × x³ × x⁴
हल:
(i) (a²) × (2a²²) × (4a²⁶)
गुणनफल = (1 × 2 × 4) × (a² × a²² × a²⁶)
= (1 × 2 × 4) × (a^2+22+26)
= 8(a⁵⁰)

(ii) (\(\frac{2}{3}\)xy) × (\(\frac{-9}{10}\)x²y²)
गुणनफल = (\(\frac{2}{3}\) × \(\frac{-9}{10}\)) × (xy × x²y²)
= \(\frac{-18}{30}\) × x³y³
= \(\frac{-3}{5}\) × x³y³

(iii) (\(\frac{-10}{3}\)pq³) × (\(\frac{6}{5}\)p³q)
गुणनफल = (\(\frac{-10}{3}\) × \(\frac{6}{5}\))(pq³ × p³q)
= \(\frac{-60}{15}\) × p⁴q⁴
= -4 p⁴q⁴

(iv) x × x² × x³ × x⁴
गुणनफल = x.x².x³.x⁴
= x^1+2+3+4
= x¹⁰.

प्रश्न 4.
(a) 3x (4x – 5) + 3 को सरल कीजिए और
(i) x = 3 एवं
(ii) x = \(\frac{1}{2}\) के लिए इसका मान ज्ञात कीजिए।

(b) (a² + a + 1) + 5 को सरल कीजिए और
(i) a = 0
(ii) a = 1
(iii) a = -1 के लिए इसका मान ज्ञात कीजिएं।
हल:
(a) 3x (4x – 5) + 3 = 12x² – 15x + 3

(i) x = 3 रेखने पर-
12 × (3)² – 15 × 3 + 3
= 12 × 9 – 45 + 3
= 108 – 45 – 3
= 66.

(ii) x = \(\frac{1}{2}\) रेखने पर-
12x² – 15x + 3
= 12 (\(\left(\frac{1}{2}\right)^{2}\))² – 15 × \(\frac{1}{2}\) + 3
= 12 × \(\frac{1}{4}\) – \(\frac{15}{2}\) + 3
= 3 – \(\frac{15}{2}\) + 3
= 6 – \(\frac{15}{2}\)
= \(\frac{12-15}{2}\)
= \(\frac{-3}{2}\)

(b) a(a² + a + 1) + 5
= a³ + a² + a + 5

(i) a = 0 रेखने पर-
a³ + a² + a + 5 = (0)³ + (0)² + 0 + 5
= 5.

(ii) a = 1 रेखने पर-
a³ + a² + a + 5 = (1)³ + (1)² + 1 + 5
= 1 + 1 + 1 + 5
= 8.

(iii) a = -1 रेखने पर-
a³ + a² + a + 5 = (-1)³ + (-1)² + (-1) + 5
= -1 + 1 – 1 + 5
= 6 – 2
= 4

प्रश्न 5.
(a) p (p – q), q(q – r) एवं r(r – p) को जोड़िए।
(b) 2x (z – x – y) एवं 2y (x – y – x) को जोडिए।
(c) 4l (10n – 3m + 2) में से 3l(l – 4m + 5n) को घटाइए।
(d) 4c (- a + b + c) में से 3a (a + b + c) – 2b (a – b + c) को घटाइए।
हल:
(a) p (p – q) = p² – pq
q(q – r) = q² – qr
r(r – p) = r² – rp
इन तीनों पदों को निम्न प्रकार जोड़ेंगे –

(b) 2x (z – x – y) = 2xz – 2x² – 2xy
2y (x – y – x) = 2yz – 2y² – 2xy
योग

(c) 4l (10n – 3m + 2) = 40ln – 12lm + 8l²
तथा 3l(l – 4m + 5n) = 3l² – 12lm + 15ln
प्रश्नानुसार, घटाने पर-

(d) 4c (- a + b + c) = -4ca + 4bc + 4c²
तथा 3a (a + b + c) – 2b (a – b + c) = 3a² + 3ab + 3ac – (2ab + 2b² – 2bc)
= 3a² + 3ab + 3ac – 2ab + 2b² – 2bc
= 3a² + ab + 3ca + 2b² – 2bc
प्रश्नानुसार, घटाने पर-

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.2

प्रश्न 1.
निम्नलिखित एकपदी युग्मों का गुणनफल ज्ञात कीजिए-
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p³, -3p
(v) 4p, 0.
हल:
(i) 4 × 7p = (4 × 7) × p
= 28p.

(ii) -4p × 7p = (-4 × 7) × (p × p)
= -28p².

(iii) -4p × 7pq = (-4 × 7) × (p × pq).
= -28p²q.

(iv) 4p3, -3p = [(4) × (-3)] × (p3 × p)
= -12 p⁴.

(v) 4p × 0 = (4 × 0) × p = 0 × p = 0.

प्रश्न 2.
निम्नलिखित एकपदी युग्मों के रूप में लम्बाई एवं चौड़ाई रखने वाले आयतों का क्षेत्रफल ज्ञात कीजिए
(p, q); (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
हल :
हम जानते हैं कि-
आयत का क्षेत्रफल = लम्बाई × चौड़ाई

प्रश्न 3.
गुणनफलों की सारणी को पूरा कीजिए-

हल:
पूर्ण तालिका निम्न प्रकार है

प्रश्न 4.
ऐसे आयताकार बक्सों का आयतन ज्ञात कीजिए जिनकी लम्बाई, चौड़ाई और ऊँचाई क्रमशः निम्नलिखित है
(i) 5a, 3a², 7a⁴,
(ii) 2p, 4p, 8r,
(iii) xy, 2x²y, 2xy²,
(iv) a, 2b, 3c.
हल:
आयताकार बक्से का आयतन = लम्बाई × चौड़ाई × ऊँचाई

(i) आयतन = 5a × 3a² × 7a⁴
= (5 × 3 × 7) × (a × a² × a⁴)
= 105a⁷

(ii) आयतन = 2p × 4q × 8r
= (2 × 4 × 8) × (p ×q × r)
= 64 pqr

(iii) आयतन = xy × 2x²y × 2xy²
= (1 × 2 × 2) × (xy × x²y × xy²)
= 4x⁴y⁴.

(iv) आयतन = a × 2b × 3c
= (1 × 2 × 3) (a × b × c)
= 6abc.

प्रश्न 5.
निम्नलिखित का गुणनफल ज्ञात कीजिए
(i) xy, yz, zx
(ii) a, -a², a³
(iii) 2, 4y, 8y², 16y³
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp.
हल:
(i) xy, yz, zx
गुणनफल = xy × yz × zx
= (x.x) × (y.y) × (z.z)
= x²y²z².

(ii) a, -a², a³
गुणनफल = a × (-a²) × (a³)
= -a⁶.

(iii) 2 × 4y × 8y² × 16y³
= (2 × 4 × 8 × 16) × (y × y² × y³)
= 1024 y⁶.

(iv) a, 2b, 3c, 6abc
गुणनफल = a × 2b × 3c × 6abc
= (1 × 2 × 3 × 6) × (a x b × c × abc)
= 36a²b²c².

(v) m, -mn, mnp.
गुणनफल = mx (-mn) × mnp
= -m³n²p.