Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.3 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.3
प्रश्न 1.
दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है । किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?
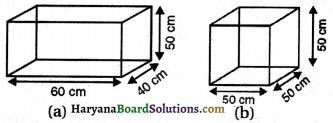
हल :
घनाभाकार डिब्बे
(a) का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (60 × 40 + 40 × 50 + 50 × 60) cm2
= 2(2400 + 2000 + 3000) cm2
= 2 × 7400 cm2
= 14800 cm2
घनाकार डिब्बे (b) का कुल पृष्ठीय क्षेत्रफल = 6 × (50)2
= 6 × 50 × 50
= 15000 cm2
डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल, डिब्बे (b) के कुल पृष्ठीय क्षेत्रफल से कम है, अतः डिब्बे (a) को बनाने मैं कम सामग्री की आवश्यकता होगी।
![]()
प्रश्न 2.
80 cm × 48 cm × 24 cm माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। ऐसे 100 सूटकेसों को रुकने के लिए 96 cm चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता होगी?
हल :
सूटकेस की ल. = 80 cm
चौ. = 48 cm
ऊँ. = 24 cm
सूटकेस की कुल सतह का क्षेत्रफल = 2(lb + bh + hl)
=2 (80 × 48 + 48 × 24 + 24 × 80)
= 2(3840 + 1152 + 1920)
= 2 × 6912
= 13824 cm2
अब, तिरपाल की चौ. = 96 cm
माना तिरपाल की ल. = x cm
∴ तिरपाल का क्षेत्रफल = l × b
= 96x cm2
∴ 96x = 13824
∴ ल., x = \(\frac{13824}{96}\) = 144 cm
अब,
100 सूटकेसों को तिरपाल से ढकने के लिए ल. = 144 × 100 cm
= \(\frac{144 \times 100}{100}\)m
∴ तिरपाल की कुल लम्बाई = 144 m
प्रश्न 3.
एक ऐसे घन की भुजा ज्ञात कीजिए, जिसका पृष्ठीय क्षेत्रफल 600 cm है।
हल :
माना घन की भुजा = x
घन का पृष्ठीय क्षेत्रफल = 6x2
दिया है पृष्ठीय क्षेत्रफल = 600
∴ 6x2 = 600
x2 = 100
अत: घन की भुजा x = 10 cm
![]()
प्रश्न 4.
रूखसार ने 1 m x 2 m x 1.5 m माप वाली एक पेटी को बाहर से पेंट किया । यदि उसने पेटी – के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया ?
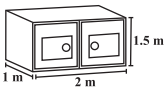
हल:
पेटी की, ल. (l) = 1 m
चौ. (b) = 2 m
ऊँ. (h) = 1.5 m
पेटी का कुल पृष्ठीय क्षेत्रफल =2 (lb + bh + hl)
= 2 (1 × 2 + 2 × 1.5 + 1 × 1.5)
= 2(2 + 3 + 1.5)
= 2 (6.5)
= 13 m2
पेटी के तल का क्षे. (जिस पर पेंट नहीं होना है) = l × b = 2 ×1
= 2 m2
अत: वह पेटी के = (13 – 2) m2
= 11 m2 क्षेत्रफल को पेंट करती है
प्रश्न 5.
डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है, जिसकी ल., चौ. और ऊँ. क्रमश: 15 m, 10 m, एवं 7 m है । पेंट की प्रत्येक कैन की सहायता से 100 m2 क्षेत्रफल को पैंट किया जा सकता है तो उस कमरे के लिए उसे पैंट की कितनी कैनों की आवश्यकता होगी?
हल:
कमरे की माप : लम्बाई (l) = 15 m
चौड़ाई (b) = 10 m
ऊँचाई (h) = 7 m
कमरे का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh +hl)
= 2(15 × 10 + 10 × 7 + 7 × 15)
= 2(150 + 70 + 105)
= 2 × 325
= 650 m2
परन्तु वह फर्श पर पेंट नहीं कर रहा है।
तब, फर्श का क्षे. = l × b.
= 15 × 10
= 150 m2
∴ पेंट किया गया क्षेत्र = 650 – 150
= 500 m2
∵ 100 m2 में आवश्यक कैन = 1
∴ 500 m2 में आवश्यक कैन = \(\frac{500}{100}\) = 5
∴ कैनों की संख्या = 5
![]()
प्रश्न 6.
वर्णन कीजिए कि निम्न आकृतियाँ किस प्रकार एकसमान हैं और किस प्रकार एक-दूसरे से भिन्न हैं? किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है ?
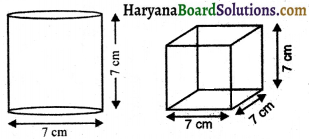
हल :
(i) समानता – दोनों की समान ऊँचाई है।
(ii) असमानता – एक बेलन तथा दूसरा घन है।
वेलन की त्रिज्या = \(\frac{7}{2}\) = 3.5 cm,
ऊँ (h) = 7 cm
∴ बेलन का पार्श्व पृष्ठीय क्षे. = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 7
= 44 x 3.5
∴ पार्श्व पृष्ठीय क्षे. = 154 cm2
घन की भुजा (1) =7 cm
घन के पार्श्व का पृष्ठीय क्षे. = 6l2
= 6 × (7)2
=6 × 49
∴ पार्श्व पृष्ठीय क्षे. = 294 cm2
अत: घन का पार्श्व पृष्ठीय क्षे. अधिक है।
प्रश्न 7.
7 m त्रिज्या और 3 m ऊंचाई वाला एक बन्द बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
हल :
टैंक की त्रिज्या = 7 m
तथा, ऊँचाई = 3 m
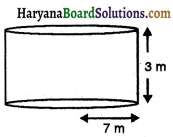
बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr(h+r) = 2 × \(\frac{22}{7}\) × 7 (3+7) m2
= 44 × (10) m2
= 440 m2
अतः आवश्यक चादर = 440 m2
![]()
प्रश्न 8.
एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल 4224 cm है । इसे इसकी ऊंचाई के अनुदिश काटकर 33 cm चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए ।
हल :
माना, आयताकार चादर की लम्बाई = l cm
तथा दिया है – चादर की चौड़ाई = 33 cm
∴ बेलन का पार्श्व पृष्ठीय क्षेत्रफल = आयताकार चादर का क्षेत्रफल
4224 = l × 33
∴ लम्बाई = 4224
∴ लम्बाई (l) = 128 cm
आयताकार चादर का परिमाप = 2 (लम्बाई + डाई)
= 2(128 + 33)
= 2 × 161
अत: चादर का परिमाप =322 cm
प्रश्न 9.
किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं । यदि सड़क रोलर का व्यास 84 cm और लम्बाई 1 m हैं तो सड़क का क्षेत्रफल ज्ञात कीजिए।

हल :
रोलर का व्यास = 84 cm
∴ अर्द्धव्यास r = 42 cm
अतः r = 10.42 m
(∵ 1 m = 100 cm)
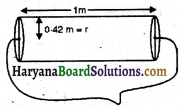
रोलर की ल. (h) = 1 m
रोलर की आकृति बेलनाकार है, तब
∵ रोलर द्वारा 1 चक्कर में तय किया क्षेत्रफल = रोलर का पृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × (0.42) × 1
= \(\frac{44 \times 42 \times 1}{7 \times 100}\)
= 2.64 m2
∵ रोलर के 1 चक्कर में चला आवश्यक क्षेत्र = 2.64 m2
∴ 750 चक्कर में आवश्यक क्षेत्र = 2.64 × 750
= 1980 m2
अतः रोलर को चक्कर चलने के लिए सड़क का क्षेत्र
= 1980 m2
![]()
प्रश्न 10.
एक कम्पनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है, जिनका व्यास 14 cm और ऊँचाई 20 cm हैं । कम्पनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है, तो लेवल का क्षेत्रफल क्या है ?
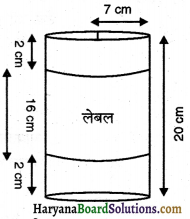
हल :
बेलन का व्यास = 14cm
∴ बेलन की त्रिज्या (r) = 7 cm
कर्तन की कुल ऊँचाई (h) = 20 cm
∴ लेवल की ऊँचाई (h) = 20 – (2 + 2)
= 20 – 4
h = 16 cm
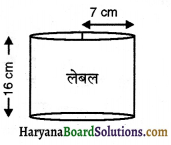
अत: चिपकाने वाले लेबल की आकृति भी बेलनाकार ही होगी, जिसकी त्रिज्य, r = 7 cm
तथा ऊँचाई (h) = 16 cm
अतः लेबल का क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 16
= 44 × 16 = 704 cm2
अतः लेबल का क्षेत्रफल = 704 cm2