HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

Class 8 /

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 1.
एक मेज के ऊपरी पृष्ठ ( सतह) का आकार समलम्ब जैसा है। यदि इसकी समान्तर भुजाएँ 1 m और 1.2 m हैं तथा इन समान्तर भुजाओं के बीच की दूरी 0.8 m है, तो इसका क्षेत्रफल ज्ञात कीजिए।
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -1
हल:
हल :
मेज के ऊपरी पृष्ठ (समलम्ब) का क्षेत्रफल = \(\frac{1}{2}\) × (समान्तर भुजाओं का योग) × ऊँचाई
= \(\frac{1}{2}\) (1+ 1.2) × 0.8
= \(\frac{1}{2}\) × 2.2 × 0.8
= 1.1 × 0.8
= 0.88 m2

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 2.
एक समलम्ब का क्षेत्रफल 34 cm और ऊंचाई 4cm है। यदि समान्तर भुजाओं में से एक की 10 cm लम्बाई है। दूसरी समान्तर भुजा की लम्बाई ज्ञात कीजिए।
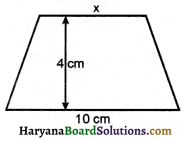
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -2
हल:
माना दुसरी समान्तर भुजा = x cm.
हम जानते हैं कि समलम्ब का क्षे. = \(\frac{1}{2}\) ×(समान्तर भुजाओं का योग) × ऊँचाई
34 = \(\frac{1}{2}\) (10+ x) × 4
2 × 34 = (10+x) × 4 (2 का पक्षान्तरण करने पर)
\(\frac{2 \times 34}{4}\) = 10 + x (4 का पक्षान्तरण करने पर)
= 10 + x = 17
∴ x = 17 – 10 = 7 (10 का पक्षान्तरण करने पर)
∴ अतः, दूसरी समान्तर भुजा = 7 cm

प्रश्न 3.
एक समलम्ब के आकार के खेत ABCD की बाड़ की लम्बाई 120 m है। यदि BC = 48 m, CD = 17 m और AD = 40 m है, तो A इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा AB समान्तर भुजाओं AD तथा BC पर लम्ब है।
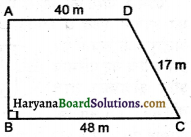
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -3
हल:
समलम्ब की भुजाएँ :
BC = 48 m
AD = 40 m
∠ABC = 90°.
D= 17 m
समलम्ब ABCD का परिमाप = 120 m
= AB + BC + CD + DA = 120
= AB+48+ 17+ 40 = 120
= AB+ 105 = 120
AB = 120 – 105 = 15
AB = 15m
अब, समलम्ब ABCD का क्षेत्रफल = \(\frac{1}{2}\) (समान्तर भुजाओं का योग) × ऊँचाई
= \(\frac{1}{2}\)(48 + 40) × 15
खेत का क्षेत्रफल = 660 m2.

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 4.
एक चतुर्भुज के आकार के खेत का विकर्ण 24 m है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गये लम्ब 8 m तथा 13 m हैं । खेत का क्षेत्रफल ज्ञात कीजिए।
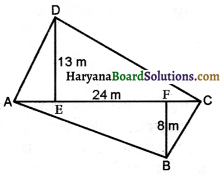
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -4
हल:
चतुर्भुज ABCD को विकर्ण AC द्वारा 13m दो त्रिभुजों में बाँटा गया है।

(i) ∆ABC का क्षे. = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 24 × 8
= 24 × 4
= 96 m2

(ii) ∆ACD का क्षे. = \(\frac{1}{2}\) × AC × DE
= \(\frac{1}{2}\) × 24 × 3
= 12 × 13
= 156 m2

चतुर्भुज ABCD का क्षे= ∆ABC का क्षे. + ∆ACD का क्षे.
= 96 + 156 = 252 m2

प्रश्न 5.
किसी समचतुर्भुज के विकर्ण 7.5cm एवं 12 cm हैं । इसका क्षेत्रफल ज्ञात कीजिए।
हल:
हम जानते हैं –
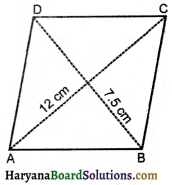
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -5
किसमचतुर्भुज का क्षेत्रफल = \(\frac{दोनों विकर्णों का गुणनफल}{2}\)
= \(\frac{12 \times 7.5}{2}\)
= 6 × 7.5
= 45.0 cm2
अत: क्षेत्रफल = 45 cm2

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 6.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा 6 cm और शीर्षलम्ब 4 cm हैं । यदि एक विकर्ण की लम्बाई 8 cin है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल :
विकर्ण AC, समचतुर्भुज ABCD को दो ΔABC तथा ΔACD में बाँटता है।
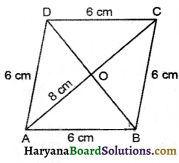
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -6
अतः समचतुर्भुज का क्षे. = ΔACD का छे + ΔABC का क्षे.
अत: \(\frac{1}{2}\)(AB+ CD) × ऊँचाई (शीर्षलम्ब)
= \(\frac{1}{2}\) × AC × OD + \(\frac{1}{2}\) × AC × OB
= \(\frac{1}{2}\)(6+6) × 4
= \(\frac{1}{2}\) × 8 × OD + \(\frac{1}{2}\) × 8 × OD
= 12 × 2 = 4 DO + 4 DO (∵ OB = OD)
24 = 8 DO (∵ OD = \(\frac{24}{3}\) = 3)
∴ विकर्ण, BD = DO + BO
= 3 + 3 = 6cm
अत: समचतुर्भुज का क्षे० = 24 cm2
तथा, विकर्ण = 6 cm

प्रश्न 7.
किसी भवन के फर्श में चतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण 45 cm तथा 30 cm लम्बाई के हैं । 14 प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।
हल :
हम जानते हैं कि,
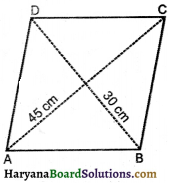
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -7
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -8
= \(\frac{45 \times 30}{2}\)
= 45 × 15.
= 675 cm2
= \(\frac{675}{100 \times 100}\) m2
= 0.0675 mm2
अत: समचतुर्भुजाकार टाइल का क्षेत्रफल = 0.0675 m2

अब, 3000 टाइलों का क्षे. = 0.0675 × 3000 m2
= 202.5 m2
3000 टाइलों का क्षेत्रफल = 202.5 m2
अब, खर्च = 202.5 × 4 = 810.0
पॉलिश कराने का खर्च = ₹810

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 8.
मोहन एक समलम्ब के आकार का खेत खरीदना चाहता है । इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समान्तर हैं और लम्बाई में दुगुनी है । यदि इस खेत का क्षेत्रफल 10500 m है2 और दो समान्तर भुजाओं के बीच की लम्बवत् दूरी 100 m है, तो नदी के साथ वाली भुजा की लम्बाई ज्ञात कीजिए।
हल :
समलम्ब का क्षे.= 10500 m2
प्रश्नानुसार, DC = 2AB
तथा, DC||AB
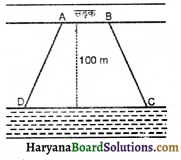
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -9
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) (AB+ CD) × 100
10500 = \(\frac{1}{2}\) (AB+ 2AB) × 100
10500 = \(\frac{3}{2}\) AB × 100
\(\frac{10500 \times 2}{10o \times 3}\) = AB = 70
∴ AB = 70 m

अत: भुजा AB = 70 m
तथा CD = 70 × 2 = 140 m

प्रश्न 9.
एक ऊपर उठे हुए। चबूतरे का ऊपरी पृष्ठ 44m अष्टभुज के आकार का है। GHb जैसा कि आकृति में दर्शाया । गया है । अष्टभुजी पृष्ठ का । क्षेत्रफल ज्ञात कीजिए।
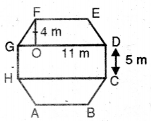
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -10
हल :
चबूतरे का ऊपरी पृष्ठ एक आयत GHCD
तथा दो समलम्ब चतुर्भुजों DEFG तथा ARCH में बँटा है।
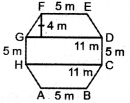
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -11
अत: ऊपरी पृष्ठ का क्षेत्रफल = आयत CDGH का क्षे. + 2 समलम्बों का क्षे.
⇒ 11 × 5 + 2 [\(\frac{1}{2}\)(5 + 4) × 4]
⇒ 55 + (5 + 4) × 4
⇒ 55 + 16 × 4
⇒ 55 + 64 = 119
अतः क्षेत्रफल = 119 m2

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 10.
एक पंचभुज आकार का बगीचा है, जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया । दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए । क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?
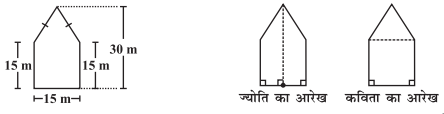
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -12
हल :
(i) ज्योति के आरेख के अनुसार-
DF भुजा के द्वारा पंचभुज को दो भागों में बाँटा गया है।
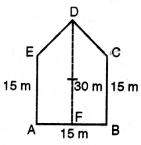
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -13
इस प्रकार, 2 समान समलम्ब चतुर्भुजों में बैंट जायेगा ।
अतः बगीचे का क्षेत्रफल = AFDE का क्षे. + FBCD का क्षे.
या 2 × समलम्ब AFDE का क्षेत्र = 2 × [\(\frac{1}{2}\)(FD + AE) × AF]
= [(30 + 15) × \(\frac{15}{2}\)]
= 45 × \(\frac{15}{2}\)
= \(\frac{675}{2}\)
= 337.5 m2

∴ बगीचे का क्षेत्रफल = 337.5 m2

(ii) कविता के आरेख के अनुसार,
पंचभुज ABCDE को दो भागों में बाँटा गया है।
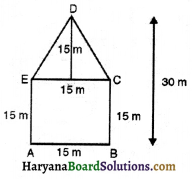
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -14
∵ दो बगीचे का क्षेत्रफल ज्ञात करने की अन्य विधि भी है।
बगीचे AEDCBA का क्षेत्रफल = वर्ग ABCE का क्षेत्रफल + AEDC का क्षेत्रफल
= 15 × 15 + \(\frac{1}{2}\) × 15 ×15
= 225 + \(\frac{1}{2}\) × 225
= 225 + 112.5 = 337.5 m2

HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 11.
संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अन्त:विमाएँ क्रमश: 24 cm × 28 cm एवं 16 cm × 20 cm हैं । यदि फ्रेम के प्रत्येक खण्ड की चौड़ाई समान है, तो प्रत्येक खण्ड का क्षेत्रफल ज्ञात कीजिए ।
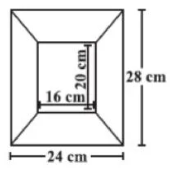
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -15
हल :
प्रत्येक खण्ड की चौड़ाई समान है।
= 28 – 20 = 8cm
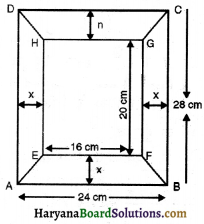
HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 -16
प्रत्येक खण्ड की चौड़ाई (x) = \(\frac{8}{2}\) = 4 cm
अत: x = 4cm

समलम्ब ABFE का क्षेत्रफल = समलम्ब DHGC का क्षे.
∴ समलम्ब ABFE का क्षे = \(\frac{1}{2}\)(24 + 16) × 4
= \(\frac{1}{2}\) × 40 × 4
= 80 cm2
तथा समलम्ब DHGC का क्षे.= 80 cm2
अब, समलम्ब, ADHE का क्षेत्रफल = समलम्ब BCGF का क्षेत्रफल
= \(\frac{1}{2}\)(28 + 20) × 4
= \(\frac{1}{2}\) × 48 × 4

∴ समलम्ब ADHE का क्षे. = 96 cm2
इसी प्रकार समलम्ब BCGF का क्षे. = 96 cm2
फ्रेम के खण्डों के क्षेत्रफल क्रमश 80 cm2, 96 cm2, 80 cm2, 96 cm2 होंगे।

Leave a Comment

Your email address will not be published. Required fields are marked *