Haryana State Board HBSE 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Intext Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Intext Questions
(पाठगत प्रश्न – पृष्ठ 210-211)
प्रश्न 1.
मोहन स्वयं अपने और अपनी बहन के लिए चाय बनाता है। वह 300 mL पानी, 2 चम्मच चीनी, 1 चम्मच चाय-पत्ती और 50 mL दूध का उपयोग करता है। यदि वह पाँच व्यक्तियों के लिए चाय बनाए, तो उसे प्रत्येक वस्तु की कितनी मात्रा की आवश्यकता होगी?
हल:
दो व्यक्तियों के लिए आवश्यक पानी की मात्रा = 300 mL
∴ पाँच व्यक्तियों के लिए आवश्यक पानी की मात्रा = \(\frac{300}{2}\) × 5mL
∴ पानी की मात्रा = 750 mL
दो व्यक्तियों के लिए आवश्यक चीनी की मात्रा = 2 चम्मच
∴ पाँच व्यक्तियों के लिए आवश्यक चीनी की मात्रा = \(\frac{2}{2}\) × 5
∴ चीनी की मात्रा = 5 चम्मच
दो व्यक्तियों के लिए आवश्यक चाय-पत्ती की मात्रा = 1 चम्मच
∴ पाँच व्यक्तियों के लिए आवश्यक चाय-पत्ती की मात्रा y
= \(\frac{1}{2}\) × 5
∴ चाय पत्ती की मात्रा = \(2 \frac{1}{2}\) चम्मच
दो व्यक्तियों के लिए आवश्यक दूध की मात्रा = 50 mL
∴ पाँच व्यक्तियों के लिए आवश्यक दूध की मात्रा
= \(\frac{50}{2}\) × 5mL
∴ = 125 mL
अतः, पाँच व्यक्तियों के लिए चाय बनाने के लिए मोहन को 750 mL पानी, 5 चम्मच चीनी, \(2 \frac{1}{2}\) चम्मच चाय-पत्ती और 125 mL दूध की आवश्यकता होगी।
![]()
(प्रयास कीजिए – पृष्ठ 212)
प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि क्या x और y अनुक्रमानुपाती हैं?
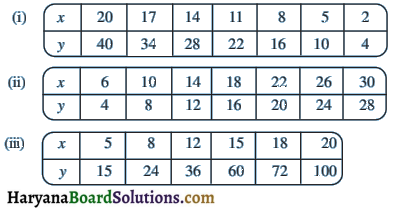
हल:
(i) प्रश्नानुसार
\(\frac{20}{40}\) = \(\frac{17}{34}\) = \(\frac{14}{28}\) = \(\frac{11}{22}\) = \(\frac{8}{16}\) = \(\frac{5}{10}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\), इस प्रकार, x और y की अनुरूप कीमत का औसत स्थिर है और \(\frac{1}{2}\) के बराबर है। अतः x और y स्थिर विचरण \(\frac{1}{2}\) के साथ अनुक्रमानुपाती हैं।
(ii) प्रश्नानुसार,
\(\frac{6}{4}\) ≠ \(\frac{10}{8}\) ≠ \(\frac{14}{12}\) ≠ \(\frac{18}{16}\) ≠ \(\frac{22}{20}\) ≠ \(\frac{26}{24}\) ≠ \(\frac{30}{28}\), इस प्रकार, x और y के अनुरूप कीमतों का औसत स्थिर नहीं है। अतः, x और y अनुक्रमानुपाती नहीं हैं
(iii) प्रश्नानुसार,
\(\frac{5}{15}\) = \(\frac{8}{24}\) = \(\frac{12}{36}\) ≠ \(\frac{15}{60}\) = \(\frac{18}{72}\) ≠ \(\frac{20}{100}\) इत्यादि इस प्रकार, x और y की अनुरूप कीमतें स्थिर नहीं हैं । अतः Jx और y अनुक्रमानुपाती नहीं हैं।
![]()
प्रश्न 2.
मूलधन = ₹ 1000, ब्याज दर = 8% वार्षिक। निम्नलिखित सारणी को भरिए तथा ज्ञात कीजिए कि, किस प्रकार का ब्याज (साधारण या चक्रवृद्धि) समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता या परिवर्तित होता है।
| समय अवधि | 1 वर्ष | 2 वर्ष | 3 वर्ष |
| साधारण ब्याज (₹ में) | |||
| चक्रवृद्धि ब्याज (₹ मे) |
हल:
दिया है-P = ₹ 1000, R = 8% वार्षिक
साधारण ब्याज के लिए
1 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×1}{100}\))
= ₹ 80
2 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×2}{100}\))
= ₹ 160
3 वर्ष का साधारण ब्याज = ₹ (\(\frac{1000×8×3}{100}\))
= ₹ 240
चक्रवृद्धि ब्याज के लिए
1 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{1}\)
= ₹ 1000 × \(\frac{108}{100}\)
= ₹ 1080
∴ 1 वर्ष का चक्रवृद्धि ब्याज = ₹ (1080 – 1000)
= ₹ 80
2 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{2}\)
= ₹ 1000 × \(\frac{108}{100}\) × \(\frac{108}{100}\)
= ₹ 1166.40
∴ 2 वर्ष का चक्रवृद्धि ब्याज = ₹ (1166.40 – 1000)
= ₹ 166.40
3 वर्ष के लिए राशि = ₹ 1000\(\left(1+\frac{8}{100}\right)^{3}\)
= ₹ 1000 × \(\frac{108}{100}\) × \(\frac{108}{100}\) × \(\frac{108}{100}\)
= ₹ 1259.712
∴ 3 वर्ष का चक्रवृद्धि ब्याज = ₹ (1259.712 – 1000)
= ₹ 259.712
∴ सारणी अग्रांकित होगी
| समय अवधि | 1 वर्ष | 2 वर्ष | 3 वर्ष |
| साधारण ब्याज (₹ में) | 80 | 160 | 240 |
| चक्रवृद्धि ब्याज (₹ मे) | 80 | 166.40 | 259.71 |
साधारण ब्याज समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता है।
![]()
(इन्हें कीजिए – पृष्ठ 216-217)
प्रश्न 1.
एक वर्गांकित कागज़ पर भिन्न-भिन्न भुजाओं के पाँच वर्ग खींचिए। निम्नलिखित सूचना को एकसारणी के रूप में लिखिए:
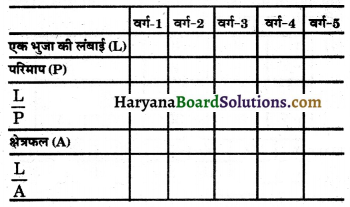
ज्ञात कीजिए कि क्या भुजा की लंबाई
(a) वर्ग के परिमाप के अनुक्रमानुपाती है।
(b) वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।
हल :
• वर्ग-1
माना वर्ग के एक भुजा की लम्बाई (L) = 3 cm
वर्ग का परिमाप (P) = (3 + 3 + 3 + 3) cm = 12 cm
\(\frac{L}{P}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
वर्ग का क्षेत्रफल (A) = 3 cm × 3 cm = 9 cm
वर्ग – 2
माना वर्ग की एक भुजा की लम्बाई (L) = 4 cm
वर्ग का परिमाप (P) = (4 + 4 + 4 + 4) cm = 16 cm
\(\frac{L}{A}\) = \(\frac{4}{16}\) = \(\frac{1}{4}\)
वर्ग का क्षेत्रफल (A) =4 cm × 4 cm = 16 cm
\(\frac{L}{A}\) = \(\frac{4}{16}\) = \(\frac{1}{4}\)
• वर्ग – 3
माना वर्ग की एक भुजा की लम्बाई (L) = 5 cm
वर्ग की परिमाप (P) = (5 + 5 + 5 + 5) cm = 20 cm
\(\frac{L}{A}\) = \(\frac{5}{20}\) = \(\frac{1}{5}\)
वर्ग का क्षेत्रफल (A) =5 cm × 5 cm = 20 cm
\(\frac{L}{P}\) = \(\frac{5}{20}\) = \(\frac{1}{5}\)
• वर्ग – 4
माना वर्ग की एक भुजा की लम्बाई (L) = 6 cm
वर्ग की परिमाप (P) = (6 + 6 + 6 + 6) cm = 24 cm
\(\frac{L}{P}\) = \(\frac{6}{24}\) = \(\frac{1}{6}\)
वर्ग का क्षेत्रफल (A) =6 cm × 6 cm = 20 cm
\(\frac{L}{A}\) = \(\frac{6}{24}\) = \(\frac{1}{6}\)
• वर्ग – 5
माना वर्ग की एक भुजा की लम्बाई (L) = 7 cm
वर्ग की परिमाप (P) = (7 + 7 + 7 + 7) cm = 24 cm
\(\frac{L}{P}\) = \(\frac{7}{28}\) = \(\frac{1}{4}\)
वर्ग का क्षेत्रफल (A) =7 cm × 7 cm = 49 cm
\(\frac{L}{A}\) = \(\frac{7}{49}\) = \(\frac{1}{7}\)
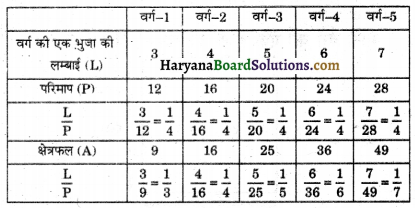
(a) भुजा की लम्बाई वर्ग के परिमाप के अनुक्रमानुपाती होती है।
(b) भुजा की लम्बाई वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।
![]()
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 217)
प्रश्न 1.
सीधा समानुपात (विचरण)’ की अब तक हल की गई समस्याओं में से कुछ को लीजिए। क्या आप सोचते हैं कि इन समस्याओं को इकाई की विधि या ऐकिक विधि (unitary method) से हल किया जा सकता है?
हल:
हम प्रश्नावली 13.1 से कुछ प्रश्न लेकर उन्हें ऐकिक विधि से निम्नानुसार हल करते हैं
प्रश्न 3:
∵ 75 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = 1 भाग
∴ 1 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = \(\frac{1}{75}\) भाग
∴ 1800 mL मूल मिश्रण के लिए आवश्यक लाल पदार्थ = \(\frac{1}{75}\) × 1800 भाग
= 24 भाग
प्रश्न 4:
∵ 6 घंटे में भरने वाली बोतलों की संख्या = 840
∴ 1 घंटे में बोतलें भरेंगी = \(\frac{840}{6}\)
∴ 5 घंटे में बोतलें भरेंगी = \(\frac{840}{6}\) × 5
= 700
प्रश्न 10:
25 मिनट अर्थात् \(\frac{25}{60}\) घंटे में, तय दूरी = 14 km
∴ 1 घंटे में तय दूरी = 14 ÷ \(\frac{25}{60}\)
= (14 × \(\frac{60}{25}\)) km
∴ 5 घंटे में तय दूरी = (14 × \(\frac{60}{25}\) × 5) km
= 168 km
![]()
(प्रयास कीजिए – पृष्ठ 219)
प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि कौन से चरों ( यहाँx और ) के युग्म परस्पर प्रतिलोम समानुपात में हैं
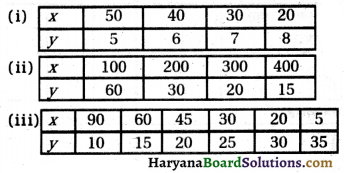
हल:
(i) प्रश्नानुसार,
x × y = 50 × 5 ≠ 40 × 6 ≠ 30 × 7 ≠ 20 × 8
इस प्रकार, x और y परस्पर व्युत्क्रमानुपाती नहीं हैं।
(ii) प्रश्नानुसार,
x × y = 100 × 60 = 200 × 30
= 300 × 20 = 400 × 15
= 6000 = स्थिर
इस प्रकार, x और y परस्पर व्युत्क्रमानुपाती हैं।
(iii) प्रश्नानुसार
x × y = 90 × 10 = 60 × 15 = 45 × 20
≠ 30 × 25 ≠ 20 × 30 ≠ 5 × 35
इस प्रकार, x और y व्युत्क्रमानुपात में नहीं हैं।