Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1 Textbook Exercise Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1
प्रश्न 1.
जैसा कि नीचे दी गई आकृति में दर्शाया गया है, एक आयताकार और एक वर्गाकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान हैं, तो किस खेत का क्षेत्रफल अधिक होगा?

हल:
वर्ग का परिमाप = 4 × भुजा
= 4 × 60
= 240 मीटर
दिया है –
वर्ग का परिमाप = आयत का परिमाप
240 = 2(लम्बाई + चौड़ाई)
240 = 2(80 + चौड़ाई)
\(\frac{240}{2}\) = 80 + चौड़ाई
120 – 80 = चौड़ाई
∴ चौड़ाई = 40 मीटर
अब, आयत का क्षेत्रफल = ल. × चौ.
= 80 × 40
= 3200 मी.
तथा वर्ग का क्षे = (भुजा)2
= 60 × 60 = 3600 मी2
अत: वर्ग का क्षेत्रफल अधिक होगा।
![]()
प्रश्न 2.
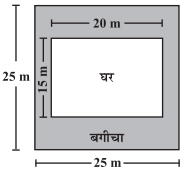
श्रीमती कौशिक के पास चित्र में दर्शाई गई मापों वाला एक वर्गाकार प्लॉट है । वह प्लॉट के बीच में एक घर बनाना चाहता है । घर के चारों ओर एक बगीचा विकसित किया गया है।₹55 प्रति वर्गमीटर की दर से इस बगीचे के विकसित करने का व्यय ज्ञात कीजिए।
हल :
वर्गाकार प्लाट की भुजा = 25m
प्लाट का क्षे. = (25)2
= 625 m2
घर की ल. = 20 m
तथा की चौ. = 15 m
घर का क्षे. = ल. × चौ.
= 20 x 15
= 300 m2
अब, बगीचे का क्षेत्रफल = प्लाट का क्षे. – घर का क्षे.
= 625 – 300
बगीचे का क्षे. = 325 m 2
अत: बगीचे को विकसित करने का खर्च = ₹325 × 55
अतः खर्च = ₹ 17875
![]()
प्रश्न 3.
जैसा कि आरेख में दर्शाया गया है एक बगीचे का आकार मध्य में आयताकार है और किनारों पर अर्द्धवृत्त के रूप में है। इस बगीचे का परिमाप और क्षेत्रफल ज्ञात कीजिए। [आयत की लम्बाई 20 – (3.5 + 3.5) मीटर है]

हल:
आयत की लम्बाई = 20 – (3.5 + 3.5)
= 20 – 7 = 13 m
आयताकार भाग का क्षेत्रफल = ल. × चौ…
= 13 × 7
= 91 m2
अब, किनारों पर बने दो अर्द्धवृत्त मिलकर एक पूरा वृत्त
बन जायेगा, जिसकी त्रिज्या r = 3.5 m होगी ।
अत: दो अर्द्धवृत्तों (एक वृत्त) का क्षे. = πr2
= \(\frac{22}{7}\) × (3.5)2
= \(\frac{22}{7}\) × \(\frac{35}{10}\) × \(\frac{35}{10}\)
= \(\frac{11 \times 35}{10}\) = \(\frac{385}{10}\)
= 38.5 m2
अतः बगीचे का कुल क्षेत्रफल = आयत का क्षे. + वृत्त का. क्षे.
= 91 + 38.5
= 129.5 m
(ii) बगीचे का परिमाप = 2 × आयत की लम्बाई + वृत्त का परिमाप (2πr)
=2 × 13 + 2 × \(\frac{22}{7}\) × 3.5
= 26 + 22
= 48 m
![]()
प्रश्न 4.
फर्श बनाने के लिए उपयोग की जाने वाली एक टाइल का आकार समान्तर चतुर्भुज का है, जिसका आधार 24cm तथा संगत ऊँचाई 10 cm है। 1080 वर्ग मीटर क्षेत्रफल के एक फर्श को ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता है ? (फर्श के कोनों को भरने के लिए आप टाइल को किसी भी रूप में तोड़ सकते हैं।)
हल:
टाइल की ल. (l) = 24 cm
तथा चौ. (b) = 10 cm
प्रत्येक टाइल का क्षे. = l × b = 24 × 10 cm2
= 240 cm2
= \(\frac{240}{100 \times 100}\) m2 (∵ 1 m = 100 cm)
∴ क्षे. = 0.024 m2 (∵ 1 m2 = 100 × 100 cm2)
![]()
\(\frac{1080}{0.024}\) = \(\frac{1080 \times 1000}{24}\)
= \(\frac{1080000}{24}\)
अत: संख्या = 45000 टाइल
![]()
प्रश्न 5.
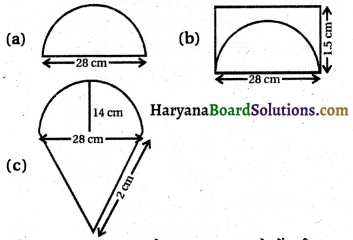
एक चींटी किसी फर्श पर बिखरे हुए विभिन्न आकारों के भोज्य पदार्थों के टुकड़ों के चारों ओर घूम रही है। भोज्य पदार्थ के किस टुकड़े के लिए चींटी को लम्बा चक्कर लगाना पड़ेगा।
हल :
(a) प्रथम टुकड़े का चक्कर लगाने में दूरी = (अर्द्धवृत्त की परिधि + 2.8 cm)
= πr + 2.8
= \(\frac{22}{7}\) × 1.4 + 2.8
= 22 × 0.2 + 2.8
= 4.4 + 2.8
= 7.2 cm
अत: कुल दूरी = 7.2 cm ………(i)
(b) चीटी बिन्दु A से चलकर B,C, D से होकर A पर आवेगी ।
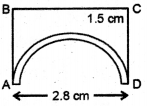
अत: चीटी द्वारा तय की गई दूरी = आयताकार तीन भुजाओं का योग + अर्द्धवृत्त की परिधि
= (1.5+2.8+ 1.5) + πr
= 5.8 + \(\frac{22}{7}\) × 1.4
= 5.8 + 22 × 0.2
= 5.8 + 4.4
∴ कुल दूरी = 10.2 cm …………. (ii)
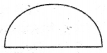
(c) चीटी द्वारा चली गई दूरी = 2 + 2 + अर्द्धवत्त की परिधि चींटी द्वारा चली गई दूरी
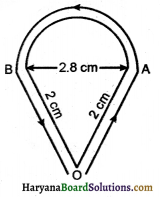
= 4 + πr
= 4+ \(\frac{22}{7}\) × 1.4
= 4 + 22 × 0.2
= 4 + 4.4 = 8.4 cm …………. (iii)
अत: समीकरण (i), (i) तथा (iii) की तुलना करने पर-
समी. (ii) के चित्र (b) (भोज्य पदार्थ के टुकड़े) के चक्कर लगने में सबसे अधिक दूरी तय करनी पड़ेगी और वह दूरी = 10.2 cm है।