HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4

Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4

प्रश्न 1.
आपको एक बेलनाकार टैंक दिया हुआ है, निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयतन:

(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा र सकता है।
(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।
(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।
हल:
(a) आयतन ज्ञात करेंगे।
(b) पृष्ठीय क्षेत्रफल ज्ञात करेंगे।
(c) आयतन ज्ञात करेंगे।

प्रश्न 2.
बेलन A का व्यास 7 cm और ऊँचाई 14 cm है। बेलन B का व्यास 14 cm और ऊँचाई 7 cm है। परिकलन किए बिना क्या आप बता सकते हैं कि इन दोनों में किसका आयतन अधिक है। दोनों बेलनों का आयतन ज्ञात करते हुए इसका सत्यापन कीजिए। जाँच कीजिए कि क्या अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

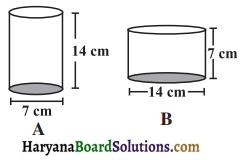
हल:
(i) बेलन A के लिए-
पहले बेलन (A) के लिए आयतन = πr²h
दूसरे बेलन (B) के लिए आयतन = π(2r)² × \(\frac{h}{2}\)
= \(\frac{4πr²h}{2}\)
= 2πr²h

अतः दूसरे बेलन (B) का आयतन पहले बेलन (A) के आयतन का दूना होगा।
अंत: दूसरे बेलन (B) का आयतन अधिक है।
त्रिज्या = \(\frac{7}{2}\) = 3.5 cm
ऊँचाई (h) = 14 cm
बेलन का आयतन = πr²h
= \(\frac{22}{7}\) × (3.5)² × 14 cm³
= \(\frac{22}{7}\) × \(\frac{35}{10}\) × \(\frac{35}{10}\) × 14 cm³
आयतन = \(\frac{44 \times 35 \times 35}{100}\) cm³
= 539 cm³
अत: बेलन A का आयतन = 539 cm³
बेलन A का पृष्ठीय क्षेत्रफल = 2πr(r+h)
= 2 × \(\frac{22}{7}\) × 3.5 (3.5 + 14)
= 2 × 22 × 0.5 × 17.5
= 22 × 17.5
= 385 cm²

(ii) बेलन B के लिए –
त्रिज्या r = \(\frac{14}{2}\) =7 cm
ऊँचाई h = 7cm बेलन का आयतन = πr²h
= \(\frac{22}{7}\) × (7)² × 7
= \(\frac{22}{7}\) × 49 × 7
= 49 × 22 cm³
अत: आयतन = 1078 cm³ = 2 × 539
= 2 × पहले बेलन A का आयतन

बेलन B का पृष्ठीय क्षेत्रफल = 2πr(r+h)
= 2 × \(\frac{22}{7}\) × 7 (7+7)
= 44 × 14 = 616 cm²
अतः बेलन B का आयतन, बेलन A के आयतन से अधिक होगा । अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

प्रश्न 3.
एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए, जिसके आधार का क्षेत्रफल 180 cm और जिसका आयतन 900 cm है।
हल :
माना, घनाभ की ऊँचाई = h
अत: घनाभ का आयतन = घनाभ के आधार का क्षेत्रफल × h
900 = 180 × h
h = \(\frac{900}{180}\) = 5
अत: घनाभ की ऊँचाई = 5 cm.

प्रश्न 4.
एक घनाभ की विमाएँ 60 cm × 54 cm × 30 cm हैं । इस घनाभ के अन्दर 6 cm भुजा वाले कितने छोटे घन रखे जा सकते हैं ?
हल:
लम्बाई (l) = 60 cm
चौड़ाई (b) = 54 cm
ऊँचाई (h) = 30 cm
घनाभ का आयतन = 60 × 54 × 30 (V = lbh)
= 97200 cm³

घन की भुजा = 6 cm
घन का आयतन = (6)³ [V = a³]
= 216 cm³

घनों की संख्या = \(\frac{97200}{216}\) = 450
अतः घनों की संख्या = 450

प्रश्न 5.
एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए, जिसका आयतन 1.54 m’ और जिसके आधार का व्यास 140 cm है?
हल:
बेलन का व्यास = 140 cm
त्रिज्या (r) = \(\frac{140}{2}\) = 70 cm
त्रिज्या (r) = 0.7 m
बेलन की ऊँचाई h = ?
बेलन का आयतन = πr²h =1.54
h = \(\frac{1.54}{\pi r^{2}}\)
h = \(\frac{1.54×7}{22 ×0.7×0.7}\)
h = 1
अतः, बेलन की ऊँचाई = 1 m

प्रश्न 6.
एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या 1.5 mऔर । लम्बाई 7 m है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञातं कीजिए।

हल:
बेलनाकार टैंक की त्रिज्या (r) = 1.5m
टैंक की लम्बाई (h) = 7m
टैंक का आयतन = πr²h
= \(\frac{22}{7}\) × (1.5)² × 7
= \(\frac{22}{7}\) × 1.5 × 1.5 × 7
= 2.25 × 22 m³

आयतन = 49.5 m²
अत: टैंक का आयतन = 49.5 m²
.. 1 m² = 1000 लीटर
49.5 m² = 49.5 x 1000 लीटर
= 49500 लीटर
टैंक में दूध की मात्रा = 49500 लीटर

प्रश्न 7.
यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो
(i) इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
(ii) इसके आयतन में कितने गुना वृद्धि होगी?
हल:
(i) माना, घन का किनारा = x
पृष्ठीय क्षेत्रफल = 6x²
अब, घन का किनारा दुगुना किया जाता है।
नया किनारा = 2x
अब, नया पृष्ठीय के. = 6(2x)²
= 6 × 4x²
नया पृष्ठीय से. = 24x²
= 4(6x²)
घन के पृष्ठीय क्षे. में 4 गुना वृद्धि होगी।

(ii) घन का आयतन = x³
भुजा (किनारा) दुगुना करने पर, आयतन = (2x)²
नया आयतन = (8x)²
अतः आयतन में 8 गुना वृद्धि होगी।

प्रश्न 8.
एक कुंड के अन्दर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108zi है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

हल:
दिया है, कुंड का आयतन = 108 m³
पानी का आयतन = 108 × 1000 लीटर = 108000 लीटर
60 लीटर पानी कुंड में गिरता है = 1 मिनट में
108000 लीटर पानी कुंड में गिरेगा है
= \(\frac{1}{60}\) × 108000 मिनट में
= 1800 मिनट
= \(\frac{1800}{60}\) घंटे
= 30 घंटे
अतः कुल समय = 30 घंटे